Арифметический квадратный корень и его свойства
Арифметическим квадратным корнем из числа a называют такое неотрицательное число b (b ≥ 0), вторая степень которого равна a.
Запишем это определение на математическом языке:
Убедимся в правильности данной записи на примере. Пусть а = 16, b = 4, тогда
Всё верно: если 4 в квадрате равно 16, значит корень из 16 равен 4.
Извлечем парочку корней:
√0 = 0;
√1 = 1;
√4 = 2;
√256 = 16 и т.д.
Обратите внимание, что подкоренное выражение неотрицательно! Извлечение корней из отрицательных чисел — это уже совсем другая история и в школьной математике не рассматривается.
Свойства арифметического квадратного корня (далее корень).
1. Корень произведения равен произведению корней (а ≥ 0, b ≥ 0).
Примеры:
2.
Примеры:
3. Корень в квадрате равен подкоренному выражению (а ≥ 0).
Примеры:
4. Корень из квадрата числа равен модулю этого числа (а — любое).
Примеры:
5. Корень из степени с основанием а и показателем n равен корню из числа а в степени n (а ≥ 0, n — натуральное).
Пример:
Свойство работает в обе стороны.
6. Квадратный корень числа в четной степени равен этому числу в степени, деленной на 2.
Пример:
Вынесение множителя за знак корня.
Рассмотрим вынесение множителя на примере: возьмем число √12.
Число 12 можно разложить на два множителя — 3 и 4; один из них извлекается. Значит, из-под корня выносится двойка (корень из 4), а под корнем остается 3.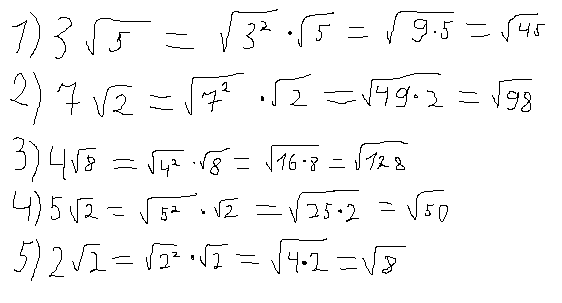
То же самое запишу на математическом языке:
Возьмем число побольше: √845.
Очевидно, что подкоренное выражение делится на 5, т.е. один из множителей равен 5, тогда второй равен 169 (169 · 5 = 845). Корень из 169 извлекается, значит из-под корня выносится множитель 13, а под корнем остается 5.
И возьмем число √28800.
Оно делится на 100, значит его можно представить в виде произведения чисел 100 и 288. Но 288 тоже можно разложить на произведение чисел 144 и 2. Это значит, что под корнем остается число 2, а выносятся сразу два множителя — 10 и 12, которые в дальнейшем нужно перемножить.
Еще есть второй способ — он короче. Здесь важно заметить, что 28800 — это произведение 14400 и 2. Результат не меняется.
Внесение множителя под знак корня.
Как в случае с вынесением рассмотрим внесение множителя под знак корня на примерах.
Возьмем число 2√3. Для внесения необходимо множитель перед корнем возвести в квадрат и умножить на подкоренное выражение.
Получившееся число записываем под корнем.
Специально взяла пример из раздела «Вынесение множителя за знак корня» для того, чтобы вы убедились в правильности данного решения. Второй этап решения (произведение корней √22 и √3), кстати говоря, всегда пропускают.
Следующий пример: 5√7.
Пятерку возводим в квадрат и умножаем на 7. Результат записываем под знаком «корня».
Успехов в учебе!
3-8Почему квадратный корень из 2 иррационален
Квадратный корень из 2
Является ли квадратный корень из 2 дробью?
Давайте предположим, что есть, и посмотрим, что получится.
Если это дробь, то мы должны быть в состоянии записать ее как упрощенную дробь, например:
m/n
(m и n оба являются целыми числами)
И мы надеемся, что когда мы возведем в квадрат получается 2:
(m/n) 2 = 2
, что равно
m 2 /n 2 = 2
или, другими словами, m 2 вдвое больше, чем . 2 :
m 2 = 2 × n 2
Попробуйте сами
Посмотрите, сможете ли вы найти значение для m и n , которое работает!
Пример : попробуем m=17 и n=12 :
m/n = 17/12
Возведение в квадрат дает
17 2 /12 2 = 289/144 = 2,0069444…
Что близко к 2, но не совсем верно Вы видите
9 9 m 2 будет дважды n 2 (289 примерно вдвое больше 144).
Можете ли вы сделать лучше?
Четное и нечетное
Теперь давайте рассмотрим идею, что m 2 = 2 × n 2
На самом деле это означает, что м 2 должно быть четным числом.
| Операция | Результат | Пример |
|---|---|---|
| Четный × Четный | Четный | 2 × 8 = 16 |
| Чет × Нечет | Четный | 2 × 7 = 14 |
| Нечетное × Четное | Четный | 5 × 8 = 40 |
| Нечетное × Нечетное | Нечетный | 5 × 7 = 35 |
А если m 2 четное, то m должно быть четным (если m было нечетным, то m 2 тоже нечетное).
м четно
И все четные числа кратны 2, значит м кратно 2 , поэтому м 2 кратно 4 .
А если m 2 кратно 4, то n 2 должно быть кратно 2 (вспомним, что m 2 /n 2 = 2).
Итак…
n тоже четно
Но подождите… если и m и n четно , мы должны быть в состоянии упростить дробь m/n.
Пример: 2/12 можно упростить до 1/6
Но мы уже говорили, что это было упрощенным…
… и если это еще не упрощено, то давайте упростим сейчас и начнем заново. Но это по-прежнему дает тот же результат: и n, и m равны . Что ж, это глупо — мы можем показать, что и n, и m равны , всегда четны |
Итак, что-то ужасно неправильно.
.. это должно быть нашим первым предположением, что квадратный корень из 2 является дробью. Не может быть.
Итак, квадратный корень из 2 не может быть записан в виде дроби .
Иррациональные
Мы называем такие числа «иррациональными» не потому, что они сумасшедшие, а потому, что их нельзя записать в виде отношения к (или дроби). И мы говорим:
«Квадратный корень из 2 иррационален»
Считается, что это первое иррациональное число, когда-либо открытое. Но есть и многое другое.
Доведение до абсурда
Между прочим, метод, который мы использовали, чтобы доказать это (сначала делая предположение, а затем проверяя, хорошо ли оно работает), называется «доказательство от противного» или «reductio ad absurdum».
Редукция до абсурда : тип логического аргумента, при котором кто-то принимает утверждение ради аргумента и получает абсурдный или нелепый результат, а затем делает вывод, что первоначальное утверждение должно было быть неверным, поскольку оно привело к абсурдному результату.
(из Википедии)
История
Много лет назад (около 500 г. до н.э.) греческие математики, такие как Пифагор, считали, что все числа можно представить в виде дробей.
И они думали, что числовая ось состоит исключительно из дробей, потому что для любых двух дробей мы всегда можем найти дробь между ними (так что мы можем смотреть все ближе и ближе на числовую прямую и находить все больше и больше дробей).
Пример: между 1/4 и 1/2 равно 1/3. Между 1/3 и 1/2 будет 2/5, между 1/3 и 2/5 будет 3/8 и так далее.
(Примечание. Самый простой способ найти дробь между двумя другими дробями — сложить верхние и нижние части, поэтому между 3/8 и 2/5 будет (3+2)/(8+5) = 5. /13).
Итак, поскольку этот процесс не имеет конца, таких точек бесконечно много. И это, кажется, заполняет числовую строку, не так ли?
И они были очень довольны этим… пока не обнаружили, что квадратный корень из 2 равен , а не дроби , и им пришлось полностью переосмыслить свои идеи!
Заключение
Квадратный корень из 2 «иррационален» (не может быть записан в виде дроби) .