Как вычислить и построить график функции тангенса в python?
Python / Статьи
Автор: admin
Примеры вычисления и построения графика функции тангенса в python
Содержание
- 1 Вычисление тангенса для заданного угла
- 2 Постром функцию касательной
Вычисление тангенса для заданного угла
Для получения тангенса заданного угла можно воспользоваться библиотекой math.
Code language: JavaScript (javascript)
import math angle = 0 result = math.tan(angle) print(result)
Результат:
Code language: CSS (css)
0.0
Примечание: функция tan предполагает, что угол задан в радианах. Чтобы преобразовать градусы в радианы в python, одним из решений является использование math.radians():
Code language: PHP (php)
import math angle = 45 # угол в градусах angle = math.radians(angle) # угол в радианах result = math.tan(angle) print(result)
Другой пример.
Code language: JavaScript (javascript)
import math angle = math.pi / 6 result = math.tan(angle) print(result)
Результат вычисления:
0. 5773502691896256
5773502691896256Code language: CSS (css)Примечание: чтобы округлить число float в python, одним из решений является использование round():
Code language: JavaScript (javascript)
import math angle = math.pi / 6 result = round(math.tan(angle), 2) print(result)
В результате вы получаете:
Code language: CSS (css)
0.58
Постром функцию касательной
import matplotlib.pyplot as plt import numpy as np import math angle_min = - 2.0 * math.pi angle_max = 2.Code language: JavaScript (javascript)0 * math.pi res = 0.01 angle_list = [a for a in np.arange(angle_min,angle_max,res)] angle_tan_list = [math.tan(a) for a in angle_list] plt.plot(angle_list, angle_tan_list) plt.title("Вычислление тангенса для заданного угла",fontsize=12) plt.ylim(-10,10) plt.savefig("tangent_function.png", bbox_inches='tight', dpi=100) plt.show()
После запуска кода получим:
Меткиmatplotlibnumpypython
что это, формула, свойства, график, примеры
Содержание:
- Что такое тангенс
- Что такое функция тангенса: формула
- Свойства функции
- Как построить график
- Примеры решения задач
Содержание
- Что такое тангенс
- Что такое функция тангенса: формула
- Свойства функции
- Как построить график
- Примеры решения задач
Что такое тангенс
Тангенсом какого-либо острого угла \(\alpha (tg \alpha)\) называют величину, выражающую отношение противоположного катета (а) к прилегающему катету (b) в треугольнике с углом 90°, то есть: \(tg \alpha = \frac{a}{b}\)
Понятие тангенса угла можно проиллюстрировать таким образом:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Если нет возможности написать самому, закажите тут.
Источник: microexcel.ru
Пример 1
Рассмотрим наглядный пример. Предположим, что катеты в треугольнике из определения тангенса имеют следующие значения: a = 3 b = 4 В таком случае справедливо записать выражение для расчета тангенса угла: \(tg \alpha = \frac{a}{b} = \frac{3}{4} = 0,75\)
Что такое функция тангенса: формула
При решении задач можно нередко встретить примеры с тригонометрическими функциями, в том числе, функцией тангенса. Эта функция обладает специфическими свойствами, которые значительно упрощают вычисления. Запись имеет следующий вид:
\(у = tg х\)
Здесь х обозначает аргумент тригонометрической функции и играет роль независимой переменной, а у определяет непосредственно функцию, то есть зависимую переменную.
Свойства функции
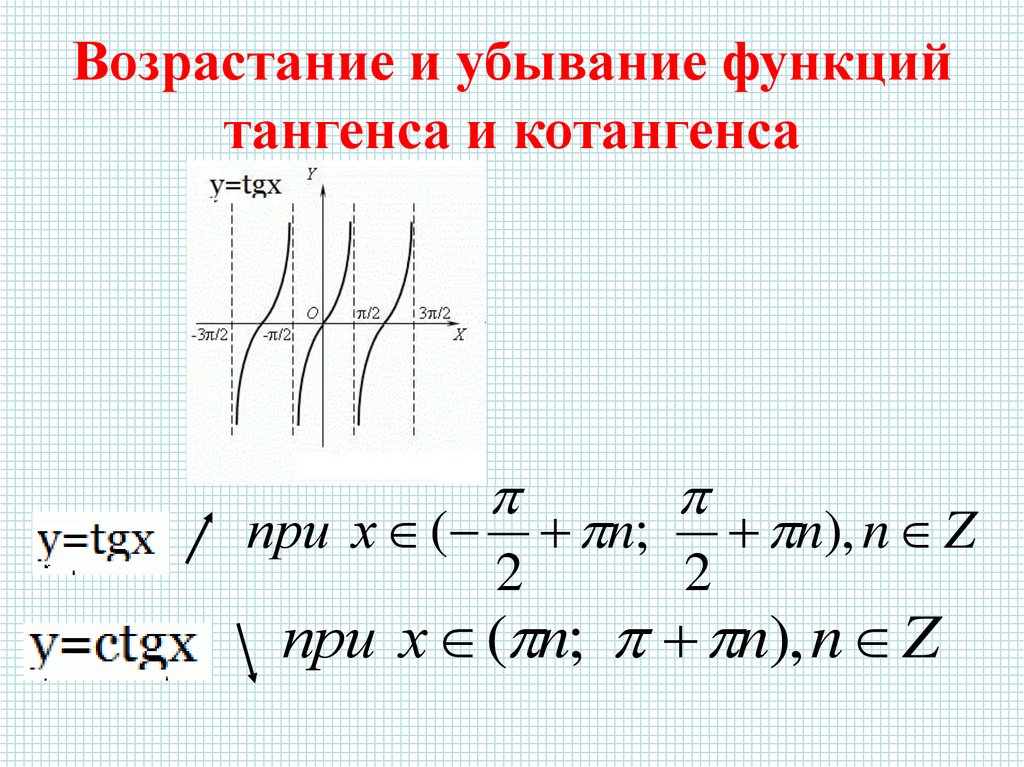
С помощью знаний свойств функций в тригонометрии достаточно просто решать самые сложные и громоздкие примеры. Перечислим закономерности, характерные для функции тангенса:
Перечислим закономерности, характерные для функции тангенса:
- Функция тангенса определяется в области \((x\ne\frac\pi2+\pi k)\), то есть на множестве, в состав которого включены действительные числа, за исключением точек, характеризующихся нулевым значением для косинуса.
- Функция на графике не имеет ограничений в верхней и нижней части, поэтому ее область значений можно записать как \(y\in\mathbb{R}\).
- Функция тангенса является нечетной, что целесообразно записать в виде соотношения \(tg(-x)=-tgx\).
- Тригонометрическая функция тангенса является периодической, а ее период составляет pi. Таким образом:\(tg(x+\pi k)=tgx\) .
- Стремление функции \(к +\infty\) можно наблюдать при сближении с левой стороны с точками \(x=\frac\pi2+\pi k\). Приближение к точке, обозначенной за a, слева формулируют таким образом: \(x\rightarrow\) \(a-0 \lim_{x\rightarrow\frac\pi2+\pi k-0} tgx=+\infty\) .
- Стремление функции \(к -\infty\) можно наблюдать при сближении с правой стороны с точками \(x=\frac\pi2+\pi k\).
 Приближение к точке, обозначенной за а, справа следует зафиксировать как \(x\rightarrow\) \(a+0 \lim_{x\rightarrow\frac\pi2+\pi k+0} tgx=-\infty\).
Приближение к точке, обозначенной за а, справа следует зафиксировать как \(x\rightarrow\) \(a+0 \lim_{x\rightarrow\frac\pi2+\pi k+0} tgx=-\infty\). - Нули рассматриваемой функции \(y_{0}=0\) определены точками \(x_0=\pi k\).
- Возрастание функции можно наблюдать на всей области, где она определена.
- Функция разрывается в точках \(x=\frac\pi2+\pi k\), которые пересечены вертикальными асимптотами. На отрезках между ними функция не прерывается, то есть \(\left(-\frac\pi2+\pi k;\ \frac\pi2+\pi k\right).\)
- Функция не обладает максимальными и минимальными значениями.
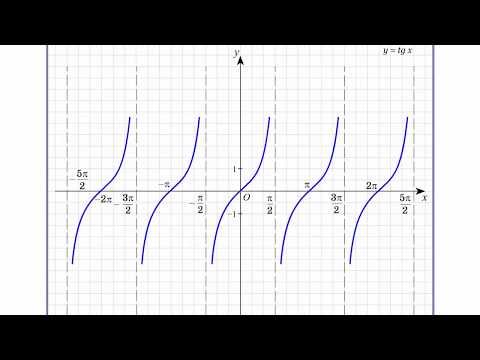
Как построить график
Как и любую другую тригонометрическую функцию, тангенс достаточно просто изобразить в системе координат. Графическое изображение функции тангенса в обобщенном виде представлено на рисунке ниже:
Источник: microexcel.ru
Построить график функции тангенса несложно. Нужно лишь последовательно выполнять действия согласно стандартному алгоритму:
- определить контрольные точки для построения;
- начертить плавную кривую линию на плоскости координат;
- для выбранного промежутка построить значения, которые расположены симметрично по отношению к началу координат;
- так как для значений функции характерны повторы с некоторым периодом, то целесообразно скопировать график для каждого из промежутков области определения;
- в результате получен график под названием тангенсоида.

Примеры решения задач
Задача 1
Требуется путем применения свойств тригонометрической функции, изученных в теоретическом разделе, записать область определения для следующей функции: \(y=\text{tg}\left( 2x+\frac{\pi }{3} \right)\)
Решение
Зная, что функция тангенса не может быть определена в точках при нулевом значении косинуса, запишем справедливое соотношение и выполним необходимые преобразования:
\(\cos \left( 2x+\frac{\pi }{3} \right)=0\)
\(2x+\frac{\pi }{3}\ne \frac{\pi }{2}+\pi n,n\in Z\)
\(x\ne \frac{\pi }{12}+\frac{\pi n}{2},n\in Z\)
В результате получена область, в которой определена функция из условия задания:
\(D(y)=\left( -\frac{\pi }{12}+\frac{\pi n}{2},\frac{\pi }{12}+\frac{\pi n}{2} \right),n\in Z\)
Ответ: \(D(y):x\in \left( -\frac{\pi }{12}+\frac{\pi n}{2},\frac{\pi }{12}+\frac{\pi n}{2} \right),n\in Z\)
Задача 2
Дано уравнение, решение которого требуется найти: \(\sin 2x-\sqrt{3}\cos 2x=0\)
Решение
Выполним преобразования исходного соотношения.
\(\sin 2x=\sqrt{3}\cos 2x\)
После деления всех частей записи на выражение \(\cos 2x\) соотношение изменится таким образом:
\(\text{tg}2x=\sqrt{3}\)
При этом ОДЗ для полученного выражения примет следующий вид:
\(\left( -\frac{\pi }{4}+\frac{\pi n}{2},\frac{\pi }{4}+\frac{\pi n}{2} \right),n\in Z.\)
Далее целесообразно приступить к решению уравнения:
\(2=\frac{\pi }{3}+\pi n,n\in Z\)
\(x=\frac{\pi }{6}+\frac{\pi n}{2},n\in Z\)
Заметим, что корни, которые получились по итогам расчетов, соответствуют ОДЗ. Можно записать ответ.
Ответ: \(x=\frac{\pi }{6}+\frac{\pi n}{2},n\in Z\)
Насколько полезной была для вас статья?
У этой статьи пока нет оценок.
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Поиск по содержимому
COCALC — Tangent Lines Примечания. SAGEWS
20. 04
04
18.04
Проект: Математика 241
Путь: 04 — Тангентные линии.
Лицензия: ДРУГОЕ
Изображение:
ubuntu2004
| Встроить | Скачать | Raw
Этот материал был разработан Аароном Трешамом из Гавайского университета в Хило и
под лицензией Creative Commons Attribution-ShareAlike 4.0 International License.
Предварительные требования:
На этой неделе мы увеличим графики функций, чтобы изучить свойство «локальной линейности». Затем найдем и начертим касательные линии.
Пример 1
Рассмотрим функцию f(x)=2ln(x)f(x)=2\ln(x)f(x)=2ln(x). Вот типичный график:
f(x)=2*ln(x) plot(f,xmin=0,xmax=10)
Что происходит, когда мы увеличиваем конкретную точку? Как выглядит график? Например, давайте увеличим масштаб точки (1,0)(1,0)(1,0).
plot(f,xmin=0,9,xmax=1,1)
На первом графике выше легко увидеть, что график непрямой, но когда мы увеличиваем кривизну, увидеть ее гораздо труднее. Давайте еще раз увеличим масштаб:
plot(f,xmin=0,99,xmax=1,01)
Когда мы приближаемся к графику fff, кажется, что график представляет собой прямую линию. Мы знаем, что это не так, но очень близко к точке (1,0)(1,0)(1,0) график представляет собой почти прямую. Это называется свойством локальной линейности. Не каждая функция обладает этим свойством, но есть много важных функций, обладающих этим свойством.
Пример 2
Рассмотрим график g(x)=cos(x)g(x)=\cos(x)g(x)=cos(x) вблизи точки (0,1)(0, 1)(0,1).
В анимации ниже мы увеличим этот график вблизи этой точки. Обратите внимание, что обе оси x и y изменятся для сохранения масштаба.
Оказывается, график cos(x)\cos(x)cos(x) обладает свойством локальной линейности в точке (0,1)(0,1)(0,1).
Пример 3
Теперь рассмотрим график h(x)=∣x∣h(x)=|x|h(x)=∣x∣ вблизи точки (0,0)(0,0)( 0,0).
plot(abs(x),xmin=-.01,xmax=.01,ymin=0,ymax=.02) #Я снова скорректировал ymin и ymax, чтобы сохранить одинаковые масштабы
Для этого функция, не имеет значения, насколько вы увеличиваете масштаб. Вы всегда получите острый угол, а не прямую линию. Это пример функции, не обладающей свойством локальной линейности в точке. [Примечание: эта функция обладает свойством локальной линейности в любой другой точке графика — везде она уже прямая.]
Из того, что мы видели выше, можно с уверенностью заключить, что одних графиков недостаточно для определения локальной линейности (в зависимости от окна просмотра изображение может выглядеть очень по-разному). Нам нужен алгебраический способ определения локальной линейности.
Касательные линии
Если функция fff обладает свойством локальной линейности в определенной точке (x0,f(x0))(x_0,f(x_0))(x0,f(x0)), то график fff выглядит как линия рядом с этой точкой. Но на какую линию это похоже?
Линия, к которой fff «близка» в точке (x0,f(x0))(x_0,f(x_0))(x0,f(x0)) называется «касательной» в этой точке, и точка (x0,f(x0))(x_0,f(x_0))(x0,f(x0)) называется «точкой касания». Чтобы найти уравнение линии, нам нужны две части информации: либо две точки на линии, либо одна точка на линии и наклон линии. Мы знаем одну точку на касательной: (x0,f(x0))(x_0,f(x_0))(x0,f(x0)). Мы не знаем вторую точку на касательной, но можем найти наклон касательной.
Чтобы найти уравнение линии, нам нужны две части информации: либо две точки на линии, либо одна точка на линии и наклон линии. Мы знаем одну точку на касательной: (x0,f(x0))(x_0,f(x_0))(x0,f(x0)). Мы не знаем вторую точку на касательной, но можем найти наклон касательной.
Во-первых, мы аппроксимируем наклон касательной, выбрав вторую точку, близкую к (x0,f(x0))(x_0,f(x_0))(x0,f(x0)). Предположим, что расстояние от x0x_0x0 равно hhh, тогда вторая точка равна (x0+h,f(x0+h))(x_0+h,f(x_0+h))(x0+h,f(x0+ час)). Мы найдем наклон линии, проходящей через эти две точки (называемой «секущей линией»).
Вот пример графика.
Теперь мы улучшим нашу аппроксимацию, делая hhh все ближе и ближе к 000, перемещая (x0+h,f(x0+h))(x_0+h,f(x_0+h))(x0+h,f( x0+h)) ближе к (x0,f(x0))(x_0,f(x_0))(x0,f(x0)).
Этот процесс звучит как ограничение, поэтому мы найдем ответ. Наклон секущей через (x0+h,f(x0+h))(x_0+h,f(x_0+h))(x0+h,f(x0+h)) и (x0,f (x0))(x_0,f(x_0))(x0,f(x0)) равно f(x0+h)−f(x0)x0+h−x0=f(x0+h)−f(x0 )h\displaystyle\frac{f(x_0+h)-f(x_0)}{x_0+h-x_0}=\frac{f(x_0+h)-f(x_0)}{h}x0+h− x0f(x0+h)−f(x0)=hf(x0+h)−f(x0) (нарастание над пробегом).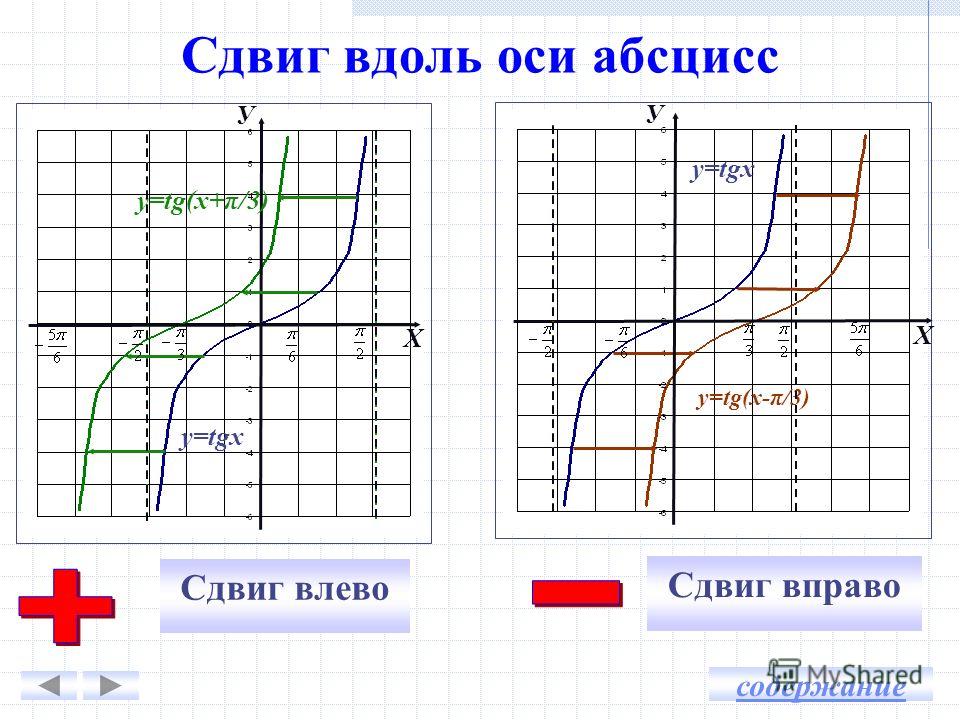
Мы хотим знать, что происходит с этим наклоном, когда hhh приближается к 000. В предельных обозначениях мы хотим найти limh→0f(x0+h)−f(x0)h\displaystyle\lim_{h\to 0} \frac{f(x_0+h)-f(x_0)}{h}h→0limhf(x0+h)−f(x0).
Если функция fff обладает свойством локальной линейности при (x0,f(x0))(x_0,f(x_0))(x0,f(x0)), то этот предел будет существовать (и наоборот). Значение этого предела представляет собой наклон касательной.
Теперь, когда у нас есть точка на линии и наклон линии, мы можем найти уравнение линии. Помните форму точка-наклон?
Точечно-наклонная форма линии: y−y0=m⋅(x−x0)y-y_0=m\cdot(x-x_0)y−y0=m⋅(x−x0), где mmm – это наклон, а (x0,y0)(x_0,y_0)(x0,y0) – точка на линии.
В этом случае (x0,y0)=(x0,f(x0))(x_0,y_0)=(x_0,f(x_0))(x0,y0)=(x0,f(x0) )) и m = limh→0f(x0+h)−f(x0)hm=\displaystyle\lim_{h\to 0}\frac{f(x_0+h)-f(x_0)}{h} m=h→0limhf(x0+h)−f(x0).
Следовательно, уравнение для касательной имеет вид y−f(x0)=m⋅(x−x0)y-f(x_0)=m\cdot(x-x_0)y−f(x0)=m⋅( х-х0). Добавление f(x0)f(x_0)f(x0) к обеим сторонам дает:
Добавление f(x0)f(x_0)f(x0) к обеим сторонам дает:
Уравнение для касательной в точке x=x0x=x_0x=x0:
y=f(x0)+m⋅(x− x0),y=f(x_0)+m\cdot(x-x_0),y=f(x0)+m⋅(x−x0),
, где m = limh→0f(x0+h)−f(x0)hm=\displaystyle\lim_{h\to 0}\frac{f(x_0+h)-f(x_0)}{h} m=h→0limhf(x0+h)−f(x0).
Это общая формула для нахождения уравнения для прямой, касательной к графику fff в точке (x0,f(x0))(x_0,f(x_0))(x0,f(x0)).
Пример 4
Чтобы увидеть, как секущие линии приближаются к касательной графически, давайте посмотрим на анимацию ниже.
Вы увидите секущие линии f(x)=2ln(x)f(x)=2\ln(x)f(x)=2ln(x) через точку (x0,f(x0) )=(1,0)(x_0,f(x_0))=(1,0)(x0,f(x0))=(1,0) и (x0+h,f(x0+h)) (x_0+h,f(x_0+h))(x0+h,f(x0+h)), где hhh начинается с 111 и приближается к 000.
Вы можете видеть, что секущие линии (зеленые) приближаются к касательной (красные) по мере того, как hhh приближается к 000.
Теперь hhh также может быть отрицательным, поэтому мы также рассмотрим секущие, когда hhh начинается с −34.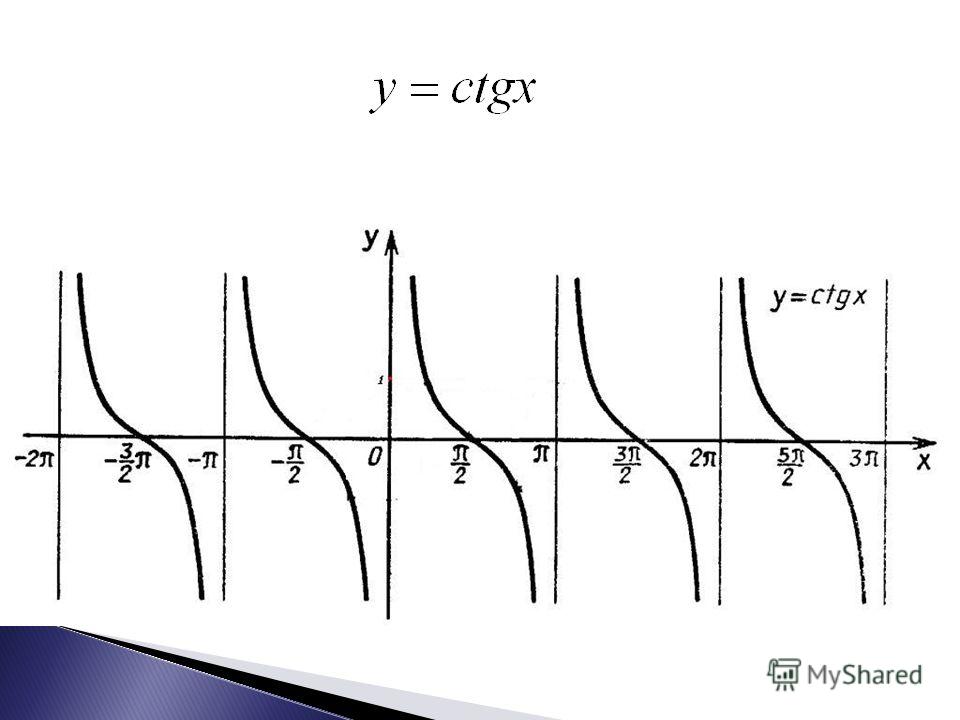 -\frac{3}{4}−43 и приближается к 000.
-\frac{3}{4}−43 и приближается к 000.
Примечание. Мы не можем начать с h=−1h=-1h=−1, так как это дает нам x0+h=0x_0+h=0x0 +h=0, которого нет в домене.
Снова секущие приближаются к касательной, когда hhh приближается к 000.
Пример 5
Теперь рассмотрим f(x)=cos(x)f(x)=\cos(x)f(x)= cos(x) и (x0,f(x0))=(0,1)(x_0,f(x_0))=(0,1)(x0,f(x0))=(0,1). Мы начнем с h=1h=1h=1 и пусть hhh приблизится к 000.
Теперь начнем с h=−1h=-1h=−1 и пусть hhh приближается к 000.
Независимо от того, приближается ли hhh к 000 слева или справа, секущие приближаются к касательной.
Теперь найдем уравнение касательной к графику f(x)=2ln(x)f(x)=2\ln(x)f(x)=2ln(x) в точке (1 ,0)(1,0)(1,0).
Во-первых, нам нужен уклон. Как мы видели выше, наклон равен limh→0f(1+h)−f(1)h\displaystyle\lim_{h\to0}\frac{f(1+h)-f(1)}{h }h→0limhf(1+h)−f(1).
%вар ч е (х) = 2 * пер (х) limit((f(1+h)-f(1))/h,h=0) # Не забывайте скобки вокруг числителя
Значит, наклон равен 2.
Теперь используем уравнение касательной: y=f(x0)+m⋅(x−x0)y=f(x_0)+m\cdot(x-x_0)y =f(x0)+m⋅(x−x0).
TL(x)=f(1)+2*(x-1) # Я буду использовать TL для "касательной линии" show(TL(x))
2 x−2\displaystyle 2 \, x — 22x−2
Теперь я нарисую функцию и касательную.
plot(f(x),xmin=0,xmax=2)+plot(TL(x),xmin=0,xmax=2,color='red')+point((1,f(1) ),color='black',pointsize=20)
Пример 7
Теперь попробуем найти касательную к g(x)=∣x∣g(x)=|x|g(x)=∣x∣ в точке (0,0)(0,0)(0,0 ). Выше мы видели, что эта функция не обладает здесь свойством локальной линейности, так что что-то должно пойти не так.
Попробуем вычислить наклон: m=limh→0∣0+h∣−∣0∣h\displaystyle m=\lim_{h\to 0}\frac{|0+h|-|0| }{h}m=h→0limh∣0+h∣−∣0∣.
Мы обнаруживаем, что предела не существует (Sage возвращает «und»).
%вар ч г (х) = абс (х) limit((g(0+h)-g(0))/h,h=0)
Обратите внимание, что односторонние пределы существуют, но не равны: 9-}\frac{-h}{h}=-1h→0−limh∣0+h∣−∣0∣=h→0−limh∣h∣=h→0−limh −h=−1
Значит, двустороннего предела не существует.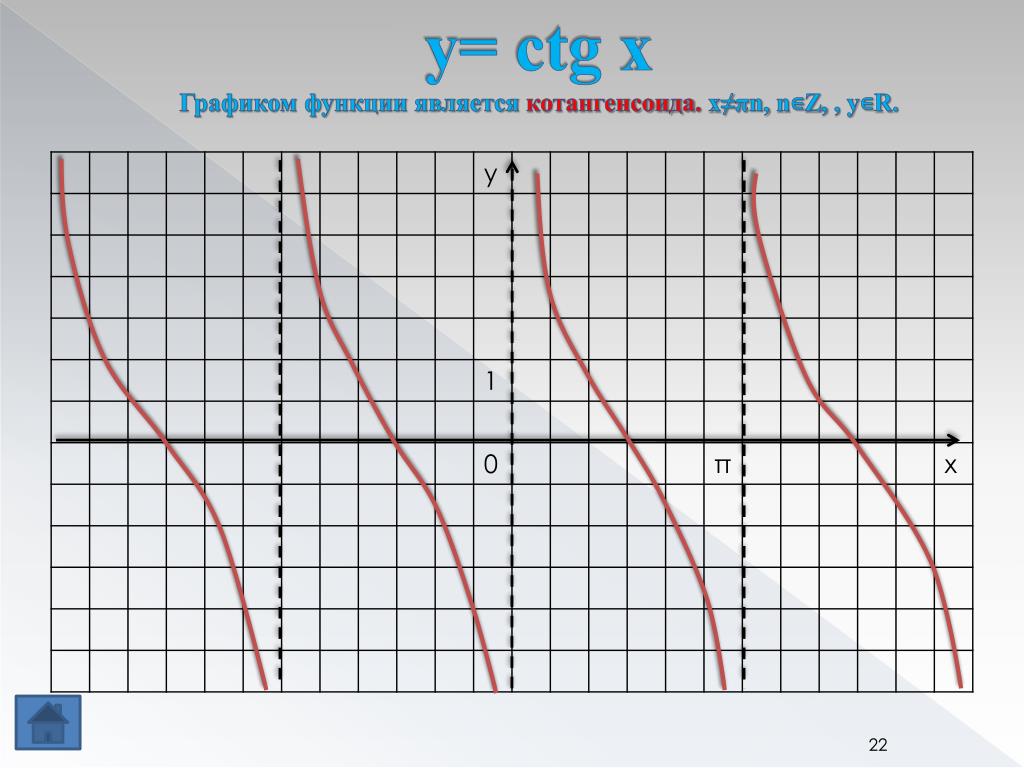
Если мы попытаемся найти наклон в любой точке, отличной от x=0x=0x=0, все будет хорошо. Давайте использовать (-5,5)(-5,5)(-5,5).
m=limh→0∣−5+h∣−∣−5∣h\displaystyle m=\lim_{h\to 0}\frac{|-5+h|-|-5|}{h }m=h→0limh∣−5+h∣−∣−5∣
%var h limit((g(-5+h)-g(-5))/h,h=0)
Теперь мы видим, что наклон касательной равен −1-1−1, поэтому касательная имеет уравнение y=g(-5)+(-1)(x-(-5))=5-(x+5)y=g(-5)+(-1)(x-(-5))=5 -(x+5)y=g(-5)+(-1)(x-(-5))=5-(x+5), или y=-xy=-xy=-x.
TL(x)=g(-5)+(-1)*(x-(-5)) show(TL(x))
−x\displaystyle -x−x
Теперь я нарисую функцию и касательную.
plot(g(x),xmin=-10,xmax=10)+plot(TL(x),xmin=-10,xmax=10,color='red',linestyle='--')+ point((-5,g(-5)),color='black',pointsize=20)
python — Как построить наклон (касательную) параболы в любой точке?
спросил
Изменено 3 года, 10 месяцев назад
Просмотрено 12 тысяч раз
Я хочу нарисовать простую иллюстрацию использования производной для определения наклона функции в любой точке.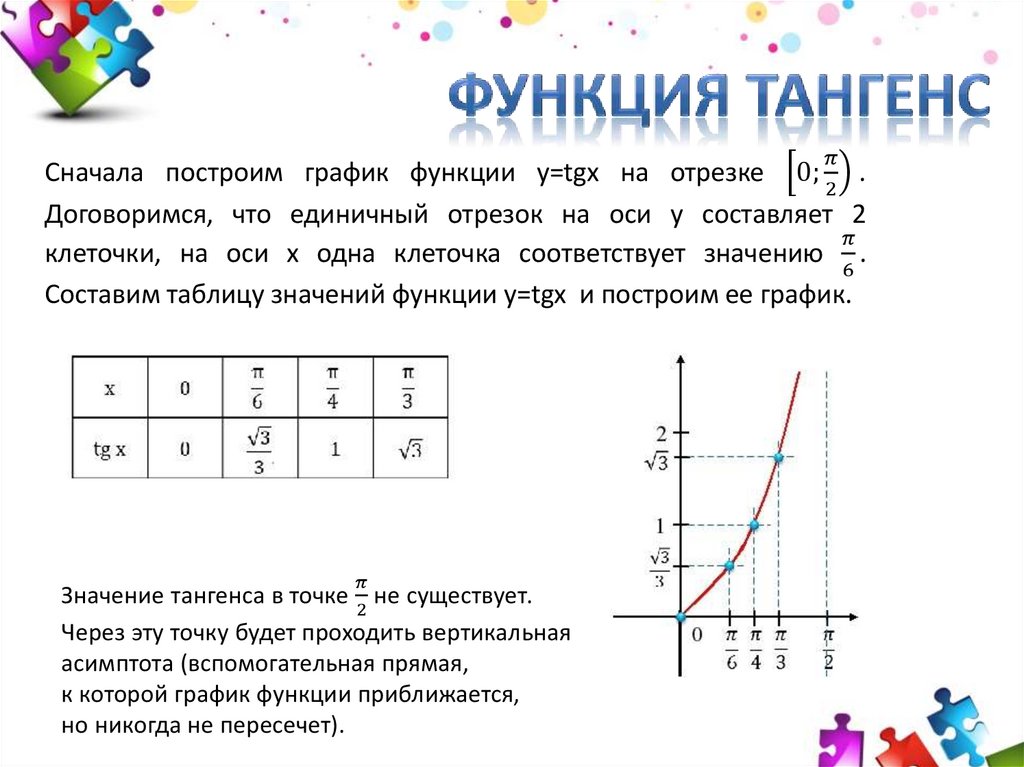 Это будет выглядеть примерно так:
Это будет выглядеть примерно так:
Я уже построил простую параболу, используя этот код:
import numpy as np
из matplotlib импортировать pyplot как plt
входы = 0,2
веса = np.arange(-6,14)
целевое_предсказание = 0,7
прогноз = входные данные * веса
ошибки = (предсказание - целевое_предсказание) ** 2
plt.xlabel("Вес")
plt.ylabel("Ошибка")
plt.plot(веса, ошибка)
Теперь я хочу добавить что-то вроде этого:
current_weight = 5 # нарисуйте короткую часть линии для обозначения наклона x = np.arange (оптимальный_вес - 3, оптимальный_вес + 3) # производная наклон = 2 * (входные данные * текущий_вес - целевой_прогноз) y = наклон*x # Как должно выглядеть это уравнение? plt.plot(x, y)
Чтобы нарисовать касательную, проходящую через current_weight .
Но я не могу понять это, вы можете помочь?
- питон
- matplotlib
- plot
Получив наклон в нужной точке, вам нужно написать уравнение для касательной, используя форму точка-наклон:
# Определить параболу защита f(x): вернуть х**2 # Определить производную параболы угол уклона (х): вернуть 2*х # Определить x диапазон данных для параболы х = np.

 0
0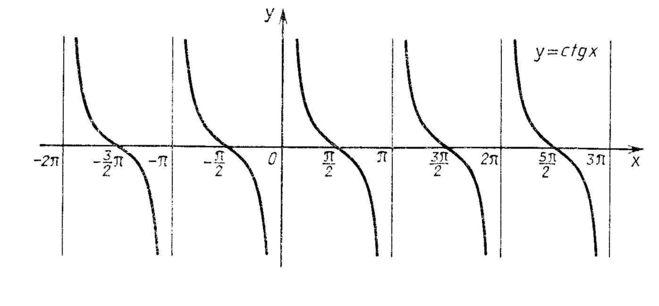 5773502691896256
5773502691896256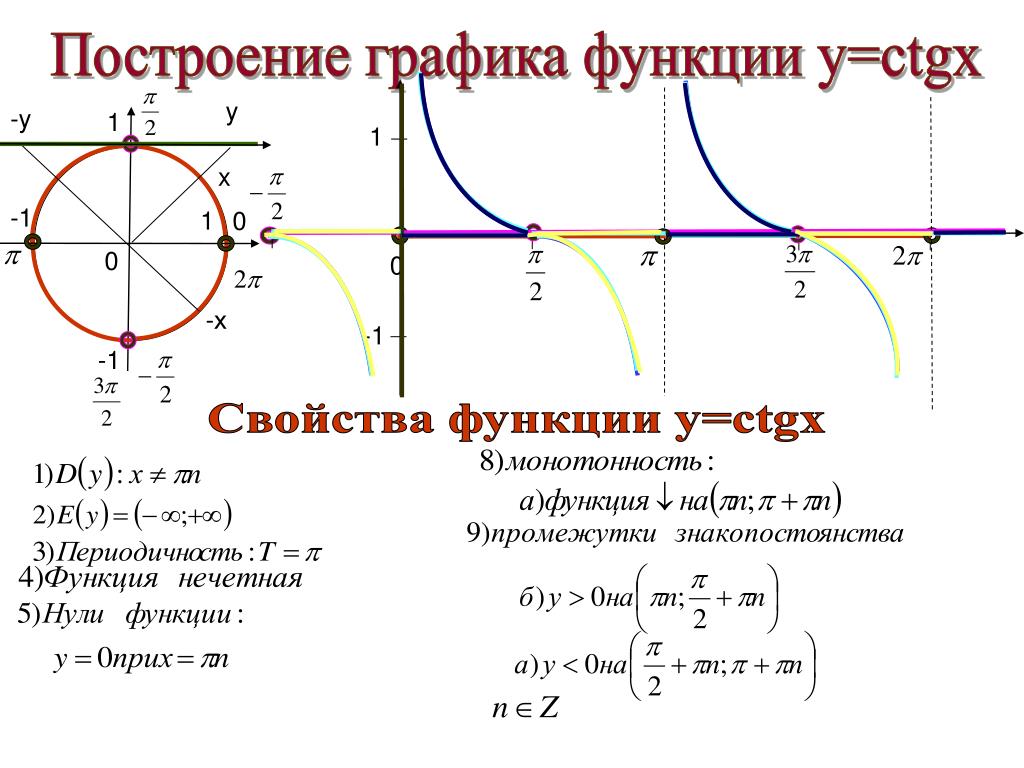 0 * math.pi
res = 0.01
angle_list = [a for a in np.arange(angle_min,angle_max,res)]
angle_tan_list = [math.tan(a) for a in angle_list]
plt.plot(angle_list, angle_tan_list)
plt.title("Вычислление тангенса для заданного угла",fontsize=12)
plt.ylim(-10,10)
plt.savefig("tangent_function.png", bbox_inches='tight', dpi=100)
plt.show()
0 * math.pi
res = 0.01
angle_list = [a for a in np.arange(angle_min,angle_max,res)]
angle_tan_list = [math.tan(a) for a in angle_list]
plt.plot(angle_list, angle_tan_list)
plt.title("Вычислление тангенса для заданного угла",fontsize=12)
plt.ylim(-10,10)
plt.savefig("tangent_function.png", bbox_inches='tight', dpi=100)
plt.show() Приближение к точке, обозначенной за а, справа следует зафиксировать как \(x\rightarrow\) \(a+0 \lim_{x\rightarrow\frac\pi2+\pi k+0} tgx=-\infty\).
Приближение к точке, обозначенной за а, справа следует зафиксировать как \(x\rightarrow\) \(a+0 \lim_{x\rightarrow\frac\pi2+\pi k+0} tgx=-\infty\).