84, 85. Наибольший общий делитель
84, 85. Наибольший общий делитель
Это надо знать
Наибольший общий делитель (НОД) двух и более чисел — это самое большее натуральное число, на которое эти числа делятся без остатка.
Пример:
Найти наибольший общий делитель чисел 15 и 35.
Найдем делители каждого числа:
15: 1, 3, 5, 15.
35: 1, 5, 7, 35.
Общие делители чисел 15 и 35: 1 и 5. Наибольший их общий делитель равен 5.
Ответ: НОД (15, 35) = 5.
Правило нахождения наибольшего общего делителя (НОД)
1) разложить числа на простые множители;
2) подчеркнуть одинаковые множители , входящие в каждое разложение этих чисел;
3) выписать подчеркнутые множители из первого разложения, найти их произведение — это и есть наибольший общий делитель.
Пример:
Найти НОД (100, 140).
Разложим оба числа на простые множители:
100 | 2 140 | 2
50 | 2 70 | 2
25 | 5 35 | 5
5 | 5 7 | 7
1 1
НОД (100, 140) = 2 ∙ 2 ∙ 5 = 20.
Ответ: НОД (100, 140) = 20.
Видеоурок
Домашнее задание
К уроку 84 (на 15.01)
П. 5.6
№ 1.221 стр. 43
Сформулируйте правило нахождения наибольшего общего делителя чисел А и В, если:
1) числа А и В взаимно простые;
2) число А кратно числу В;
Приведите примеры!!!
№ 1. 221
221
Найдите наибольший общий делитель чисел:
1) 72 и 35; 2) 120 и 77; 3) 55 и 165; 4) 328 и 8; 5) 60, 240 и 20; 6) 1620, 135 и 15.
К уроку 85 (на 18.01)
П. 5.6
№ 5.108 стр. 122
Срезали 48 цветков розовых, 64 цветка белых цикламентов и 80 декоративных веточек. Какое наибольшее число одинаковых букетов можно составить из этих растений?
№ 5.109 стр. 122
Для новогодних гирлянд школьники подготовили флажки разного цвета: 960 красных, 480 желтых, 720 синих и 680 зеленых. Какое наибольшее количество одинаковых гирлянд можно изготовить из этих флажков, если флажков каждого цвета во всех гирляндах будет поровну?
№ 5.342 стр. 173 Задача на повторение
Из двух городов, находящихся на расстоянии 700 км друг от друга, одновременно навстречу друг другу выехали два поезда. Скорость одного из поездов 80 км/ч. Найдите скорость другого поезда, если через 2 ч после начала движения между поездами было 200 км. 3x-1 = 820…
3x-1 = 820…
Друзья помогите. Голову сломала.
Если размер сторон треугольника АВ и ВС равен 46,5 см а ВС и СА равен 50см и СА и АВ равны 47,5 то какой периметр треугольника?
…
Математика
Литература
Алгебра
Русский язык
Геометрия
Английский язык
Химия
Физика
Биология
Другие предметы
История
Обществознание
Окружающий мир
География
Українська мова
Українська література
Қазақ тiлi
Беларуская моваИнформатика
Экономика
Музыка
Право
Французский язык
Немецкий язык
ОБЖ
Психология
GCF, равный 72 и 120
GCF, равный 72 и 120, — это наибольшее возможное число, которое делит 72 и 120 точно без остатка. Делители 72 и 120 равны 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72 и 1, 2, 3, 4, 5, 6, 8, 10, 12, 15. , 20, 24, 30, 40, 60, 120 соответственно. Существует 3 наиболее часто используемых метода нахождения GCF 72 и 120: деление в длину, алгоритм Евклида и разложение на простые множители.
Делители 72 и 120 равны 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72 и 1, 2, 3, 4, 5, 6, 8, 10, 12, 15. , 20, 24, 30, 40, 60, 120 соответственно. Существует 3 наиболее часто используемых метода нахождения GCF 72 и 120: деление в длину, алгоритм Евклида и разложение на простые множители.
| 1. | GCF 72 и 120 |
| 2. | Список методов |
| 3. | Решенные примеры |
| 4. | Часто задаваемые вопросы |
Что такое GCF 72 и 120?
Ответ: НГК 72 и 120 равно 24.
Объяснение:
НГК двух ненулевых целых чисел, x(72) и y(120), есть наибольшее натуральное число m(24) который делит и x (72), и y (120) без остатка.
Методы определения GCF 72 и 120
Давайте рассмотрим различные методы определения GCF 72 и 120.
- Метод длинного деления
- Список общих факторов
- Использование алгоритма Евклида
GCF 72 и 120 путем длинного деления
GCF 72 и 120 — это делитель, который мы получаем, когда остаток становится равным 0 после многократного длинного деления.
- Шаг 1: Разделите 120 (большее число) на 72 (меньшее число).
- Шаг 2: Поскольку остаток ≠ 0, разделим делитель шага 1 (72) на остаток (48).
- Шаг 3: Повторяйте этот процесс до тех пор, пока остаток не станет равным 0.
Соответствующий делитель (24) представляет собой НОД чисел 72 и 120.
НОД чисел 72 и 120 путем перечисления общих делителей
- Факторы числа 72: 12, 18, 24, 36, 72
- Факторы 120: 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60, 120
Существует 8 общих делителей чисел 72 и 120: 1, 2, 3, 4, 6, 8, 12 и 24. Следовательно, наибольший общий делитель чисел 72 и 120 равен 24. 120 по алгоритму Евклида
Согласно алгоритму Евклида, GCF(X, Y) = GCF(Y, X mod Y)
где X > Y, а mod — оператор по модулю.
Здесь X = 120 и Y = 72
- GCF(120, 72) = GCF(72, 120 mod 72) = GCF(72, 48)
- GCF(72, 48) = GCF(48, 72 mod 48) = GCF(48, 24)
- GCF(48, 24) = GCF(24, 48 mod 24) = GCF(24, 0)
- GCF(24, 0) = 24 (∵ GCF(X, 0) = |X|, где X ≠ 0)
Следовательно, значение GCF 72 и 120 равно 24.
☛ Также проверьте:
- GCF 120 и 168 = 24
- GCF 16 и 40 = 8
- GCF 64 и 80 = 16
- GCF 8 и 40 = 8
- GCF 10 и 12 = 2
- GCF 24 и 32 = 8
- GCF 22 и 33 = 11
GCF 72 и 120 Примеры
Пример 1. Найдите НОКФ чисел 72 и 120, если их НОКП равен 360. ⇒ GCF(72, 120) = (72 × 120)/360 = 24
Следовательно, наибольший общий делитель 72 и 120 равен 24,9.0003Пример 2: Найдите наибольшее число, которое точно делит 72 и 120.
Решение:
Наибольшее число, которое точно делит 72 и 120, является их наибольшим общим делителем, т. е. НОД 72 и 120.
⇒ Множители 72 и 120:- Множители 72 = 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72
- Коэффициенты 120 = 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60, 120
Таким образом, GCF 72 и 120 равен 24.

Пример 3: Для двух чисел GCF = 24 и LCM = 360. Если одно число равно 120, найдите другое число.
Решение:
Дано: GCF (x, 120) = 24 и НОК (x, 120) = 360
∵ GCF × LCM = 120 × (x)
⇒ x = (GCF × LCM)/120
⇒ х = (24 × 360)/120
⇒ х = 72
Следовательно, другое число равно 72.
перейти к слайдуперейти к слайдуперейти к слайду
Готовы посмотреть на мир глазами математика?
Математика лежит в основе всего, что мы делаем. Наслаждайтесь решением реальных математических задач на живых уроках и станьте экспертом во всем.
Записаться на бесплатный пробный урок
Часто задаваемые вопросы о GCF 72 и 120
Что такое GCF 72 и 120?
GCF 72 и 120 равен 24 . Чтобы вычислить наибольший общий делитель 72 и 120, нам нужно разложить каждое число на множители (множители 72 = 1, 2, 3, 4, 6, 8, 9). , 12, 18, 24, 36, 72; множители 120 = 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60, 120) и выбрать наибольший множитель, который точно делит и 72, и 120, т.е. , 24.
, 12, 18, 24, 36, 72; множители 120 = 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60, 120) и выбрать наибольший множитель, который точно делит и 72, и 120, т.е. , 24.
Каковы методы нахождения GCF 72 и 120?
Существует три широко используемых метода нахождения GCF 72 и 120 .
- Путем простой факторизации
- Длинным делением
- По алгоритму Евклида
Какая связь между LCM и GCF 72, 120?
Следующее уравнение можно использовать для выражения связи между наименьшим общим кратным (НОК) и НОД 72 и 120, т. е. НОД × НОК = 72 × 120.
Как найти НОД 72 и 120 методом деления на длинные ?
Чтобы найти НГК 72, 120 с помощью метода деления в длину, 120 нужно разделить на 72. Соответствующий делитель (24), когда остаток равен 0, принимается за НГК.
Как найти GCF 72 и 120 с помощью простой факторизации?
Чтобы найти НОК 72 и 120, мы найдем простую факторизацию данных чисел, т. е. 72 = 2 × 2 × 2 × 3 × 3; 120 = 2 × 2 × 2 × 3 × 5,
е. 72 = 2 × 2 × 2 × 3 × 3; 120 = 2 × 2 × 2 × 3 × 5,
⇒ Поскольку 2, 2, 2, 3 являются общими элементами в простой факторизации чисел 72 и 120. Следовательно, GCF(72, 120) = 2 × 2 × 2 × 3 = 24
☛ Что такое простое число?
Если GCF 120 и 72 равен 24, Найдите его LCM.
GCF(120, 72) × LCM(120, 72) = 120 × 72
Так как GCF 120 и 72 = 24
⇒ 24 × НОК(120, 72) = 8640
Следовательно, НОК = 360
.
☛ Калькулятор наибольшего общего делителя
Скачать БЕСПЛАТНЫЕ учебные материалы
GCF и LCM
LCM (наименьший общий кратный) и HCF (наибольший общий множитель)
Что такое LCM (наименьший общий кратный)?В арифметике LCM или наименьшее общее кратное двух чисел a и b , обозначается как LCM (a,b) является наименьшим положительным или делимым целым числом. как a , так и b .
LCM i s также называется Наименьший общий делитель
Пример:
Возьмем два натуральных числа 3 и 4, задача состоит в том, чтобы найти НОК(3, 4).
Решение:
- Кратность 3: 3,6,9,12,15,18,21,24…
- Кратность 4: 4,8,12,16,20,24, 28…
Общие множители 3 и 4 равны 12, 24…, Таким образом, наименьшее общее кратное равно 12.
Следовательно, НОК(3, 4) = 12
Как найти LCM?
Существует 3 способа найти наименьшее общее кратное двух чисел.
- НОК методом листинга
- НОК методом простой факторизации
- НОК методом деления
1. НОК методом листинга:
Мы можем найти общие кратные двух или более чисел, перечислив их кратные. И из этих общих кратных и наименьшим общим кратным считается НОК двух заданных чисел.
Выполните следующие шаги, чтобы вычислить НОК двух чисел A и B методом перечисления:
- Сначала запишите первые несколько кратных A и B.
- Отметьте общие кратные из кратных обоих чисел.
- Выберите наименьшее отмеченное общее кратное. Следовательно, это приводит к LCM (A, B).
Пример:
Найдите НОК двух натуральных чисел 2 и 6.
Решение:
- Кратные 2: 2,4, 6 ,8,10, 12 ,14…
- Кратные 6: 6 , 12 ,18,24, 54… 900 множители 2 и 6 равны 6, 12…, Таким образом, наименьшее общее кратное равно 6.
Следовательно, НОК(2, 6) = 6
2. НОК методом деления:
Мы можем найти LCM, используя метод деления заданных чисел. Это можно сделать, разделив числа на обычное простое число, и эти простые множители используются для вычисления НОК этих чисел.
Выполните следующие действия, чтобы вычислить НОК двух чисел A и B методом деления:
- Сначала найдите простое число, которое является множителем хотя бы одного из заданных чисел. Запишите это простое число слева от данных чисел.
- Если простое число в шаге 1 является множителем числа, то разделите число на простое число и под ним запишите частное. Если простое число в шаге 1 не является делителем числа, то запишите число в строке ниже, как оно есть. Продолжайте действия до тех пор, пока в последнем ряду не останется 1.
Пример:
Возьмем два натуральных числа 3 и 4, задача состоит в том, чтобы найти НОК(3, 4).
Решение:НОК(3,4) = 12
НОК является произведением всех этих простых чисел.
Следовательно, НОК(3, 4) = 12
3. НОК методом простой факторизации:
Мы можем найти НОК, используя метод простой факторизации заданных чисел.
Выполните следующие действия, чтобы вычислить НОК двух чисел с помощью метода простой факторизации:
- Сначала найдите простые множители данных чисел, используя метод повторного деления.
- Запишите эти числа в виде экспоненты и найдите произведение только тех простых множителей, которые имеют наибольшую мощность.
- Произведение этих множителей с наивысшими степенями есть НОК заданных чисел
Пример:
Найдите НОК двух натуральных чисел 120 и 300.
из 120: 2*2*2*3*5 = 2 3 *3 1 *5 1
Разложение числа 300 на простые множители: 2*2*3*5*5 = 2 2 *3 1 *5 2 Теперь , найдите произведение только тех множителей, которые имеют наибольшую степень среди них. Это будет 2 3 * 3 1 * 5 2 = 8 * 3 * 25 = 600 . Фактор)?
Наивысший общий делитель (HCF) двух чисел — это максимально возможное число, которое полностью делит оба числа.
Наибольший общий делитель (HCF) также известен как наибольший общий делитель (GCD).
Х.К.Ф. также называют наибольшим общим делителем (GCF).
Как найти HCF?
Существует 3 метода расчета HCF двух чисел:
- HCF методом листинга факторов
- HCF методом простой факторизации
- HCF методом деления
1. HCF методом перечисления множителей
Здесь мы перечисляем множители каждого числа и находим общие множители этих чисел. Затем среди общих факторов определяем наибольший общий фактор.
Пример:
Найдите HCF чисел 32 и 14.
Решение: Сначала запишите множители 32 и 14.
- , 8, 16, 32
- Делители числа 14: 1, 2, 7, 14
Мы видим, что 1, 2 являются единственными общими делителями чисел 32 и 14. Тогда как 2 является наибольшим среди всех общих делителей.

Следовательно, HCF 32 и 14 равен 2.2. HCF методом простой факторизации
Мы можем найти HCF, используя метод простой факторизации заданных чисел.
Выполните следующие шаги, чтобы вычислить HCF заданных чисел, используя метод простой факторизации:
- Сначала найдите общие простые делители данных чисел.
- Умножьте эти общие простые множители, чтобы получить HCF этих чисел.
Пример:
Найдите HCF чисел 80 и 90.
Решение:
- Простые множители числа 80: 2 * 928 * 003
- Простые делители числа 90: 2 * 3 * 3 * 5.
Мы видим, что 2, 5 являются единственными общими делителями чисел 80 и 9.0, Теперь HCF 80 и 90 будет произведением общих простых множителей, равных 2 и 5.
Следовательно, HCF 80 и 90 равен 10.3. HCF методом деления
HCF двух чисел можно рассчитать, используя метод деления.
Выполните следующие действия, чтобы рассчитать HCF заданных чисел с помощью метода деления
- Сначала мы разделим большее число на меньшее и проверим остаток.
- Затем выполните оставшуюся часть предыдущего шага, так как новый делитель и делитель предыдущего шага станут новым делимым. После этого снова выполняем длинное деление.
- Продолжайте процесс деления до тех пор, пока в остатке не будет 0. Следует отметить, что последним делителем будет HCF этих двух чисел.
Пример:
Найдите HCF 30 и 42.
Решение:
HCF 30 и 42
Следовательно, HCF из 30 и 42 — 6.
6. на LCM и HCF:
- Вопрос 1: Два числа находятся в соотношении 5:11. Если их HCF равен 7, найдите числа.
Решение: Пусть числа будут 5м и 11м. Поскольку 5:11 уже является уменьшенным соотношением, «m» должно быть HCF. Итак, числа 5 x 7 = 35 и 11 x 7 = 77.
- Вопрос 2: Найдите длину доски, с помощью которой можно точно измерить длины 4 м 50 см, 9 м 90 см, и 16 м 20 см в наименьшее время.
Решение: Давайте сначала переведем каждую длину в см. Итак, длины 450 см, 990 см и 1620 см. Теперь нам нужно найти длину самой большой доски, которую можно использовать для измерения этих длин, поскольку для самой большой доски потребуется наименьшее время. Для этого нам нужно взять HCF 450, 990 и 1620. 450 = 2 x 3 x 3 x 5 x 5 = 2 x 3 2 x 5 2 990 = 2 x 3 x 3 x 5 x 11 = 2 x 3 2 x 5 x 11 1620 = 2 x 2 x 3 x 3 x 3 x 3 x 5 = 2 2 x 3 4 x 5 Следовательно, HCF (450, 990, 1620) = 2 x 3 x 3 x 5 = 90 Таким образом, мы Нужна доска длиной 90 см, чтобы измерить заданные длины за наименьшее время.
- Вопрос 3: Найдите наибольшее число, которое при делении 70 и 50 дает остатки 1 и 4 соответственно.
Решение: Искомое число оставляет остатки 1 и 4 при делении 70 и 50 соответственно.Это означает, что число точно делит 69 и 46. Итак, нам нужно найти HCF 69 (3 x 23) и 46 (2 x 23). HCF (69, 46) = 23 Таким образом, 23 — искомое число.
- Вопрос 4: Найдите наибольшее число, которое делится на 64, 136 и 238 так, чтобы в каждом случае оставался один и тот же остаток.
Решение: Чтобы найти искомое число, нам нужно найти HCF (136-64), (238-136) и (238-64), т. е. HCF (72, 102, 174). 72 = 2 3 x 3 2 102 = 2 x 3 x 17 174 = 2 x 3 x 29 Следовательно, HCF (72, 102, 174) = 2 x 3 = 6, следовательно, 6 — это искомое число.
- Вопрос 5: Найдите наименьшее число, которое при делении на 5,7,9 и 12 дает один и тот же остаток 3 в каждом случае
Решение: В этих типах вопросов нам нужно найти НОК делители и прибавляем к ним общий остаток (3). Итак, НОК (5, 7, 9, 12) = 1260 Следовательно, искомое число = 1260 + 3 = 1263
- Вопрос 6: Найдите наибольшее четырехзначное число, которое точно делится на 15, 21 и 28.
разделив 9999 на 420, получим в остатке 339. Следовательно, требуемое число равно 9660
- Вопрос 7: Полицейские в трех разных местах на земле дают свисток через каждые 42 секунды, 60 секунд и 78 секунд соответственно. Если они все одновременно дадут свисток в 9:30:00 часов, то в какое время они снова свистят вместе
Решение: Все они снова свистят одновременно после интервала, равного LCM их индивидуальных циклов свистка. Итак, НЦМ (42, 60, 78) = 2 х 3 х 7 х 10 х 13 = 5460 Следовательно, они снова дадут свисток одновременно через 5460 сек, т. е. через 1 час 31 мин, т. е. в 11:01: 00 часов.
- Вопрос 8: Найдите наименьшее число, которое при делении на 6,7,8 дает в остатке 3, а при делении на 9не оставляет остатка.
Решение: НОК (6, 7, 8) = 168 Итак, число имеет вид 168m + 3. Теперь 168m + 3 должно делиться на 9. Мы знаем, что число делится на 9, если сумма число его цифр кратно 9.При m = 1 число равно 168 + 3 = 171, сумма цифр которого равна 9. Следовательно, искомое число равно 171.
- Вопрос 9: Два числа в соотношении 2:3. Если произведение их LCM и HCF равно 294, найдите числа.
Решение: Пусть обыкновенное отношение равно «m». Итак, числа 2м и 3м. Теперь мы знаем, что произведение чисел равно произведению LCM и HCF. => 2 м x 3 м = 294 => м 2 = 49 => m = 7 Следовательно, числа равны 14 и 21.
- Вопрос 10: Прямоугольное поле размерами одинаковые квадратные плитки. Найдите размер каждой плитки и необходимое количество плиток.
Решение: Нам нужно найти такой размер квадратной плитки, чтобы определенное количество плиток точно покрывало поле, не оставляя незамощенных участков. Для этого находим ВКФ длины и ширины поля. HCF (180, 105) = 15 Следовательно, размер каждой плитки = 15 м x 15 м. Кроме того, количество плиток = площадь поля / площадь каждой плитки => Количество плиток = (180 x 105) / (15 x 15) = > Количество плиток = 84 Следовательно, нам нужно 84 плитки, каждая размером 15м х 15м.
- Вопрос 11: Три прямоугольных поля площадью 60 м 2 , 84 м 2 , и 108 м 2 разделить на одинаковые прямоугольные клумбы, каждая длиной 6 м. Найдите ширину каждой клумбы.
Решение: Нам нужно разделить каждое большое поле на меньшие клумбы так, чтобы площадь каждой клумбы была одинаковой. Итак, мы находим HCF больших полей, что дает нам площадь меньшего поля. HCF (60, 84, 108) = 12 Теперь эта HCF представляет собой площадь (в м 2 ) каждой клумбы. Кроме того, площадь прямоугольного поля = длина х ширина => 12 = 6 х ширина => ширина = 2 м Следовательно, каждая клумба будет иметь ширину 2 м.
- Вопрос 12: Найдите максимальное количество учеников, среди которых можно распределить 182 шоколада и 247 конфет так, чтобы каждый ученик получил одинаковое количество каждого из них. Кроме того, найдите количество шоколадок и конфет, которые получит каждый ученик.

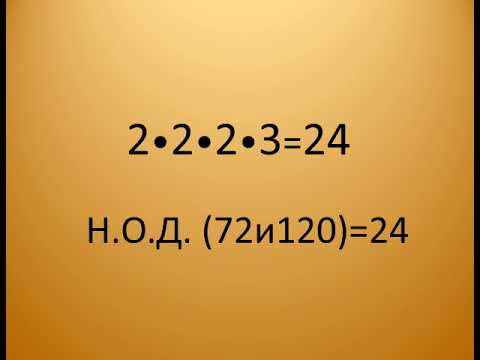

 Наибольший общий делитель (HCF) также известен как наибольший общий делитель (GCD).
Наибольший общий делитель (HCF) также известен как наибольший общий делитель (GCD). 


 Это означает, что число точно делит 69 и 46. Итак, нам нужно найти HCF 69 (3 x 23) и 46 (2 x 23). HCF (69, 46) = 23 Таким образом, 23 — искомое число.
Это означает, что число точно делит 69 и 46. Итак, нам нужно найти HCF 69 (3 x 23) и 46 (2 x 23). HCF (69, 46) = 23 Таким образом, 23 — искомое число.  разделив 9999 на 420, получим в остатке 339. Следовательно, требуемое число равно 9660
разделив 9999 на 420, получим в остатке 339. Следовательно, требуемое число равно 9660 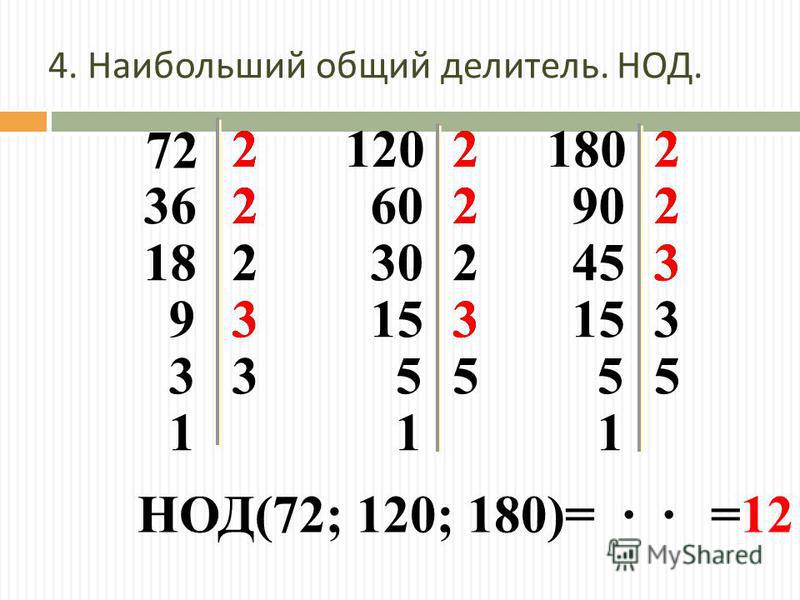 При m = 1 число равно 168 + 3 = 171, сумма цифр которого равна 9. Следовательно, искомое число равно 171.
При m = 1 число равно 168 + 3 = 171, сумма цифр которого равна 9. Следовательно, искомое число равно 171. 
