методы умножения, примеры с объяснением
Известно, что знак корня является квадратным корнем из некоторого числа. Однако знак корня означает не только алгебраическое действие, но и применяется в деревообрабатывающем производстве — в расчете относительных размеров.
Если вы хотите узнать, как умножить корни «с» или «без» множителей, то эта статья для вас. В ней мы рассмотрим методы умножения корней:
- без множителей;
- с множителями;
- с разными показателями.
Метод умножения корней без множителей
Алгоритм действий:
Убедиться, что у корня одинаковые показатели (степени). Вспомним, что степень записывается слева над знаком корня. Если нет обозначения степени, это значит, что корень квадратный, т.е. со степенью 2, и его можно умножать на другие корни со степенью 2.
ПримерПример 1: 18×2=?
Пример 2: 10×5=?
Пример 3: 33×93=?
Далее необходимо перемножить числа под корнем.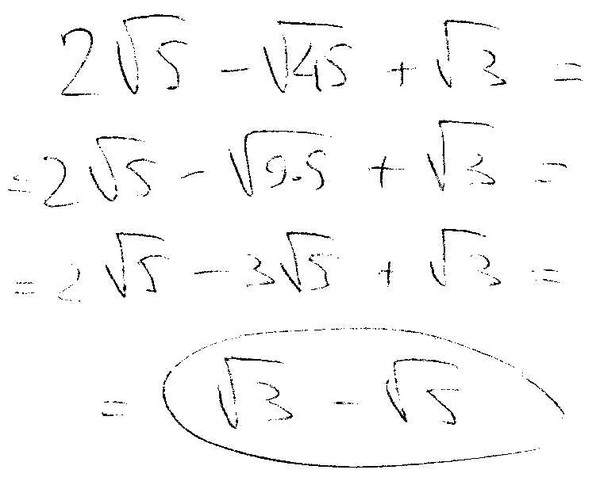
Пример 1: 18×2=36
Пример 2: 10×5=50
Пример 3: 33×93=273
Упростить подкоренные выражения. Когда мы умножаем корни друг на друга, мы можем упростить полученное подкоренное выражение до произведения числа (или выражения) на полный квадрат или куб:
ПримерПример 1: 36=6. 36 — квадратный корень из шести (6×6=36).
Пример 2: 50=(25×2)=(5×5)×2=52. Число 50 раскладываем на произведение 25 и 2. Корень из 25 — 5, поэтому выносим 5 из-под знака корня и упрощаем выражение.
Пример 3: 273=3. Кубический корень из 27 равен 3: 3×3×3=27.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать заданиеМетод умножения показателей с множителями
Алгоритм действий:
Умножить множители. Множитель — число, которое стоит перед знаком корня. В случае отсутствия множителя, он, по умолчанию, считается единицей. Далее необходимо перемножить множители:
ПримерПример 1: 32×10=3?3×1=3
Пример 2: 43×36=12?4×3=12
Умножить числа под знаком корня. Как только вы перемножили множители, смело умножайте числа, стоящие под знаком корня:
Как только вы перемножили множители, смело умножайте числа, стоящие под знаком корня:
Пример 1: 32×10=3(2×10)=320
Пример 2: 43×36=12(3×6)=1218
Упростить подкоренное выражение. Далее следует упростить значения, которые стоят под знаком корня, — требуется вынести соответствующие числа за знак корня. После этого, необходимо перемножить числа и множители, которые стоят перед знаком корня:
ПримерПример 1: 320=3(4×5)=3(2×2)×5=(3×2)5=65
Пример 2: 1218=12(9×2)=12(3×3)×2=(12×3)2=362
Метод умножения корней с разными показателями
Алгоритм действий:
Найти наименьшее общее кратное (НОК) показателей. Наименьшее общее кратное — наименьшее число, делящееся на оба показателя.
Необходимо найти НОК показателей для следующего выражения:
53×22
Показатели равны 3 и 2. Для этих двух чисел наименьшим общим кратным является число 6 (оно делится без остатка и на 3, и на 2).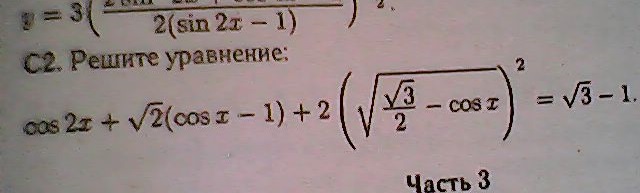 Для умножения корней необходим показатель 6.
Для умножения корней необходим показатель 6.
Записать каждое выражение с новым показателем:
56×26
Найти числа, на которые нужно умножить показатели, чтобы получить НОК.
В выражении 53 необходимо умножить 3 на 2, чтобы получить 6. А в выражении 22 — наоборот, необходимо умножить на 3, чтобы получить 6.
Возвести число, которое стоит под знаком корня, в степень равную числу, которое было найдено в предыдущем шаге. Для первого выражения 5 нужно возвести в степень 2, а втором — 2 в степень 3:
2→56=5263→26=236
Возвести в степень выражения и записать результат под знаком корня:
526=(5×5)6=256236=(2×2×2)6=86
Перемножить числа под корнем:
(8×25)6
Записать результат:
(8×25)6=2006
По возможности необходимо упростить выражение, но в данном случае оно не упрощается.
Автор: Ирина
Преподаватель математики и информатики.
3 плюс корень из 3
Вы искали 3 плюс корень из 3? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и корень из 2 плюс корень из 3, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «3 плюс корень из 3».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте.
Где можно решить любую задачу по математике, а так же 3 плюс корень из 3 Онлайн?
Решить задачу 3 плюс корень из 3 вы можете на нашем сайте https://pocketteacher.ru. Бесплатный
онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо
сделать — это просто
ввести свои данные в решателе.
Корни и степени. Квадратный корень, кубический корень.
Степенью называется выражение вида .
Здесь — основание степени, — показатель степени.
Степень с натуральным показателем
Проще всего определяется степень с натуральным (то есть целым положительным) показателем.
По определению, .
Выражения «возвести в квадрат» и «возвести в куб» нам давно знакомы.
Возвести число в квадрат — значит умножить его само на себя.
.
Возвести число в куб — значит умножить его само на себя три раза.
.
Возвести число в натуральную степень — значит умножить его само на себя раз:
Степень с целым показателем
Показатель степени может быть не только натуральным (то есть целым положительным), но и равным нулю, а также целым отрицательным.
По определению,
.
Это верно для . Выражение 00 не определено.
Определим также, что такое степень с целым отрицательным показателем.
Конечно, все это верно для , поскольку на ноль делить нельзя.
Например,
Заметим, что при возведении в минус первую степень дробь переворачивается
Показатель степени может быть не только целым, но и дробным, то есть рациональным числом. В статье «Числовые множества» мы говорили, что такое рациональные числа. Это числа, которые можно записать в виде дроби , где — целое, — натуральное.
Здесь нам понадобится новое понятие — корень -степени. Корни и степени — две взаимосвязанные темы. Начнем с уже знакомого вам арифметического квадратного корня.
Корни и степени — две взаимосвязанные темы. Начнем с уже знакомого вам арифметического квадратного корня.
Арифметический квадратный корень из числа — это такое неотрицательное число, квадрат которого равен .
Согласно определению,
В школьной математике мы извлекаем корень только из неотрицательных чисел. Выражение для нас сейчас имеет смысл только при .
Выражение всегда неотрицательно, т.е. . Например, .
Свойства арифметического квадратного корня:
Кубический корень
Аналогично, кубический корень из — это такое число, которое при возведении в третью степень дает число .
Например, , так как ;
, так как ;
, так как .
Обратите внимание, что корень третьей степени можно извлекать как из положительных, так и из отрицательных чисел.
Теперь мы можем дать определение корня -ной степени для любого целого .
Корень -ной степени
Корень -ной степени из числа — это такое число, при возведении которого в -ную степень получается число .
Например,
Заметим, что корень третьей, пятой, девятой — словом, любой нечетной степени, — можно извлекать как из положительных, так и из отрицательных чисел.
Квадратный корень, а также корень четвертой, десятой, в общем, любой четной степени можно извлекать только из неотрицательных чисел.
Итак, — такое число, что . Оказывается, корни можно записывать в виде степеней с рациональным показателем. Это удобно.
По определению,
в общем случае .
Сразу договоримся, что основание степени больше 0.
Например,
Выражение по определению равно .
При этом также выполняется условие, что больше 0.
Например,
Запомним правила действий со степенями:
— при перемножении степеней показатели складываются
— при делении степени на степень показатели вычитаются
— при возведении степени в степень показатели перемножаются
Ты нашел то, что искал? Поделись с друзьями!
Покажем, как применяются эти формулы в заданиях ЕГЭ по математике:
1.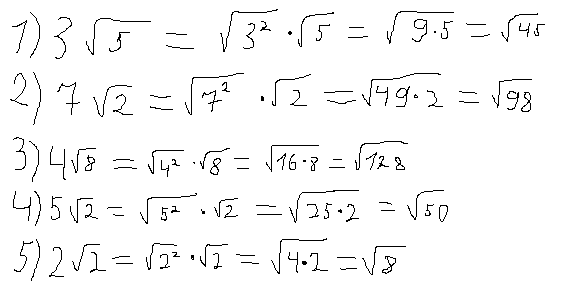 2=400\\
\hline \end{array}\]
2=400\\
\hline \end{array}\]
Факт 3.
Какие действия можно выполнять с квадратными корнями?
\(\bullet\) Сумма или разность квадратных корней НЕ РАВНА квадратному корню из суммы или разности, то есть \[\sqrt a\pm\sqrt b\ne \sqrt{a\pm b}\] Таким образом, если вам нужно вычислить, например, \(\sqrt{25}+\sqrt{49}\), то первоначально вы должны найти значения \(\sqrt{25}\) и \(\sqrt{49}\), а затем их сложить. Следовательно, \[\sqrt{25}+\sqrt{49}=5+7=12\] Если значения \(\sqrt a\) или \(\sqrt b\) при сложении \(\sqrt
a+\sqrt b\) найти не удается, то такое выражение дальше не преобразуется и остается таким, как есть. Например, в сумме \(\sqrt
2+ \sqrt {49}\) мы можем найти \(\sqrt{49}\) – это \(7\), а вот \(\sqrt
2\) никак преобразовать нельзя, поэтому \(\sqrt 2+\sqrt{49}=\sqrt
2+7\). Дальше это выражение, к сожалению, упростить никак нельзя
\(\bullet\) Произведение/частное квадратных корней равно квадратному корню из произведения/частного, то есть \[\sqrt a\cdot \sqrt b=\sqrt{ab}\quad \text{и}\quad
\sqrt a:\sqrt b=\sqrt{a:b}\] (при условии, что обе части равенств имеют смысл)
Пример: \(\sqrt{32}\cdot \sqrt 2=\sqrt{32\cdot
2}=\sqrt{64}=8\);
\(\sqrt{768}:\sqrt3=\sqrt{768:3}=\sqrt{256}=16\);
\(\sqrt{(-25)\cdot (-64)}=\sqrt{25\cdot 64}=\sqrt{25}\cdot \sqrt{64}=
5\cdot 8=40\). \(\bullet\) Пользуясь этими свойствами, удобно находить квадратные корни из больших чисел путем разложения их на множители.
\(\bullet\) Пользуясь этими свойствами, удобно находить квадратные корни из больших чисел путем разложения их на множители.
Рассмотрим пример. Найдем \(\sqrt{44100}\). Так как \(44100:100=441\), то \(44100=100\cdot 441\). По признаку делимости число \(441\) делится на \(9\) (так как сумма его цифр равна 9 и делится на 9), следовательно, \(441:9=49\), то есть \(441=9\cdot 49\).
Таким образом, мы получили: \[\sqrt{44100}=\sqrt{9\cdot 49\cdot 100}=
\sqrt9\cdot \sqrt{49}\cdot \sqrt{100}=3\cdot 7\cdot 10=210\] Рассмотрим еще один пример: \[\sqrt{\dfrac{32\cdot 294}{27}}=
\sqrt{\dfrac{16\cdot 2\cdot 3\cdot 49\cdot 2}{9\cdot 3}}= \sqrt{
\dfrac{16\cdot4\cdot49}{9}}=\dfrac{\sqrt{16}\cdot \sqrt4 \cdot
\sqrt{49}}{\sqrt9}=\dfrac{4\cdot 2\cdot 7}3=\dfrac{56}3\]
\(\bullet\) Покажем, как вносить числа под знак квадратного корня на примере выражения \(5\sqrt2\) (сокращенная запись от выражения \(5\cdot
\sqrt2\)). Так как \(5=\sqrt{25}\), то \[5\sqrt2=\sqrt{25}\cdot \sqrt2=\sqrt{25\cdot 2}=\sqrt{50}\] Заметим также, что, например,
1) \(\sqrt2+3\sqrt2=4\sqrt2\),
2) \(5\sqrt3-\sqrt3=4\sqrt3\)
3) \(\sqrt a+\sqrt a=2\sqrt a\). 2\), поэтому \(\sqrt{16}=4\). А вот извлечь корень из числа \(3\), то есть найти \(\sqrt3\), нельзя, потому что нет такого числа, которое в квадрате даст \(3\).
2\), поэтому \(\sqrt{16}=4\). А вот извлечь корень из числа \(3\), то есть найти \(\sqrt3\), нельзя, потому что нет такого числа, которое в квадрате даст \(3\).
Такие числа (или выражения с такими числами) являются иррациональными. Например, числа \(\sqrt3, \ 1+\sqrt2, \ \sqrt{15}\) и т.п. являются иррациональными.
Также иррациональными являются числа \(\pi\) (число “пи”, приблизительно равное \(3,14\)), \(e\) (это число называют числом Эйлера, приблизительно оно равно \(2,7\)) и т.д.
\(\bullet\) Обращаем ваше внимание на то, что любое число будет либо рациональным, либо иррациональным. А вместе все рациональные и все иррациональные числа образуют множество, называющееся множеством действительных (вещественных) чисел. Обозначается это множество буквой \(\mathbb{R}\).
Значит, все числа, которые на данный момент мы знаем, называются вещественными числами.
Факт 5.
\(\bullet\) Модуль вещественного числа \(a\) – это неотрицательное число \(|a|\), равное расстоянию от точки \(a\) до \(0\) на вещественной прямой. 2\\
&2>2,25 \end{aligned}\] Видим, что мы получили неверное неравенство. Следовательно, наше предположение было неверным и \(\sqrt 2-1<0,5\).
2\\
&2>2,25 \end{aligned}\] Видим, что мы получили неверное неравенство. Следовательно, наше предположение было неверным и \(\sqrt 2-1<0,5\).
Заметим, что прибавление некоторого числа к обеим частям неравенства не влияет на его знак. Умножение/деление обеих частей неравенства на положительное число также не влияет на его знак, а умножение/деление на отрицательное число меняет знак неравенства на противоположный!
Возводить обе части уравнения/неравенства в квадрат можно ТОЛЬКО ТОГДА, когда обе части неотрицательные. Например, в неравенстве из предыдущего примера возводить обе части в квадрат можно, в неравенстве \(-3<\sqrt2\) нельзя (убедитесь в этом сами)!
\(\bullet\) Следует запомнить, что \[\begin{aligned}
&\sqrt 2\approx 1,4\\[1ex]
&\sqrt 3\approx 1,7 \end{aligned}\] Знание приблизительного значения данных чисел поможет вам при сравнении чисел!
\(\bullet\) Для того, чтобы извлечь корень (если он извлекается) из какого-то большого числа, которого нет в таблице квадратов, нужно сначала определить, между какими “сотнями” оно находится, затем – между какими “десятками”, а потом уже определить последнюю цифру этого числа. 2=168\cdot 168=28224\).
2=168\cdot 168=28224\).
Следовательно, \(\sqrt{28224}=168\). Вуаля!
Квадратный корень из 3;2;5 — Квадратный Корень
Квадратный корень из числа 3 — положительное действительное число, которое при умножении само на себя даёт число 3.
Его приблизительным значением с 69 цифрами после запятой является:
Округленное значение 1.732 является правильным с точностью до 0,01 %. Приблизительной правильной дробью является (1,7321 42857…).
Квадратный корень из 3 является иррациональным числом. Также известен как Феодоровская постоянная, названная в честь Феодора Киренского.
Может быть выражен в виде непрерывной дроби [1; 1, 2, 1, 2, 1, 2, …].
Геометрия
Квадратный корень из 3 равен длине между параллельными сторонами правильного шестиугольника со сторонами 1.Если равносторонний треугольник со сторонами длиной 1 делится на две равные половины, пересечением внутреннего угла для составления прямого угла с одной стороной, то получившийся прямоугольный треугольник имеет гипотенузу со стороной 1 и катеты длиной 1/2 и Поэтому тангенс 60° равен
Так же, это расстояние между параллельными сторонами правильного шестиугольника со сторонами 1.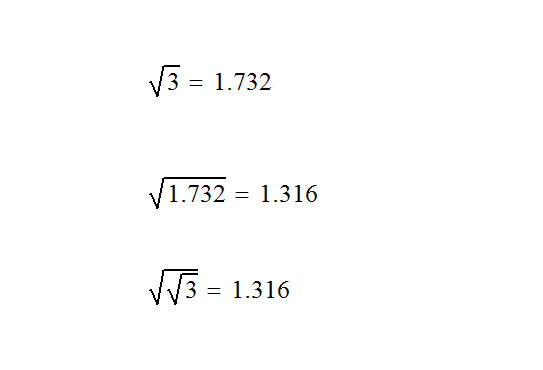
является длиной диагонали куба со стороной 1.
Использование в других областях
Энергетика
При трехфазной системе токов модуль напряжения между двумя фазами (линейное напряжение) в больше модуля фазного напряжения
Квадратный корень из числа 2 — положительное вещественное число, которое при умножении само на себя даёт число 2. Обозначение: Приведём значение корня из 2 с 65 знаками после запятой:
- 1,414 213 562 373 095 048 801 688 724 209 698 078 569 671 875 376 948 073 176 679 737 99…
Геометрически корень из 2 можно представить как длину диагонали квадрата со стороной 1 (это следует из теоремы Пифагора). Вероятно, это было первое известное в истории математики иррациональное число (то есть число, которое нельзя точно представить в виде дроби).
Квадратный корень из 2 равен длине гипотенузы в прямоугольном треугольнике с длиной катетов 1. Квадратный корень из 2.Хорошим и часто используемым приближением к является дробь .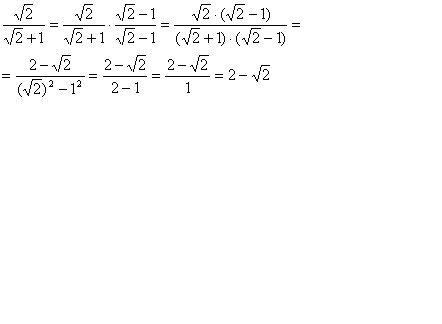 Несмотря на то, что числитель и знаменатель дроби лишь двузначные
целые, оно отличается от реального значения меньше, чем на 1/10000.
Несмотря на то, что числитель и знаменатель дроби лишь двузначные
целые, оно отличается от реального значения меньше, чем на 1/10000.
История
Вавилонская глиняная табличка с примечаниями.Вавилонская глиняная табличка (ок. 1800—1600 до н. э.) даёт приближённое значение в четырёх шестидесятеричных цифрах, что составляет 8 десятичных цифр:
Другое раннее приближение этого числа в древнеиндийском математическом тексте, Шульба-сутры (ок. 800—200 до н. э.) даётся следующим образом:
Пифагорейцы обнаружили, что диагональ квадрата несоизмерима с его стороной, или на современном языке, что квадратный корень из двух является иррациональным. Мало что известно с определённостью о времени и обстоятельствах этого выдающегося открытия, но традиционно его авторство приписывается Гиппасу из Метапонта.
Алгоритмы вычисления
Существует множество алгоритмов для вычисления значения квадратного
корня из двух. В результате алгоритма получается приблизительное
значение в виде обыкновенной или десятичной дроби. Самый популярный алгоритм для этого, который используется во многих
компьютерах и калькуляторах, это вавилонский метод вычисления квадратных
корней. Он состоит в следующем:
Самый популярный алгоритм для этого, который используется во многих
компьютерах и калькуляторах, это вавилонский метод вычисления квадратных
корней. Он состоит в следующем:
Чем больше повторений в алгоритме (то есть, чем больше «n»), тем лучше приближение квадратного корня из двух. Каждое повторение приблизительно удваивает количество правильных цифр. Приведём несколько первых приближений:
- 3/2 = 1.5
- 17/12 = 1.416…
- 577/408 = 1.414215…
- 665857/470832 = 1.4142135623746…
В 1997 году Ясумаса Канада вычислил значение √2 до 137,438,953,444 десятичных знаков после запятой. В феврале 2007 года рекорд был побит: Сигэру Кондо вычислил 200 миллиардов десятичных знаков после запятой в течение 13 дней и 14 часов, используя процессор 3.6 GHz с 16 ГБ ОЗУ. Среди математических констант только было вычислено более точно.
Свойства квадратного корня из двух
Половина √2 приблизительно равна 0. 70710 67811 86548; эта величина даёт в геометрии и тригонометрии координаты единичного вектора, образующего угол 45° с координатными осями:
70710 67811 86548; эта величина даёт в геометрии и тригонометрии координаты единичного вектора, образующего угол 45° с координатными осями:
Одно из интересных свойств √2 состоит в следующем:
- .Потому что
Это является результатом свойства серебряного сечения.
Другое интересное свойство √2:
Квадратный корень из двух может быть выражен в мнимых единицах i используя только квадратные корни и арифметические операции:
- и
Квадратный корень из 2 является единственным числом, отличным от 1, чья бесконечная тетрация равна его квадрату.
Квадратный корень из двух может быть также использован для приближения :
С точки зрения высшей алгебры, является корнем многочлена и поэтому является целым алгебраическим числом. Множество чисел вида , где — рациональные числа, образует алгебраическое поле. Оно обозначается и является подполем поля вещественных чисел.
Доказательство иррациональности
Применим доказательство от противного: допустим, рационален, то есть представляется в виде несократимой дроби , где и — целые числа. Возведём предполагаемое равенство в квадрат:
- .
Отсюда следует, что чётно, значит, чётно и . Пусть , где целое. Тогда
Следовательно, чётно, значит, чётно и . Мы получили, что и чётны, что противоречит несократимости дроби . Значит, исходное предположение было неверным, и — иррациональное число.
Непрерывная дробь
Квадратный корень из двух может быть представлен в виде непрерывной дроби:
Подходящие дроби данной непрерывной дроби дают приближённые значения, быстро сходящиеся к точному квадратному корню из двух. Способ их вычисления прост: если обозначить предыдущую подходящую дробь , то последующая имеет вид . Скорость сходимости здесь меньше, чем у метода Ньютона, но вычисления гораздо проще. Выпишем несколько первых приближений:
Квадрат последней приведенной дроби равен (округлённо) 2,000000177.
Размер бумаги
Квадратный корень из двух является пропорцией формата бумаги ISO 216. Соотношение сторон таково, что при разрезании листа пополам параллельно его короткой стороне получатся два листа той же пропорции.
Квадратный корень из числа 5 — положительное действительное число, которое при умножении само на себя даёт число 5. Это иррациональное и алгебраическое число.[1]
Его приблизительное значение с 59 цифрами после запятой является:
Округлённое значение 2.236 является правильным с точностью до 0,01 %. Компьютерная вычисленная точность составляет не менее 1 000 000 знаков.[2]
Может быть выражено в виде непрерывной дроби [2; 4, 4, 4, 4, 4, 4, …], последовательно это дроби:
Вавилонский метод
Вычисление корня из 5, начиная с r0 = 2, где rn+1 = (rn + 5/rn) / 2:
Золотое сечение
√5/2 — диагональ половины квадрата, представляет собой геометрическое представление о золотом сечении.
Золотое сечение φ — среднее арифметическое 1 и корня из 5.[3]
() алгебраически можно выразить так:
Числа Фибоначчи могут быть выражены через корень из 5 так:
Отношение √5 к φ и наоборот дают интересные зависимости непрерывных дробей с числами Фибоначчи и числами Люка:[4]
Алгебра
Кольцо содержит числа вида , где a и b целые числа и мнимое число . Это кольцо является примером области целостности, не являющейся факториальным кольцом.
Число 6 представляется в данном кольце двумя способами:
Поле — абелево расширение рациональных чисел.
Теорема Кронекера — Вебера утверждает, что корень из 5 можно выразить линейной комбинацией корней из единицы:
Тождества Рамануджана
Корень из 5 появляется во множестве тождеств Рамануджана с непрерывными дробями. [5][6]
[5][6]
Например, случай непрерывных дробей Роджерса-Рамануджана:
Найти модуль с корнем
☰
Как известно, модуль числа — это его абсолютное значение, без учета знака. Модуль всегда неотрицателен. Это значит, что он может быть равен либо положительному числу, либо нулю.
Таким образом, если дается положительное число или ноль, то их модуль будет равен им самим. А вот для отрицательного числа, его модуль будет иметь противоположное значение, т. е. являться противоположным числом. Так
|–3| = 3,
|–1,345| = 1,345.
Если представить числовую прямую (координатную прямую), то можно сказать, что на том расстоянии, на котором от нуля находится отрицательное число в одну сторону, на том же расстоянии от нуля находится его модуль, но в другую сторону.
Однако как найти модуль числового выражения, если его вычислить проблематично. Например, в выражениях с корнями когда получаются иррациональные числа. Пусть требуется найти модуль √2 – 2. Понятно, что здесь получится отрицательное число, т. к. 2 определенно больше √2. Следовательно, модулем этого выражения будет противоположное число. Но каково оно?
Например, в выражениях с корнями когда получаются иррациональные числа. Пусть требуется найти модуль √2 – 2. Понятно, что здесь получится отрицательное число, т. к. 2 определенно больше √2. Следовательно, модулем этого выражения будет противоположное число. Но каково оно?
Чтобы получить противоположное число, надо умножить его на –1. Обычно просто приписывают к нему знак минуса. Если число отрицательное, то минус на минус дает плюс, и в результате получается положительное. Например, для –5 противоположное –(–5) = 5. Поэтому, когда берется модуль отрицательного числа, то можно не просто писать |–1,2| = |1,2|, а расписывать действие подробно:
|–1,2| = –(–1,2) = 1,2
Сделаем то же самое по отношению к выражению √2 – 2, коли мы уже знаем, что это отрицательное число:
|√2 – 2| = –(√2 – 2) = –√2 + 2 = 2 – √2
Таким образом, при вычислении модуля выражения с корнем следует придерживаться следующего алгоритма:
- Определить, является ли число положительным или отрицательным.

- Если число положительное или 0, то его модуль будет равен ему самому.
- Если число отрицательное, то умножить его на –1, после чего преобразовать выражение к удобному виду.
Теперь обратим внимание на следующее. Выше было сказано, что модуль отрицательного числа отстоит от точки отсчета (нуля) на таком же расстоянии (но в другую сторону), как и само это число. Однако в примере с корнем мы видим, что само выражение и его модуль не выглядят такими уж идентичными по абсолютному значению. Трудно сказать, действительно ли √2 – 2 отстоит от нуля на таком же расстоянии как 2 – √2.
Однако это так. Если записать отрицательное число с корнем как –2 + √2, то понятно, что мы получаем число, которое больше –2, т. е. находится от –2 ближе к нулю на √2. Модуль же числа равен 2 – √2. Это число, которое меньше 2 на √2. То есть тоже находится от 2 ближе к нулю на √2.
Пределы с иррациональностями. Примеры раскрытия неопределённостей.
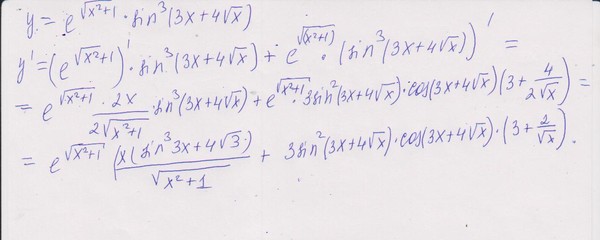 3-8}=\frac{5}{384}$.
3-8}=\frac{5}{384}$.Пример №6
Найти $\lim_{x\to 2}\frac{\sqrt[5]{3x-5}-1}{\sqrt[3]{3x-5}-1}$.
Решение
Так как $\lim_{x\to 2}(\sqrt[5]{3x-5}-1)=0$ и $\lim_{x\to 2}(\sqrt[3]{3x-5}-1)=0$, то мы имеем дело с неопределенностью $\frac{0}{0}$. В таких ситуациях, когда выражения под корнями одинаковы, можно использовать способ замены. Требуется заменить выражение под корнем (т.е. $3x-5$), введя некоторую новую переменную. Однако простое использование новой буквы ничего не даст. Представьте, что мы просто заменили выражение $3x-5$ буквой $t$. Тогда дробь, стоящая под пределом, станет такой: $\frac{\sqrt[5]{t}-1}{\sqrt[3]{t}-1}$. Иррациональность никуда не исчезла, – лишь несколько видоизменилась, что нисколько не облегчило задачу.
Здесь уместно вспомнить, что корень может убрать лишь степень. Но какую именно степень использовать? Вопрос не тривиален, ведь у нас два корня. Один корень пятого, а другой – третьего порядка. Степень должна быть такой, чтобы одновременно убрать оба корня! Нам нужно натуральное число, которое одновременно делилось бы на $3$ и на $5$. 2+1+1}=\frac{3}{5}.
$$
2+1+1}=\frac{3}{5}.
$$
Ответ: $\lim_{x\to 2}\frac{\sqrt[5]{3x-5}-1}{\sqrt[3]{3x-5}-1}=\frac{3}{5}$.
Сложение и вычитание радикалов (квадратные корни)
Purplemath
Так же, как и «обычные» числа, квадратные корни можно складывать. Но возможно, вам не удастся упростить сложение до одного числа. Как «нельзя добавлять яблоки и апельсины», так и нельзя комбинировать «непохожие» радикальные термины. Чтобы можно было объединить радикальные термины вместе, эти термины должны иметь одну и ту же радикальную часть.
Упростить:
Поскольку радикал в каждом члене один и тот же (является квадратным корнем из трех), то это «одинаковые» термины. Это означает, что я могу комбинировать термины.
Это означает, что я могу комбинировать термины.
MathHelp.com
У меня два радикала копии, добавлены еще три копии. Всего получается пять копий:
Этот средний шаг в круглых скобках показывает рассуждение, которое оправдывает окончательный ответ.Возможно, вам никогда не понадобится «показывать» этот шаг, но это то, о чем вы должны думать.
Упростить:
Коренная часть одинакова во всех терминах, поэтому я могу добавить это дополнение.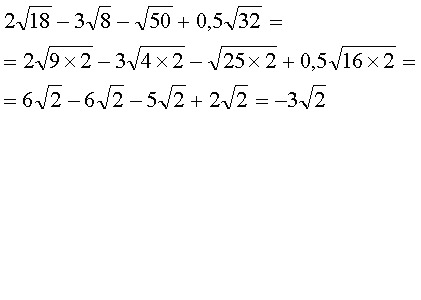 Чтобы помочь мне понять, что первый термин означает «одну копию квадратного корня из трех», я вставлю «понял» «1»:
Чтобы помочь мне понять, что первый термин означает «одну копию квадратного корня из трех», я вставлю «понял» «1»:
Не думайте, что выражения с непохожими радикалами нельзя упростить.Возможно, что после упрощения радикалов выражение действительно может быть упрощено.
Упростить:
Чтобы упростить радикальное сложение, я должен сначала посмотреть, могу ли я упростить каждый радикальный термин. В данном конкретном случае квадратные корни упрощаются «полностью» (то есть до целых чисел):
Упростить:
У меня есть три копии радикала плюс еще две копии, что дает мне… Погодите! Я могу упростить эти радикалы до целых чисел:
Не волнуйтесь, если вы не сразу увидите упрощение. Если бы я не заметил до конца, что радикальное упрощение, мои шаги были бы другими, но мой окончательный ответ был бы таким же:
Если бы я не заметил до конца, что радикальное упрощение, мои шаги были бы другими, но мой окончательный ответ был бы таким же:
Упростить:
Могу объединить только радикалы «лайки». Первый и последний члены содержат квадратный корень из трех, поэтому их можно комбинировать; средний член содержит квадратный корень из пяти, поэтому его нельзя комбинировать с другими.Итак, в этом случае я получу два термина в своем ответе.
Я начну с перестановки терминов, чтобы соединить «похожие» термины вместе, и вставив «понятый» 1 во второй член квадратного корня из трех:
Насколько мне известно, нет предпочтительного упорядочивания терминов в такого рода выражениях, поэтому выражение
также должно быть приемлемым ответом.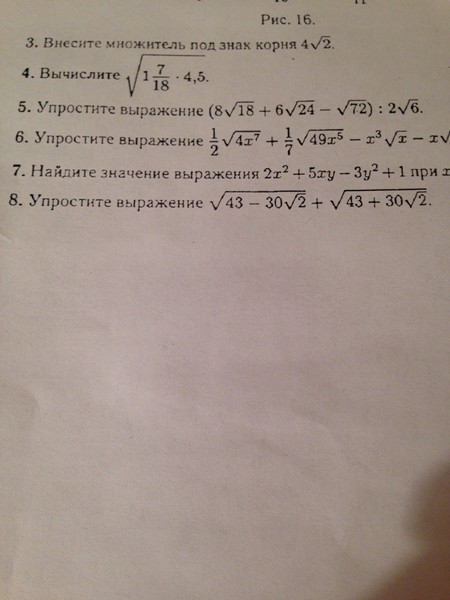
Упростить:
Насколько мне известно, это «непохожие» термины, и я не могу их объединить.Но восьмерка в радикале первого члена множится как 2 × 2 × 2. Это означает, что я могу вытащить 2 из радикала. В этот момент у меня будут термины «нравится», которые я могу комбинировать.
Упростить:
Я могу упростить большинство радикалов, и это позволит хотя бы немного упростить:
Упростить:
В этих двух терминах есть «непохожие» радикальные части, и я не могу извлечь ничего из любого из радикалов.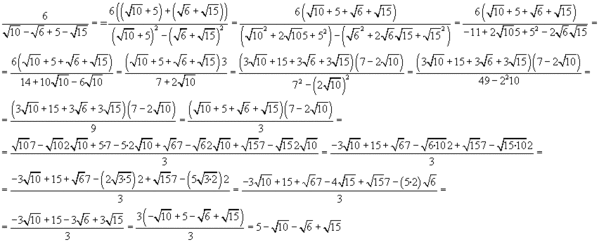 Тогда я не могу дальше упрощать выражение
Тогда я не могу дальше упрощать выражение
(выражение уже полностью упрощено)
Развернуть:
Чтобы расширить это выражение (то есть умножить его, а затем упростить), мне сначала нужно извлечь квадратный корень из двух через круглые скобки:
Как видите, упрощение включало превращение продукта радикалов в один радикал, содержащий значение продукта (2 × 3 = 6).Вы должны ожидать, что вам придется манипулировать радикальными продуктами в обоих «направлениях».
Развернуть:
Как и в предыдущем примере, мне нужно умножить через круглые скобки.
Развернуть:
Наверное, проще будет это умножение «по вертикали».
Упрощение дает мне:
Выполняя вертикальное умножение, я мог лучше отслеживать свои шаги. Вы должны использовать тот метод умножения, который вам больше подходит. Но знайте, что вертикальное умножение — это не временная уловка для начинающих студентов; Я до сих пор использую эту технику, потому что обнаружил, что при этом я постоянно быстрее и точнее.
Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в нахождении радикалов. Попробуйте выполнить указанное упражнение или введите свое собственное. Затем нажмите кнопку, чтобы сравнить свой ответ с ответом Mathway.
Затем нажмите кнопку, чтобы сравнить свой ответ с ответом Mathway.
(Нажмите «Нажмите, чтобы просмотреть шаги», чтобы перейти непосредственно на сайт Mathway для платного обновления.)
URL: https: // www.purplemath.com/modules/radicals3.htm
Калькулятор квадратного корня. Найдите квадратный корень за один простой шаг.
Наш калькулятор квадратного корня вычисляет квадратный корень любого положительного числа, которое вы хотите. Просто введите выбранный номер и ознакомьтесь с результатами. Все рассчитывается быстро и автоматически ! С помощью этого инструмента вы также можете оценить квадрат желаемого числа (просто введите значение во второе поле), что может оказаться большим подспорьем в поиске точных квадратов по формуле квадратного корня. Вы боретесь с основными арифметическими операциями: сложение квадратных корней, вычитание квадратных корней, умножение квадратных корней или деление квадратных корней? Уже нет! В следующем тексте вы найдете подробное объяснение о различных свойствах квадратного корня, например, как упростить квадратный корень, с множеством различных примеров . Из этой статьи вы раз и навсегда узнаете, как находить квадратные корни!
Вы боретесь с основными арифметическими операциями: сложение квадратных корней, вычитание квадратных корней, умножение квадратных корней или деление квадратных корней? Уже нет! В следующем тексте вы найдете подробное объяснение о различных свойствах квадратного корня, например, как упростить квадратный корень, с множеством различных примеров . Из этой статьи вы раз и навсегда узнаете, как находить квадратные корни!
Вы когда-нибудь задумывались, каково происхождение символа квадратного корня √? Уверяем вас, что эта история не так проста, как вы могли подумать вначале.Происхождение символа корня восходит к древним временам, как происхождение знака процента.
Если вам нужен график квадратного корня или свойства функции квадратного корня, перейдите непосредственно в соответствующий раздел (просто нажмите на ссылки выше!). Здесь мы объясняем, что такое производная квадратного корня, используя определение фундаментального квадратного корня; мы также подробно рассмотрим, как вычислять квадратные корни из экспонент или квадратные корни из дробей. Наконец, если вы будете достаточно настойчивы, вы обнаружите, что квадратный корень из отрицательного числа на самом деле возможен.Таким образом, мы вводим комплексных чисел , которые находят широкое применение в физике и математике.
Наконец, если вы будете достаточно настойчивы, вы обнаружите, что квадратный корень из отрицательного числа на самом деле возможен.Таким образом, мы вводим комплексных чисел , которые находят широкое применение в физике и математике.
Символ квадратного корня √
Операция извлечения квадратного корня из числа была известна еще в древности. Самая ранняя глиняная табличка с правильным значением √2 = 1,41421 до 5 знаков после запятой происходит из Вавилонии (1800 г. до н.э. — 1600 г. до н.э.) . Многие другие документы показывают, что квадратные корни также использовали древние египтяне, индийцы, греки и китайцы. Однако происхождение корневого символа √ все еще остается в значительной степени спекулятивным.
- Многие ученые считают, что квадратные корни происходят от буквы «r» — первой буквы латинского слова Radix, означающего корень,
- другая теория утверждает, что символ квадратного корня был взят из арабской буквы ج , которая была помещена в исходной форме ﺟ в слове جذر — корень (арабский язык пишется справа налево).

Первое использование символа квадратного корня √ не включало горизонтальную «черту» над числами внутри символа квадратного корня (или радикала), √‾.«Бар» на латыни известен как vinculum, что означает облигация . Хотя радикальный символ с винкулумом сейчас используется в повседневной жизни, мы обычно опускаем эту черту во многих текстах, например, в статьях в Интернете. Обозначение высших степеней корня было предложено Альбертом Жираром, который поместил указатель степени в начало знака корня, например, ³√ или ⁴√.
Последний вопрос: почему операция извлечения квадратного корня называется корнем независимо от ее истинного происхождения? Объяснение станет более очевидным, если мы запишем уравнение x = ⁿ√a в другой форме: xⁿ = a.x называется корнем или радикалом, потому что это скрытое основание a. Таким образом, слово радикальный не означает далеко идущий или крайний , а вместо этого фундаментальный, достигающий первопричины .
Определение квадратного корня
В математике традиционными операциями с числами являются сложение, вычитание, умножение и деление. Тем не менее, мы иногда добавляем в этот список некоторые более сложные операции и манипуляции: квадратных корней , возведение в степень, логарифмические функции и даже тригонометрические функции (например,г., синус и косинус). В этой статье мы сосредоточимся только на определении квадратного корня.
Квадратный корень из заданного числа x представляет собой каждое число y , квадрат которого y² = y * y дает исходное число x . Следовательно, формула квадратного корня может быть выражена как:
√x = y ⟺ x = y² ,
, где ⟺ — математический символ, который означает тогда и только тогда, когда . Каждое положительное действительное число всегда имеет два квадратных корня — первый положительный, а второй отрицательный. (0,5)
(0,5)
В геометрической интерпретации квадратный корень из данной площади квадрата дает длину его стороны. Вот почему в названии √ есть слово , квадрат . Аналогичная ситуация и с кубическим корнем ∛ . Если вы берете кубический корень из объема куба, вы получаете длину его ребер. В то время как квадратные корни используются при рассмотрении площади поверхности, кубические корни полезны для определения величин, относящихся к объему, например плотности.
Как найти квадратный корень?
Может быть, мы не очень скромны, но мы думаем, что лучший ответ на вопрос, как найти квадратный корень, прост: используйте калькулятор квадратного корня! Вы можете использовать его как на компьютере, так и на смартфоне, чтобы быстро вычислить квадратный корень из заданного числа.К сожалению, бывают ситуации, когда можно рассчитывать только на себя, что тогда? Чтобы подготовиться к этому, вы должны запомнить несколько основных идеальных квадратных корней:
- квадратный корень из 1:
√1 = 1, так как1 * 1 = 1; - квадратный корень из 4:
√4 = 2, так как2 * 2 = 4; - квадратный корень из 9:
√9 = 3, так как3 * 3 = 9; - квадратный корень из 16:
√16 = 4, так как4 * 4 = 16; - квадратный корень из 25:
√25 = 5, так как5 * 5 = 25; - квадратный корень из 36:
√36 = 6, так как6 * 6 = 36; - квадратный корень из 49:
√49 = 7, так как7 * 7 = 49; - квадратный корень из 64:
√64 = 8, так как8 * 8 = 64; - квадратный корень из 81:
√81 = 9, так как9 * 9 = 81; - квадратный корень из 100:
√100 = 10, так как10 * 10 = 100; - квадратный корень из 121:
√121 = 11, так как11 * 11 = 121; - квадратный корень из 144:
√144 = 12, так как12 * 12 = 144;
Приведенные выше числа являются простейшими квадратными корнями, потому что каждый раз вы получаете целое число.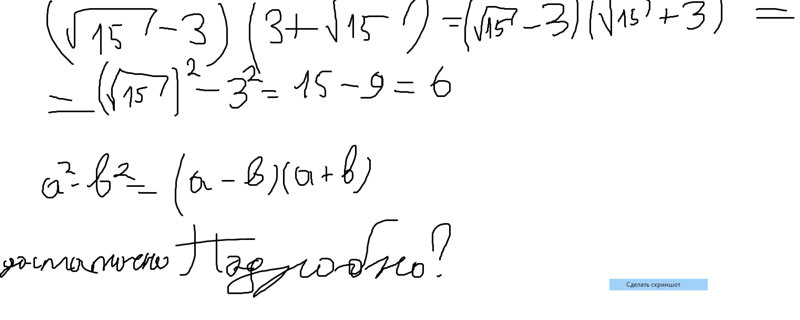 Попробуй их запомнить! Но что делать, если есть число, у которого нет такого красивого квадратного корня? Есть несколько решений. Прежде всего, вы можете попробовать спрогнозировать результат методом проб и ошибок . Допустим, вы хотите вычислить квадратный корень из
Попробуй их запомнить! Но что делать, если есть число, у которого нет такого красивого квадратного корня? Есть несколько решений. Прежде всего, вы можете попробовать спрогнозировать результат методом проб и ошибок . Допустим, вы хотите вычислить квадратный корень из 52 :
- Вы знаете, что
√49 = 7и√64 = 8, поэтому√52должно быть между7и8. - Число
52ближе к49(фактически ближе к7), поэтому вы можете попробовать угадать, что√52— это7.3. - Затем возводите в квадрат
7,3, получая7,3² = 53,29(как говорит формула квадратного корня), что больше, чем52. Вы должны попробовать с меньшим числом, скажем,7.2. - Квадрат
7,2равен51,84. Теперь у вас меньшее число, но оно намного ближе к52. Если эта точность вас устраивает, можете закончить оценку здесь. В противном случае вы можете повторить процедуру с выбранным числом от
Если эта точность вас устраивает, можете закончить оценку здесь. В противном случае вы можете повторить процедуру с выбранным числом от 7.2и7,3, например,7,22и так далее и так далее.
Другой подход состоит в том, чтобы сначала упростить квадратный корень, а затем использовать приближения квадратных корней простых чисел (обычно с округлением до двух знаков после запятой):
- квадратный корень из 2:
√2 ≈ 1,41, - квадратный корень из 3:
√3 ≈ 1,73, - квадратный корень из 5:
√5 ≈ 2,24, - квадратный корень из 7:
√7 ≈ 2.65, - квадратный корень из 11:
√11 ≈ 3,32, - квадратный корень из 13:
√13 ≈ 3,61, - квадратный корень из 17:
√17 ≈ 4,12, - квадратный корень из 19:
√19 ≈ 4,34и т. Д.
Давайте попробуем снова найти квадратный корень из 52 . Вы можете упростить его до
Вы можете упростить его до √52 = 2√13 (вы узнаете, как упростить квадратный корень в следующем разделе), а затем замените √13 ≈ 3,61 . Наконец, произведем умножение √52 ≈ 2 * 3.61 = 7,22 . Результат такой же, как и раньше!
Вы можете проверить, является ли число простым или нет, с помощью нашего калькулятора простых чисел. Простое число — это натуральное число (больше единицы), которое не может быть получено как произведение двух меньших натуральных чисел. Например, 7 — простое число, потому что вы можете получить его, только умножив 1 * 7 или 7 * 1 . С другой стороны, число 8 не является простым, потому что вы можете сформировать его, умножив 2 * 4 или 4 * 2 (помимо произведения 1 и самого 8).
Калькулятор квадратного корня
В некоторых случаях вам не нужно знать точный результат вычисления квадратного корня. В этом случае наш калькулятор квадратного корня — лучший вариант для оценки значения каждого квадратного корня, который вы хотите . Например, предположим, вы хотите узнать, больше ли
Например, предположим, вы хотите узнать, больше ли 4√5 , чем 9 . Из калькулятора вы знаете, что √5 ≈ 2,23607 , поэтому 4√5 ≈ 4 * 2,23607 = 8,94428 . Он очень близок к 9 , но не больше его! Калькулятор квадратного корня дает окончательное значение с относительно высокой точностью (до пяти цифр в приведенном выше примере).С помощью калькулятора значащих цифр вы можете вычислить этот результат до любого количества значащих цифр.
Помните, что наш калькулятор автоматически пересчитывает числа, введенные в любое из полей. Вы можете найти квадратный корень из определенного числа, заполнив первое окно, или получить квадрат числа, введенного вами во втором окне. Второй вариант удобен в для нахождения точных квадратов , которые необходимы во многих аспектах математики и естественных наук.Например, если вы введете 17 во второе поле, вы обнаружите, что 289 — это полный квадрат.
В некоторых приложениях извлечения квадратного корня, особенно относящихся к таким наукам, как химия и физика, предпочтение отдается результатам в научной нотации. Короче говоря, ответ в научном представлении должен иметь десятичную точку между первыми двумя ненулевыми числами и будет представлен как десятичная дробь, умноженная на 10, возведенная в степень. Например, число 0.00345 записывается как 3,45 * 10⁻³ в экспоненциальном представлении, тогда как 145,67 записывается как 1,4567 * 10² в экспоненциальном представлении. Результаты, полученные с помощью калькулятора квадратного корня, можно преобразовать в научную нотацию с помощью калькулятора экспоненциальной записи.
Как упростить извлечение квадратного корня?
Во-первых, давайте спросим себя, какие квадратные корни можно упростить. Чтобы ответить на него, вам нужно взять число, стоящее после символа квадратного корня, и найти его множители.Если какой-либо из его множителей является квадратным числом (4, 9, 16, 25, 36, 49, 64 и т. Д.), То вы можете упростить квадратный корень. Почему эти числа квадратные? Они могут быть соответственно выражены как 2², 3², 4², 5², 6², 7² и так далее. Согласно определению квадратного корня, вы можете назвать их полными квадратами . У нас есть специальный инструмент, называемый калькулятором коэффициентов, который может быть здесь очень кстати. Давайте посмотрим на несколько примеров:
Д.), То вы можете упростить квадратный корень. Почему эти числа квадратные? Они могут быть соответственно выражены как 2², 3², 4², 5², 6², 7² и так далее. Согласно определению квадратного корня, вы можете назвать их полными квадратами . У нас есть специальный инструмент, называемый калькулятором коэффициентов, который может быть здесь очень кстати. Давайте посмотрим на несколько примеров:
- Можете ли вы упростить √27? С помощью упомянутого выше калькулятора вы получаете множители 27: 1, 3, 9, 27.(1/2) ⟺ √ (x * y) = √x * √y ,
Как вы можете использовать эти знания? Аргумент квадратного корня обычно не является точным квадратом, который можно легко вычислить, но он может содержать точный квадрат среди своих множителей. Другими словами, вы можете записать это как умножение двух чисел, где одно из чисел представляет собой полный квадрат, например,
45 = 9 * 5(9 — это полный квадрат). Требование наличия по крайней мере одного множителя , который представляет собой полный квадрат, необходимо для упрощения квадратного корня. (1/2) = √9 * √5 = 3√5 .
(1/2) = √9 * √5 = 3√5 .Вы успешно упростили свой первый квадратный корень! Конечно, вам не нужно записывать все эти расчеты. Если вы помните, что квадратный корень равен степени половины , вы можете сократить их. Попрактикуемся в упрощении квадратных корней на некоторых других примерах:
- Как упростить квадратный корень из 27?
√27 = √ (9 * 3) = √9 * √3 = 3√3; - Как упростить квадратный корень из 8?
√8 = √ (4 * 2) = √4 * √2 = 2√2; - Как упростить квадратный корень из 144?
√144 = √ (4 * 36) = √4 * √36 = 2 * 6 = 12.
В последнем примере вам вообще не нужно было упрощать квадратный корень, потому что 144 — это полный квадрат. Вы можете просто вспомнить, что 12 * 12 = 144. Однако мы хотели показать вам, что с помощью процесса упрощения вы также можете легко вычислить квадратные корни из полных квадратов. Это полезно, когда имеет дело с большими числами .

Наконец, вы можете спросить, как упростить корни более высокого порядка, например, кубические корни. Фактически, этот процесс очень похож на квадратные корни, но в случае кубических корней вы должны найти хотя бы один множитель, который является идеальным кубом , а не полным квадратом, т.е.е., 8 = 2³, 27 = 3³, 64 = 4³, 125 = 5³ и так далее. Затем вы делите свое число на две части и кладете под кубический корень. Возьмем следующий пример упрощения ³√192:
∛192 = ∛ (64 * 3) = ∛64 * ∛3 = 4∛3На первый взгляд это может показаться немного сложным, но после некоторой практики вы сможете упростить корни в своей голове . Доверься нам!
Сложение, вычитание, умножение и деление квадратных корней
Сложение квадратных корней и вычитание квадратных корней
К сожалению, сложение или вычитание квадратных корней не так просто, как сложение / вычитание обычных чисел.
 Например, если 2 + 3 = 5, это не означает, что √2 + √3 равно √5. Это неправильно! Чтобы понять, почему это так, представьте, что у вас есть два разных типа фигур: треугольники 🔺 и круги 🔵. Что произойдет, если вы добавите один треугольник к одному кругу 🔺 + 🔵? Ничего такого! У вас остались один треугольник и один круг 🔺 + 🔵. С другой стороны, что происходит, когда вы пытаетесь добавить три треугольника к пяти треугольникам: 3 🔺 + 5 🔺? У нас получится восемь треугольников 8 🔺.
Например, если 2 + 3 = 5, это не означает, что √2 + √3 равно √5. Это неправильно! Чтобы понять, почему это так, представьте, что у вас есть два разных типа фигур: треугольники 🔺 и круги 🔵. Что произойдет, если вы добавите один треугольник к одному кругу 🔺 + 🔵? Ничего такого! У вас остались один треугольник и один круг 🔺 + 🔵. С другой стороны, что происходит, когда вы пытаетесь добавить три треугольника к пяти треугольникам: 3 🔺 + 5 🔺? У нас получится восемь треугольников 8 🔺.Сложение квадратного корня очень похоже на это.Результат сложения √2 + √3 по-прежнему равен √2 + √3. Вы не можете упростить это дальше. Однако это другая ситуация, когда оба квадратных корня имеют одинаковое число под символом корня . Затем мы можем складывать их как обычные числа (или треугольники). Например, 3√2 + 5√2 равно 8√2. То же самое и с вычитанием квадратных корней. Давайте посмотрим на другие примеры, иллюстрирующие это свойство квадратного корня:
- Что такое
6√17 + 5√17? Ответ:6√17 + 5√17 = 11√17; - Что такое
4√7 - 7√7? Ответ:4√7 - 7√7 = -3√7; - Что такое
2√2 + 3√8? Ответ:2√2 + 3√8 = 2√2 + 6√2 = 8√2, потому что мы упростили √8 = √ (4 * 2) = √4 * √2 = 2√2; - Что такое
√45 - √20? Ответ:√45 - √20 = 3√5 - 2√5 = √5, потому что мы упростили √45 = √ (9 * 5) = √9 * √5 = 3√5 и √20 = √ (4 * 5) = √4 * √5 = 2√5; - Что такое
7√13 + 2√22? Ответ:7√13 + 2√22, мы не можем упростить это дальше; - Что такое
√3 - √18? Ответ:√3 - √18 = √3 - 3√2, мы не можем упростить это дальше, чем это, но мы, по крайней мере, упростили √18 = √ (9 * 2) = √9 * √2 = 3√ 2. (1/2) ⟺ √x * √y = √ (x * y) .
(1/2) ⟺ √x * √y = √ (x * y) .В отличие от сложения, вы можете умножить на каждые два квадратных корня. Помните, что умножение имеет коммутативные свойства , это означает, что порядок, в котором умножаются два числа, не имеет значения. Несколько примеров должны прояснить этот вопрос:
- Что такое
√3 * √2? Ответ:√3 * √2 = √6; - Что такое
2√5 * 5√3? Ответ:2√5 * 5√3 = 2 * 5 * √5 * √3 = 10√15, потому что умножение коммутативно; - Что такое
2√6 * 3√3? Ответ:2√6 * 3√3 = 2 * 3 * √6 * √3 = 6√18 = 18√3, мы упростили √18 = √ (9 * 2) = √9 * √2 = 3√ 2.(1/2) ⟺ √x / √y = √ (x / y) .Все, что вам нужно сделать, это заменить знак умножения на деление. Однако деление не является коммутативным оператором ! Вы должны отдельно вычислять числа перед квадратными корнями и числа под квадратными корнями.
 (1/2) .(1/2) ⟺ √x / √y = √ (x / y) ,
(1/2) .(1/2) ⟺ √x / √y = √ (x / y) ,, где
x / y— дробная часть. Ниже вы можете найти несколько примеров квадратных корней из дроби:- квадратный корень из 4/9:
√ (4/9) = √4 / √9 = 2/3, - квадратный корень из 1/100:
√ (1/100) = √1 / √100 = 1/10, - квадратный корень из 1/5:
√ (1/5) = √1 / √5 = 1 / √5 = √5 / 5.
Оставлять корни в знаменателе — не очень хорошая привычка. Вот почему мы избавились от него в последнем примере.Мы просто умножили числитель и знаменатель на одно и то же число (мы всегда можем это сделать, так как число, которое мы умножаем на 1), в данном случае на
√5.Функция квадратного корня и график
Функции играют жизненно важную роль не только в математике, но и во многих других областях, таких как физика, статистика или финансы. Функция
f (x)— это не что иное, как формула, которая говорит, как значениеf (x)изменяется с аргументомx. Чтобы увидеть некоторые примеры, ознакомьтесь с нашими финансовыми инструментами, созданными финансовыми специалистами, например, калькулятор сложных процентов или калькулятор будущей стоимости.Там вы найдете несколько функций, которые можно применить в реальной жизни. Они очень полезны, если вы хотите знать, как рассчитать сложные проценты или оценить будущую стоимость аннуитета.
Чтобы увидеть некоторые примеры, ознакомьтесь с нашими финансовыми инструментами, созданными финансовыми специалистами, например, калькулятор сложных процентов или калькулятор будущей стоимости.Там вы найдете несколько функций, которые можно применить в реальной жизни. Они очень полезны, если вы хотите знать, как рассчитать сложные проценты или оценить будущую стоимость аннуитета.Ниже вы можете найти график квадратного корня, состоящий из половины параболы . Проверьте его и попробуйте проверить, например, является ли функция квадратного корня
x = 93иx = 164(как и должно быть).Давайте вернемся к функции квадратного корня
f (x) = √xи исследуем ее основные свойства .Мы рассматриваем только положительную частьf (x)(как вы можете видеть на графике квадратного корня выше). Итак, функция квадратного корня:- — непрерывный и растущий для всех неотрицательных
x, - является дифференцируемым для всех положительных
x(см. Производную квадратного корня для получения дополнительной информации),
Производную квадратного корня для получения дополнительной информации), - приближается к пределу бесконечности , когда
xприближается к бесконечности (lim √x → ∞, когдаx → ∞), - — это действительное число для всех неотрицательных
xи комплексное число для всех отрицательныхx(подробнее об этом мы пишем в разделе квадратного корня из отрицательного числа).
Вы, наверное, уже заметили, что квадратный корень из площади квадрата дает длину его стороны. Эта функция используется в одном из наших строительных калькуляторов — калькуляторе квадратных метров. Если вы планируете что-либо отремонтировать в будущем, эти инструменты могут вам очень помочь. Не забывайте их использовать!
Производная квадратного корня
Производная функции сообщает нам, насколько быстро эта функция изменяется вместе со своим аргументом.
 Один из простейших примеров в физике — это положение объекта и его скорость (скорость изменения положения).Допустим, функция
Один из простейших примеров в физике — это положение объекта и его скорость (скорость изменения положения).Допустим, функция x (t)описывает, как расстояние движущегося автомобиля от определенной точки изменяется со временемt. Вы знаете, что определяет, насколько быстро меняется пройденное вами расстояние? Ответ — скорость машины! Таким образом, производная положенияx (t)— это скоростьv (t)(скорость также может зависеть от времени). Для обозначения производной мы обычно используем апострофv (t) = x '(t)или символ производнойv (t) = dx (t) / dt.(-1/2) = 1 / (2√x) .Так как число в отрицательной степени больше этого числа на единицу, оценка вывода будет включать дроби. У нас есть инструмент, который может оказаться незаменимым при сложении или вычитании дробей с разными знаменателями. Он называется калькулятором НОК и объясняет, как найти наименьшее общее кратное.
Производная квадратного корня необходима для получения коэффициентов в так называемом разложении Тейлора .
 Мы не хотим вдаваться в подробности слишком глубоко, поэтому, вкратце, ряд Тейлора позволяет вам аппроксимировать различные функции с помощью многочленов, которые намного проще вычислить.Например, разложение Тейлора
Мы не хотим вдаваться в подробности слишком глубоко, поэтому, вкратце, ряд Тейлора позволяет вам аппроксимировать различные функции с помощью многочленов, которые намного проще вычислить.Например, разложение Тейлора √ (1 + x)вокруг точкиx = 0дается следующим образом:√ (1 + x) = 1 + 1/2 * x - 1/8 * x² + 1/16 * x³ - 5/128 * x⁴ + ...,, что действительно для
-1 ≤ x ≤ 1. Хотя в приведенном выше выражении содержится бесконечное количество членов, чтобы получить приблизительное значение, вы можете использовать всего несколько первых членов. Давай попробуем! Приx = 0,5и первых пяти членах вы получаете:√ (1,5) = 1 + 1/2 * 0.5 - 1/8 * 0,25 + 1/16 * 0,125 - 5/128 * 0,0625,√ (1,5) ≈ 1,2241,, а действительное значение, предоставленное нашим калькулятором, составляет
√ (1,5) ≈ 1,2247. Достаточно близко!Пока что это было много математики и уравнений.
 Для тех из вас, кто достаточно настойчив, мы подготовили следующий раздел, в котором объясняется, как вычислить квадратный корень из отрицательного числа.
Для тех из вас, кто достаточно настойчив, мы подготовили следующий раздел, в котором объясняется, как вычислить квадратный корень из отрицательного числа.Корень квадратный из отрицательного числа
В школе вас, вероятно, учили, что квадратного корня из отрицательного числа не существует.Это верно, когда вы рассматриваете только действительные числа. Давным-давно для выполнения сложных вычислений математикам приходилось вводить более общий набор чисел — комплексные числа , . Их можно выразить в следующей форме:
х = а + Ь * я,, где
x— комплексное число с действительной частьюaи мнимой частьюb. Что отличает комплексное число от действительного, так это мнимое числоi.Вот несколько примеров комплексных чисел:2 + 3i,5i,1,5 + 4i,2. Вы можете быть удивлены, увидев там2, что является реальным числом. Да, но это тоже комплексное число с
Да, но это тоже комплексное число с b = 0. Комплексные числа — это обобщение действительных чисел.Пока что воображаемое число
i, наверное, до сих пор для вас загадка. Что это вообще такое? Что ж, хотя это может показаться странным, это определяется следующим уравнением:я = √ (-1),, и это все, что вам нужно для вычисления квадратного корня из каждого числа, независимо от того, положительное оно или нет.Давайте посмотрим на несколько примеров:
- квадратный корень из -9:
√ (-9) = √ (-1 * 9) = √ (-1) √9 = 3i, - квадратный корень из -13:
√ (-13) = √ (-1 * 13) = √ (-1) √13 = i√13, - квадратный корень из -49:
√ (-49) = √ (-1 * 49) = √ (-1) √49 = 7i.
Разве это не просто? Эта проблема не возникает с кубическим корнем, поскольку отрицательное число можно получить, умножив три одинаковых отрицательных числа (чего нельзя сделать с двумя отрицательными числами).
 Например:
Например:³√ (-64) = ³√ [(- 4) * (- 4) * (- 4)] = -4.Это, вероятно, все, что вам следует знать о квадратных корнях. Мы ценим, что вы остались с нами до этого момента! В качестве награды испеките себе что-нибудь сладкое 🙂 Воспользуйтесь нашим калькулятором идеальных блинов, чтобы узнать, как приготовить идеальный блин, каким бы он вам ни нравился. Вам может понадобиться наш калькулятор граммов в чашки, чтобы помочь вам в этом. Он работает в обоих направлениях, то есть для преобразования граммов в чашки и преобразования чашек в граммы.А если вы спросите себя: «Сколько калорий мне нужно есть в день?», Воспользуйтесь нашим удобным калькулятором калорий!
FAQ
Может ли число иметь более одного квадратного корня?
Да, на самом деле все положительные числа имеют 2 квадратных корня , один положительный, а другой равный первому, но отрицательный. Это потому, что если вы умножите два негатива вместе, негативы аннулируются и результат будет положительным.

Как найти квадратный корень без калькулятора?
- Вычислите квадратного корня.Ближайшее квадратное число приемлемо, если вы в затруднении.
- Разделите число, из которого вы хотите найти квадратный корень, на оценку.
- Добавьте оценку к результату шага 2.
- Разделите результат шага 3 на 2. Это ваша новая оценка .
- Повторите шаги 2–4 с новой оценкой. Чем больше раз это повторяется, тем точнее будет результат.
Как вычислить квадратные корни?
- Найдите ближайший квадрат над и под числом, которое вы думаете.
- Квадратный корень будет между квадратными корнями этих чисел.
- Близость числа к квадратному корню указывает, насколько близок корень. Например, 26 очень близко к 25, поэтому корень будет очень близок к 5.
- Попробуйте несколько раз разобраться в этом .
Является ли квадратный корень из 2 рациональным числом?
Нет, квадратный корень из 2 не является рациональным .
 Это связано с тем, что, когда 2 записывается как дробь, 2 / 1 , она никогда не может иметь только четные показатели, и поэтому рациональное число не может быть возведено в квадрат для его создания.
Это связано с тем, что, когда 2 записывается как дробь, 2 / 1 , она никогда не может иметь только четные показатели, и поэтому рациональное число не может быть возведено в квадрат для его создания.Как избавиться от квадратного корня?
В алгебре возведение в квадрат обеих частей уравнения избавит от любых квадратных корней . Результатом этой операции является то, что квадратные корни будут заменены любым числом, из которого они находили квадратный корень.
Являются ли квадратные корни рациональными?
Некоторые квадратные корни являются рациональными , а другие — нет. Вы можете определить, является ли квадратный корень рациональным или нет, выяснив, может ли число, которое вы извлекаете квадратным корнем, быть выражено только с помощью четных показателей (например,грамм. 4 = 2 2 /1 2 ). Если может, его корень рациональный .
Является ли квадратный корень из 5 рациональным числом?
Квадратный корень из 5 дает , а не рациональное число .
 Это связано с тем, что 5 не может быть выражено дробью, если числитель и знаменатель имеют четные показатели. Это означает, что рациональное число нельзя возвести в квадрат, чтобы получить 5.
Это связано с тем, что 5 не может быть выражено дробью, если числитель и знаменатель имеют четные показатели. Это означает, что рациональное число нельзя возвести в квадрат, чтобы получить 5.Является ли квадратный корень из 7 рациональным числом?
Результатом квадратного корня 7 является иррациональное число .7 не может быть записано как дробь только с четными показателями, а это означает, что число, возведенное в квадрат для достижения 7, не может быть выражено как дробь целых чисел, и поэтому не является рациональным.
Какова производная квадратного корня из x?
Производная квадратного корня x равна x — 1 / 2 / 2 или 1 / 2SQRT (x) . Это связано с тем, что квадратный корень из x может быть выражен как x 1 / 2 , от которого обычно происходит дифференцирование.
Как найти квадратный корень из десятичной дроби?
- Преобразует десятичную дробь в дробь .

- Найдите любые квадратные корни дроби или оцените их. Сделайте дробью, равной квадратному корню, который вы нашли в квадрате.
- Отмените квадратный корень и квадрат, оставив дробь.
- Запишите дробь как десятичную в качестве окончательного ответа.
Кубики и кубики
Чтобы понять кубические корни, сначала мы должны понять кубики…
Как построить число в кубе
Чтобы куб число, просто умножьте на 3 раза …
Пример: Что такое 3 Cubed?
3 куба = = 3 × 3 × 3 = 27 Примечание: пишем «3 В кубе «как 3 3
(маленький 3 означает число появляется трижды при умножении)Кубики От 0
3 до 6 30 кубов = 0 3 = 0 × 0 × 0 = 0 1 куб = 1 3 = 1 × 1 × 1 = 1 2 куба = 2 3 = 2 × 2 × 2 = 8 3 куба = 3 3 = 3 × 3 × 3 = 27 4 куба = 4 3 = 4 × 4 × 4 = 64 5 кубов = 5 3 = 5 × 5 × 5 = 125 6 кубов = 6 3 = 6 × 6 × 6 = 216 Кубический корень
Кубический корень идет в другом направлении:
3 в кубе равно 27, поэтому кубический корень из 27 это 3
3 27 Кубический корень числа.
 ..
..
… специальное значение, которое при в кубе дает исходное число.Кубический корень из 27 равен …
… 3 , потому что , когда 3 в кубе , вы получаете 27 .Примечание: когда вы видите «корень», подумайте о
«Я знаю дерево , но какой корень его породил? »
В данном случае дерево — «27», а корень куба — «3».
Вот еще несколько кубиков и кубических корней:
4
64
5
125
6
216
Пример: Что такое кубический корень из 125?
Ну, мы просто случайно знаем, что 125 = 5 × 5 × 5 (если вы используете 5 трижды при умножении получится 125).
 ..
..… итак, кубический корень из 125 равен 5
Символ кубического корня
Это специальный символ, обозначающий «кубический корень», это «радикальный» символ (используется для квадратных корней) с маленькой тройкой, чтобы означать куб корень.
Вы можете использовать это так: (мы говорим «кубический корень из 27 равен 3»)
Вы также можете кубить отрицательные числа в куб
Взгляните на это:
Когда мы кубим +5, получаем +125: +5 × +5 × +5 = +125
Когда мы кубим −5, получаем −125: −5 × −5 × −5 = −125
Таким образом, кубический корень из −125 равен −5
Идеальные кубики
Идеальные кубики — это кубики целых чисел:
Perfect
Кубики0 0 1 1 2 8 3 3 9111 9111 9111 9111 9111 9111 9113 5 125 6 216 7 343 8 9111 10 1000 11 1331 12 1728 13 9111 1 191 13 9112 9111 11 19111 9111 15 3375 Легко вычислить кубический корень из идеального куба, но он действительно сложно вычислить другие кубические корни.

Пример: что такое кубический корень из 30?
Итак, 3 × 3 × 3 = 27 и 4 × 4 × 4 = 64, поэтому мы можем угадать ответ от 3 до 4.
- Попробуем 3,5: 3,5 × 3,5 × 3,5 = 42,875
- Попробуем 3,2: 3,2 × 3,2 × 3,2 = 32,768
- Попробуем 3,1: 3,1 × 3,1 × 3,1 = 29,791
Мы приближаемся, но очень медленно … в этот момент я достаю свой калькулятор, и он говорит:
3.1072325059538588668776624275224 …
… но цифры продолжают повторяться, без всякого рисунка. Так что даже калькулятор ответит только приближение !
(Дополнительная литература: такие числа называются сурдами, которые являются особым типом иррациональных чисел)Как умножить квадратный корень
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту.
 Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т.
 д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.{2} = \ left (-3 \ right) \ cdot \ left (-3 \ right) = 9 $$
д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.{2} = \ left (-3 \ right) \ cdot \ left (-3 \ right) = 9 $$3 и -3 считаются квадратными корнями из 9.
Все положительные действительные числа имеют два квадратных корня, один положительный квадратный корень и один отрицательный квадратный корень. Положительный квадратный корень иногда называют главным квадратным корнем. Причина, по которой у нас есть два квадратных корня, проиллюстрирована выше. Произведение двух чисел положительно, если оба числа имеют одинаковый знак, как в случае с квадратами и квадратными корнями
. {2} = a \ cdot a = \ left (-a \ right) \ cdot \ left (-a \ right) $$
{2} = a \ cdot a = \ left (-a \ right) \ cdot \ left (-a \ right) $$Квадратный корень записывается с помощью символа корня √, а число или выражение внутри символа корня, обозначенное ниже a, называется подкоренным выражением.
$$ \ sqrt {a} $$
Чтобы указать, что нам нужен как положительный, так и отрицательный квадратный корень из подкоренной части, мы помещаем символ ± (читается как плюс минус) перед корнем.
$$ \ pm \ sqrt {9} = \ pm 3 $$
У нуля один квадратный корень, равный 0.
$$ \ sqrt {0} = 0 $$
Отрицательные числа не имеют действительных квадратных корней, поскольку квадрат либо положительный, либо 0.
Если квадратный корень целого числа является другим целым числом, квадрат называется полным квадратом.Например, 25 — это идеальный квадрат, так как
$$ \ pm \ sqrt {25} = \ pm 5 $$
Если подкоренное выражение не является точным квадратом, то есть квадратный корень не является целым числом, вам нужно приблизительно вычислить квадратный корень
$$ \ pm \ sqrt {3} = \ pm 1.
 73205 … \ приблизительно \ pm 1,7 $$
73205 … \ приблизительно \ pm 1,7 $$Квадратные корни из чисел, не являющихся полным квадратом, являются членами иррациональных чисел. Это означает, что они не могут быть записаны как частное двух целых чисел. Десятичная форма иррационального числа не прерывается и не повторяется.Иррациональные числа вместе с рациональными числами составляют действительные числа.
ВидеоурокПриблизительно квадратный корень из 250
Промежуточная алгебра
Урок 41: Рационализация знаменателей и числителей
радикальных выражений
WTAMU > Виртуальная математическая лаборатория> Алгебра среднего уровняЦели обучения
После завершения этого руководства вы сможете: - Рационализируйте одночленные знаменатели рациональных выражений.

- Рационализируйте числители рациональных выражений, состоящие из одного члена.
- Рационализируйте двухчленные знаменатели рациональных выражений.
Введение
В этом уроке мы поговорим о рационализации знаменателя и числитель рациональных выражений.Отзыв из учебника 3: Наборы чисел, рациональное число — это число, которое может быть записанным как одно целое число над другим. Отзыв из учебника 3: Наборы чисел, что иррациональное число не является тем, что трудно рассуждать, но это число, которое нельзя записать как одно целое число над другим. Это неповторяющаяся десятичная дробь. Один Пример иррационального числа — это когда у вас есть корень выражения это не идеальный корень, например квадратный корень из 7 или куб корень из 2.
 Итак, когда мы рационализируем знаменатель или числитель
мы хотим избавить его от радикалов.
Итак, когда мы рационализируем знаменатель или числитель
мы хотим избавить его от радикалов.Учебник
Рационализация знаменателя
(с одним членом)Когда радикал содержит выражение, не являющееся полным корнем, например, квадратный корень из 3 или кубический корень из 5, он называется иррациональное число . Итак, чтобы рационализировать знаменатель , нам нужно избавиться от всех радикалов, которые находятся в знаменателе.
Шаг 1.
 Умножьте числитель и знаменатель на радикал.
это избавит от радикала в знаменателе.
Умножьте числитель и знаменатель на радикал.
это избавит от радикала в знаменателе. Если радикал в знаменателе является квадратным корнем, умножьте квадратным корнем, который даст вам идеальный квадрат под корнем при умножении на знаменатель.Если радикал в знаменателе является кубическим корнем, затем вы умножаете его на кубический корень, что даст вам идеальный куб под корнем при умножении на знаменатель и т. д.
Обратите внимание, что фраза «полный квадрат» означает что из него можно извлечь квадратный корень. Так же, как «идеально куб «означает, что мы можем извлечь кубический корень числа, и поэтому вперед.
Имейте в виду, что если умножить числитель и знаменатель точно так же дроби будут эквивалентны.

Шаг 3: При необходимости упростите дробь.
Будьте осторожны.Вы не можете отменить фактор, который находится снаружи радикала с тем, что находится внутри радикала. Чтобы чтобы исключить общие факторы, они должны быть оба внутри одного радикала или быть вне радикала.
Пример 1 : Рационализируйте знаменатель. Шаг 1.
 Умножьте числитель и знаменатель на радикал.
это избавит от радикала в знаменателе.
Умножьте числитель и знаменатель на радикал.
это избавит от радикала в знаменателе. Поскольку в знаменателе стоит квадратный корень, то нам нужно умножить на квадратный корень из выражения, которое даст нам идеальный квадрат под корнем в знаменателе.
Квадратные корни удобны для работы с этим типом задач, потому что если подкоренное выражение — это не идеальный квадрат, нам просто нужно умножить это само по себе, и тогда у нас есть идеальный квадрат.
Итак, в этом случае мы можем добиться этого, умножив верх и низ корнем квадратным из 6:
* Мног. число и ден. корнем из 6
число и ден. корнем из 6
* Den. теперь имеет идеальный квадрат под квадратным корнем
* кв.корень 36 равен 6
* Разделите общий множитель 2
Будьте осторожны при уменьшении такой дроби. Это действительно заманчиво чтобы отменить 3, которая находится за пределами радикала, с 6, которая находится внутри радикала последней дроби.
 Вы не можете этого сделать, если
они оба находятся внутри одного радикала или оба вне радикала, как
4 в числителе и 6 в знаменателе были во втором
до последней дроби.
Вы не можете этого сделать, если
они оба находятся внутри одного радикала или оба вне радикала, как
4 в числителе и 6 в знаменателе были во втором
до последней дроби.
Пример 2 : Рационализируйте знаменатель. Шаг 1. Умножьте числитель и знаменатель на радикал. это избавит от радикала в знаменателе.
Поскольку в знаменателе стоит кубический корень, нам нужно умножить кубическим корнем из выражения, которое даст нам идеальный куб под радикал в знаменателе.

Итак, в этом случае мы можем добиться этого, умножив верхнюю и нижнюю корень кубический из:
* Mult. число и ден. корень кубический из
* Den.теперь есть идеальный куб под корнем куба
* Кубический корень из 27 куб равен 3 a
Как обсуждалось в примере 1, мы не сможем отменить 3 с 18 в нашей последней дроби, потому что 3 находится за пределами радикал, а 18 находится внутри радикала.

Кроме того, мы не можем брать кубический корень из чего-либо под радикалом. Итак, ответ, который у нас есть, настолько упрощен, насколько мы можем его получить.
Рационализация числителя
(с одним членом)Как упоминалось выше, когда радикал не может быть оценен, для Например, квадратный корень из 3 или кубический корень из 5, он называется иррациональным . номер .Итак, чтобы рационализировать числитель , нам нужно избавиться от всех радикалов, которые находятся в числителе. Обратите внимание, что это те же основные шаги для рационализируя знаменатель, мы просто применим к числителю.

Шаг 1. Умножьте числитель и знаменатель на радикал. это избавит от корня в числителе.
Если радикал в числителе является квадратным корнем, умножьте квадратным корнем, который даст вам идеальный квадрат под корнем при умножении на числитель. Если радикал в числителе является кубическим корнем, затем вы умножаете его на кубический корень, что даст вам идеальный куб под корнем при умножении на числитель и т. д…
Обратите внимание, что фраза «полный квадрат» означает что из него можно извлечь квадратный корень. Так же, как «идеально куб «означает, что мы можем извлечь кубический корень числа, и поэтому вперед.

Имейте в виду, что если умножить числитель и знаменатель точно так же дроби будут эквивалентны.
Шаг 3: При необходимости упростите дробь.
Будьте осторожны. Вы не можете отменить фактор, который находится снаружи радикала с тем, что находится внутри радикала. Чтобы чтобы исключить общие факторы, они должны быть оба внутри одного радикала или быть вне радикала.
Пример 3 : Рационализируйте числитель. Шаг 1. Умножьте числитель и знаменатель на радикал. это избавит от корня в числителе.
Поскольку у нас в числителе квадратный корень, то нам нужно умножить квадратным корнем из выражения, которое даст нам полный квадрат под корнем в числителе.
Итак, в этом случае мы можем добиться этого, умножив верхнюю и нижнюю корнем квадратным из 5:
* Mult. число и ден. корнем из 5
* Чис.теперь имеет идеальный квадрат под квадратным корнем
* кв. корень 25 равен 5
Как обсуждалось выше, мы не сможем отменить 5 с помощью 30 в нашей последней дроби, потому что 5 находится вне радикала а 30 — внутри радикала.
Кроме того, мы не можем извлечь квадратный корень из чего-либо под корнем. Итак, ответ, который у нас есть, настолько упрощен, насколько мы можем его получить.
Пример 4 : Рационализируйте числитель. Шаг 1. Умножьте числитель и знаменатель на радикал. это избавит от корня в числителе.
Поскольку у нас в числителе кубический корень, нам нужно умножить кубическим корнем из выражения, которое даст нам идеальный куб под радикал в числителе.
Итак, в этом случае мы можем добиться этого, умножив верхнюю и нижнюю корень кубический из:
* Мног.число и ден. корень кубический из
* Чис. теперь есть идеальный куб под корнем куба
* Кубический корень из 8 x куба равно 2 x
Как обсуждалось выше, мы не сможем компенсировать 2 x квадратом 4 x в нашей последней дроби, потому что 2 x находится за пределами корня а квадрат 4 x находится на внутренней стороне радикальный.
Кроме того, мы не можем брать кубический корень из чего-либо под радикалом. Итак, ответ, который у нас есть, настолько упрощен, насколько мы можем его получить.
Рационализация знаменателя
(с двумя членами)Выше мы говорили о рационализации знаменателя одним членом. Опять же, рационализация знаменателя означает избавление от любых радикалов в знаменатель.
Поскольку теперь у нас есть два термина, нам придется подойти к нему по-другому чем когда у нас был один семестр, но цель все та же.
Шаг 1: Найдите сопряжение знаменателя.
Сопряжение бинома можно найти, изменив знак между два условия, но соблюдайте тот же порядок терминов.
a + b и a — b являются конъюгатами друг друга.
Шаг 2: Умножьте числитель и знаменатель дроби конъюгатом, найденным на шаге 1.
Имейте в виду, что если умножить числитель и знаменатель точно так же дроби будут эквивалентны.
Шаг 4: При необходимости упростите дробь.
Будьте осторожны. Вы не можете отменить фактор, который находится снаружи радикала с тем, что находится внутри радикала. Чтобы чтобы исключить общие факторы, они должны быть оба внутри одного радикала или быть вне радикала.
Пример 5 : Рационализировать знаменатель Шаг 1: Найдите сопряжение знаменателя.
Как правило, конъюгатом a + b является a — b и наоборот.
Итак, каким было бы сопряжение нашего знаменателя?
Похоже конъюгат.
Шаг 2: Умножьте числитель и знаменатель дроби конъюгатом, найденным на шаге 1.
Никакого упрощения по этой проблеме сделать нельзя, поэтому окончательный ответ:
Пример 6 : Рационализируйте знаменатель. Шаг 1: Найдите сопряжение знаменателя.
Как правило, конъюгатом a + b является a — b и наоборот.
Итак, каким было бы сопряжение нашего знаменателя?
Похоже конъюгат.
Шаг 2: Умножьте числитель и знаменатель дроби конъюгатом, найденным на шаге 1.
* 12 — это (4) (3) и кв.корень из 4 равен 2
* 18 равен (9) (2), а квадратный корень из 9 равен 3
Практические задачиЭто практические задачи, которые помогут вам следующий уровень. Это позволит вам проверить и понять, понимаете ли вы эти типы проблем. Математика работает так же, как что-нибудь иначе, если вы хотите добиться успеха в этом, вам нужно практиковаться Это. Даже лучшие спортсмены и музыканты получали помощь и много практиковаться, практиковаться, практиковаться, чтобы хорошо освоить свой вид спорта или инструмент. На самом деле не бывает слишком много практики.
Чтобы получить максимальную отдачу от них, вы должны работать проблема на свой собственный, а затем проверьте свой ответ, щелкнув ссылку для ответ / обсуждение для этой проблемы . По ссылке вы найдете ответ а также любые шаги, которые позволили найти этот ответ.
Практика Задача 1a: Рационализируйте знаменатель.
Практика Задача 2a: Рационализируйте числитель.
Практика Задача 3a: Рационализируйте знаменатель.
Нужна дополнительная помощь по этим темам?
Последний раз редактировал Ким Сьюард 21 июля 2011 г.
Авторские права на все содержание (C) 2001 — 2011, WTAMU и Kim Seward. Все права защищены.Основы квадратного корня (примеры и ответы)
Обновлено 8 декабря 2020 г.
Ли Джонсон
Квадратные корни часто встречаются в математических и естественных задачах, и любой ученик должен овладеть основами квадратного корня, чтобы ответьте на эти вопросы. Квадратные корни спрашивают, «какое число при умножении само на себя дает следующий результат», и поэтому их вычисление требует, чтобы вы относились к числам немного по-другому.Однако вы можете легко понять правила извлечения квадратного корня и ответить на любые вопросы, связанные с ними, независимо от того, требуют ли они прямого вычисления или просто упрощения.
TL; DR (слишком долго; не читал)
Квадратный корень спрашивает вас, какое число при умножении на само дает результат после символа √. Итак, √9 = 3 и √16 = 4. Технически каждый корень имеет положительный и отрицательный ответ, но в большинстве случаев положительный ответ — это тот, который вас заинтересует.
Вы можете множить квадратные корни на множители, как и обычные числа , поэтому √ ab = √ a √ b , или √6 = √2√3.
Что такое квадратный корень?
Квадратные корни — это противоположность возведения числа в квадрат или его умножения на само себя. Например, три в квадрате равно девяти (3 2 = 9), поэтому квадратный корень из девяти равен трем. В символах это
\ sqrt {9} = 3
Символ «√» говорит вам извлекать квадратный корень из числа, и вы можете найти его на большинстве калькуляторов.
Помните, что каждое число на самом деле имеет два квадратных корня.2 = 9 \ text {и} \ sqrt {9} = ± 3
, где ± вместо «плюс или минус». Во многих случаях вы можете игнорировать отрицательные квадратные корни чисел, но иногда важно помнить, что каждое число имеет два корня.
Вас могут попросить извлечь «кубический корень» или «корень четвертой степени» из числа. Кубический корень — это число, которое при двойном умножении на себя равно исходному числу. Корень четвертой степени — это число, которое при трехкратном умножении на себя равно исходному числу.{1/3}
Упрощение квадратных корней
Одна из самых сложных задач, которые вам, возможно, придется выполнить с квадратными корнями, — это упрощение больших квадратных корней, но вам просто нужно следовать некоторым простым правилам, чтобы ответить на эти вопросы. Вы можете разложить на множители квадратные корни так же, как и обычные числа. Так, например, 6 = 2 × 3, поэтому
\ sqrt {6} = \ sqrt {2} × \ sqrt {3}
Упрощение больших корней означает выполнение факторизации шаг за шагом и запоминание определения квадратного корня.Например, √132 — большой корень, и может быть трудно понять, что делать. Однако вы можете легко увидеть, что оно делится на 2, поэтому вы можете написать
\ sqrt {132} = \ sqrt {2} \ sqrt {66}
Однако 66 также делится на 2, поэтому вы можете написать:
\ sqrt {2} \ sqrt {66} = \ sqrt {2} \ sqrt {2} \ sqrt {33}
В этом случае квадратный корень из числа, умноженный на другой квадратный корень, просто дает исходное число ( из-за определения квадратного корня), поэтому
\ sqrt {132} = \ sqrt {2} \ sqrt {2} \ sqrt {33} = 2 \ sqrt {33}
Короче говоря, вы можете упростить квадратные корни используя следующие правила
\ sqrt {a × b} = \ sqrt {a} × \ sqrt {b} \\ \ sqrt {a} × \ sqrt {a} = a
Что такое квадратный корень…
Используя приведенные выше определения и правила, вы можете найти квадратные корни из большинства чисел.Вот несколько примеров, которые стоит рассмотреть.
Квадратный корень из 8
Его нельзя найти напрямую, потому что это не квадратный корень из целого числа. Однако использование правил для упрощения дает:
\ sqrt {8} = \ sqrt {2} \ sqrt {4} = 2 \ sqrt {2}
Квадратный корень из 4
. простой квадратный корень из 4, который равен √4 = 2. Задачу можно точно решить с помощью калькулятора, а √8 = 2,8284 ….
Квадратный корень из 12
Используя тот же подход, попробуйте найдите квадратный корень из 12.Разделите корень на факторы, а затем посмотрите, сможете ли вы снова разделить его на факторы. Попробуйте это как практическую задачу, а затем посмотрите на решение ниже:
\ sqrt {12} = \ sqrt {2} \ sqrt {6} = \ sqrt {2} \ sqrt {2} \ sqrt {3} = 2 \ sqrt {3}
Опять же, это упрощенное выражение может либо использоваться в задачах по мере необходимости, либо точно рассчитываться с помощью калькулятора. Калькулятор показывает, что
\ sqrt {12} = 2 \ sqrt {3} = 3.4641….
Корень квадратный из 20
Корень квадратный из 20 можно найти таким же образом:
\ sqrt {20} = \ sqrt {2} \ sqrt {10} = \ sqrt {2} \ sqrt {2} \ sqrt {5} = 2 \ sqrt {5} = 4.4721….
Квадратный корень из 32
Наконец, возьмите квадратный корень из 32, используя тот же подход:
\ sqrt {32} = \ sqrt {4} \ sqrt {8}
Здесь, обратите внимание, что мы уже вычислил квадратный корень из 8 как 2√2, а √4 = 2, поэтому:
\ sqrt {32} = 2 × 2 \ sqrt {2} = 4 \ sqrt {2} = 5,657 ….
Квадратный корень отрицательного числа
Хотя определение квадратного корня означает, что отрицательные числа не должны иметь квадратного корня (поскольку любое число, умноженное на само по себе, дает в результате положительное число), математики сталкивались с ними как с частью задач по алгебре и разработал решение.«Мнимое» число i используется для обозначения «квадратного корня из минус 1», а любые другие отрицательные корни выражаются как кратные i . Итак,
\ sqrt {-9} = \ sqrt {9} × i = ± 3i
Эти задачи более сложные, но вы можете научиться решать их, основываясь на определении i и стандартных правилах для корнеплоды.
Примеры вопросов и ответов
Проверьте свое понимание квадратных корней, упростив по мере необходимости, а затем вычислив следующие корни:
\ sqrt {50} \\ \ sqrt {36} \\ \ sqrt {70} \\ \ sqrt {24} \\ \ sqrt {27}
Попытайтесь решить их, прежде чем смотреть ответы ниже:
\ sqrt {50} = \ sqrt {2} \ sqrt {25} = 5 \ sqrt {2} = 7.071 \\ \ sqrt {36} = 6 \\ \ sqrt {70} = \ sqrt {7} \ sqrt {10} = \ sqrt {7} \ sqrt {2} \ sqrt {5} = 8,637 \\ \ sqrt {24} = \ sqrt {2} \ sqrt {12} = \ sqrt {2} \ sqrt {2} \ sqrt {6} = 2 \ sqrt {6} = 4,899 \\ \ sqrt {27} = \ sqrt { 3} \ sqrt {9} = 3 \ sqrt {3} = 5,196
. - квадратный корень из 4/9:
- Что такое
- Как упростить квадратный корень из 27?



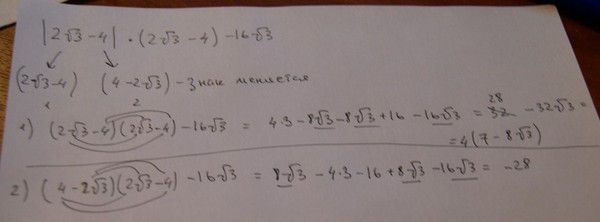 Если эта точность вас устраивает, можете закончить оценку здесь. В противном случае вы можете повторить процедуру с выбранным числом от
Если эта точность вас устраивает, можете закончить оценку здесь. В противном случае вы можете повторить процедуру с выбранным числом от  (1/2) = √9 * √5 = 3√5 .
(1/2) = √9 * √5 = 3√5 .
 Например, если 2 + 3 = 5, это не означает, что √2 + √3 равно √5. Это неправильно! Чтобы понять, почему это так, представьте, что у вас есть два разных типа фигур: треугольники 🔺 и круги 🔵. Что произойдет, если вы добавите один треугольник к одному кругу 🔺 + 🔵? Ничего такого! У вас остались один треугольник и один круг 🔺 + 🔵. С другой стороны, что происходит, когда вы пытаетесь добавить три треугольника к пяти треугольникам: 3 🔺 + 5 🔺? У нас получится восемь треугольников 8 🔺.
Например, если 2 + 3 = 5, это не означает, что √2 + √3 равно √5. Это неправильно! Чтобы понять, почему это так, представьте, что у вас есть два разных типа фигур: треугольники 🔺 и круги 🔵. Что произойдет, если вы добавите один треугольник к одному кругу 🔺 + 🔵? Ничего такого! У вас остались один треугольник и один круг 🔺 + 🔵. С другой стороны, что происходит, когда вы пытаетесь добавить три треугольника к пяти треугольникам: 3 🔺 + 5 🔺? У нас получится восемь треугольников 8 🔺. (1/2) ⟺ √x * √y = √ (x * y) .
(1/2) ⟺ √x * √y = √ (x * y) .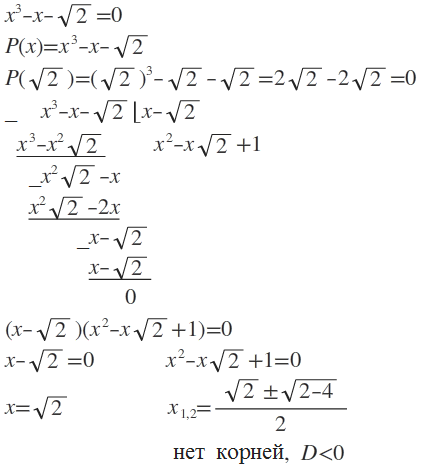 (1/2) .(1/2) ⟺ √x / √y = √ (x / y) ,
(1/2) .(1/2) ⟺ √x / √y = √ (x / y) , Чтобы увидеть некоторые примеры, ознакомьтесь с нашими финансовыми инструментами, созданными финансовыми специалистами, например, калькулятор сложных процентов или калькулятор будущей стоимости.Там вы найдете несколько функций, которые можно применить в реальной жизни. Они очень полезны, если вы хотите знать, как рассчитать сложные проценты или оценить будущую стоимость аннуитета.
Чтобы увидеть некоторые примеры, ознакомьтесь с нашими финансовыми инструментами, созданными финансовыми специалистами, например, калькулятор сложных процентов или калькулятор будущей стоимости.Там вы найдете несколько функций, которые можно применить в реальной жизни. Они очень полезны, если вы хотите знать, как рассчитать сложные проценты или оценить будущую стоимость аннуитета. Производную квадратного корня для получения дополнительной информации),
Производную квадратного корня для получения дополнительной информации), Один из простейших примеров в физике — это положение объекта и его скорость (скорость изменения положения).Допустим, функция
Один из простейших примеров в физике — это положение объекта и его скорость (скорость изменения положения).Допустим, функция  Мы не хотим вдаваться в подробности слишком глубоко, поэтому, вкратце, ряд Тейлора позволяет вам аппроксимировать различные функции с помощью многочленов, которые намного проще вычислить.Например, разложение Тейлора
Мы не хотим вдаваться в подробности слишком глубоко, поэтому, вкратце, ряд Тейлора позволяет вам аппроксимировать различные функции с помощью многочленов, которые намного проще вычислить.Например, разложение Тейлора  Для тех из вас, кто достаточно настойчив, мы подготовили следующий раздел, в котором объясняется, как вычислить квадратный корень из отрицательного числа.
Для тех из вас, кто достаточно настойчив, мы подготовили следующий раздел, в котором объясняется, как вычислить квадратный корень из отрицательного числа. Да, но это тоже комплексное число с
Да, но это тоже комплексное число с  Например:
Например:
 Это связано с тем, что, когда 2 записывается как дробь, 2 / 1 , она никогда не может иметь только четные показатели, и поэтому рациональное число не может быть возведено в квадрат для его создания.
Это связано с тем, что, когда 2 записывается как дробь, 2 / 1 , она никогда не может иметь только четные показатели, и поэтому рациональное число не может быть возведено в квадрат для его создания. Это связано с тем, что 5 не может быть выражено дробью, если числитель и знаменатель имеют четные показатели. Это означает, что рациональное число нельзя возвести в квадрат, чтобы получить 5.
Это связано с тем, что 5 не может быть выражено дробью, если числитель и знаменатель имеют четные показатели. Это означает, что рациональное число нельзя возвести в квадрат, чтобы получить 5.
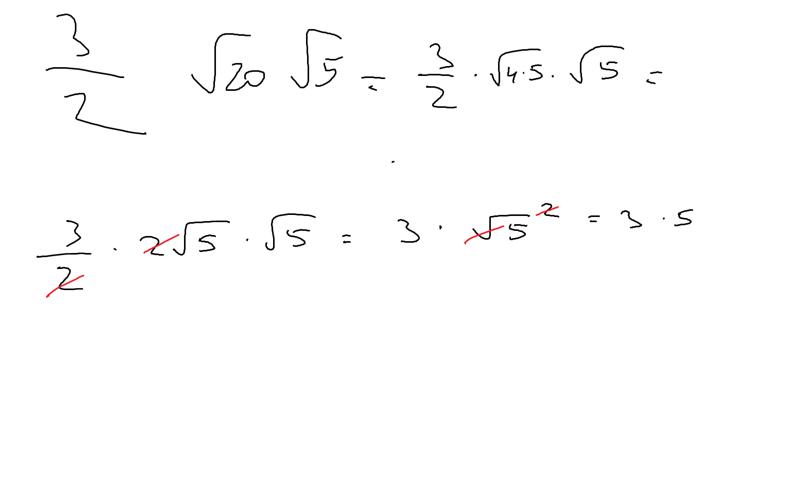 ..
..  ..
..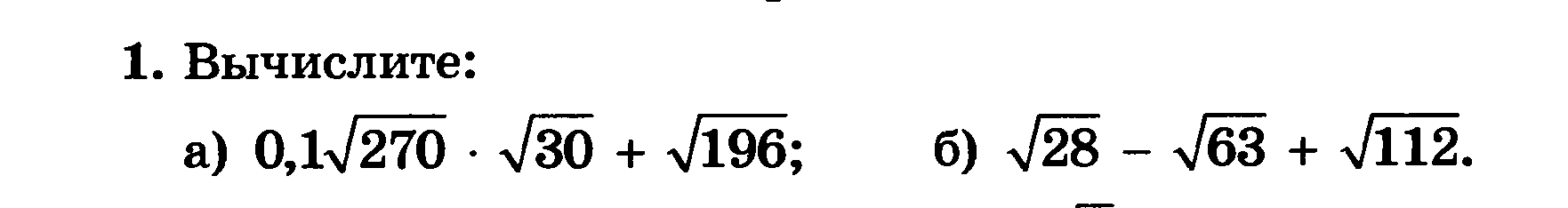
 Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.{2} = \ left (-3 \ right) \ cdot \ left (-3 \ right) = 9 $$
д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.{2} = \ left (-3 \ right) \ cdot \ left (-3 \ right) = 9 $$ {2} = a \ cdot a = \ left (-a \ right) \ cdot \ left (-a \ right) $$
{2} = a \ cdot a = \ left (-a \ right) \ cdot \ left (-a \ right) $$ 73205 … \ приблизительно \ pm 1,7 $$
73205 … \ приблизительно \ pm 1,7 $$
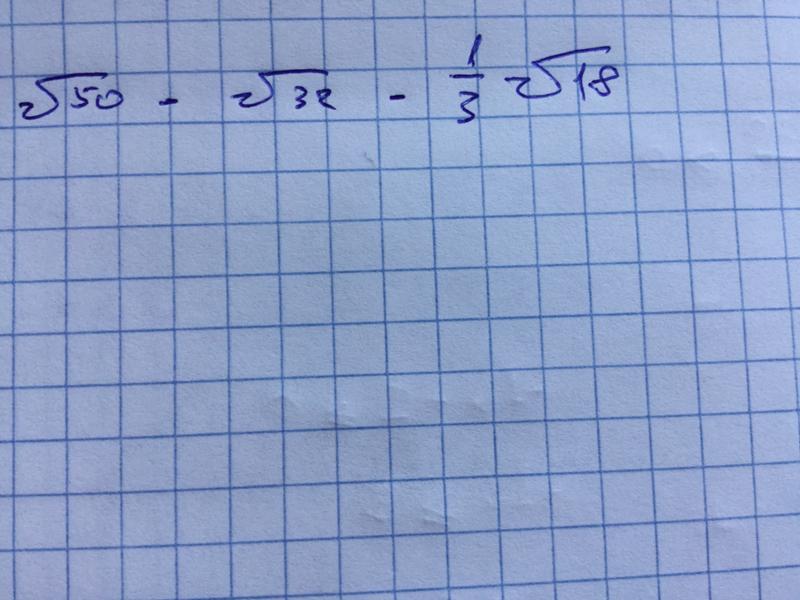 Итак, когда мы рационализируем знаменатель или числитель
мы хотим избавить его от радикалов.
Итак, когда мы рационализируем знаменатель или числитель
мы хотим избавить его от радикалов. Умножьте числитель и знаменатель на радикал.
это избавит от радикала в знаменателе.
Умножьте числитель и знаменатель на радикал.
это избавит от радикала в знаменателе. 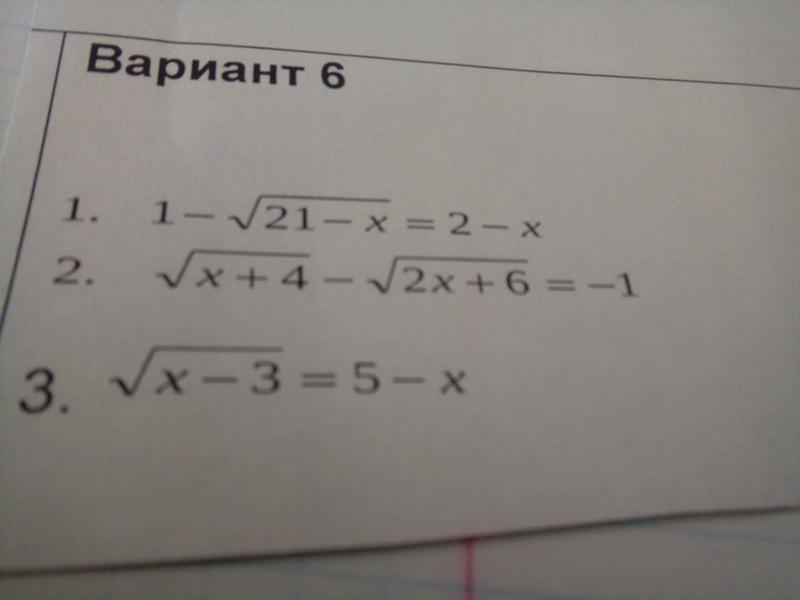
 Умножьте числитель и знаменатель на радикал.
это избавит от радикала в знаменателе.
Умножьте числитель и знаменатель на радикал.
это избавит от радикала в знаменателе.  число и ден. корнем из 6
число и ден. корнем из 6  Вы не можете этого сделать, если
они оба находятся внутри одного радикала или оба вне радикала, как
4 в числителе и 6 в знаменателе были во втором
до последней дроби.
Вы не можете этого сделать, если
они оба находятся внутри одного радикала или оба вне радикала, как
4 в числителе и 6 в знаменателе были во втором
до последней дроби.


