| 1 | Найти точное значение | sin(30) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2 | Найти точное значение | sin(45) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3 | Найти точное значение | sin(30 град. ) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4 | Найти точное значение | sin(60 град. ) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 5 | Найти точное значение | tan(30 град. ) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6 | Найти точное значение | arcsin(-1) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7 | Найти точное значение | sin(pi/6) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 8 | cos(pi/4) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 9 | Найти точное значение | sin(45 град. ) ) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 10 | Найти точное значение | sin(pi/3) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 11 | Найти точное значение | arctan(-1) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 12 | Найти точное значение | cos(45 град. ) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 13 | Найти точное значение | cos(30 град. ) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 14 | Найти точное значение | tan(60) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 15 | Найти точное значение | csc(45 град. ) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 16 | Найти точное значение | tan(60 град. ) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 17 | Найти точное значение | sec(30 град. ) ) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 18 | Найти точное значение | cos(60 град. ) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 19 | Найти точное значение | cos(150) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 20 | Найти точное значение | sin(60) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 21 | Найти точное значение | cos(pi/2) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 22 | Найти точное значение | tan(45 град. ) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 24 | Найти точное значение | csc(60 град. ) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 25 | Найти точное значение | sec(45 град. ) ) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 26 | Найти точное значение | csc(30 град. ) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 27 | Найти точное значение | sin(0) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 28 | Найти точное значение | sin(120) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 29 | Найти точное значение | cos(90) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 30 | Преобразовать из радианов в градусы | pi/3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 31 | Найти точное значение | tan(30) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 32 | Преобразовать из градусов в радианы | 45 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 33 | Найти точное значение | cos(45) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 35 | Преобразовать из радианов в градусы | pi/6 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 36 | Найти точное значение | cot(30 град. ) ) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 37 | Найти точное значение | arccos(-1) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 38 | Найти точное значение | arctan(0) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 39 | Найти точное значение | cot(60 град. ) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 40 | Преобразовать из градусов в радианы | 30 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 42 | Найти точное значение | sin((5pi)/3) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 43 | Найти точное значение | sin((3pi)/4) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 44 | Найти точное значение | tan(pi/2) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 45 | Найти точное значение | sin(300) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 46 | Найти точное значение | cos(30) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 47 | Найти точное значение | cos(60) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 48 | Найти точное значение | cos(0) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 49 | Найти точное значение | cos(135) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 50 | Найти точное значение | cos((5pi)/3) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 51 | Найти точное значение | cos(210) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 52 | Найти точное значение | sec(60 град. ) ) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 53 | Найти точное значение | sin(300 град. ) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 54 | Преобразовать из градусов в радианы | 135 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 55 | Преобразовать из градусов в радианы | 150 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 58 | Преобразовать из градусов в радианы | 89 град. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 59 | Преобразовать из градусов в радианы | 60 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 60 | Найти точное значение | sin(135 град. ) ) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 61 | Найти точное значение | sin(150) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 62 | Найти точное значение | sin(240 град. ) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 63 | Найти точное значение | cot(45 град. ) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 65 | Найти точное значение | sin(225) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 66 | Найти точное значение | sin(240) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 67 | Найти точное значение | cos(150 град. ) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 68 | Найти точное значение | tan(45) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 69 | Вычислить | sin(30 град.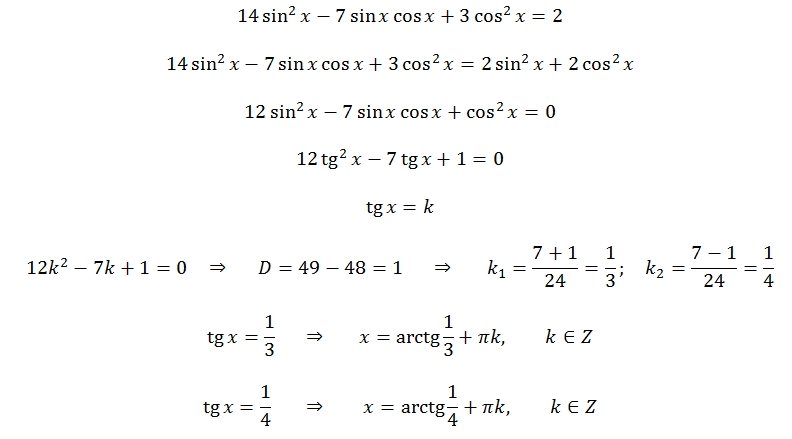 ) ) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 70 | Найти точное значение | sec(0) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 71 | Найти точное значение | cos((5pi)/6) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 72 | Найти точное значение | csc(30) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 74 | Найти точное значение | tan((5pi)/3) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 75 | Найти точное значение | tan(0) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 76 | Вычислить | sin(60 град. ) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 79 | Найти точное значение | sin((7pi)/4) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 80 | Найти точное значение | arcsin(-1/2) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 81 | sin((4pi)/3) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 82 | Найти точное значение | csc(45) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 83 | Упростить | arctan( квадратный корень из 3) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 84 | Найти точное значение | sin(135) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 85 | Найти точное значение | sin(105) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 86 | Найти точное значение | sin(150 град.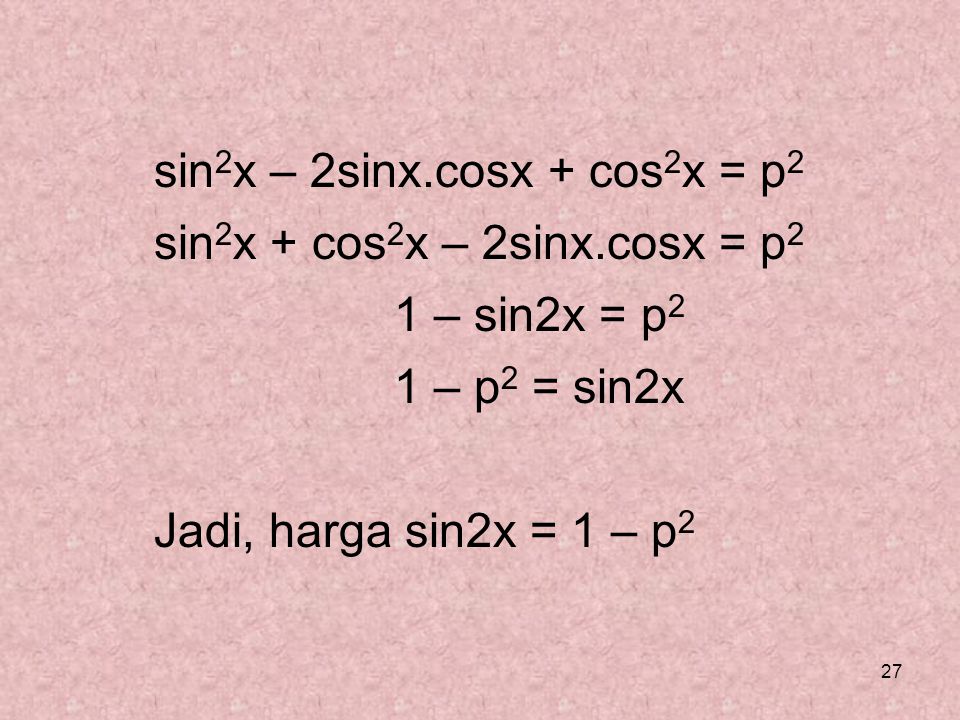 ) ) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 87 | Найти точное значение | sin((2pi)/3) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 88 | Найти точное значение | tan((2pi)/3) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 89 | Преобразовать из радианов в градусы | pi/4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 90 | Найти точное значение | sin(pi/2) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 91 | Найти точное значение | sec(45) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 92 | Найти точное значение | cos((5pi)/4) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 93 | Найти точное значение | cos((7pi)/6) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 94 | Найти точное значение | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 95 | Найти точное значение | sin(120 град.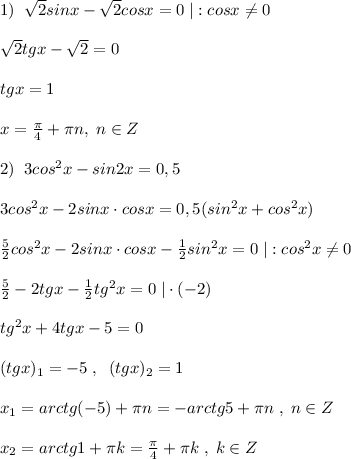 4x + 3cos2x + 1 = 0. Найдите все корни, принадлежащие отрезку [пи;3пи]. 4x + 3cos2x + 1 = 0. Найдите все корни, принадлежащие отрезку [пи;3пи].
Решение: 2*(1-cos2x)²/4+3cos2x+1=0 (1-cos2x)²+6cos2x+2=0 1-2cos2x+cos²2x+6cos2x+2=0 cos²2x+4cos2x+3=0 a=cosx a²+4a+3=0,a1+a2=-4 U a1*a2=3 a1=-1,cosx=-1⇒x=π+2πn a2=-3,cosx=-3∉[-1;1] x=π;3π
2 sin⁴x +3cos2x +1=0 Пусть у=sin²x При у=1 2 2 При у=2 x∈[π; 3π] x=-π +2πn 0.75 ≤ n ≤ 1.75 n=1 x= -π + 2π *1 = 3π 2 2 Ответ: 3π ; 5π Решите уравнение sinx=cosxи найдите его корни, принадлежащие отрезку [ -360;0]Решение: sinx=cosx по формуле получаем sinx-cosx=0 (корень из 2)sin(x-(п/4))=0 sin(x-(п/4))=0 х-(п/4))=Пn x=(п/4)+Пn -360<=(п/4)+Пn <=0 -360- 0.785<=Пn<=0-0.785 -360.785/3.14<=n<=-0.785/3,14 -144<=n<=-0.25, т.к n — целое то n=-144, -143……….-1 получаеться надо будет подставлять все эти числа в n но это очень много. Найдите корни уравнения, принадлежащие отрезку [0;2п]:cos x — sin x*cos x = 0 Указать наименьший корень. Ответ в градусах.
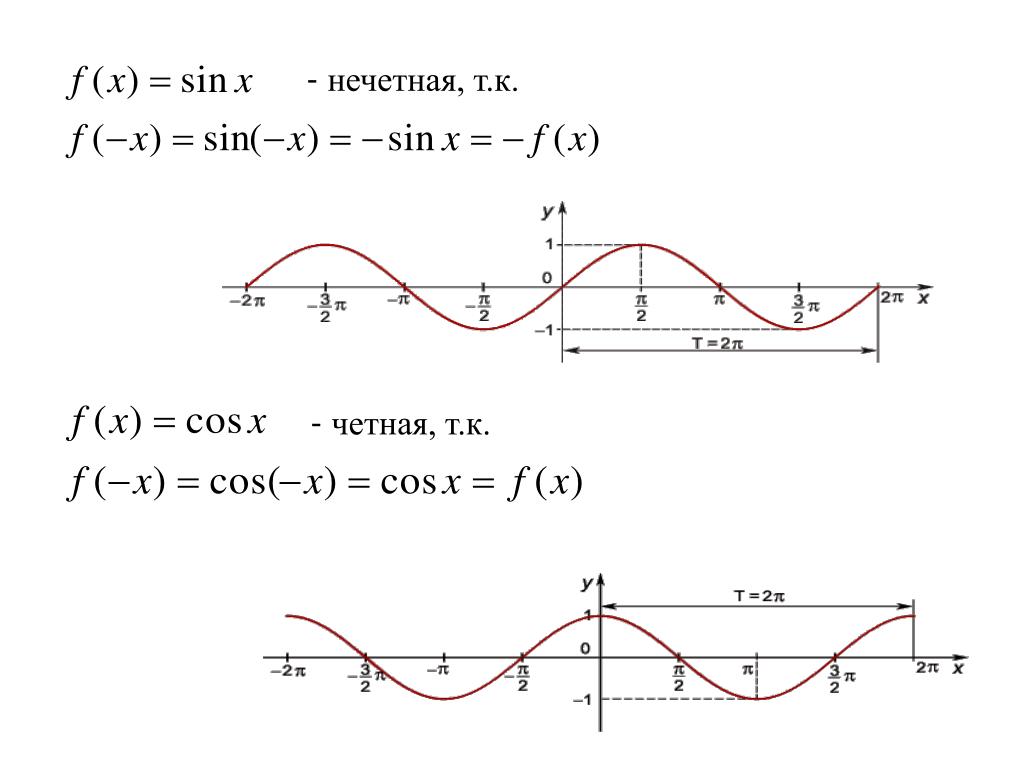
cosx-sinx*cosx=0 x=П/2 + 2Пn, n∈z П/2 — наименьший корень Ответ: 90° . Решите уравнение IsinxI-5sinx+4cosx=0Найдите все корни принадлежащие отрезку [-3п;-3п/2]Решение: Есть 2 варианта 1) sinx <0 тогда |sinx|=-sinx -sinx-5sinx+4cosx=0 -6sinx+4cosx=0 6sinx=4cosx 3sinx=2cosx так как sinx <0, то и cosx<0. Учитывая это возведем обе стороны в квадрат 9sin²x=4cos²x 9sin²x=4(1-sin²x) 9sin²x=4-4sin²x 13sin²x=4 sinx=-2/√13 (х находится в третьей четверти тригонометрического круга ) x=π+arcsin(2/√13)+2πn в отрезок [-3п;-3п/2] попадает х= -3π+arcsin(2/√13) 2) sinx >=0 тогда |sinx|=sinx sinx-5sinx+4cosx=0 -4sinx+4cosx=0 4sinx=4cosx sinx=cosx x=π/4+2πn (х находится в первой четверти тригонометрического круга ) в отрезок [-3п;-3п/2] попадает х= -2π+π/4=-7π/4 Ответ:х= -3π+arcsin(2/√13) и -7π/4 cos2x+3sinx-2=0Решите уравнение и найдите все корни, принадлежащие отрезку [П и пять пи на два]Решение: А)cos2x + 3sinx — 2 = 0 cos²x — sin²x + 3sinx — 2 =0 1-sin²x — sin²x + 3sinx — 2 = 0 -2sin²x + 3sinx — 1 = 0 |*(-1) 2sin²x — 3sinx + 1 =0 Обозначим: sinx= t, тогда 2t² — 3t + 1 = 0 D= 9 — 8 = 1 t₁= 1, t₂ = 1/2 (1) sinx= 1 б) x₁= π/2+2πn, n ∈ z x₂= (-1)^k π/6 + πk, k∈z При остальных целых значениях n и k, значения х выходят за пределы заданного отрезка. 123 4 5 > >> ЕГЭ.Математика профильный уровень(Задания на тригонометрию) а) Решите уравнение 2cos2x=√3sin(3π/2+x). а) Решите уравнение 4sin2x+√2tgx=0. а) Решите уравнение (5sin2x–3sinx)/(5cosx+4)=0 Решить уравнение 1/tg2x+3/sinx+3=0 а) Решите уравнение 2sin2x=√3cos(π/2–x) а) Решите уравнение (6cos2x–8cosx–1)√5tgx=0 а) Решите уравнение 3sin2x + 3cos2x = 4 а) Решите уравнение 3tg2x+(6–2√2)/cosx + 3–4√2 = 0 а) Решите уравнение (1/49)cos2x=72–2cosx а) Решите уравнение (cos2x–1)2=10sin2x–4 а) Решите уравнение (√2cosx–1)/√–5cosx=0 а) Решите уравнение (2cosx–√3)/√7sinx=0 а) Решите уравнение cos2x–2√2sin(π/2+x)–2=0 а) Решите уравнение log–cosx(1–0. а) Решите уравнение 4sinx·tgx·21/cosx=8tgx. a) Решите уравнение (2cos2x+sinx–2)√5tgx=0 а) Решите уравнение (16sinx)cosx=(1/4)√3sinx а) Решите уравнение 2cos2x–cosx–1=0 Открыть страницу с решением к задаче (решений: 1) а) Решить уравнение log4(4sin22x)=2–log2(–2tgx) (4cos2x–1)· корень из (5–x)=0 а) Решить уравнение cos2x+3√3sin(3π/2+x)–5=0 5/(sin2(11 pi/2+x)) +8/cos x –4=0 (64cosx)sinx=8√3cosx а) Решите уравнение cos2x – 14cos2x – 7sin2x = 0 а)Решите уравнение 4sin2x+tgx=0 а)Решите уравнение 4sin2x=tgx а)Решите уравнение 2sin2x–3cosx–3=0 а) Решите уравнение 2sin2x = √3cos(π/2–x) а) Решите уравнение 5/(cos2x)+7/sin(5π/2–x)+2=0 Решить уравнение (49cosx)sinx = 7√2cosx и найти все корни этого уравнения, принадлежащие отрезку [5π/2;4π] а) Решите уравнение 2sin3x – 2sinx + cos2x = 0. б) Найдите все корни этого уравнения, принадлежащие отрезку [–7π/2; –2π] Решите уравнение (0,25sinx)cosx = 2–√2sinx, найдите корни на промежутке [2π; 7π/2] a) Решите уравнение 6sin2x–5sinx–4=0 а) Решите уравнение (36cosx)sinx = (1/6)√2sinx б) Найдите все корни этого уравнения, принадлежащие отрезку [–π; π/2]. а) Решите уравнение sinx2x/cos(x+3π/2) = 1 б) Найдите все корни этого уравнения принадлежащие отрезку [–4π; –5π/2] Открыть страницу с решением к задаче (решений: 1) а) Решите уравнение 2sin2x = √3cos(3π/2+x) б) Найдите все корни этого уравнения, принадлежащие промежутку [–3π; –3π/2] Решить уравнение 4sin2x–12sinx+5=0,в ответе укажите корни, принадлежащие отрезку [–π;2π]. а) Решите уравнение 5cos2x – 12cosx + 4 = 0. a) 2cos2x+4cos(3π/2–x)+1 = 0 решить уравнение cos2x =2cosx – 1 решить уравнение а) 4x–2x+3+12 = 0 1) 2sin(x/3+π/4)=1 Открыть страницу с решением к задаче (решений: 1) sin4 x + cos4 x +cos2x=0. Открыть страницу с решением к задаче (решений: 1) а) Решить уравнение cos2x+2√2sin(π/2 + x)–2=0 Открыть страницу с решением к задаче (решений: 1) а) Решите уравнение sin2x–2√3cos2x–4sinx+4√3cosx=0 Открыть страницу с решением к задаче (решений: 1) Решить уравнение sin(3πx/2–π/3)=cos(π/6–πx) Открыть страницу с решением к задаче (решений: 1) а) Решите уравнение cos(2x+π/4) + cos(2x–π/4) + 4sinx = 2 + √2(1–sinx) Открыть страницу с решением к задаче (решений: 1) а) Решите уравнение √10–18cosx = 6cosx–2 Открыть страницу с решением к задаче (решений: 1) а) Решить уравнение cos2x – √2cos(3π/2 + x) – 1 = 0 Открыть страницу с решением к задаче (решений: 1) 8sin2(x) · (3–2sin2(x))–9 = 0 на отрезке [–π/2;π] Открыть страницу с решением к задаче (решений: 1) (26cos2x−23cosx+5) / (13sinx−12)=0 Открыть страницу с решением к задаче (решений: 1) a) Решите уравнение sin3x=2cos(π/2–x) Открыть страницу с решением к задаче (решений: 1) а) Решите уравнение (1/16)cosx+3·(1/4)cosx–4=0 Открыть страницу с решением к задаче (решений: 1) (cos2x + √3sinx – 1) / (tgx–√3) = 0 Открыть страницу с решением к задаче (решений: 1) 1. cos2x/(sin2x+1) =0 Открыть страницу с решением к задаче (решений: 1) a) 4sin42x+3cos4x–1=0 решите уравнение Открыть страницу с решением к задаче (решений: 1) а) 2sin4x+3cos2x+1=0 решите уравнение Открыть страницу с решением к задаче (решений: 2) Решить уравнение sin 5x = sin 3x Открыть страницу с решением к задаче (решений: 1) 4cos3x + 3√2sin2x=8cosx Открыть страницу с решением к задаче (решений: 5) 4cos2x–8cos(π/2–x)+1=0 Открыть страницу с решением к задаче (решений: 3) Решите уравнение (sinx–√3/2)·√3x2–7x+4=0 Открыть страницу с решением к задаче (решений: 2) Решите |cosx+sinx| = √2sin2x Открыть страницу с решением к задаче (решений: 1) а) Решите sinx(2sinx–3ctgx)=3 Открыть страницу с решением к задаче (решений: 1) а) Решите 7tg2x – 1/cosx + 1 = 0 Открыть страницу с решением к задаче (решений: 3) а) Решите 4tg2x + 3/cosx + 3 = 0 Открыть страницу с решением к задаче (решений: 1) Решите (2cos2x–5cosx+2) · log11(–sinx)=0 Открыть страницу с решением к задаче (решений: 1) a) Решите 36sin2x = 62sinx Открыть страницу с решением к задаче (решений: 1) a) Решите 1/sin2x – 3/sinx +2 = 0 Открыть страницу с решением к задаче (решений: 1) a) Решите 2cos2(3π/2+x) = sin2x Открыть страницу с решением к задаче (решений: 1) a) Решите 2√3cos2·(3π/2+x)–sin2x=0 Открыть страницу с решением к задаче (решений: 1) a) Решите 10sinx = 2sinx·5–cosx Открыть страницу с решением к задаче (решений: 1) а) Решите (27cosx)sinx = 33cosx/2 Открыть страницу с решением к задаче (решений: 1) a) Решите 15cosx = 3cosx·5sinx Открыть страницу с решением к задаче (решений: 1) a) Решите уравнение cos2x+sin(π/2+x)+1=0 Открыть страницу с решением к задаче (решений: 1) а) Решите уравнение √3sin2x+3cos2x=0 Открыть страницу с решением к задаче (решений: 1) а) Решите уравнение cosx(2cosx+tgx)=1. Открыть страницу с решением к задаче (решений: 1) a) Решите уравнение 1/tg2x+3/sinx+3=0 Открыть страницу с решением к задаче (решений: 1) а) Решите уравнение 2sin2x+cosx+4sinx+1=0 Открыть страницу с решением к задаче (решений: 1) Решите уравнение (cox–1)(tgx+√3)·√cosx=0 Открыть страницу с решением к задаче (решений: 1) Решите уравнение 2tgx·cos2x–cosx=0 Открыть страницу с решением к задаче (решений: 1) а) Решите уравнение 7sin2x+8cosx–8=0 Открыть страницу с решением к задаче (решений: 3) а) Решите уравнение 6sin2x–5sinx–4=0 Открыть страницу с решением к задаче (решений: 3) а) Решите уравнение tg2x+5tgx+6=0 Открыть страницу с решением к задаче (решений: 1) а) Решите уравнение 1/tg2x–1/sinx=1 Открыть страницу с решением к задаче (решений: 1) а) Решите уравнение 7sin2x+4sinxcosx–3cos2x=0 Открыть страницу с решением к задаче (решений: 1) а) Решите уравнение log2(3sinx–cosx)+log2(cosx)=0 Открыть страницу с решением к задаче (решений: 2) a) Решите уравнение: log5(cosx – sin2x + 25) = 2 Открыть страницу с решением к задаче (решений: 1) a) Решите уравнение: cos2x + sin2x = 0,25 б) Найдите все корни этого уравнения, принадлежащие отрезку [3p ; 9p/2] Открыть страницу с решением к задаче (решений: 2) a) Решите уравнение: 6sin2x + 5sin(p/2 – x) – 2 = 0 б) Найдите все корни этого уравнения, принадлежащие отрезку [–5p ; –7p/2] Открыть страницу с решением к задаче (решений: 1) Решите уравнение (2cos2x+cosx–1)√–sinx=0 Открыть страницу с решением к задаче (решений: 1) Решите уравнение 6cos2x–7cosx–5=0 . Открыть страницу с решением к задаче (решений: 1) Решите уравнение tgy–4sin2y–2sin2y=2cos2y–ctgy Открыть страницу с решением к задаче (решений: 1) Решите уравнение sin4x–sinx=0 Открыть страницу с решением к задаче (решений: 1) a) Решите уравнение 4cos4x–4cos2x+1=0 Открыть страницу с решением к задаче (решений: 1) а) Решите уравнение cos2x=1–cos(π/2–x). Открыть страницу с решением к задаче (решений: 1) Решите уравнение 6sin2x+7cosx–7=0 и найдите корни, принадлежащие отрезку [–3π;–π] Открыть страницу с решением к задаче (решений: 1) Решите уравнение 3sin2x+5sinx+2=0 и найдите корни, принадлежащие отрезку [π/2;2π] Открыть страницу с решением к задаче (решений: 2) а) Решите уравнение cos2x+2cos2x–sin2x=0 Открыть страницу с решением к задаче (решений: 1) Решите уравнение (6cos2x–5cosx–4)√–43sinx=0 Открыть страницу с решением к задаче (решений: 1) а) Решите уравнение 3/sin(π–x)–1/sin2x=2 Открыть страницу с решением к задаче (решений: 1) a) Решите уравнение 1/cos2x+3tgx–5 = 0 Открыть страницу с решением к задаче (решений: 1) a) Решите уравнение 2sin2x+(2–√2)cosx+√2–2=0 Открыть страницу с решением к задаче (решений: 1) Решить уравнение cos3x+sin2x=0 Открыть страницу с решением к задаче (решений: 1) Решить уравнение sin3x+sin4x+sin5x=0 Открыть страницу с решением к задаче (решений: 1) Решить уравнение sin2x–cosx=0 Открыть страницу с решением к задаче (решений: 1) Решить уравнение 4cosx–3sinx=5 Открыть страницу с решением к задаче (решений: 1) Решить уравнение 2cos4x+cos2x=1 Открыть страницу с решением к задаче (решений: 1) a) Решить уравнение √2cos2x=sin(x–π/2) Открыть страницу с решением к задаче (решений: 1) а) Решите уравнение sin2x=sin(π/2+x) Открыть страницу с решением к задаче (решений: 1) а) Решите уравнение cos2x+3sin2x=1,25 Открыть страницу с решением к задаче (решений: 1) а) Решите уравнение cos2x+0,5=cos2x. Открыть страницу с решением к задаче (решений: 1) а) Решите уравнение 4cos3x+3sin(x–π/2)=0. Открыть страницу с решением к задаче (решений: 1) а) Решите уравнение sin2x=2sinx–cosx+1 Открыть страницу с решением к задаче (решений: 1) а) Решите данное уравнение 2cos2x+2sin2x=3. Открыть страницу с решением к задаче (решений: 1) Решите уравнение 6sin2x+sin2x=2 Открыть страницу с решением к задаче (решений: 1) Решите уравнение Sin2x+Cos4x=0 Открыть страницу с решением к задаче (решений: 2) а) Решите уравнение cos2x=1–cos(π/2–x) Открыть страницу с решением к задаче (решений: 2) а) Решите уравнение cos(3π/2+2x)=cosx Открыть страницу с решением к задаче (решений: 1) Решите уравнение 3sin2x–4cosx+3sinx–2=0 Открыть страницу с решением к задаче (решений: 1) Решить систему: Открыть страницу с решением к задаче (решений: 0) Решить систему: Открыть страницу с решением к задаче (решений: 1) Найдите корни уравнения 2cos2х + 5sinx = 4, принадлежащие промежутку [–5; l]. Открыть страницу с решением к задаче (решений: 1) Решить уравнение (2x+1)(x+1)(2x+3)/√sin(π·x)=0 Ответ: проверить Открыть страницу с решением к задаче (решений: 1) Решите уравнение sin2x=cos(pi/2–x) Открыть страницу с решением к задаче (решений: 1) Решить уравнения 2sin2x–5sinxcosx+2cos2x=0 Открыть страницу с решением к задаче (решений: 2) Решите уравнение cos4x–cos2x=0 Методы решения тригонометрических уравнений — презентация онлайнМЕТОДЫ РЕШЕНИЯ 2. ЦЕЛЬ:Систематизировать, обобщить,расширить знания и умения, связанные с применением методов решения тригонометрических уравнений № № метода Методы Sin x/3 — cos 6x = 2 4(б) 4 5 sinx – 2 cosx = 1 3, 2(б,в) 5 sin3x cos2x = 1 1.  Разложение на множители. Разложение на множители.2.Введение новой переменной: а) сведение к квадратному; б) универсальная подстановка; в) введение вспомогательного аргумента. 3. Сведение к однородному уравнению. 4. Использование свойств функций, входящих в уравнение: а) обращение к условию равенства тригонометрических функций; б) использование свойства ограниченности функции. 1 Уравнения 2 3 4(б) (cos x – sin x ) 1,2(б,в), 3 7 1 – sin2x = cos x – sin x 1,2(б,в)3 8 cos3x = sin x 4(а) 9 4 – cos2 x = 4 sin x 2(а) 10 sin3x – sin5x = 0 4(б) 11 tg 3x tg(5x + /3) = 1 4(а) 12 2 tg x/2 — cos x = 2 6 cos2x = 1,2(а,б,в) ,3,4(а) 1. Какие методы решения тригонометрических уравнений вы знаете? 2. Определите и ответьте, какими методами нужно решать данные тригонометрические уравнения? а) sin 2x – cos x = 0 б) 2sin²x — 5sinx = -3 в) cos²x – sin²x = sinx – cosx г) sin2 x – 3sinx cosx + 2cos²x = 0 3.  Решите простейшие тригонометрические уравнения: Решите простейшие тригонометрические уравнения:Некоторые типы тригонометрических уравнений. 1. Уравнения, сводящиеся к квадратным, относительно cos х = t, sin х = t. A sin2 x + B cosx + C = 0 A cos2 x + В sinx + C = 0 Решаются методом введения новой переменной. 2.Однородные уравнения первой и второй степени. I степени. II степени. A sinx + B cosx = 0 : cosx A tg x + B = 0 A sin2 x + B sinx cosx + A cos2 x = 0 A tg2 x + B tgx + C = 0 : cos2x Решаются методом разложения на множители и методом введения новой переменной. 3. Уравнение вида: А sinx + B cosx = C. А, В, С 0 Применимы все методы. 4. Понижение степени. 2 А cos2x + В cos x = C. A cos2x + B sin 2 x = C. Решаются методом разложения на множители. A sin2x + B sin 2 x = C. 2 A sin2x + B cos x = C. 2 2 sin x cos x). Сводятся к однородным уравнениям С = С( Формулы. Универсальная подстановка. 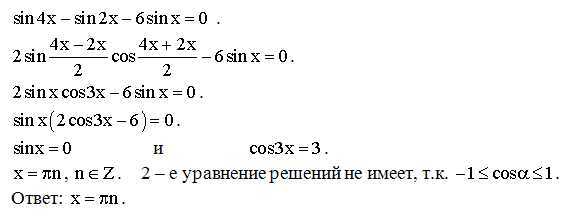 x 2tg 2 ; sinx x 1 tg 2 2 x 1 — tg 2; cosx x 1 tg 2 2 2 x 2 ; tgx x 1 tg 2 2 2tg х + 2 n; Проверка обязательна! Понижение степени. cos 2 x = (1 + cos2x ) : 2 sin 2 x = (1 – cos 2x) : 2 Метод вспомогательного аргумента. a cosx +b sinx заменим на C sin(x+ ), где С a 2 b 2 ; b а cos = ; — вспомогательный аргумент. sin = ; С С Сведение к однородному. Уравнения вида Пример. 5 sin2 x + A sin2x + B sin2 x = C, Asin2x + Bcos2 x = C. 3 sinx cosx + 6 cos2 x = 5. Разложение на множители. Пример. cos 2 x — 2 cosx = 4 sinx — sin2x Проблемы ,возникающие при решении тригонометрических уравнений 1.Потеря корней: делим на g(х). опасные формулы (универсальная подстановка). Этими операциями мы сужаем область определения. 2. Лишние корни: возводим в четную степень. умножаем на g(х) (избавляемся от знаменателя).  Этими операциями мы расширяем область определения. Уравнение 2 sin x 3 cos x 0 . Уравнение 2 sin x 3 cos x 0 . Поделив уравнение на cos x , получим 2tgx 3 0 , tgx 3 3 x arctg n, n . 2 , 2 При решении этой задачи обе части уравнения 2 sin x 3 cos x 0 были поделены на cos x . Напомним, что при делении уравнения на выражение, содержащее неизвестное, могут быть потеряны корни. Поэтому нужно проверить, не являются ли корни уравнения cos x 0 корнями данного уравнения. Если cos x 0 , то из уравнения 2 sin x 3 cos x 0 следует, что sin x 0 . Однако sin x и cos x не могут одновременно равняться нулю, так как они связаны равенством sin 2 x cos 2 x 1 . Следовательно, при делении a sin x b cos x 0, где a 0 , b 0 , на cos x (или sin x ) уравнения получаем уравнение, равносильное данному. Решить уравнение cos²x + sinx cosx = 0 1) Делить на cosx нельзя, так как в условии не указано , что cosx не равен нулю.  Но можно утверждать, что sinx не равен нулю, так как Но можно утверждать, что sinx не равен нулю, так какв противном случае cosx равен 0, что невозможно , так как sin²xcos²x =1. Значит можно разделить на sin²x. 2) Решим уравнение разложением на множители: cos²x + sinx cosx = 0, сosx(cosx + sinx ) = 0, сosx = 0 x 2 или n, n ; cosx + sinx = 0, tg x=-1, x 4 k , k ; Уравнения, линейные относительно sin x и cos x а sin x + в cos x = с. Если а=в=0, а с не равно 0, то уравнение теряет смысл; Если а=в=с=0, то х – любое действительное число, то есть уравнение обращается в тождество. Рассмотрим случаи, когда а,в,с не равны 0. Примеры: 2 sin x cos x 2 3 sin 5x — 4 cos 5x = 2 2 sin 3x + 5 cos 3x = 8. Последнее уравнение не имеет решений, так как левая часть его не превосходит 7. Уравнения, этого вида можно решить многими способами: с помощью универсальной подстановки, выразив sin x и cos x через tgх ; сведением уравнения к однородному; введением вспомогательного аргумента и другими.  Решение этих уравнений существует при a 2 b 2 c 2 2 sin x cos x 2 Данное уравнение является уравнением вида a sin x b cos x c , (1) где a 0 , b 0 , c 0 , которое можно решить другим способом. Разделим обе части этого уравнения на a 2 b 2 : a a2 b sin x 2 a a2 b Введем вспомогательный аргумент cos a a2 b c cos x 2 a 2 b 2. , такой, что (2) b , sin 2 . a2 b2 Такое число существует, так как 2 2 a b 2 1. 2 2 2 a b a b Таким образом, уравнение можно записать в виде sin x cos cos x sin sin( x ) c a b c 2 a2 b2 2 , . Последнее уравнение является простейшим тригонометрическим уравнением. Уравнение 2 sin x cos x 2 . x x x — sin2 x и 2 2 2 2 x x 2 правую часть уравнения в виде 2 2 1 2(sin cos 2 ,) 2 2 Используя формулы sin x = 2 sin записывая cos , cos x = cos2 x x x x x x cos cos 2 sin 2 2 sin 2 2 cos 2 , 2 2 2 2 2 2 x x x x x 3 sin2 4 sin cos cos2 0. 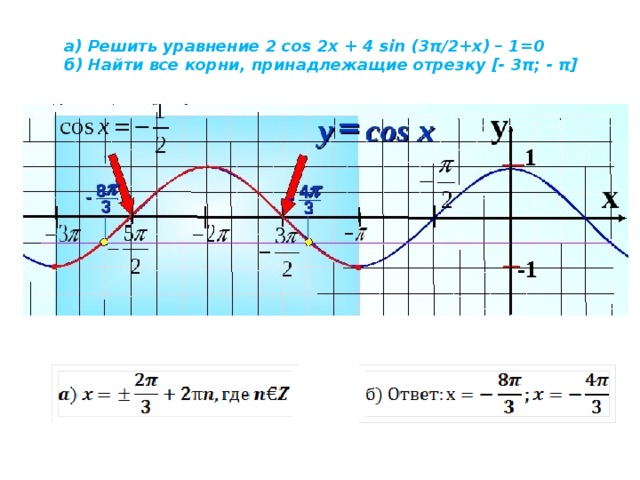 Поделив это уравнение на cos 2 , Поделив это уравнение на cos 2 ,2 2 2 2 2 x 2 x 4tg 1 0. получим равносильное уравнение 3tg 2 2 x 1 . Обозначая tg y , получаем 3 y 2 4 y 1 0 , откуда y1 1, y2 2 3 x 1 x 1 1 tg , arctg n, x 2arctg 2 n, n . 1) 2 3 2 3 3 x x 2) tg 1, n, x 2 n, n ; 2 2 4 2 получаем 4 sin Ответ: x 2 2 n, n ; x 2arctg 1 2 n, n . 3 16. Решить уравнениеРЕШИТЬ УРАВНЕНИЕ4sin²x – 4sinx – 3 = 0 2cos²x – sinx – 1 = 0 17. Ответы.ОТВЕТЫ.4sin²x — 4 sinx – 3 = 0 ( -1)n+1 П/6 +Пn, n Z. 2 сos²x – sin x – 1 = 0 ±П/6 +Пn; -П/2+2Пn, n Z. 18. Решить уравнениеРЕШИТЬ УРАВНЕНИЕ4 sin x 3 cos x 5. Решить уравнение 4 sin x 3 cos x 5. Здесь a 4, b 3, c 5, a 2 b2 5 Поделим обе части уравнения на 5: 4 3 sin x cos x 1. 5 5 4 Введем вспомогательный аргумент , такой, что cos , Исходное уравнение можно записать в виде 5 3 sin .  5 sin x cos cos x sin , 1 sin( x ) , 1 4 4 откуда x 2 n, где arccos , x arccos 2 n, n Z 2 5 2 5 Ответ: x 4 arccos 2 n, n . 2 5 6 =30° sin x 1 2 cos x 3 2 3 3 tg x ctg x 3 4 =45° 2 2 2 2 3 = 60° 3 2 1 2 1 3 1 3 3 А 0° 2 = 90° =180° 3 2 =270° 2 =360° sin x 0 1 0 -1 0 cos x 1 0 -1 0 1 tg x 0 — 0 — 0 ctg x — 0 — 0 —
(cos x)/(1 + sinx) + (1 + sinx)/(cosx) = 2 в4 885 результатов
Страницы
Тригонометрические функции — вопросы с ответами Представлен набор вопросов по тригонометрии, связанных с тригонометрическими функциями.
|

 25 ≤ n ≤ 1.25
25 ≤ n ≤ 1.25 2(\frac{\pi}{2} + x) = -cosx \). Найдите все корни, принадлежащие отрезку [\(-\frac{5\pi}{2};-\pi \)].
2(\frac{\pi}{2} + x) = -cosx \). Найдите все корни, принадлежащие отрезку [\(-\frac{5\pi}{2};-\pi \)].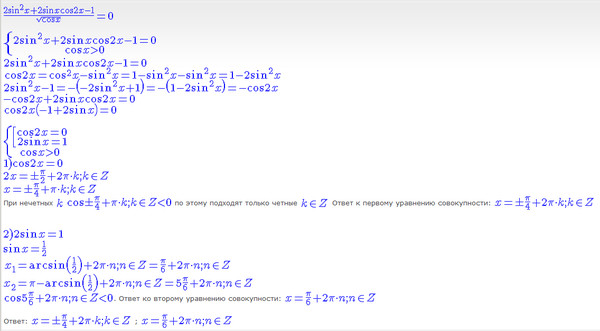
 2+3V2у-3=0.
2+3V2у-3=0. 5sinx)=2
5sinx)=2

 5 решить уравнение
5 решить уравнение

 –sinx=10/3
–sinx=10/3 Укажите его корни, принадлежащиеотрезку [–π;2π]
Укажите его корни, принадлежащиеотрезку [–π;2π]
 )/3
)/3
 ..пожалуйста, помогите мне
..пожалуйста, помогите мне a) Определить точное значение cosx b) Определить точное значение siny
a) Определить точное значение cosx b) Определить точное значение siny x и g(x)= синкс 93 Д. -cos х + 120 х Э. sin х
x и g(x)= синкс 93 Д. -cos х + 120 х Э. sin х f(x) растет быстрее, чем g(x), когда x стремится к бесконечности. g(x) растет быстрее, чем f(x), когда x стремится к бесконечности. f(x) и g(x) растут с той же скоростью, что и x стремится к бесконечности. Ставка
f(x) растет быстрее, чем g(x), когда x стремится к бесконечности. g(x) растет быстрее, чем f(x), когда x стремится к бесконечности. f(x) и g(x) растут с той же скоростью, что и x стремится к бесконечности. Ставка (n) означает n-ю производную от y по x. 92(1/2 года)
(n) означает n-ю производную от y по x. 92(1/2 года) е. 0 ≤ θ < 2π) уравнения cos(2θ)cos(θ) = sin(2θ)sin(θ). Пожалуйста, может кто-нибудь помочь и показать все работы Спасибо
е. 0 ≤ θ < 2π) уравнения cos(2θ)cos(θ) = sin(2θ)sin(θ). Пожалуйста, может кто-нибудь помочь и показать все работы Спасибо Какой
Какой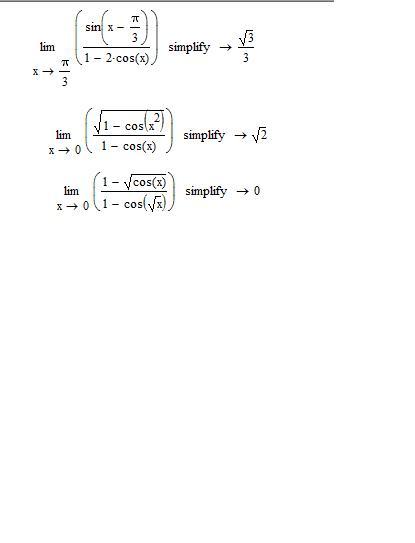 На интервале [0, 2pi] каковы решения уравнения sin3xcos2x = -cos3xsin2x + 1? пи/10 и пи/2? 2. Каково значение tan75degrees? √(3) + 1)/(1 — √(3))? 3. Значение cos (130 градусов) cos (130 градусов) + sin (10 градусов) sin (10 градусов)? Не
На интервале [0, 2pi] каковы решения уравнения sin3xcos2x = -cos3xsin2x + 1? пи/10 и пи/2? 2. Каково значение tan75degrees? √(3) + 1)/(1 — √(3))? 3. Значение cos (130 градусов) cos (130 градусов) + sin (10 градусов) sin (10 градусов)? Не (cos 2x) — (cos x)=0
(cos 2x) — (cos x)=0 Я знаю, что нужно использовать формулу cos(A+B), но я просто не уверен в своей способности решить ее правильно.
Я знаю, что нужно использовать формулу cos(A+B), но я просто не уверен в своей способности решить ее правильно. Используйте аппроксимацию касательной, чтобы найти координату y точки на кривой с координатой x pi/3 + pi/180.
Используйте аппроксимацию касательной, чтобы найти координату y точки на кривой с координатой x pi/3 + pi/180. Выразите A в градусах и запишите числовые значения с точностью до 2 знаков после запятой. Так что я совершенно не понимаю, как вообще начать
Выразите A в градусах и запишите числовые значения с точностью до 2 знаков после запятой. Так что я совершенно не понимаю, как вообще начать A — w1=cos(35°)+isin(35°) w2=cos(125°)+isin(125°) w3=cos(215°)+isin(215°) w4=cos(305°)+ isin(305°) B — w1 =cos(40°)+isin(40°) w2
A — w1=cos(35°)+isin(35°) w2=cos(125°)+isin(125°) w3=cos(215°)+isin(215°) w4=cos(305°)+ isin(305°) B — w1 =cos(40°)+isin(40°) w2 Решения и ответы даны.
Решения и ответы даны. Следовательно
Следовательно
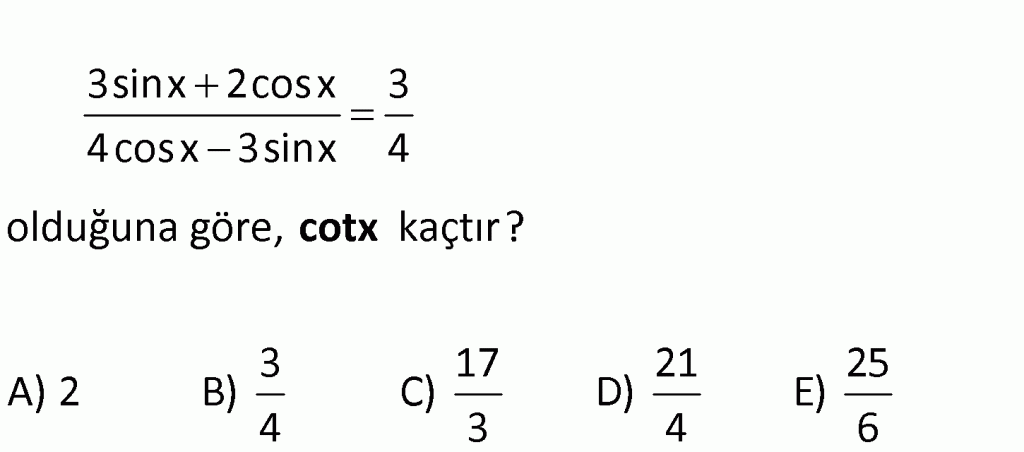 Найдите точное значение cos (x).
Найдите точное значение cos (x). Следовательно
Следовательно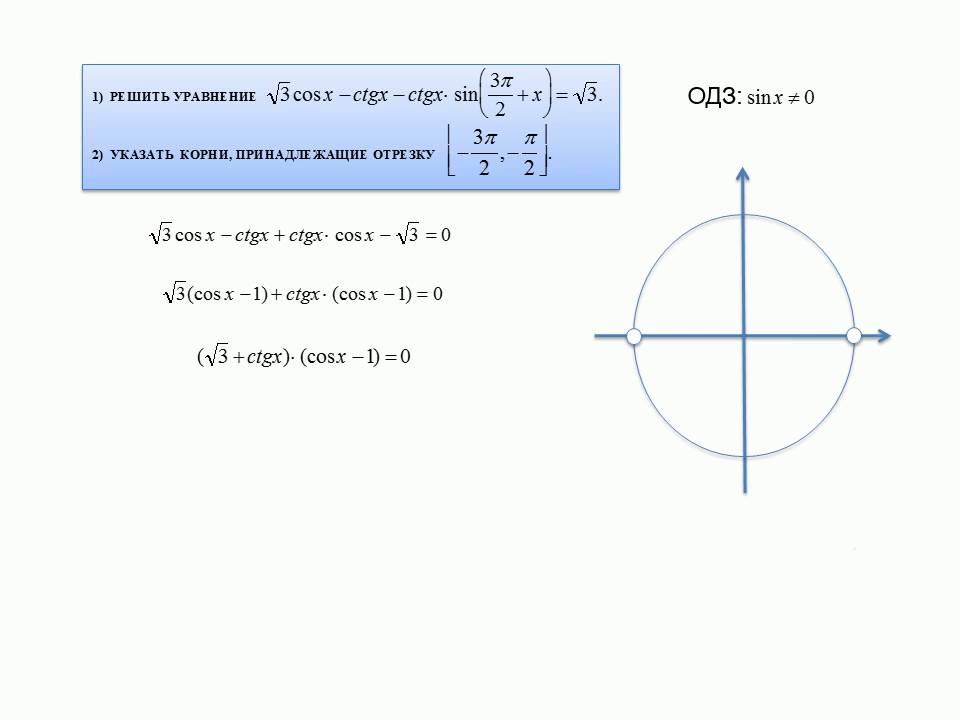

 Найдите cos (x + y) через a и b.
Найдите cos (x + y) через a и b. Найдите sin (3x) и cos (3x).
Найдите sin (3x) и cos (3x).