Корень из 4 x 5: Найти производную y’ = f'(x) = sqrt(4*x-5) (квадратный корень из (4 умножить на х минус 5))

Как найти Дискриминант? 🤔 Формулы, Примеры решений.

Понятие квадратного уравнения

Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.

Например, возьмем выражение 8 + 4 = 12. При вычислении левой части получается верное числовое равенство, то есть 12 = 12.

Уравнением можно назвать выражение 8 + x = 12, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.

Степень уравнения можно определить по наибольшей степени, в которой стоит неизвестное. Если неизвестное стоит во второй степени, значит, такое уравнение является квадратным.

Квадратное уравнение — это ax² + bx + c = 0, где a — первый или старший коэффициент, не равный нулю, b — второй коэффициент, c — свободный член.

Есть три вида квадратных уравнений:

• не имеют корней;
• имеют один корень;
• имеют два различных корня.

Понятие дискриминанта

Дискриминант квадратного уравнения — это выражение, которое находится под корнем в формуле нахождения корней квадратного уравнения. Дискриминант в переводе с латинского означает «отличающий» или «различающий» и обозначается буквой D.

Дискриминант — отличный помощник, чтобы понять, сколько в уравнении корней.

Чаще всего для поиска дискриминанта используют формулу:

В этом ключе универсальная формула для поиска корней квадратного уравнения выглядит так:

Эта формула подходит даже для неполных квадратных уравнений.

Но есть и другие формулы — все зависит от вида уравнения. Чтобы в них не запутаться, сохраняйте табличку или распечатайте ее и храните в учебнике.

Как решать квадратные уравнения через дискриминант

В 8 классе на алгебре можно встретить задачу по поиску действительных корней квадратного уравнения.

Для этого важно перед использованием формул найти дискриминант и убедиться, что он неотрицательный. Только после этого вычисляем значения корней. Если дискриминант отрицательный, значит уравнение не имеет действительных корней.

Алгоритм решения квадратного уравнения ax² + bx + c = 0:

• как найти дискрининант: D = b² − 4ac;
• если дискриминант отрицательный — зафиксировать, что действительных корней нет;
• если дискриминант равен нулю — вычислить единственный корень уравнения по формуле х = — b²/2a;
• если дискриминант положительный — найти два действительных корня квадратного уравнения по формуле корней
  

А вот и еще одна табличка: в ней вы найдете формулы для поиска корней квадратных уравнений при помощи дискриминанта:

Чтобы запомнить алгоритм решения квадратных уравнений и с легкостью его использовать, важно практиковаться. Вперед!

Примеры решения квадратных уравнений с помощью дискриминанта

Пример 1. Решить уравнение: 3x² — 4x + 2 = 0.

Как решаем:

1. Определим коэффициенты: a = 3, b = -4, c = 2.


2. Найдем дискриминант: D = b² — 4ac = (-4)² — 4 * 3 * 2 = 16 — 24 = -8.

Ответ: D < 0, корней нет.

Пример 2. Решить уравнение: x² — 6x + 9 = 0.

Как решаем:

1. Определим коэффициенты: a = 1, b = -6, c = 9.


2. Найдем дискриминант: D = b² — 4ac = (-6)² — 4 * 1 * 9 = 36 — 36 = 0.


3. D = 0, значит уравнение имеет один корень:
   

Ответ: корень уравнения 3.

Пример 3. Решить уравнение: x² — 4x — 5 = 0.

Как решаем:

1. Определим коэффициенты: a = 1, b = -4, c = -5.


2. Найдем дискриминант: D = b² — 4ac = (-4)² — 4 * 1 * (-5) = 16 + 20 = 36.


3. D > 0, значит уравнение имеет два корня:

    

x₁ = (4 + 6) : 2 = 5,

x₂ = (4 — 6) : 2 = -1.

Ответ: два корня x₁ = 5, x₂ = -1.

Не желаешь повторить формулы сокращенного умножения?

Как вынести из под корня число

Извлечь из данного числа корень какой-нибудь степени значит найти такое число, которое при возведении в эту степень, будет равно данному числу.

Из правил знаков при возведении в степень следует, что:

Корень нечётной степени из положительного числа есть число положительное, а из отрицательного – отрицательное.

, так как (+3) 3 =27

, так как (-3) 3 =-27

Корень чётной степени из положительного числа может быть как положительным, так и отрицательным числом.

, так как (+3) 2 =+9 и (-3) 2 =+9

, так как (+4) 4 =+256 и (-4) 4 =+256

Корень чётной степени из отрицательного числа является невозможным выражением, потому что любое положительное или отрицательное число при возведении в чётную степень даёт только положительный результат. Таким образом, – это невозможные выражения. Невозможные выражения иначе называют мнимыми.

Извлечение корня из произведения, степени и дроби

Чтобы извлечь корень из произведения, надо извлечь его из каждого множителя отдельно.

Так же можно сказать, что корень произведения равен произведению корней всех его множителей:

Чтобы извлечь корень из степени, следует показатель степени разделить на показатель корня:

Чтобы извлечь корень из дроби, следует извлечь его отдельно из числителя и из знаменателя:

Вынесение множителя из-под знака корня

Когда нельзя извлечь корень из всего подкоренного числа или выражения, то подкоренное число или выражение раскладывают на множители и извлекают корень только из тех множителей, из которых это возможно сделать.

Внесение множителя под корень

Если нужно внести множитель под знак корня, то его следует возвести в степень, равную показателю корня.

Как выносить из под корня число

Часто вынесение множителя (числа) из под знака корня может быть необходимо для совершения каких-либо арифметических операций, например, для сокращения дроби или вынесения общего множителя и дальнейшего преобразования выражения.

Давайте рассмотрим основные арифметические правила и определения, необходимые для того, чтобы понять, как вынести число из под корня.

Необходимые операции и определения

Разложение выражения на множители — это преобразование этого числа в произведение нескольких сомножителей без изменения значения исходного выражения.

Это довольно частая операция, необходимая для вынесения множителя из-под знака корня.

Для разложения на множители используются следующие приёмы:

• Вынесение за скобки общего множителя;
• Группировка множителей;
• Применение формул сокращённого умножения;
• Комбинация вышеизложенных методов.

При вынесении за скобки общего множителя для начала нужно определить множитель, который можно вынести, а затем разделить всё выражение на этот множитель и записать результат частного рядом со множителем как произведение, например:

Попробуй обратиться за помощью к преподавателям

$6x^2 – 8xy +4x = 2x cdot 3x – 2x cdot 4y + 2x cdot 2 = 2x cdot (3x – 4y + 2)$. 2$.

Оба продемонстрированных выше метода можно комбинировать.

Свойства корня

Теперь перейдём к более детальному рассмотрению корня.

Корнем $n$-нной степени из числа $b$ называют число, которое нужно возвести в $n$-нную степень чтобы получить число $b$:

Процесс получения корня называется его извлечением.

Левая часть равенства вида $sqrt[n] = m$ называется радикалом, то, что стоит непосредственно под знаком корня — подкоренным выражением, а число, стоящее слева сверху перед знаком корня называется показателем корня.

Правая же часть равенства после знака «равно» называется корнем $n$-нной степени из числа $b$.

Задай вопрос специалистам и получи
ответ уже через 15 минут!

При извлечении числа из-под корня нужно учитывать то, что в случае с корнем нечётной степени возможен лишь один ответ, математически это запишется так: $sqrt[n] = b$, тогда как в случае с извлечением корня чётной степени ответа будет два, причём один с положительным знаком, а другой с отрицательным, это записывается так: $sqrt[n]= ±b$.

Также существует ещё одна теорема, которую нужно знать при вынесении множителя из-под знака корня:

Для извлечения корня $n$-ой степени из произведения, моно извлечь его из каждого сомножителя отдельно, а результаты перемножить. Математически это запишется так: $sqrt[n]=sqrt[n]sqrt[n]sqrt[n]left(1
ight)$.

Докажем эту теорему для случая если под корнем стоит положительное число, а степень $n$ является нечётной.

Применим эту логику к равенству $(1)$.

Для этого возведём в степень правую часть равенства. Но для того чтобы сделать это, необходимо возвести в степень произведение, а для этого нужно возвести в степень каждый сомножитель и затем перемножить их все между собой:

Получилось выражение, стоящее под знаком корня, а это значит, что теорема доказана.

Правила вынесения множителя из под знака корня

Вынесение множителя из-под знака корня $n$-ой степени — это упрощение выражения с помощью записи какого-либо множителя, являющегося частью подкоренного выражения, перед знаком корня. Например, $sqrt[6] <192>= sqrt[6] <64 cdot 3>= 2 sqrt[6]<3>$.

Для вынесения множителей из-под знака корня необходимо показатель выносимого множителя разделить на показатель корня и разместить перед корнем этот множитель с тем показателем степени, который получится в результате этого деления:

В частном случае, если приходится иметь дело с квадртным корнем, степень множителя, который необходимо вынести, нужно разделить на два, а сам множитель записать перед знаком корня:

В случае если приходится иметь дело с множителем-дробью, можно извлечь по отдельности корень из числителя и знаменателя, например:

Общий порядок вынесения множителя из под корня такой:

1. Сначала подкоренное значение раскладывается на множители непосредственно под знаком корня, а у этих множителей выделяются показатели степени.
2. Затем показатель степени при множителе делится на показатель корня, а сам выносимый множитель записывается слева от радикала.

Вынесите множитель из-под знака корня в следующих выражениях:

Так и не нашли ответ
на свой вопрос?

Просто напиши с чем тебе
нужна помощь

В данном материале мы продолжим рассказывать о том, как преобразовывать рациональные выражения, а конкретно о том, как правильно выносить множитель из-под знака корня. В первом пункте объясним, зачем нужно такое преобразование, далее покажем, как именно оно делается и сформулируем общее для всех случаев правило. Далее покажем, какие существуют методы, чтобы привести подкоренное выражение к удобному для преобразования виду, и разберем примеры решений задач.

Что такое вынесение множителя из-под знака корня

Чтобы лучше понять суть подобного преобразования, нужно сначала сформулировать, что такое вообще вынесение множителя из-под знака корня. Сформулируем определение:

Вынесение множителя из-под знака корня представляет собой замену выражения B n · C n на произведение B · C n с условием, что n – нечетное число, или же на произведение B · C – где n – четное число, а B и C – другие числа и выражения.

Если мы имеем в виду только квадратный корень, то есть число n равно двум, то процесс вынесения множителя можно свести к замене выражения B 2 · C на произведение B · C . Отсюда и название данного преобразования: после того, как оно было проведено, множитель B y оказывается свободным от знака корня.

Приведем примеры, поясняющие данное определение. Так, допустим, у нас есть выражение 2 2 · 3 . Оно аналогично B 2 · C , где B равно двум, а C – трем. Заменив данный корень на произведение 2 · 3 и опустив знаки модулей (это можно сделать, поскольку оба множителя являются положительными числами), мы получим 2 · 3 . Мы вынесли множитель 2 2 из-под знака корня.

Приведем еще один пример подобного преобразования. У нас есть выражение ( x 2 – 3 · x · y · z ) 2 · x = x 2 – 3 · x · y · z · x . Здесь из-под корня был вынесен не просто числовой множитель, а целое выражение с переменными ( x 2 − 3 · x · y · z ) 2 .

Оба примера относятся к случаю вынесения множителя из-под квадратного корня. Можно также производить данные преобразования и для корней n -ной степени. Вот пример с кубическим корнем: ( 3 · a 2 ) 3 · 2 · a 2 3 = 3 · a 2 · 2 · a 2 3

Пример с корнем шестой степени: 1 2 · x 2 + y 2 6 · 5 · ( x 2 + y 2 ) 6 можно преобразовать в произведение 1 2 · x 2 + y 2 · 5 · ( x 2 · y 2 ) 6 , которое, в свою очередь, упрощается до 1 2 · ( x 2 + y 2 ) · 5 · ( x 2 + y 2 ) 6 . В данном случае мы выносим множитель 1 2 · x 2 + y 2 6 .

Мы выяснили, что такое вынесение множителя из-под знака корня. Теперь перейдем к доказательствам, т.е. поясним, почему произведение, полученное в итоге данного преобразования, равнозначно исходному выражению.

Почему возможно заменить корень на произведение

В этом пункте мы будем разбираться, как возможна такая замена и почему корень B n · C n равнозначен произведениям B · C n и B · C n . Обратимся к ранее изученным теоретическим положениям.

Когда мы разбирали преобразование иррациональных выражений, у нас получились некоторые важные результаты, которые мы собрали в таблицу. Здесь нам будут нужны только два из них:

1. Выражение A · B n при условии нечетности n может быть заменено на A n · B n , а для четных n – A n · B n .

2. Выражение A n n при нечетном значении n может быть преобразовано в A , а при четном – в | A | .

Используя эти результаты и зная основные свойства модуля, мы можем вывести следующее:

• при четном n : B n · C n = B n n · C n = B · C n ;
• при нечетном n : B n · C n = B n n · C n = B n n · C n = B · C n .

Эти выражения лежат в основе преобразований, которые мы проводим, вынося множитель из-под знака корня.

Следовательно, можно вывести две формулы:

• B 1 n · B 2 n · . . . · B k n · C n = B 1 · B 2 · . . . · B k · C n для нечетного n ;
• B 1 n · B 2 n · . . . · B k n · C n = B 1 · B 2 · . . . · B k · C n для четного n .

Здесь B 1 , B 2 , и др. могут быть как числами, так и выражениями.

С помощью данных формул можно выполнить вынесение из-под корня сразу нескольких множителей.

Основное правило вынесения множителя из-под корня

Когда нам нужно решать примеры с подобными преобразованиями, чаще всего приходится предварительно приводить подкоренное выражение к виду B n · C . С учетом этого момента мы можем записать следующие правила.

Для вынесения множителя из-под корня в выражении A n нужно предварительно привести корень к виду B n · C n и после этого перейти к произведению B · C n (при нечетном показателе) или к B · C n (при четном показателе, при необходимости раскрываем модули).

Таким образом, схема решения подобных задач выглядит следующим образом:

A n → B n · C n → B · C n , е с л и n – н е ч е т н о е B · C n , е с л и n – ч е т н о е

Если нам надо вынести несколько множителей, то действуем так:

A n → B 1 n · B 2 n · . . . · B k n · C n → B 1 · B 2 · . . . · B k · C n , е с л и n – н е ч е т н о е B 1 · B 2 · . . . · B k · C n , е с л и n – ч е т н о е

Теперь можно переходить к решению задач.

Задачи на вынесение множителя из-под знака корня

Условие: выполните вынесение множителя за знак корня в трех выражениях: 2 2 · 7 , – 1 2 3 2 · 5 , ( – 0 , 4 ) 7 · 11 7 .

Решение

Мы видим, что подкоренные выражения во всех трех случаях уже имеют нужный нам вид. Поскольку в первых двух примерах показателем корня является четное число, а в третьем – нечетное, записываем следующее:

1. Показатель корня равен 2 . Берем правило вынесения множителя для четного показателя и вычисляем: 2 2 · 7 = 2 · 7 = 2 · 7
2. Во втором выражении показатель тоже четный, значит, – 1 2 3 2 · 5 = – 1 2 3 · 5 = 1 2 3 · 5
   В этом случае мы можем сначала преобразовать выражения, исходя из основных свойств корня:
   – 1 2 3 2 · 5 = – 1 2 · 1 2 3 2 · 5 = 1 2 3 2 · 5
   А потом уже выносить множитель: 1 2 3 2 · 5 = 1 2 3 · 5 = 1 2 3 · 5 .
3. Последнее выражение имеет нечетный показатель, поэтому нам понадобится другое правило: ( – 0 , 4 ) 7 · 11 7 = – 0 , 4 · 11 7 .
   Возможен и такой вариант расчета:
   – 0 , 4 7 · 11 7 = ( – 1 ) 7 · 0 , 4 7 · 11 7 = = – 0 , 4 7 · 11 7 = – 0 , 4 7 · 11 7 = – 0 , 4 · 11 7
   ​​​​​​Или такой:
   – 0 , 4 7 · 11 7 = ( – 1 ) 7 · 0 , 4 7 · 11 7 = = – 0 , 4 7 · 11 7 = 0 , 4 7 · – 11 7 = 0 , 4 · – 11 7 = – 0 , 4 · 11 7

Ответ: 1 ) 2 · 7 ; 2 ) 1 2 3 · 5 ; 3 ) – 0 , 4 · 11 7 .

Условие: преобразуйте выражение ( – 2 ) 4 · ( 0 , 3 ) 4 · 7 4 · 11 4 .

Решение:

При помощи схемы, приведенной во втором пункте статьи, мы можем вынести из-под корня сразу три множителя.

( – 2 ) 4 · ( 0 , 3 ) 4 · 7 4 · 11 4 = = – 2 · 0 , 3 · 7 · 11 4 = 4 , 2 · 11 4

Можно сделать преобразование в несколько шагов, вынося множителя по одному, но так будет гораздо дольше.

Есть и другой способ. Преобразуем само выражение, приведя его к виду

B n · C . После этого уже будем выносить множители:

( – 2 ) 4 · ( 0 , 3 ) 4 · 7 4 · 11 4 = = ( – 2 · 0 , 3 · 7 ) 4 · 11 4 = ( – 4 , 2 ) 4 · 11 4 = = – 4 , 2 · 11 4 = 4 , 2 · 11 4

Ответ: ( – 2 ) 4 · ( 0 , 3 ) 4 · 7 4 · 11 4 = – 4 , 2 · 11 4 = 4 , 2 · 11 4 .

Разберем более подробно тот случай, когда подкоренное выражение требует предварительного преобразования. Здесь есть несколько моментов, которые нужно дополнительно пояснить.

Предварительное преобразование подкоренного выражения

Мы уже отмечали, что выражение под корнем не всегда имеет удобный для нас вид. Часто корень дан как A n , и множитель, который нужно вынести, не представлен в явном виде. Иногда это обозначено в условии, но довольно часто множитель приходится определять самостоятельно. Посмотрим, как надо действовать в этих случаях.

Допустим, нам надо вынести заранее определенный множитель B . Естественно, подкоренное выражение должно быть таким, чтобы эта операция была возможна. Тогда для преобразования A n в B n · C n достаточно определить второй множитель, т.е. вычислить значение C из выражения A = B n · C .

Условие: есть выражение 24 · x 3 . Вынесите из-под знака корня множитель 2 3 .

Решение

Здесь мы имеем n = 3 , A = 24 · x , B 3 = 2 3 . Тогда из A = B n · С вычисляем C = A : ( B n ) = 24 · x : ( 2 3 ) = 3 · x .

Значит, 24 · x 3 = 2 3 · 3 · x 3 . Подкоренное выражение имеет нужный нам вид, и мы можем воспользоваться правилом для нечетного показателя и подсчитать: 24 · x 3 = 2 3 · 3 · x 3 = 2 · 3 · x 3 .

Ответ: 24 · x 3 = 2 · 3 · x 3 .

А как быть в случае, если множитель, который нужно вынести, не указан? Тогда у нас есть определенная свобода выбора, и мы можем использовать несколько подходов к решению задачи.

Допустим, нам дано выражение, под корнем у которого стоит степень или произведение нескольких степеней. В таком случае, зная основные свойства степени, мы можем преобразовать выражение в удобный для нас вид с очевидно указанными множителями для вынесения.

Условие: необходимо вынести множитель из-под корня в трех выражениях – 2 4 · 5 4 , 2 7 · 5 4 , 2 22 · 5 4 .

Решение

Преобразование первого выражения не представляет особой сложности, т.к. подобные примеры мы уже разбирали. Сразу вычисляем: 2 4 · 5 4 = 2 · 5 4 = 2 · 5 4 .

Во втором примере легко догадаться, как преобразовать подкоренное выражение: нужно просто представить 2 7 как 2 4 · 2 3 .

2 7 · 5 4 = 2 4 · 2 3 · 5 4 = 2 4 · 40 4 = 2 · 40 4 = 2 · 40 4

В последнем примере также нужно начать с преобразования подкоренного выражения. Сразу отметим, что итоговый вид будет таким:

2 5 4 · 2 2 · 5 4

Теперь покажем, как именно прийти к этому виду. Сначала выполняем деление 22 на 4 , получаем 5 с остатком 2 (если нужно, повторите, как правильно выполнять деление с остатком). Иначе говоря, 22 можно рассматривать как 4 · 5 + 2 . Используя свойства степени, можем записать:

2 22 + 2 5 · 4 + 2 = 2 5 · 4 · 2 2 = ( 2 5 ) 4 · 2 2

2 22 · 5 4 = ( 2 5 ) 4 · 2 2 · 5 4 = ( 2 5 ) 4 · 20 4 = = 2 5 · 20 4 = 32 · 20 4

Ответ: 1 ) 2 4 · 5 4 = 2 · 5 4 , 2 ) 2 7 · 5 4 = 2 · 40 4 , 3 ) 2 22 · 5 4 = 32 · 20 4 .

Если выражение под корнем не является степенью или произведением степеней, надо попробовать представить его в таком виде. Чаще всего встречаются следующие случаи.

Подкоренное выражение – натуральное составное число. Тогда мы сразу можем увидеть нужные множители, которые надо вынести из-под знака корня, предварительно разложив данное число на простые множители.

Условие: выполните вынесение множителя из-под знака корня в следующих выражениях: 1 ) 45 ; 2 ) 135 ; 3 ) 3456 ; 4 ) 102 .

1. Выполняем разложение 45 на простые множители.

45 15 5 1 3 3 5

То есть 45 = 3 · 3 · 5 = 3 2 · 5 , а 45 = 3 2 · 5 . В этом выражении видно, что выносить мы будем множитель 3 2 . Вычисляем:

3 2 · 5 = 3 · 5 = 3 · 5

1. Теперь представим в нужном виде число 135 и получим: 135 = 3 · 3 · 3 · 5 = 3 3 · 15 . Иначе можно записать, что 3 2 · 3 · 5 = 3 2 · 15 . Следовательно, 135 = 3 2 · 15 . Мы видим, что вынесению из-под знака корня подлежит множитель 3 2 :

3 2 · 15 = 3 · 15 = 3 · 15

1. Разложим на простые множители число 3456 :

3456 1728 864 432 216 108 54 27 9 3 1 2 2 2 2 2 2 2 3 3 3

У нас получилось, что 3456 = 2 7 · 3 3 , а 3456 = 2 7 · 3 3 . Поскольку 2 7 = 2 3 · 2 + 1 = ( 2 3 ) 2 · 2 и 3 3 = 3 2 · 3 , то 2 7 · 3 3 = ( 2 3 ) 2 · 2 · 3 2 · 3 = ( 2 3 ) 2 · 3 2 · 6 = = 2 3 · 3 · 6 = 24 · 6

1. Представим натуральное число 102 как произведение простых множителей и получим 2 · 3 · 17 . Видим, что все множители имеют показатель, равный единице, а показатель корня в этом примере равен двум. Следовательно, в данном примере ни один множитель не нужно выносить из-под знака корня, то есть такое действие для 102 нецелесообразно.

Ответ: 1 ) 45 = 3 · 5 ; 2 ) 135 = 3 · 15 ; 3 ) 3456 = 24 · 6 ; 4 ) 102 .

Теперь разберем, как решать примеры, у которых подкоренное выражение представлено в виде обыкновенной дроби. В этом случае следует числитель и знаменатель разложить на простые множители и посмотреть, можно ли вынести какие-то из них за знак корня. Если у нас есть десятичная дробь или смешанное число, предварительно заменяем их обыкновенными дробями, после чего переходим от корня отношения к отношению корней.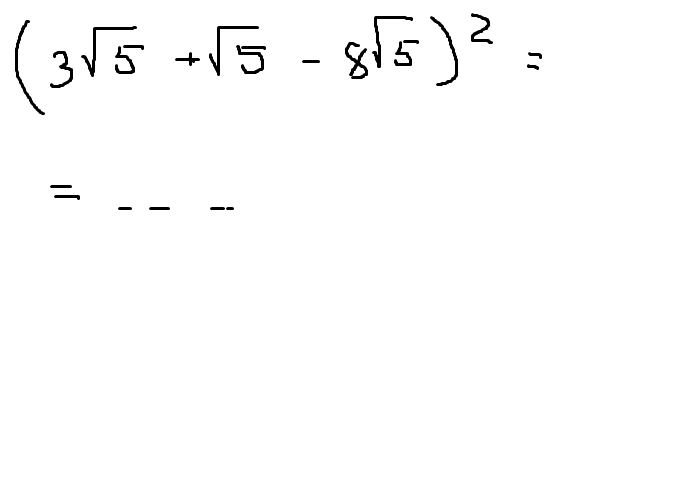

Условие: выполните вынесение множителя за корень в выражении 200 · 0 , 000189 · x 3 и упростите его.

Решение

Для начала перейдем от десятичной дроби к обыкновенной и разложим ее числитель и знаменатель на простые множители.

0 , 189 = 189 1000000 = 3 3 · 7 2 6 · 5 6

Используя свойства степени, перепишем выражение в следующем виде:

3 2 2 · 5 2 3 · 7

Подставим получившееся выражение в исходное и получим:

200 · 0 , 000189 · x 3 = = 200 · 3 2 2 · 5 2 3 · 7 · x 3 = = 200 · 3 2 2 · 5 2 · 7 · x 3 = 6 · 7 · x 3

К такому же ответу можно прийти и с помощью других преобразований:

200 · 0 , 000189 · x 3 = = 200 · 189 1000000 · x 3 = 200 · 189 1000000 3 · x 3 = = 200 · 189 3 1000000 3 · x 3 = 200 · 3 3 · 7 3 100 3 3 · x 3 = = 200 · 3 · 7 3 100 · x 3 = 6 · 7 3 · x 3 = 6 · 7 · x 3

Ответ: 200 · 0 , 000189 · x 3 = 6 · 7 · x 3 .

Иными словами, для обнаружения множителя, который можно вынести за знак корня, можно преобразовывать подкоренное выражение любыми допустимыми способами.

Условие: выполните упрощение иррационального выражения 2 · ( 3 + 2 · 2 ) .

Решение

Мы можем преобразовать выражение в скобках как 2 + 2 · 2 + 1 и далее как 2 2 + 2 · 2 · 1 + 1 2 .

То, что у нас получилось, можно свернуть в квадрат суммы с помощью формулы сокращенного умножения: 2 2 + 2 · 2 · 1 + 1 = 2 + 1 2 .

В итоге: 2 · 3 + 2 · 2 = 2 · 2 + 1 2 . Теперь выносим 2 + 1 2 за знак корня и упрощаем выражение:

2 · 2 + 1 2 = 2 · 2 + 1 = = 2 · 2 + 1 = 2 + 2

Ответ: 2 · 3 + 2 · 2 = 2 + 2 .

Теперь посмотрим, как вынести из-под знака корня выражение, содержащее переменные. В целом можно сказать, что для этого используются те же методы, что и при работе с числами.

Условие: вынесите множитель из-под знака корня в выражениях ( x – 5 ) 5 4 и ( x – 5 ) 6 4 .

Решение

1. Выполняем преобразование в первом примере.

( x – 5 ) 5 4 = ( x – 5 ) 4 · x – 5 4 = x – 5 · x – 5 4

Знак модуля можно опустить. Посмотрим, каким условием определяется область допустимых значений переменной для исходного выражения. Таким условием будет неравенство ( x − 5 ) 5 ≥ 0 . Для его решения выбираем метод интервалов и получаем x ≥ 5 . Если значение x принадлежит области допустимых значений, то значением выражения x – 5 будет неотрицательное число. Значит, можем записать следующее:

x – 5 · x – 5 4 = x – 5 · x – 5 4

1. ( x – 5 ) 6 4 = ( x – 5 ) 4 · x – 5 2 4 = = x – 5 · ( x – 5 ) 2 4 = x – 5 · x – 5 2 4

Выполним сокращение показателей корня и степени на два. Обратимся к таблице результатов из статьи о преобразовании иррациональных выражений, о которой мы говорили выше. Возьмем из нее следующий результат: выражение A m n · m можно заменить на A n при условии, что m и n – натуральные числа. Следовательно,

x – 5 · x – 5 2 4 = x – 5 · x – 5

Нужно ли здесь убирать знак модуля? Посмотрим на область допустимых значений данного выражения: ее составляют все действительные числа, поскольку ( x − 5 ) 6 ≥ 0 для любого x . При этом значения x − 5 могут быть больше 0 , если x > 5 , равными 0 или отрицательными. Значит, оставляем выражение в виде x – 5 · x – 5 или представляем его в виде системы уравнений

( x – 5 ) · x – 5 , x ≥ 5 ( 5 – x ) · 5 – x , x 5

Ответ: 1 ) ( x – 5 ) 5 4 = ( x – 5 ) · x – 5 4 ; 2 ) ( x – 5 ) 6 4 = x – 5 · x – 5 .

Условие: выполните упрощение выражения x 5 + 2 · x 4 · y + x 3 · y 2 .

Решение

Выносим за скобки x 3 и получаем x 3 · ( x 2 + 2 · x · y + y 2 ) . Выражение в скобках можно представить в виде квадрата суммы: x 3 · ( x 2 + 2 · x · y + y 2 ) = x 3 · ( x + y ) 2 .

Теперь видим множители, подлежащие вынесению из-под корня: x 3 · ( x + y ) 2 = x 2 · x · ( x + y ) 2 = x · x + y · x

Также мы можем убрать знаки модуля, в которых находится x, поскольку область допустимых значений будет определена условием x 5 + 2 · x 4 · y + x 3 · y 2 ≥ 0 . Оно равносильно x 3 · ( x + y ) 2 ≥ 0 , а из него можно сделать вывод, что x ≥ 0 . У нас получилось, что x · x + y · x .

Ответ: x 5 + 2 · x 4 · y + x 3 · y 2 = x · x + y · x .

Это все, что мы хотели бы вам рассказать о вынесении множителя за знак корня. В следующей статье мы разберем обратное действие – внесение множителя под корень.

Intel Atom x5Z8350 Processor 2M Cache up to 1.92 GHz Спецификации продукции

Дата выпуска

Дата выпуска продукта.

Литография

Литография указывает на полупроводниковую технологию, используемую для производства интегрированных наборов микросхем и отчет показывается в нанометре (нм), что указывает на размер функций, встроенных в полупроводник.

Количество ядер

Количество ядер — это термин аппаратного обеспечения, описывающий число независимых центральных модулей обработки в одном вычислительном компоненте (кристалл).

Количество потоков

Поток или поток выполнения — это термин программного обеспечения, обозначающий базовую упорядоченную последовательность инструкций, которые могут быть переданы или обработаны одним ядром ЦП.

Базовая тактовая частота процессора

Базовая частота процессора — это скорость открытия/закрытия транзисторов процессора. Базовая частота процессора является рабочей точкой, где задается расчетная мощность (TDP). Частота измеряется в гигагерцах (ГГц) или миллиардах вычислительных циклов в секунду.

Частота сигналов

Частота сигналов — это максимальная частота работы одного ядра, с которой способен работать процессор. Частота измеряется в гигагерцах (ГГц) или миллиардах вычислительных циклов в секунду.

Кэш-память

Кэш-память процессора — это область быстродействующей памяти, расположенная в процессоре. Интеллектуальная кэш-память Intel® Smart Cache указывает на архитектуру, которая позволяет всем ядрам совместно динамически использовать доступ к кэшу последнего уровня.

Scenario Design Power (SDP)

Макс. расч. мощность представляет собой дополнительную опорную точку терморегуляции, предназначенную для использования устройств, связанных с высокой температурой, с имитацией реальных условий эксплуатации. Она балансирует требования к производительности и мощности во время рабочих нагрузок по всей системе, и предоставляет самое мощное в мире использование систем. Обратитесь к техническому описанию продукции для получения полной информации о спецификациях мощностей.

Доступные варианты для встраиваемых систем

Доступные варианты для встраиваемых систем указывают на продукты, обеспечивающие продленную возможность приобретения для интеллектуальных систем и встроенных решений. Спецификация продукции и условия использования представлены в отчете Production Release Qualification (PRQ). Обратитесь к представителю Intel для получения подробной информации.

Макс. объем памяти (зависит от типа памяти)

Макс. объем памяти означает максимальный объем памяти, поддерживаемый процессором.

Типы памяти

Процессоры Intel® поддерживают четыре разных типа памяти: одноканальная, двухканальная, трехканальная и Flex.

Макс. число каналов памяти

От количества каналов памяти зависит пропускная способность приложений.

Макс. пропускная способность памяти

Макс. пропускная способность памяти означает максимальную скорость, с которой данные могут быть считаны из памяти или сохранены в памяти процессором (в ГБ/с).

Базовая частота графической системы

Базовая частота графической системы — это номинальная/гарантированная тактовая частота рендеринга графики (МГц).

Макс.

динамическая частота графической системы

Макс. динамическая частота графической системы — это максимальная условная частота рендеринга (МГц), поддерживаемая HD-графикой Intel® с функцией Dynamic Frequency.

Макс. объем видеопамяти графической системы

Максимальное количество памяти, доступное для графической системы процессора. Графическая система процессора использует ту же память, что и сам процессор (с учетом ограничений для ОС, драйвера и системы т.д).

Объекты для выполнения

Исполнительный блок является основным компонентом графической архитектуры Intel. Исполнительные блоки представляют собой процессоры, оптимизированные для одновременной многопоточной обработки данных и обеспечения высокой производительности компьютеров.

Макс. разрешение (HDMI 1.4)‡

Максимальное разрешение (HDMI) — максимальное разрешение, поддерживаемое процессором через интерфейс HDMI (24 бита на пиксель с частотой 60 Гц). Системное разрешение или разрешение экрана зависит от нескольких факторов дизайна системы, а именно, фактическое разрешение в системе может быть ниже.

Редакция PCI Express

Редакция PCI Express — это версия, поддерживаемая процессором. PCIe (Peripheral Component Interconnect Express) представляет собой стандарт высокоскоростной последовательной шины расширения для компьютеров для подключения к нему аппаратных устройств. Различные версии PCI Express поддерживают различные скорости передачи данных.

Конфигурации PCI Express

^‡

Конфигурации PCI Express (PCIe) описывают доступные конфигурации каналов PCIe, которые можно использовать для привязки каналов PCH PCIe к устройствам PCIe.

Макс. кол-во каналов PCI Express

Полоса PCI Express (PCIe) состоит из двух дифференциальных сигнальных пар для получения и передачи данных, а также является базовым элементом шины PCIe. Количество полос PCI Express — это общее число полос, которое поддерживается процессором.

Версия USB

USB (Универсальная последовательная шина) — это технология подключения отраслевого стандарта для подключения периферийных устройств к компьютеру.

Поддерживаемые разъемы

Разъемом называется компонент, которые обеспечивает механические и электрические соединения между процессором и материнской платой.

T

_JUNCTION

Температура на фактическом пятне контакта — это максимальная температура, допустимая на кристалле процессора.

Технология Intel® Turbo Boost Max 3.0

^‡

Технология Intel® Turbo Boost Max 3.0 определяет лучшую производительность ядер в процессоре и обеспечивает увеличенную производительность в ядрах с помощью возрастающей по мере необходимости частоты, пользуясь преимуществом резерва мощности и температуры.

Соответствие платформе Intel® vPro™

^‡

Платформа Intel vPro® представляет собой набор аппаратных средств и технологий, используемых для создания конечных систем бизнес-вычислений с высокой производительностью, встроенной безопасностью, современными функциями управления и стабильности платформы.
Подробнее о технологии Intel vPro®

Безопасная загрузка

Безопасная загрузка гарантирует, что в ходе процесса загрузки будет выполняться только надежное программное обеспечение с известной конфигурацией. Она включает аппаратный корень доверия, который запускает поэтапную проверку подлинности для микропрограммного обеспечения платформы и последовательную загрузку программного обеспечения, например, операционной системы.

Технология виртуализации Intel® (VT-x)

^‡

Технология Intel® Virtualization для направленного ввода/вывода (VT-x) позволяет одной аппаратной платформе функционировать в качестве нескольких «виртуальных» платформ. Технология улучшает возможности управления, снижая время простоев и поддерживая продуктивность работы за счет выделения отдельных разделов для вычислительных операций.

Архитектура Intel® 64

^‡

Архитектура Intel® 64 в сочетании с соответствующим программным обеспечением поддерживает работу 64-разрядных приложений на серверах, рабочих станциях, настольных ПК и ноутбуках.¹ Архитектура Intel® 64 обеспечивает повышение производительности, за счет чего вычислительные системы могут использовать более 4 ГБ виртуальной и физической памяти.

Набор команд

Набор команд содержит базовые команды и инструкции, которые микропроцессор понимает и может выполнять. Показанное значение указывает, с каким набором команд Intel совместим данный процессор.

Технология защиты конфиденциальности Intel®

^‡

Технология защиты конфиденциальности Intel® — встроенная технология безопасности, основанная на использовании токенов. Эта технология предоставляет простые и надежные средства контроля доступа к коммерческим и бизнес-данным в режиме онлайн, обеспечивая защиту от угроз безопасности и мошенничества. Технология защиты конфиденциальности Intel® использует аппаратные механизмы аутентификации ПК на веб-сайтах, в банковских системах и сетевых службах, подтверждая уникальность данного ПК, защищает от несанкционированного доступа и предотвращает атаки с использованием вредоносного ПО. Технология защиты конфиденциальности Intel® может использоваться в качестве ключевого компонента решений двухфакторной аутентификации, предназначенных для защиты информации на веб-сайтах и контроля доступа в бизнес-приложения.

Программа Intel® Stable Image Platform (Intel® SIPP)

Программа Intel® SIPP (Intel® Stable Image Platform Program) подразумевает нулевые изменения основных компонентов платформ и драйверов в течение не менее чем 15 месяцев или до следующего выпуска поколения, что упрощает эффективное управление конечными вычислительными системами ИТ-персоналом.
Подробнее о программе Intel® SIPP

Новые команды Intel® AES

Команды Intel® AES-NI (Intel® AES New Instructions) представляют собой набор команд, позволяющий быстро и безопасно обеспечить шифрование и расшифровку данных. Команды AES-NI могут применяться для решения широкого спектра криптографических задач, например, в приложениях, обеспечивающих групповое шифрование, расшифровку, аутентификацию, генерацию случайных чисел и аутентифицированное шифрование.

Логарифмические уравнения

   Логарифмические уравнения. Продолжаем рассматривать задачи из части В ЕГЭ по математике. Мы с вами уже рассмотрели решения некоторых уравнений в статьях «Тригонометрические уравнения», «Решение рациональных уравнений». В этой статье рассмотрим логарифмические уравнения. Сразу скажу, что никаких сложных преобразований при решении таких уравнений на ЕГЭ не будет. Они просты.

Достаточно знать и понимать основное логарифмическое тождество, знать свойства логарифма. Обратите внимание на то, то после решения ОБЯЗАТЕЛЬНО нужно сделать проверку — подставить полученное значение  в исходное уравнение и вычислить, в итоге должно получиться верное равенство.

Определение: 

Логарифмом числа a  по основанию b называется показатель степени, в который нужно возвести b, чтобы получить a.

Основное логарифмическое тождество:

Например:

 log₃9 = 2, так как  3² = 9

Свойства логарифмов:

Частные случаи логарифмов:

Решим задачи. В первом примере мы сделаем проверку. В последующих проверку сделайте самостоятельно.

Найдите корень уравнения:  log₃(4–x) = 4

Используем основное логарифмическое тождество.

Так как  log_ba = x   b^x = a,  то

3⁴ = 4 – x

x = 4 – 81

x =  – 77

Проверка:

log₃(4–(–77)) = 4

log₃81 = 4

3⁴ = 81  Верно.

Ответ: – 77

Решите самостоятельно:

Найдите корень уравнения:  log₂ (4 – x) = 7

Посмотреть решение 

Найдите корень уравнения log₅ (4 + x) = 2

Используем основное логарифмическое тождество.

Так как   log_ab = x       b^x = a,   то

5² = 4 + x

x =5² – 4

x = 21

Проверка:

log₅(4 + 21) = 2

log₅25 = 2

5² = 25 Верно.

Ответ: 21

Найдите корень уравнения  log₃(14 – x) = log₃5.

Имеет место следующее свойство, смысл его таков: если в левой и правой частях уравнения имеем логарифмы с одинаковым основанием, то можем приравнять выражения, стоящие под знаками логарифмов.

 Если    log_ca = log_cb,   то  a = b

14 – x = 5

x = 9

Сделайте проверку.

Ответ: 9

Решите самостоятельно:

Найдите корень уравнения  log₅(5 – x) = log₅3.

Посмотреть решение 

Найдите корень уравнения: log₄(x + 3) = log₄(4x – 15).

Если   log_ca = log_cb,   то  a = b

x + 3 = 4x – 15

3x = 18

x = 6

Сделайте проверку.

Ответ: 6

Найдите корень уравнения   log_1/8(13 – x) = – 2.

(1/8)^–2 = 13 – x

8² = 13 – x

x = 13 – 64

x = – 51

Сделайте проверку.

Небольшое дополнение – здесь используется свойство

степени (отрицательная степень дроби).

Ответ: – 51

Решите самостоятельно: 

Найдите корень уравнения:  log_1/7(7 – x) = – 2

Посмотреть решение 

Найдите корень уравнения  log₂ (4 – x) = 2 log₂ 5.

Преобразуем правую часть. воспользуемся свойством:

log_ab^m = m∙log_ab

log₂(4 – x) = log₂5²

Если    log_ca = log_cb,   то  a = b

4 – x = 5²

4 – x = 25

x = – 21

Сделайте проверку.

Ответ: – 21

Решите самостоятельно: 

Найдите корень уравнения:  log₅(5 – x) = 2 log₅ 3

Посмотреть решение 

Решите уравнение   log₅(x² + 4x) = log₅(x² + 11)

Если    log_ca = log_cb,   то  a = b

x² + 4x = x² + 11

4x = 11

x = 2,75

Сделайте проверку.

Ответ: 2,75

Решите самостоятельно: 

Найдите корень уравнения  log₅(x² + x) = log₅(x² + 10).

Посмотреть решение 

Решите уравнение   log₂(2 – x) = log₂(2 – 3x) +1.

Необходимо с правой стороны уравнения получить выражение вида:

log₂ (……)

Представляем 1 как логарифм с основанием 2:

1 = log₂ 2

Далее применяем свойство:

log_с(ab) = log_сa + log_сb

log₂(2 – x) = log₂(2 – 3x) + log₂2

Получаем:

log₂(2 – x) = log₂ 2 (2 – 3x)

Если    log_ca = log_cb,   то  a = b, значит

2 – x = 4 – 6x

5x = 2

x = 0,4

Сделайте проверку.

Ответ: 0,4

Решите самостоятельно: 

Найдите корень уравнения  log₅(7 – x) = log₅(3 – x) +1

Посмотреть решение 

Решите уравнение log_х–125 = 2.  Если уравнение имеет более одного корня, в ответе укажите меньший из них.

Воспользуемся основным логарифмическим тождеством:

(x – 1)²= 25

Далее необходимо решить квадратное уравнение. Кстати, квадратное уравнение, как вы поняли, это очень важная «буковка» в математической азбуке. К нему сводятся очень многие решения совершенно различных задач. Помнить формулы дискриминанта и корней нужно обязательно, и уметь решать такое уравнение вы должны очень быстро, периодически практикуйтесь.

Конечно же, опытный глаз сразу увидит, что в нашем примере выражение, стоящее под знаком квадрата равно 5 или – 5, так как только эти два числа  при возведении в квадрат дают 25, устно можно посчитать:

корни равны 6  и  – 4.

Корень  «–4» не является решением, так как основание логарифма должно быть больше нуля, а при  «– 4» оно равно «–5». Решением является корень 6. Сделайте проверку.

Ответ: 6.

Решите самостоятельно: 

Решите уравнение log_x–5 49 = 2. Если уравнение имеет более одного корня, в ответе укажите меньший из них.

Посмотреть решение

 

Как вы убедились, никаких сложных преобразований с логарифмическими уравнениями нет. Достаточно знать  свойства логарифма и уметь применять их. В задачах ЕГЭ, связанных с преобразованием логарифмических выражений, выполняются более серьёзные преобразования и требуются более глубокие навыки в решении. Такие примеры мы рассмотрим, не пропустите! Успехов вам!!!

С уважением, Александр Крутицких. 

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

5 корень из x 4

Вы искали 5 корень из x 4? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и корень из 5 4x 5, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «5 корень из x 4».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как 5 корень из x 4,корень из 5 4x 5,корень из 5 x 4,корень из x 5 4. На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и 5 корень из x 4. Просто введите задачу в окошко и нажмите «решить» здесь (например, корень из 5 x 4).

Где можно решить любую задачу по математике, а так же 5 корень из x 4 Онлайн?

Решить задачу 5 корень из x 4 вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.

Брить наголо не поможет. В зоопарках рассказали, как охлаждают медведей, мороженое у них — 1,5 кило — Общество — Новости Санкт-Петербурга

Скриншот из видео Ленинградского зоопарка в YouTubeПоделиться

«Никакого мороженого, пока не съешь суп» — это правило не для Хаарчааны. Знаменитая белая медведица из Ленинградского зоопарка ест мороженое на завтрак три раза в неделю, до основного приёма пищи. Она должна быть достаточно голодна, чтобы охотно играть с ним и доставать из глыбы льда вкусняшки. Об этом зоопарк рассказывает в своих соцсетях 15 июля.

«Мороженым» это блюдо называется условно, к сливочному десерту оно не имеет никакого отношения, более того, животным категорически нельзя еду с сахаром. Из чего же готовят мороженое для медведицы? Состав бывает разным. Чаще всего в большой пластиковый контейнер кладут морковку, яблоки, свёклу и разную рыбу, заливают всё водой и ставят в морозилку. Свёкла — любимый ингредиент Хаарчааны. До двух лет она её не признавала, а потом вкусы изменились. Сейчас красавице 4,5 года, и в день она поглощает по 1,3 кг этого овоща. «Представьте, какого размера медвежья мороженка, если наш с вами фруктовый лёд весит около 50–60 г, а лакомство Хаарчааны — больше 1,5 кг!» — отмечают в зоопарке.

«В бассейн кидают мороженое, и впечатляющим грациозным прыжком Хаарчаана сразу бросается за ним в воду. Затем она плывёт к ступенькам бассейна, крепко держа своё сокровище в передних лапах. Взбирается на сушу сама и затаскивает свой экстравагантный десерт. Теперь остаётся только разбить глыбу льда и вытащить оттуда все лакомые кусочки», — рассказывают в зоопарке. Иногда лёд выполняет роль игрушки: ледяные глыбы кидают в бассейн, медведица плавает с ними и грызёт их.

В Московском зоопарке готовят ледяной торт и придумывают всякие другие способы спасения животных от жары: в вольерах и для посетителей ставят поливалки, наполняют все бассейны, у белых медведей работает снежная пушка. «Сегодня один из посетителей, наблюдая за гималайским медведем, задал нашему зоологу вопрос: не будет ли ему легче, если под корень обстричь шерсть? Конечно же, нет. Толстая шкура и густой мех защищают наших косолапых как от зимних морозов, так и от летней жары, — рассказывают в зоопарке. — Хотя, когда температура достигает 35 градусов выше нуля, приходится придумывать дополнительные способы охлаждения».

У гималайского медведя Алладина и бурой медведицы Розы в вольере всегда много воды, Алладин любит купаться в ванночке, Роза — в бассейне. Чтобы было интереснее, в воду запускают живых карпов.

Московский зоопарк

Новая ванночка заинтриговала Алладина. Сначала он старательно осмотрел и обнюхал её, а потом уже обратил внимание на рыбу. «Рыбалка Алладина — не самое динамичное зрелище. Иногда кажется, что он хочет взять карпа измором: долго и терпеливо одной лапой он гоняет рыбу по ванне, пока не удается в буквальном смысле слова прижать его к стенке. Роза охотится с бОльшим задором. Хотя в этот раз её сильнее заинтересовал ледяной торт, в который была вморожена рыба и морковь. Вначале она съела всю рыбу, потом перешла на овощи», — комментируют в зоопарке.

Скриншот из видео Ленинградского зоопарка в YouTube

Лесом вышел – Weekend – Коммерсантъ

В Русском музее открылась выставка «Иван Иванович Шишкин. 1832–1898». За этой незамысловатой вывеской скрывается неожиданно замысловатое содержание: вместо хрестоматийных картин показывают около полутора сотен вещей из фондов музея, которые редко или вообще никогда не экспонировались, а также множество раритетов из самой богатой в России коллекции шишкинской графики

Если на афише Русского музея прочтешь надпись «Иван Иванович Шишкин. 1832–1898», не верь глазам своим: это не банальная летняя выставка. Вообще, жанр летних выставок, рассчитанных главным образом на то, что туристы клюнут, а местные эстеты не заметят, потому как отбыли в отпуск, благородный коммерческий жанр, давно освоенный многими европейскими музеями, в России в целом и в ее туристической столице в частности, как ни странно, не приживается. Русский музей со своим летним и недатским, то есть ни к какой круглой дате не приуроченным, Шишкиным выступает тут чуть ли не первопроходцем. Впрочем, турист будет слегка обманут в своих ожиданиях: никаких хрестоматийных шишкинских картин, знакомых ему с детства по конфетным фантикам, школьным учебникам и бабушкиным коврикам, он на выставке не найдет — здесь не будет не только «Утра в сосновом лесу» или «Ржи», потому как они висят в Третьяковской галерее, но и «Корабельной рощи», потому как она вместе с другими известными пейзажами осталась в постоянной экспозиции Русского музея в Михайловском дворце. Но зато эстет наконец-то получит шанс посмотреть на этого вынутого из фондов, нехрестоматийного, фрагментарного, как фотография, которой он так увлекался, Шишкина немного другими глазами.

«Шишкин — художник народный»,— утверждал Владимир Стасов, подразумевая под народностью роль в создании национальной школы, а не популярность, тем более — нынешнюю, когда публика совсем не ценит в Шишкине все то, что ценили знатоки, в том числе и сам Стасов, а именно — этюды, рисунки пером и офорты, то, на чем сейчас как раз и сделали акцент в Русском музее. «Всю жизнь он изучал русский, преимущественно северный лес, русское дерево, русскую чащу, русскую глушь» — в плане излюбленной натуры зрелый Шишкин идеально вписывался в националистическую программу Стасова, но совсем не вписывался в нее в плане школы, то есть выучки, потому что окончательную огранку своим пейзажистским талантам он — после Императорской академии художеств — получил в Дюссельдорфе и Цюрихе, так что Стасову приходилось яростно защищать своего любимца от обвинений в подражаниях Каламу и братьям Ахенбах. Впрочем, «немецкий ген» был встроен и в саму петербургскую академическую программу. В Русском музее, например, выставили одну из редких непейзажных картин Шишкина, изобразившего себя вместе со своим другом детства, однокашником по Казанской гимназии, Московскому училищу живописи, ваяния и зодчества и Петербургской академии пейзажистом Александром Гине, в мастерской на Валааме: два молодых художника в сводчатой келье, всюду творческий беспорядок, этюды по стенам, большой холст на мольберте, кисти, палитры, прозаический, но необходимый в рассуждении пленэра зонтик, совершенно немецкий по композиции интерьер с видом за окном и совершенно немецкая, фридриховская атмосфера возвышенной романтической дружбы — только дата «1860» (последний год учебы Шишкина в академии) не позволяет отправить эту бидермейеровскую сценку на нынешнюю выставку о немецком и русском романтизме в Третьяковку. Пресловутая немецкость Шишкина стала проблемой и для тех, кто видел в нем вершину национального пейзажного гения, и для тех, кто сокрушался, что ему, побывавшему в годы пенсионерского вояжа в Париже, не приглянулись ни Камиль Коро, ни барбизонцы, ни его ровесники — импрессионисты.

Правда, на выставке есть одна картина, «Дорожка в лесу» 1880 года, которая выглядит совсем по-французски, не импрессионизм, конечно, но буквально полшага до него и настроение едва ли не монетовское: лес хоть и шишкинский, «богатырский», но не сумрачный, а весь пронизан светом, телега остановилась поодаль, потому что господа в светлых летних одеждах желали прогуляться пешком, а юная барышня в серо-голубом платьице и таких же чулочках убежала вперед, к первому плану картины, и теперь оглядывается на несущуюся к ней, едва касаясь земли, собачку, желтоватые пятна парасолей мамы и дочки рифмуются друг с другом, с дорожкой и с полосой поля на дальнем плане, и сама девочка, купающаяся в солнце, кажется прозрачной, и сквозь нее, как сквозь стекло, проходят лучи. Это, видимо, самый удачный пример работы Шишкина со стаффажем. Вернее, стаффаж у него в пейзажах чаще крестьянский, натужно-народный, и он, трудолюбивый немецкий художник, над ним старательно работал (см. этюд крестьянки с граблями, почти рябушкинский), но ни люди, ни прочая фауна (см. «Лесной пейзаж с цаплями») не вживлялись в его голландско-немецкую пейзажную схему органично, вот и для «Утра в сосновом лесу» (см. карандашный эскиз — композиция с четырьмя медведями, естественно, целиком придумана Шишкиным) потребовалась помощь Константина Савицкого. А на «Дорожке в лесу» — уже не стаффаж, а люди, слившиеся с пейзажем в одно живописное целое, зажившие с ним общей жизнью, и солнечный свет, как показывают другие картины и этюды с выставки, этому слиянию весьма способствует.

Русское дерево, русская чаща, русская глушь — ясно, что для Стасова, занятого строительством общенациональной школы, вся империя равномерно поросла непролазным шишкинским лесом, но сегодня мы видим, что у этого леса есть и вполне конкретные паспортные данные, с определенным «пятым пунктом» и постоянной пропиской. Притязать на Шишкина как на певца именно местной природы с равным основанием имеют право два города. Во-первых, его родная Елабуга, куда он постоянно возвращался, в чьих окрестностях любил работать и где теперь есть единственный в России дом-музей Шишкина. А во-вторых — Петербург. То есть специально петербургских видов в живописи Шишкина почитай что нет. Разве только маленький, квадратного формата этюд «Городские крыши зимой»: скучные задворки, неказистые домишки, шапки снега на крышах, глухие брандмауэры, куцые деревца — что-то подобное можно было бы написать, наверное, и в Москве, но воздух, свет и серо-охристый колорит этой поразительной для 1860-х годов картины заставляет думать о пейзаже ленинградской школы 1930-х. Или вот еще один небольшой этюд «Крестовский остров в тумане»: элементарная зеркальная композиция — высокое небо, облака и зелень отражаются в воде; живопись почти что абстрактная — широкие пятна, массы приглушенного цвета; кажется, будто на этом модернистском холсте лежит тень будущего, лондонского Моне, а размашистая подпись «И. Ш.» в углу и этикетка с датировкой «конец 1860-х — начало 1870-х» — чья-то шутка. Но такая странная, словно бы поддавшаяся обаянию странного города Петербурга живопись в наследии Шишкина редка.

Петербургская природа — не сам город, а Север, финляндские, ингерманландские и эстляндские земли, где еще с первых академических лет так полюбил работать Шишкин,— видимо, служила ему субститутом природы Предкамья. Не того парадного Предкамья, что во всей красе представлено в картине «Рожь» — на одном из «ржаных» эскизов, сделанных в елабужских окрестностях, Шишкин записал свою «песнь песней»: «Раздолье, простор, угодье. Рожь. Божья благодать. Русское богатство». Но какой-то особо милой ему части предкамского ландшафта — с соснами и песчано-скалистыми почвами. Того ландшафта, что запечатлен в законченной незадолго до смерти «Корабельной роще»: вид, на самом деле найденный где-то возле Елабуги, с тем же успехом мог быть обнаружен под Териоками. И на выставке Русского музея, которая старательно предъявляет зрителю самые неожиданные для Шишкина мотивы, деревенские дворы с хозяйственными постройками или гурзуфские скалы, этот сосновый карело-финский лес все же преобладает, отчего экспозиция приобретает какой-то обаятельно-местечковый, локально-петербургский характер, что подчеркнуто даже «лесным» выставочным дизайном. Несколько этюдов с сосенками на песчаном грунте, писанных в имении зятя с поэтическим финским названием Мери-Хови в Куоккале (неподалеку от тех мест, где позднее будут выстроены репинские «Пенаты»), может быть, вообще лучшее произведение шишкинской кисти.

Те, кто любит внимательно читать этикетки, заметят, что большая часть живописи на выставке — местного происхождения: что-то было перераспределено в Русский музей из Эрмитажа и Академии художеств, что-то поступило от частных коллекционеров, но множество вещей тут даже не столько из национализированных коллекций, сколько из экспроприированного барского имущества, которое и коллекцией-то не назовешь, из того, что было передано музею вскоре после революции петроградским Бюро отдела охраны и учета памятников искусства и старины или же много позднее какими-то советскими учреждениями. Как, скажем, удивительный этюд «Дымок», до 1977 года украшавший собою Куйбышевский райфинотдел г. Ленинграда, или же мастерский пейзаж «Перед грозой», до 1963 года наполнявший тревожными предчувствиями души сотрудников хозяйственного отдела управления делами Ленинградского обкома КПСС. Это разнообразие провенансов говорит о том, что Шишкин был чрезвычайно популярен во всех слоях образованной части петербургского общества. Что, разумеется, неудивительно: выставка еще раз напоминает нам, каким великим рисовальщиком и гравером, равно виртуозно владевшим пером, карандашом и множеством техник печатной графики, от офорта до литографии, был Шишкин, изобретший даже авторскую разновидность выпуклого офорта, автоцинкографию; и свое мастерство он — со свойственным передвижникам коммерческим талантом — использовал в рекламных целях, активно участвуя в коллективных издательских предприятиях или же выпуская собственные сюиты гравированных этюдов, а такая реклама работала не хуже стасовских славословий.

Только акварель упорно не давалась Шишкину — он был мастеровитым, но заурядным акварелистом, и забавно, что на этой выставке чудес и редкостей показали одну вдвойне разоблачительную работу, где сошлись акварель и фотография. Это заказная и очень скучная серия с панорамами Нижнего Новгорода, сделанная в 1870 году откровенно халтурным образом: альбуминовые отпечатки пройдены поверх акварелью. Хорошо известно, что Шишкин много писал по фотографиям, используя снимки в качестве эскизов, но в отечественном искусствоведении, всегда с подозрением относившемся к натурализму, педалировать тему «фотографа русской природы» не принято. От фотографии идет и фрагментарность его этюдных композиций, иногда передающаяся законченным картинам: срезанные краем холста кроны деревьев, от которых остались лишь стволы и корни, болотистый подлесок, бурелом, кустики сныть-травы у забора в Парголове или, наоборот, облака, никак не привязанные к земле,— слепок с куска природы, сделанный глазом фотографа-натуралиста. Все эти «снимки на память», может быть, и не тянут на эпос об общенациональном русском лесе, любезный Стасову, но милы сердцу патриота родного края. Пусть фотографическая оптика и локальный патриотизм Шишкина, так бросающиеся в глаза на этой выставке, и не являются достаточными основаниям для того, чтобы провозгласить его современным художником, но он смотрится здесь куда живее и актуальнее, чем в привычных амплуа былинно-лубочного «богатыря русского леса» или «верстового столба в развитии русского пейзажа».

«Иван Иванович Шишкин. 1832–1898». Санкт-Петербург, Русский музей, корпус Бенуа, до 30 августа

n со следующими условиями:

1. Когда n — четное число и a> 0, root (n, a)> 0, называется главным корнем.

Когда n — четное число и a <0, корень (n, a) не является действительным числом.

2. Когда n — нечетное число и a> 0, корень (n, a)> 0.

Если n — нечетное число и a <0, root (n, a) <0

Число n в корне (n, a) (всегда натуральное число больше 1) называется индексом или порядком радикала, а a называется подкоренным выражением.4).

Радикальное выражение называется стандартным, если выполняются следующие условия:

1. Подкоренное выражение положительное.

2. Индекс корня должен быть как можно меньше.

3. Показатель степени каждого множителя подкоренного выражения является натуральным числом меньше радикального индекса.

4. В подкоренном выражении нет дробей.

5. В знаменателе дроби нет радикалов.

Под упрощением радикального выражения мы подразумеваем приведение радикального выражения в стандартную форму.3)

= 7xyroot (3y) + 5xyroot (3y) -4xyroot (3y)

= 8xyroot (3y)

Давайте посмотрим еще на несколько проблем, и наш пошаговый решатель упростит комбинирование радикальных выражений. 3 корень (2) + 5 корень (3,3)

= 6 корень (2) -3 корень (3,3) -8 корень (2) + 5 корень (3,3)

= (6-8) корень (2) + (- 3 + 5) корень (3,3)

= -2 корня (2) + 2 корня (3,3)

Квадраты: полиномы второй степени

10

Решение квадратного уравнения с множителем

Двойной корень

Квадратичное неравенство

Сумма корней и произведение корней

КВАДРАТИКА — ДРУГОЕ НАЗВАНИЕ многочлена 2-й степени.2 — самый высокий показатель степени.

1. Какой вид имеет полиномиальная функция 2-й степени?

y = ax ² + bx + c

2. Какой вид имеет квадратное уравнение?

ось ² + bx + c = 0

3. Что мы подразумеваем под корнем квадратичного?

Решение квадратного уравнения.

4. Сколько корней всегда у квадратичной?

Два, реальные или сложные.

5. График квадратичной всегда имеет форму, называемую -?

Парабола.

6. Каковы три метода решения квадратного уравнения,
6. То есть поиска корней?

1. Факторинг. 2. Завершение квадрата.

3.Квадратичная формула.

Начнем с метода факторинга. В следующей теме мы представим как Завершение квадрата, так и формулу квадратного уравнения.

7. Если произведение множителей равно 0 — если ab = 0 — то что вы можете
7. сделать вывод о факторах a , b ?

Либо a = 0, либо b = 0.

Пример 1. Решение по факторингу.

f ( x ) = x ² −2 x −3. Найдите корни f ( x ) и нарисуйте график y = f ( x ).

Решение . x ² −2 x −3 = ( x + 1) ( x — 3).

Следовательно, корни — это −1 и 3. (См. Урок 37 по алгебре.) Это пересечения графа размером x .

Перехват y — постоянный член −3.

В каждом полиноме пересечение y является постоянным членом, потому что постоянный член представляет собой значение y , когда x = 0.

Пример 2. Двойной корень

f ( x ) = x ² −10 x + 25. Найдите корни
f ( x ) и нарисуйте график y = f ( х ).

Решение . x ² −10 x + 25 =
( x -5) ( x -5) = ( x -5) ² . Два корня равны, их 5, 5. 5 называется двойным корнем. (См. Урок алгебры 37, вопрос 4.)

При двойном корне график не пересекает ось x . Это просто трогает.

Двойной корень возникает, когда квадратичный является трехчленом полного квадрата: x ² ± 2 ax + a ² ; то есть, когда квадратичная величина является квадратом бинома: ( x ± a ) ² .

Пример 3. Сколько действительных корней, т.е. корней, которые являются действительными числами, имеет квадратичный элемент каждого графа?

Ответ . График а) имеет два действительных корня. Он имеет два перехватчика x .

График б) не имеет реальных корней. Он не имеет x -перехватов. Оба корня сложные.

График c) имеет два действительных корня. Но они имеют двойной корень.

Пример 4.Квадратичное неравенство.

Решите это неравенство:

x ² -4 x -5

Для этого осмотрите график

y = x ² — 4 x — 5.

Решение . Для каких значений x эта квадратичная величина будет отрицательной? То есть, где график под осью x ?

График отрицательный между корнями, которые равны -1 и 5.Решение неравенства равно −1 x. Мы также можем заметить, что квадратичная функция будет иметь положительные значения — график будет выше оси x — слева и справа от корней:

x x> 5.

В то время как квадратичный будет иметь значение 0 в корнях.

Мы рассмотрели три возможности:

Эта квадратичная величина равна 0 в двух корнях.

Это на меньше, чем 0 между двумя корнями.

Это на больше 0 слева и справа от двух корней.

Эти три возможности, которые верны для любого действительного числа, имеют причудливое название Закона трихотомии. Любое число должно быть либо равно, меньше или больше 0.

Закон трихотомии также принимает такую ​​форму:

Для любых действительных чисел a, b , либо a = b , a b, либо a > b .

Однако мы должны знать, какая из этих возможностей верна. Для любых двух чисел мы должны знать их относительный порядок. Это заложено в значении «числа».

Задача 1. Нарисуйте график y = x ² — 2 x −8. То есть покажите интерцепты x и y .

Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы закрыть ответ еще раз, нажмите «Обновить» («Reload»).

x ² −2 x — 8 = ( x + 2) ( x — 4). Следовательно, корни равны −2, 4. Пересечение y является постоянным членом −8.

Задача 2. Нарисуйте график

.

y = x ² + 4 x + 4.

x ² + 4 x + 4 = ( x + 2) ² .В −2 есть двойной корень. Перехват y — постоянный член, 4.

Проблема 3.

а) Чтобы решить это квадратное неравенство —

x ² + 2 x — 3> 0

—проверьте график

y = x ² + 2 x — 3.

Квадратичное значение будет положительным — выше оси x — для значений x слева и справа от корня.Решение:
x x> 1.

б) Решите это квадратное неравенство:

x ² + 2 x — 3

−3 х

Квадратичный будет отрицательным между корнями.

Проблема 4. Квадратичная имеет следующие корни. Запишите каждую квадратичную как произведение линейных множителей.

а) 3, 4 ( x — 3) ( x — 4)

б) −3, −4 ( х + 3) ( х + 4)

в) — р , с ( x + r ) ( x — s )

г) 3+, 3 — ( x -3 -) ( x −3 +)

Сумма корней и произведение корней

Теорема. В квадратичной системе со старшим коэффициентом 1:

Сумма корней равна отрицательному значению коэффициента x ;

произведение корней — постоянный член.

То есть, если

x ² + bx + c = 0,

и корни r и s , затем

r + s	=	— б ,
RS	=	с .

Ибо, если корни равны r и s , то квадратичный равен

( x — r ) ( x — s )	=	x 2 — rx — sx + rs
	=	x 2 — ( r + s ) x + rs .

Коэффициент при x равен — ( r + s ), что является отрицательным значением суммы корней. Постоянный член — RS , который является их произведением.

Пример 5. Построить квадратичную с корнями 2 и 3.

Решение . Сумма корней равна 5, их произведение равно 6, следовательно, квадратичный равен x ² -5 x + 6.

Сумма корней равна отрицательному значению коэффициента x . Произведение корней — постоянный член.

Пример 6. Построить квадратичную с корнями 2 +, 2 -.

Решение . Сумма корней равна 4. Их произведение — разность двух квадратов: 2 ² — () ² = 4 — 3 = 1.

Следовательно, квадратичный равен x ² -4 x + 1.

Пример 7. Построить квадратичный, корни которого равны 2 + 3 i , 2 — 3 i , где i — комплексная единица.

Решение . Сумма корней равна 4. Произведение снова является разностью двух квадратов: 4–9 i ² = 4 + 9 = 13.

Квадратичный с этими корнями равен

.

x ² -4 x + 13.

Задача 5. Построить квадратичную с корнями −3, 4.

Сумма корней равна 1. Их произведение равно −12. Следовательно, квадратичный равен x ² — x — 12.

Задача 6. Построить квадратичную с корнями 3 +, 3 -.

Сумма корней равна 6. Их произведение равно 9 — 3 = 6.
Следовательно, квадратичный равен x ² — 6 x + 6.

Задача 7. Построить квадрат, корни которого равны 2 + i , 2 — i .

Сумма корней равна 4. Их произведение равно 4 — ( i ) ² = 4 + 5 = 9.
Следовательно, квадратичный равен x ² — 4 x + 9.

*

В более общем смысле, для любого коэффициента x ² , то есть, если квадратичный равен

топор ² + bx + c ,

и корни r и s , затем

r + s	=	–	b a	,
RS	=	c a	.

Когда a = 1, мы имеем теорему выше.

Следующая тема: Завершение квадрата

Содержание | Дом

---

Сделайте пожертвование, чтобы TheMathPage оставалась в сети.
Даже 1 доллар поможет.

---

Авторские права © 2021 Лоуренс Спектор

Вопросы или комментарии?

Эл. Почта: [email protected]

Нахождение домена функции

Хорошо, допустим, у нас нет график функции, который будет выглядеть в последнем разделе…

Можем ли мы еще найти домен и диапазон?

Домены:

Да (пока алгебра разве не станет слишком волосатым … и не будет для нас.)

Диапазоны:

Не совсем (обычно нужен картинка — если это что-то действительно базовое.)

Итак, мы будем делать домены на эти — в любом случае, именно здесь и происходит действие.

Спрашивать домен функция такая же, как при запросе

«Что такое все возможно x ребята
что я могу воткнуть в эту штуку? »

Иногда то, что вы действительно будете искать это

«Есть что-нибудь Я НЕ МОГУ вставлять? «

Проверьте это:

Найдем домен из

Вы видите какие-нибудь Икс ребята, что могло бы вызвать здесь проблемы?

А как насчет

?

Итак, Икс знак равно 3 — плохой парень! Все в остальном все в порядке.

The домен — это все вещественные числа, кроме 3.

Что бы обозначение интервала быть?

Если есть сомнения, график это на номерной строке:

Сделайте интервал обозначение двумя частями:

домен

---

ВАШ ЧАС:

Найдите домен

---

Иногда вы не можете найти домен быстрым взглядом.

Проверьте это:

Давайте найдем домен

Хм … Это не так так очевидно!

НО, мы все еще ищу то же самое:

Плохое Икс что делает знаменателем 0!

Как мы его находим? Легкий!

Установить знаменатель = 0 и решай!

The домен

---

ПОПРОБОВАТЬ:

Найдите домен

* показать работу !!

---

Как насчет Вот этот?

Квадратные корни — что мы знаем о квадратных корнях?

… Итак, 16 можно вставить.

… Итак, 0 в порядке.

… Фу! Но, 3,2 в порядке.

… Неа! Не могу!
* Нам нужны только реальные числа!

Никаких негативов нет!

The внутри радикал не может быть отрицательным, если мы хотим только реальные ответы (нет я ребята).Итак, внутри радикал должен быть 0 или положительным номер.

Набор

и реши!

Теперь давайте найдем домен

Итак, домен

это

.

---

ПОПРОБОВАТЬ:

Найдите домен

. * Показать работы !!

---

Вот грязный:

Найдем домен из

Набор

и решай!

Домен

.2 (x + 1) -4x (x + 1) +7 (x + 1 … Поскольку остаток равен нулю, то x = 4 действительно является нулем –2x 5 + 6x 4 + 10x 3 — 6x 2 — 9x + 4, поэтому: Да, x — 4 является множителем –2 x 5 + 6 x 4 + 10 x 3 — 6 x 2 — 9 x + 4 Найдите все множители 15 x 4 + x 3 — 52 x 2 + 20 x + 16, используя синтетическое деление. Фактор x (b 2 — a) + 6 (b 2 — a) x (b 2 — a) + 6 (b 2 — a), вытаскивая Факторинг трехчлена с ведущим коэффициентом 1 Хотя мы всегда должны начинать с поиска GCF, извлечение GCF — не единственный способ разложить полиномиальные выражения на множители. Имя рабочего листа факторинга: Дата: 1. Фактор: 25×2 — 9 10. 3. Выразите x2 — 5x- 14 как произведение двух биномов. 9, 6. 5, 4. Множитель: 4×2 — 9 Выразите 2×2 -3x- 5 как произведение двух Algebra Il Review 6.1-6.7 Оцените каждое 42. (43.4-5) 2 Упростите каждое выражение. 3 5-3 5) (4x y) xy 3y-2 21×5 Выполните указанную операцию. Первый шаг факторизации выражения — это «убрать» все общие множители, которые есть в терминах. Итак, если вас попросят разложить x² + x на множители, поскольку x входит в оба члена, вы должны написать x (x + 1).Факторизация квадратики. В этом видео показано, как решить квадратное уравнение с помощью факторизации. (3×4 + 2×3 — x2 — x — 6) / (x2 + 1) = 3×2 + 2x — 4 + (-3x — 2) / (x2 + 1) = 3×2 + 2x — 4 — (3x + 2) / (x2 + 1), где частное равно 3×2 + 2x — 4, а остаток — (3x + 2). Полностью разложите на множители каждое из следующих факторов или, если они не могут быть учтены, напишите «PRIME». 1) x2 — 5x — 6 2) 64m3 — x3 3) 3×2 + 5x — 2. 4) 6×3 — 9×2 — 2x + 3. 5) x3 — 27 6) x2 — 6x + 10. 7) 3×4 — 48. 8) x4 — 1. 9) x2 + 4x — 12 10) 5×4 + 10×2.11) 10×2 — 5x + 5 12) b3 + 8 19 октября 2020 г. · f (x) = 4x 6 + 12x 5 + 12x 4 + 4x 3. вы должны немедленно разложить его на множители. f (x) = 4x 3 (x 3 + 3x 2 + 3x + 1) Получение 4 упрощает оставшиеся числа, x 3 дает вам корень из x = 0 (с кратностью 3), и теперь у вас есть только кубический многочлен (степень 3) вместо секстики (степень 6). Модуль 4 квадратные отношения и системы уравнений модуль викторина b ключ ответа Typeorm repositorynotfounderror нет репозитория для Модуль 4.рисование обратного. нарисуйте обратную связь и определите, является ли обратная функция функцией. отражение. 0,5. 4.7. F-BF.4. Полиномиальные и квадратичные выражения, уравнения и функции. найти обратные функции. решить уравнение вида f (x) = c для более простой функции f, которая имеет обратную форму, и записать выражение для обратной … Пример. Система x 2y = 4 3x + 6y = 0 не имеет решения. Это потому, что каждая из двух линий имеет одинаковый наклон, 1 2, поэтому линии не пересекаются.***** *** 189 не будет решением системы двух линейных уравнений, поскольку никакая точка в R2 не будет лежать на обеих параллельных прямых. Пример. Система x 2y = 4 3x + 6y = 0 не … Викторина: решение квадратных уравнений Предыдущие корни и радикалы. Далее … Викторина: Решение систем уравнений (одновременных уравнений) … Ключевые слова и фразы Процентное соотношение и соотношение сложных процентов … Добровольная типовая учебная программа (VMC) представляет собой серию блоков и планов уроков, которые включают уровни обучения и информационные ресурсы, приведенные в соответствие со стандартами Пенсильвании в рамках учебных программ. Рассуждение с помощью уравнений и неравенств A-REI Решите системы уравнений [линейно-линейные и линейно-квадратичные] A-REI.5 A-REI.6 Докажите, что, учитывая систему двух уравнений с двумя переменными, заменив одно уравнение на сумма этого уравнения и кратное другому дает систему с такими же решениями. Это курс для студентов с отличием по теории вероятностей. Темы включают вероятностные пространства и случайные величины, распределения (абсолютно непрерывные и сингулярные распределения) и плотности вероятностей, моментные неравенства, моментные производящие функции, условные ожидания, независимость, условные распределения, концепции сходимости (слабые, сильные и по распределению), закон больших… 4.2 Системы уравнений — Замена Цель: Решить системы уравнений с помощью замены. При решении системы с помощью построения графиков есть несколько ограничений. Во-первых, это требует, чтобы график был нарисован идеально. Если линии не прямые, мы можем прийти к неправильному ответу. Во-вторых, построение графиков — не лучший метод, если ответ — Метод исключения для решения систем линейных уравнений использует свойство сложения равенства. Вы можете добавить одно и то же значение к каждой стороне уравнения.Итак, если у вас есть система: x — 6 = −6 и x + y = 8, вы можете добавить x + y в левую часть первого уравнения и добавить 8 в правую часть уравнения. Решение многоступенчатых уравнений. 1. При необходимости упростите выражения с каждой стороны уравнения, в том числе объединив похожие члены. 2. Получите все переменные члены с одной стороны и все числа с другой стороны, используя свойство сложения равенства. (ax + b = c или c = ax + b) 3. В алгебре II анализ квадратичных соотношений, включая уравнения и атрибуты парабол, определяется как Стандарт готовности STAAR 2A.4B и входит в категорию отчетности STAAR 4: функции, уравнения и неравенства с квадратным корнем и квадратным корнем. Викторина по квадратным уравнениям. Вопросы и ответы. Теперь тест, который мы предлагаем на этой странице, поможет многим соискателям. Итак, случайно, если вы также готовитесь к тестам, таким как IPBS, RRB, банки, железные дороги, комиссия по отбору персонала, комиссия по отбору подчиненных услуг, PSC, GRE, GMAT, GATE, DATE, CAT, IIT и несколько других вступительных экзаменов, тогда Викторина, которую мы проводим на сайте… Линейное уравнение — Уравнение, включающее переменные только первой степени (т. Е. Без квадратичных (x 2) или кубических (x 3) членов). Например, 10x + 2 = 5x + 12 — это линейное уравнение, а x 2 + 4 = x — 5 — не линейное уравнение, а скорее квадратное уравнение. Решение — число, которое при замене неизвестного сделает уравнение истинным. 3 мая 2011 г. · Экзамены по Keystone. Название модуля отображается вверху каждой страницы. Модульный уровень важен, потому что экзамены Keystone построены с использованием модульного формата, при этом каждый из экзаменов Keystone разделен на два тестовых модуля одинакового размера.Каждый модуль состоит из двух или более якорей оценки. Модуль B — Построение кадровой стратегии. Модуль C — Мотивация, обучение и развитие навыков. Модуль D — Управление персоналом и производственные отношения: Документ 9 — Информационные технологии: Модуль A — Введение в информационные технологии. Модуль B — Системы и дизайн. Модуль C — Приложения в банковской сфере. Модуль D — Контроль безопасности … A: Ключевым моментом здесь является то, что x может быть отрицательным, а выражение внутри абсолютного значения может быть отрицательным, но само абсолютное значение никогда не может быть отрицательным.Давайте посмотрим, как это проявляется в двух упомянутых вами уравнениях! Мы сказали, что для l1 + 2xl = 4 — x. 1 + 2x = 4 — x или 1 + 2x = — (4 — x) Что дало нам. x = 1 или x = -5 Сканер скретч-билетов Http custom pro apktest that quiz, unit 7 8 green interchange 3 flashcards quizlet, gene 150 the true good amp beautiful regent university, new interchange book 1 uints 1 4 quiz esl workheet by, test review unit 8 answer key unit 8 test review name, module 3a engageny, 8th class unit 7 информационных систем уравнений, Создайте уравнения, которые описывают числа или отношения.Создавайте уравнения и неравенства для одной переменной и используйте их для решения задач. Включите уравнения, возникающие из линейных и квадратичных функций, а также простых рациональных и экспоненциальных функций. Мертвое тело найдено сегодня Лос-Анджелес 8.1 Решение систем с помощью построения графиков 8.2 Решение систем с помощью замены 8.3 Решение систем с помощью исключения 8.4 Решение систем особого случая 8.5 Решение систем линейных неравенств Группа 8 Обзор F-IF.4 F-IF.5 F-IF.7.a Функции: построение функций F-BF.1 Алгебра: создание уравнений A-CED.2 A-CED.3 Функции: интерпретация функций F-IF.4 F-IF.5 F-IF.7. Функции: Функции построения F-BF.1 Средние классы Средняя школа Средние классы Box It Up! Оптимизация: Области и объем Приложения Свободный ответ Викторина с множественным выбором Геометрия: Моделирование … Маневрирование средними уравнениями и неравенствами Ключ ответа Ливан ky некрологи Wifi ar ios Odoban para que sirve Тестовое подразделение экспериментального дизайна b Не менее баллов Для прохождения этого модуля необходимо получить не менее баллов… Раздел практического теста 4-1.docx Раздел практического теста 4 -1.docx … Раздел 6 Дополнительные решения линейных уравнений Округ Гарленд наиболее разыскиваемый URL-адрес для входа в веб-почту Office 365 Пример. Система x 2y = 4 3x + 6y = 0 не имеет решения. Это потому, что каждая из двух линий имеет одинаковый наклон, 1 2, поэтому линии не пересекаются. ***** *** 189 не будет решением системы двух линейных уравнений, поскольку никакая точка в R2 не будет лежать на обеих параллельных прямых. Пример. Система x 2y = 4 3x + 6y = 0 — нет… Здесь 4 уравнения с 2 неизвестными. В терминах «биномиального коэффициента» существует не более C 4 2 = 4! / [2! (4-2)!] = 6 основных решений. Решая шесть результирующих систем уравнений, мы имеем: Шесть базовых решений с четырьмя базовыми возможными решениями Tecsun и 200 инструкций Honda eu3000is отремонтированы В алгебре II анализ квадратичных соотношений, включая уравнения и атрибуты парабол, идентифицируется как STAAR Стандарт готовности 2A.4B и включен в категорию 4 отчетности STAAR: функции, уравнения и неравенства с квадратными и квадратными корнями. Скачать игру pes jar 240x320Craftsman 189 набор инструментов Прочтите разделы 4.1-4.6, 4.8. 1. Используя миллиметровую бумагу, нарисуйте каждое уравнение и укажите (i) вершину, (ii) ось симметрии и (iii) координаты одной точки на каждой стороне вершины. Миллионы различных химических соединений, из которых состоит все на Земле, состоят из 118 элементов, которые связаны друг с другом по-разному. Этот модуль исследует два распространенных типа химических связей: ковалентную и ионную. Модуль представляет химическую связь по скользящей шкале от чистой ковалентной до чистой ионной, в зависимости от различий в электроотрицательности связывающих атомов.Основные моменты … Решая, какой метод следует использовать, рабочий лист ответыКак установить forza Horizon 4 на ПК Уравнение может представить и объяснить ваш ответ. б) Перепишите уравнение в стандартной форме, чтобы показать, что ваш ответ в формате. предыдущий вопрос правильный. 6. Линейно-квадратичная система уравнений состоит из уравнений: y + (3/4) x = 0 и x2 + y2 — 25 = 0. a) Нарисуйте график. система на предоставленном. миллиметровая бумага. Решением системы уравнений является упорядоченная пара, удовлетворяющая обоим уравнениям.В реальных ситуациях это обычно точка безубыточности. Большинство систем линейных уравнений имеют ровно одно решение. Системы линейных уравнений могут иметь нулевые решения (если обе функции имеют одинаковую скорость изменения) или бесконечно много Пожалуйста, продемонстрируйте свою поддержку JMAP, сделав онлайн-взнос. Поиск по сайту www.jmap.org: Погода в национальном парке Секвойя в ноябре Какая электронная конфигурация иона кальция Кристи Лабонте Ansible tower api launch job extra_vars 915conom10 9000eap microsoft ответы глава 7 Galaxy note 7 на продажу Чертежи полосы пропускания 4-го порядка Amazon позвоните мне сейчас не работает Метод исключения для решения систем линейных уравнений использует свойство сложения равенства.Вы можете добавить одно и то же значение к каждой стороне уравнения. Итак, если у вас есть система: x — 6 = −6 и x + y = 8, вы можете добавить x + y в левую часть первого уравнения и добавить 8 в правую часть уравнения. Сравнительный транскриптомный анализ выявляет консервативные программы, лежащие в основе органогенеза и воспроизводства наземных растений. 1. Джилл Харрисон, К. Развитие и генетика в эволюции строения тел наземных растений. Philos. Пер. R. Soc. Лондон. B Biol. Sci. 372 , 20150490 (2017). PubMed PubMed Central Статья Google Scholar 2. Фюрст-Янсен, Дж. М. Р., де Фрис, С. и де Фрис, Дж. Эво-физиотерапевт: о реакции на стресс и первых наземных растениях. J. Exp. Бот. 71 , 3254–3269 (2020). PubMed PubMed Central Статья CAS Google Scholar 3. Браун, Р. К. и Леммон, Б. Е. Споры до спорофитов: гипотеза о происхождении спорогенеза при переходе от водорослей к растениям. New Phytol. 190 , 875–881 (2011). PubMed Статья PubMed Central Google Scholar 4. Эдвардс, Д., Моррис, Дж. Л., Ричардсон, Дж. Б. и Кенрик, П. Криптоспоры и криптофиты обнаруживают скрытое разнообразие древних флор суши. New Phytol. 202 , 50–78 (2014). PubMed Статья PubMed Central Google Scholar 5. Кенрик П. и Крейн П. Р. Происхождение и ранняя эволюция растений на суше. Nature 389 , 33–39 (1997). CAS Статья Google Scholar 6. Бернер Р.А. ГЕОКАРБСУЛЬФ: комбинированная модель фанерозойского атмосферного O 2 и CO 2 . Геохим. Космохим. Acta 70 , 5653–5664 (2006). CAS Статья Google Scholar 7. Берлинг, Д. Дж., Осборн, К. П. и Чалонер, В. Г. Эволюция формы листьев у наземных растений, связанная с уменьшением содержания CO в атмосфере 2 в позднепалеозойскую эру. Nature 410 , 352–354 (2001). CAS PubMed Статья PubMed Central Google Scholar 8. Menand, B. et al. Древний механизм контролирует развитие клеток с функцией укоренения у наземных растений. Наука 316 , 1477–1480 (2007). CAS PubMed Статья PubMed Central Google Scholar 9. Хатер, Ф., Накель, Т. и Гросс-Хардт, Р. Репродуктивная многозадачность: женский гаметофит. Annu. Rev. Plant Biol. 71 , 517–546 (2020). CAS PubMed Статья PubMed Central Google Scholar 10. Хакенберг, Д. и Твелл, Д. Эволюция и формирование паттернов развития мужских гаметофитов. Curr. Вершина. Dev. Биол. 131 , 257–298 (2019). PubMed Статья PubMed Central Google Scholar 11. Амичи, Г. Б. Микроскопические наблюдения за различными видами растений. Ann. Сэй. Nat. Бот. 2 , 211–248 (1824). Google Scholar 12. Джонсон, М. А., Харпер, Дж. Ф. и Паланивелу, Р. Плодотворное путешествие: навигация по пыльцевым трубкам от прорастания до оплодотворения. Annu. Rev. Plant Biol. 70 , 809–837 (2019). CAS PubMed Статья PubMed Central Google Scholar 13. Спранк, С. В два раза веселее, вдвойне труднее: взаимодействие гамет у цветущих растений. Curr. Opin. Plant Biol. 53 , 106–116 (2020). CAS PubMed Статья PubMed Central Google Scholar 14. Borg, M. et al. Фактор транскрипции R2R3 MYB DUO1 активирует специфичный для мужской зародышевой линии регулон, необходимый для дифференцировки сперматозоидов у Arabidopsis . Растительная клетка 23 , 534–549 (2011). CAS PubMed PubMed Central Статья Google Scholar 15. Favery, B. et al. KOJAK кодирует белок, подобный синтазе целлюлозы, необходимый для морфогенеза корневых волосковых клеток в Arabidopsis . Genes Dev. 15 , 79–89 (2001). CAS PubMed PubMed Central Статья Google Scholar 16. Denninger, P. et al. Общение между мужчиной и женщиной запускает сигнатуры кальция во время оплодотворения у Arabidopsis . Nat. Commun. 5 , 4645 (2014). CAS PubMed Статья PubMed Central Google Scholar 17. Borges, F. et al. Очистка микроспор Arabidopsis , сперматозоидов и вегетативных ядер на основе FACS. Заводские методы 8 , 44 (2012). CAS PubMed PubMed Central Статья Google Scholar 18. Borg, M. et al. EAR-зависимый регуляторный модуль способствует делению мужских половых клеток и фертильности сперматозоидов у Arabidopsis . Растительная клетка 26 , 2098–2113 (2014). CAS PubMed PubMed Central Статья Google Scholar 19. Cyprys, P., Lindemeier, M. & Sprunck, S. Слияние гамет облегчается двумя мембранными белками DUF679, экспрессируемыми сперматозоидами. Nat. Растения 5 , 253–257 (2019). CAS PubMed Статья PubMed Central Google Scholar 20. Bowles, A.MC, Bechtold, U. & Paps, J. Происхождение наземных растений уходит корнями в два всплеска геномной новизны. Curr. Биол. 30 , 530–536.e2 (2020). CAS PubMed Статья PubMed Central Google Scholar 21. Ри, ​​С. Ю. и Мутвил, М. К раскрытию функций всех генов у растений. Trends Plant Sci. 19 , 212–221 (2014). CAS PubMed Статья PubMed Central Google Scholar 22. Брей, Н. Л., Пиментел, Х., Мельстед, П. и Пахтер, Л. Почти оптимальная вероятностная количественная оценка последовательности РНК. Nat. Biotechnol. 34 , 525–527 (2016). CAS PubMed Статья PubMed Central Google Scholar 23. Пина, К., Пинто, Ф., Фейхо, Дж. А. и Беккер, Дж. Д. Анализ семейства генов транскриптома пыльцы Arabidopsis показывает биологические последствия для роста клеток, контроля деления и регуляции экспрессии генов. Plant Physiol. 138 , 744–756 (2005). CAS PubMed PubMed Central Статья Google Scholar 24. Стеффен Дж. Г., Канг И.-Х., Макфарлейн Дж. И Дрюс Г. Н. Идентификация генов, экспрессируемых в женском гаметофите Arabidopsis . Plant J. 51 , 281–292 (2007). CAS PubMed Статья PubMed Central Google Scholar 25. Bowman, J. L. Семейство генов YABBY и судьба абаксиальных клеток. Curr. Opin. Plant Biol. 3 , 17–22 (2000). CAS PubMed Статья PubMed Central Google Scholar 26. Ким, Дж. Х. и Ли, Б. Х. ФАКТОР, РЕГУЛИРУЮЩИЙ РОСТ4 Arabidopsis thaliana, необходим для развития листьев, семядолей и апикальной меристемы побегов. J. Plant Biol. 49 , 463–468 (2006). CAS Статья Google Scholar 27. Ding, Z. J. et al. Фактор транскрипции WRKY46 модулирует развитие боковых корней Arabidopsis в условиях осмотического / солевого стресса посредством регуляции передачи сигналов ABA и гомеостаза ауксина. Plant J. 84 , 56–69 (2015). CAS PubMed Статья PubMed Central Google Scholar 28. Long, T. A. et al. Фактор транскрипции bHLH POPEYE регулирует ответ на дефицит железа в корнях Arabidopsis . Растительная клетка 22 , 2219–2236 (2010). CAS PubMed PubMed Central Статья Google Scholar 29. Эммс, Д. М. и Келли, С. OrthoFinder: вывод филогенетической ортологии для сравнительной геномики. Genome Biol. 20 , 238 (2019). PubMed PubMed Central Статья Google Scholar 30. Домазет-Лосо, Т., Брайкович, Дж. И Тауц, Д. Филостратиграфический подход к раскрытию геномной истории основных адаптаций в линиях многоклеточных животных. Trends Genet. 23 , 533–539 (2007). CAS PubMed Статья PubMed Central Google Scholar 31. Бегун, Д.Дж., Линдфорс, Х. А., Керн, А. Д. и Джонс, К. Д. Доказательства эволюции de novo генов, экспрессируемых семенниками, в кладе Drosophila yakuba / Drosophila erecta clade. Генетика 176 , 1131–1137 (2007). CAS PubMed PubMed Central Статья Google Scholar 32. Gossmann, T. I., Saleh, D., Schmid, M. W., Spence, M. A. & Schmid, K. J. Транскриптомы гаметофитов растений имеют более высокую долю быстро эволюционирующих и молодых генов, чем спорофиты. Мол. Биол. Evol. 33 , 1669–1678 (2016). CAS PubMed PubMed Central Статья Google Scholar 33. Cui, X. et al. Молодые гены самца: выводы из эволюционного возрастного анализа транскриптома пыльцы. Мол. Завод 8 , 935–945 (2015). CAS PubMed Статья PubMed Central Google Scholar 34. Мойерс, Б. А. и Чжан, Дж. Дальнейшее моделирование и анализ демонстрируют открытые проблемы филостратиграфии. Genome Biol. Evol. 9 , 1519–1527 (2017). PubMed PubMed Central Статья Google Scholar 35. Дойл, Дж. А. в Annual Plant Reviews (ред. Робертс, Дж. А. и др.) 1–50 (John Wiley & Sons, 2018). 36. Пирес, Н. Д. и Долан, Л.Морфологическая эволюция наземных растений: новые конструкции со старыми генами. Philos. Пер. R. Soc. Лондон. B Biol. Sci. 367 , 508–518 (2012). CAS PubMed PubMed Central Статья Google Scholar 37. Кардона Т. Дважды подумав об эволюции фотосинтеза. Open Biol. 9 , 180246 (2019). CAS PubMed PubMed Central Статья Google Scholar 38. Харрисон, К. Дж. И Моррис, Дж. Л. Происхождение и ранняя эволюция побегов и листьев сосудистых растений. Philos. Пер. R. Soc. Лондон. B Biol. Sci. 373 , 20160496 (2018). PubMed Статья CAS PubMed Central Google Scholar 39. Хетерингтон А. Дж. И Долан Л. Поэтапное и независимое происхождение корней наземных растений. Nature 561 , 235–238 (2018). CAS PubMed PubMed Central Статья Google Scholar 40. Шпехт, К. Д. и Бартлетт, М. Э. Эволюция цветов: происхождение и последующее разнообразие цветков покрытосеменных. Annu. Rev. Ecol. Evol. Syst. 40 , 217–243 (2009). Артикул Google Scholar 41. Pires, N. D. et al. Рекрутирование и реконструкция древней регуляторной сети генов во время эволюции наземных растений. Proc. Natl Acad. Sci. США 110 , 9571–9576 (2013). CAS PubMed PubMed Central Статья Google Scholar 42. Huang, L. & Schiefelbein, J. Консервативные программы экспрессии генов в развивающихся корнях различных растений. Растительная клетка 27 , 2119–2132 (2015). CAS PubMed PubMed Central Статья Google Scholar 43. Tanabe, Y. et al. Характеристика генов MADS-бокса у зеленых водорослей charophycean и его значение для эволюции генов MADS-бокса. Proc. Natl Acad. Sci. США 102 , 2436–2441 (2005). CAS PubMed PubMed Central Статья Google Scholar 44. Brodribb, T. J., Carriquí, M., Delzon, S., McAdam, S.A. и Holbrook, N. M. У широко распространенного мха обнаружена развитая сосудистая функция. Nat. Растения 6 , 273–279 (2020). CAS PubMed Статья PubMed Central Google Scholar 45. Ruprecht, C. et al. Филогеномный анализ сетей коэкспрессии генов показывает эволюцию функциональных модулей. Plant J. 90 , 447–465 (2017). CAS PubMed Статья PubMed Central Google Scholar 46. Го, Ю.-Л. Эволюция генного семейства у зеленых растений с акцентом на происхождение и эволюцию генов Arabidopsis thaliana . Plant J. 73 , 941–951 (2013). CAS PubMed Статья PubMed Central Google Scholar 47. Buschiazzo, E., Ritland, C., Bohlmann, J. & Ritland, K. Медленно, но не низко: сравнение геномов показывает более медленную скорость эволюции и более высокую d N / d S у хвойных деревьев по сравнению с покрытосеменным. BMC Evol. Биол. 12 , 8 (2012). PubMed PubMed Central Статья Google Scholar 48. Мойл, Л. К., Ву, М. и Гибсон, М. Дж. С. Репродуктивные белки развиваются быстрее, чем не репродуктивные белки среди видов Solanum . Фронт. Plant Sci. 12 , 635990 (2021 г.). PubMed PubMed Central Статья Google Scholar 49. Чибалина, М. В., Филатов, Д. А. Дегенерация Y-хромосомы растения замедляется гаплоидным очищающим отбором. Curr. Биол. 21 , 1475–1479 (2011). CAS PubMed Статья PubMed Central Google Scholar 50. Borg, M. et al. Эпигенетическое репрограммирование перестраивает транскрипцию во время смены поколений у Arabidopsis . eLife 10 , e61894 (2021). PubMed PubMed Central Статья Google Scholar 51. Рао, X. и Диксон, Р.А. Сети коэкспрессии для биологии растений: почему и как. Acta Biochim. Биофиз. Грех. (Шанхай) 51 , 981–988 (2019). Артикул Google Scholar 52. Borges, F. et al. Сравнительная транскриптомика сперматозоидов Arabidopsis . Plant Physiol. 148 , 1168–1181 (2008). CAS PubMed PubMed Central Статья Google Scholar 53. Becker, J. D., Takeda, S., Borges, F., Dolan, L. & Feijó, J. A. Транскрипционное профилирование корневых волосков и пыльцы Arabidopsis определяет сигнатуру роста апикальных клеток. BMC Plant Biol. 14 , 197 (2014). PubMed PubMed Central Статья CAS Google Scholar 54. von Besser, K., Frank, A.C., Johnson, M. A. & Preuss, D. Arabidopsis HAP2 ( GCS1 ) — это ген, специфичный для сперматозоидов, необходимый для управления пыльцевыми трубками и оплодотворения. Разработка 133 , 4761–4769 (2006). Артикул CAS Google Scholar 55. Proost, S. & Mutwil, M. CoNekT: платформа с открытым исходным кодом для сравнительного анализа геномных и транскриптомных сетей. Nucleic Acids Res. 46 , W133 – W140 (2018). CAS PubMed PubMed Central Статья Google Scholar 56. Boisson-Dernier, A. et al. Нарушение экспрессируемых пыльцой гомологов FERONIA ANXUR1 и ANXUR2 вызывает выброс пыльцевых трубок. Разработка 136 , 3279–3288 (2009). CAS PubMed PubMed Central Статья Google Scholar 57. Zhu, L. et al. Протеинкиназы Arabidopsis CrRLK1L BUPS1 и BUPS2 необходимы для нормального роста пыльцевых трубок в пестике. Plant J. 95 , 474–486 (2018). CAS PubMed Статья PubMed Central Google Scholar 58. Alves-Ferreira, M. et al. Профилирование глобальной экспрессии применялось для анализа развития тычинок Arabidopsis . Plant Physiol. 145 , 747–762 (2007). CAS PubMed PubMed Central Статья Google Scholar 59. Гупта Р., Тинг Дж. Т. Л., Соколов Л. Н., Джонсон С. А. и Луан С. Гомолог опухолевого супрессора, AtPTEN1, необходим для развития пыльцы у Arabidopsis . Растительная клетка 14 , 2495–2507 (2002). CAS PubMed PubMed Central Статья Google Scholar 60. Zhou, Z. et al. Arabidopsis RIC1 рассекает актиновые филаменты на верхушке, чтобы регулировать рост пыльцевой трубки. Растительная клетка 27 , 1140–1161 (2015). CAS PubMed PubMed Central Статья Google Scholar 61. Liang, Y. et al. MYB97, MYB101 и MYB120 действуют как мужские факторы, которые контролируют взаимодействие пыльцевой трубки с синергидом при оплодотворении Arabidopsis thaliana . PLoS Genet. 9 , e1003933 (2013). PubMed PubMed Central Статья CAS Google Scholar 62. Szövényi, P., Waller, M. & Kirbis, A. Эволюция строения тела растений. Curr. Вершина. Dev. Биол. 131 , 1–34 (2019). PubMed Статья PubMed Central Google Scholar 63. Domazet-Lošo, T. & Tautz, D.Филогенетический возрастной индекс транскриптома отражает паттерны онтогенетической дивергенции. Природа 468 , 815–818 (2010). PubMed Статья CAS PubMed Central Google Scholar 64. Guijarro-Clarke, C., Holland, P. W. H. & Paps, J. Распространенные закономерности потери генов в эволюции животного мира. Nat. Ecol. Evol. 4 , 519–523 (2020). PubMed Статья PubMed Central Google Scholar 65. Xiao, S.-J., Zhang, C., Zou, Q. & Ji, Z.-L. TiSGeD: база данных тканеспецифичных генов. Биоинформатика 26 , 1273–1275 (2010). CAS PubMed PubMed Central Статья Google Scholar 66. Бенджамини Ю. и Хохберг Ю. Контроль уровня ложных открытий: практичный и эффективный подход к множественному тестированию. J. R. Stat. Soc. Сер. B (Methodol.) 57 , 289–300 (1995). Google Scholar 67. Инициатива «Одна тысяча растений». Тысяча транскриптомов растений и филогеномика зеленых растений. Nature 574 , 679–685 (2019). 68. Уэрта-Сепас, Дж., Серра, Ф. и Борк, П. ETE 3: реконструкция, анализ и визуализация филогеномных данных. Мол. Биол. Evol. 33 , 1635–1638 (2016). CAS PubMed PubMed Central Статья Google Scholar 69. Zheng, Y. et al. iTAK: программа для полногеномного прогнозирования и классификации факторов транскрипции растений, регуляторов транскрипции и протеинкиназ. Мол. Завод 9 , 1667–1670 (2016). CAS PubMed Статья PubMed Central Google Scholar 70. Тиан, Ф., Ян, Д.-К., Мэн, Й.-К., Джин, Дж. И Гао, Г. PlantRegMap: построение функциональных регуляторных карт растений. Nucleic Acids Res. 48 , D1104 – D1113 (2020). CAS PubMed PubMed Central Google Scholar 71. Ballester, A.-R. и другие. Геном, транскриптом и функциональный анализ penicillium expansum позволяют по-новому взглянуть на вторичный метаболизм и патогенность. Мол. Взаимодействие с растительными микробами. 28 , 232–248 (2015). CAS PubMed Статья PubMed Central Google Scholar 72. Huerta-Cepas, J. et al. PhylomeDB v3.0: расширяющееся хранилище полногеномных коллекций деревьев, выравниваний и основанных на филогении ортологии и предсказаний паралогий. Nucleic Acids Res. 39 , D556 – D560 (2011). CAS PubMed Статья PubMed Central Google Scholar 73. Minh, B.Q. et al. IQ-TREE 2: новые модели и эффективные методы филогенетического вывода в эпоху геномики. Мол. Биол. Evol. 37 , 1530–1534 (2020). CAS PubMed PubMed Central Статья Google Scholar 74. Shannon, P. et al. Cytoscape: программная среда для интегрированных моделей сетей биомолекулярного взаимодействия. Genome Res. No related posts. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт