Длина окружности, формула как найти длину окружности
Если вы не знаете, как обозначается длина окружности, то знак окружности выглядит вот так — l
Как найти длину окружности через диаметр
Диаметр — отрезок, который соединяет две точки окружности и проходит через её центр. Формула длины окружности через диаметр:
l=πd, где
π— число пи — математическая константа, равная 3,14
d — диаметр окружности
Как найти длину окружности через радиус
Радиус окружности — отрезок, который соединяет центр окружности с точкой на окружности. Формула длины окружности через радиус:
l=2πr , где
π — число пи, равное 3,14
r — радиус окружности
Как вычислить длину окружности через площадь круга
Если вам известна площадь круга, вы также можете узнать длину окружности:
где:
π — число пи, равное 3,14
S — площадь круга
Как найти длину окружности через диагональ вписанного прямоугольника
Как измерить окружность, если в нее вписан прямоугольник:
l=πd, где
d — диагональ прямоугольника
Как вычислить длину окружности через сторону описанного квадрата
Давайте рассмотрим, как найти длину окружности, если она вписана в квадрат и нам известна сторона квадрата:
l=πa, где
π — математическая константа, равная 3,14
a — сторона квадрата
Как найти длину окружности через стороны и площадь вписанного треугольника
Можно найти, чему равна длина окружности, если в нее вписан треугольник и известны все три его стороны, а также известна его площадь:
где:
π — математическая константа, она всегда равна 3,14
a — первая сторона треугольника
b — вторая сторона треугольника
c — третья сторона треугольника
S — площадь треугольника
Как найти длину окружности через площадь и полупериметр описанного треугольника
Можно определить, чему равна длина окружности, если круг вписан в треугольник, и известны следующие параметры: площадь треугольника и его полупериметр.
Периметр — это сумма всех сторон треугольника. Полупериметр равен половине этой суммы, то есть чтобы его найти, вам нужно рассчитать периметр и поделить его на два.
где:
π — математическая константа, равная 3,14
S — площадь треугольника
p — полупериметр треугольника
Как вычислить длину окружности через сторону вписанного правильного многоугольника
Разбираемся, как в этом случае измерить окружность. Для этого необходимо посчитать, сколько сторон у многоугольника, а также знать длину стороны многоугольника. Напомним, что у правильного многоугольника все стороны равны, как у квадрата.
Формула вычисления длины окружности:
где:
π — математическая константа, равная 3,14
a — сторона многоугольника
N — количество сторон многоугольника
Задачи для решения
Давайте тренироваться! Двигаемся от простого к сложному:
 Найти длину окружности, диаметр которой равен 5 см.
Найти длину окружности, диаметр которой равен 5 см.
Решение. Итак, нам известен диаметр окружности, значит для вычисления длины заданной окружности берем формулу:
l=πd
Подставляем туда известные переменные и получается, что длина окружности равна
l=πd=3,14·5=15,7(см)
Ответ: 15,7 (см)
Задача 2. Чему равна длина окружности, описанной около правильного треугольника со стороною a = 4√3 дм
Решение. Радиус окружности равен Подставим туда наши переменные и получим
Теперь, когда нам известен радиус окружности и есть формула длины окружности через радиус l=2πr, мы можем подставить наши данные и получить решение задачи.
Так и сделаем:
l=2πr=2·π·4≈2·3,14·4=25,12(дм)
Ответ: l=25,12(дм)
Окружность, круг, сегмент, сектор. Формулы и свойства
Определение. Окружность — это совокупность всех точек на плоскости, которые находятся на одинаковом расстоянии от заданной точки О, которая называется центром окружности.
Определение. Единичная окружность — окружность, радиус которой равна единице.
Определение. Круг — часть плоскости, ограничена окружностью.
Определение. Радиус окружности R — расстояние от центра окружности О до любой точки окружности.
Определение. Диаметр окружности D — отрезок, который соединяет две точки окружности и проходит через ее центр.
Основные свойства окружности
1. Диаметр окружности равен двум радиусам.D = 2r
2. Кратчайшее расстояние от центра окружности к секущей (хорде) всегда меньше радиуса.
3. Через три точки, которые не лежат на одной прямым, можно провести только одну окружность.
4. Среди всех замкнутых кривых с одинаковой длиной, окружность имеет наибольшую площадь.
5. Если две окружности соприкасаются в одной точке, то эта точка лежит на прямой, что проходит через центры этих окружностей.
Формулы длины окружности и площади круга
Формулы длины окружности
1. Формула длины окружности через диаметр:
Формула длины окружности через диаметр:L = πD
2. Формула длины окружности через радиус:L = 2πr
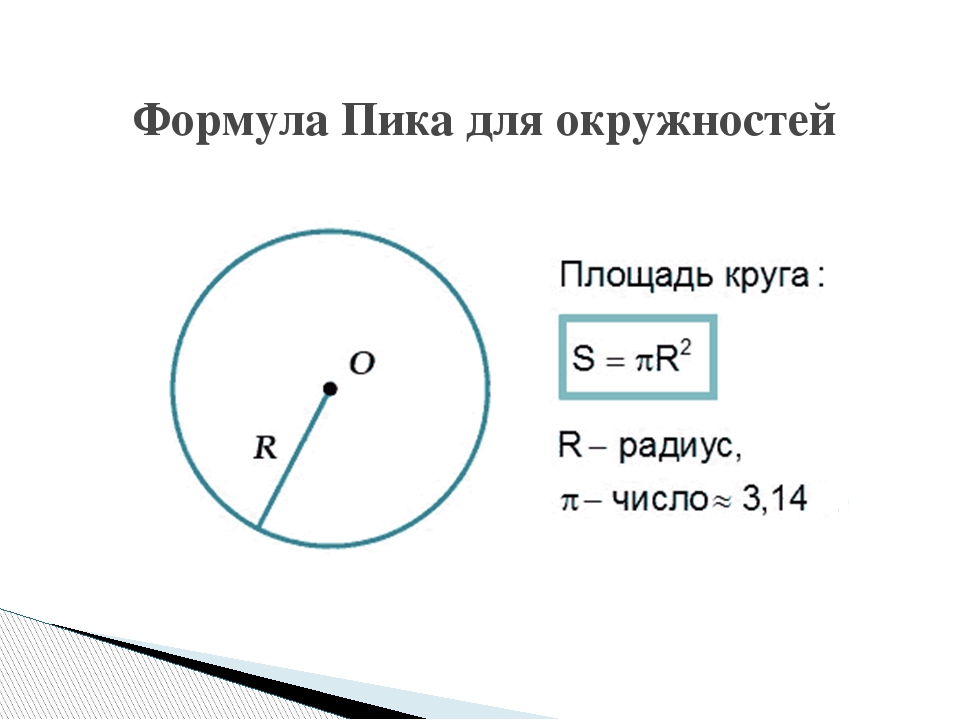
Формулы площади круга
1. Формула площади круга через радиус:S = πr2
2. Формула площади круга через диаметр:S = πD24
Уравнение окружности
1. Уравнение окружности с радиусом r и центром в начале декартовой системы координат:r2 = x2 + y2
2. Уравнение окружности с радиусом r и центром в точке с координатами (a, b) в декартовой системе координат:r2 = (x — a)2 + (y — b)2
3. Параметрическое уравнение окружности с радиусом r и центром в точке с координатами (a, b) в декартовой системе координат:| { | x = a + r cos t |
| y = b + r sin t |
Касательная окружности и ее свойства
Определение. Касательная окружности — прямая, которая касается окружности только в одной точке.
Основные свойства касательных к окружности
1. Касательная всегда перпендикулярна к радиусу окружности, проведенного в точке соприкосновения.
2. Кратчайшее расстояние от центра окружности к касательной равна радиусу окружности.
3. Если две касательные, с точками соприкосновения B и C, на одной окружности не параллельны, то они пересекаются в точке A, а отрезок между точкой соприкосновения и точкой пересечения одной касательной равен таком же отрезке на другой касательной:AB = AC
Также, если провести прямую через центр окружности О и точку пересечения A этих касательных, то углы образованный между этой прямой и касательными будут равны:Секущая окружности и ее свойства
Определение. Секущая окружности — прямая, которая проходит через две точки окружности.
Основные свойства секущих
1. Если с точки вне окружности (Q) выходят две секущие, которые пересекают окружность в двух точках A и B для одной секущей и C и D для другой секущей, то произведения отрезков двух секущих равны между собою:AQ ∙ BQ = CQ ∙ DQ
2. Если из точки Q вне окружности выходит секущая прямая, что пересекает окружность в двух точках A и B, и касательная с точкой соприкосновения C, то произведение отрезков секущей равна квадрату длины отрезка касательной:
Если из точки Q вне окружности выходит секущая прямая, что пересекает окружность в двух точках A и B, и касательная с точкой соприкосновения C, то произведение отрезков секущей равна квадрату длины отрезка касательной:AQ ∙ BQ = CQ2
Хорда окружности ее длина и свойства
Определение. Хорда окружности — отрезок, который соединяет две точки окружности.
Длина хорды
1. Длина хорды через центральный угол и радиус: AB = 2r sin α2 2. Длина хорды через вписанный угол и радиус:AB = 2r sin α
Основные свойства хорд
1. Две одинаковые хорды стягивают две одинаковые дуги:если хорды AB = CD, то
дуги ◡ AB = ◡ CD
2. Если хорды параллельные, то дуги между ними будут одинаковые:если хорды AB ∣∣ CD, то
◡ AD = ◡ BC
3. Если радиус окружности перпендикулярен к хорде, то он разделяет хорду пополам в точке их пересечения:если OD ┴ AB, то
AC = BC
4. Если две хорды AB и CD пересекаются в точке Q, то произведение отрезков, что образовались при пересечении, одной хорды равны произведению отрезков другой хорды:AQ ∙ BQ = DQ ∙ QC
5. Хорды с одинаковой длиной находятся на одинаковом расстоянии от центра окружности.
Хорды с одинаковой длиной находятся на одинаковом расстоянии от центра окружности.если хорды AB = CD, то
ON = OK
6. Чем больше хорда тем ближе она к центру.если CD > AB, то
ON < OK
Центральный угол, вписанный угол и их свойства
Определение. Центральный угол окружности — угол, вершиной которого есть центр окружности.
Определение. Угол вписанный в окружность — угол, вершина которого лежит на окружности, а стороны угла пересекают окружность.
Основные свойства углов
1. Все вписанные углы, которые опираются на одну дугу — равны. 2. Вписанний угол, который опирается на диаметр будет прямым (90°). 3. Вписанный угол равен половине центрального угла, что опирается на ту же дугуβ = α2
4. Если два вписанных угла опираются на одну хорду и находятся по различные стороны от нее, то сумма этих углов равна 180°.α + β = 180°
Определение. Дуга окружности (◡) — часть окружности, которая соединяет две точки на окружности.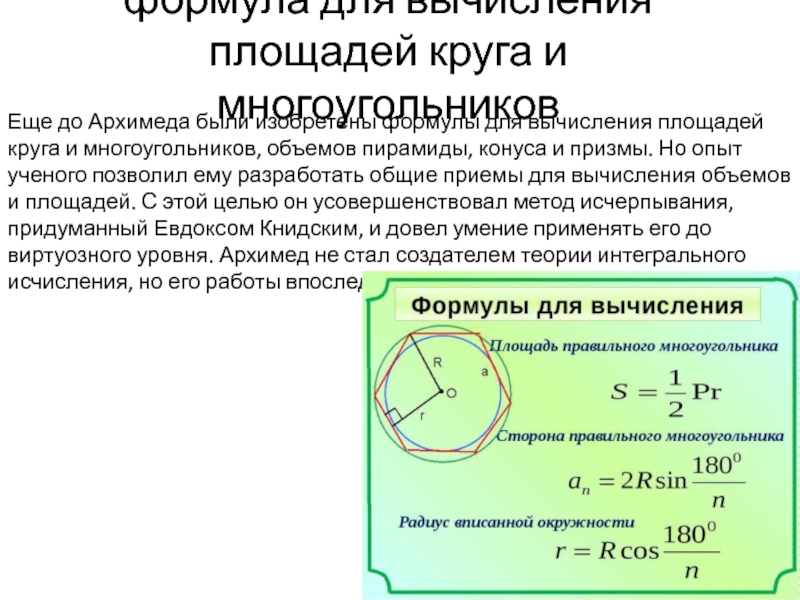
Определение. Градусная мера дуги — угол между двумя радиусами, которые ограничивают эту дугу. Градусная мера дуги всегда равна градусной мере центрального угла, который ограничивает эту дугу своими сторонами.
Формула длины дуги через центральный угол (в градусах):l = πr180°∙ α
Определение. Полуокружность — дуга в которой концы соединены диаметром окружности.
Определение. Полукруг (◓) — часть круга, которая ограничена полуокружностью и диаметром.
Определение. Сектор (◔) — часть круга, которая ограничена двумя радиусами и дугой между этими радиусами.
Формула. Формула площади сектор через центральный угол (в градусах)S = πr2360°∙ α
Определение. Сегмент — часть круга, которая ограничена дугой и хордой, что соединяет ее концы.
Определение. Концентрические окружности — окружности с различными радиусами, которые имеют общий центр.
Определение. Кольцо — часть плоскости ограниченная двумя концентрическими окружностями.
Формула расчета длины окружности
Окружностью называется ряд равноудалённых точек от одной точки, которая, в свою очередь, является центром этой окружности. Окружность имеет также свой радиус, равный расстоянию этих точек от центра.
Отношение длины, какой либо окружности к её диаметру, для всех окружностей одинаково. Это отношение есть число, являющееся математической константой, которое обозначается греческой буквой π.
Определение длины окружности
Формула расчёта длинны окружности
Произвести расчёт окружности можно по следующей формуле:
L = πD = 2πr
r – радиус окружности
D – диаметр окружности
L – длина окружности
π – 3.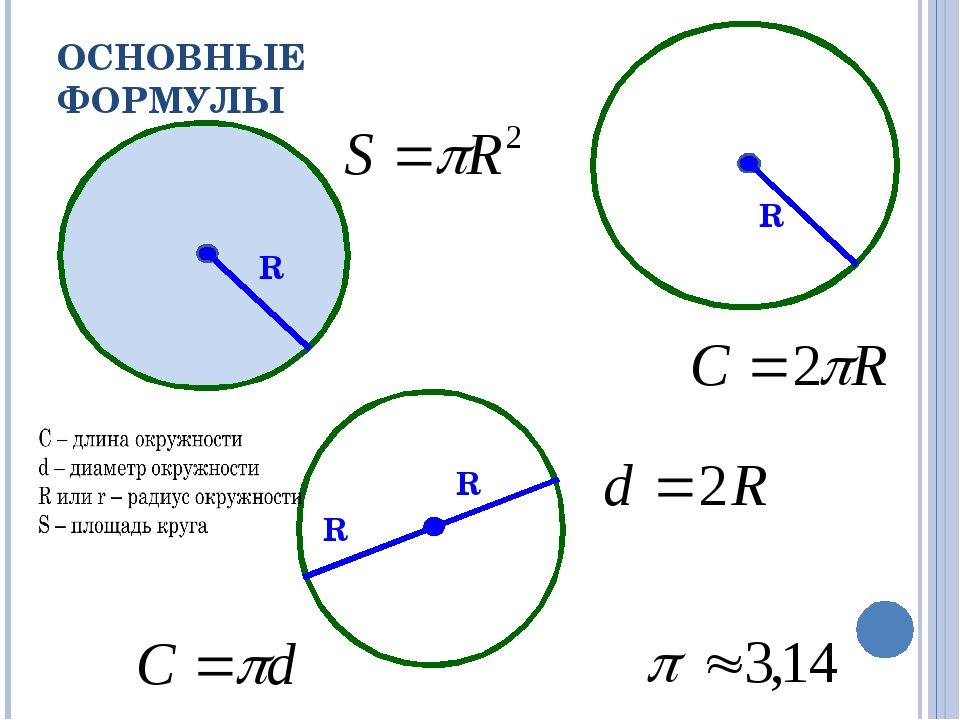 14
14
Пример нахождения длинны окружности
Задача:
Вычислить длину окружности, имеющей радиус 10 сантиметров.
Формула для вычисления дины окружности имеет вид:
L = πD = 2πr
где L – длина окружности, π – 3,14, r – радиус окружности, D – диаметр окружности.
Таким образом, длина окружности, имеющей радиус 10 сантиметров равна:
L = 2 × 3,14 × 10 = 31,4 сантиметра
Окружность представляет собой геометрическую фигуру, являющуюся совокупностью всех точек на плоскости, удаленных от заданной точки, которая называется ее центром, на некоторое расстояние, не равное нулю и именуемое радиусом. Определять ее длину с различной степенью точности ученые умели уже в глубокой древности: историки науки считают, что первая формула для вычисления длины окружности была составлена примерно в 1900 году до нашей эры в древнем Вавилоне.
С такими геометрическими фигурами, как окружности, мы сталкиваемся ежедневно и повсеместно. Именно ее форму имеет внешняя поверхность колес, которыми оснащаются различные транспортные средства. Эта деталь, несмотря на свою внешнюю простоту и незатейливость, считаются одним из величайших изобретений человечества, причем интересно, что аборигены Австралии и американские индейцы вплоть до прихода европейцев совершенно не имели понятия о том, что это такое.
По всей вероятности, самые первые колеса представляли собой отрезки бревен, которые насаживались на ось. Постепенно конструкция колеса совершенствовалась, их конструкция становилась все более и более сложной, а для их изготовления требовалось использовать массу различных инструментов. Сначала появились колеса, состоящие из деревянного обода и спиц, а затем, для того, чтобы уменьшить износ их внешней поверхности, ее стали обивать металлическими полосами. Для того чтобы определить длины этих элементов, и требуется использовать формулу расчета длины окружности (хотя на практике, вероятнее всего, мастера это делали «на глаз» или просто опоясывая колесо полосой и отрезая требуемый ее участок).
Следует заметить, что колесо используется отнюдь не только в транспортных средствах. Например, его форму имеет гончарный круг, а также элементы шестеренок зубчатых передач, широко применяемых в технике. Издавна колеса использовались в конструкциях водяных мельниц (самые древние из известных ученым сооружений такого рода строились в Месопотамии), а также прялок, применявшихся для изготовления нитей из шерсти животных и растительных волокон.
Окружности нередко можно встретить и в строительстве. Их форму имеют достаточно широко распространенные круглые окна, очень характерные для романского архитектурного стиля. Изготовление этих конструкций – дело весьма непростое и требует высокого мастерства, а также наличия специального инструмента. Одной из разновидностей круглых окон являются иллюминаторы, устанавливаемые в морских и воздушных судах.
Таким образом, решать задачу определения длины окружности часто приходится инженерам-конструкторам, разрабатывающим различные машины, механизмы и агрегаты, а также архитекторам и проектировщикам. Поскольку число π, необходимое для этого, является бесконечным, то с абсолютной точностью определить этот параметр не представляется возможным, и поэтому при вычислениях учитывается та ее степень, которая в том или ином конкретном случае является необходимой и достаточной.
Поскольку число π, необходимое для этого, является бесконечным, то с абсолютной точностью определить этот параметр не представляется возможным, и поэтому при вычислениях учитывается та ее степень, которая в том или ином конкретном случае является необходимой и достаточной.
| Окружность круга P | |||
| Результат | |||
Длина окружности: Площадь круга: | |||
Круг (окружность) – геометрическая фигура на плоскости, все точки которой равноудалены от данной точки (центр круга). Круг (окружность) – геометрическая фигура на плоскости, все точки которой равноудалены от данной точки (центр круга). | |||
| Числовая характеристика | Рисунок | Формула |
| Площадь круга | , где R – радиус круга, D – диаметр круга Посмотреть доказательство | |
| Площадь сектора | , если величина угла α выражена в радианах Посмотреть доказательство | |
, если величина угла α выражена в градусах Посмотреть доказательство | ||
| Площадь сегмента | , если величина угла α выражена в радианах Посмотреть доказательство | |
, если величина угла α выражена в градусах Посмотреть доказательство |
| Площадь круга |
, где R – радиус круга, D – диаметр круга Посмотреть доказательство |
| Площадь сектора |
, если величина угла α выражена в радианах Посмотреть доказательство * * * , если величина угла α выражена в градусах Посмотреть доказательство |
| Площадь сегмента |
, если величина угла α выражена в радианах Посмотреть доказательство * * * , если величина угла α выражена в градусах Посмотреть доказательство |
Центральный угол, вписанный угол и их свойства
Определение.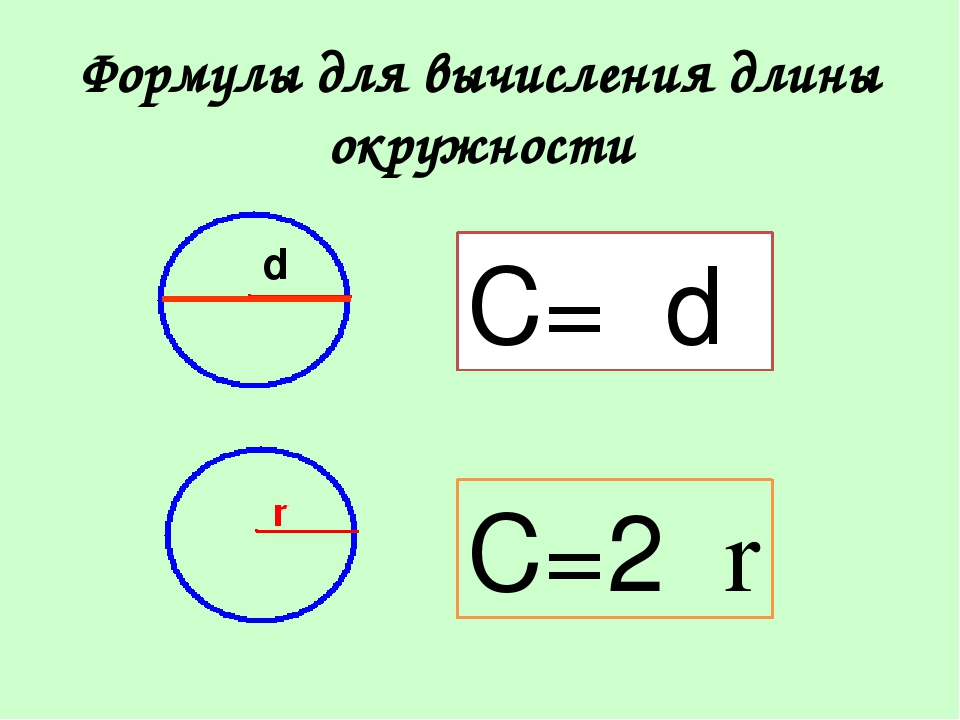 Центральный угол окружности – угол, вершиной которого есть центр окружности.
Центральный угол окружности – угол, вершиной которого есть центр окружности.
Определение. Угол вписанный в окружность – угол, вершина которого лежит на окружности, а стороны угла пересекают окружность.
Связанные определения
- Центральный угол в окружности — это угол, образованный двумя радиусами.
- Радиус кривизны кривой — это радиус окружности, имеющей с этой кривой касание второго порядка.
Примеры задач
Задание 1
Длина окружности равняется 87,92 см. Найдите ее радиус.
Решение:
Используем первую формулу (через периметр):
Задание 2
Найдите радиус круга, если его площадь составляет 254,34 см2.
Решение:
Воспользуемся формулой, выраженной через площадь фигуры:
Длина дуги
Рассмотрим дугу окружности, изображённую на рисунке 3, и обозначим её длину символом L(α), где буквой α обозначена величина соответствующего центрального угла.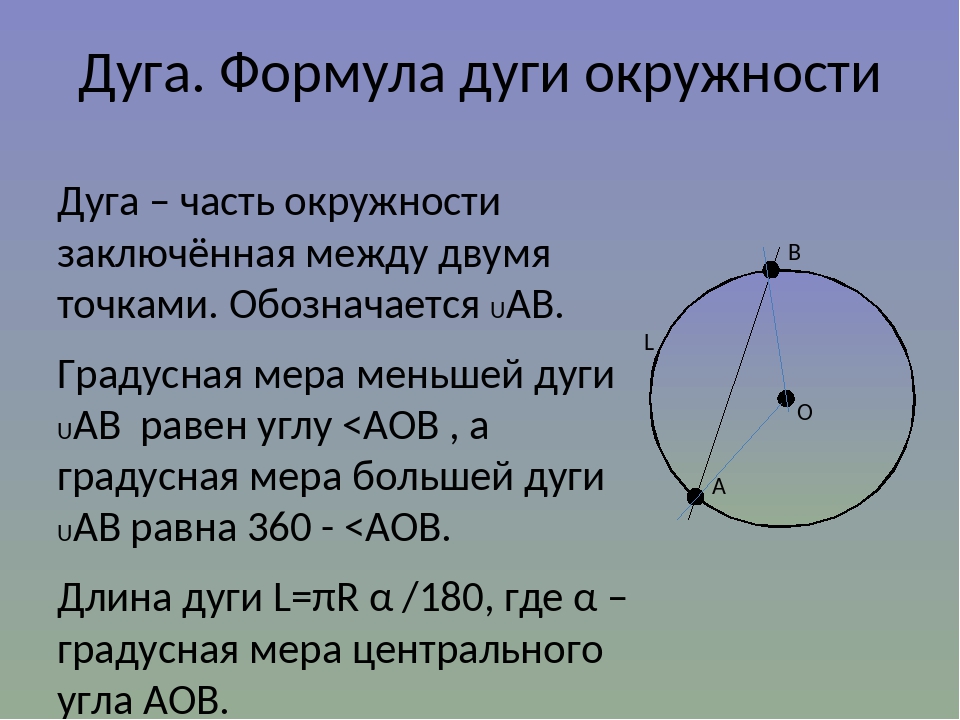
Рис.3
В случае, когда величина α выражена в градусах, справедлива пропорция
из которой вытекает равенство:
В случае, когда величина α выражена в радианах, справедлива пропорция
из которой вытекает равенство:
Уравнение окружности
1. Уравнение окружности с радиусом r и центром в начале декартовой системы координат:r2 = x2 + y2
2. Уравнение окружности с радиусом r и центром в точке с координатами (a, b) в декартовой системе координат:r2 = (x – a)2 + (y – b)2
3. Параметрическое уравнение окружности с радиусом r и центром в точке с координатами (a, b) в декартовой системе координат:| { | x = a + r cos t |
| y = b + r sin t |
Углы между двумя хордами
Случай 1: два секущие пересекаются внутри окружности.
Когда две секущие пересекаются внутри окружности, величина образованных угла, в два раза меньше суммы величин дуг, на которые они опираются. На рисунке дуга AB и дуга CD равны 60° и 50° тогда углы 1 и 2 равны Случай 2: две секущие пересекаются вне окружности.
Иногда секущие пересекаются за пределами окружности. Когда это случается, величина образующихся углов равна половине разности дуг, на которые они опираются.
Через площадь и полупериметр описанного треугольника
Разделите площадь описанного треугольника на его полупериметр.
- r — искомый радиус окружности.
- S — площадь треугольника.
- p — полупериметр треугольника (равен половине от суммы всех сторон).
Основные свойства касательных к окружности
1. Касательная всегда перпендикулярна к радиусу окружности, проведенного в точке соприкосновения.
2. Кратчайшее расстояние от центра окружности к касательной равна радиусу окружности.
3. Если две касательные, с точками соприкосновения B и C, на одной окружности не параллельны, то они пересекаются в точке A, а отрезок между точкой соприкосновения и точкой пересечения одной касательной равен таком же отрезке на другой касательной:
AB = AC
Также, если провести прямую через центр окружности О и точку пересечения A этих касательных, то углы образованный между этой прямой и касательными будут равны:
∠ОAС = ∠OAB
Обобщения
Радиусом множества , лежащего в метрическом пространстве с метрикой , называется величина . Например, радиус n-размерного гиперкуба со стороной s равен
Через диагональ вписанного прямоугольника
Диагональ прямоугольника является диаметром окружности, в которую он вписан. А диаметр, как мы уже вспомнили, в два раза больше радиуса. Поэтому достаточно разделить диагональ на два.
- R — искомый радиус окружности.
- d — диагональ вписанного прямоугольника.
 Напомним, она делит фигуру на два прямоугольных треугольника и является их гипотенузой — стороной, лежащей напротив прямого угла. Поэтому, если диагональ неизвестна, её можно найти через соседние стороны прямоугольника с помощью теоремы Пифагора.
Напомним, она делит фигуру на два прямоугольных треугольника и является их гипотенузой — стороной, лежащей напротив прямого угла. Поэтому, если диагональ неизвестна, её можно найти через соседние стороны прямоугольника с помощью теоремы Пифагора. - a, b — стороны вписанного прямоугольника.
Площадь круга, онлайн расчет
Вместо заключения
Чтобы еще больше понять, насколько важно понятие РАДИУС, вспомните инструмент, с помощью которого можно начертить окружность. Это циркуль и выглядит он вот так.
Пользоваться им просто. Ножка с острым концом ставится в центр будущей окружности. А ножка с грифелем прочерчивает линию. А расстояние, на котором они будут друг от друга, и есть РАДИУС.
Источники
- https://mnogoformul.ru/dlina-okruzhnosti-ili-perimetr-kruga
- https://allcalc.
 ru/node/783
ru/node/783 - https://KtoNaNovenkogo.ru/voprosy-i-otvety/radius-chto-ehto-takoe-kak-najti-radius-okruzhnosti-formula.html
- https://dobriy-sovet.ru/kak-najti-radius-kruga/
- https://www.calc.ru/radius-kruga.html
- https://Lifehacker.ru/kak-najti-radius-okruzhnosti/
- https://poschitat.online/radius-okruzhnosti
- https://ru.wikihow.com/%D0%BD%D0%B0%D0%B9%D1%82%D0%B8-%D1%80%D0%B0%D0%B4%D0%B8%D1%83%D1%81-%D0%BA%D1%80%D1%83%D0%B3%D0%B0
- https://www.resolventa.ru/demo/diaggia6.htm
- https://ru.onlinemschool.com/math/formula/circle/
- https://dic.academic.ru/dic.nsf/ruwiki/6846
- https://MicroExcel.ru/radius-kruga/
- https://www.math20.com/ru/geometria/krugi.html
Длина окружности. Решение задач на длину окружности и площадь круга
Длина окружности
Длина любой окружности больше своего диаметра в одно и то же число раз, а именно, приблизительно в 3,14 раза. Для обозначения этой величины используется маленькая (строчная) греческая буква
Для обозначения этой величины используется маленькая (строчная) греческая буква π
(пи):
Таким образом, длину окружности (C) можно вычислить, умножив константу π на диаметр (D), или умножив π на удвоенный радиус, так как диаметр равен двум радиусам. Следовательно, формула длины окружности будет выглядеть так:
C = πD = 2πR,
где C — длина окружности, π — константа, D — диаметр окружности, R — радиус окружности.
Так как окружность является границей круга, то длину окружности можно также назвать длиной круга или периметром круга.
Задачи на длину окружности
Задача 1. Найти длину окружности, если её диаметр равен 5 см.
Решение: Так как длина окружности равна π умноженное на диаметр, то длина окружности с диаметром 5 см будет равна:
C ≈ 3,14 · 5 = 15,7 (см).
Ответ: 15,7 см.
Задача 2. Найти длину окружности, радиус которой равен 3,5 м.
Решение: Сначала найдём диаметр окружности, умножив длину радиуса на 2:
D = 3,5 · 2 = 7 (м),
теперь найдём длину окружности, умножив π на диаметр:
C ≈ 3,14 · 7 = 21,98 (м).
Ответ: 21,98 м.
Задача 3. Найти радиус окружности, длина которой равна 7,85 м.
Решение: Чтобы найти радиус окружности по её длине, надо длину окружности разделить на 2π:
следовательно, радиус будет равен:
| R | ≈ | 7,85 | = | 7,85 | = 1,25 (м). |
| 2 · 3,14 | 6,28 |
Ответ: 1,25 м.
Задачи на площадь круга
Задача 1.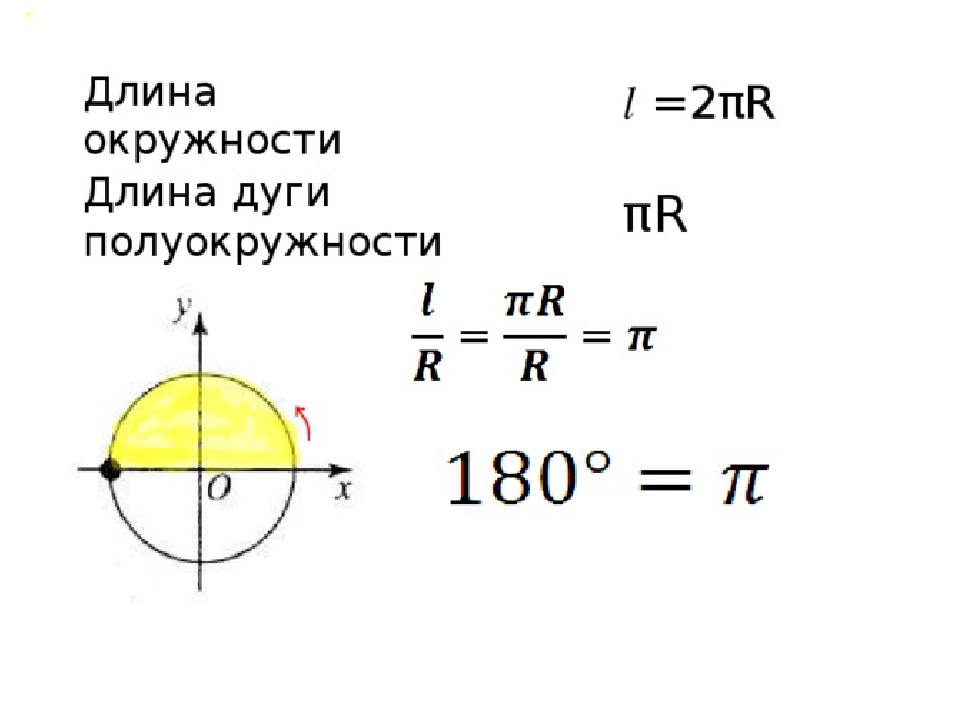 Найти площадь круга, если его радиус равен 2 см.
Найти площадь круга, если его радиус равен 2 см.
Решение: Так как площадь круга равна π умноженное на радиус в квадрате, то площадь круга с радиусом 2 см будет равна:
S ≈ 3,14 · 22 = 3,14 · 4 = 12,56 (см2).
Ответ: 12,56 см2.
Задача 2. Найти площадь круга, если его диаметр равен 7 см.
Решение: Сначала найдём радиус круга, разделив его диаметр на 2:
7 : 2 = 3,5 (см),
теперь вычислим площадь круга по формуле:
S = πr2 ≈ 3,14 · 3,52 = 3,14 · 12,25 = 38,465 (см2).
Данную задачу можно решить и другим способом. Вместо того чтобы сначала находить радиус, можно воспользоваться формулой нахождения площади круга через диаметр:
| S = π | D2 | ≈ 3,14 · | 72 | = 3,14 · | 49 | = |
| 4 | 4 | 4 |
| = | 153,86 | = 38,465 (см2). |
| 4 |
Ответ: 38,465 см2.
Задача 3. Найти радиус круга, если его площадь равна 12,56 м2.
Решение: Чтобы найти радиус круга по его площади, надо площадь круга разделить π, а затем из полученного результата извлечь квадратный корень:
r = √S : π ,
следовательно, радиус будет равен:
r ≈ √12,56 : 3,14 = √4 = 2 (м).
Ответ: 2 м.
Формулы круга и окружности
Понятие окружности и круга
Перед тем, как ввести основные формулы для окружности и круга, введем, непосредственно понятия окружности и круга, и связанные с ними определения.
Определение 1
Окружностью будем называть такую геометрическую фигуру, которая будет состоять из всех таких точек, которые находятся на одинаковом расстоянии от какой-либо заданной точки.
Определение 2
Центром окружности будем называть точку, которая задается в рамках определения 1. 0}{n}}=\frac{2τ}{2τ’}$
0}{n}}=\frac{2τ}{2τ’}$
Получаем, что отношение $\frac{ρ}{ρ’}=\frac{2τ}{2τ’}$ будет верным независимо от значения числа сторон вписанных правильных многоугольников. То есть
$\lim_{n→∞}(\frac{ρ}{ρ’})=\frac{2τ}{2τ’}$
С другой стороны, если бесконечно увеличивать число сторон вписанных правильных многоугольников (то есть $n→∞$), будем получать равенство:
$\lim_{n→∞}(\frac{ρ}{ρ’})=\frac{C}{C’}$
Из последних двух равенств получим, что
$\frac{C}{C’}=\frac{2τ}{2τ’}$
То есть
$\frac{C}{2τ}=\frac{C’}{2τ’}$
Видим, что отношение длины окружности к его удвоенному радиусу всегда одно и тоже число, независимо от выбора окружности и ее параметров, то есть
$\frac{C}{2τ}=const$
Эту постоянную принять называть числом «пи» и обозначать $π$. Приближенно, это число будет равняться $3,14$ (точного значения этого числа нет, так как оно является иррациональным числом). Таким образом
$\frac{C}{2τ}=π$
Окончательно, получим, что длина окружности (периметр круга) определяется формулой
$C=2πτ$
Площадь круга
Будем выводить площадь $S$ произвольного круга с помощью радиуса окружности, ограничивающей его, равного $τ$. 2=\frac{πα}{4}$
2=\frac{πα}{4}$
Ответ: $C=πα$, $S=\frac{πα}{4}$.
Формула нахождения окружности. Как найти и чему будет равна длина окружности
Инструкция
Сначала надо исходные данные к задаче. Дело в том, что ее условии не может быть явно сказано, какова радиуса окружности . Вместо этого в задаче может быть дана длина диаметра окружности . Диаметр окружности — отрезок, который объединяет между собой две противоположные точки окружности , проходя через ее центр. Проанализировав определения окружности , можно сказать, что длина диаметра удвоенной длине радиуса.
Теперь можно принять радиус окружности равным R. Тогда для длины окружности необходимо воспользоваться формулой:
L = 2πR = πD, где L — длина окружности , D — диаметр окружности , который всегда в 2 раза радиуса.
Обратите внимание
Окружность можно вписать в многоугольник, либо описать вокруг него. При этом, если окружность вписана, то она в точках касания со сторонами многоугольника будет делить их пополам. Чтобы узнать радиус вписанной окружности, нужно поделить площадь многоугольника на половину его периметра:
Чтобы узнать радиус вписанной окружности, нужно поделить площадь многоугольника на половину его периметра:
R = S/p.
Если окружность описана вокруг треугольника, то ее радиус находится по следующей формуле:
R = a*b*c/4S, где a, b, c — это стороны данного треугольника, S — площадь треугольника, вокруг которого описана окружность.
Если требуется описать окружность вокруг четырехугольника, то это можно будет сделать при соблюдении двух условий:
Четырехугольник должен быть выпуклым.
В сумме противоположные углы четырехугольника должны составлять 180°
Полезный совет
Помимо традиционного штангенциркуля, для начертания окружности можно применять и трафареты. В современных трафаретах включены окружность разных диаметров. Данные трафареты можно приобрести в любом магазине канцтоваров.
Источники:
- Как найти длину окружности?
Окружность — замкнутая кривая линия, все точки которой находятся на равном расстоянии от одной точки. Эта точка — центр окружности, а отрезок между точкой на кривой и ее центром называется радиусом окружности.
Инструкция
Если через центр окружности провести прямую линию, то ее отрезок между двумя точками пересечения этой прямой с окружностью называется диаметром данной окружности. Половина диаметра, от центра до точки пересечения диаметра с окружность — это радиус
окружности. Если окружность разрезать в произвольной точке, выпрямить и измерить, то полученная величина является длиной данной окружности.
Начертите несколько окружностей разным раствором циркуля. Визуальное сравнение позволяет сделать вывод, что больший диаметр очерчивает больший круг, ограниченный окружностью с большей длиной. Следовательно, между диаметром окружности и ее длиной существует прямо пропорциональная зависимость.
По физическому смыслу параметр «длина окружности» соответствует , ограниченного ломаной линией. Если вписать в окружность правильный n-угольник со стороной b, то периметр такой фигуры Р равен произведению стороны b на число сторон n: Р=b*n. Сторона b может быть определена по формуле: b=2R*Sin (π/n), где R — радиус окружности, в которую вписали n-угольник.
При увеличении числа сторон периметр вписанного многоугольника будет все больше приближаться к L. Р= b*n=2n*R*Sin (π/n)=n*D*Sin (π/n). Зависимость между длиной окружности L и ее диаметром D постоянна. Отношение L/D=n*Sin (π/n) при стремлении числа сторон вписанного многоугольника к бесконечности стремится к числу π, постоянной величине, называемой «число пи» и выраженной бесконечной десятичной дробью. Для расчетов без применения вычислительной техники принимается значение π=3,14. Длина окружности и ее диаметр связаны формулой: L= πD. Для окружности разделите ее длину на число π=3,14.
Множество предметов в окружающем мире имеют круглую форму. Это колеса, круглые оконные проемы, трубы, различная посуда и многое другое. Подсчитать, чему равна длина окружности, можно, зная ее диаметр или радиус.
Существует несколько определений этой геометрической фигуры.
- Это замкнутая кривая, состоящая из точек, которые располагаются на одинаковом расстоянии от заданной точки.

- Это кривая, состоящая из точек А и В, являющихся концами отрезка, и всех точек, из которых А и В видны под прямым углом. При этом отрезок АВ – диаметр.
- Для того же отрезка АВ эта кривая включает все точки С, такие, что отношение АС/ВС неизменно и не равняется 1.
- Это кривая, состоящая из точек, для которых справедливо следующее: если сложить квадраты расстояний от одной точки до двух данных других точек А и В, получится постоянное число, большее 1/2 соединяющего А и В отрезка. Это определение выводится из теоремы Пифагора.
Обратите внимание! Есть и другие определения. Круг – это область внутри окружности. Периметр круга и есть ее длина. По разным определениям круг может включать или не включать саму кривую, являющуюся его границей.
Определение окружности
Формулы
Как вычислить длину окружности через радиус? Это делается по простой формуле:
где L – искомая величина,
π – число пи, примерно равное 3,1413926.
Обычно для нахождения нужной величины достаточно использовать π до второго знака, то есть 3,14, это обеспечит нужную точность. На калькуляторах, в частности инженерных, может быть кнопка, которая автоматически вводит значение числа π.
Обозначения
Для нахождения через диаметр существует следующая формула:
Если L уже известно, можно легко узнать радиус или диаметр. Для этого L нужно поделить на 2π или на π соответственно.
Если уже дана круга, нужно понимать, как найти длину окружности по этим данным. Площадь круга равняется S = πR2. Отсюда находим радиус: R = √(S/π). Тогда
L = 2πR = 2π√(S/π) = 2√(Sπ).
Вычислить площадь через L также несложно: S = πR2 = π(L/(2π))2 = L2/(4π)
Резюмируя, можно сказать, что существует три основных формулы:
- через радиус – L = 2πR;
- через диаметр – L = πD;
- через площадь круга – L = 2√(Sπ).
Число пи
Без числа π решить рассматриваемую задачу не получится. Число π впервые и было найдено как отношение длины окружности к ее диаметру. Это сделали еще древние вавилоняне, египтяне и индийцы. Нашли они его довольно точно – их результаты отличались от известного сейчас значения π не больше, чем на 1%. Постоянную приближали такими дробями как 25/8, 256/81, 339/108.
Число π впервые и было найдено как отношение длины окружности к ее диаметру. Это сделали еще древние вавилоняне, египтяне и индийцы. Нашли они его довольно точно – их результаты отличались от известного сейчас значения π не больше, чем на 1%. Постоянную приближали такими дробями как 25/8, 256/81, 339/108.
Далее значение этой постоянной считали не только с позиции геометрии, но и с точки зрения математического анализа через суммы рядов. Обозначение этой константы греческой буквой π впервые использовал Уильям Джонс в 1706 году, а популярно оно стало после работ Эйлера.
Сейчас известно, что эта постоянная представляет собой бесконечную непериодическую десятичную дробь, она иррациональна, то есть ее нельзя представить в виде отношения двух целых чисел. С помощью вычислений на суперкомпьютерах в 2011 году узнали 10-триллионный знак константы.
Это интересно! Для запоминания нескольких первых знаков числа π были придуманы различные мнемонические правила.
Некоторые позволяют хранить в памяти большое число цифр, например, одно французское стихотворение поможет запомнить пи до 126 знака.
Если вам необходима длина окружности, онлайн-калькулятор поможет в этом. Таких калькуляторов существует множество, в них нужно только ввести радиус или диаметр. У некоторых из них есть обе эти опции, другие вычисляют результат только через R. Некоторые калькуляторы могут рассчитать искомую величину с разной точностью, нужно указать число знаков после запятой. Также с помощью онлайн-калькуляторов можно посчитать площадь круга.
Такие калькуляторы легко найти любым поисковиком. Также существуют мобильные приложения, которые помогут решить задачу, как найти длину окружности.
Полезное видео: длина окружности
Практическое применение
Решать такую задачу чаще всего необходимо инженерам и архитекторам, но и в быту знание нужных формул тоже может пригодиться. Например, требуется обернуть бумажной полоской торт, испеченный в форме с поперечником 20 см. Тогда не составит труда найти длину этой полоски:
Тогда не составит труда найти длину этой полоски:
L = πD = 3,14 * 20 = 62,8 см.
Другой пример: нужно построить забор вокруг круглого бассейна на определенном расстоянии. Если радиус бассейна 10 м, а забор нужно поставить на расстоянии 3 м, то R для полученной окружности будет 13 м. Тогда ее длина равна:
L = 2πR = 2 * 3,14 * 13 = 81,68 м.
Полезное видео: круг — радиус, диаметр, длина окружности
Итог
Периметр круга легко рассчитать по простым формулам, включающим диаметр или радиус. Также можно найти искомую величину через площадь круга. Решить эту задачу помогут онлайн-калькуляторы или мобильные приложения, в которые нужно ввести единственное число – диаметр или радиус.
Понятие окружности
Определение 1
Окружность — геометрическая фигура, состоящая из всех точек, расположенных на равном расстоянии от заданной точки.
Определение 2
В рамках определения 1, заданная точка называется центром окружности.
Определение 3
Отрезок, соединяющий центр окружности с любой ее точкой называется радиусом окружности $(r)$ (Рис. 1).
Рисунок 1. Окружность с центром в точке $O$ и радиусом $r$
Уравнение окружности
Выведем уравнение окружности в декартовой системе координат $xOy$. Пусть центр окружности $C$ имеет координаты $(x_0,y_0)$, а радиус окружности равен $r$. Пусть точка $M$ с координатами $(x,y)$ — произвольная точка этой окружности (рис. 2).
Рисунок 2. Окружность в декартовой системе координат
Расстояние от центра окружности до точки $M$ вычисляется следующим образом
Но, так как $M$ лежит на окружности, то по определению 3, получаем $CM=r$. Тогда получим следующее
Уравнение (1) и есть уравнение окружности с центром в точке $(x_0,y_0)$ и радиусом $r$.
В частности, если центр окружности совпадает с началом координат. То уравнение окружности имеет вид
Длина окружности
Выведем формулу длины окружности $C$ через её радиус. Для этого рассмотрим две окружности с длинами $C$ и $C»$ и радиусами $R$ и $R»$. Впишем в ним правильные $n-угольники$ с периметрами $P$ и $P»$ и длинами сторон $a$ и $a»$ соответственно. Как нам известно, сторона вписанного -угольника равна
Для этого рассмотрим две окружности с длинами $C$ и $C»$ и радиусами $R$ и $R»$. Впишем в ним правильные $n-угольники$ с периметрами $P$ и $P»$ и длинами сторон $a$ и $a»$ соответственно. Как нам известно, сторона вписанного -угольника равна
Тогда, получим
Следовательно
Неограниченно увеличивая количество сторон правильных многоугольников $n$ получим, что
Отсюда, получаем
Получили, что отношение длины окружности к её диаметру постоянное число для любой окружности. Эту константу принято обозначать числом $\pi \approx 3,14$. Таким образом, получим
Формула (2) и есть формула для вычисления длины окружности.
Площадь круга
Определение 4
Круг — часть плоскости, ограниченной окружностью.
Выведем формулу для вычисления площади круга.
Рассмотрим следующую ситуацию. Пусть нам дана окружность с радиусом $R$. Обозначим её площадь через $S$. В нее вписан правильный -угольник с площадью $S_n$, в который, в свою очередь вписана окружность с площадью ${S»}_n$ (рис. 2=2$, $C=2\sqrt{2}\pi $, $S=2\pi $
2=2$, $C=2\sqrt{2}\pi $, $S=2\pi $
Окружностью называют кривую линию, которая ограничивает собой круг. В геометрии фигуры плоские, поэтому определение относится к двухмерному изображению. Предполагается, что все точки этой кривой удалены от центра круга на равное расстояние.
У окружности есть несколько характеристик, на основе которых производят расчеты, связанные с этой геометрической фигурой. В их число входит: диаметр, радиус, площадь и длина окружности. Эти характеристики взаимосвязаны, то есть для их вычисления достаточно информации хотя бы об одной из составляющих. Например, зная только радиус геометрической фигуры по формуле можно найти длину окружности, диаметр, и ее площадь.
- Радиус окружности – это отрезок внутри окружности, соединённый с ее центром.
- Диаметр – это отрезок внутри окружности, соединяющий ее точки и проходящий через центр. По сути, диаметр – это два радиуса. Именно так выглядит формула для его вычисления: D=2r.
- Есть еще одна составляющая окружности – хорда.
 Эта прямая, которая соединяет две точки окружности, но не всегда проходит через центр. Так вот ту хорду, которая через него проходит, тоже называют диаметром.
Эта прямая, которая соединяет две точки окружности, но не всегда проходит через центр. Так вот ту хорду, которая через него проходит, тоже называют диаметром.
Как узнать длину окружности? Сейчас выясним.
Длина окружности: формула
Для обозначения этой характеристики выбрана латинская буква p. Еще Архимед доказал, что отношение длины окружности к ее диаметру является одним и тем же числом для всех окружностей: это число π, которое приблизительно равно 3,14159. Формула для вычисления π выглядит так: π = p/d. Согласно этой формуле, величина p равна πd, то есть длина окружности: p= πd. Поскольку d (диаметр) равен двум радиусам, то эту же формулу длины окружности можно записать как p=2πr.Рассмотрим применение формулы на примере простых задач:
Задача 1
У основания царь-колокола диаметр равен 6,6 метров. Какова длина окружности основания колокола?
- Итак, формула для вычисления окружности — p= πd
- Подставляем имеющееся значение в формулу: p=3,14*6,6= 20,724
Ответ: длина окружности основания колокола 20,7 метра.
Задача 2
Искусственный спутник Земли вращается на расстоянии 320 км от планеты. Радиус Земли – 6370 км. Какова длина круговой орбиты спутника?
- 1.Вычислим радиус круговой орбиты спутника Земли: 6370+320=6690 (км)
- 2.Вычислим длину круговой орбиты спутника по формуле: P=2πr
- 3.P=2*3,14*6690=42013,2
Ответ: длина круговой орбиты спутника Земли 42013,2 км.
Способы измерения длины окружности
Вычисление длины окружности на практике используется не часто. Причиной тому приблизительное значение числа π. В быту для поиска длины круга используют специальный прибор – курвиметр. На окружности отмечают произвольную точку отсчета и ведут от нее прибор строго по линии, пока опять не дойдут до этой точки.
Как найти длину окружности? Нужно просто держать в голове незамысловатые формуля для вычислений.
Таким образом, длину окружности (C ) можно вычислить, умножив константу π на диаметр (D ), или умножив π на удвоенный радиус, так как диаметр равен двум радиусам. Следовательно, формула длины окружности будет выглядеть так:
Следовательно, формула длины окружности будет выглядеть так:
C = πD = 2πR
где C — длина окружности, π — константа, D — диаметр окружности , R — радиус окружности.
Так как окружность является границей круга , то длину окружности можно также назвать длиной круга или периметром круга.
Задачи на длину окружности
Задача 1. Найти длину окружности, если её диаметр равен 5 см.
Так как длина окружности равна π умноженное на диаметр, то длина окружности с диаметром 5 см будет равна:
C ≈ 3,14 · 5 = 15,7 (см)
Задача 2. Найти длину окружности, радиус которой равен 3,5 м.
Сначала найдём диаметр окружности, умножив длину радиуса на 2:
D = 3,5 · 2 = 7 (м)
теперь найдём длину окружности, умножив π на диаметр:
C ≈ 3,14 · 7 = 21,98 (м)
Задача 3. Найти радиус окружности, длина которой равна 7,85 м.
Чтобы найти радиус окружности по её длине, надо длину окружности разделить на 2π
Площадь круга
Площадь круга равна произведению числа π на квадрат радиуса. Формула нахождения площади круга :
S = πr 2
где S — площадь круга, а r — радиус круга.
Так как диаметр круга равен удвоенному радиусу, то радиус равен диаметру, разделённому на 2:
Задачи на площадь круга
Задача 1. Найти площадь круга, если его радиус равен 2 см.
Так как площадь круга равна π умноженное на радиус в квадрате, то площадь круга с радиусом 2 см будет равна:
S ≈ 3,14 · 2 2 = 3,14 · 4 = 12,56 (см 2)
Задача 2. Найти площадь круга, если его диаметр равен 7 см.
Сначала найдём радиус круга, разделив его диаметр на 2:
7: 2 = 3,5 (см)
теперь вычислим площадь круга по формуле:
S = πr 2 ≈ 3,14 · 3,5 2 = 3,14 · 12,25 = 38,465 (см 2)
Данную задачу можно решить и другим способом. Вместо того чтобы сначала находить радиус, можно воспользоваться формулой нахождения площади круга через диаметр:
Вместо того чтобы сначала находить радиус, можно воспользоваться формулой нахождения площади круга через диаметр:
| S = π | D 2 | ≈ 3,14 | 7 2 | = 3,14 | 49 | = | 153,86 | = 38,465 (см 2) |
| 4 | 4 | 4 | 4 |
Задача 3. Найти радиус круга, если его площадь равна 12,56 м 2 .
Чтобы найти радиус круга по его площади, надо площадь круга разделить π , а затем из полученного результата извлечь квадратный корень:
r = √S : π
следовательно радиус будет равен:
r ≈ √12,56: 3,14 = √4 = 2 (м)
Число
πДлину окружности предметов, окружающих нас, можно измерить с помощью сантиметровой ленты или верёвки (нитки), длину которой потом можно померить отдельно. Но в некоторых случаях померить длину окружности трудно или практически невозможно, например, внутреннюю окружность бутылки или просто длину окружности начерченной на бумаге.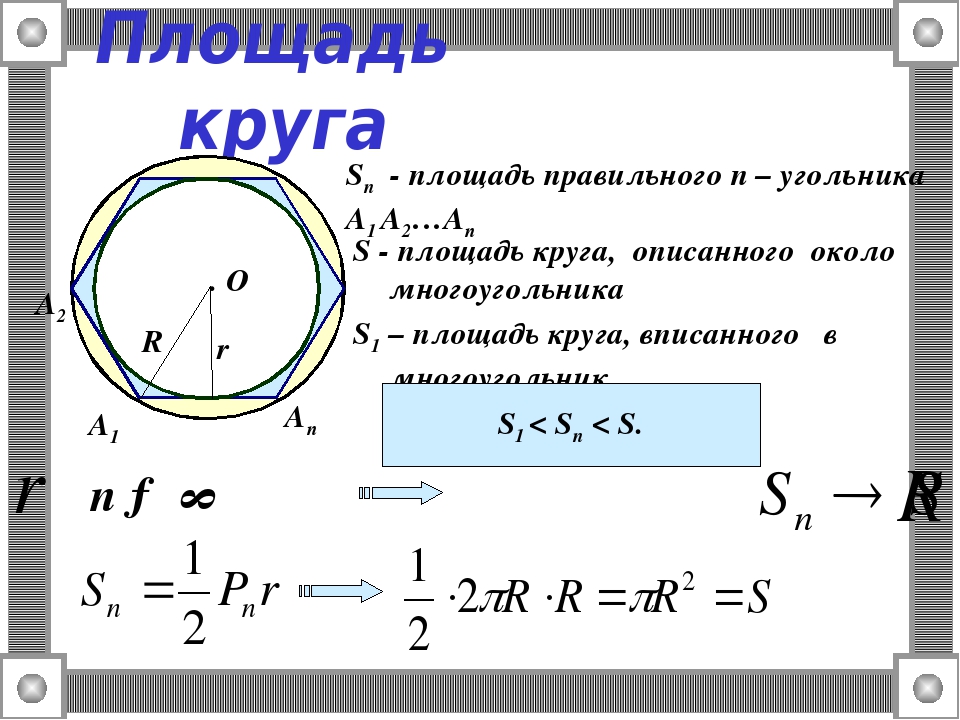 В таких случаях можно вычислить длину окружности, если известна длина её диаметра или радиуса.
В таких случаях можно вычислить длину окружности, если известна длина её диаметра или радиуса.
Чтобы понять, как это можно сделать, возьмём несколько круглых предметов, у которых можно измерить и длину окружности и диаметр. Вычислим отношение длины к диаметру, в итоге получим следующий ряд чисел:
Из этого можно сделать вывод, что отношение длины окружности к её диаметру это постоянная величина для каждой отдельной окружности и для всех окружностей в целом. Это отношение и обозначается буквой π .
Используя эти знания, можно по радиусу или диаметру окружности находить её длину. Например, для вычисления длины окружности с радиусом 3 см нужно умножить радиус на 2 (так мы получим диаметр), а полученный диаметр умножить на π . В итоге, с помощью числа π мы узнали, что длина окружности с радиусом 3 см равна 18,84 см.
Формула окружности
Набор всех точек на плоскости, которые равноудалены от фиксированной точки, определяемой как центр, называется окружностью.
Формулы с кружками часто содержат математическую константу пи, обозначаемую как π; π ≈ 3,14159. π определяется как отношение длины окружности к ее диаметру. Две из наиболее широко используемых формул круга — это формулы для окружности и площади круга.
Формула окружности круга
Длина окружности C — это мера расстояния по окружности.Его можно найти по формуле
С = 2πr
где r — радиус окружности.
При использовании диаметра d окружности:
С = πd
Если площадь круга A известна:
Формула площади круга
Площадь круга — это плоская область, ограниченная окружностью круга. Его можно найти по формуле
А = πr 2
где r — радиус окружности.
При использовании диаметра d окружности:
Если длина окружности C известна:
Уравнение окружности
В координатной геометрии круг можно выразить с помощью ряда уравнений, основанных на различных ограничениях.
С центром в исходной точке
Учитывая, что точка (x, y) лежит на окружности радиуса r с центром в начале координатной плоскости, она образует прямоугольный треугольник со сторонами x и y и гипотенузой r. Это позволяет нам использовать теорему Пифагора, чтобы найти, что уравнение для этого круга в стандартной форме:
x 2 + y 2 = r 2
Это верно для любой точки на окружности, поскольку любая точка на окружности находится на равном расстоянии r от центра.
По центру в любом месте
Чтобы найти уравнение для окружности в координатной плоскости, не центрированной в начале координат, мы используем формулу расстояния. Этот метод также можно использовать для поиска уравнения для круга с центром в начале координат, но в таком случае использование уравнения из предыдущего раздела было бы более эффективным.
Учитывая круг радиуса r с центром в точке (h, k), мы можем использовать формулу расстояния, чтобы найти, что:
где (x, y) — любая точка на окружности.
Возводя обе части уравнения в квадрат, получаем уравнение круга:
(x — h) 2 + (y — k) 2 = r 2
Обратите внимание, что если центр окружности находится в начале координат, (0, 0), то и h, и k в приведенном выше уравнении равны 0, и уравнение сводится к тому, что мы получили в предыдущем разделе:
x 2 + y 2 = r 2
Пример:
Найдите уравнение окружности с центром (4, -3) и радиусом 5.
Подставляя координаты центра и радиуса, получаем
(x — 4) 2 + (y — (-3)) 2 = 5 2
(x — 4) 2 + (y + 3) 2 = 25
Общая форма круга
Уравнение круга в общем виде:,
x 2 + y 2 + Dx + Ey + F = 0
, где D, E и F — действительные числа.
Чтобы упростить определение центра и радиуса окружности, заданной в общем виде, мы можем преобразовать уравнение в стандартную форму.
Пример:
Найдите центр и радиус окружности с помощью уравнения
x 2 + y 2 + 4x — 12y — 9 = 0
Сначала сгруппируйте члены x и y.
x 2 + 4x + y 2 — 12y = 9
Завершая квадрат, получаем:
x 2 + 4x + 4 + y 2 — 12 лет + 36 = 9 + 4 + 36
(x + 2) 2 + (y — 6) 2 = 49 = 7 2
Итак, центр равен (-2, 6), а радиус равен 7.
формул круга — что такое формулы круга? Примеры
Прежде чем выучить все формулы круга, давайте вспомним, что такое круг. Круг определяется как набор точек, расположенных на равном расстоянии от фиксированной точки на плоскости. Неподвижная точка называется центром круга. Радиус — это расстояние от центра круга до границы круга. Давайте разберемся во всех формулах круга на решенных примерах.
Что такое круглые формулы?
Параметры, такие как площадь, длина окружности, радиус круга, могут быть рассчитаны с использованием всех формул круга. Различные формулы круга для вычисления различных параметров данного круга могут быть выражены как
Различные формулы круга для вычисления различных параметров данного круга могут быть выражены как
- Диаметр окружности D = 2 × r
- Окружность круга C = 2 × π × r
- Площадь круга A = π × r 2
Где,
- r = радиус окружности
- d = диаметр круга
- c = окружность круга
Список всех формул круга
Ниже приведен список всех формул окружности для ваших простых вычислений для окружности с радиусом ‘r’.
| Параметры | Формулы круга |
| Формула диаметра круга | D = 2 × r |
| Формула окружности круга | С = 2 × π × |
| Формула площади круга | А = π × r 2 |
Хотите найти сложные математические решения за секунды?
Воспользуйтесь нашим бесплатным онлайн-калькулятором для решения сложных вопросов.С Cuemath находите решения простым и легким способом.
Забронируйте бесплатную пробную версию Класс
Примеры формул круга
Решим несколько интересных задач, используя формулу периметра круга.
Пример 1: Найдите площадь кругового парка, радиус которого равен 200 м.
Решение:
Найти: Площадь парка.
Дано:
Радиус парка = 200 м
Используя одну из формул для всех кругов (формула площади круга),
Площадь круга = π × r 2
= Π × 200 2
= Π × 40000
Ответ: Площадь кругового парка 40000π м 2 .
Пример 2: Используя формулу периметра окружности, найдите радиус окружности, имеющей длину окружности 100 дюймов.
Решение:
Найти: Радиус окружности
Дано: Окружность = 100 из
Используя формулу периметра круга,
Периметр круга или окружности = 2 π r
2 π г = 100
2 × 22/7 × r = 100
г = 100 × 7/44
г = 15.909 дюймов
Ответ: Радиус окружности = 15,909 дюйма
Пример 3: Радиус окружности 8 дюймов. Используя формулу круга, вычислите длину окружности круга.
Решение:
Для штрафа: длина окружности
Дано: r = 8 дюймов
Формула периметра круга = 2 π r
C = 2 × (22/7) × (8)
Ответ: Окружность круга равна 50.28 дюймов.
Часто задаваемые вопросы по формуле круга
Что такое формула периметра полукруга?
Полукруг — это половина полного круга. Следовательно, если периметр формулы полукруга равен 1/2 (2π r) = π r единиц.
Что такое формула диаметра круга?
Формула диаметра круга определяется как двойной радиус.
Следовательно, D = 2r, где r — радиус окружности.
Что такое формула периметра круга?
Формула периметра круга задается как 2 π r, где ‘r’ — радиус, а π постоянна со значением (3.14 или 22/7).
Как рассчитать радиус по формуле круга?
Длина окружности в формуле круга равна 2 π r. Если мы знаем значение длины окружности круга, то, подставив это значение в формулу, мы можем вычислить радиус «r».
r = (длина окружности) / 2 π.
Уравнение окружности
Круг — это набор всех точек на плоскости на заданном расстоянии (называемый радиус ) из заданной точки (называемой центром.)
Отрезок, соединяющий две точки на окружности и проходящий через центр, называется отрезком. диаметр круга.
Предположить, что ( Икс , у ) — координаты точки на изображенной окружности. Центр находится в ( час , k ) , а радиус р .
Использовать Формула расстояния найти уравнение круга.
( Икс 2 — Икс 1 ) 2 + ( у 2 — у 1 ) 2 знак равно d
Заменять ( Икс 1 , у 1 ) знак равно ( час , k ) , ( Икс 2 , у 2 ) знак равно ( Икс , у ) а также d знак равно р .
( Икс — час ) 2 + ( у — k ) 2 знак равно р
Выровняйте каждую сторону.
( Икс — час ) 2 + ( у — k ) 2 знак равно р 2
Уравнение окружности с центром ( час , k ) и радиус р единиц ( Икс — час ) 2 + ( у — k ) 2 знак равно р 2 .
Формулы круга в математике | Площадь, окружность, сектор, хорда, круговая дуга
Свойства круга в математике | Дуга, Периметр, Отрезок окружности
Окружность можно определить как геометрическое место всех точек, равноудаленных от центральной точки. Здесь мы обсуждаем около свойств круга , формул круга , таких как площадь , периметр , длина дуги, длина сегмента, площадь сегмента .. . пр.
Терминология, связанная с кругами в математике:
Начало координат: Это центральная (равноудаленная) точка круга.Здесь «O» — начало круга.
Радиус: Расстояние от центра круга до любой точки вокруг него Окружность называется Радиус окружности. Обычно обозначается буквой «r».
Диаметр: Наибольшее расстояние от одного конца круга до другого конца круга называется диаметром круга. Обычно обозначается буквой «D». Диаметр круга = 2 x Радиус круга. я. е D = 2r.
Дуга окружности: Это часть окружности окружности. Большая дуга называется большой, а меньшая — вспомогательной.
Сектор круга: Это часть площади круга между двумя радиусами (круговой клин).
Хорда: Отрезок линии внутри круга, который касается двух точек на окружности, называется хордой окружности.
Окружность: Расстояние по окружности называется окружностью или периметром окружности.
Пи (π ): Это число, равное 3,141592… или 22/7.
пи (π ) = (окружность) / (диаметр) любого круга.
Касательная окружности: линия, перпендикулярная радиусу, которая касается ТОЛЬКО одной точки на окружности.
Секанс окружности : линия, пересекающая окружность в двух точках, она называется Секанс окружности .
Свойства круга:
- Конгруэнтность : Две окружности могут быть конгруэнтными тогда и только тогда, когда они имеют равных радиусов.
- Перпендикуляр от центра окружности к хорде делит хорду пополам. Обратное также верно.
- Биссектрисы двух хорд окружности пересекаются в центре.
- Может быть одна и только одна окружность, проходящая через три или более неколлинеарных точек.
- Если две окружности пересекаются в двух точках, то прямая, проходящая через центры, представляет собой серединный перпендикуляр к общей хорде.
- Если две хорды окружности равны, то центр окружности лежит на биссектрисе двух хорд.
- Равные хорды окружности или совпадающие окружности равноудалены от центра.
- Хорды, расположенные на одинаковом расстоянии от центра круга, равны друг другу по длине.
- Градус дуги окружности равен удвоенному углу, образуемому ею в любой точке альтернативного сегмента окружности.
- Равные хорды окружности (или равных окружностей) соединены равными углами в центре (в соответствующих центрах). Верно и обратное.
- Если сумма противоположных углов четырехугольника равна 180 °, то четырехугольник является вписанным.
- Секущая означает линию, пересекающую окружность в двух точках. Касательная означает, что это линия, которая касается круга ровно в одной точке.
- В двух концентрических окружностях хорда большего круга, касающаяся меньшего круга, делится пополам в точке контакта.
Круговые формулы в математике:
Площадь и длина окружности:
Здесь Начало круга = O, Диаметр = D и Радиус = r
Площадь круга (A) = π r 2 = (π / 4) D 2 = 0,7854 D 2
Окружность круга (C) = 2 π r = π Д.
Площадь круга = (1/2) x окружность x радиус
A = (1/2) x C x r
Диаметр окружности (D) = √ (A / 0.7854).
Дуга и сектор круга:
Здесь угол между двумя радиусами равен ”θ” в градусах. . И сектор круга AOB.
Длина дуги окружности (l) (второстепенная) = (θ / 360) x 2 π r = θ π r / 180
Площадь сектора (второстепенная) = (θ / 360) x π r 2
Если угол θ выражен в радианах, то
Площадь сектора = (θ / 2) r 2
Секторный угол окружности θ = (180 x l) / (π r).
Отрезок окружности и периметр отрезка:
Здесь радиус окружности = r, угол между двумя радиусами равен ”θ” в градусах.
Площадь сегмента круга = Площадь сектора — Площадь ΔOAB.
Площадь сегмента = (θ / 360) x π r 2 — (1/2) x sinθ x r 2
Периметр отрезка = (θ π r / 180) + 2r sin (θ / 2).
Длина хорды окружности = 2 √ [h (2r — h)] = 2r sin (θ / 2).
Дуга Длина сегмента круга = l = 0,01745 x r x θ
Онлайн калькулятор для расчета площади отрезка круга
Площадь кругового кольца:
Здесь радиус большого круга = R и Dia = D,
Радиус малого круга = r и диаметр = d,
Площадь кругового кольца = 0,7854 (D 2 — d 2 ) = (π / 4) (D 2 — d 2 )
Площадь кругового кольца = π (R 2 — r 2 ).
Формула пересечения хорд в окружности:
Здесь AB и CD — две окружные хорды, пересекающиеся каждая в точке E.
Тогда AE: EB = DE: EC.
Формула длины касательных окружностей:
Здесь Две окружности, начало O и O ’и радиус равны r1 и r2 соответственно.
Прямая общая касательная AB и поперечная общая касательная = CD
Длина прямой общей касательной AB = √ [(Расстояние между двумя исходными точками) 2 — (r1 -r2) 2 ]
= √ [(OO ’) 2 — (r1 -r2) 2 ]
Длина общей поперечной касательной AB = √ [(Расстояние между двумя исходными точками) 2 — (r1 + r2) 2 ]
= √ [(OO ’) 2 — (r1 + r2) 2 ]
Геометрия по математике
Формулы двухмерных фигур.
Четырехугольник Недвижимости | Трапеция, параллелограмм, Ромб
Типы треугольников с примерами | Свойства треугольника
Система счисления.Категории номеров
Правила делимости чисел
Формулы суммы n последовательных чисел
Методы поиска HCF и LCM
Проблемы и решения GCD и LCM
Привет, друзья Спасибо за чтение. Надеюсь, вам понравилось. Оставляйте отзывы, комментарии и, пожалуйста, не забудьте поделиться ими.
как рассчитать площадь круга
Поскольку формула для площади круга возводит в квадрат радиус , площадь большего круга всегда в 4 (или 2 2 ) раз больше меньшего круга. Подумайте об этом: вы удваиваете число (что означает × 2), а затем возводите его в квадрат (то есть возводите в квадрат 2) — что приводит к новой области, которая в четыре раза меньше.
Вы можете убедиться, что это соотношение верно, если вы выберете некоторые фактические значения для радиуса круга. 2 $$
$$ A_ {больше} = \ color {красный} {4} \ cdot A_ {меньше} \\ A_ {больше} = \ color {красный} {4} \ cdot 9 \ pi \\ A_ {больше} = 36 \ пи $$
Это соотношение сохраняется независимо от выбранного вами радиуса.
Сделаем исходный радиус = 5.
| Меньший круг | Большой круг |
|---|---|
| радиус $$ = 5 $$ | радиус $$ = 5 \ cdot 2 = 10 $$ |
| A = $$ \ pi (5) ^ 2 $$ | A = $$ \ pi (10) ^ 2 $$ |
| A = $$ 25 \ pi $$ | A = $$ 100 \ pi $$ |
$$ A_ {больше} = \ color {красный} {4} \ cdot A_ {меньше} \\ A_ {больше} = \ color {красный} {4} \ cdot 25 \ pi \\ A_ {больше} = 100 \ пи $$
Площадь круга | Формула для радиуса, диаметра и окружности
Содержание
- Какова площадь круга?
- Как найти площадь круга
Какова площадь круга?
Круг — это не квадрат, а площадь круга (количество внутреннего пространства, заключенного в круг) измеряется в квадратных единицах.Найти площадь квадрата несложно: длина умножена на ширину.
Круг, однако, имеет только диаметр или расстояние в поперечнике. У него нет четко видимой длины и ширины, поскольку круг (по определению) — это набор всех точек, равноудаленных от данной точки в центре.
Тем не менее, имея только диаметр или половину диаметра (радиус ), или даже только длину окружности (расстояние вокруг), вы можете вычислить площадь любого круга.
Как найти площадь круга
Напомним, что отношение между длиной окружности и ее диаметром всегда одинаковое, 3.14159265, пи или π. Это число π, умноженное на квадрат радиуса круга, дает вам площадь внутренней части круга в квадратных единицах.
Формула площади круга
Если вам известен радиус r в любых единицах измерения (мм, см, м, дюймы, футы и т. Д.), Используйте формулу π r 2 , чтобы найти площадь, A:
Ответом будут квадратные единицы линейных единиц, такие как мм2, см2, м2, квадратные дюймы, квадратные футы и так далее.
Вот круг радиусом 7 метров. Какая у него площадь?
[вставить чертеж круга шириной 14 м с обозначенным радиусом 7 м]
А = π · r2
А = π × 72
А = π × 49
A = 153,9380 м2
Площадь круга с использованием диаметра
Если вам известен диаметр d в любых единицах измерения, возьмите половину диаметра, чтобы получить радиус r в тех же единицах.
Вот комплекс недвижимости Сан-Сити, штат Аризона, круглого города диаметром 1.07 километров. Какой район Сан-Сити?
Сначала найдите половину заданного диаметра, чтобы получить радиус:
1,072 = 0,535 км = 535 м
Подставьте радиус в нашу формулу:
А = π · r2
А = π × 5352
А = π × 286,225
A = 899 202,3572 м2
Чтобы преобразовать квадратные метры, м2, в квадратные километры, км2, разделите на 1000000:
A = 0,8992 км2
Самый западный круглый жилой комплекс Сан-Сити имеет площадь почти 1 квадратный километр!
Как рассчитать площадь круга
Попробуйте эти вычисления площади для четырех разных кругов.Будь осторожен; некоторые указывают радиус r, а некоторые — диаметр d.
Не забудьте взять половину диаметра, чтобы найти радиус, прежде чем возводить радиус в квадрат и умножать на π.
Проблемы
- Велосипедное колесо диаметром 406 мм
- Колесо обозрения London Eye радиусом 60 метров
- Велосипедное колесо диаметром 26 дюймов
- Самая большая пицца в мире имела радиус 61 фут 4 дюйма (736 дюймов)
Не заглядывайте в ответы, пока не произведете расчеты!
ответов
- Велосипедное колесо диаметром 406 мм имеет радиус r 203 мм:
- Радиус 60 метров колеса обозрения «Лондонский глаз»:
- Велосипедное колесо диаметром 26 дюймов имеет радиус r 13 дюймов:
- Самая большая пицца в мире с радиусом 736 дюймов:
А = πr2
A = π × 203 мм2
А = 637.7433 мм2
А = πr2
A = π × 60 м2
A = 188,4955 м2
А = πr2
A = π × 13 дюйм2
A = 530,9291 дюйм2
А = πr2
A = π × 736 дюйм2
A = 1 701 788,17 дюймов2
То есть 11817.97 квадратных футов пиццы! Ням! В любом случае, как вы справились с четырьмя задачами?
Площадь круга по окружности
Если вы не знаете, что такое радиус или диаметр, но знаете длину окружности C, вы можете все же найти площадь.
Формула площади и окружности
Окружность (расстояние по окружности) находится по следующей формуле:
С = 2πr
Это означает, что мы можем взять формулу окружности и «решить для r», что даст нам:
г = C2π
Мы можем заменить r в нашей исходной формуле этим новым выражением:
А = π C2π2
Это выражение упрощается до следующего:
Эта формула работает каждый раз!
Как найти площадь по окружности
Вот красивая пиццы разумного размера , которую вы можете разделить с тремя друзьями.Вы знаете, что окружность вашей пиццы составляет 50,2655 дюйма, но вы не знаете ее общую площадь. Вы хотите знать, сколько квадратных дюймов пиццы вам понравится.
[вставить мультяшный рисунок типичной 16-дюймовой пиццы, но не указывать диаметр]
Замените C в формуле на 50,2655 дюйма:
А = 50.265524π
А = 2,526,62044π
A = 201,0620 дюйм2
Поровну разделите эту общую площадь для полноразмерной пиццы между четырьмя друзьями, и каждый из вас получит 50.2655 дюйм2 пиццы! Это примерно треть квадратного фута на каждого из вас! Ням ням!
Следующий урок:
Площадь сектора круга
Калькулятор площади круга
Калькулятор площади круга помогает вычислить поверхность круга с учетом диаметра или радиуса . Наш инструмент работает в обоих направлениях — независимо от того, ищете ли вы для вычисления площади или радиуса для области , вы нашли нужное место ◔
Мы дадим вам обзор наиболее важной информации, касающейся площади круга, его диаметра и радиуса.Мы изучим , как найти площадь круга , поговорим о формуле площади круга и обсудим другие разделы математики, в которых используется то же уравнение.
Как рассчитать площадь круга? Формула площади круга
Итак, давайте посмотрим, как найти площадь круга. Есть несколько способов добиться этого. Здесь мы можем вычислить площадь круга , используя диаметр или , используя радиус .
| 💡 Диаметр — это линия, которая пересекает центр фигуры и касается обоих ее полей.Радиус начинается в центре фигуры и заканчивается на краю фигуры. |
Диаметр круга можно найти, умножив радиус круга на два:
Диаметр = 2 * Радиус
Площадь окружности радиуса. Калькулятор радиуса круга использует следующую формулу площади круга:
Площадь круга = π * r 2
Площадь окружности диаметром. Калькулятор диаметра круга использует следующее уравнение:
Площадь круга = π * (d / 2) 2
Где:
- π примерно равно 3,14 . Неважно, хотите ли вы найти площадь круга, используя диаметр или радиус — вам нужно будет использовать эту константу почти в каждом случае.
Теперь, когда вы знаете, как рассчитать площадь круга, мы рекомендуем вам попробовать другие наши калькуляторы кругов:
> Сектор круга — это сечение круга между двумя радиусами.Вы можете думать об этом как о гигантском куске пиццы. > Это «отрезанная» часть круга, ограниченная хордой или секущей. > Это угол с вершиной в центре, руки которого доходят до окружности.Как использовать калькулятор площади круга? Диаметр к площади и радиус к площади.
Вы можете легко вычислить все, площадь круга, его диаметр и радиус, , используя наш калькулятор площади круга в мгновение ока:
Определите , является ли ваше заданное значение диаметром или радиусом , используя изображение справа и определения, доступные в разделе выше (вы можете рассчитать площадь круга, используя диаметр, а также радиус) .
Введите значение в соответствующее поле калькулятора .
Это не заняло много времени — ваши результаты ! Мы решили включить пошаговое решение и все самые важные данные прямо под калькулятором.
Вот как быстро вычислить площадь круга 😉
Зачем нам нужны калькуляторы площади круга?
Площадь круга, найденная с помощью калькуляторов радиуса и диаметра , служит основой для многих других уравнений — не только в математике, но и в повседневной жизни! Вот несколько примеров, когда знание того, как найти площадь круга, может быть полезно:
Нам нужно знать площадь поверхности круга, чтобы рассчитать объем конуса и его площадь 🎉
Ваша вечеринка с пиццей не была бы полной без нашего инструмента для пиццы на основе калькулятора диаметра к площади 🍕
Мы используем вычисления, подобные этому, при получении информации о сфере, например, об объеме сферы.

 Принципиальной разницы, большую букву писать или маленькую, нет.
Принципиальной разницы, большую букву писать или маленькую, нет.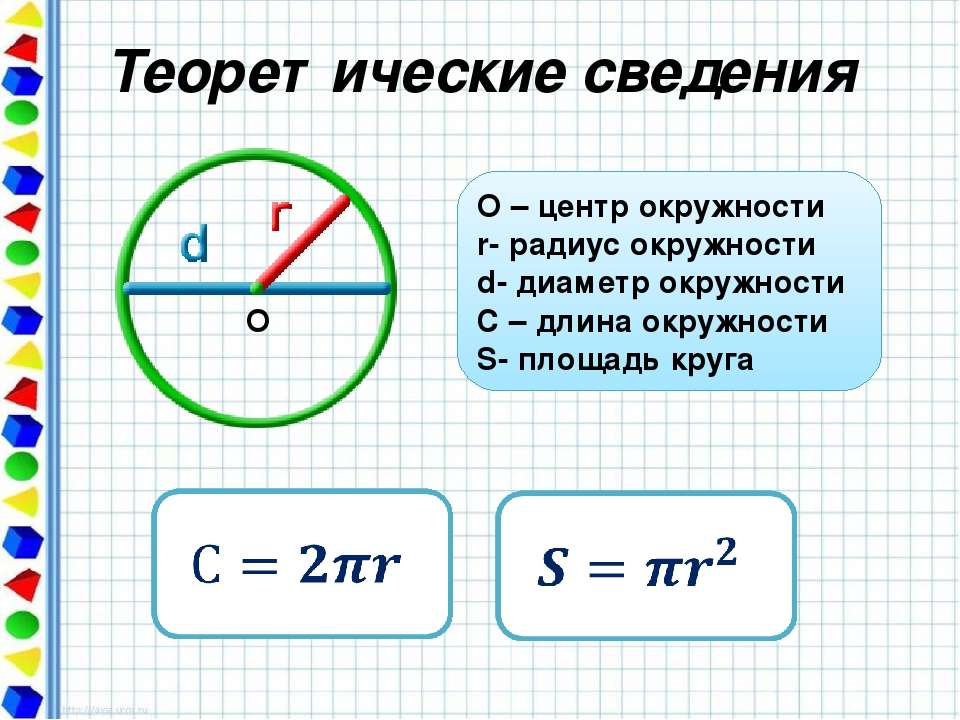 Формула для расчета длины окружности C=2πr, в которой C является длиной окружности, π=3,14, а r — это как раз искомый радиус.
Формула для расчета длины окружности C=2πr, в которой C является длиной окружности, π=3,14, а r — это как раз искомый радиус.
 Это мы продемонстрировали только что.
Это мы продемонстрировали только что. Значение площади сектора подставляется вместо переменной , а значение центрального угла вместо переменной .
Значение площади сектора подставляется вместо переменной , а значение центрального угла вместо переменной .
 Напомним, она делит фигуру на два прямоугольных треугольника и является их гипотенузой — стороной, лежащей напротив прямого угла. Поэтому, если диагональ неизвестна, её можно найти через соседние стороны прямоугольника с помощью теоремы Пифагора.
Напомним, она делит фигуру на два прямоугольных треугольника и является их гипотенузой — стороной, лежащей напротив прямого угла. Поэтому, если диагональ неизвестна, её можно найти через соседние стороны прямоугольника с помощью теоремы Пифагора. ru/node/783
ru/node/783
 Некоторые позволяют хранить в памяти большое число цифр, например, одно французское стихотворение поможет запомнить пи до 126 знака.
Некоторые позволяют хранить в памяти большое число цифр, например, одно французское стихотворение поможет запомнить пи до 126 знака.