Лучший ответ по мнению автора | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||
02.16
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука
| Похожие вопросы |
У Красной Шапочки в корзине.
..
В треугольнике ABC известно, что AC=6, BC=8, угол C равен 90°. Найдите радиус описанной около этого треугольника окружность. На пишите пожалуйста решение
—+—+—=30 Заполните пустые места используя данные числа (1,3,5,7,9,11,13,15) Одно и тоже число можно использовать несколько раз.
Площадь равнобедренного треугольника равна 81 корень 3 .Длина боковой стороны равна 18.Найти косинус угла ,лежащего напротив основания треугольника , если известно что этот угол тупой
Полый алюминиевый куб с ребром…
Пользуйтесь нашим приложением
Интересные Новости — Новости в России и мире, самая оперативная информация: темы дня, обзоры, анализ. Фото и видео с места событий, инфографика, радиоэфир, подкасты
Кулинария
Сколько по времени тушить голубцы: ошибка, которую допускают хозяйки
00
Голубцы считаются блюдом праздничным. Готовить их достаточно долго и сложно. Однако во время семейных торжеств они часто есть на столе.
Кулинария
На каком масле поджарить белые грибы, чтобы не превратить их в сухарики: хитрости кулинаров
00
Грибы, если их добавить к основному блюду, соусу или гарниру, украсят любой обед или ужин. Жареные грибы – это полноценное блюдо, отличный источник белка
Кулинария
Половина ложки — и картофель в мундире точно не разварится: что положить в кастрюлю
00
Нередко хозяйкам приходится прибегать к такому способу приготовления картофеля, как варка овоща в мундире. Если положить в кастрюлю клубень, с которого
Кулинария
Какую хитрость используют хозяйки, чтобы бутерброды с икрой не заветрились
00
Бутерброды с красной икрой – это хорошая закуска на праздничный стол. Они уместны при любом торжестве: день рождения, фуршет, новогодние торжества.
Кулинария
3 приправы, которыми можно заменить соль: о чем не догадываются хозяйки
00
Одна из самых распространенных специй – соль. Умеренное употребление соли не скажется на здоровье, однако ее избыток может негативно сказаться на давлении
Кулинария
Как приготовить картофель в мундире с сыром – не стыдно и гостям подать
00
Считается, что картофель в мундире не стоит рассматривать как самостоятельное блюдо, а если так, то как что-то очень примитивное. Но если проявить малую
Кулинария
Непростительная ошибка хозяек, из-за которой кофе в турке всегда горчит
00
Приготовленный по всем правилам кофе всегда получается вкусный и ароматный. Для приготовления качественного кофе все имеет значение: сорт зерен, их помол
Кулинария
Одна хитрость – и вареная свекла будет храниться долго: об этом не расскажут повара
00
Сварить свеклу можно по-разному: за 1 час, за 2 часа, за 15 минут. Все зависит от того, чем пользоваться при варке свеклы: или плитой, или мультиваркой
Кулинария
Квашеная капуста: добавьте один продукт, который сделает капусту бесподобной
00
Квашеная капуста должна получиться в меру кислой и хрустящей, только при сочетании этих показателей можно говорить, что она вкусная. Такую капусту можно
Кулинария
Как сделать мясо мягким и сочным: для маринада понадобится один ингредиент
00
Существует несколько типов маринадов, состоящих из трех основных ингредиентов: маринады на основе масла и кислоты, масла и приправ, кислоты и приправ
Видео-урок: Умножение и деление квадратных корней
Стенограмма видео
В этом видео мы будем умножение подкоренных выражений и упрощение результатов. Помните, что радикальные выражения точные формы чисел, которые включают радикалы или корневые знаки, такие как корень пять или семь корень три и все в таком духе.
Тогда наш первый вопрос: экспресс пять корней пять раз корень 45 в его простейшей форме.
Итак, радикалы в их простейшем
формы имеют подкоренные, эти биты здесь под корневыми знаками, как можно меньше
быть после факторизации любых квадратных факторов. Итак, во-первых, эта пятерка
против корня пять означает пять раз корень пять. И далее, мы должны упростить
корень 45.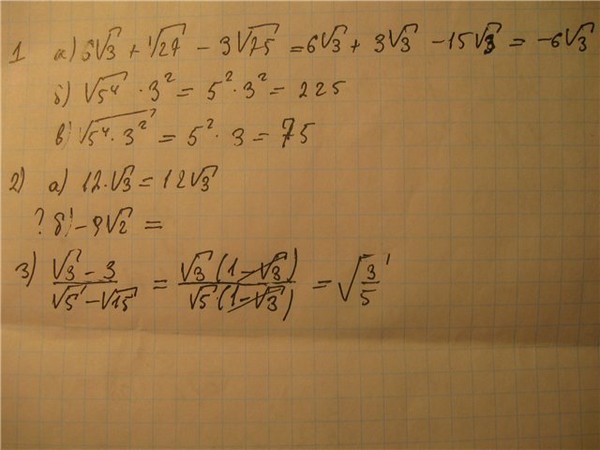
А теперь попробуем
найти самый большой квадратный множитель числа 45, который мы можем найти. И основная техника выполнения
это попробуй разделить на два, потом на три, потом на четыре, потом на пять и так далее
на. И посмотрите, есть ли какие-либо результаты, которые
мы получаем квадратные числа. И первое, с чем мы сталкиваемся, это
также будет самый большой квадратный множитель. Значит, 45 разделить на два нельзя.
работай. 45 разделить на три равно 15. Но это не квадратное число. 45 разделить на четыре не входит
45 точно. 45 разделить на пять будет девять. И это квадратное число. Так что это наша самая большая площадь
фактор. Так что я собираюсь переписать 45 как девять
раз пять.
А теперь корень девять раз по пять,
мы собираемся разделить на корень девять раз корень пять. И причина этого в том,
этот корень девять равен трем.
Девять — это идеальный квадрат, поэтому корень
девять это всего лишь три. Теперь с умножением это не
независимо от того, в каком порядке вы умножаете вещи. Вы получите то же самое
результат. Так что я собираюсь поменяться местами с корнем
пять и три в середине и умножьте вещи вместе в этом порядке. Итак, у нас есть пять раз три
15. И квадратный корень из пяти раз
квадратный корень из пяти равен всего пяти. И 15 умножить на пять будет 75, так что
ответ 75.
Следующий вопрос экспресс четыре корня семь раз два корня 49 в простейшей форме.
Теперь пара моментов, когда мы
посмотрите на это, четыре справа от корня семь означает четыре раза корень
Семь. И двое прямо против
корень 49 означает удвоенный корень 49. Но также 49 является полным квадратом, поэтому
корень 49 ровно семь. Таким образом, мы можем переписать это как четыре
раз корень семь раз два раза семь.
И следующий вопрос, используйте Распределительное свойство умножения пятикратное увеличение три минус два раза квадратный корень из пяти.
Распределительное имущество
умножение говорит нам, что это означает, что пять раз три отнять пять раз два
корень пять. И пять раз три — это 15.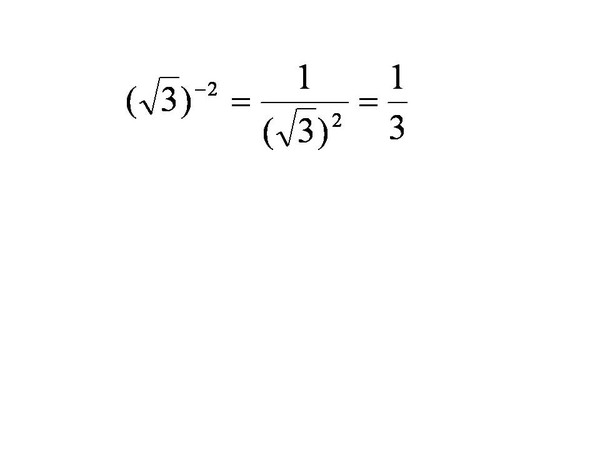
И пять раз два корень пять, ну
это означает, что пять раз два раза корень пять. И пять умножить на два будет 10, так что
10 корень пять. Итак, у нас есть 15 минус 10 корень
пять. И это не упростит
далее, таков наш ответ.
Теперь следующий вопрос: упростите три корня трижды два плюс пять корень три.
Так что будем использовать дистрибутив
свойство умножения делать три корня трижды два. И тогда мы собираемся добавить три
корень трижды пять корень три. Теперь давайте перепишем это со всеми
правильные знаки умножения там. И давайте поменяем вещи вокруг
немного, потому что не имеет значения, в каком порядке вы умножаете вещи вместе. Таким образом, мы получаем трижды два
раз корень три плюс три раза пять раз корень три раза корень три. Ну, трижды два — шесть. Таким образом, этот бит становится шестикратным корнем
три или просто шесть корень три.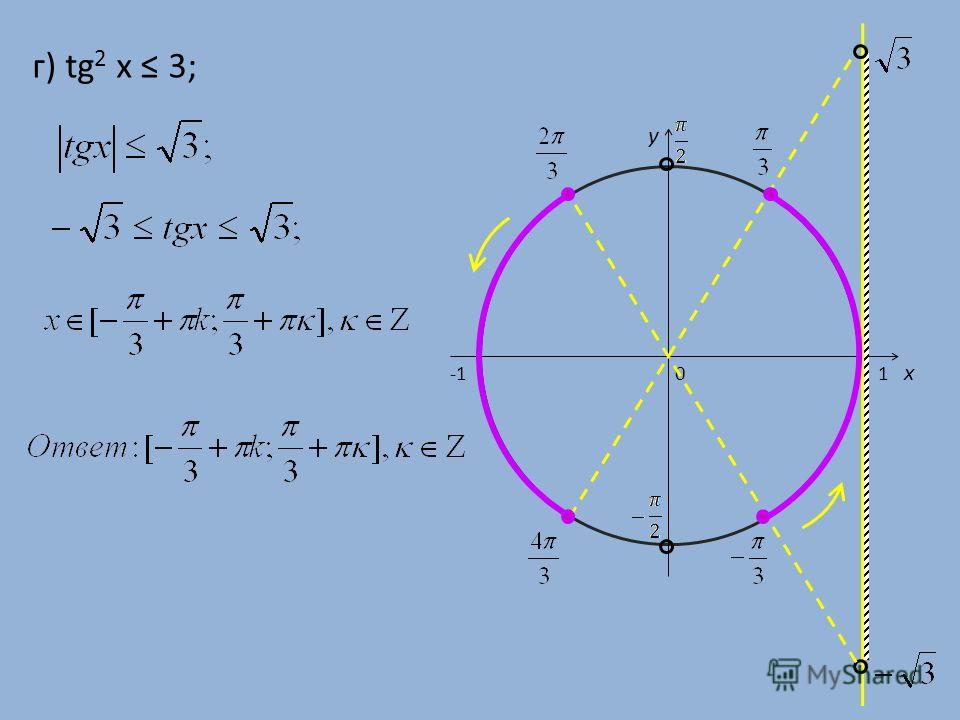
Теперь наш следующий вопрос замусорен с отрицательными знаками. Так что мы должны быть действительно, действительно осторожный.
Нам нужно упростить отрицательный три корня два раза минус четыре убери два корня два.
Прежде всего, я положу
скобки вокруг отрицательных чисел. Просто чтобы убедиться, что мы знаем, что
они отрицательны, и мы не забываем знак минус. А затем мы воспользуемся
распределительное свойство умножения делать отрицательные три корня два раза отрицательными
четыре. И тогда мы собираемся забрать
минус три корня два раза два корня два.
Теперь этот бит здесь просто означает
минус три раза корень два раза минус четыре. И потому что они умножаются
вместе, я могу расположить их в любом порядке, который мне нравится. И так же с этими терминами
здесь я собираюсь объединить все радикальные термины и все остальные термины
все вместе.
Хорошо, давайте разберем эти
вещи и умножать вещи вместе. Так что я получил отрицательный три раза
отрицательное четыре, что положительное 12. И это умножается на корень
два. Тогда у нас есть отрицательный три раза
два, что минус шесть. И квадратный корень из двух раз
квадратный корень из двух, что равно двум. Так что это в целом правая рука
выражение здесь становится отрицательным шесть раз два, что равно отрицательному числу 12. Таким образом, мы получили 12 корней два.
отнимем минус 12. Ну, если мы отнимем минус 12,
это то же самое, что добавить 12.
И корень два не упростит вниз
больше, так что это наш ответ, 12 корень два плюс 12.
Следующая остановка, мы должны упростить два набора скобок, умноженных вместе, корень три плюс пять и корень три минус четыре. И для этого мы собираемся умножьте каждый член в первой скобке на каждый член во второй скобке, как это. Так что это дает нам root три раза корень три. И тут мы получили root три раза минус четыре. Итак, мы собираемся забрать корень три раза минус четыре, которые мы собираемся написать четыре перед корнем три. Таким образом, получается отрицательный корень из четырех три. Тогда у нас пять положительных результатов корень три, так что это положительная пятерка корень три.
И, наконец, пятикратное отрицательное значение
четыре, что составляет минус 20. И, глядя на них, мы получаем
корень трижды корень три.
Ну это только три. Тогда у нас есть отрицательная четверка
эти коренные тройки. А потом прибавляем пять корней
тройки к тому. Так что это даст нам позитив
один корень три или просто положительный корень три, как мы могли бы написать. И, наконец, мы только что получили отрицательный
20 в конце. Таким образом, объединяя подобные термины, мы получили
три отнять 20 будет минус 17. И тогда у нас только один корень
три самостоятельно. Так что ответ отрицательный 17 плюс
корень три. И, как и все эти вопросы,
на самом деле не имеет значения, в каком порядке вы записываете эти термины. Таким образом, вы можете написать корень три минус
17. На самом деле есть повод сделать
это потому, что довольно часто нам не нравится вести с такими негативными знаками. Итак, корень три минус 17 — это еще один
совершенно хороший ответ.
Наш следующий вопрос — семь
плюс корень пять раз семь минус корень пять.
Есть два разных способа
мы можем подойти к этому. Так что мы сделаем их обоих, а затем
вы можете сравнить между ними. И первый способ заключается в том, чтобы просто
умножьте каждое слагаемое во второй скобке на каждое слагаемое в первой скобке. И это дает нам семь раз семь
равно 49. Семь раз отрицательный корень пять равен
минус семь корень пять. Затем корень пять раз по семь, ну
Я сделаю это наоборот. Семь раз корень пять, так что это
положительная семь корень пять. И, наконец, пять раз root
отрицательный корень пять. Ну, квадратный корень из пяти раз
квадратный корень из пяти равен всего пяти. И положительные времена отрицательные делают
отрицательный, так что это будет минус пять. Итак, у нас есть отрицательный корень из семи.
пять плюс семь корень пять. Ну, они собираются отменить каждый
другой аут.
Так что ничего не останется
середина. Так что у нас осталось 49минус
пять, что равно 44.
Таким образом, умножая скобки
вот так, не особо сложно. И это дало нам наш простой ответ
из 44. Но давайте еще раз посмотрим на
вопрос. Если вы узнаете эту форму, то есть
разность двух квадратов. Если вы вспомните свой факторинг
квадратичных чисел, 𝑎 в квадрате минус 𝑏 в квадрате, поэтому одно квадратное число убирает другое
квадратное число, можно разложить так. 𝑎 плюс 𝑏 раз 𝑎 минус 𝑏. И если мы допустим, что 𝑎 равно семи и 𝑏
равный корню пять, что даст нам семь плюс корень пять раз семь минус корень
пять, что мы и пытаемся сделать. Так что это просто 𝑎 в квадрате минус 𝑏
в квадрате. Другими словами, семь в квадрате минус
корень пять в квадрате. Ну семь в квадрате это 49, и корень
пять раз корень пять всего пять.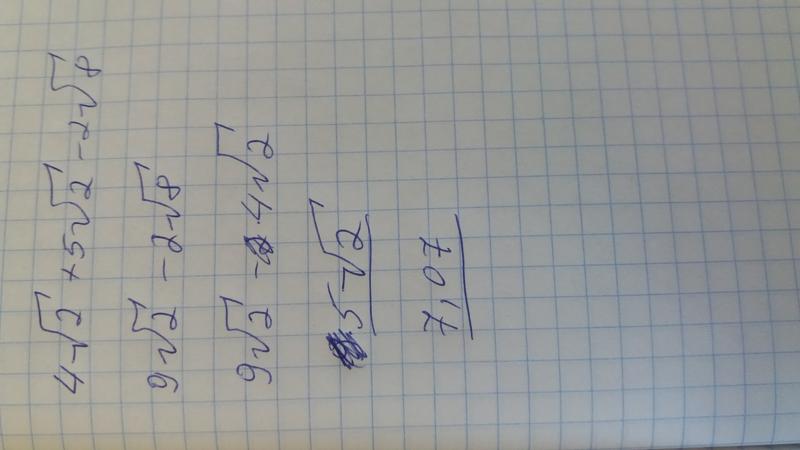
Итак, у нас сразу 49 минус
пять, что равно 44.
Итак, пока вы помните правило два квадрата, и вы держите такие вещи в своем мозгу. Тогда этот вопрос может на самом деле дает вам меньше работы, чтобы сделать этот путь, чем у вас был другой путь.
Теперь наш следующий вопрос, упростите шесть корень семь минус четыре корень два раза шесть корень семь плюс четыре корень два.
И если мы заглянем внутрь этих
скобки, у нас есть шесть корней семь в обоих местах. И у нас есть четыре корня два в обоих
места. Таким образом, мы вычитаем в одном, добавляя
в другом. Это как последний
вопрос. это разница двух квадратов
вопрос. И на этот раз 𝑎 это корень из шести
семь, а 𝑏 — это корень четыре из двух. Таким образом, мы можем переписать это как шесть корней
семь в квадрате минус корень четыре из двух в квадрате.
И шесть раз корень семь все
квадрат означает шесть раз корень семь раз шесть раз корень семь. И четыре корня два все в квадрате означает
четыре раза корень два раза четыре раза корень два. И с умножением, помни,
не имеет значения, в каком порядке мы умножаем эти вещи вместе. Так что я просто немного
реорганизовать это.
Так что просто поменяв порядок, который я
умножить некоторые из этих терминов вместе означает, что я собрал радикалы вместе и
остальные числа. Так что у меня есть шесть раз шесть раз
корень семь раз корень семь и четыре раза четыре раза корень два раза корень два. Ну шесть умножить на шесть будет 36, а корень
семь раз корень семь это просто семь. Итак, у меня 36 умножить на семь. И тогда четырежды четыре
шестнадцать. И корень два раза корень два
два. Таким образом, это упрощается до 36 раз
семь минус 16 умножить на два.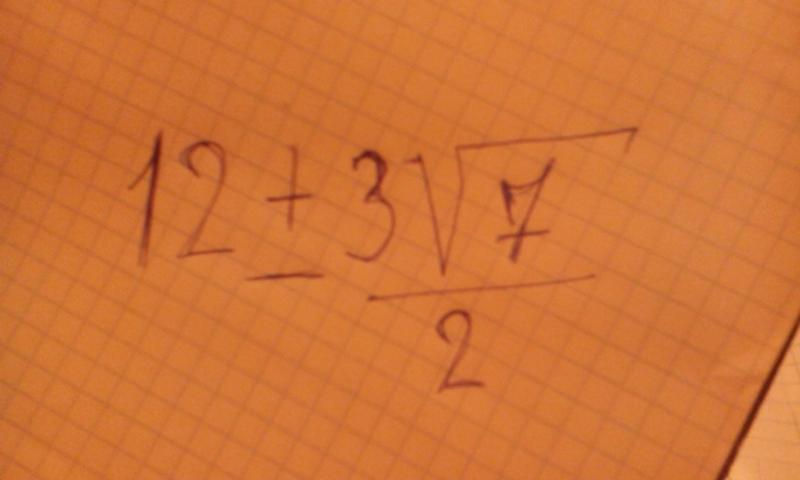
Теперь, я уверен, вы все знакомы
с вашей таблицей умножения на 36. Итак, 36 умножить на семь — это 252.
очевидно. И 16 умножить на два равно 32. Тогда 252 минус 32, это дает нам наше
ответ, 220.
Теперь наш следующий вопрос, упростите корень пять минус корень шесть все в квадрате.
Будьте очень осторожны, когда делаете
такого рода вопросы. Самая распространенная ошибка просто
люди смотрят на это, особенно в пылу экзамена, и думают: «О, это
корень из пяти во всех квадратах минус корень из шести во всех квадратах». И так они заканчивают тем, что делают пять с минусом
шесть. Теперь это совершенно неправильно. Вы всегда должны писать это в
полный; что-то в квадрате — это то, что умножается на себя. Итак, корень пять минус корень шесть все
в квадрате корень пять минус корень шесть раз корень пять минус корень шесть. И мы должны умножить каждый член
во второй скобке на каждое слагаемое в первой скобке.
Так что это корень пять раз корень
пять, и тогда у нас есть корень пять, умноженный на отрицательный корень шесть. Это минус корень пять корень
шесть. И тогда у нас есть минус корень шесть
раз корень пять.
Ну неважно в каком порядке
вы умножаете их вместе в. Так что я собираюсь положить это как корень пять
корень шесть снова. И это отрицательные времена положительные,
так что опять минус. И тогда у нас есть отрицательный корень
шесть раз отрицательный корень шесть или отрицательный раз отрицательный положительный. Итак, глядя на эти выражения,
у нас есть корень пять раз корень пять, что всего пять. И у нас есть корень шесть раз корень
шесть, что всего шесть. На самом деле, это плюс шесть. Итак, корень пять раз корень шесть
также то же самое, что и корень пять раз шесть. Итак, мы видели это раньше, когда
мы убрали и упростили эти сурды или эти радикалы.
Но это работает по-другому, как
хорошо. Итак, корень пять раз, корень шесть — это корень.
пять раз шесть, и это корень 30. Таким образом, у нас есть отрицательный корень 30 взять
прочь еще один корень 30.
Теперь давайте посмотрим на условия; собрать подобные термины. Пять плюс шесть равно 11 и минус корень 30 убери другой корень 30 минус два корня 30. Теперь смотрим содержимое этого радикал, 30. Давайте подумаем о факторах 30. Ну, у 30 много факторов. Но глядя на них, только один номер квадрата. И это не поможет нам в этой ситуации, чтобы уменьшить размер числа. Поэтому мы не можем еще больше упростить тот радикал или тот сурд. Так что это наш ответ, 11 минус два корень 30.
Давайте перейдем к нашему предпоследнему тогда вопрос.
Корень семь раз три корень семь
минус пять минус два раза четыре минус пять корень семь.
Ну, мы будем использовать Распределительное свойство умножения для решения этого вопроса. Итак, глядя на первые скобки во-первых, у нас есть корень семь раз три корень семь, что то же самое, что корень семь раз три раза корень семь. Затем мы получили root семь раз минус пять. Итак, мы убираем корень семь умножить на пять, что равно пятикратному корню семь. Затем мы собираемся сделать минус два умножить на четыре, что составляет минус восемь. Итак, мы убираем восемь. И минус два раза минус пять корень семь. ну минус два раза минус пять — это положительное число 10. Таким образом, у нас есть положительный корень из 10. Семь.
Хорошо, давайте пролистаем здесь. Теперь, в этом первом семестре, мы
получил корень семь раз корень семь раз три. Ну, корень семь раз корень семь
равно семи, а семь раз три равно 21.
И мы не можем упростить второе
срок, так что минус пять корень семь. А у нас минус восемь. Точно так же мы не можем упростить
последний семестр. Теперь 21 отнять восемь будет 13. И минус пять корень семь плюс
10 корень семь положительный пять корень семь. А так как у семерки нет
квадратные множители больше единицы, мы не можем упростить это дальше. Итак, 13 плюс пять корень семь это наш
отвечать.
Наконец, просто для развлечения, давайте попробуем ответить на этот довольно каверзный вопрос.
Упростить квадратный корень из 15 плюс квадратный корень из 19, умноженный на квадратный корень из 15 минус квадратный корень из 19 все в квадрате.
Теперь, если вы платили
внимание на протяжении всего видео, вы, вероятно, замечаете факт: «О, это выглядит
как разность двух квадратов!» Но не совсем в том формате,
это? Итак, разница двух квадратов
говорит, что 𝑎 в квадрате минус 𝑏 в квадрате равно 𝑎 плюс 𝑏 умножить на 𝑎 минус 𝑏.
И мы почти у цели. Но у нас есть эта проблема
два квадрата над скобками здесь. Итак, если мы немного перестроим
тогда мы сможем использовать это. Итак, давайте посмотрим на это. Ну, корень 15 плюс корень 19все
квадрат — это просто корень 15 плюс корень 19, умноженный на корень 15 плюс корень 19. Итак, это первые скобки
разбирается и аналогично со вторым.
Теперь у нас есть четыре комплекта
скобки, все перемножаются вместе. И когда мы умножаем вещи
вместе, на самом деле не имеет значения, в каком порядке мы их делаем. Так что я собираюсь переставить их. Так что я просто поменял местами
порядок средних двух наборов скобок там. И это оставило меня с корнем 15
плюс корень 19умножить на корень 15 минус корень 19 все умножить на корень 15 плюс корень 19 умножить на корень
15 минус корень 19. Теперь каждый из них отличается
из двух квадратов формата, который мы искали.
Итак, если 𝑎 — корень 15, а 𝑏 — корень
19, у нас есть этот образец здесь. И у нас тоже есть здесь. А это значит, что 𝑎 в квадрате
корень 15 в квадрате, что равно 15. А 𝑏 в квадрате — это корень 19 во всех
в квадрате, что равно 19. И 𝑎 в квадрате минус 𝑏 в квадрате равно
15 минус 19.
Итак, вернемся к нашему вопросу. тогда. У нас есть 𝑎 плюс 𝑏 раз 𝑎 минус 𝑏 раз 𝑎 плюс 𝑏 раз 𝑎 минус 𝑏. И 𝑎 плюс 𝑏 раз 𝑎 минус 𝑏 равно то же, что 𝑎 в квадрате минус 𝑏 в квадрате. И, как мы только что сказали, 𝑎 в квадрате минус 𝑏 в квадрате равно 15 минус 19. А 15 минус 19 отрицательное четыре. Так что это становится отрицательным четыре раза отрицательная четверка, которая является положительной 16.
Итак, помня о нашей разнице
два квадрата и небольшая реорганизация, чтобы получить правильный формат
потому что это избавило нас от огромного количества размножения.
И дал нам очень простой ответ
из 16 вместо всего этого хлама здесь, с которого мы начали в
начало вопроса.
Хорошо, удачи в умножении тогда радикальные выражения.
Common Core Algebra I.Unit 9.Lesson 1.Квадратные корни, алгебра 1
электронная инструкция
20 сентября 2016 г.
2177 просмотров
В одиночку, добро пожаловать на еще один общий урок алгебры ядра. По E математике инструкции. Меня зовут Кирк Вейлер, и сегодня мы будем делать первый урок по квадратным корням из раздела 9. Прежде чем мы начнем, позвольте мне напомнить вам, что вы можете найти рабочий лист для этого видео и домашнее задание, нажав на описание видео или посетив наш веб-сайт по адресу WWW точка E math инструкциям точка com. Кроме того, не забывайте о QR-кодах в верхней части каждого из наших рабочих листов. Используйте свой телефон или планшет, чтобы отсканировать этот код, и вы перейдете к видео, которое идет с этим уроком.
Хорошо, давайте начнем. Я надеюсь, что квадратные корни — это то, что вы видели раньше. Все в порядке? Безусловно, в математике кое-что появилось раньше. И сегодня мы их рассмотрим. Начнем с вроде, если хотите, простых задач на квадратный корень. В первом упражнении найдите значение каждого из следующих основных квадратных корней, напишите причину своего ответа в виде уравнения умножения. Теперь у вас есть хорошая возможность проверить, насколько хорошо вы помните квадратные корни. Я понимаю, что дроби и буква E и буква F могут быть немного сложными. Так что, если это проблема, я бы не слишком беспокоился об этом. Но сейчас остановите видео и посмотрите, сможете ли вы вычислить каждый из следующих квадратных корней. У каждого из них есть только один ответ. Так что не записывайте два, даже если вы думаете, что это правильно. Поставьте видео на паузу. Хорошо, давайте пройдемся по ним. Итак, квадратные корни всегда отвечают на очень забавный вопрос. Они всегда отвечают на следующий вопрос.
Какое число в квадрате даст мне 25? И ответ там 5. Хорошо? Почему? Это право разума. Ну, это потому, что 5 умножить на 5 или еще лучше, 5 в квадрате равно 25. Квадратный корень и возведение в квадрат обратны друг другу. Их противоположности друг другу. Хорошо? Итак, квадратный корень из 9, ну это три. Почему? Потому что трижды три равно 9. Квадратный корень из ста, ну, это равно десяти. Почему? Потому что десять раз десять равно сотне. Квадратный корень из нуля довольно забавный. У меня будут даже студенты, дошедшие до предварительного исчисления, которые будут сбиты с толку этим. Но это не должно сбивать с толку. Квадратный корень из нуля равен нулю. Почему? Потому что ноль умножить на ноль равно нулю. Теперь, как напоминание, о дробях. Не беспокойтесь об этих двоих ни на минуту. Когда вы перемножаете дроби вместе, скажем, в одну треть, позвольте мне избавиться от этого. Одна треть умножить на две пятых. Что вы всегда делаете, так это умножаете числители два раза один на два. И вы умножаете знаменатели трижды на 5, это 15.
Мы можем использовать это, чтобы понять, что квадратный корень из одной четвертой должен быть половиной, и причина в том, что половина, умноженная на половину, равна одной четвертой, верно? Один раз один — один, два раза два — четыре. Все в порядке? Точно так же квадратный корень из 64 9должно быть 8 третей. Почему? Потому что 8 третей умножить на 8 третей, 8 умножить на 8 — это 64. Три раза по три — 9. Хорошо? Таким образом, квадратные корни, по сути, отвечают на вопрос, какое число мне нужно умножить само на себя, другими словами, какое число мне нужно возвести в квадрат, чтобы получить число под квадратным корнем? Число под корнем квадратным под корнем квадратным имеет особое название. Это называется радикал. Радикальная рука. Это не тот термин, который будет использовать множество учителей, но некоторые из них будут. И это удобно, в отличие от того, чтобы говорить такие вещи, как число под квадратным корнем. Так что я иногда говорю число квадратного корня, а иногда я говорю ратическую руку.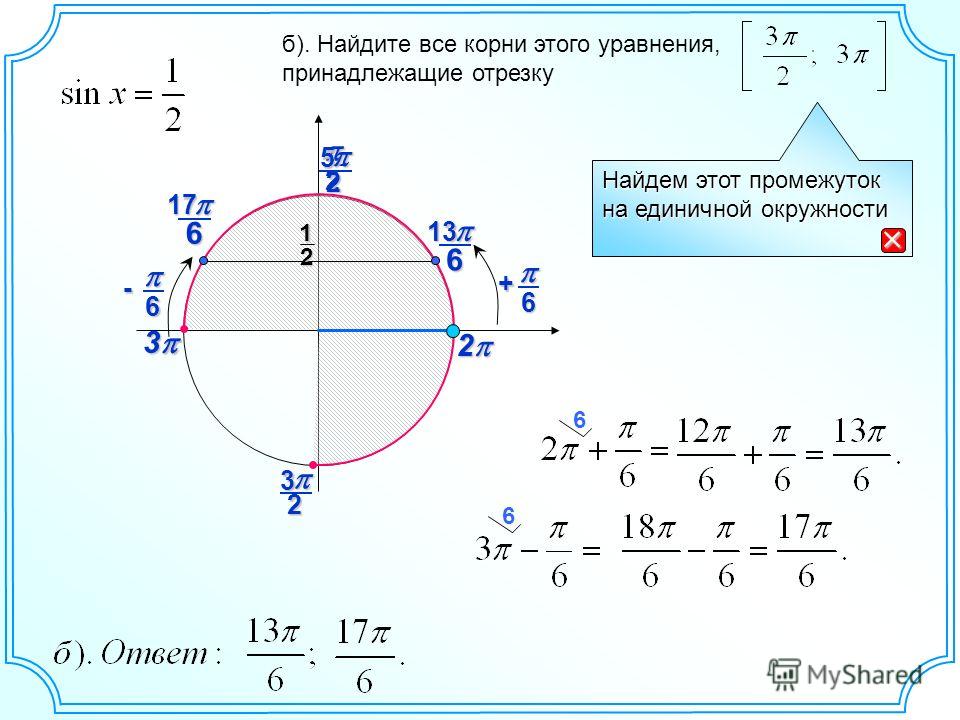
Хорошо? В любом случае, запишите все, что вам нужно, чтобы поставить видео на паузу, и тогда мы продолжим. Хорошо, поехали. Перейдем к следующей странице. Итак, из каждого положительного числа есть два квадратных корня. И причина этого в том, что произведение двух отрицаний положительно, верно? Итак, мы знаем, что отрицательное и отрицательное, отрицательное, умноженное на отрицательное, является положительным и является произведением двух положительных. Это положительно? И из-за этого каждое положительное целое число имеет два квадратных корня. Знаете, например, да? Минус три раза минус три равно 9, а трижды три равно 9. Таким образом, и положительная тройка, и отрицательная тройка являются законными квадратными корнями из 9. Аналогично, отрицательная единица 5, умноженная на отрицательную единицу 5, эта 25-я и одна 5-я, умноженная на одну пятую, составляет одну 25-ю. Так что оба они являются законными квадратными корнями из одной 25-й. Итак, вы можете спросить, или вы можете спросить, ну, почему я тогда не поставил два ответа для каждой проблемы в номере один? Ну, это потому, что нам нужно знать.
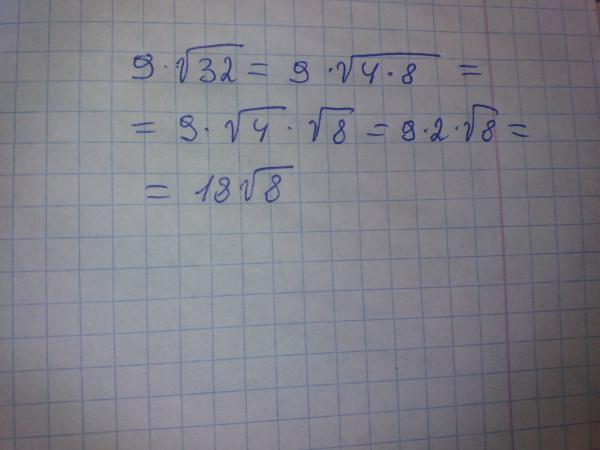Нам нужен способ узнать, говорим ли мы о положительном квадратном корне числа или об отрицательном квадратном корне числа. Все в порядке? Итак, о каком квадратном корне мы говорим, будет определяться просто тем, имеет ли квадратный корень отрицательное значение. Другими словами, квадратный корень из 9это три. Но отрицательный квадратный корень из 9 равен отрицательному трем. Итак, когда вы видите символ квадратного корня и не видите перед ним отрицательного значения, тогда мы говорим о том, что известно как принцип. Квадратный корень. И да, это принцип у парня, который сидит в углу кабинета. Парень или женщина, которая сидит в углу кабинета, прошу прощения. И там действительно не должно быть места. Но это называется принципом квадратного корня. А еще есть отрицательный квадратный корень. Таким образом, если не указано иное, вы определяете, о каком из них вы говорите, по тому, есть ли отрицательное или положительное значение перед квадратным корнем, или визуально говоря отрицательное или не отрицательное.
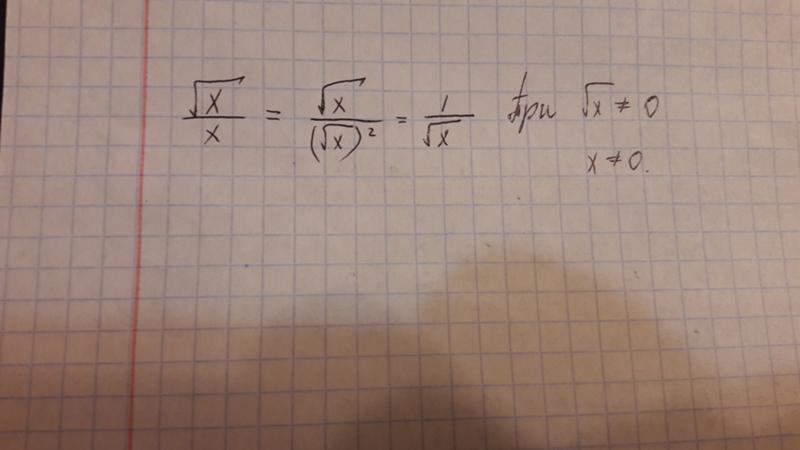Все в порядке. Позвольте мне очистить текст. А затем давайте продолжим и решим еще несколько задач с квадратными корнями. Все в порядке. Упражнение два, это должно быть кусок пирога. Назовите все квадратные корни каждого из следующих чисел. Все в порядке? Поставьте видео на паузу и сделайте это. Что ж, как мы только что обсуждали, каждое число имеет два квадратных корня, и вы, возможно, только что записали их, но позвольте мне подчеркнуть. Один из них будет положительным квадратным корнем из четырех, что равно двум. И одним из них будет отрицательный квадратный корень из четырех, то есть отрицательная двойка. В этой задаче одним из них будет положительный квадратный корень из 36, что равно 6. И одним из них будет отрицательный квадратный корень из 36, что равно отрицательному числу 6. Здесь один из них будет положительным квадратным корнем из единицы. 16-й, который будет одной четвертой, и один из них будет отрицательным квадратным корнем из одного 16-го. Что будет отрицательной одной четвертой.
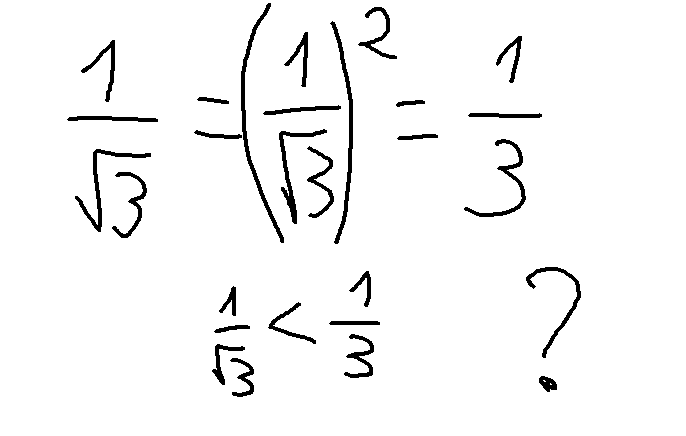И снова, если вы просто записали все это без символов квадратного корня, это нормально, но я просто хочу подчеркнуть, что именно так мы собираемся отметить разницу между положительными и отрицательными значениями. Все в порядке. Я собираюсь прояснить это, продолжив нашу довольно простую работу с квадратным корнем до второй половины урока. Хорошо, вот оно. Давайте перейдем к следующей проблеме, хорошо? Итак, третье упражнение — это относительно простой вопрос с несколькими вариантами ответов, но оно, как обычно, включает в себя некоторые обозначения функций, верно? F из X равно квадратному корню из X плюс три. Что из следующего является значением F из 46, верно? Итак, опять же, это больше, чем что-либо еще о записи функций, верно? И просто зная, что, когда вы видите это, вы не должны бояться. Вы должны просто вставить 46. В этом случае везде, где есть X, поэтому мы сначала складываем эти числа, мы получаем квадратный корень из 49., и это вышло. Все в порядке. Так достаточно просто. Хорошо, вам просто нужно понять обозначение функций и то, что означает символ квадратного корня.
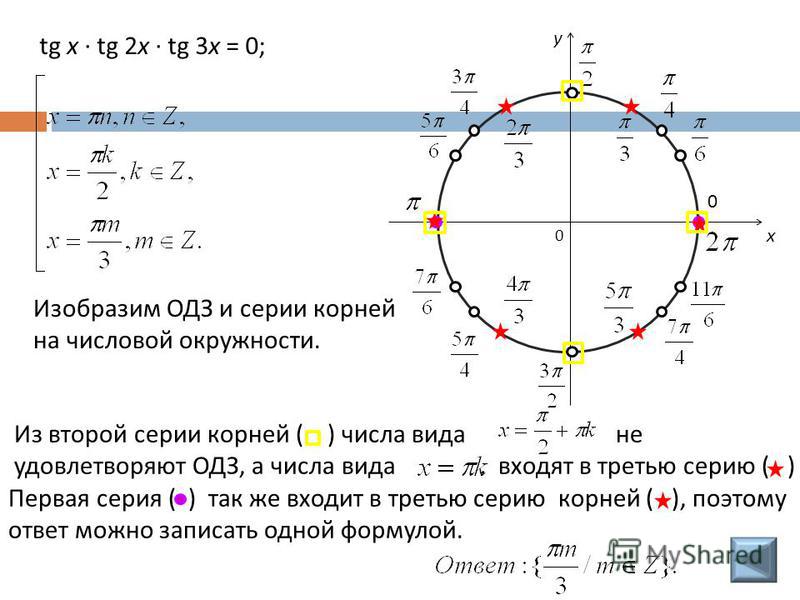Но это все равно важно, верно? Это может быть сложно, особенно обозначение функций. Итак, я собираюсь очистить текст от всего, что вам нужно. Все в порядке. И продолжим двигаться дальше. Хорошо? Теперь следующая проблема может показаться вам немного глупой. Хорошо? Но его цель — проиллюстрировать одно из самых важных свойств квадратных корней. Все в порядке? И это свойство имеет какое-то отношение к продуктам. Итак, давайте сделаем А и Б вместе. Тогда я заставлю тебя сделать C и D самостоятельно. Силы упражнений определяют ценность каждого из следующих продуктов, верно? Итак, эта штука говорит: эй, найди произведение квадратного корня из четырех, умноженного на квадратный корень из 9.. Ну, квадратный корень из четырех равен двум. Квадратный корень из 9 равен трем, так что произведение равно 6. Однако буква B говорит о квадратном корне из четырех, умноженных на 9. Что ж, это означает, что мы должны сначала произвести произведение четырех, умноженных на 9, что равно 36, а затем мы должны найти квадратный корень из 36.
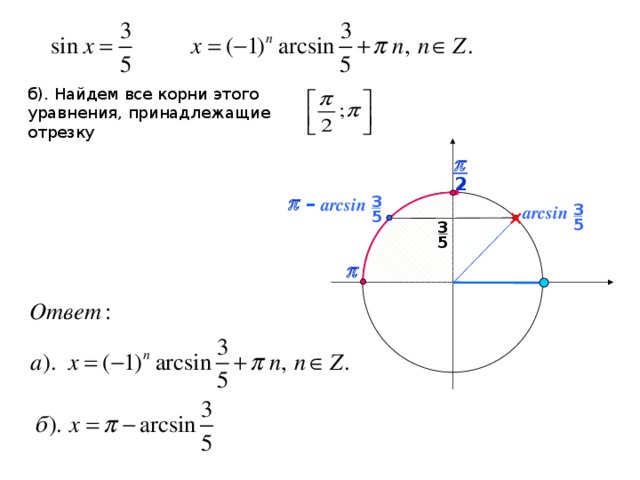Но ведь это 6, верно? О, да. Интересно, это совпадение, да? Я имею в виду, почти кажется, что когда мы умножаем два квадратных корня вместе, мы могли бы сначала умножать радикалы, числа под квадратным корнем, а затем извлекать квадратный корень, или мы могли бы сначала извлекать квадратные корни, а затем умножить. В любом случае, почему бы вам не решить задачи C и D, чтобы проверить, сохраняется ли схема. Хорошо, давайте сделаем это. В то время как квадратный корень из четырех раз больше квадратного корня из 25, квадратный корень из четырех равен двум. Квадратный корень из 25 равен 5, а два раза по 5 равно десяти. С другой стороны, если мы сначала умножим ратические руки четыре раза на 25, мы получим 100. А квадратный корень из ста равен десяти. Так что да, шаблон продолжает действовать, верно? И это иллюстрирует, как я уже сказал, одно из самых важных свойств квадратных корней. Это и есть квадратные корни, если хотите, уважайте умножение. Или поиграйте с умножением, как бы вы ни думали об этом.
В любом случае, мы собираемся официально рассмотреть его через минуту, но я собираюсь убрать этот текст. Так что остановите видео прямо сейчас, запишите все, что вам нужно, а потом мы его очистим. Хорошо, давайте перейдем к следующей странице. Таким образом, свойство умножения квадратного корня говорит, что если мы собираемся умножить два квадратных корня вместе, мы можем сделать это, сначала умножив числа под квадратным корнем, два радикала, а затем возьмем квадратный корень. Как ни странно, мы собираемся использовать это свойство чуть ли не чаще в обратном порядке. То есть, если у нас есть произведение двух чисел под квадратным корнем, то мы можем разбить это произведение как произведение двух отдельных квадратных корней. Все в порядке? Вот как мы собираемся использовать это свойство. По крайней мере в основном. Но мы сделаем немного этого, используя что-то вроде этой первой версии здесь. Все в порядке? Итак, я собираюсь прояснить это, а затем мы собираемся попрактиковаться в некоторых задачах, связанных с этим свойством.
Хорошо? Итак, одно из непосредственных действий, которые мы можем сделать с этим свойством, — это умножение недружественных квадратных корней, верно? Это дружественные квадратные корни, такие как квадратный корень из четырех и квадратный корень из 9.и квадратный корень из 25. А еще есть недружественные, такие как квадратный корень из двух и квадратный корень из 8. Но наше свойство говорит: смотрите, если я получил квадратный корень из двух умноженных на квадратный корень из 8 , то я могу на самом деле разбить это на квадратный корень из двух, умноженных на 8, который является квадратным корнем из 16, и это четыре. Вот и все. Теперь, конечно, мы могли бы перемножить эти два числа вместе и получить число под квадратным корнем, которое не было бы идеальным квадратом, а 16 — это идеальный квадрат. Но оказывается, что в этих задачах так бывает много. Таким образом, квадратный корень из 12, умноженный на квадратный корень из трех, будет таким же, как квадратный корень из 12, умноженный на три.
12 умножить на три — это 36, а квадратный корень из 36 — это 6. Хорошо, выглядит хорошо. Как насчет буквы С? Почему бы тебе не поставить видео на паузу и не сделать это самому? Хорошо, надеюсь, у вас есть десять, это окончательный ответ. Потому что, как и раньше, мы можем сначала умножить радикалы. 20 умножить на 5 будет 100. И тогда квадратный корень из ста равен десяти. Хорошо? Таким образом, одним из непосредственных следствий свойства умножения квадратных корней является то, что если у вас есть два квадратных корня, умножающих друг друга, может быть проще всего сначала умножить радикалы, а затем извлечь квадратный корень. Может быть. Все в порядке. Так что я собираюсь прояснить это. А затем мы поговорим о другом важном последствии этого свойства. И это при упрощении квадратных корней. Теперь, что значит упростить квадратный корень? Это означает, что нужно найти эквивалентное выражение, то есть идентичное число. Но где все совершенные квадратные множители были удалены из неустойчивой руки.
Все в порядке. Так вот, это на самом деле процедура, которую вы собираетесь изучить, которая специально обязательна, если вы сдаете математику или общую базовую алгебру в штате Нью-Йорк. Если вы изучаете общую базовую алгебру в других штатах, это может быть не то, что вам нужно изучать на общем базовом уровне. Или общая базовая алгебра одного уровня. Но давайте прыгнем в него. Это своего рода забавный процесс. Это не так уж сложно. И давайте посмотрим, как это работает. Хорошо? Итак, мы собираемся сделать это на одном конкретном примере. Упражнение номер 6 говорит букву а, перечислите первые десять правильных квадратов. Совершенные квадраты — это числа, у которых есть хорошие квадратные корни, например, один квадрат равен единице. Итак, идеальный квадрат. Два в квадрате четыре. Итак, идеальный квадрат. Три в квадрате 9. Итак, идеальный квадрат. Четыре в квадрате — это 16. Итак, 16 — это полный квадрат. 5 в квадрате равно 25. Это идеальный квадрат. 6 в квадрате равно 36. Идеальный квадрат.
7 в квадрате равно 49. Идеальный квадрат. 8 в квадрате равно 64. Идеальный квадрат. 9 в квадрате равно 81. Идеальный квадрат. А десять в квадрате — это сто. В первой десятке нет ничего волшебного. На самом деле, вам, возможно, придется пройти мимо этого. Возможно, вам придется перейти к 11 в квадрате, 12 в квадрате, 13 в квадрате, но это довольно редко. Итак, теперь давайте поиграем с буквой B, которая говорит, теперь рассмотрим квадратный корень из 18. Итак, 18 не является идеальным квадратом, верно? Посмотри на это. Один, четыре, 9, 16, 25, 36 и так далее. 18 не входит в их число. Но один из тех, на самом деле два из тех, но давайте исключим первый. Я действительно не забочусь об этом. Хорошо, один из них делит 18 красиво. И это 9. Верно? В частности, 18 равно 9 умножить на два. Итак, смотрите, что мы собираемся делать сейчас. Теперь мы собираемся обратить этот процесс вспять, верно? Квадратный корень из 18 равен квадратному корню из 9 умножить на два. Потому что очевидно, что 9 умножить на два равно 18.
Так что это правда, несмотря ни на что. Мне было бы все равно, какое имущество мы использовали. Но теперь это свойство квадратных корней говорит, что мы можем переписать это как квадратный корень из 9.умножить на квадратный корень из двух. С квадратным корнем из 9 мы можем что-то сделать. Можно сказать, три. Квадратный корень из двух, с которым мы ничего не можем сделать, поэтому мы должны оставить его как квадратный корень из двух. И это все. Квадратный корень из 18 равен трем умножениям на квадратный корень из двух, и они действительно одинаковы. Если вы возьмете калькулятор и наберете квадратный корень из 18, введите. А потом набираешь трижды квадратный корень из двух, вводишь. Вы получите точно такое же и уродливое, десятичное выражение. Хорошо? Итак, давайте проясним это. А затем попрактикуйтесь в упрощении квадратных корней. Ключевое модное слово здесь, извините, я должен был указать на это раньше, было простейшей, радикальной формой, простейшей радикальной формой. В любом случае, я собираюсь это выяснить.
Так что скопируйте то, что вам нужно. Хорошо, поехали. Давайте двигаться дальше. Хорошо, в верхней части страницы я перечислил первые 12 идеальных квадратов, и на самом деле наименее релевантным является номер один. Нас никогда не будет волновать тот факт, что это идеальный квадрат. Так что дело не в том, что это не идеальный квадрат. Я просто не хочу об этом заботиться. Итак, в нем говорится, выпишите каждый из следующих квадратных корней и простейшую радикальную форму. Итак, вот что мы хотим сделать. Мы хотим найти самый большой из них, который красиво делится на 8. И это четыре. Все в порядке? Другими словами, 8 — это то же самое, что четыре раза по два. Но затем мы можем использовать это свойство квадратных корней, чтобы переписать это как квадратный корень из четырех, умноженный на квадратный корень из двух, а затем мы можем преобразовать квадратный корень из четырех в два. Так что извлеките квадратный корень из того, что вы можете, и оставьте то, что вы не можете. Все в порядке? Так что я могу найти квадратный корень из четырех равен двум.
Но квадратный корень из двух, я должен оставить именно так. Хорошо, давайте посмотрим на квадратный корень из 45. Мы подумаем об этих числах, какое число туда входит. Очевидно, что вам не нужно подниматься выше 45. Но самый большой, самый большой совершенный квадрат что входит в 45 это 9, правильно? 45 — это 9, умноженное на 5. Это означает, что теперь я могу разбить это, так как квадратный корень из 9, умноженный на квадратный корень из 5, всегда ставит на первое место полный квадрат. Квадратный корень из 9, я могу найти это три. Квадратный корень из 5 я не могу найти, поэтому просто оставляю так. Ладно, буква С, я хочу показать тебе кое-что крутое. Хорошо, потому что ученики часто совершают ошибку. Взгляните на квадратный корень из 48 и очень и очень законно. Они возьмут свой калькулятор и скажут, хорошо, квадратный корень из 48 разделить на четыре. И они узнают, эй, ты же знаешь, что 48 делится на четыре, верно? Итак, 48 — это на самом деле четыре раза по 12. Хорошо, поэтому они разобьют его на квадратный корень из четырех, умноженный на квадратный корень из 12.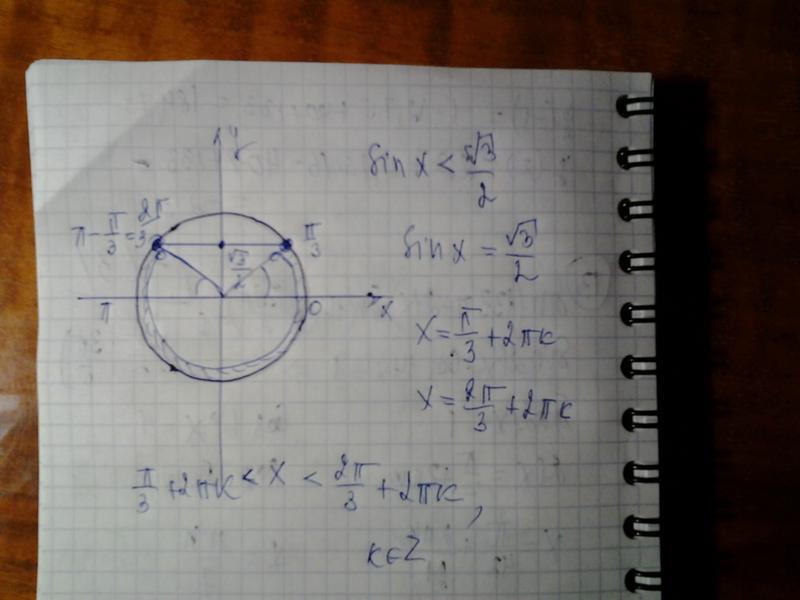
Квадратный корень из четырех равен двум, и тогда они оставят это так. Между прочим, нет никаких сомнений в том, что квадратный корень из 48 в два раза больше квадратного корня из 12. Здесь мы сделали все, что законно. Проблема в том, что в числе 12 тоже есть идеальный квадрат. Правильно? Позвольте мне избавиться от этого. Правильно. Таким образом, мы можем взять квадратный корень из 12 и разбить его на квадратный корень из четырех, умноженный на квадратный корень из трех. Но тогда это будет дважды два корня Таймс-сквер из трех. Что будет четыре корень три. В этом нет ничего плохого. Это мой окончательный ответ. Это простейшая радикальная форма. У этой удивительно важной фразы простейшая корневая форма. Но если я сделал это в два шага, это означает, что на самом деле есть больший совершенный квадрат, который красиво делится на 48. На самом деле, больший квадрат, который красиво делится на 16. Таким образом, квадратный корень из 48 такой же, как квадратный корень из 16 раз по три. Таким образом, квадратный корень из 16 умножается на квадратный корень из трех, а квадратный корень из 16 равен четырем.
А квадратный корень из трех — это квадратный корень из трех. Все в порядке. Теперь нет абсолютно ничего, ничего, ничего, ничего плохого. С уменьшением вот так. Это эквивалентно сокращению, скажем, 12 восемнадцатых. И вы сказали: о, я знаю, что в них обоих входит два. Итак, вы сделали это и получили 6 девятых, а потом сказали: «О, подождите секунду». Нет, я не знаю. Я собираюсь разделить это на три в этом на три. И получить две трети. Это было бы хорошо. Вы знаете, вы можете сделать это в два шага, или вы можете сделать это в один шаг, разделив и числитель, и знаменатель на 6. Я не хочу этого прямо сейчас. Вернемся к этому. Хорошо, теперь есть негатив перед этим. Это не имеет большого значения. Мы просто должны не потерять его. Итак, мы рассматриваем все эти проблемы. И мы говорим, ладно, не проблемы, но мы смотрим на все эти числа и говорим, что самое большое из тех, что входят в 75, это 25. Итак, я сейчас разложу это на отрицательный корень 25. раз корень три. Не кладите туда два негатива, тогда у вас будет позитив.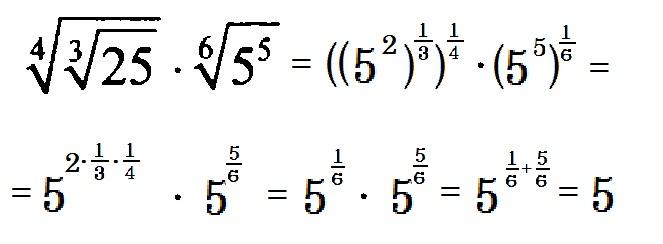
Квадратный корень из 25, я могу уменьшить минус 5, квадратный корень из трех. Я ничего не могу сделать с таким отрицательным корнем Таймс-сквер из 30. Корень Таймс-сквер из трех. Все в порядке. Я бы хотел, чтобы вы сами поиграли с E и F. Поставьте видео на паузу, продлите до 5 минут. Калькулятор может даже пригодиться, чтобы понять, какие идеальные квадраты входят в эти числа. А потом посмотрите, что у вас получится. Хорошо, давайте пройдемся по ним. Таким образом, самый большой совершенный квадрат, входящий в число 72, равен 36. Фактически, 36 умножить на два равно 72. Итак, я разделяю этот конец квадратного корня из 36 и квадратного корня из двух, квадратного корня из 36 на 6, и я оставить квадратный корень из двух. Хорошо, квадратный корень из минус 500. Извините. Это было плохо. Отрицательный квадратный корень из 500 — это не квадратный корень из минус 500. Мы поговорим об этом подробнее в следующий раз. Что ж, самый большой совершенный квадрат, входящий в число 500, равен 100. Затем я могу разбить его на отрицательный квадратный корень из ста.
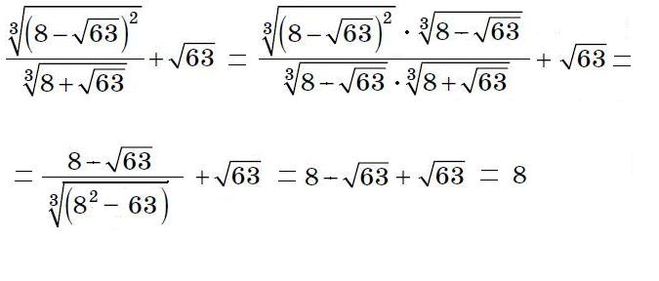Корень Таймс-сквер из 5, и тогда это будет отрицательная десятка. Раз root 5. Ладно. И вот как мы упрощаем квадратный корень. Хорошо, извлекая все множители совершенных квадратов. Хорошо, остановите видео сейчас и запишите все, что вам нужно. Это будет важным навыком для нас в будущих задачах. Хорошо, поехали. Давайте закончим урок. Итак, сегодня мы увидели много разного. Мы рассмотрели основную идею квадратного корня. Мы узнали, что квадратные корни любых положительных чисел всегда идут парами. И мы научились различать принцип квадратного корня. Это положительный, а отрицательный квадратный корень просто зависит от того, был ли отрицательный перед радикалом или нет. Затем мы увидели это важное свойство квадратных корней, свойство произведения, верно? Это позволило нам найти произведение двух квадратных корней, но также позволило нам упростить квадратные корни, вытащив их совершенные квадратные множители. Все в порядке. А пока, однако, я хотел бы поблагодарить вас за то, что вы присоединились ко мне для еще одного общего урока основной алгебры по математической инструкции E.