Красивый способ извлечения квадратного корня без калькулятора | Строю для себя
Добрый день, уважаемые гости и подписчики моего канала!
Помните, как учили нас в школе извлекать квадратные корни без калькулятора? Скорее, эта операция уже давно забылась, поскольку является сложной. Несмотря на то, что подобные вычисления очень редко применимы в быту, — есть метод, который вряд ли можно забыть, вычислив с его помощью хотя бы один раз любой квадратный корень.
Единственное, что потребуется вспомнить, это таблицу квадратов чисел, которая изучается в старших классах, как и таблица умножения в начальных:
Обычно, чтобы извлечь квадратный корень без электронных вычислительных устройств, мы вынуждены производить подбор числа, выполняя обратную операцию — путем возведения его в квадрат и так до тех пор, пока «не промахнемся»!
Итак, оригинальный способ:
Пусть нам нужно вычислить квадратный корень из 200.
Обратившись к таблице квадратов, можно понять, что число 200 находится между 196 (14^2) и 225 (15^2).
2 и находим значение Y, после чего еще точнее вычисляем искомый квадратный корень из 200:
Далее, оперируем с этим полученным числом, либо приводим к общему знаменателю и вычисляем.
Вычислив значение, получим 14.14 , что соответствует правильному значению, округленному до сотых:
Если требуется еще точнее, то операция повторяется, и каждый раз, производя одинаковые действия, мы увеличиваем точность вычисления.
Способ достойный и заслуживает внимания!
Надеюсь, статья Вам понравилась и стала полезной!
——
Читайте также:
WD-40: мифы и надуманные свойства. Где в быту нельзя использовать WэDэшку?
«Зачем мять виноград?» — ответила бабуля, — давай покажу, как сделать вино без лишних усилий
«Срочно продам дом. Собственник». Как за 20 минут понять, что перед вами дом на продажу? (8 признаков)
Таблица квадратных корней | Алгебра
В таблице приведены квадратные корни натуральных чисел от 1 до 100.
|
√1 = 1 √4 = 2 √9 = 3 √16 = 4 √25 = 5 √36 = 6 √49 = 7 √64 = 8 √81 = 9 √100 = 10 |
√121 = 11 √144 = 12 √169 = 13 √196 = 14 √225 = 15 √256 = 16 √289 = 17 √324 = 18 √361 = 19 √400 = 20 |
√441 = 21 √484 = 22 √529 = 23 √576 = 24 √625 = 25 √676 = 26 √729 = 27 √784 = 28 √841 = 29 √900 = 30 |
√961 = 31 √1089 = 33 √1156 = 34 √1225 = 35 √1296 = 36 √1369 = 37 √1444 = 38 √1521 = 39 √1600 = 40 |
|
√1681 = 41 √1764 = 42 √1849 = 43 √1936 = 44 √2025 = 45 √2116 = 46 √2209 = 47 √2304 = 48 √2401 = 49 √2500 = 50 |
√2601 = 51 √2704 = 52 √2809 = 53 √2916 = 54 √3025 = 55 √3136 = 56 √3249 = 57 √3364 = 58 √3481 = 59 √3600 = 60 |
√3721 = 61 √3844 = 62 √3969 = 63 √4096 = 64 √4225 = 65 √4356 = 66 √4489 = 67 √4624 = 68 √4761 = 69 √4900 = 70 |
√5041 = 71 √5184 = 72 √5329 = 73 √5476 = 74 √5625 = 75 √5776 = 76 √5929 = 77 √6084 = 78 √6241 = 79 √6400 = 80 |
|
√6561 = 81 √6724 = 82 √6889 = 83 √7056 = 84 √7225 = 85 √7396 = 86 √7569 = 87 √7744 = 88 √7921 = 89 √8100 = 90 |
√8281 = 91 √8464 = 92 √8649 = 93 √8836 = 94 √9025 = 95 √9216 = 96 √9409 = 97 √9604 = 98 √9801 = 99 √10000 = 100 |
||
Квадратный корень из 3;2;5 — Квадратный Корень
Квадратный корень из числа 3 — положительное действительное число, которое при умножении само на себя даёт число 3.
Его приблизительным значением с 69 цифрами после запятой является:
Округленное значение 1.732 является правильным с точностью до 0,01 %. Приблизительной правильной дробью является (1,7321 42857…).
Квадратный корень из 3 является иррациональным числом. Также известен как Феодоровская постоянная, названная в честь Феодора Киренского.
Может быть выражен в виде непрерывной дроби [1; 1, 2, 1, 2, 1, 2, …].
Геометрия
Квадратный корень из 3 равен длине между параллельными сторонами правильного шестиугольника со сторонами 1.Если равносторонний треугольник со сторонами длиной 1 делится на две равные половины, пересечением внутреннего угла для составления прямого угла с одной стороной, то получившийся прямоугольный треугольник имеет гипотенузу со стороной 1 и катеты длиной 1/2 и Поэтому тангенс 60° равен
Так же, это расстояние между параллельными сторонами правильного шестиугольника со сторонами 1.
является длиной диагонали куба со стороной 1.
Использование в других областях
Энергетика
При трехфазной системе токов модуль напряжения между двумя фазами (линейное напряжение) в больше модуля фазного напряжения
Квадратный корень из числа 2 — положительное вещественное число, которое при умножении само на себя даёт число 2. Обозначение: Приведём значение корня из 2 с 65 знаками после запятой:
- 1,414 213 562 373 095 048 801 688 724 209 698 078 569 671 875 376 948 073 176 679 737 99…
Геометрически корень из 2 можно представить как длину диагонали квадрата со стороной 1 (это следует из теоремы Пифагора). Вероятно, это было первое известное в истории математики иррациональное число (то есть число, которое нельзя точно представить в виде дроби).
Хорошим и часто используемым приближением к является дробь .
Несмотря на то, что числитель и знаменатель дроби лишь двузначные
целые, оно отличается от реального значения меньше, чем на 1/10000.
История
Вавилонская глиняная табличка с примечаниями.Вавилонская глиняная табличка (ок. 1800—1600 до н. э.) даёт приближённое значение в четырёх шестидесятеричных цифрах, что составляет 8 десятичных цифр:
Другое раннее приближение этого числа в древнеиндийском математическом тексте, Шульба-сутры (ок. 800—200 до н. э.) даётся следующим образом:
Пифагорейцы обнаружили, что диагональ квадрата несоизмерима с его стороной, или на современном языке, что квадратный корень из двух является иррациональным. Мало что известно с определённостью о времени и обстоятельствах этого выдающегося открытия, но традиционно его авторство приписывается Гиппасу из Метапонта.
Алгоритмы вычисления
Существует множество алгоритмов для вычисления значения квадратного
корня из двух. В результате алгоритма получается приблизительное
значение в виде обыкновенной или десятичной дроби.
Самый популярный алгоритм для этого, который используется во многих
компьютерах и калькуляторах, это вавилонский метод вычисления квадратных
корней.
Он состоит в следующем:
Чем больше повторений в алгоритме (то есть, чем больше «n»), тем лучше приближение квадратного корня из двух. Каждое повторение приблизительно удваивает количество правильных цифр. Приведём несколько первых приближений:
- 3/2 = 1.5
- 17/12 = 1.416…
- 577/408 = 1.414215…
- 665857/470832 = 1.4142135623746…
В 1997 году Ясумаса Канада вычислил значение √2 до 137,438,953,444 десятичных знаков после запятой. В феврале 2007 года рекорд был побит: Сигэру Кондо вычислил 200 миллиардов десятичных знаков после запятой в течение 13 дней и 14 часов, используя процессор 3.6 GHz с 16 ГБ ОЗУ. Среди математических констант только было вычислено более точно.
Свойства квадратного корня из двух
Половина √2 приблизительно равна 0.70710 67811 86548; эта величина даёт в геометрии и тригонометрии координаты единичного вектора, образующего угол 45° с координатными осями:
Одно из интересных свойств √2 состоит в следующем:
- .
Потому что
Потому чтоЭто является результатом свойства серебряного сечения.
Другое интересное свойство √2:
Квадратный корень из двух может быть выражен в мнимых единицах i используя только квадратные корни и арифметические операции:
- и
Квадратный корень из 2 является единственным числом, отличным от 1, чья бесконечная тетрация равна его квадрату.
Квадратный корень из двух может быть также использован для приближения :
С точки зрения высшей алгебры, является корнем многочлена и поэтому является целым алгебраическим числом. Множество чисел вида , где — рациональные числа, образует алгебраическое поле. Оно обозначается и является подполем поля вещественных чисел.
Доказательство иррациональности
Применим доказательство от противного: допустим, рационален, то есть представляется в виде несократимой дроби , где и — целые числа. Возведём предполагаемое равенство в квадрат:
- .
Отсюда следует, что чётно, значит, чётно и . Пусть , где целое. Тогда
Следовательно, чётно, значит, чётно и . Мы получили, что и чётны, что противоречит несократимости дроби . Значит, исходное предположение было неверным, и — иррациональное число.
Непрерывная дробь
Квадратный корень из двух может быть представлен в виде непрерывной дроби:
Подходящие дроби данной непрерывной дроби дают приближённые значения, быстро сходящиеся к точному квадратному корню из двух. Способ их вычисления прост: если обозначить предыдущую подходящую дробь , то последующая имеет вид . Скорость сходимости здесь меньше, чем у метода Ньютона, но вычисления гораздо проще. Выпишем несколько первых приближений:
Квадрат последней приведенной дроби равен (округлённо) 2,000000177.
Размер бумаги
Квадратный корень из двух является пропорцией формата бумаги ISO 216.
Соотношение сторон таково, что при разрезании листа пополам параллельно
его короткой стороне получатся два листа той же пропорции.
Квадратный корень из числа 5 — положительное действительное число, которое при умножении само на себя даёт число 5. Это иррациональное и алгебраическое число.[1]
Его приблизительное значение с 59 цифрами после запятой является:
Округлённое значение 2.236 является правильным с точностью до 0,01 %. Компьютерная вычисленная точность составляет не менее 1 000 000 знаков.[2]
Может быть выражено в виде непрерывной дроби [2; 4, 4, 4, 4, 4, 4, …], последовательно это дроби:
Вавилонский метод
Вычисление корня из 5, начиная с r0 = 2, где rn+1 = (rn + 5/rn) / 2:
Золотое сечение
√5/2 — диагональ половины квадрата, представляет собой геометрическое представление о золотом сечении.() алгебраически можно выразить так:
Числа Фибоначчи могут быть выражены через корень из 5 так:
Отношение √5 к φ и наоборот дают интересные зависимости непрерывных дробей с числами Фибоначчи и числами Люка:[4]
Алгебра
Кольцо содержит числа вида , где a и b целые числа и мнимое число .
Это кольцо является примером области целостности, не являющейся факториальным кольцом.
Число 6 представляется в данном кольце двумя способами:
Поле — абелево расширение рациональных чисел.
Теорема Кронекера — Вебера утверждает, что корень из 5 можно выразить линейной комбинацией корней из единицы:
Тождества Рамануджана
Корень из 5 появляется во множестве тождеств Рамануджана с непрерывными дробями.[5][6]
Например, случай непрерывных дробей Роджерса-Рамануджана:
делители, простота, двоичный вид, куб, квадрат
Укажите число, чтобы получить всю информацию о нем:| Четность: |
Число 200 является четным. |
| Сумма цифр: | 2 |
| Произведение цифр: | 0 |
| Количество цифр: | 3 |
| Все делители числа | 1 2 4 5 8 10 20 25 40 50 100 200 |
| Количество делителей | 12 |
| Сумма делителей | 465 |
| Простое число |
Составное число |
| Квадратный корень | 14,142135623731 |
| Кубический корень | 5,84803547642573 |
| Квадрат | 40000 |
| Куб | 8000000 |
| Обратное число | 0,005 |
| Предыдущее число: 199 | Следующее число: 201 |
Описание числа 200
Рациональное положительное число 200
является трехзначным.
Оно записывается 3 цифрами.
Сумма цифр, из которых состоит число 200, равна 2, а их произведение равно 0.
Число 200 является четным.
Всего число 200 имеет 12 делителей:
1,
2,
4,
5,
8,
10,
20,
25,
40,
50,
100,
200,
. Сумма делителей равна 465. Куб числа 200 равен 40000, а квадрат составляет 8000000.
Квадратный корень рассматриваемого числа равен 14,142135623731. Кубический корень равен 5,84803547642573.
Число, которое является обратным к числу 200, выглядит как 0,005.
© 2020 — ZeroInf
Как извлечь корень 13-й степени из 200-значного числа за считанные секунды: Из жизни: Lenta.ru
85 877 066 894 718 045 602 549 144 850 158 599 202 771 247 748 960 878 023 151 390 314 284 284 465 842 798 373 290 242 826 571 823 153 045 030 300 932 591 615 405 929 429 773 640 895 967 991 430 381 763 526 613 357 308 674 592 650 724 521 841 103 664 923 661 204 223.
А вам слабо?
Прочитали? Запомнили число? Нет? Странно. А сколько в нем было цифр, не обратили внимания? Тоже нет? Ну а хотя бы четное оно было или нечетное, скажете, не подсматривая? Опять нет? А простое илисоставное?
А сколько времени вам понадобилось для того, чтобы прочесть предыдущие два абзаца? Если вы просто пробегали глазами, то несколько секунд, если всерьез пытались ответить на вопросы — то больше, может быть, даже минута. Человеку-калькулятору Алексису Лемэру нужно примерно столько же времени, чтобы безошибочно извлечь из этого числа корень тринадцатой степени. В уме. Это включая ознакомление с числом и оглашение ответа. Количество цифр Лемэру, правда, подсчитывать не надо — он и так заранее знает, что их ровно двести.
Двести — потому что сто для Лемэра — это слишком просто, корень 13-й степени из стозначного числа он научился находить менее, чем за четыре секунды, и решил, что дальше совершенствоваться уже некуда.
Тринадцатый корень
Извлечение корня 13-й степени из очень больших чисел — традиционная форма соревнований по быстрым вычислениям в уме.
Найти корень сложнее, чем возвести в степень — это нельзя сделать напрямую, перемножив числа в столбик. Почему именно 13-й?На самом деле сложность вычисления определяется не столько степенью корня, сколько длиной числа: чем оно длиннее, тем труднее найти ответ. Но и степень корня имеет значение: от нее зависит, во-первых, количество потенциально подходящих, но ошибочных ответов, во-вторых, количество заранее известных закономерностей, которым будет подчиняться ответ.
Шаг алгоритма извлечения квадратного корня в столбик Изображение с сайта guidescope.com.
Lenta.ru
Задания подбираются так, чтобы ответ являлся целым числом. Например, для стозначного числа ответом теоретически могут являться 7992563 числа: от 41246264 до 49238826 (все прочие числа при возведении в тринадцатую степень дают не стозначное число). Для двухсотзначного таких возможностей во много раз больше: 393544396177593 (без малого четыреста триллионов). Поэтому у профессионалов извлечение корня из стозначного числа считается забавой для начинающих, а вот из двухсотзначного — уже нормальным заданием.
Количество потенциальных ответов зависит от степени корня сложным образом. «Официальный сайт корня 13-й степени» приводит такую шкалу сложности для некоторых степеней: 10>15>12>13=17=137=23=7>667>9=19>11=31>101>1001>4>3>2>1. Особенно трогательно смотрится единица в конце (корень первой степени — это, разумеется, само число).
13 — простое число, поэтому вычисление корня нельзя свести к пошаговому нахождению более простых корней. Например, корень девятой степени из 512 (для тех, кто не знает его наизусть, конечно) можно вычислить, найдя корень третьей степени — 8, а затем найдя корень третьей степени из него — 2. С тринадцатью такой номер не пройдет.
Никаким особым закономерностям «тринадцатый» корень тоже не подчиняется. Можно разве что отметить, что последняя цифра корня всегда совпадает с последней цифрой числа, из которого он извлекается. Это помогает, но не очень.
До недавнего времени книга рекордов Гиннесса фиксировала замечательные результаты по извлечению корня, однако сейчас прекратила, обосновав это тем, что сложность задачи зависит еще и от числа, случайно выданного в качестве задания: для каких-то чисел она проще, для каких-то — сложнее.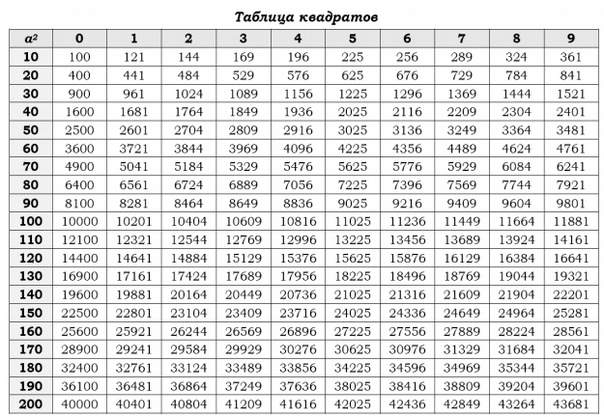
Пока непонятно, как можно было бы стандартизовать эту сложность, поэтому книга временно прекратила официальную регистрацию рекордов.
Кто такие рекордсмены и как они это делают
Был предложен один из таких тестов: понять, каким образом при пересечении куба плоскостью может получиться шестиугольник. Это не очень сложно, сказал Колмогоров (Андрей Николаевич — гениальный математик, великий российский ученый — прим «Ленты.ру»), но каждый претендующий на то, чтобы выбрать математику профессией, должен уметь представить себе соответствующий чертеж. А уж кто не умеет, тому разумно поискать другую профессию. Тут Колмогоров дал всем минуты три для самостоятельного решения, после чего нарисовал на доске куб и стал пересекать его плоскостью. Как он ни старался, шестиугольник у него не получился. Он слегка разозлился, стер куб и перешел к следующей теме.
В. А. Успенский, «Колмогоров, каким я его помню».
Последние замечательные результаты в области быстрых вычислений в уме принадлежат французу Алексису Лемэру и австрийцу немецкого происхождения Герту Миттрингу.
Интересно, что их деятельность в обычной жизни явно связана с их поразительными способностями: 27-летний Лемэр занимается искусственным интеллектом, а 41-летний Миттринг — проблемами одаренных детей.
Один из предыдущих держателей рекорда, ныне покойный голландец Виллем (Вим) Клейн, зарабатывал на жизнь непосредственно своим искусством. Сначала он выступал в составах различных трупп вместе с огнеглотателями, человеком-змеей и прочими циркачами, затем читал занимательные лекции, а затем с конца пятидесятых до середины семидесятых годов работал ни много ни мало в ЦЕРНе «живым компьютером» — «программистом и числовым аналитиком». Клейн по заказам физиков проводил сложные вычисления в уме, с распространением компьютеров начал помогать составлять программы.
Как находить корни (в уме, на бумаге, на компьютере) — учит специальный раздел математики, теория чисел. Клейна, Миттринга, Лемэра и им подобных можно назвать практиками чисел. Разумеется, практики чисел могут не только вычислять корни — они могут проводить и другие вычисления, запоминать огромные объемы информации (необязательно только числовой) и заниматься прочей гимнастикой чистого разума.
Как они это делают? Во-первых, знают и, что еще более важно, чувствуют (одно дело — знать механически, другое — глубоко понимать) специальные алгоритмы (при необходимости — придумывают сами). Знают на память таблицы квадратов, кубов, логарифмов (которые тоже могут пригодиться при вычислении корня). Во-вторых, ежедневно тренируют память, устный счет и прочие необходимые навыки. В-третьих, видимо, обладают некоторыми врожденными способностями, которые обычные люди приобрести не в состоянии.
Лемэр говорит, что воспринимает числа не просто как ряды цифр. Логично — за четыре секунды невозможно даже вдумчиво прочитать стозначное число цифру за цифрой. Он воспринимает число целостно и «видит» ответ — наверное, без совершения всех необходимых промежуточных операций. Числа ассоциируются у него со словами, со зрительными образами — короче говоря, мозг работает особым образом.
Подобным образом человек, выучивший в школе таблицу умножения, решивший без калькулятора несколько тысяч примеров и обладающий хоть какими-то способностями к устному счету, может изумлять тех, кто таблицы умножения не знает и без калькулятора считать не умеет.
Просто разница в умениях не столь поразительна, как в случае с практиками чисел типа Лемэра.
Интересно, что такие способности могут сочетаться и с обычным интеллектом, и с высоким, и с низким: известно множество примеров идиотов-гениев — людей с низкими или даже патологическими низкими умственными способностями, которые, однако, демонстрируют в чем-то одном, вроде извлечения корней из огромных чисел, поразительные способности.
Основная задача человеческого интеллекта — скорее не в этом, а в умении делать обобщения, проводить аналогии, видеть похожее в непохожем, необычное в обычном (и обычное в необычном), наконец, заниматься творчеством.
А корень тринадцатой степени из числа, приведенного в начале статьи, кстати, равен 2396232838850303. Пересчитывать будете?
| Сумма цифр | 2 |
| Произведение цифр | 0 |
| Произведение цифр (без учета ноля) | 2 |
| Все делители числа | 1, 2, 4, 5, 8, 10, 20, 25, 40, 50, 100, 200 |
| Наибольший делитель из ряда степеней двойки | 8 |
| Количество делителей | 12 |
| Сумма делителей | 465 |
| Простое число? | Нет |
| Полупростое число? | Нет |
| Обратное число | 0. 005 |
| Римская запись | CC |
| Индо-арабское написание | ٢٠٠ |
| Азбука морзе | ..— —— —— |
| Факторизация | 2 * 2 * 2 * 5 * 5 |
| Двоичный вид | 11001000 |
| Троичный вид | 21102 |
| Восьмеричный вид | 310 |
| Шестнадцатеричный вид (HEX) | C8 |
| Перевод из байтов | 200 байтов |
| Цвет | RGB(0, 0, 200) или #0000C8 |
| Наибольшая цифра в числе (возможное основание) | 2 (3, троичный вид) |
| Перевод троичной записи в десятичную | 18 |
| Число Фибоначчи? | Нет |
| Нумерологическое значение | 2 женственность, чувствительность, интуиция, близость, поддержка, доверие, сотрудничество, мир, дипломатичность |
| Синус числа | -0. 8732972972139946 |
| Косинус числа | 0.4871876750070059 |
| Тангенс числа | -1.7925274837903817 |
| Натуральный логарифм | 5.298317366548036 |
| Десятичный логарифм | 2.3010299956639813 |
| Квадратный корень | 14. 142135623730951 |
| Кубический корень | 5.848035476425732 |
| Квадрат числа | 40000 |
| Перевод из секунд | 3 минуты 20 секунд |
| Дата по UNIX-времени | Thu, 01 Jan 1970 00:03:20 GMT |
| MD5 | 3644a684f98ea8fe223c713b77189a77 |
| SHA1 | 9f9af029585ba014e07cd3910ca976cf56160616 |
| Base64 | MjAw |
| QR-код числа 200 |
Калькулятор настольный Casio JW-200SC-PK, премиум
Настольный калькулятор Casio JW-200SC-PK не только стильно выглядит, но и имеет необходимые для работы бухгалтера, товароведа, экономиста функции.
Casio JW-200SC-PK умеет конвертировать валюты, рассчитывать налоги и проценты, выводить итоговую сумму. У модели есть специальные кнопки для смены знаков и коррекции ввода. Можно выбрать режим десятичной точки.
Главным отличием этого настольного калькулятора, конечно, является яркий дизайн. Нежный розовый цвет привлекает внимание: Casio JW-200SC-PK не затеряется в сумке или среди бумаг! Корпус модели металлический, поэтому можно не бояться падений и ударов. Угол наклона дисплея можно регулировать.
РАСЧЕТ ПРОЦЕНТОВ: ЛОГИКА CASIO
Процент
Определите число, составляющее 5% от числа 200.
200 Х 5 % = 10
Увеличение
Увеличьте число 100 на 5%.
100 Х 5 % + = 105
Скидка
Уменьшите число 100 на 5%.
100 Х 5 % — = 96
Отношение
Сколько процентов составляет число 30 от числа 60. Найдите процентное соотношение.
30 ÷ 60 % = 50
Наценка
От какого числа нужно отнять 20%, чтобы получить число 100.
100 ÷ 20 % = 125
Например, Вы закупили товар и планируете в скором времени объявить на него 20% скидку, но не можете опустить цену ниже 100. Если Вы просто прибавите 20% к числу 100 (получится 120), а затем сделаете скидку 20%, то опуститесь ниже минимальной цены (получится 96). Если воспользоваться функцией «Наценка», то получится искомое число – 125.
Процентное изменение
На сколько процентов нужно увеличить число 10, чтобы получить число 12.
12 – 10 % = 20
Например, Вы хотите сделать размер торговой наценки такой, чтобы розничная цена была равна 12, закупая по оптовой цене 10. Эта функция поможет найти размер процента торговой наценки.
Квадратный корень из 200 — Как найти квадратный корень из 200?
Знаете ли вы, что древние греки представили идею, что квадратный корень из целых положительных чисел, которые не являются точными квадратами, являются иррациональными числами? Квадратный корень из 200 — одно из таких иррациональных чисел.
В этой главе мы вычислим квадратный корень из 200 методом долгого деления вместе с решенными примерами.
Давайте посмотрим, что такое квадратный корень из 200.
- Квадратный корень из 200 : √ 200 = 14.14213
- Квадрат 200: 200 2 = 40000
Что такое квадратный корень из 200?
Квадратный корень из 200 — это значение, которое получается после извлечения квадратного корня из 200.
Является ли квадратный корень из 200 рациональным или иррациональным?
Невозможно найти такое целое число, которое при возведении в квадрат дает 200. Его можно приблизительно записать в виде квадрата 14,142, которое является неповторяющимся и непрерывным десятичным числом.Это показывает, что это не идеальный квадрат, что также доказывает, что квадратный корень из 200 является иррациональным числом.
Как найти квадратный корень из 200?
Квадратный корень из 200 находится с помощью следующих шагов:
- Проверьте, является ли число точным квадратом. 200 не является точным квадратом, так как его нельзя разбить на произведение двух одинаковых чисел.
- Если число представляет собой полный квадрат, его можно записать в следующем формате: √ x 2 = x.
- Если число не является точным квадратом, квадратный корень определяется методом деления в столбик. Его также можно записать в упрощенной радикальной форме квадратного корня.
- В этом случае 200 не является точным квадратом, поэтому его квадратный корень находится с использованием метода деления в длину. Упрощенная радикальная форма квадратного корня из 200 приведена ниже.
200 не является точным квадратом, так как его нельзя разбить на произведение двух одинаковых чисел.Упрощенная радикальная форма квадратного корня из 200
200 может быть записано как произведение 2 и 100. Оно задается как:
√ 200 = √ 2 × 10 2
2 не является точным квадратом, поэтому остается в пределах корней.Следовательно, квадратный корень из 200 в радикальной форме упрощается как 10 √ 2.
Квадратный корень из 200 методом длинных делений
Значение квадратного корня из 200 методом длинного деления состоит из следующих шагов:
- Шаг 1 : Начиная справа, мы объединим цифры в пары, поместив над ними полосу.
- Шаг 2 : Найдите такое число, которое при умножении на само себя дает меньше или равно 200.Итак, число 14. Положив делитель 14, мы получим частное 14, а остаток 200 — 196 = 4.
- Шаг 3 : Удвойте делитель и введите его с пробелом справа. Угадайте наибольшую возможную цифру, чтобы заполнить пробел, который также станет новой цифрой в частном, так что, когда новый делитель умножается на новое частное, произведение меньше или равно деленному. Разделите и запишите остаток. Повторите этот процесс, чтобы получить нужные десятичные разряды.
Следовательно, √ 200 = 14,142
Изучите квадратные корни с помощью иллюстраций и интерактивных примеров
Сложные вопросы:
- Как Хейли найдет квадратный корень из 200, используя метод деления в длину до трех знаков после запятой?
- Как Билли выразит квадратный корень из 200 в его упрощенной радикальной форме?
Советы и хитрости:
- 200 не является точным квадратом, следовательно, его квадратный корень является иррациональным числом. Отсюда следует, что квадратный корень из любого числа «n», которое не является полным квадратом, всегда будет иррациональным числом.
Отсюда следует, что квадратный корень из любого числа «n», которое не является полным квадратом, всегда будет иррациональным числом.Что такое упрощенная версия квадратного корня 200?
Квадратный корень из 200 в простейшей форме равен 10 √ 2.
Чему равен 200 квадратный корень?
200 — квадратный корень из 40000.
200 — это идеальный квадрат?
Нет, 200 — не идеальный квадрат.
Можно ли упростить квадратный корень из 200?
Корень квадратный из 200 можно упростить как 10 √ 2.
Является квадратный корень из 200 рациональным или иррациональным?
Корень квадратный из 200 иррационально.
Является ли квадратный корень из 200 действительным числом?
Да, квадратный корень 200 является действительным числом.
Квадратный корень из 200 (√200)
Здесь мы определим, проанализируем, упростим и вычислим квадратный корень из 200.Начнем с определения, а затем ответим на несколько общих вопросы о квадратном корне из 200. Затем мы покажем вам различные способы вычисления квадратного корня из 200 с учетом и без компьютер или калькулятор. У нас есть чем поделиться, так что приступим!
Корень квадратный из 200 определения
Квадратный корень из 200 в математической форме записывается со знаком корня √200. Мы называем это квадратным корнем из 200 в радикальной форме. Квадратный корень из 200 — это величина (q), которая при умножении сама на себя будет равна 200.
√200 = q × q = q 2
Является ли 200 идеальным квадратом?
200 — это полный квадрат, если квадратный корень из 200 равен целому числу. Как мы подсчитали дальше на этой странице квадратный корень из 200 не является целым числом.
200 — не идеальный квадрат.
Корень квадратный из 200 является рациональным или иррациональным?
Квадратный корень из 200 — рациональное число, если 200 — полный квадрат. Это иррациональное число, если оно не является полным квадратом.Поскольку 200 не является точным квадратом, это иррациональное число. Это означает, что ответ на «корень квадратный из 200?» будет бесконечное число десятичных знаков. Десятичные дроби не прерываются, и вы не можете преобразовать их в точную дробь.
√200 — иррациональное число
Можно ли упростить квадратный корень из 200?
Вы можете упростить 200, если можете уменьшить 200 внутри корня. Мы называем этот процесс «упрощением сурда». Корень квадратный из 200 можно упростить.
√200 = 10√2
Как вычислить квадратный корень из 200 с помощью калькулятора
Самый простой и утомительный способ вычислить квадратный корень из 200 — использовать калькулятор! Просто введите 200, а затем √x, чтобы получить ответ. Мы сделали это с помощью нашего калькулятора и получили следующий ответ с 9 десятичными числами:
√200 ≈ 14,142135624
Как вычислить квадратный корень из 200 на компьютере
Если вы используете компьютер с Excel или Numbers, вы можете ввести SQRT (200) в ячейку, чтобы получить квадратный корень из 200.Ниже приведен результат с 13 знаками после запятой. Мы называем это квадратным корнем из 200 в десятичной форме.
SQRT (200) ≈ 14,1421356237310
Что такое квадратный корень из 200 с округлением?
Квадратный корень из 200, округленный до ближайшей десятой, означает, что вам нужна одна цифра после десятичной точки. Квадратный корень из 200, округленный до сотых, означает, что вы хотите две цифры после десятичной точки. Квадратный корень из 200, округленный до ближайшей тысячной, означает, что вам нужны три цифры после десятичной точки.
10-я: √200 ≈ 14,1
100-я: √200 ≈ 14,14
1000-я: √200 ≈ 14,142
Что такое квадратный корень из 200 в дроби?
Как мы уже говорили выше, поскольку квадратный корень из 200 является иррациональным числом, мы не можем превратить его в точную дробь. Однако мы можем преобразовать его в приблизительную дробь, используя квадратный корень из 200, округленный до сотых.
√200
≈ 14,14 / 1
≈ 1414/100
≈ 14 7/50
Что такое квадратный корень из 200, записанный с показателем степени?
Все квадратные корни можно преобразовать в число (основание) с дробной степенью.Квадратный корень из 200 — не исключение. Вот правило и ответ в «квадратный корень из 200, преобразованный в основание с показателем степени?»:
√b = b ½
√200 = 200 ½
Как найти квадратный корень из 200 методом деления в длину
Здесь мы покажем вам, как вычислить квадратный корень из 200, используя метод длинного деления с точностью до одного десятичного знака. Это потерянный искусство того, как они вычисляли квадратный корень из 200 вручную до того, как были изобретены современные технологии.
Шаг 1)
Задайте 200 в парах по две цифры справа налево и присоедините один набор 00, потому что нам нужен один десятичный разделитель:
Шаг 2)
Начиная с первого набора: наибольший полный квадрат, меньший или равный 2, равен 1, а квадратный корень из 1 равен 1. Таким образом, поместите 1 вверху и 1 внизу следующим образом:
Шаг 3)
Вычислите 2 минус 1 и укажите разницу ниже. Затем перейдите к следующему набору чисел.
Шаг 4)
Удвойте число, выделенное зеленым сверху: 1 × 2 = 2. Затем используйте 2 и нижнее число, чтобы решить эту задачу:
2? ×? ≤ 100
Знаки вопроса «пустые» и такие же «пустые». Методом проб и ошибок мы обнаружили, что наибольшее число «пробел» может быть равно 4. Замените вопросительные знаки в задаче на 4, чтобы получить:
24 × 4 = 96.
Теперь введите 4 вверху и 96 внизу:
Шаг 5)
Вычислите 100 минус 96 и укажите разницу ниже.Затем перейдите к следующему набору чисел.
Шаг 6)
Удвойте число, выделенное зеленым сверху: 14 × 2 = 28. Затем используйте 28 и нижнее число, чтобы решить эту задачу:
28? ×? ≤ 400
Знаки вопроса «пустые» и такие же «пустые». Методом проб и ошибок мы обнаружили, что наибольшее число, которое может быть пустым, равно 1. Теперь введите 1 сверху:
Это оно! Ответ сверху. Квадратный корень из 200 с точностью до одной десятичной дроби равен 14,1. Вы заметили, что последние два шага повторяют предыдущие два шага.Вы можете добавлять десятичные дроби с помощью просто добавляя новые подходы по 00 и повторяя последние два шага снова и снова.
Квадратный корень числа
Введите другое число в поле ниже, чтобы получить квадратный корень из числа и другую подробную информацию, как вы получили для 200 на этой странице.
Банкноты
Помните, что отрицательное умножение на отрицательное равно положительному. Таким образом, квадратный корень из 200 не только дает положительный ответ. что мы объяснили выше, но также и отрицательный аналог.
На этой странице мы часто упоминаем точные квадратные корни. Вы можете использовать список идеальных квадратов для справки.
Квадратный корень из 201
Вот следующее число в нашем списке, о котором у нас есть столь же подробная информация о квадратном корне.
Авторские права | Политика конфиденциальности | Заявление об ограничении ответственности | Контакт
WTAMU > Виртуальная математическая лаборатория> Алгебра среднего уровня Цели обучения
Введение
Учебник
Нужна дополнительная помощь по этим темам? |
Коэффициент квадратного корня из 200 (коэффициент √200)
Здесь мы покажем вам, как получить множители квадратного корня из 200 (множители √200). Мы определяем множители квадратного корня из 200 как любые целое число (целое число) или квадратный корень, который можно равномерно разделить на квадратный корень из 200. Кроме того, если вы разделите √200 на коэффициент √200, получится приводит к другому коэффициенту √200.
Сначала мы найдем все квадратные корни, которые можно равномерно разделить на квадратный корень из 200. Мы делаем это, находя все множители 200 и добавьте к ним радикал (√) следующим образом:
√1, √2, √4, √5, √8, √10, √20, √25, √40, √50, √100 , и √200
Затем мы найдем все целые числа, которые можно равномерно разделить на квадратный корень из 200. Мы делаем это, сначала идентифицируя полные квадратные корни из приведенного выше списка:
√1, √4, √25, √100
Затем мы извлекаем квадратный корень из совершенных квадратных корней, чтобы получить целые числа, которые мы можем равномерно разделить на квадратный корень из 200.
1, 2, 5, 10
Множители квадратного корня из 200 — это два приведенных выше списка вместе. Таким образом, множители квадратного корня из 200 (квадратные корни и целые числа) следующие:
1, 2, 5, 10, √1, √2, √4, √5, √8, √10, √20, √25, √40, √50, √100 и √200
Как мы уже говорили выше, квадратный корень из 200, деленный на любой из его множителей, приведет к другому его множителю. Следовательно, если разделить √200 на любой из
факторов, указанных выше, вы увидите, что это приводит к одному из других факторов.
Что вы можете сделать с этой информацией? Во-первых, вы можете получить квадратный корень из 200 в простейшей форме. Квадратный корень из 200 упрощенное — это наибольший целочисленный множитель, умноженный на квадратный корень из 200, деленный на наибольший полный квадратный корень. Таким образом, вот математика для получения квадратного корня из 200 в его простейшей радикальной форме:
√200
= 10 × (√200 ÷ √100)
= 10√2
Калькулятор коэффициента квадратного корня
Вам нужно множители другого квадратного корня? Хорошо, введите квадратный корень в поле ниже.
Коэффициенты квадратного корня 201
Надеемся, эта информация была полезной. Хотите узнать больше? Если это так, перейдите сюда, чтобы получить множители следующего квадратного корня в нашем списке.
Авторские права | Политика конфиденциальности | Заявление об ограничении ответственности | Контакт
Как упростить извлечение квадратного корня из 200 по математике класса 8 CBSE
Подсказка: Прежде всего, запишите утверждение, данное в приведенной выше задаче, в математическое выражение.Итак, квадратный корень из 200 математически записывается как $ \ sqrt {200} $, а квадратный корень из 32 математически записывается как $ \ sqrt {32} $. Теперь индивидуально упростите $ \ sqrt {200} $ и $ \ sqrt {32} $, а затем вычтите второе упрощение квадратного корня из первого. Полное пошаговое решение:
В приведенной выше задаче нас просят упростить вычитание квадратного корня 32 из квадратного корня 200. {2}} \ times 2} $
Теперь, вынимая квадрат чисел из квадратный корень получаем,
$ \ begin {align}
& \ sqrt {32} = \ left (2 \ times 2 \ right) \ sqrt {2} \\
& \ Rightarrow \ sqrt {32} = 4 \ sqrt {2} \\
\ end {align} $
Следовательно, мы упростили квадратный корень из 32 как $ 4 \ sqrt {2} $.
Вычитая квадратный корень 32 из квадратного корня 200, мы получаем
$ 10 \ sqrt {2} -4 \ sqrt {2} $
Принимая $ \ sqrt {2} $ как общее из приведенного выше выражения, мы получаем ,
$ \ begin {align}
& \ Rightarrow \ sqrt {2} \ left (10-4 \ right) \\
& = \ sqrt {2} \ left (6 \ right) \\
& = 6 \ sqrt {2} \\
\ end {align} $
Следовательно, решение указанной выше задачи равно $ 6 \ sqrt {2} $.
Примечание: Ошибка, которая могла быть возможна в приведенной выше проблеме, заключается в записи разложения на простые множители чисел 200 и 32.Здесь вы можете пропустить один или два множителя 200 и 32, поэтому, чтобы исправить эту проблему, лучше умножить все множители и затем продолжить.
Например, для коэффициент, который мы написали для 200, равен:
$ 200 = 2 \ умножить на 5 \ умножить на 5 \ раз 2 \ раз 2 \ раз 2 $
Чтобы проверить, пропустили ли мы какой-либо из факторов или нет, мы собираемся умножить все коэффициенты, записанные на правой стороне приведенного выше уравнения.
$ \ Rightarrow 200 = 200 $
Отрицательный квадратный корень 200?
кв. (-200).Найдите квадратный корень из -200 или любого другого действительного числа, положительного или отрицательного. Вот ответы на такие вопросы, как: Квадратный корень 200? или каков квадратный корень из -200? Используйте калькулятор квадратного корня ниже, чтобы найти квадратный корень любого действительного числа, положительного или отрицательного. См. Также на этой странице таблицу квадратного корня от 1 до 100.
Что такое квадратный корень? Определение квадратного корня
Квадратный корень из числа «x» — это такое число y, что y 2 = x, другими словами, число y, квадрат которого равен y.Например, 14 — это квадратный корень из 196, потому что 14 2 = 14 • 14 = 196, -14 — квадратный корень из 196, потому что (-14) 2 = (-14) • (-14) = 196. При написании математики люди часто используют sqrt (x) для обозначения квадратного корня из x. Узнайте больше о квадратном корне здесь: Квадратный корень — Википедия и здесь: Квадратный корень — Wolfram
квадратный символ?
Вот символ квадратного корня. Он обозначается √, известным как знак корня или основание.
Квадратный корень Таблица 1-100
Квадратные корни от 1 до 100 с округлением до тысячных.
| число | квадрат | квадрат корень | ||||
|---|---|---|---|---|---|---|
| 1 | 1 | 1.000 | ||||
| 2 | 4 | 1,414 | ||||
| 3 | 9 | 1,732 | ||||
| 4 | 90182,236 | |||||
| 6 | 36 | 2,449 | ||||
| 7 | 49 | 2.646 | ||||
| 8 | 64 | 2,828 | ||||
| 9 | 81 | 3,000 | ||||
| 10 | 100 | 3,162 | 144 | 3,464 | ||
| 13 | 169 | 3,606 | ||||
| 14 | 196 | 3,742 | ||||
| 15 | 225 3 | |||||
| 16 | 256 | 4.000 | ||||
| 17 | 289 | 4,123 | ||||
| 18 | 324 | 4,243 | 903 903 903 903 903 903 903 903 19 | 400 | 4,472 | |
| 21 | 441 | 4,583 | ||||
| 22 | 484 | 4,690 | ||||
| 23 | 529 903.796 | |||||
| 24 | 576 | 4,899 | ||||
| 25 | 625 | 5,000 |
| число | квадрат | квадрат корень | ||||||
|---|---|---|---|---|---|---|---|---|
| 26 | 676 | 5,099 | ||||||
| 27 | 729 | 5,196 | ||||||
| 28 | 784 | 5,292 | ||||||
| 8307 | ||||||||
| 85 | ||||||||
| 30 | 900 | 5,477 | ||||||
| 31 | 961 | 5,568 | ||||||
| 32 | 1,024 | 5,657 | 1,156 | 5,831 | ||||
| 35 | 1,225 | 5,916 | ||||||
| 36 | 1,296 | 6.000 | ||||||
| 37 | 1,369083 | |||||||
| 38 | 1,444 | 6,164 | ||||||
| 39 | 1,521 | 6,245 | ||||||
| 40 | 1,600 | 6,325 | ||||||
| 1,600 | 6,325 | |||||||
| 6,4 | 1,764 | 6,481 | ||||||
| 43 | 1,849 | 6,557 | ||||||
| 44 | 1936 | 6,633 | ||||||
| 45 | 2,0708 | |||||||
| 46 | 2,116 | 6,782 | ||||||
| 47 | 2,209 | 6,856 | ||||||
| 48 | 2,304 | 9018 9018 | 2,303 | 9018 9018 | 2,500 | 7,071 |
| число | квадрат | квадрат корень | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 51 | 2601 | 7.141 | |||||||
| 52 | 2,704 | 7,211 | |||||||
| 53 | 2,809 | 7,280 | |||||||
| 54 | 2,916 | 2,916 | 7.310 | 3,136 | 7,483 | ||||
| 57 | 3,249 | 7,550 | |||||||
| 58 | 3,364 | 7,616 | |||||||
| 59307 7,616 | |||||||||
| 59 30 | |||||||||
| 60 | 3,600 | 7,746 | |||||||
| 61 | 3,721 | 7,810 | |||||||
| 62 | 3,844 | 903 903 903 903 903 7,819 903 | 4,096 | 8,000 | |||||
| 65 | 4,225 | 8,062 | |||||||
| 66 | 4,356 | 8,124 | |||||||
| 67 | 90,303185|||||||||
| 68 | 4,624 | 8,246 | |||||||
| 69 | 4,761 | 8,307 | |||||||
| 70 | 4,900 | 8,310 | 4,900 | 8,310 | 4,900 | 8,310 | 5,184 | 8,485 | |
| 73 | 5,329 | 8,544 | |||||||
| 74 | 5,476 | 8,602 | |||||||
| 75307 5,6725 660 |
| число | квадрат | квадрат корень | ||||||
|---|---|---|---|---|---|---|---|---|
| 76 | 5,776 | 8.718 | ||||||
| 77 | 5,929 | 8,775 | ||||||
| 78 | 6,084 | 8,832 | 9018 9018 | 8,832 | 8,944 | |||
| 81 | 6,561 | 9.000 | ||||||
| 82 | 6,724 | 9,055 | ||||||
| 83 | 6,889 | 9,110 | ||||||
| 84 | 7,056 | 9,165 903 903 903 187 9,165 903 | 7,396 | 9,274 | ||||
| 87 | 7,569 | 9,327 | ||||||
| 88 | 7,744 | 9,381 | ||||||
| 89 7307,9318 9,381434 | ||||||||
| 90 | 8,100 | 9,487 | ||||||
| 91 | 8,281 | 9,539 | ||||||
| 92 | 8,464 | 9,519 9018 | 8,464 | 9,519 9018 | 8,836 | 9,695 | ||
| 95 | 9,025 | 9,747 | ||||||
| 96 | 9,216 | 9,798 | ||||||
| 97 | 9,409849||||||||
| 98 | 9,604 | 9,899 | ||||||
| 99 | 9,801 | 9,950 | ||||||
| 100 | 10,000 | |||||||
| Число | Sqrt | ||
|---|---|---|---|
| 196 | 14,000 | ||
| 197 | 14,036 | ||
| 198 | |||
| 198 | 14,019 | 107 | |
| 201 | 14,177 | ||
| 202 | 14,213 | ||
| 203 | 14,248 | ||
| 204 | 14,283 | Примеры квадратного корняУпрощение радикальных выражений — ChiliMathРадикальное выражение состоит из трех частей: — радикальный символ , подкоренный элемент и индекс В этом руководстве основное внимание уделяется упрощению радикальных выражений с индексом 2. {16}} |
Что делает их идеальными квадратами?
Обратите внимание, что квадратный корень из каждого числа выше дает целочисленный ответ.Думайте о них как о числах с идеальным поведением.
Кроме того, эти числа представляют собой точные квадраты, потому что все они могут быть выражены как экспоненциальные числа с четной степенью. Степень не обязательно должна быть постоянно равной «2». Пока степени являются четными числами, такими как 2, 4, 6, 8 и т. Д., Они считаются полными квадратами. С одной стороны, пара любых чисел — это идеальный квадрат!
Более того, приведенные выше выражения переменных также являются точными квадратами, потому что все переменные имеют четные показатели или степени.
Примеры упрощения радикальных выражений
Пример 1: Упростите радикальное выражение \ sqrt {16}.
Это легкий! Число 16, очевидно, является точным квадратом, потому что я могу найти целое число, которое при умножении само на себя дает целевое число. Должно быть 4, так как (4) (4) = 4 2 = 16. Таким образом, ответ
.Ниже приведен снимок экрана с ответом калькулятора, который подтверждает наш ответ.
Пример 2: Упростите радикальное выражение \ sqrt {60}.
Вы можете методом проб и ошибок найти число, когда возведение в квадрат дает 60. Перебирая некоторые квадраты натуральных чисел…
Ответом должно быть некоторое число n , которое находится между 7 и 8. Таким образом, мы ожидаем, что квадратный корень из 60 должен содержать десятичные значения. Чтобы упростить это радикальное число, попробуйте разложить его на множители так, чтобы один из множителей был точным квадратом. При беглом осмотре число 4 представляет собой идеальный квадрат, на который можно разделить 60.
Итак, наш ответ…
А для нашего калькулятора проверьте…
Какое правило я использовал, чтобы разбить их как произведение квадратных корней? Вот!
Запомните приведенное ниже правило, поскольку вы будете использовать его снова и снова.
ПРОДУКТ ПРАВИЛО КВАДРАТНЫХ КОРНЕЙ
- Это означает, что квадратный корень из произведения a и b равен произведению их индивидуальных квадратных корней.
Пример 3: Упростите радикальное выражение \ sqrt {72}.
Всегда ищите точный квадрат подкоренного выражения. После проб и ошибок я обнаружил, что любой из идеальных квадратов 4, 9 и 36 может разделить 72.Итак, что мне выбрать? На самом деле должен работать любой из трех коэффициентов точного квадрата. Однако лучший вариант — это самый большой из возможных, потому что это значительно сокращает количество шагов в решении.
Сравните, что произойдет, если я упросту радикальное выражение, используя каждый из трех возможных коэффициентов полного квадрата. Выбор самого большого делает решение очень коротким и точным.
Ничего страшного, если вы когда-нибудь начнете с меньших абсолютных квадратов. Вам просто нужно убедиться, что вы еще больше упростили оставшееся подкоренное выражение (содержимое внутри радикального символа).Повторяйте процесс до тех пор, пока подкоренное выражение не перестанет иметь точный квадратный множитель.
Похоже, калькулятор согласен с нашим ответом. Большой!
Пример 4: Упростите радикальное выражение \ sqrt {48}.
Другой способ решить эту проблему — выполнить разложение на простые множители для подкоренного выражения. Затем выразите простые числа как можно точнее. Парные простые числа выйдут из символа квадратного корня, а простое простое число останется внутри.
И он проверяет, когда решается в калькуляторе.
Пример 5: Упростите радикальное выражение \ sqrt {200}.
Давайте найдем квадратный множитель подкоренного выражения. Хотя 25 может делить 200, наибольшее число равно 100. Затем выразите подкоренное выражение как произведение квадратных корней и упростите. 4}}.
Подкоренное выражение содержит как числа, так и переменные. Разберемся с ними отдельно.
Для числового члена 12 его наибольший коэффициент полного квадрата равен 4. Теперь что касается переменных, мне нужно разбить их на пары, поскольку квадратный корень любой парной переменной — это просто сама переменная. Решение этой проблемы должно выглядеть примерно так…
Стандартный способ записи окончательного ответа — поместить все термины (как числа, так и переменные), которые находятся за пределами радикального символа , перед терминов, оставшихся внутри.7}}.
Для этой проблемы мы собираемся решить ее двумя способами. Цель состоит в том, чтобы показать, что есть более простой способ приблизиться к этому, особенно когда показатели переменных становятся больше.
Метод спаривания : Это обычный способ, при котором мы группируем переменные в две, а затем применяем операцию извлечения квадратного корня, чтобы вывести переменную за пределы радикального символа. Вы увидите, что для больших мощностей этот метод может быть утомительным и трудоемким.
«Разделение четных степеней» Метод : Вы не можете найти это имя ни в одном учебнике алгебры, потому что я его придумал.Однако ключевая концепция есть. Основной подход состоит в том, чтобы выразить каждую переменную как произведение членов с четными и нечетными показателями. Если термин уже имеет четную силу, вам нечего делать. В противном случае вам нужно выразить как некоторую четную степень плюс 1 .
Помните, что получение квадратного корня из «чего-то» эквивалентно возведению этого «чего-то» в дробную степень {1 \ более 2}.
Проще говоря, разделите показатель этого «чего-то» на 2.
- По этой причине мы хотим выразить их с помощью четных степеней, поскольку любое четное число делится на 2 .{13}}}.
Практика с рабочими листами
Возможно, вас заинтересует:
Решение радикальных уравнений
.
Сложение и вычитание радикальных выражений
Умножение радикальных выражений
Рационализация знаменателя