| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | cos(pi/4) | ||
| 9 | Найти точное значение | sin(45 град. |
|
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) |
|
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) |
|
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) |
|
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) |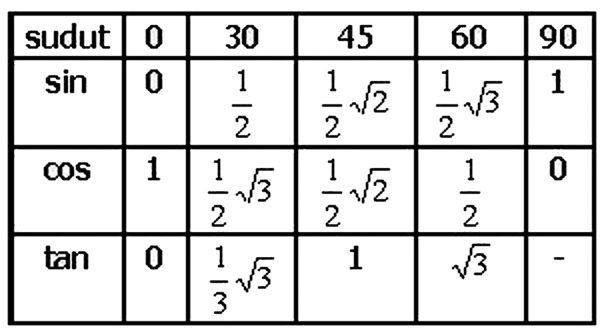
|
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) |
|
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | ||
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) |
|
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град.
) |
|
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | ||
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град. ) |
|
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) |
|
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | ||
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | sin(45 град. ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) |
|
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) |
|
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) |
|
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) |
|
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) |
|
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) |
|
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) |
|
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град. ) |
|
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
функций — Касательные и корни уравнений.
Во-первых, вы сделали что-то великое: вы рассмотрели задачу, которой, вероятно, не было в вашем учебнике, тщательно проанализировали ее, сделали ошибки и исправили их.
Это ужасно!
Хорошо, продолжаю отвечать на ваши вопросы (и встречно отвечать на некоторые).
Во-первых, понятие «тангенс», которое вы используете, обычно не называется (теми, кто занимается вычислениями) «тангенсом». Ваше представление о том, что прямая $L$ касается кривой $C$, состоит в том, что $L$ и $C$ имеют общую точку $P$ и в этой точке $P$ имеют одинаковый наклон, а вблизи $P$ кривая $C$ лежит по одну сторону от $L$. Это почти правильно… за исключением того, что пункт «одна сторона» не включен в определение. Поэтому мы часто говорим, что если $f$ — функция, график которой представляет собой кривую $C$, а $L$ и $C$ пересекаются в точке $P$ и имеют один и тот же наклон в точке $P$, то «$L$ касательная к $f$ в точке $P$», независимо от того, пересекаются ли там $L$ и $C$.
Тем не менее, для многочленов это интересная и полезная концепция.
Позвольте мне перейти к разговору о функциях.
Если $f(x)$ — полиномиальная функция и $g(x) = mx + b$ — прямая (т.
е. $m$ отлична от нуля) и $f(a) = g(a)$ для какое-то $a$, то мы говорим, что $f$ и $g$ пересекаются, или «соглашаемся на нулевой порядок»; если $f(a) = g(a) = 0$, мы говорим, что они имеют общий корень. Если наклоны $f$ и $g$ одинаковы, то мы говорим, что они «согласуются с первым порядком». В этом случае уравнение $f(x) — g(x) = 0$ имеет (по крайней мере) двойной корень в $a$, и действительно, для полиномов это можно назвать «определением» производной: линейная функция $g$, обладающая тем свойством, что $f(x) — g(x)$ имеет двойной корень в точке $a$ [или наклон этой прямой], может быть названа производной $f$ в точке $a$ .
Корень может иметь более высокий порядок; это может быть тройной корень или корень четвертой степени и т. д. И, как вы заметили, для повторяющихся корней с нечетным числом (когда $f$ является многочленом) это указывает на пересечение в точке $x = a$, тогда как для четных количество повторяющихся корней, это указывает на то, что вблизи $x = a$ график $f$ лежит по одну сторону от своей касательной.
2} & x \ne 0 \end{case}
$$
Его касательная в точке $x = 0$ является осью $x$ (что требует некоторой работы, чтобы показать!), но эта касательная бесконечно часто пересекает график $f$ в любой окрестности $x = 0$. Ой!
Существует также стандартный пример (который я не буду приводить, потому что он, вероятно, использует вещи, с которыми вы еще не сталкивались) непостоянной функции $f$ со свойством $f(0) = 0$ и $ f'(0) = 0$, поэтому его касательная в точке $0$ является осью $x$. Но при $x = 0$ график $f$ пересекает свою касательную «в бесконечном порядке», т. е. если максимально хорошо аппроксимировать $f$ вблизи нуля полиномом степени $n$, то этот полином будет иметь $ n$ укореняется в $0$… и это верно для любого $n$. Мы говорим, что функция $f$ «чрезвычайно плоская» при $x = 0$. Такие функции на самом деле важны для «построения разделов единицы» (что бы это ни значило!) позже, т. е. они не просто дурацкие примеры, но на самом деле представляют собой важные явления в математике.
Мой ответ теперь почти такой же длинный, как и ваш вопрос, и я надеюсь, что ответил на большую часть того, что вы спросили.
Моя любимая книга, помогающая людям понять подобные вопросы, — « Исчисление » Майкла Спивака. Возможно, лучше было бы назвать ее чем-то вроде «Введение в анализ», но как бы вы ее ни называли, это сокровище.
Метод Ньютона
Метод Ньютона
Метод Ньютона
Попробуйте найти корень
y
= e x — 4x
Как ни старайся, не существует алгебраического метода, позволяющего найти этот корень.
Аппроксимируем решение следующим образом:
График показывает, что решение находится между 0 и 2.
Наше первоначальное предположение:
x
= 1
Теперь проведите касательную через (1,f(1)). Следующий
посмотрите, где касательная пересекает ось x.
Касательная линия является близкой
аппроксимация кривой для близких значений, следовательно, точка пересечения
касательная близка к точке пересечения кривой с абсциссой. Касательная линия
имеет уравнение
y — f(1) = f ‘(1)(x — 1)
Пересечение x происходит, когда y = 0, следовательно,
-f(1)
= f ‘(1)(x — 1)
решение для x,
ф(1)
Икс
= 1 —
f ‘(1)
Этот x не будет истинным корнем, но будет будет лучшим предположением, чем x = 1. Мы будем использовать это (назовите это x 2 ) как наш второе предположение. Следующая игра в ту же игру:
е(х 2 )
х 3
= x 2 —
ф'(х 2 )
На графике ниже показана эта конструкция. Синяя линия первая касательная линия, а фиолетовая линия — вторая касательная линия.
Продолжайте этот процесс, чтобы получить
|
е (х n ) |
Для нашего примера это выражение
.
Используйте калькулятор или компьютер, чтобы найти значения.
х 1 = 1, х 2 = 0,
x 3 = 0,3333, x 4 = 0,3572,
х 5 = 0,3574, х 6 = 0,3574
Мы видим, что 0,3574 — это корень с точностью до 4
десятичные разряды.
Упражнение
Оценка
с использованием метода Ньютона.
Подсказка: найдите корень x 2 — 5.
Когда метод Ньютона не работает
-
Если наша первая догадка (или любые последующие догадки) точка, в которой проходит горизонтальная касательная, то эта линия никогда не будет ударить по оси x, и метод Ньютона не сможет найти корень. Если есть горизонтальная касательная, то производная равна нулю, и мы не может делиться на f ‘(x), так как формула требует.
-
Если наши догадки колеблются туда-сюда, то метод Ньютона не будет работать.
-
Если есть два корня, у нас должно быть первое предположение вблизи интересующего нас корня, иначе метод Ньютона найдет неправильный корень.
-
Если корней нет, то метод Ньютона не работает Найди это. (Это может быть неприятно, когда вы используете свой калькулятор найти корень.
Пример
Объясните, почему метод Ньютона не может найти корень
f(x) = x 1/3
с начальным предположением x = 1.
Раствор
У нас есть
f ‘(x) = 1/3 x -2/3
так что
х п 1/3
х н+1 = х н —
= x n — 3x n = -2x n
1/3 х -2/3
Это дает нам
х 1 = 1, х 2 = -2(1) = -2
х 3 = -2(-2) = 4, х 4 = -2(4) = -8
Эти числа растут (в абсолютном значении) вместо
сходящийся.