Математическое уравнение третьей степени
- Главная
- Калькуляторы
- Математика
- Алгебра
- Кубическое уравнение
Кубическим уравнением является полиномиальное уравнение третьей степени. Общий вид ax3+bx2+cx+d=0, где a ≠ 0.
Кубическое уравнение имеет вид ax3 + bx2 + сх + d = 0. В уравнение должно присутствовать х3, в противном случае уравнение не будет кубическим, но некоторые или все из В, С и D могут быть равны нулю. Бесплатный онлайн калькулятор для расчета уравнения третьей степени, используется для нахождения корней кубического уравнения.
3 + bx2 + cx + d = 0
| x³ + | x² + | x+ | d = 0 |
| X1: | + | i | ||
| X2: | + | i | ||
| X3: | + | i |
Формула кубического уравнения:
- q = (3c- b2)/9
- r = -27d + b(9c-2b2)
- s = r + √(discriminant)
- t = r — √(discriminant)
- term1 = √(3.
 0)*((-t + s)/2)
0)*((-t + s)/2) - r13= 2 * √(q)
- x1=(- term1 + r13*cos(q3/3) )
- x2=(- term1 + r13*cos(q3+(2*∏)/3) )
- x3=(- term1 + r13*cos(q3+(4*∏)/3) )
Кубическое уравнение:
ax3 + bx2 + cx + d = 0,
где,
- a = коэффициент x 3
- b = коэффициент x2
- c = коэффициент x
- d = constant.
Формула:
x1 = -term1 + r13 * cos(q3 / 3)
x2 = -term1 + r13 * cos(q3 + (2 * ∏) / 3)
x3 = -term1 + r13 * cos(q3 + (4 * ∏) / 3)
term1 и r13 формула:
q = (3c — b2) / 9
r = (-27d + b(9c — 2b2)) / 54
discriminant(Δ) = q3 + r2
r13 = 2 * √ (q)
Если discriminant(Δ) > 0 term1 = (b/3. 0)
0)
еще
- s = r + √ discriminant(Δ)
- t = r — √ discriminant(Δ)
- term1 = √ (3.0) * ((-t + s) / 2)
Пример:
Вычислить корни (x1, x2, x3) уравнения третьей степени, x 3 — 4x2 — 9x + 36 = 0
Шаг 1:
Из приведенного выше уравнения, значение a = 1, b = — 4, c = — 9 и d = 36.
Шаг 2:
Найдем значения q и r
q = ((3*-9) — (-4)2) / 9 = -4.77778
r = (-27*36+(-4)*(9*(-9)-2*(-4)2))/54 = -9.62963
Шаг 3:
Найдем значение дискриминанта, обозначается как знак дельта (Δ)
discriminant(Δ)= q3 + r2
discriminant(Δ) = (-4.77778)3 + (-9.62963)2 = -16.3333
Значение дискриминанта меньше 0
Шаг 4:
Найдем term1 и r13
Если Δ< 0, term1 = (b/3.
term1 = -1.33333
r13 = 2 * √(q)
где, q = -q = 4.77778
r13 = 2 * √ 4.77778 = 4.371626
Шаг 5:
Подставляем значения term1 и r13 в формулу кубического уравнения
x1 = -term1 + r13 * cos(q3 / 3)
x1 = 1.33333 + 4.371626 x cos(4.777783 / 3) = 4
x2 = -term1 + r13 * cos(q3 + (2 * ∏) / 3)
x2 = 1.33333 + 4.371626 x cos(4.777783 + (2 * ∏)/ 3) = -3
x3 = -term1 + r13 * cos(q3 + (4 * ∏) / 3)
x3 = 1.33333 + 4.371626 x cos(4.777783 + (4 * ∏)/ 3) = -3
Шаг 6:
Мы получили корни уравнения, x1 = 4, x2 = -3 и x3 = -3.

Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!
Алгебра Калькулятор Расчёт Уравнение 3405
Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!
Массаж головы и уравнения третьей степени
Многие люди знакомы с приятным ощущением в мышцах после спортивных нагрузок — организм радуется правильному физическому утомлению. Но сегодня речь пойдёт об аналогичном воздействии на мозг: если подумать о чём-то сложном и интересном, то можно получить массу удовольствия.
Тонкость здесь в том, что задача должна быть именно увлекательной и сопротивляющейся, а не тупой и рутинной. Например, недавно меня спросили: А почему в школьной программе нет изучения уравнений третьей степени? Они же почти такие же простые, как и квадратные уравнения, просто на один корень больше.
Что здесь можно ответить? Ответ будет ниже, а пока я покажу упражнение, которое полезно выполнить любому, кто задаётся таким же вопросом. А после упражнения будет пара важных мыслей.
А после упражнения будет пара важных мыслей.
Сконструируйте кубическое уравнение, у которого корнями являются числа 1, 2 и 3. Сделать это легко: (x-1)(x-2)(x-3)=0. Теперь давайте раскроем скобки, чтобы получить канонический вид уравнения третьей степени
Получаем: x3 — 6x2 + 11x — 6 = 0.
Другими словами, коэффициенты кубического уравнения следующие: a=1, b=-6, c=11, d=-6. Всё просто, как и в статье о квадратных уравнениях 🙂
Продолжаем движение. Как найти корни кубического уравнения, зная его коэффициенты? Можно вычислить дискриминант:
Посчитали? (сколько минут это заняло?) Это число позволяет нам выяснить, сколько же корней у этого простого уравнения (оказывается, у него три действительных корня). Заметьте, что нам очень повезло — все коэффициенты являются целыми числами, поэтому считать дискриминант было очень приятно.
Что делать дальше? Давайте искать корни. Формула очень простая:
Любому нормальному человеку не хочется подставлять в эти формулы даже целые числа, потому что придётся исписать немало бумаги. А представьте, что было бы, если бы у нас коэффициенты были иррациональными числами!
А представьте, что было бы, если бы у нас коэффициенты были иррациональными числами!
Метод решения «в лоб» не вдохновляет (заметьте, что по крайней мере с простыми квадратными уравнениями таких проблем нет). Давайте тогда попробуем применить метод Кардано:
Можно сделать замену , чтобы избавиться от коэффициента b (перед квадратом). Предлагаю проделать это. Впрочем, это не обязательно — можно сразу пройти по ссылке на страницу, где автоматически формируется решение этим методом: посмотреть решение по формуле Кардано (нужные коэффициенты я уже вбил).
Нравится такое решение? И это для простейшего уравнения, у которого корни 1, 2 и 3. Заметьте, что оно ещё достаточно короткое для такой задачи. Проблема в том, что сколько-нибудь сложное кубическое уравнение «решать человеком» очень неэффективно. Если квадратные уравнения проявляются в очень большом количестве задачек, то кубические нужны не так уж часто. А учитывая, как тяжело даётся их решение на бумаге (и очень высока вероятность арифметической ошибки, потому что проводится масса бессмысленных действий), крайне тяжело обосновать их плотное использование в школе.
Кстати, обычно если составитель задачи никак не может избавиться от необходимости решения кубического уравнения, то он так корректирует условие, чтобы корень был простой: 1, -1 или какой-то такой. Тогда школьник может легко поделить полином третьей степени на (x-x0), где x0 — угаданный корень, чтобы получить нулевой остаток и квадратное уравнение, которое уже совсем легко решить.
Поэтому, полагаю, Вы согласитесь со следующим моим ответом на подобные вопросы:
1. Есть не так много задач, в рамках которых возникают кубические уравнения;
2. Даже очень простое уравнение третьей степени (у которого не получается угадать один корень) требует много времени и сил, отвлекая ученика от настоящей работы мозга;
3. Поэтому нецелесообразно тратить время детей на рутинную работу, а лучше направить их силы на освоение сложных и интересных математических проблем. Знать об уравнениях третьей степени очень даже полезно, но вот регулярно их решать руками — явный перебор.
А сейчас будет важная мысль. Вот я показал вам эти формулы, но разве это было очень познавательно? Скорее нет, чем да. Но легко понять, что проблема не в кубических уравнениях, а в том, как я их только что подал. Недавно мы говорили о пяти уровнях обучения. Только что был пятый — я скучно дал формулы, не сообщив ничего важного об интереснейшей теме — о кубических уравнениях. Но ведь Кардано, который придумал эту остроумную замену (или кто-то до него) получил массу удовольствия. И это был отличный массаж мозга! Тысячи школьников и студентов, которым их учитель аккуратно подсказал, чтобы они почти сами сообразили, как можно справиться с достаточно сложным классом уравнений — они тоже получили массу удовольствия и пользы для развития своего мозга. Вроде бы те же уравнения, а какая большая разница!
Вот я показал вам эти формулы, но разве это было очень познавательно? Скорее нет, чем да. Но легко понять, что проблема не в кубических уравнениях, а в том, как я их только что подал. Недавно мы говорили о пяти уровнях обучения. Только что был пятый — я скучно дал формулы, не сообщив ничего важного об интереснейшей теме — о кубических уравнениях. Но ведь Кардано, который придумал эту остроумную замену (или кто-то до него) получил массу удовольствия. И это был отличный массаж мозга! Тысячи школьников и студентов, которым их учитель аккуратно подсказал, чтобы они почти сами сообразили, как можно справиться с достаточно сложным классом уравнений — они тоже получили массу удовольствия и пользы для развития своего мозга. Вроде бы те же уравнения, а какая большая разница!
Поэтому я не призываю отказываться от уравнений третьей степени, но прошу не вдалбливать формулы в бедные детские головы. Пользы от знания подобных формул в тысячи раз меньше, чем от их (почти) самостоятельного вывода. Поэтому гораздо лучше осилить вывод более простых формул, чем выучить эти.
Поэтому гораздо лучше осилить вывод более простых формул, чем выучить эти.
А как же массировать ребёнку мозг? Всё зависит от его возраста.
Меня, например, примерно в возрасте шестиклассника очень впечатлил тот факт, что бывают числа, не представимые в виде отношения двух целых чисел. Само число «корень из двух» я себе представлял, но осознать, что оно не является рациональным — это было круто!
Потом ещё помню, как удивительно было осознать, что натуральных чисел ровно столько же, сколько рациональных (тогда я не знал о мощностях множеств, поэтому позволяю себе такие нестрогие формулировки). Как же так? Вроде бы между двумя подряд идущими натуральными числами есть бесконечно много рациональных… Но это, оказывается, не аргумент. Понять такое — это для школьника очень круто!
Ещё интереснее было потом понять, что вещественных чисел не просто бесконечно много, но гораздо больше чем натуральных. Это уже ни в какие ворота не лезло: я вроде бы понимал, что и натуральных, и вещественных чисел бесконечно много. Но как одних может быть больше, чем других? Или вот ещё вопросик: а бывает ли множество, в котором элементов больше, чем во множестве натуральных чисел, но меньше, чем во множестве вещественных?
Но как одних может быть больше, чем других? Или вот ещё вопросик: а бывает ли множество, в котором элементов больше, чем во множестве натуральных чисел, но меньше, чем во множестве вещественных?
Есть масса интересных свойств, которые может (почти) самостоятельно понять человек с любым уровнем подготовки, если у него есть желание (другими словами, если он уже ощущал кайф от процесса познания).
Хорошего вам дня! И удовольствия от размышлений!
Решение уравнений третей и четвёртой степени. Уравнения разных степеней Решение уравнений третьей и четвертой степени
- В начале 16в. многие математики бились над решением алгебраических уравнений 3 – ей степени.
- Решения линейных и квадратных уравнений были известны еще в античности, а кубические уравнения долго не поддавались.
Исторические факты.
Большой вклад в решение уравнений 3 и 4 степеней внесли итальянские математики 16 века:
- Спицион Даль Ферро (1465-1526) и его ученик Фиори
Н. Тарталья (1499-1557)
Тарталья (1499-1557)
- Д. Кардано (1501-1576) его ученик – Л. Феррари
Р. Бомбелли (1530-1572)
Итальянские математики 16 в. сделали крупнейшее математическое открытие. Они нашли формулы для решения уравнений третьей и четвертой степеней.
Рассмотрим произвольное кубическое уравнение:
И покажем, что с помощью подстановки его можно преобразить к виду:
Положим т.е. Тогда данное уравнение
примет вид
В 16 в. было распространено соревнование между учеными, проводившееся в форме диспута. Математики предлагали друг другу определенное число задач, которые нужно было решить к началу поединка. Выигрывал тот, кто решил большее число задач.
Антонио Фиоре постоянно участвовал в турнирах и всегда выигрывал, так как владел формулой для решения кубических уравнений. Победитель получал денежное вознаграждение, ему предлагали почетные, высоко оплачиваемые должности.
Тарталья преподавал математику в Вероне, Венеции, Брешии.
И приложил все силы для его решения. Отыскав формулу, Тарталья решил все задачи, предложенные ему Фиоре, и выиграл турнир. Через день после поединка он нашел формулу для решения уравнения
Это было величайшее открытие. После того как в Древнем Вавилоне была найдена формула для решения квадратных равнений, выдающиеся математики в течение двух тысячелетий безуспешно пытались найти формулу для решений кубических уравнений. Метод решения Тарталья держал втайне.
Рассмотрим уравнение
Тарталья использовал подстановку:
Из уравнения он получил:
Для u и v получена система
Значит, они являются корнями квадратного уравнения
Следовательно, для отыскания х имеем формулу
- Ее называют сейчас формулой Кардано, так как она впервые была опубликована в 1545 г. в книге Кардано «Великое искусство, или Об алгебраических правилах».
- Джироламо Кардано (1501-1576) окончил университет в Падуе.
 Его главным занятием была медицина. Кроме того, он занимался философией, математикой, астрологией, составлял гороскопы Петрарки, Лютера, Христа, английского короля Эдуарда 6. Папа римский пользовался услугами Кардано — астролога и покровительствовал ему. Кардано умер в Риме. Существует легенда, что он покончил жизнь самоубийством в тот день, который предсказал, составляя собственный гороскоп, как день своей смерти.
Его главным занятием была медицина. Кроме того, он занимался философией, математикой, астрологией, составлял гороскопы Петрарки, Лютера, Христа, английского короля Эдуарда 6. Папа римский пользовался услугами Кардано — астролога и покровительствовал ему. Кардано умер в Риме. Существует легенда, что он покончил жизнь самоубийством в тот день, который предсказал, составляя собственный гороскоп, как день своей смерти.
Изложим метод Феррари. Запишем общее уравнение четвертой степени:
С помощью подстановки его можно привести к виду
Используя метод дополнения до полного квадрата, запишем:
Феррари ввел параметр и получил:
Учитывая, получим
В левой части уравнения стоит полный квадрат, а в правой — квадратный трехчлен относительно х. Чтобы правая часть была полным квадратом, необходимо и достаточно, чтобы дискриминант квадратного трехчлена равнялся нулю.
- Кубические уравнения Феррари решил по формуле Кардано.
- Пусть — корень уравнения.
 Тогда уравнение запишется в виде
Тогда уравнение запишется в виде - Отсюда получаем два квадратных уравнения:
- Они дают четыре корня исходного уравнения.
Приведем пример. Рассмотрим уравнение
Легко проверить, что -корень этого уравнения.
По формуле находим:
Как понять выражение На этот вопрос первым ответил инженер Рафаэль Бомбелли (ок. 1526-1573), работавший в Болонье В 1572 г. он издал книгу «Алгебра», в которую ввел в математику число i , такое, что
Бомбелли сформулировал правила операций с числом
Согласно теории Бомбелли, выражение можно записать так:
А корень уравнения, имеющий вид, можно записать так:
Проблема
решения уравнений третьей и четвертой
степени в радикалах не вызывалась особой
практической необходимостью. Ее появление
косвенным образом свидетельствовало
о постепенном переходе математики к
более высокому уровню ее развития, когда
математическая наука развивается не
только под влиянием запросов практики,
но и в силу своей внутренней логики. После решения квадратных уравнений
естественно было перейти к решению
кубических уравнений.
После решения квадратных уравнений
естественно было перейти к решению
кубических уравнений.
Уравнения третьей и четвертой степени были решены в Италии в XVI в.
Итальянские математики рассматривали три вида кубических уравнений:
Рассмотрение трех видов кубических уравнений вместо одного связано с тем, что, хотя математикиXVI в. были знакомы с отрицательными числами, но они еще долго не считались настоящими числами, и ученые стремились записывать уравнения только с положительными коэффициентами.
Исторически сложилось так, что сначала алгебраисты занялись уравнением первого типа
Первоначально
его решил профессор Болонского
университета Сципион дель Ферро, но
полученное решение не опубликовал, а
сообщил его своему ученику Фиоре. С
помощью секрета решения этого уравнения
Фиоре победил на нескольких математических
турнирах. Тогда такие турниры были
распространены в Италии. Заключались
они в том, что два противника в присутствии
нотариуса обменивались заранее
обусловленным числом задач и договаривались
о сроке для их решения. Победитель
получал известность и нередко выгодную
должность. В 1535 г. Фиоре вызвал на такой
поединок любого, кто хочет с ним сразиться.
Вызов принял Тарталья.
Победитель
получал известность и нередко выгодную
должность. В 1535 г. Фиоре вызвал на такой
поединок любого, кто хочет с ним сразиться.
Вызов принял Тарталья.
Никколо Тарталья (1500-1557) рано остался сиротой и вырос в бедности, не получив никакого образования. Тем не менее он был хорошо знаком с математикой того времени и зарабатывал себе на жизнь частными уроками математики. Незадолго до поединка с Фиоре он сумел самостоятельно решить уравнение (1). Поэтому когда противники встретились, Тарталья смог за несколько часов решить задачи Фиоре; все они оказались на уравнении (1). Что касается Фиоре, то он и за много дней не решил ни одной из 30 разнообразных задач Тартальи. Победителем турнира был признан Тарталья. Известие о его победе распространилось по всей Италии. Он стал заведовать кафедрой математики в университете города Вероны.
Метод Тартальи заключался в следующем. Он полагал в уравнении (1) , гдеu и v – новые неизвестные. Получим:
Положим
в последнем уравнении
. Образуется система уравнений
Образуется система уравнений
которая сводится к квадратному уравнению. Из нее находим:
,
Вскоре после турнира Тарталья легко решил кубические уравнения второго и третьего типа. Например, для уравнения второго типа он применил подстановкукоторая привела к формуле
(3)
Известие
об успехи Тартальи дошло до Кардано.
Джироламо Кардано (1501-1576) окончил
медицинский факультет университета в
Павии и был врачом в Милане. Он являлся
ученым, не менее талантливым, чем
Тарталья, и гораздо более разносторонним:
он занимался медициной, математикой,
философией и астрологией. Кардано
задумал написать книгу энциклопедического
характера по алгебре, и она была бы
неполна без решения кубических уравнений.
Он обратился к Тарталье с просьбой
сообщить его способ решения этих
уравнений. Тарталья не соглашался, и
тогда Кардано поклялся на Евангелии
никому не сообщать секрета решения
кубических уравнений. По-видимому,
Тарталья собирался сам написать книгу
по алгебре, включив в нее и свое открытие,
но из-за занятости и из-за того, что
издание было делом дорогостоящим,
откладывал свое намерение. В конце
концов в 1545 г. Кардано выпустил свою
монографию под названием «Великое
искусство», в которую вошло и открытие
«моего друга Тартальи». Тарталья был
разгневан нарушением клятвы и выступил
в печати с разоблачением Кардано.
Кончилось тем, что лучший ученик Кардано
вызвал Тарталью на публичный поединок.
Поединок состоялся в 1548 г. в Милане и
закончился, при не вполне ясных
обстоятельствах, поражением Тартальи.
Формулы корней кубического уравнения
получили в истории название формул
Кардано, хотя сам Кардано в своей книге
и не приводил формул, а излагал алгоритм
решения кубического уравнения.
В конце
концов в 1545 г. Кардано выпустил свою
монографию под названием «Великое
искусство», в которую вошло и открытие
«моего друга Тартальи». Тарталья был
разгневан нарушением клятвы и выступил
в печати с разоблачением Кардано.
Кончилось тем, что лучший ученик Кардано
вызвал Тарталью на публичный поединок.
Поединок состоялся в 1548 г. в Милане и
закончился, при не вполне ясных
обстоятельствах, поражением Тартальи.
Формулы корней кубического уравнения
получили в истории название формул
Кардано, хотя сам Кардано в своей книге
и не приводил формул, а излагал алгоритм
решения кубического уравнения.
Книга Кардано «Великое искусство» сыграло значительную роль в истории алгебры. В частности, в ней он доказал, что полное уравнение третье степени с помощью подстановки сводится к уравнению без члена с квадратом неизвестного, т.е. к одному из трех видов кубических уравнений, рассмотренных в начале параграфа. Осовременивая изложение, возьмем кубическое уравнение общего вида
с произвольными по знаку коэффициентами вместо тех нескольких типов кубических уравнений, которыми занимался Кардано, и положим в нем
.
Нетрудно проверить, что последнее уравнение не содержит члена с квадратом неизвестного, так как сумма членов, содержащих равна нулю:
.
Аналогично Кардано доказал, что в полном уравнении четвертой степени можно избавиться от члена с кубом неизвестного. Для этого в уравнении четвертой степени общего вида
достаточно положить .
Позднее Ф. Виет знакомое нам кубическое уравнение решил с помощью остроумной подставкиБудем иметь:
.
Положим в последнем уравнении . Из полученного квадратного уравнения находимt ; затем вычислими, наконец,
Уравнение четвертой степени решил Феррари. Он решал его на примере
(без члена с кубом неизвестного), но вполне общим способом.
Прибавим к обеим частям уравнения (4) , с тем, чтобы дополнить левую часть до квадрата суммы:
Теперь прибавим к обеим частям последнего уравнения сумму
где t – новое неизвестное:
Так
как левая часть уравнения (5) есть квадрат
суммы, то и правая часть есть квадрат,
а тогда дискриминант квадратного
трехчлена равен нулю:
Впрочем, вXVI
в.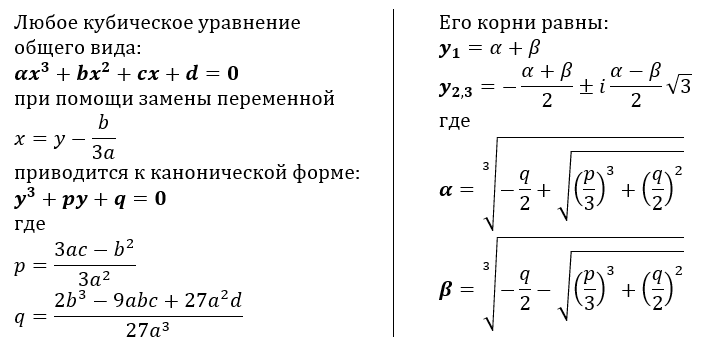 это уравнение писали в виде
это уравнение писали в виде
Уравнение (6) является кубическим. Найдем из него t уже знакомым способом, подставим это значение t в уравнение (5) и извлечем из обеих частей полученного уравнения квадратный корень. Образуется квадратное уравнение(точнее, два квадратных уравнения).
Приведенный здесь способ решения уравнения четвертой степени вошел в книгу Кардано.
По воззрениям того времени, правило решения кубического уравнения второго типа по формуле (3) нельзя применять в том случае, когда
; c современной точки зрения, в этом случае приходится проводить операции над мнимыми числами. Например, уравнение
имеет действительный корень ; кроме того, оно имеет еще два действительных (иррациональных) корня. Но по формуле (3) получаем:
Каким образом из мнимых («воображаемых», как тогда говорили) чисел получается действительное число? Это случай кубического уравнения получил название неприводимого.
Подробно
неприводимый случай разобрал итальянский
математик Рафаэль Бомбелли в книге
«Алгебра», изданной в 1572 г. В формуле
(3) он объяснил эту ситуацию тем, что
первый кубический корень равен
а второй –a-bi
(где a
и b-
действительные числа, t-мнимая
единица), так что их сумма дает
В формуле
(3) он объяснил эту ситуацию тем, что
первый кубический корень равен
а второй –a-bi
(где a
и b-
действительные числа, t-мнимая
единица), так что их сумма дает
т.е. действительное число.
Бомбелли привел правила действий над комплексными числами.
После выхода книги Бомбелли математикам постепенно становится ясно, что в алгебре без комплексных чисел не обойтись.
Нажав на кнопку «Скачать архив», вы скачаете нужный вам файл совершенно бесплатно.
Перед скачиванием данного файла вспомните о тех хороших рефератах, контрольных, курсовых, дипломных работах, статьях и других документах, которые лежат невостребованными в вашем компьютере. Это ваш труд, он должен участвовать в развитии общества и приносить пользу людям. Найдите эти работы и отправьте в базу знаний.
Мы и все студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будем вам очень благодарны.
Чтобы скачать архив с документом, в поле, расположенное ниже, впишите пятизначное число и нажмите кнопку «Скачать архив»
Подобные документы
Описание жизни Италии и мира того времени, когда жил и творил Джироламо Кардано. Научная деятельность математика, обзор его математических трудов и поиск решения кубических уравнений в радикалах. Способы решений уравнений третьей и четвертой степеней.
Научная деятельность математика, обзор его математических трудов и поиск решения кубических уравнений в радикалах. Способы решений уравнений третьей и четвертой степеней.
курсовая работа , добавлен 26.08.2011
История развития математической науки в Европе VI-XIV вв., ее представители и достижения. Развитие математики эпохи Возрождения. Создание буквенного исчисления, деятельность Франсуа Виета. Усовершенствование вычислений в конце XVI – начале XVI вв.
презентация , добавлен 20.09.2015
Европейская математика эпохи Возрождения. Создание буквенного исчисления Франсуа Виет и метода решения уравнений. Усовершенствование вычислений в конце XVI – начале XVII веков: десятичные дроби, логарифмы. Установление связи тригонометрии и алгебры.
презентация , добавлен 20.09.2015
Из истории десятичных и обыкновенных дробей. Действия над десятичными дробями. Сложение (вычитание) десятичных дробей. Умножение десятичных дробей. Деление десятичных дробей.
реферат , добавлен 29.05.2006
Греческая математика и её философия. Взаимосвязь и совместный путь философии и математики от начала эпохи возрождения до конца XVII века. Философия и математика в эпохе Просвещения. Анализ природы математического познания немецкой классической философии.
дипломная работа , добавлен 07.09.2009
Уравнение в дробях количества знаков после запятой, выполнение сложения и вычитания, не обращая внимания на запятую. Практическая значимость теории десятичных дробей. Самостоятельная работа с последующей проверкой результатов, выполнение вычислений.
презентация , добавлен 02.07.2010
Изучение возникновения математики и использования математических методов Древнем Китае. Особенности задач китайцев по численному решению уравнений и геометрических задач, приводящих к уравнениям третьей степени. Выдающиеся математики Древнего Китая.
Решение уравнений высших степеней – история полная драматизма, разочарования и радости открытия. В течение почти 700 лет математики разных стран пытались найти приёмы решения уравнений третьей, четвёртой и более высоких степеней.
В течение почти 700 лет математики разных стран пытались найти приёмы решения уравнений третьей, четвёртой и более высоких степеней.
Со времен Омара Хайяма ученые средневековья почти 400 лет искали формулу для решения уравнений третьей степени.
Паоло Вальмес за свое открытие поплатился жизнью. Инквизиция отправила Вальмеса на костер. Однако трагедии и неудачи не смогли остановить прогресс.
Омар Хайям(1048 – 1123)
В своих математических трудах таджикский ученый описал все возможные виды уравнений третьей степени и рассмотрел геометрический способ их решения.
Николо Тарталья (1499 – 1557)
Решил уравнение в радикалах
Джероламо Кардано(1501 – 1576)
Обобщил приемы решения разных видов кубических уравнений. Независимо от Тартальи открыл формулу корней («формула Кардано»).
Франсуа Виет (1540 – 1603)
Установил, каким образом корни уравнения выражаются через коэффициенты. Поставил вопрос о существовании решения уравнений произвольных степеней в радикалах
Паоло Руффини (1765 – 1822)
Пытался доказать невозможность алгебраического решения общих уравнений выше четвертой степени.
Жозеф Луи Лагранж (1736 – 1813)
Искал признаки уравнений высших степеней, разрешимых в радикалах
Нильс Хенрик Абель (1802 – 1829)
Доказал неразрешимость в радикалах уравнения пятой степени и более высоких степеней в общем случае.
Эварист Галуа (1811 – 1832)
Нашел необходимое и достаточное условие, которому удовлетворяет алгебраическое уравнение, разрешимое в радикалах.
Уравнения разных степеней
Ровесник Леонардо да Винчи, профессор Сципион дель Ферро из Болоньи (ум.1526) посвятил всю жизнь решению различных алгебраических уравнений. Затруднения, связанные с неудобными обозначениями неизвестных величин, были огромны.
Как мы показали выше, важнейшие достижения математиков средневековой Европы относились к области алгебры, к усовершенствованию ее аппарата и символики. Региомонтан обогатил понятие числа, введя радикалы и операции над ними. Это позволяло ставить проблему решения возможно более широкого класса уравнений в радикалах. И в этой именно области были достигнуты первые успехи – решены в радикалах уравнения 3-й и 4-й степени.
И в этой именно области были достигнуты первые успехи – решены в радикалах уравнения 3-й и 4-й степени.
Ход событий, связанных с этим открытием, освещается в литературе разноречиво. В основном он таков. Профессор университета в Болонье Сципион дель Ферро вывел формулу для нахождения положительного корня конкретных уравнений вида х 3 + рх = q (p›0, q ›0). Он держал ее в тайне, приберегая как оружие против своих противников в научных диспутах, но перед смертью сообщил эту тайну своему родственнику и преемнику по должности Аннибалу делла Наве и ученику своему – Фиоре.
В начале 1535 года должен был состояться научный поединок между Фиоре с Николо Тарталья (1500–1557). Последний был талантливым ученым, выходцем из бедной семьи, зарабатывавшим себе на жизнь преподаванием математики и механики в городах Северной Италии. Узнав, что Фиоре владеет формулой Ферро и готовит своему противнику задачи на решение кубических уравнений, Тарталья сумел заново открыть эту формулу.
На диспуте Фиоре предложил Тарталье несколько вопросов, требующих умения решать уравнения третьей степени. Но Тарталья уже нашел раньше сам решение таких уравнений и, мало того, не только одного того частного случая, который был решен Ферро, но и двух других частных случаев. Тарталья принял вызов и сам предложил Фиоре свои задачи. Результатом состязания было полное поражение последнего. Тарталья решил предложенные ему задачи в продолжение двух часов, между тем как Фиоре не мог решить ни одной задачи, предложенной ему (с обеих сторон было 30 задач).
Вскоре Тарталья смог решать уравнения вида х 3 = рх + q (p›0, q ›0). Наконец он сообщил, что уравнения вида х 3 + q = px сводятся к предыдущему виду, но не дал способа сведения. Тарталья долго не публиковал своего результата. Причин этому было две: во-первых, та же причина, которая останавливала и Ферро. Во-вторых, невозможность справиться с неприводимым случаем. Последний состоит в том, что есть уравнения х 3 = рх + q которые имеют действительный положительный корень. Однако формула Тартальи не давала решения в том случае, когда надо было извлекать корень из отрицательных чисел, так как не было возможности правильно трактовать мнимые числа, получающиеся при этом. Неприводимый случай появлялся у Тартальи и в уравнениях вида х 3 + q = px.
Однако формула Тартальи не давала решения в том случае, когда надо было извлекать корень из отрицательных чисел, так как не было возможности правильно трактовать мнимые числа, получающиеся при этом. Неприводимый случай появлялся у Тартальи и в уравнениях вида х 3 + q = px.
Однако его труд не пропал даром. С 1539 года кубическими уравнениями начинает заниматься Кардано (1501–1576). Услышав об открытии Тартальи, он приложил много усилий, чтобы выманить тайну у осторожного и недоверчивого ученого для публикации в своей книге «Великое искусство, или о правилах алгебры». Только когда Кардано поклялся над Евангелием и дал честное слово дворянина, что не откроет способа Тартальи для решения уравнений и даже запишет его в виде непонятной анаграммы, Тарталья согласился раскрыть свою тайну. Он показал правила решений кубических уравнений, изложив их в стихах, причем довольно туманно.
Однако Кардано не только понял эти правила, но и нашел доказательства для них. Невзирая на данное им обещание, он опубликовал способ Тартальи, и способ этот известен до сих пор под именем «правила Кардана». А книга появилась в 1545 году.
А книга появилась в 1545 году.
Вскоре было открыто и решение уравнений 4-й степени. Итальянский математик Д. Колла предложил задачу, для решения которой известных до той поры правил были недостаточно, а требовалось умение решать биквадратные уравнения. Большинство математиков считало эту задачу неразрешимою. Но Кардано предложил ее своему ученику Луиджи Феррари, который решил задачу, и даже нашел способ решать уравнения 4-й степени вообще, сводя их к уравнениям 3-й степени.
Столь быстрые и поразительные успехи в нахождении формулы решения уравнений 3-й и 4-й степени поставили перед математиками проблему отыскания решений уравнений любых степеней. Огромное число попыток, усилия виднейших ученых не приносили успеха. В поисках протекло около 300 лет. Только в XIX веке Абель (1802–1829) доказал, что уравнения степени п›4, вообще говоря, в радикалах не решаются.
На пути создания общей теории алгебраических уравнений и способов их решения стояли еще два препятствия: сложность, неудобство получаемых формул и неразъясненность неприводимого случая. Первое составляло чисто практическое неудобство. Его Кардано устраняет, предлагая находить корни уравнений приближенно с помощью правила двух ложных положений, по существу применяемого и в наши дни в виде простой, или линейной, интерполяции. Второе препятствие имеет более глубокие корни, а попытки его преодоления привели к весьма важным следствиям.
Первое составляло чисто практическое неудобство. Его Кардано устраняет, предлагая находить корни уравнений приближенно с помощью правила двух ложных положений, по существу применяемого и в наши дни в виде простой, или линейной, интерполяции. Второе препятствие имеет более глубокие корни, а попытки его преодоления привели к весьма важным следствиям.
Плодотворная и смелая попытка справиться с неприводимым случаем принадлежит итальянскому математику и инженеру Р. Бомбелли из Болоньи. В сочинении «Алгебра» (1572) он ввел формально правила действий над мнимыми и комплексными числами.
Данный текст является ознакомительным фрагментом.Корни или нули многочленов степени выше 2
Темы в
ПРЕДВАРИТЕЛЬНАЯ РАБОТА
Содержание | Дом
13
Факторная теорема
Основная теорема алгебры
Стратегия поиска корней
Теорема о целочисленном корне
Сопряженные пары
Доказательство теоремы о факторах
Доказательство теоремы о целочисленном корне
В ЭТОЙ ТЕМЕ мы увидим, как найти корни многочлена степени больше 2. Это будет зависеть от предыдущей темы: Синтетическое деление.
Это будет зависеть от предыдущей темы: Синтетическое деление.
Мы видели в этой теме то, что называется факторной теоремой.
Факторная теорема. x − r является множителем многочлена P ( x ) тогда и только тогда, когда r является корнем P ( x ).
Это означает, что если многочлен можно разложить, например, следующим образом:
P ( х ) = ( х — 1)( х + 2)( х + 3)
, то теорема говорит нам, что корни равны 1, −2 и −3.
И наоборот, если мы знаем, что корни многочлена равны −2, 1 и 5, то многочлен имеет следующие множители:
( х + 2)( х — 1)( х — 5).
Затем мы могли бы умножить и узнать полином, который имеет эти три корня.
Ниже мы увидим, как доказывается факторная теорема.
Задача 1.
a) Используйте теорему о множителях, чтобы доказать: ( x + 1) является множителем x 5 + 1,
Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы снова закрыть ответ, нажмите «Обновить» («Reload»).
Сначала решай задачу сам!
−1 является корнем из x 5 + 1. Ибо (−1) 5 + 1 = −1 + 1 = 0,
Следовательно, согласно теореме о факторах,
[ x −(−1)] = ( x + 1) является фактором.
б) Используйте синтетическое деление, чтобы найти другой множитель.
Следовательно, x 5 + 1 = ( x + 1)( x 4 − x 3 + x 2 − x + 1)
Следуя той же процедуре, мы можем доказать:
( x + a ) является коэффициентом x 5 + a 5 ,
и вообще:
( х + ) является коэффициентом x n + a n , где n нечетно.
Основная теорема алгебры
Следующее называется основной теоремой алгебры:
Многочлен степени n имеет хотя бы один корень, действительный или комплексный.
Это кажущееся простым утверждение позволяет нам заключить:
Многочлен P ( x ) степени n имеет ровно n корней, действительных или комплексных.
Если старший коэффициент P ( x ) равен 1, то Факторная теорема позволяет нам заключить:
P ( x ) = ( x — r n )( x — r — r — 9004). . . ( x − r 2 )( x − r 1 )
Следовательно, многочлен третьей степени, например, будет иметь три корня. А если все они настоящие, то его график будет выглядеть примерно так:
Ибо три корня — это три точки пересечения x .
Примечание: Если представить, что график начинается слева от y -ось, то этот график начинается ниже оси x . Почему? Потому что в любом многочлене в конечном итоге будет доминировать старший член. Если старший член положителен, а полином имеет нечетную степень, то когда x является большим отрицательным числом, то есть далеко слева от начала координат, тогда нечетная степень отрицательного числа сам по себе отрицателен. График будет ниже оси x .
Если старший член положителен, а полином имеет нечетную степень, то когда x является большим отрицательным числом, то есть далеко слева от начала координат, тогда нечетная степень отрицательного числа сам по себе отрицателен. График будет ниже оси x .
Что касается многочлена четвертой степени, то у него будет четыре корня. А если все они настоящие, то его график будет выглядеть примерно так:
Здесь крайний левый график представляет собой над по оси x . Ибо, когда полином имеет четную степень (и старший коэффициент положительный), то четная степень отрицательного числа будет положительной . График будет над осью x .
Пример 1. Запишите многочлен с целыми коэффициентами, имеющий следующие корни: −1, ¾.
Решение . Поскольку −1 — корень, то ( x + 1) — множитель. Что касается корня ¾, то у нас было бы решение
.| х | = | 3 4 |
| что подразумевает | ||
| 4 x | = | 3 |
| 4 x − 3 | = | 0 |
Коэффициенты равны (4 x − 3)( x + 1).
Многочлен равен 4 x 2 + x − 3,
.Задача 2. Определить многочлен, корни которого равны −1, 1, 2, и начертить его график.
Коэффициенты равны ( x + 1)( x — 1)( x — 2). При умножении полином равен ( x 2 — 1) ( x — 2) =
x 3 — 2 x 2 — x + 2.
9002 здесь.Точка пересечения y представляет собой постоянный член 2. В каждом многочлене отрезок y является постоянным членом, поскольку постоянный член представляет собой значение y , когда x = 0,
Задача 3. Определить многочлен с целыми коэффициентами, корни которого равны −½, −2, −2, и начертить график.
Коэффициенты равны (2 x + 1)( x + 2) 2 . При умножении полиномиальное составляет (2 x + 1) ( x 2 + 4 x + 4) =
2 x 3 + x 2 3 + x 2 + 12 + 12 + 12 + 12 + 12888 + 12 888 + 12888 + 12 888 + 12 8888, x + 4.
Вот график:
−2 — двойной корень. График не пересекает ось x .
Вопрос. Если r является корнем многочлена p ( x ), тогда при делении p ( x ) на x − r , что следует ожидать от 34 остатка 90?
0. Поскольку r является корнем, то x − r является множителем из p ( x ).
Задача 4. Является ли x = 2 корнем этого многочлена:
x 6 − 3 x 5 + 3 x 4 − 3 x 3 + 3 x 2 −3 x + 2 ?
Используйте синтетическое деление, чтобы разделить многочлен на x − 2, и посмотрите на остаток.
Остаток равен 0. 2 — корень многочлена.
Урок 12
Пример 2. Найти три корня из
P ( х ) = х 3 − 2 х 2 − 9 х 9 ,
учитывая тот
корень 3.
Раствор. Поскольку 3 является корнем P ( x ), то, согласно теореме о множителях, x − 3 является множителем. Следовательно, разделив P ( x ) на x − 3, мы можем найти другой, квадратичный множитель.
У нас есть
| x 3 − 2 x 2 − 9 x + 18 | = | ( х 2 + х — 6)( х — 3) |
| = | ( х — 2)( х + 3)( х — 3) | |
Три корня: 2, −3, 3.
Опять же, поскольку x — 3 является множителем от P ( x ), остаток равен 0.
Задача 5. Нарисуйте график этого полинома
.у = х 3 — 2 х 2 — 5 х + 6,
, учитывая, что один корень равен −2.
Поскольку −2 — корень, то ( x + 2) — множитель. Чтобы найти другой квадратичный множитель, разделите полином на x + 2. Обратите внимание, что корень −2 находится в прямоугольнике:
. У нас есть
| x 3 4 − 1 2 2 − 5 x + 6 | = | ( x 2 − 4 x + 3)( x + 2) |
| = | ( х — 1)( х — 3)( х + 2) | |
Три корня: 1, 3, −2. Вот график:
Стратегия поиска корней
Какова же тогда стратегия нахождения корней многочлена степени n > 2?
Нам нужно дать или мы должны угадать корень r . Затем мы можем разделить многочлен на x − r и, следовательно, получить множитель многочлена, который будет на одну степень меньше. Если мы сможем найти корень этого множителя, мы сможем продолжить процесс, каждый раз уменьшая степень, пока не дойдем до квадратного числа, которое мы всегда сможем решить.
Если мы сможем найти корень этого множителя, мы сможем продолжить процесс, каждый раз уменьшая степень, пока не дойдем до квадратного числа, которое мы всегда сможем решить.
Вот теорема, которая поможет нам угадать корень.
Теорема о целом корне. Если целое число является корнем многочлена с целыми коэффициентами и старшим коэффициентом ±1, то это целое число является коэффициент постоянного члена.
Мы докажем это ниже.
Эта теорема о целочисленном корне является примером более общей теоремы о рациональном корне:
Если рациональное число r/s является корнем многочлена с целыми коэффициентами, то целое число r является множителем постоянного члена, а целое число s является множителем старшего коэффициента.
Пример 3. Каковы возможные целые корни x 3 − 4 x 2 + 2 x + 4?
Ответ. Если есть целые корни, то они будут множителями постоянного члена 4; а именно: ±1, ±2, ±4.
Если есть целые корни, то они будут множителями постоянного члена 4; а именно: ±1, ±2, ±4.
Итак, является ли 1 корнем? Чтобы ответить, мы разделим многочлен на x — 1 и будем надеяться на остаток 0,
.| 1 | – 4 | + 2 | + 4 | |1 |
| + 1 | – 3 | – 1 | ||
| ————————————————————— ————————————————— —— | ||||
| 1 | − 3 | – 1 | + 3 | |
Остаток не равен 0. 1 не является корнем. Попробуем −1:
.| 1 | – 4 | + 2 | + 4 | |−1 |
| – 1 | + 5 | − 7 | ||
| ————————————————————— ————————————————— —— | ||||
| 1 | − 5 | + 7 | − 3 | |
Остаток снова не 0. Попробуем 2:
Попробуем 2:
| 1 | – 4 | + 2 | + 4 | |2 |
| + 2 | – 4 | − 4 | ||
| ————————————————————— ————————————————— —— | ||||
| 1 | − 2 | − 2 | + 0 | |
Да! 2 это корень. У нас есть
x 3 − 4 x 2 + 2 x + 4 = ( х 2 — 2 х — 2)( х — 2)
Теперь мы можем найти корни квадратного уравнения, составив квадрат. Как мы нашли в Теме 11:
х = 1 ±
Следовательно, три корня равны:
1 + , 1 — , 2.
Проблема 6.
а) Каковы возможные целые корни этого многочлена?
x 3 − 2 x 2 − 3 x + 1
±1. Они являются единственными факторами постоянного члена.
Они являются единственными факторами постоянного члена.
б) Имеет ли этот многочлен целые корни?
Нет, потому что ни 1, ни −1 не сделают этот многочлен равным 0. Синтетическое деление на оба ±1 не дает в остатке 0,
.Задача 7. Разложите этот полином на произведение линейных множителей.
x 3 + 2 x 2 − 5 x − 6
Мы должны найти корни. Возможные целые корни: ± 1, ± 2, ± 3, ± 6. Синтетическое деление показывает, что −1 — это корень.
Таким образом,
| х 3 + 2 х 2 − 5 х 9 − 16 | = | ( х + 1)( х 2 + х — 6) |
| = | ( х + 1)( х + 3)( х -2) | |
Сопряженные пары
Если иррациональное число a + является корнем, то его сопряженное a − также является корнем. (См. Навыки алгебры, урок 28.) И если комплексное число a + bi — это корень, то и его сопряженное, a − bi .
(См. Навыки алгебры, урок 28.) И если комплексное число a + bi — это корень, то и его сопряженное, a − bi .
Пример 4. Многочлен P ( x ) имеет следующие корни:
−2, 1 + , 5 i .
Какова наименьшая степень, которую может иметь P ( x )?
Ответ . 5. Поскольку, поскольку 1 + является корнем, то и его сопряженный корень 1 − . А с 5 i — это корень, как и его сопряжение, −5 i .
P ( x ) имеет по крайней мере эти 5 корней:
-2, 1 ± , ±5 i .
Задача 8. Построить многочлен, имеющий следующий корень:
а) 2 +
Поскольку 2 + является корнем, то и 2 − тоже. Следовательно, по теореме о сумме и произведении корней они являются корнями х 2 − 4 х + 1.
Тема 10
б) 2 − 3 i
Поскольку 2 − 3 i является корнем, то и 2 + 3 i является корнем. Опять же, согласно теореме о сумме и произведении корней, они являются корнями х 2 — 4 х + 13.
Опять же, согласно теореме о сумме и произведении корней, они являются корнями х 2 — 4 х + 13.
См. раздел 10, пример 7.
Задача 9. Построить полином, корни которого равны 1 и 5 и .
Поскольку 5 i является корнем, то и его сопряженное число равно -5 i . Они будут корнями квадратного множителя многочлена. Сумма этих корней равна 0. Произведение равно 25. Следовательно, квадратичный множитель равен ( x 2 + 25).
Далее, поскольку 1 — корень, то ( x — 1) — множитель. Следовательно, полином равен
.( х — 1)( х 2 + 25) = х 3 — х 2 + 25 х — 25.
Problem 10. Let f ( x ) = x 5 + x 4 + x 3 + x 2 − 12 x − 12. One root есть, а другой — −2 i .
One root есть, а другой — −2 i .
Если f ( x ) имеет целые корни, сколько их может быть?
Один. Это многочлен 5-й степени и имеет 5 корней. Два и -. И два из них 2 i и −2 i .
Задача 11. Может ли многочлен 5-й степени иметь 2 действительных корня и 3 мнимых корня?
Нет. Так как мнимые корни всегда идут парами, то если есть мнимые корни, то их всегда будет четное число.
Рассмотрим график полинома 5-й степени с положительным старшим членом. Когда x является большим отрицательным числом, график находится ниже оси x . Когда x является большим положительным числом, оно выше оси x . Следовательно, график должен пересечь ось x хотя бы один раз. Теперь можете ли вы нарисовать график так, чтобы он пересекал ось x ровно дважды? Нет, ты не можешь. Многочлен нечетной степени должен иметь нечетное число действительных корней.
Доказательство теоремы о факторах
x − r является множителем многочлена P ( x )
тогда и только тогда, когда
r является корнем P ( x x ).
Во-первых, если ( x − r ) является множителем P ( x ), то P ( r ) будет иметь множитель ( 90−3 r ), 3 01031 r , равно 0. Это составит P ( r ) = 0. Это означает, что r является корнем.
Обратно, если r является корнем P ( x ), то P ( r ) = 0. что при делении P ( x ) на x − r , остаток равен 0.0031 Р ( х ).
Вот что мы хотели доказать.
Доказательство теоремы о целочисленном корне
Если целое число является корнем многочлена, коэффициенты которого являются целыми числами, а старший коэффициент равен ±1, то это целое число представляет собой множитель постоянного члена.
Пусть целое число r будет корнем этого многочлена:
P ( x ) = ± x n + a n −1 x n −1 + a n −2 x n −2 + . . . + a 2 x 2 + a 1 x + a 0 , , где и являются целыми числами. Тогда так как r это корень, Р ( р ) =
± г п + a n −1 r n −1 + a n −2 r n −2 + . . . + a 2 r 2 + a 1 r + a 0 40 = Транспонировать постоянный член a 0 , и коэффициент r от остальных слагаемых: R (± R N −1 + A N —1 R N — 2 +. Теперь все числа и являются целыми числами; поэтому выражение в скобках является целым числом, которое для удобства будем называть — к: r(−q) = − a 0 , или rq = a 0 . Таким образом, постоянный член a 0 можно разложить на множители как rq , если r и q оба являются целыми числами. Таким образом, при этих условиях r является множителем постоянного члена. Вот что мы хотели доказать. Следующая тема: Множественные корни Содержание | Дом Пожалуйста, сделайте пожертвование, чтобы TheMathPage оставался онлайн. Copyright © 2021 Лоуренс Спектор Вопросы или комментарии? Электронная почта: [email protected] формула корней полинома третьей степени Зарегистрирован: 11. Зарегистрирован: 25. Зарегистрирован: 14.10.2001 Дата регистрации: 24.04.2004 Зарегистрирован: 14.10.2001 Зарегистрирован: 14.07.2002 Полином третьей степени имеет вид p(x) = ax 3 + bx 2 + cx + d где ‘a’ не равно нулю. Он также называется кубическим полиномом, так как он имеет степень 3. Пример: 5x 3 + 2x 2 + 3x + 7 является кубическим полиномом или полиномом третьей степени, поскольку наивысшая степень выражения равна 3 или степень старшего члена равна 3. полином третьей степени имеет четыре точки пересечения, функция пересекает ось x только раз три раз. + a 1 ) = − a 0
+ a 1 ) = − a 0
Даже 1 доллар поможет. Формула корней полинома третьей степени
Похожие темы:
изучение промежуточной алгебры |
матлаб решает уравнения |
калькулятор квадратичного коэффициента 2 varibales |
как решить алгебру с ti 89 |
как решить линейное программирование с ti-83 |
тригонометрия ти-83 задачи |
одновременный решатель уравнений |
шестой класс математической вероятности |
как рассчитать уравнения алгебры? Автор Сообщение musicolmidget  01.2003
01.2003
От: Размещено: Пятница, 29 декабря, 20:02 Привет, я учусь в старшей школе и нуждаюсь в серьезной помощи в формуле полиномиальных корней третьей степени. Мои оценки по математике ужасны, и я решил что-то с этим сделать. Я ищу веб-сайт, который позволит мне ввести вопрос и дает подробное пошаговое решение; в основном это должно провести меня через все это. Мне очень нужно улучшить свои оценки, поэтому, пожалуйста, помогите мне. Наверх nxu  10.2006
10.2006
Откуда: Сибирь, Российская Федерация Размещено: Суббота, 30 декабря, 09:21 Верно! Спаси, Господи, нас, студентов, от зла формулы многочленных корней третьей степени. Когда я был там, я сталкивался с теми же проблемами, что и вы. Я всегда путался в коррекционной алгебре, алгебре колледжа и предварительной алгебре. Я был худшим в формуле корней полинома третьей степени, пока не узнал об алгебраике. Это действительно полезно, и я определенно рекомендую его. Лучшая особенность программного обеспечения заключается в том, что оно также поможет вам изучить алгебру, а не просто дать ответы.  Я нашел Algebrator эффективным и уверен, что он поможет и вам. Ваше здоровье.
Я нашел Algebrator эффективным и уверен, что он поможет и вам. Ваше здоровье. Наверх Техей-Мечиал
От: Размещено: Воскресенье, 31 декабря, 21:56. Ага! Я с тобой согласен! Гарантия возврата денег, которая предоставляется при покупке Algebrator, является одним из привлекательных вариантов.  В случае, если вы недовольны предложенной вам помощью по какой-либо математической теме, вы можете получить возмещение платежа, который вы сделали для покупки Algebrator в течение количества дней, указанного на этикетке. Прежде чем размещать заказ, загляните на https://graph-inequality.com/solving-systems-of-linear-equations-by-graphing.html, потому что там содержится много информации о темах, по которым вы можете ожидать чтобы получить помощь.
В случае, если вы недовольны предложенной вам помощью по какой-либо математической теме, вы можете получить возмещение платежа, который вы сделали для покупки Algebrator в течение количества дней, указанного на этикетке. Прежде чем размещать заказ, загляните на https://graph-inequality.com/solving-systems-of-linear-equations-by-graphing.html, потому что там содержится много информации о темах, по которым вы можете ожидать чтобы получить помощь. Наверх TortniX
От: Размещено: Понедельник, 01 января, 07:45 О, круто ! Спасибо .  Я вдруг чувствую себя счастливым, зная, что помощь рядом. Я хотел бы попробовать это немедленно. С кем я должен поговорить, чтобы купить эту программу? Я не могу дождаться, чтобы получить эту программу сейчас.
Я вдруг чувствую себя счастливым, зная, что помощь рядом. Я хотел бы попробовать это немедленно. С кем я должен поговорить, чтобы купить эту программу? Я не могу дождаться, чтобы получить эту программу сейчас. Наверх Техей-Мечиал
От: Размещено: Среда, 03 января, 08:36 Я постоянный пользователь Алгебратора.  Это не только помогает мне быстрее выполнять домашнюю работу, но и предлагает подробные объяснения, которые облегчают понимание концепций. Я настоятельно рекомендую использовать его, чтобы помочь улучшить навыки решения проблем.
Это не только помогает мне быстрее выполнять домашнюю работу, но и предлагает подробные объяснения, которые облегчают понимание концепций. Я настоятельно рекомендую использовать его, чтобы помочь улучшить навыки решения проблем. Наверх ЗалевиЛ
Откуда: плавающие в свете, никогда не забываемые Размещено: Четверг, 04 января, 09:10 Его можно заказать прямо здесь — https://graph-inequality.  com/inequalities-and-applications-1.html. Друг сказал мне, что они даже предлагают гарантию возврата денег «без каких-либо условий», так что закажите копию, я уверен, вам понравится.
com/inequalities-and-applications-1.html. Друг сказал мне, что они даже предлагают гарантию возврата денег «без каких-либо условий», так что закажите копию, я уверен, вам понравится. Наверх Что является примером полинома 3-й степени?
Может ли полином третьей степени иметь четыре точки пересечения?
 24 апреля 2014 г.
24 апреля 2014 г. Сколько членов в многочлене третьей степени?
Многочлены третьей степени могут иметь 3 возможных нуля из-за: — Поскольку степень многочлена указывает количество нулей в…
Сколько корней может иметь многочлен третьей степени?
Основная теорема алгебры утверждает, что степень многочлена — это максимальное количество корней, которое имеет многочлен. Уравнение третьей степени имеет не более три корня . Многочлен четвертой степени имеет не более четырех корней.
Многочлен четвертой степени имеет не более четырех корней.
Может ли многочлен третьей степени не иметь действительных корней?
Как квадратное уравнение может иметь два действительных корня, так и кубическое уравнение может иметь три . Но в отличие от квадратного уравнения, которое может не иметь действительного решения, кубическое уравнение всегда имеет хотя бы один действительный корень.
Может ли многочлен 3-й степени иметь 4 корня?
Нет, нельзя . Многочлен нечетной степени должен иметь нечетное число действительных корней. r является корнем P(x). Во-первых, если (x − r) является множителем P(x), то P(r) будет иметь множитель (r − r), равный 0.
Многочлен нечетной степени должен иметь нечетное число действительных корней. r является корнем P(x). Во-первых, если (x − r) является множителем P(x), то P(r) будет иметь множитель (r − r), равный 0.
Что такое термин третьей степени?
: применение к заключенному психических или физических пыток с целью получения признания .
Как написать полиномиальное уравнение?
К напишите общее уравнение для многочлен с определенной степенью, надо знать степень полином (значение n или, другими словами, значение показателя степени переменной наивысшей степени).
 Многочлены второй степени называются квадратичными многочленами . Их общее уравнение : P (y) 2 = k 1 y 2 + k2 y + k 3 = 0.
Многочлены второй степени называются квадратичными многочленами . Их общее уравнение : P (y) 2 = k 1 y 2 + k2 y + k 3 = 0.
Как узнать, является ли уравнение полиномом?
Определение наличия 9(n-1) + . . .
Как решить это полиномиальное уравнение?
Для решить многочлен найти сумму членов. Сумма полинома равна 0. Постарайтесь запомнить аббревиатуру \\»FOIL\\» при решении полиномов . ФОЛЬГА расшифровывается как First, Outside, Inside, Last. Давайте посмотрим, как решить многочлен уравнения . Поместите свой полином в стандартную форму, от самой высокой степени до самой низкой степени.


 0)*((-t + s)/2)
0)*((-t + s)/2) Его главным занятием была медицина. Кроме того, он занимался философией, математикой, астрологией, составлял гороскопы Петрарки, Лютера, Христа, английского короля Эдуарда 6. Папа римский пользовался услугами Кардано — астролога и покровительствовал ему. Кардано умер в Риме. Существует легенда, что он покончил жизнь самоубийством в тот день, который предсказал, составляя собственный гороскоп, как день своей смерти.
Его главным занятием была медицина. Кроме того, он занимался философией, математикой, астрологией, составлял гороскопы Петрарки, Лютера, Христа, английского короля Эдуарда 6. Папа римский пользовался услугами Кардано — астролога и покровительствовал ему. Кардано умер в Риме. Существует легенда, что он покончил жизнь самоубийством в тот день, который предсказал, составляя собственный гороскоп, как день своей смерти. Тогда уравнение запишется в виде
Тогда уравнение запишется в виде Многочлены второй степени называются квадратичными многочленами . Их общее уравнение : P (y) 2 = k 1 y 2 + k2 y + k 3 = 0.
Многочлены второй степени называются квадратичными многочленами . Их общее уравнение : P (y) 2 = k 1 y 2 + k2 y + k 3 = 0.