Cos 2x график: Mathway | Популярные задачи

2

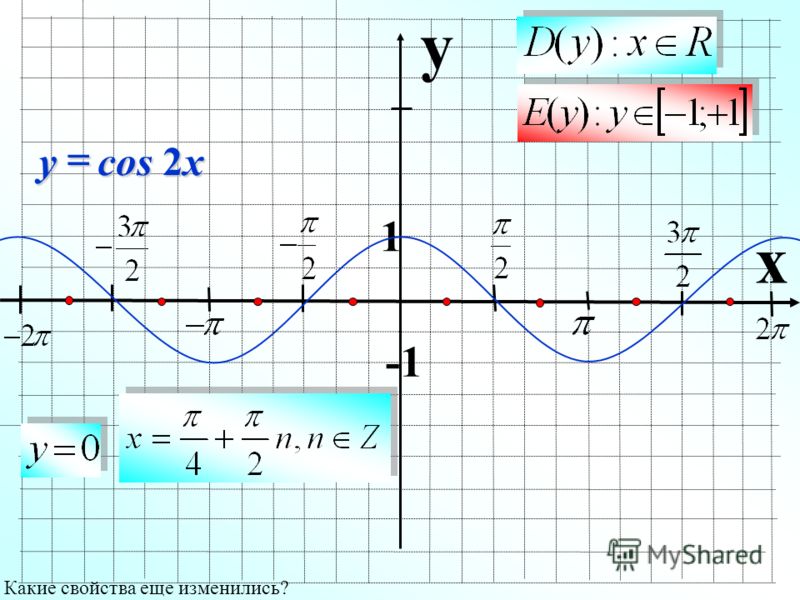
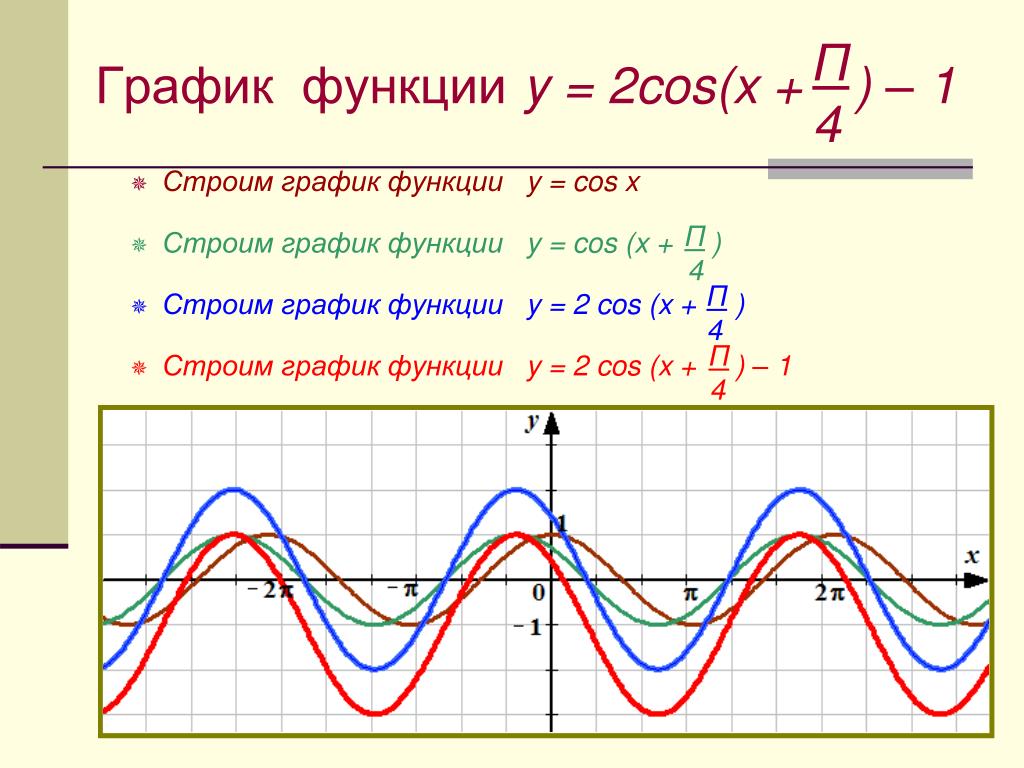
Графики тригонометрических функций кратных углов. Графики тригонометрических функций кратных углов График функции y 2 cos x

«Графики функций и их свойства» — y = ctg x. 4) Ограниченность функции. 3) Нечётная функция. (График функции симметричен относительно начала координат). y = tg x. 7) Функция непрерывна на любом интервале вида (?k; ? + ?k). Функция y = tg x непрерывна на любом интервале вида. 4) Функция убывает на любом интервале вида (?k; ? + ?k). График функции y = tg x называется тангенсоидой.

«График функции Y X» — Шаблон параболы у = х2. Чтобы увидеть графики, щелкни мышкой. Пример 2. Построим график функции y = x2 + 1, опираясь на график функции y=x2 (щелчок мышкой). Пример 3. Докажем, что графиком функции у = х2 + 6х + 8 является парабола, и построим график. График функции y=(x — m)2 является параболой с вершиной в точке (m; 0).

«Математика графики» — Как можно строить графики? Наиболее естественно функциональные зависимости отражаются с помощью графиков. Интересное применение: рисунки,… Зачем мы изучаем графики? Графики элементарных функций. Что вы можете нарисовать с помощью графиков? Рассматриваем применение графиков в учебных предметах: математике, физике,…

«Построение графиков с помощью производной» — Обобщение. Построить эскиз графика функции. Найти асимптоты графика функции. График производной функции. Дополнительное задание. Исследовать функцию. Назвать промежутки убывания функции. Самостоятельная работа учащихся. Расширить знания. Урок закрепления изученного материала. Оцените свои умения. Точки максимума функции.

«Графики с модулем» — Отобрази «нижнюю» часть в верхнюю полуплоскость. Модуль действительного числа. Свойства функции y = |x|. |x|. Числа. Алгоритм построения графика функции. Алгоритм построения. Функция y= lхl. Свойства. Самостоятельная работа. Нули функции. Советы великих. Решение самостоятельной работы.

«Уравнение касательной» — Уравнение касательной. Уравнение нормали. Если,то и кривые пересекаются под прямым углом.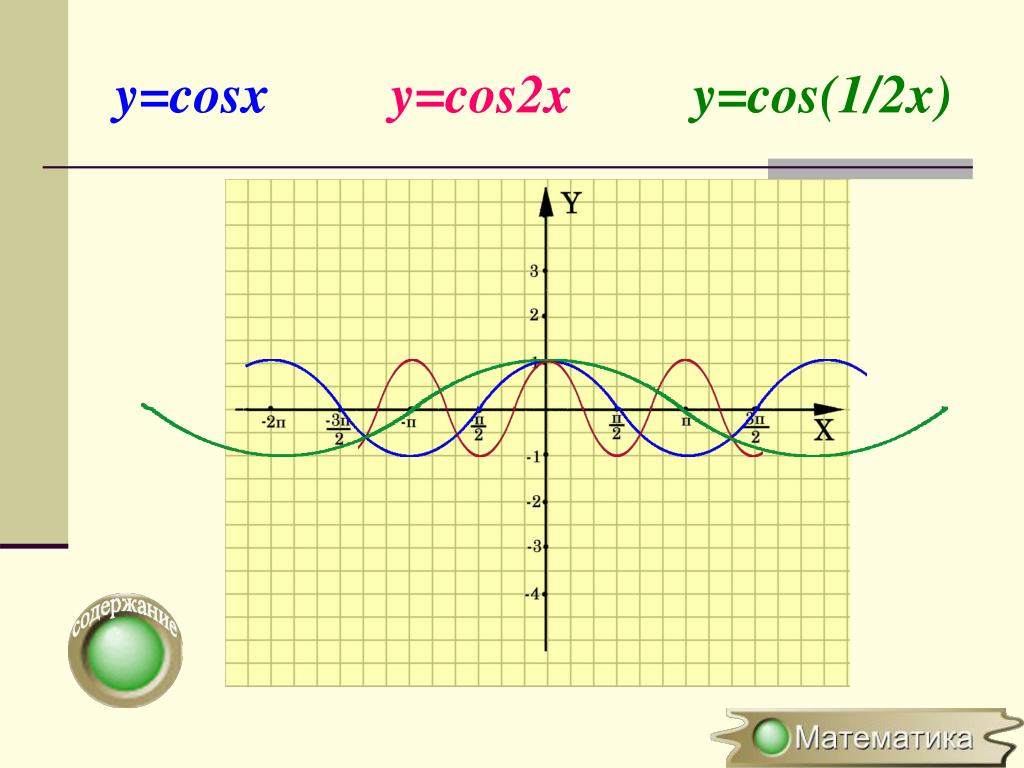

Условия параллельности и перпендикулярности двух прямых. Угол между графиками функций. Уравнение касательной к графику функции в точке. Пусть функция дифференцируема в точке. Пусть прямые заданы уравнениями и.

Всего в теме 25 презентаций

Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.

Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 10 класса
Алгебраические задачи с параметрами, 9–11 классы
Программная среда «1С: Математический конструктор 6.1»

Что будем изучать:
1. Определение.
2. График функции.
3. Свойства функции Y=cos(X).
4. Примеры.

Определение функции косинуса у=cos(x)

Ребята, мы уже познакомились с функцией Y=sin(X).

Давайте вспомним одну из формул привидения : sin(X + π/2) = cos(X).

Благодаря этой формуле, мы можем утверждать, что функции sin(X + π/2) и cos(X) тождественны, и их графики функций совпадают.

График функции sin(X + π/2) получается из графика функции sin(X) параллельным переносом на π/2 единиц влево. Это и будет график функции Y=cos(X).

График функции Y=cos(X) так же называют синусоидой.

Свойства функции cos(x)

Запишем свойства нашей функции:
• Область определения – множество действительных чисел.
• Функция четная. Давайте вспомним определение четной функции. Функция называется четной, если выполняется равенство y(-x)=y(x). Как мы помним из формул привидения: cos(-x)=-cos(x), определение выполнилось, тогда косинус – четная функция.
• Функция Y=cos(X) убывает на отрезке и возрастает на отрезке [π; 2π]. В этом мы можем убедиться на графике нашей функции.
• Функция Y=cos(X) ограничена снизу и сверху. Данное свойство следует из того, что
  -1 ≤ cos(X) ≤ 1
• Наименьшее значение функции равно -1 (при х = π + 2πk). Наибольшее значение функции равно 1 (при х = 2πk).
• Функция Y=cos(X) является непрерывной функцией. Посмотрим на график и убедимся, что у нашей функции нет разрывов, это и означает непрерывность.
• Область значений отрезок [- 1; 1]. Это также хорошо видно из графика.
• Функция Y=cos(X) — периодическая функция. Посмотрим опять на график и увидим, что функция принимает одни и те же значения через некоторые промежутки.

Примеры с функцией cos(x)

1. Решить уравнение cos(X)=(x — 2π) 2 + 1

Решение: Построим 2 графика функции: y=cos(x) и y=(x — 2π) 2 + 1 (см. рисунок).

y=(x — 2π) 2 + 1 — это парабола, смещенная вправо на 2π и вверх на 1. Наши графики пересекаются в одной точке А(2π;1), это и есть ответ: x = 2π.

2. Построить график функции Y=cos(X) при х ≤ 0 и Y=sin(X) при x ≥ 0

Решение: Чтобы построить требуемый график, давайте построим два графика функции по «кусочкам». Первый кусочек: y=cos(x) при х ≤ 0. Второй кусочек: y=sin(x)
при x ≥ 0. Изобразим оба «кусочка» на одном графике.

3. Найти наибольшее и наименьшее значение функции Y=cos(X) на отрезке [π; 7π/4]

Решение: Построим график функции и рассмотрим наш отрезок [π; 7π/4]. На графике видно, что наибольшие и наименьшие значения достигаются на концах отрезка: в точках π и 7π/4 соответственно.

Ответ: cos(π) = -1 – наименьшее значение, cos(7π/4) = наибольшее значение.

4. Построить график функции y=cos(π/3 — x) + 1

Решение: cos(-x)= cos(x), тогда искомый график получится путем переноса графика функции y=cos(x) на π/3 единиц вправо и 1 единицу вверх.

Задачи для самостоятельного решения

1)Решить уравнение: cos(x)= x – π/2.
2) Решить уравнение: cos(x)= — (x – π) 2 — 1.
3) Построить график функции y=cos(π/4 + x) — 2.
4) Построить график функции y=cos(-2π/3 + x) + 1.
5) Найти наибольшее и наименьшее значение функции y=cos(x) на отрезке .
6) Найти наибольшее и наименьшее значение функции y=cos(x) на отрезке [- π/6; 5π/4].

Теперь мы рассмотрим вопрос о том, как строить графики тригонометрических функций кратных углов ωx , где ω — некоторое положительное число.

Для построения графика функции у = sin ωx сравним эту функцию с уже изученной нами функцией у = sin x . Предположим, что при х = x 0 функция у = sin х принимает значение, равное у 0 . Тогда

у 0 = sin x 0 .

Преобразуем это соотношение следующим образом:

Следовательно, функция у = sin ωx при х = x 0 / ω принимает то же самое значение у 0 , что и функция у = sin х при х = x 0 . А это означает, что функция у = sin ωx повторяет свои значения в ω раз чаще, чем функция у = sin x . Поэтому график функции у = sin ωx получается путем «сжатия» графика функции у = sin x в ω раз вдоль оси х.

Например, график функции у = sin 2х получается путем «сжатия» синусоиды у = sin x вдвое вдоль оси абсцисс.

График функции у = sin x / 2 получается путем «растяжения» синусоиды у = sin х в два раза (или «сжатия» в 1 / 2 раза) вдоль оси х.

Поскольку функция у = sin ωx повторяет свои значения в ω раз чаще, чем функция
у = sin x , то период ее в ω раз меньше периода функции у = sin x . Например, период функции у = sin 2х равен 2π / 2 = π , а период функции у = sin x / 2 равен π / x / 2 = 4π .

Интересно провести исследование поведения функции у = sin аx на примере анимации, которую очень просто можно создать в программе Maple :

Аналогично строятся графики и других тригонометрических функций кратных углов. На рисунке представлен график функции у = cos 2х , который получается путем «сжатия» косинусоиды

у = cos х в два раза вдоль оси абсцисс.

График функции у = cos x / 2 получается путем «растяжения» косинусоиды у = cos х вдвое вдоль оси х.

На рисунке вы видите график функции у = tg 2x , полученный «сжатием» тангенсоиды у = tg x вдвое вдоль оси абсцисс.

График функции у = tg x / 2 , полученный «растяжением» тангенсоиды у = tg x вдвое вдоль оси х.

И, наконец, анимация, выполненная программой Maple:

Упражнения

1. Построить графики данных функций и указать координаты точек пересечения этих графиков с осями координат. Определить периоды данных функций.

а). y = sin 4x / 3 г). y = tg 5x / 6 ж). y = cos 2x / 3

б). у= cos 5x /

3 д). у = ctg 5x / 3 з). у= ctg x / 3

в). y = tg 4x / 3 е). у = sin 2x / 3

2. Определить периоды функций у = sin (πх) и у = tg ( πх / 2 ).

3. Приведите два примера функции, которые принимают все значения от -1 до +1 (включая эти два числа) и изменяются периодически с периодом 10.

4 *. Приведите два примера функций, которые принимают все значения от 0 до 1 (включая эти два числа) и изменяются периодически с периодом π / 2 .

5. Приведите два примера функций, которые принимают все действительные значения и изменяются периодически с периодом 1.

6 *. Приведите два примера функций, которые принимают все отрицательные значения и нуль, но не принимают положительные значения и изменяются периодически с периодом 5.

y = 2 sin x cos 2x, z = cos2 2x sin x.

⇐ ПредыдущаяСтр 4 из 4

______________________________________________________________________________

Вариант № 13

1. Создать таблицу расчета функции при х Î [-2, 1.5]. Построить график функции.

Создать таблицу расчета функций при х Î [-2, 2]. Построить графики в одной системе координат.    

y = 3 sin px – cos 2px sin px, z = cos2px – 2sin³ px.

________________________________________________________________________________________________________________

Вариант № 14

1. Создать таблицу расчета функции при

х Î [-1.5, 1.5]. Построить график функции.

2. Создать таблицу расчета функций при х Î [-2, 2]. Построить графики в одной системе координат.    

y = sin 2px cos px – 2cos²3px , z = 2 cos²2px – 4 sin^3px.

_____________________________________________________________________________________________________________________

Вариант № 15

1. Создать таблицу расчета функции при х Î [-1.8, 1.8]. Построить график функции.

2. Создать таблицу расчета функций при х Î [0, 3]. Построить графики в одной системе координат.    

y = 3sin px cos px, z = cos³px sin^2px.

Вариант № 16

1.

Создать таблицу расчета функции при х Î [-2, 1.8]. Построить график функции.

2. Создать таблицу расчета функций при х Î [-3, 0]. Построить графики в одной системе координат.    

y = 3sin 2px cos 3px, z = cos³4px sin^2px.

___________________________________________________________________________________________________________________

Вариант № 17

1.

Создать таблицу расчета функции при х Î [-1.7, 1.5]. Построить график функции.

2. Создать таблицу расчета функций при х Î [-3, 0]. Построить графики в одной системе координат.    

y = 2sin px cos 3px, z = cos²3px – cospx sin^px.

_________________________________________________________________________________________________________________

Вариант № 18

1.

Создать таблицу расчета функции при х Î [-1.5, 1.8]. Построить график функции.

2. Создать таблицу расчета функций при х Î [-3, 0]. Построить графики в одной системе координат.    

y = sin 2px + sin 2px cos px, z = 2cospx – cos3px sin² px.

___________________________________________________________________________________________________________________

Вариант № 19

1. Создать таблицу расчета функции при х Î [-1.4, 1.9]. Построить график функции.

2.

Создать таблицу расчета функций при х Î [0, 3]. Построить графики в одной системе координат.    

y =2 sin px cos px + 2 sin 3px cos 2px, z = 3cos²px – cos2px

________________________________________________________________________________________________________________

Вариант № 20

1. Создать таблицу расчета функции при х Î [-1.4, 1.4]. Построить график функции.

2.

Создать таблицу расчета функций при х Î [0, 2]. Построить графики в одной системе координат.    

y = 3 sin 2px cos px + sin 3px, z = 3cos^{2px sin2 px – cos4px}

 

 

Вариант № 21

1.

Создать таблицу расчета функции при хÎ[-2, 2]. Построить график функции

2. Создать таблицу расчета функций при х Î [-2, 2]. Построить графики в одной системе координат.    

y = 2 sin x cos 2x, z = cos2 2x sin x.

______________________________________________________________________________

Вариант № 22

1. Создать таблицу расчета функции при х Î [-2, 2]. Построить график функции.

2. Создать таблицу расчета функций при х Î [-2, 2]. Построить графики в одной системе координат.    

y = 3 sin 2px – 3cos px,  z = cos²2px – 2sin px.

________________________________________________________________________________________________________________

Вариант № 23

1. Создать таблицу расчета функции при х Î [-2, 1.5]. Построить график функции.

2.

Создать таблицу расчета функций при х Î [-2, 2]. Построить графики в одной системе координат.    

y = 3 sin px – cos 3px sin 2px, z = 2cos2px – 2sin³ px.

______________________________________________________________________________

Вариант № 24

1. Создать таблицу расчета функции при х Î [-1.5, 1.5]. Построить график функции.

2. Создать таблицу расчета функций при х Î [-2, 2]. Построить графики в одной системе координат.    

y = 3sin 2px cos px – cos²3px , z = 2 cos²2px – 3 sin^3px.

__________________________________________________________________________________________________________________

Вариант № 25

1.

Создать таблицу расчета функции при х Î [-1.8, 1.8]. Построить график функции.

2. Создать таблицу расчета функций при х Î [0, 3]. Построить графики в одной системе координат.    

y = 2sin px 3cos px, z = cos²px sin^px.

⇐ Предыдущая1234

3-8 9 Оценить квадратный корень из 12 10 Оценить квадратный корень из 20 11 Оценить квадратный корень из 50 94 18 Оценить квадратный корень из 45 19 Оценить квадратный корень из 32 20 Оценить квадратный корень из 18 92

Как построить график y cos 2x класс 11 по математике CBSE

Подсказка: Сначала найдите амплитуду, период, фазовый сдвиг и вертикальный сдвиг для заданной периодической функции.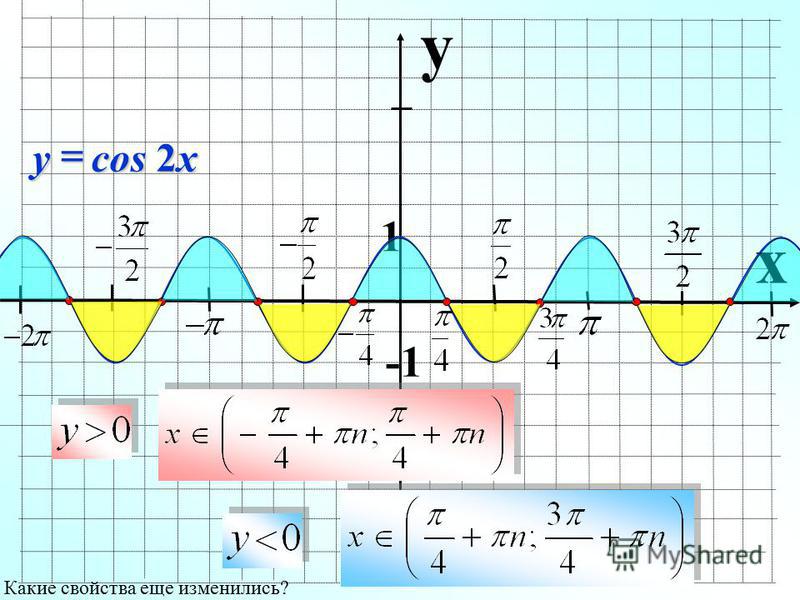 Выберите несколько точек для построения графика. Найдите точку при $x = 0$, $x = \dfrac{\pi }{4}$, $x = \dfrac{\pi }{2}$, $x = \dfrac{{3\pi}} {4}$, $x = \pi $. Занесите точки в таблицу. Затем постройте график тригонометрической функции, используя амплитуду, период, фазовый сдвиг, вертикальный сдвиг и точки.

Используемая формула:
Период: Период идет от одного пика к другому (или от любой точки к следующей точке совпадения).
Амплитуда: Амплитуда — это высота от центральной линии до пика (или впадины). Или мы можем измерить высоту от самой высокой до самой низкой точки и разделить их на $2$.
Фазовый сдвиг: Фазовый сдвиг показывает, насколько функция смещена по горизонтали от обычного положения.
Сдвиг по вертикали: Сдвиг по вертикали показывает, насколько функция смещена по вертикали от обычного положения.

Полный пошаговый ответ:
Используйте форму $a\cos\left( {bx — c} \right) + d$, чтобы найти амплитуду, период, фазовый сдвиг и вертикальный сдвиг.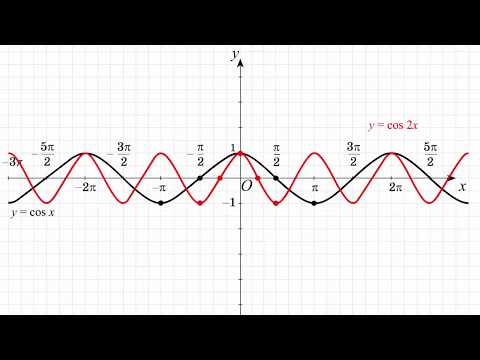
Сравните данное уравнение $y = \cos 2x$ с $a\cos \left( {bx — c} \right) + d$ и найдите переменные $a,b,c$ и $d$.
$a = 1$, $b = 2$, $c = 0$ и $d = 0$.
Найдите амплитуду $\left| а \право|$.
Здесь $a = 1$.
Амплитуда, $\left| а \право| = 1$.
Период функции можно вычислить с помощью $\dfrac{{2\pi }}{{\left| б \право|}}$.
Период: $\dfrac{{2\pi}}{{\left| b \right|}}$
Замените $b$ на $2$ в формуле для периода.
Период: $\dfrac{{2\pi}}{{\left| 2 \right|}}$
Абсолютное значение — это расстояние между числом и нулем.
Расстояние между $0$ и $2$ равно $2$.
Период: $\dfrac{{2\pi }}{2}$
Отмените общий делитель $2$.
Период: $\dfrac{{\not{2}\pi }}{{\not{2}}}$
Разделите $\pi $ на $1$.
Период: $\pi $
Найдите фазовый сдвиг по формуле $\dfrac{c}{b}$.
Фазовый сдвиг функции можно вычислить по $\dfrac{c}{b}$.
Фазовый сдвиг: $\dfrac{c}{b}$
Замените значения $c$ и $b$ в уравнении для фазового сдвига.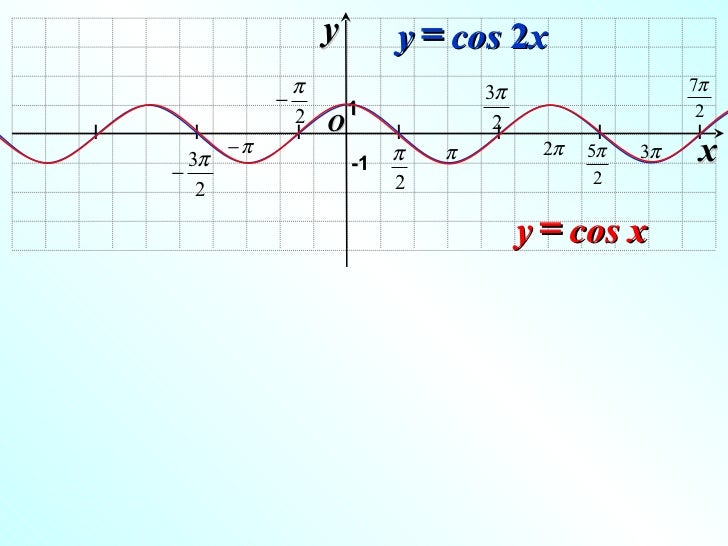
Фазовый сдвиг: $\dfrac{0}{2}$
Разделите $0$ на $2$.
Фазовый сдвиг: $0$
Найдите вертикальное смещение $d$.
Сдвиг по вертикали: $0$
Теперь нам нужно составить список свойств тригонометрической функции.
Амплитуда: $1$
Период: $\pi $
Фазовый сдвиг: $0$($0$ вправо)
Вертикальный сдвиг: $0$ 909:13 Также выбираем несколько точек для построения графика.
Найдите точку $x = 0$.
Замените в выражении переменную $x$ на $0$.
$f\left( 0 \right) = \cos \left( {2\left( 0 \right)} \right)$
Умножить $2$ на $0$.
$f\left( 0 \right) = \cos \left( 0 \right)$
Точное значение $\cos \left( 0 \right)$ равно $1$.
$ \Rightarrow f\left( 0 \right) = 1$
Окончательный ответ: $1$.
Найдите точку $x = \dfrac{\pi }{4}$.
Замените в выражении переменную $x$ на $\dfrac{\pi }{4}$.
$ \Rightarrow f\left( {\dfrac{\pi }{4}} \right) = \cos \left( {2\left({\dfrac{\pi }{4}} \right)} \right )$
Отмените общий делитель $2$.
Фактор $2$ из $4$.
$ \Rightarrow f\left( {\dfrac{\pi} {4}} \right) = \cos \left( {2\left({\dfrac{\pi}}{{2\left( 2 \right) }}} \right)} \right)$
Отменить общий множитель.
$ \Rightarrow f\left( {\dfrac{\pi} {4}} \right) = \cos \left( {\not{2}\left({\dfrac{\pi}}{{2 \times \ not{2}}}} \right)} \right)$
Перепишите выражение.
$ \Rightarrow f\left( {\dfrac{\pi }{4}} \right) = \cos \left( {\dfrac{\pi }{2}} \right)$
Точное значение $\ потому что \left( {\dfrac{\pi }{2}} \right)$ равно $0$.
$ \Rightarrow f\left( {\dfrac{\pi }{4}} \right) = 0$
Окончательный ответ: $0$.
Также нам нужно найти точку $x = \dfrac{\pi }{2}$.
Замените в выражении переменную $x$ на $\dfrac{\pi }{2}$.
$ \Rightarrow f\left( {\dfrac{\pi} {2}} \right) = \cos \left( {2\left({\dfrac{\pi} {2}} \right)} \right )$
Отменить общий делитель $2$.
$ \ Rightarrow f \ left ( {\ dfrac {\ pi} {2}} \ right) = \ cos \ left ( {\ not {2} \ left ( {\ dfrac {\ pi } {\ not {2 }}}} \right)} \right)$
Перепишите выражение.
$ \Rightarrow f\left( {\dfrac{\pi }{2}} \right) = \cos \left( \pi \right)$
Примените опорный угол, найдя угол с эквивалентными тригонометрическими значениями в первой квадрант.
Сделайте выражение отрицательным, поскольку косинус отрицателен во втором квадранте.
$ \Rightarrow f\left( {\dfrac{\pi }{2}} \right) = — \cos \left( 0 \right)$
Точное значение $\cos\left( 0 \right)$ равно $1$.
$ \Rightarrow f\left( {\dfrac{\pi }{2}} \right) = — 1 \times 1$
Умножьте $ — 1$ на $1$.
$ \Rightarrow f\left( {\dfrac{\pi }{2}} \right) = — 1$
Окончательный ответ: $ — 1$.
Опять же, нам нужно найти точку $x = \dfrac{{3\pi }}{4}$.
Замените в выражении переменную $x$ на $\dfrac{{3\pi }}{4}$.
$ \Rightarrow f\left( {\dfrac{{3\pi}}{4}} \right) = \cos \left( {2\left( {\dfrac{{3\pi}}}{4}} \справа)} \справа)$
Отменить общий делитель $2$.
$ \ Rightarrow f \ left ( {\ dfrac {{3 \ pi}} {4}} \ right) = \ cos \ left ( {2 \ left ( {\ dfrac {{3 \ pi}} {{2 \ left( 2 \right)}}} \right)} \right)$
Отменить общий множитель.
$ \Rightarrow f\left( {\dfrac{{3\pi}}{4}} \right) = \cos \left( {\not{2}\left({\dfrac{{3\pi}} {{2 \cdot \not{2}}}} \right)} \right)$
Перепишите выражение.
$ \Rightarrow f\left( {\dfrac{{3\pi}}{4}} \right) = \cos \left({\dfrac{{3\pi}}{2}} \right)$
Примените опорный угол, найдя угол с эквивалентными тригонометрическими значениями в первом квадранте.
$ \Rightarrow f\left( {\dfrac{{3\pi}}{4}} \right) = — \cos \left({\dfrac{\pi }{2}} \right)$
Точное значение $\cos\left({\dfrac{\pi}{2}}\right)$ равно $0$.
$ \Rightarrow f\left( {\dfrac{{3\pi}}{4}} \right) = 0$
Окончательный ответ: $0$.
Найдите точку $x = \pi $.
Замените в выражении переменную $x$ на $\pi $.
$ \Rightarrow f\left( \pi \right) = \cos \left( {2\left( \pi \right)} \right)$
$2\pi $ — это полный поворот, поэтому замените на $0$.
$ \Rightarrow f\left( \pi \right) = \cos \left( 0 \right)$
Точное значение $\cos \left( 0 \right)$ равно $1$.
$ \Rightarrow f\left( \pi \right) = 1$
Окончательный ответ: $1$.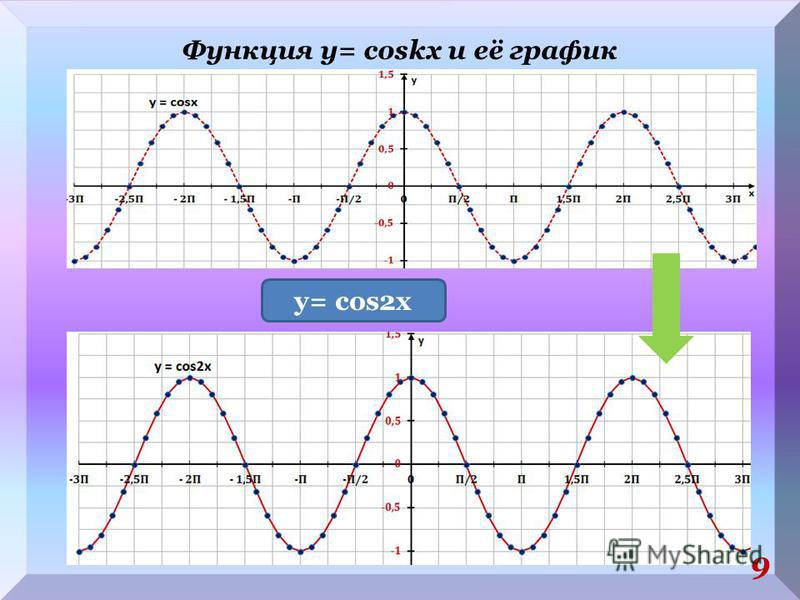
Список точек в таблице.

$ x $	$ f \ left (x right) $
$ 0 $	$ 1 $
$ \ dfrac {\ pi} {4} $	444 $ \ dfrac {\ pi} {4} $	4444 $ $ $ \ dfrac {\ pi}} $	4444444444444 40004 $ $ \ dfrac {\ pi}} $	444444 40004 $ $ \ dfrac $
$\dfrac{\pi }{2}$	$ — 1$
$\dfrac{{3\pi }}{4}$	$0$
$\pi $	$1$

, фазовый сдвиг, вертикальный сдвиг и точки.
Амплитуда: $1$
Период: $\pi $
Фазовый сдвиг: $0$($0$ вправо)
Вертикальный сдвиг: $0$

$x$	$f\left( x \right )$
$0$	$1$
$\dfrac{\pi }{4}$	$0$
$\dfrac{\pi }{2}$	$ — 1$
$\dfrac{3 pi }}{4}$	$0$
$\pi $	$1$

Примечание.
$2\cos x$ — удвоенный косинус угла $x$. Он находится между $-2$ и $2$.
$\cos 2x$ — косинус угла $2x$. Это в два раза больше угла $x$. Значение $\cos 2x$ находится между $-1$ и $1$.

Производная cos(2x) с доказательствами и графиками

Доказательство производной косинуса двойных углов с использованием цепного правила

Поскольку это составная функция, формула цепного правила используется в качестве основы для вывода косинуса из двойного угла. Косинус тригонометрической функции будет внешней функцией f(u) в составной функции cos(2x) , а моном 2x будет внутренней функцией g(x) .

В качестве предварительного условия для этой темы вам следует ознакомиться с формулой цепного правила, посетив эту статью: Цепное правило деривативов. Кроме того, вы можете посетить эту статью для доказательства производной функции косинуса: Производная косинуса, cos(x).

Предположим, нас попросили получить производную от

$latex F(x) = \cos{(2x)}$

Мы можем идентифицировать две функции, составляющие F(x) . В этом сценарии есть косинус тригонометрической функции и моном. Очевидно, что данная функция косинуса является внешней функцией, а моном 2x — это внутренняя функция. Мы можем установить внешнюю функцию как

$latex f(u) = \cos{(u)}$

, где

$latex u = 2x$

Установка монома 2x в качестве внутренней функции f (u) , обозначив его как g(x) , мы получим

$latex f(u) = f(g(x))$

$latex g(x) = 2x$

$latex u = g(x)$

Получение внешней функции f(u) с использованием производной косинуса через u , имеем

$latex f(u) = \cos{(u)}$

$latex f'(u) = -\sin{(u)}$

Вывод внутренней функции g(x ) с использованием степенного правила, так как это моном, мы имеем

$latex g(x) = 2x$

$latex g'(x) = 2$

Алгебраически умножая производную внешней функции $latex f'( u)$ производной от внутренней функции $latex g'(x)$, имеем

$latex \frac{dy}{dx} = f'(u) \cdot g'(x)$

$latex \frac{dy}{dx} = (-\sin{(u)}) \cdot (2)$

Подставив u в f'(u) , мы получим

$latex \frac{dy}{dx} = (-\sin{(u)}) \cdot (2)$

$latex \frac{dy}{dx} = – (\sin{(2x)} \cdot (2))$

$latex \frac{dy}{dx} = – ((2) \cdot \sin{(2x )})$

В этом случае мы предпочитаем не применять тригонометрическое тождество двойного угла для косинуса, так как это сделает формулу производной менее упрощенной.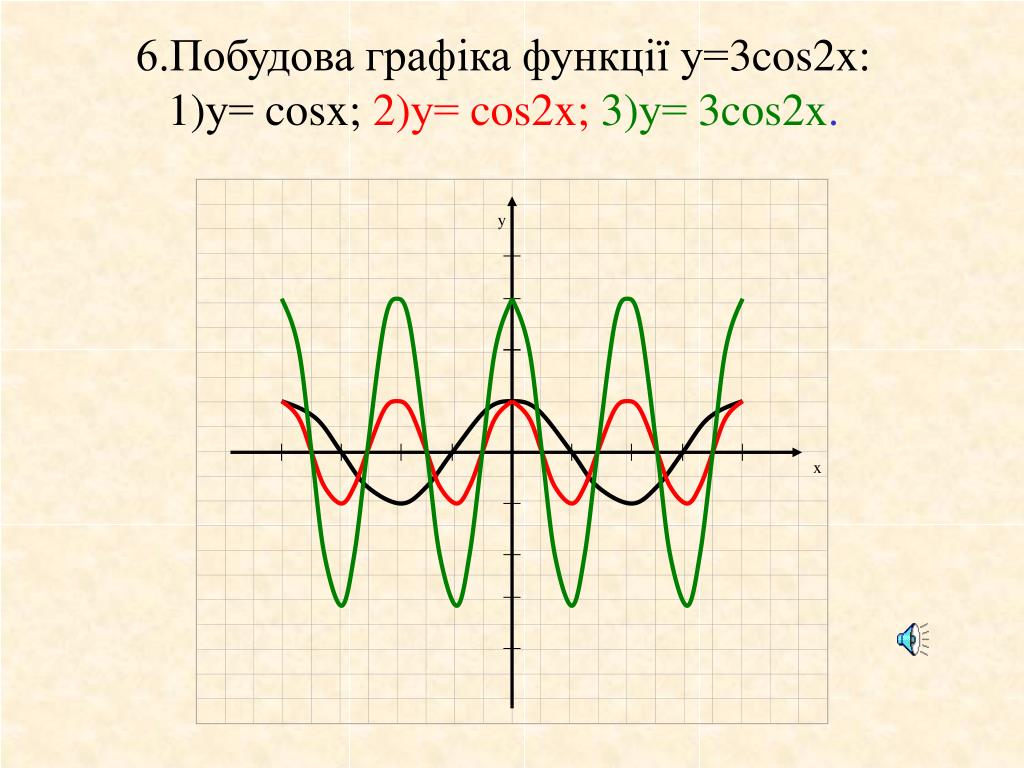 Следовательно, это приводит нас к производной формуле cos(2x)

$latex \frac{d}{dx} \cos{(2x)} = -2\sin{(2x)}$

---

Как найти косинус двойного угла?

Как упоминалось выше, косинус двойного угла является сложной функцией косинуса тригонометрической функции и одночлена 2x . Эту функцию легко вывести, и вместо того, чтобы все время использовать метод цепного правила, мы можем просто использовать проверенную формулу производной для косинуса двойного угла.

МЕТОД 1: Когда косинус двойного угла

2x должен быть получен через ту же переменную х .

$латекс \frac{d}{dx} \left( \cos{(2x)} \right) = -2\sin{(2x)}$

Шаг 1: Проанализируйте, является ли $latex \cos{(2x)}$ функцией одной и той же переменной $latex x$ или f(x) . Если $latex \cos{(2x)}$ является функцией других переменных, таких как f(t) или f(y) , будет использоваться неявное дифференцирование, которое выходит за рамки этой статьи.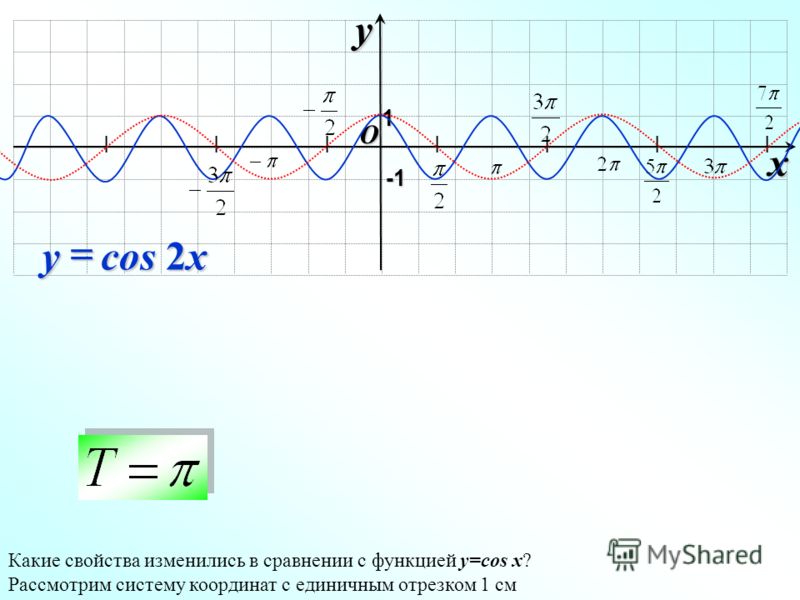

Шаг 2: Непосредственно применить проверенную формулу производной косинуса двойного угла.

$latex \frac{dy}{dx} = -2\sin{(2x)}$

Если больше ничего не нужно упрощать, это будет окончательный ответ.

СПОСОБ 2: Когда дано косинус функции $latex v \times 2$ и выводится через

x.

$латекс \frac{d}{dx} \left( \cos{(2v)} \right) = -2\sin{(2v)} \cdot \frac{d}{dx} ( в)$

Шаг 1: Выразите функцию в виде $latex G(x) = \cos{(2v)}$, где $latex v$ представляет любую функцию, отличную от x .

Шаг 2: Рассмотрим $latex \cos{(2x)}$ как внешнюю функцию $latex g(v)$ и $latex v$ как внутреннюю функцию $latex h(x)$ составная функция $latex G(x)$. Отсюда имеем

$latex g(v) = \cos{(2v)}$

и

$latex h(x) = v$

Шаг 3: Получите производную внешней функции $latex g(v)$, которая должна использовать производную косинуса двойного угла, выраженную через $latex v$.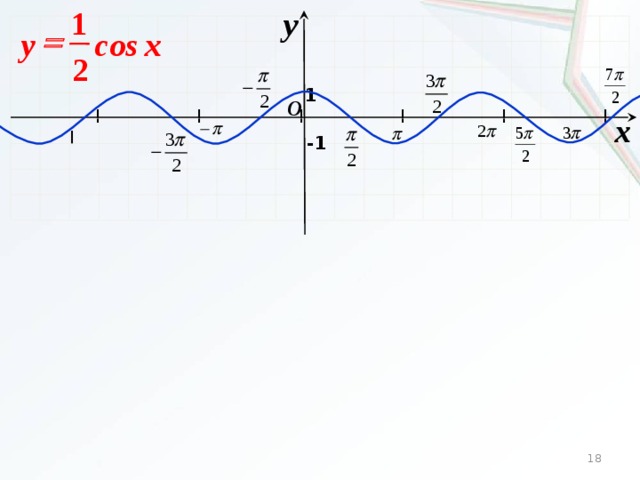

$latex \frac{d}{du} \left( \cos{(2v)} \right) = -2\sin{(2v)}$

Шаг 4: Получить производную внутренней функции $latex h(x) = v$. Используйте соответствующее производное правило, применимое к $latex v$.

Шаг 5: Примените основную формулу цепного правила путем алгебраического умножения производной внешней функции $latex g(v)$ на производную внутренней функции $latex h(x)$

$latex \frac{dy}{dx} = \frac{d}{du} (g(v)) \cdot \frac{d}{dx} (h(x))$

$latex \frac{dy}{dx} = (-2\sin{ (2v)}) \cdot \frac{d}{dx} (v)$

Шаг 6: Подставить $latex v$ в $latex g'(v)$

Шаг 7: Упростите и примените любой функциональный закон, когда это применимо, чтобы завершить ответ.

---

График

cos(2x) VS. его производная

Учитывая функцию

$latex f(x) = \cos{(2x)}$

ее график показан как

И, как мы уже знаем, путем получения $latex f(x) = \ cos{(2x)}$, мы получаем

$latex f'(x) = -2\sin{(2x)}$

, что на графике отображается как

Если проиллюстрировать оба графика в одном, мы получим

Глядя на различия между этими функциями на основе этих графиков, вы можете видеть, что исходная функция $latex f(x) = \cos{(2x)}$ имеет область определения

$latex (-\infty,\infty)$ или все действительные числа

и существуют в диапазоне

$latex [-1,1]$

, тогда как производная $latex f'(x) = -2\sin{(2x)}$ имеет область определения

$latex (-\infty,\infty)$ или всех действительных чисел

и существует в диапазоне

$latex [-2, 2]$

График Сравнение

cos(2x) и cos(x) , а также их производных

Графики, показанные ниже, иллюстрируют разницу между $latex \cos{(2x)}$ и $latex \ потому что {(х)} $

и в терминах их производных

---

Примеры

Ниже приведены некоторые примеры получения косинуса двойного угла с использованием первого или второго метода, в зависимости от того, какой из них более применим.

ПРИМЕР 1

Получение: $latex f(\beta) = \cos{(2\beta)}$

Решение:

Анализ двойного косинуса угол, он должен быть выведен через $latex\beta$. Следовательно, мы можем использовать первый метод для вывода этой проблемы.

Шаг 2: Непосредственно применить формулу производной косинуса двойного угла через $latex\beta$. Поскольку дальнейшее упрощение не требуется, окончательный ответ будет следующим:

$latex f'(\beta) = -2\sin{(2\beta)}$

ПРИМЕР 2

Получение: $latex G (x) = \cos{(2\ln{(x)})}$

Решение: Анализ данного косинуса функции умножить на два, это косинус логарифмической функции, умноженный на два. Следовательно, мы можем использовать второй метод для вывода этой проблемы.

Шаг 1: Выразите функцию в виде $latex G(x) = \cos{(2v)}$, где $latex v$ представляет собой любую функцию, отличную от x .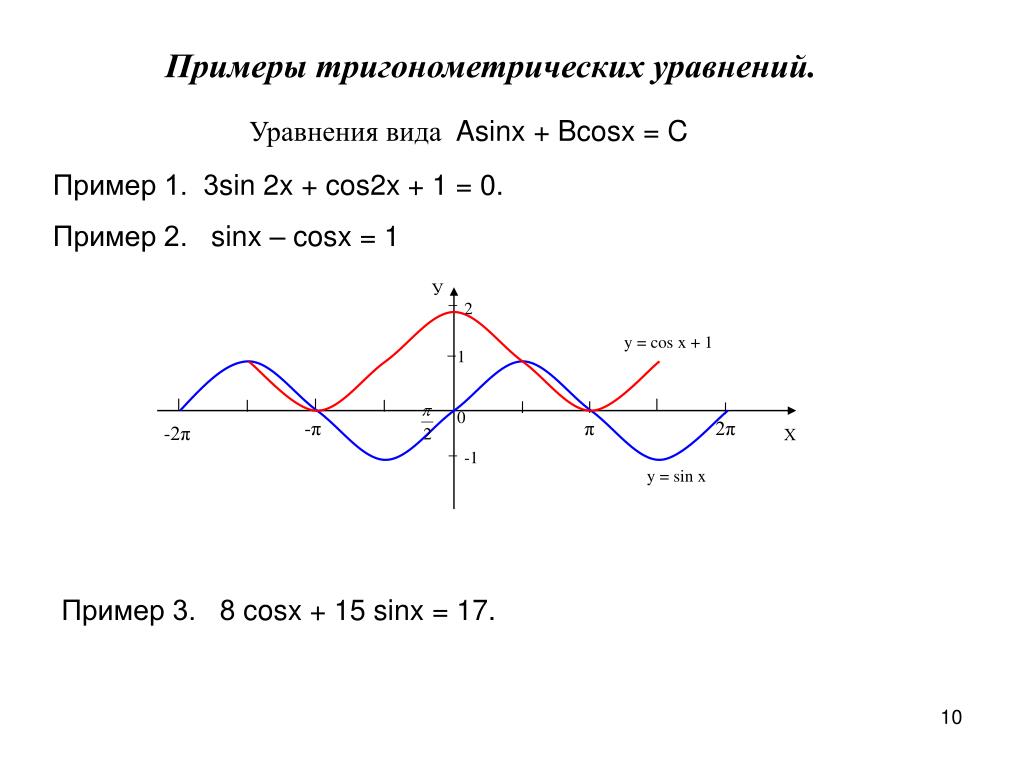 В этой задаче

$latex v = \ln{(x)}$

Мы заменим это позже, когда доработаем производную задачи.

Шаг 2: Рассмотрим $latex \cos{(2v)}$ как внешнюю функцию $latex g(v)$ и $latex v$ как внутреннюю функцию $latex h(x)$ составного функция $латекс G(x)$. Для этой задачи у нас есть

$latex g(v) = \cos{(2v)}$

и

$latex h(x) = v = \ln{(x)}$

Шаг 3: Получите производная внешней функции $latex g(v)$, которая должна использовать производную косинуса двойного угла через $latex v$.

$latex \frac{d}{du} \left( \cos{(2v)} \right) = -2\sin{(2v)}$

Шаг 4: Получите производную от внутренняя функция $latex h(x)$ или $latex v$. Поскольку наш $latex v$ в этой задаче является логарифмической функцией, мы будем использовать производную логарифмических функций для получения $latex v$.

$латекс \frac{d}{dx}(h(x)) = \frac{d}{dx} (\ln{(x)})$

$латекс \frac{d}{dx}( h(x)) = \frac{1}{x}$

Шаг 5: Примените основную формулу цепного правила, алгебраически умножив производную внешней функции $latex g(v)$ на производную внутренней функция $latex h(x)$

$latex \frac{dy}{dx} = \frac{d}{du} (g(v)) \cdot \frac{d}{dx} (h(x) )$

$латекс \frac{dy}{dx} = (-2\sin{(2v)}) \cdot \left(\frac{1}{x}\right)$

Шаг 6: Подставить $latex v$ в $latex g'(v)$

$latex \frac{dy}{dx} = (-2\sin{(2v)}) \cdot \left (\frac{1}{x}\right)$

$латекс \frac{dy}{dx} = (-2\sin{(2(\ln{(x)}))}) \cdot \left (\frac{1}{x}\right)$

Шаг 7: Упростите и примените любой закон функции, когда это применимо, чтобы получить окончательный ответ.

No related posts.