Корни в квадратном уравнении: Частный случай нахождения корней квадратного уравнения — урок. Алгебра, 8 класс.

2 + b*x + c = 0,где x- переменная, a,b,c – константы; a<>0. Задача состоит в отыскании корней уравнения.

Геометрический смысл квадратного уравнения

Графиком функции, которая представлена квадратным уравнением является парабола. Решения (корни) квадратного уравнения — это точки пересечения параболы с осью абсцисс (х). Из этого следует, что есть три возможных случая:
1) парабола не имеет точек пересечения с осью абсцисс. Это означает, что она находится в верхней плоскости с ветками вверх или нижней с ветками вниз. В таких случаях квадратное уравнение не имеет действительных корней (имеет два комплексных корня).

2) парабола имеет одну точку пересечения с осью Ох. Такую точку называют вершиной параболы, а квадратное уравнение в ней приобретает свое минимальное или максимальное значение. В этом случае квадратное уравнение имеет один действительный корень (или два одинаковых корня).

3) Последний случай на практике интересный больше — существует две точки пересечения параболы с осью абсцисс. 2 и осуществим преобразование

Отсюда находим

Формула дискриминанта и корней квадратного уравнения

Дискриминантом называют значение подкоренного выраженияЕсли он положительный то уравнение имеет два действительных корня, вычисляемые по формулеПри нулевом дискриминант квадратное уравнение имеет одно решение (два совпадающих корня), которые легко получить из приведенной выше формулы при D=0При отрицательном дискриминант уравнения действительных корней нет. Однако исують решения квадратного уравнения в комплексной плоскости, и их значение вычисляют по формуле

Теорема Виета

Рассмотрим два корня квадратного уравнения и построим на их основе квадратное уравнение.С записи легко следует сама теорема Виета: если имеем квадратное уравнение видато сумма его корней равна коэффициенту p, взятому с противоположным знаком, а произведение корней уравнения равен свободному слагаемому q. Формульная запись вышесказанного будет иметь видЕсли в классическом уравнении константа а отлична от нуля, то нужно разделить на нее все уравнение, а затем применять теорему Виета. 2+x-6=0.

Решение: В случаях когда есть малые коэффициенты при х целесообразно применять теорему Виета. По ее условию получаем два уравнения

С второго условия получаем, что произведение должно быть равно -6. Это означает, что один из корней отрицателен. Имеем следующую возможную пару решений{-3;2}, {3;-2}. С учетом первого условия вторую пару решений отвергаем.
Корни уравнения равны

 

Задача 5. Найти длины сторон прямоугольника, если его периметр 18 см, а площадь 77 см².

Решение: Половина периметра прямоугольника равна сумме соседних сторон. Обозначим х – большую сторону, тогда 18-x меньшая его сторона. Площадь прямоугольника равна произведению этих длин:
х(18-х)=77;
или
х²-18х+77=0.
Найдем дискриминант уравнения

Вычисляем корни уравнения

Если х=11, то 18-х=7, наоборот тоже справедливо (если х=7 , то 21-х=9).

 

Задача 6. Разложить квадратное 10x²-11x+3=0 уравнения на множители.

Решение: Вычислим корни уравнения, для этого находим дискриминант

Подставляем найденное значение в формулу корней и вычисляем

Применяем формулу разложения квадратного уравнения по корнями

Раскрыв скобки получим тождество.

Квадратное уравнение с параметром

Пример 1. При каких значениях параметра а, уравнение (а-3)х²+(3-а)х-1/4=0 имеет один корень?

Решение: Прямой подстановкой значения а=3 видим, что оно не имеет решения. Далее воспользуемся тем, что при нулевом дискриминанте уравнение имеет один корень кратности 2. Выпишем дискриминант

упростим его и приравняем к нулю

Получили квадратное уравнение относительно параметра а, решение которого легко получить по теореме Виета. Сумма корней равна 7, а их произведение 12. Простым перебором устанавливаем, что числа 3,4 будут корнями уравнения. Поскольку решение а=3 мы уже отвергли в начале вычислений, то единственным правильным будет — а=4. Таким образом, при а=4 уравнение имеет один корень. 2+(2а+6)х-3а-9=0 имеет более одного корня?

Решение:Рассмотрим сначала особые точки, ими будут значения а=0 и а=-3. При а=0 уравнение упростится до вида 6х-9=0; х=3/2 и будет один корень. При а= -3 получим тождество 0=0.
Вычислим дискриминант

и найдем значения а при котором оно положительно

С первого условия получим а>3. Для второго находим дискриминант и корни уравнения


Определим промежутки где функция принимает положительные значения. Подстановкой точки а=0 получим 3>0. Итак, за пределами промежутка (-3;1/3) функция отрицательная. Не стоит забывать о точке а=0, которую следует исключить, поскольку в ней исходное уравнение имеет один корень.
В результате получим два интервала, которые удовлетворяют условию задачи

Подобных задач на практике будет много, постарайтесь разобраться с заданиями самостоятельно и не забывайте учитывать условия, которые взаимоисключают друг друга. Хорошо изучите формулы для решения квадратных уравнений, они довольна часто нужны при вычислениях в разных задачах и науках.

Квадратное уравнение: формула корней, как их решать и примеры

Квадратное уравнение — это уравнение вида ax² + bx + c, где a, b, c — некоторые числа (причём обязательно a ≠ 0),

В таком уравнении:

• x — переменная, которая присутствует в таком уравнении во второй степени,
• a — первый коэффициент,
• b — второй коэффициент,
• c — свободный член.

Ещё такое уравнение называется квадратный трёхчлен, т.к. самая большая степень в нём квадрат и он состоит из 3 одночленов.

Для решения таких уравнений сначала находится дискриминант по этой формуле:

Эту формулу нужно выучить наизусть.

Если:

• D < 0 <=> корней не существует,
• D = 0 <=> есть один корень,
• D > 0 <=> есть два корня.

Пример: x² – x – 3 = 0; a = 1, b = –1, c = –3, D = (–1)² – 4×1×(–3) = 1 + 12 = 13, D > 0 <=> есть два корня.

Когда уже точно известно, что корни существуют, и известно количество этих корней, можно приступить к их поиску с помощью этой формулы:

Корни таких уравнений находят с помощью этой формулы.

Пример: x² – x – 3 = 0; a = 1, b = –1, c = –3, D = 13.

X1,2 = ((–(–1)) ±√13)/(2×1) =>

x1 = (1 + √13)/2 ≈ (1 + 3,60555)/2 ≈ 2,302775

x2 = (1 – √13)/2 ≈ (1 – 3,60555)/2 ≈ -1,302775

Примеры

Пример 1

20x² – 15x – 10 = 0

Лучше сразу выписать так: a = 20, b = – 15, c = – 10.

1. Ищем дискриминант: формула D = b² – 4ac <=> D = (– 15)² – 4 × 20 × (– 10) = 225 + 800 = 1025; D > 0 <=> значит есть два корня.

2. Ищем эти корни: формула корней

2.1. Разбиваем формулу на две части, первый корень:

Уравнение 20x² – 15x – 10 = 0, где a = 20, b = – 15, c = – 10; D =1025.

x1 = ((–(–15)) + √ 1025)/(2×20) = (15 + 32,0156) / 40 ≈ 1,17539

2.2. Второй корень:

Уравнение 20x² – 15x – 10 = 0, где a = 20, b = – 15, c = – 10; D =1025.

x2 = ((–(–15)) – √ 1025)/(2×20) ≈ (15 – 32,0156) / 40 ≈ -0,42539

Пример 2

–x² +6x + 18 = 0

a = –1, b = 6, c = 18

Дискриминант D = b² – 4ac

D = 6² – 4×(–1)×(18) = 36 + 72 = 108, D > 0 <=> есть два корня

Ищем корни:

a = –1, b = 6, c = 18, D = 108

X1,2 = ((–6) ±√108)/(2×(–1)) =>

x1 = ((–6) +√108)/(–2) = ((–6) + 10,3923)/(–2) = – 2,19615

x2 = ((–6) –√108)/(–2) = ((–6) – 10,3923)/(–2) = 8,19615

Как разложить квадратный трёхчлен на множители?

Продолжим с примером уравнения 20x² – 15x – 10 = 0

Мы уже нашли корни

x1 ≈ 1,17539, x2 ≈ -0,42539

Выносим коэффициент x² за скобки, и оба корня ставятся с противоположными знаками таким образом:

20x² – 15x – 10 = 20 (x – 1,17539) (x+0,42539)

Хотите проверить? Открываем скобки и проверяем

20 (x – 1,17539) (x+0,42539) = 20 (x²–1,17539x + 0,42539x–0,42539×1,17539) = 20 (x²–0,75x – 0,4999991521) =

20 x²–15x–9,999983042

Погрешность в 0,000016958 должна быть из-за округления в предыдущих расчётах.

Виды квадратных уравнений

Полное и неполное квадратное уравнение

В полном уравнении присутствуют все три его члена (ax² + bx + c = 0). В противном случае уравнение неполное, например:

–x² – 9 = 0 (отсутствует bx)

x² + 16x = 0 (отсутствует с)

–5x² = 0 (отсутствуют bx и с)

Т.е. это когда коэффициент с = 0 или b = 0 (или оба одновременно равны нулю). Внимание: о том, что «a» может быть равно нулю, не говорится, т.к. таким образом уравнение станет линейным (ax + b = 0).

Как решать неполное квадратное уравнение?

Способ решения, когда b=0

5x² – 5 = 0

5x² = 5, делим всё на 5

x² = 1

x = ± √1 ⇔ x = 1 или x = –1

Первый способ решения, когда c=0 (это быстрый метод)

Пример:

x² + 16x = 0 (выносим x за скобки)

x (x + 16) = 0, таким образом, либо x = 0, либо то, что в скобках, равно нулю,

x = 0 или (x + 16)= 0

(x + 16)= 0 ⇔ x = – 16

Второй способ решения, когда c=0

Неполное уравнение (c=0, b=0 или когда оба равны нулю) можно решить по той же системе, как и полное, правильно выписав коэффициенты (но это долго и нерационально).

Например:

x² + 16x = 0

a = 1, b = 16, c = 0 (здесь отсутствует c, значит он равен нулю)

Дискриминант: D = b² – 4ac = 16² – 4×1×0 = 16² = 256 >0, есть два корня.

Ищем корни X1,2 = ((–b) ±√D)/(2×(a)) =>

X1,2 = ((–16) ± √256)/(2×(1)) =>

x1 = ((–16) + √256)/(2×(1)) = ((–16) + 16)/2 = 0

x2 = ((–16) – √256)/(2×(1)) = ((–16) – 16)/2 = –32/2 = – 16

Способ решения, когда b=0 и c=0

Например:

3x² = 0

Делим всё на 3

x² = 0

x = 0

Приведённое квадратное уравнение

Чтобы получить приведённое квадратное уравнение, нужно лишь разделить обе части уравнения на a:

x² + px + q = 0, где:

p = b/a

q = c/a

Примеры:

3x² – 6x = 0 (делим всё на 3) ⇔ x² – (6/3)x = 0 ⇔ x² – 2x = 0 (неполное приведённое)

2x² – 4x – 2 = 0 (делим всё на 2) ⇔ x² – (4/2)x – (2/2) = 0 ⇔ x² – 2x – 1 = 0 (полное приведённое)

Геометрический смысл решения корней квадратных уравнений

Корни квадратного уравнения ещё являются и нулями функции, т. е. если вы ищете нули функции (в каких точках функция пересекает ось Ox), то вы их найдёте именно через этот процесс: поймёте, если они существуют, рассчитав дискриминант, затем найдёте их, используя формулу корней.

Вспомним наш пример уравнения 20x² – 15x – 10 = 0.

Мы сделали график 20x² – 15x – 10, на котором видно, что наши корни (x1 ≈ 1,17539, x2 ≈ -0,42539) являются нулями этой функции.Другой пример, в котором есть только один нуль, функция 3x². Здесь х = 0.Функция x² + 1 не имеет корней, это мы и видим на графике функции (она не пересекает ось Ox).

Узнайте также, что такое Теорема Виета и Парабола.

Как решать квадратные уравнения / Бери и делай

Решение квадратных уравнений — это важная тема в школьном курсе алгебры. Если хотите освежить знания, помочь подросткам с уроками или впервые знакомитесь с этим вопросом, воспользуйтесь нашей простой инструкцией, где собраны несколько способов решения квадратных уравнения.

Мы в «Бери и Делай» постарались максимально просто и понятно объяснить эту тему, а в конце статьи добавили бонус, благодаря которому вы сможете за секунды решать подобные уравнения.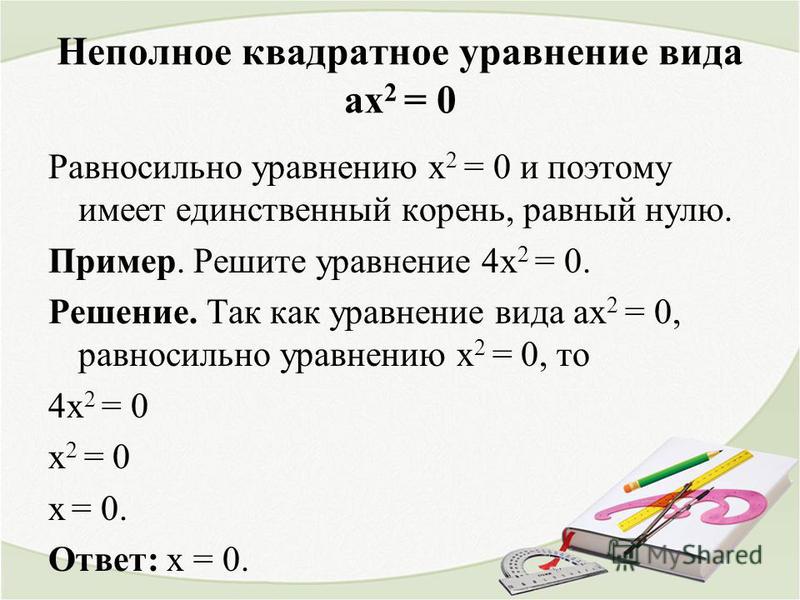

Что такое уравнение

Уравнение — это равенство, где есть переменная, чье значение нужно найти. Выражение 3 + x = 9 — это уравнение с переменной x. Именно ее значение нужно найти.

Корнем уравнения называют такое значение переменной, при подстановке которого уравнение превращается в верное равенство. Если в вышеуказанное уравнение мы подставим вместо x число 5, то получим 3 + 5 = 8, что противоречит правой части уравнения. Если вместо x взять число 6, то получим 3 + 6 = 9, а значит, 6 является корнем уравнения.

Решая уравнения, мы ищем все его корни или доказываем, что их не существует.

Что такое квадратное уравнение

Это уравнение вида ax² + bx + c = 0, где корнем является значение переменной x, обращающее квадратный трехчлен в 0, а само квадратное уравнение — в верное равенство. Другими словами, благодаря наличию x² это уравнение является квадратным.

Квадратное уравнение содержит коэффициенты:

• а — старший или первый коэффициент, не равный 0 (иначе это линейное уравнение)
• b — второй коэффициент
• c — свободный член

Не всегда новичкам легко определить коэффициенты уравнения, потому что b и c вместе или по отдельности могут равняться 0.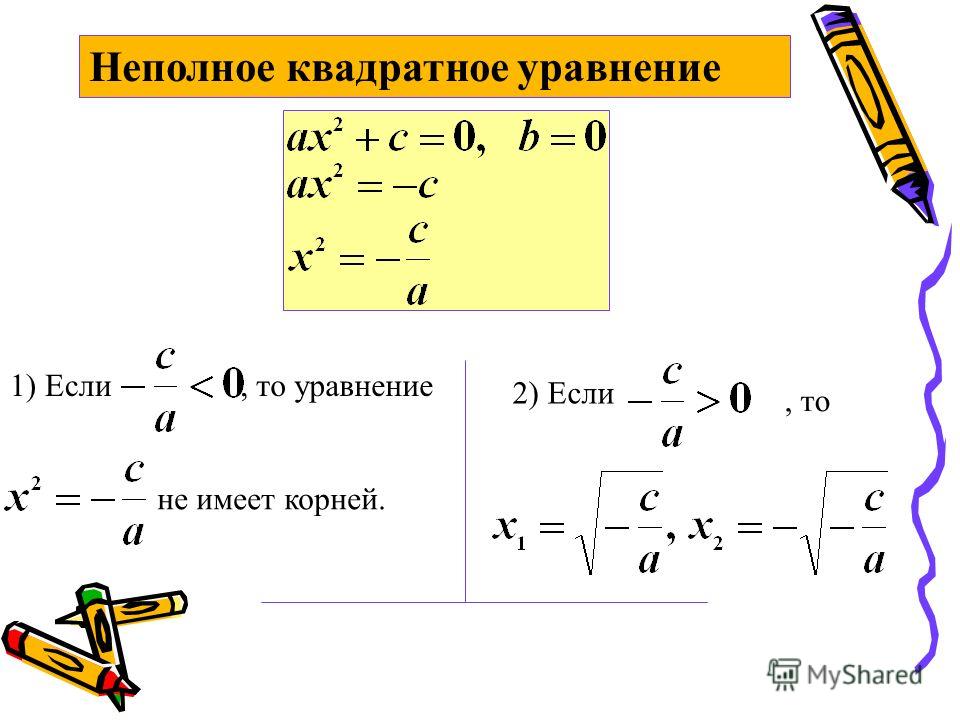 Обратите внимание, как могут выглядеть квадратные уравнения и их коэффициенты:

О чем важно знать:

• В уравнении x² + 7x + 1 = 0 старший коэффициент равен 1. Такие квадратные уравнения называются приведенными. Если старший коэффициент отличается от 1, например равен 2, как в примере 2ײ + 7x + 1 = 0, то это неприведенное квадратное уравнение.
• По условию в квадратном уравнении a ≠ 0. Но другие коэффициенты могут равняться 0, например x² + 5x = 0, или 5ײ = 0, или x² + 5 = 0. Если коэффициенты b и c равны по отдельности или вместе 0, то квадратное уравнение называется неполным. Соответственно, у полного квадратного уравнения все коэффициенты отличны от нуля.
• Как привести уравнение к виду ax² + bx + c = 0? Допустим, у нас есть уравнение x² — 3x — 5 = 11 — 3x. В этом случае нужно сделать так, чтобы в правой части остался только 0: x² — 3x — 5 — 11 + 3x = 0. Полученное уравнение можно сократить до x² — 16 = 0. Получилось приведенное неполное квадратное уравнение, где коэффициенты а = 1, b = 0, c = —16.

Как решать неполные квадратные уравнения

Существует 3 типа неполных квадратных уравнений:

• ax² = 0, где коэффициенты b = 0 и c = 0
• ax² + c = 0, при b = 0
• ax² + bx = 0, при c = 0

• Как решить уравнение типа ax² = 0

У этого уравнения коэффициенты b и c равны 0, но а ≠ 0. Если уравнение ax² = 0 разделить на некое число a (которое по условию не равняется 0), то получим x² = 0. Получается, что корнем уравнения является 0, так как 0² = 0. Других корней у уравнения нет. Значит, любое неполное квадратное уравнение ax² = 0 имеет только один корень x = 0.

На картинке выше в качестве примера мы решили уравнение —8ײ = 0 и выяснили, что корень x = 0.

Вывод: уравнение типа ax² = 0 имеет только один корень x = 0.

• Как решить уравнение типа ax² + с = 0

В этом типе уравнения b = 0, но c ≠ 0 и а ≠ 0. Преобразуем уравнения, перенеся свободный член в правую часть: ax² = —c. Теперь разделим обе части на первый коэффициент a и получим x² = —c/а.

Если c/а < 0, то уравнение x² = —c/а не имеет корней, потому что квадрат любого числа равен неотрицательному числу. Если же c/а > 0, то уравнение имеет 2 корня.

На картинке выше мы решили уравнение 8ײ + 5 = 0, выяснив, что у него нет корней.

Вывод: уравнение типа ax² + с = 0 не имеет корней или имеет 2 корня, которые при возведении в квадрат дают x² = —c/а.

• Как решить уравнение типа ax² + bx = 0

В таком типе уравнения c = 0, но а ≠ 0. Чтобы решить его, можно использовать метод разложения на множители. Возьмем многочлен в левой части и разложим его на множители, убрав за скобки общий множитель х. Получим: x × (ax + b) = 0. Отсюда получаем, что х = 0 или ax + b = 0. Во втором случае мы имеем уже линейное уравнение, чей корень равен x = −b/a. Получается, что у уравнения ax² + bx = 0 имеется 2 корня: x₁ = 0 и x₂= −b/a.

На картинке выше мы решили уравнение 8ײ + 8x = 0, определив два корня: x₁ = 0 и x₂ = −1.

Вывод: уравнение типа ax² + bx = 0 имеет 2 корня, это x₁ = 0 и x₂= −b/a.

Что такое дискриминант и формула для нахождения корней

Определить количество корней квадратного уравнения можно и не решая его, с помощью выражения дискриминанта (обозначается буквой D), в которое подставляют коэффициенты квадратного уравнения.

Свойства дискриминанта подскажут, сколько корней имеет уравнение:

• если D < 0, корней нет
• если D = 0, то есть один корень. Вычислить его можно по формуле х = −b/2a
• если D > 0, то есть 2 различных корня. В этом случае их можно вычислить по формуле:

Обратите внимание, что в этой формуле тоже есть дискриминант, он находится под корнем. Это универсальная формула для нахождения корней квадратного уравнения. Как ею пользоваться?

Допустим, нужно вычислить корни уравнения x² — 5x + 6 = 0.

Шаг № 1: Запишем квадратное уравнение и определим его коэффициенты. В данном случае мы имеем: a = 1, b = —5, c = 6. Вычислим значение дискриминанта по формуле D = b² — 4ac. Получим, что D = 1. Получается, у нашего уравнения 2 корня.

Шаг № 2: Найдем корни уравнения через формулу с дискриминантом, подставив в нее коэффициенты.

Шаг № 3: Произведем вычисления и получим значения двух корней. Получаем, что уравнение x² — 5x + 6 = 0 имеет 2 корня: x₁ = 3 и x₂ = 2. Готово!

Как решить квадратное уравнение, разложив его на множители

Мы уже пользовались этим способом выше, когда решали неполное уравнение типа ax² + bx = 0. Разложить на множители можно любое квадратное уравнение, но этим стоит заниматься только в том случае, если это облегчит расчеты.

Например, попробуем решить уравнение х² + 10х — 24 = 0. Сначала разложим левую часть на множители и получим х² + 10х — 24 = х² + 12х — 2х — 24 = х(х + 12) — 2(х + 12) = (х + 12)(х — 2). Теперь наше уравнение можно записать как (х + 12)(х — 2) = 0. Получается, что хотя бы один из множителей равен нулю. Если (х + 12) = 0, то х = —12. Если (х — 2) = 0, то х = 2.

Тогда уравнение х² + 10х — 24 = 0 имеет 2 корня: x₁ = −12 и x₂ = 2.

Как быстро решать квадратные уравнения с помощью теоремы Виета

Согласно теореме Виета, сумма корней x₁ и x₂ в уравнении x² + bx + c = 0 равна второму коэффициенту с противоположным знаком, а произведение этих же корней равняется свободному члену или c (мы изобразили это на картинке выше). Другими словами, получается, что корни уравнения фактически спрятаны внутри коэффициентов уравнения.

Благодаря этому, если вы имеете дело с приведенным квадратным уравнением (у которого a = 1), то эта теорема может помочь вам быстро найти корни уравнения.

В качестве примера возьмем уравнение x² — 8x + 15 = 0. Это приведенное квадратное уравнение (т. е. старший коэффициент равен 1), а D = 4, а значит, корня точно 2. Воспользуемся теоремой Виета и получим следующие равенства:

x₁ + x₂ = 8

x₁ × x₂ = 15

Нам надо найти такие 2 числа, которые в сумме дают 8, а их произведение равно 15. Методом подстановки получаем x₁ = 3 и x₂ = 5. На всякий случай проверим, решив уравнение с помощью формулы для нахождения корней. Подставим коэффициенты в формулу, произведем вычисления и получим: х₁ = (8 — 2) / 2 = 3 и x₂ = (8 + 2) / 2 = 5. Все верно!

Важно: использовать теорему Виета следует в тех случаях, когда это облегчит расчеты.

Бонус: хитрость, которая позволяет быстро находить корни квадратного уравнения

Попробуем пошагово быстро решить квадратное уравнение 27ײ — 12х + 1 = 0 с помощью этой хитрости:

Шаг № 1: В уравнении 27ײ — 12х + 1 = 0 обратим внимание на второй коэффициент, который равен —12.

Шаг № 2: Подберем 2 таких числа, которые в сумме дают —12. При этом их произведение должно равняться числу 27, которое является произведением a и с, т. е. это 27 × 1 = 27. В нашем случае это числа —9 и —3.

Шаг № 3: Теперь поменяем у этих чисел знаки на противоположные, получив 9 и 3. И разделим каждое из них на число первого коэффициента уравнения, т. е. в нашем случае на 27. Получим 2 числа: это 9/27 и 3/27. Эти числа можно сократить, получив 1/3 и 1/9. Они и являются корнями уравнения, т. е. уравнение 27ײ — 12х + 1 = 0 имеет 2 корня: x₁ = 1/3 и x₂ = 1/9. На всякий случай можно проверить себя, решив уравнение с помощью формулы для нахождения корней.

Внимание: в апреле 2022 года мы исправили фактические неточности в этой статье.

Линейные, квадратные и кубические уравнения

На этой странице вы узнаете:

• Почему неизвестное обозначают через x?
• Как находить корни квадратного уравнения, не считая их?
• Как дискриминант может повлиять на количество корней уравнения?

Понятие уравнения

Главный секрет математики в том, что любую задачу можно решить уравнением. А решить уравнение – значит найти все его корни или доказать, что их нет.

Давай разберемся как это сделать.

Вспомним, что:

Уравнение – это равенство, содержащее неизвестное, обозначенное буквой.

Корнем уравнения называется такое значение неизвестного, при котором уравнение становится верным равенством.

Например, число 8 будет корнем уравнения 2x — 3 = 5 + x, потому что равенство 2 * 8 — 3 = 5 + 8 верное.

Почему неизвестное обозначают через x? Арабские математики в IX веке для записи формул использовали слова. Неизвестную величину они называли “шей”, что буквально Арабские математики в IX веке для записи формул использовали слова. Неизвестную величину они называли “шей”, что буквально означает “нечто”. Выглядело это примерно так: Позднее испанские ученые переводили записи на свой язык. Они записывали неизвестное как xei, поскольку в их языке отсутствовал звук [ш]. С появлением формул слово сократилось до одной буквы x.

Линейные уравнения

Что же такое линейное уравнение?

Линейное уравнение – это уравнение, в котором неизвестная находится в степени 1.

Вид линейного уравнения:

ax + b=0 , где 
х – неизвестная
а – коэффициент при неизвестной
b – свободный член

Стоит отметить, что а и b в таком уравнение известны, также оба этих числа можно называть коэффициентами.

Как же решить такое уравнение?

Для решения линейного уравнения нужно выразить х и найти числовое значение, то есть сделать такие преобразования, чтобы в одной части уравнения осталась только неизвестная, а в другой собралось все остальное.

Преобразования, которые можно совершать:

1. Переносить слагаемое в другую часть уравнения с противоположным знаком.

x — 5 = 0
x = 0 + 5
x = 5

2. Умножать или делить обе части уравнение на одно и то же число или выражение, которое не равно нулю.

3x = 12  | : 3
x = 4

Давайте рассмотрим решение линейного уравнения на следующем примере

2(x + 5) — 4x + 2 = 0

1. Сначала раскроем скобки
   2x + 10 — 4x + 2 = 0

2. Для упрощения сложим подобные слагаемые
   -2x + 12 = 0

3. Теперь перенесем слагаемое без неизвестной в правую часть и разделим обе части уравнения на коэффициент при неизвестной, то есть выразим х
   -2x = -12 | : (-2)
   x = 6

Значение неизвестной найдено, а значит единственное решение данного уравнения 6

С линейными уравнениями можно столкнуться и в жизни. 

Допустим, нам нужно приготовить 570 грамм теста на пирожки.  

Обозначим вес одной части за x. Составим и решим уравнение для получения этого количества теста:

12x + 6x + x = 570
19x = 570
x = 30

Мы узнали, что одна часть — это 30 грамм. Теперь посчитаем сколько грамм продуктов нам потребуется.

• Мука: 12 * 30 = 360 грамм
• Вода: 6 * 30 = 180 грамм
• Растительное масло: 1 * 30 = 30 грамм 

Квадратные уравнения

Мы уже знаем, что такое линейное уравнение. Но как же выглядит квадратное?

Квадратное уравнение – это уравнение, в котором неизвестная находится в степени 2.

Вид квадратного уравнения:

ax² + bx + c = 0 , где
х — неизвестная
а и b – коэффициенты при неизвестной
с – свободный член

Стоит отметить, что а, b и с – известные числа.

Какими бывают квадратные уравнения?

Эти виды квадратных уравнений отличаются тем, что у полного квадратного уравнения есть оба коэффициента и свободный член, а у неполного может отсутствовать или второй коэффициент, или свободный член.

Решение несколько неполных квадратных уравнений на примере:

x2 + 2x = 0 x * (x + 2) = 0 Ответ: 0 и -2

x2 — 4 = 0 x2 = 4 x = ±2 Ответ: 2 и -2

Полное квадратное уравнение может иметь 2 корня, 1 корень или не иметь корней. Количество корней зависит от дискриминанта

Что такое дискриминант?

Дискриминант в квадратном уравнении — это выражение, которое ищется по следующей формуле, где а, b и с берутся из уравнения:

D = b² — 4 ⋅ a ⋅ c

Как дискриминант может повлиять на количество корней уравнения? Если D > 0, то уравнение имеет 2 корня. Если D = 0, то уравнение имеет 1 корень. Если D < 0, то уравнение не имеет корней.

Дискриминант нужен не только для определения количества корней, но и для их нахождения одним из способов.

Способы решения квадратных уравнений:

1. Решение через дискриминант

   Корни квадратного уравнения находятся по этим формулам, где а и b берутся из уравнения, а D – это дискриминант:

\(\large x_{1} = \frac{-b + \sqrt{D}}{2 ⋅ a}\)
\(\large x_{2} = \frac{-b — \sqrt{D}}{2 ⋅ a}\)

2. По теореме Виета

Как находить корни квадратного уравнения, не считая их? По теореме Виета корни нужно подбирать, поэтому она удобна для нахождения рациональных корней. Данная теорема заключается в связывании корней уравнения и коэффициентов многочлена системой двух уравнений.

где а, b и с – коэффициенты квадратного уравнения
x₁ и x₂ – корни квадратного уравнения

Давайте рассмотрим решение квадратного уравнения на следующем примере

2x² — 5x — 3 = 0

1 способ:

1. Найдем дискриминант 

D = (-5)² — 4 ⋅ 2 ⋅ (-3) = 25 + 24 = 49

2. Дискриминант больше нуля, следовательно, у уравнения 2 корня, найдем их

\(\large x_{1} = \frac{-(-5) + \sqrt{49}}{2 ⋅ 2} = 3\)
\(\large x_{2} = \frac{-(-5) — \sqrt{49}}{2 ⋅ 2} = -12\)

Решениями уравнения являются числа 3 и -12.

2 способ:

1. Запишем систему по теореме Виета

2. Теперь подберем такие два числа, чтобы их сумма была \(\frac{5}{2}\), а произведение -\(\frac{3}{2}\), это будут числа 3 и -12.

Значит, решениями уравнения являются числа 3 и -12.

Кубические уравнения

Перейдем к последнему виду уравнений. Что же такое кубическое уравнение и как оно выглядит?

Кубическое уравнение – это уравнение, в котором неизвестная находится в степени 3.

Вид кубического уравнения:

ax³ + bx² + cx + d = 0, где
х — неизвестная
а, b и с – коэффициенты при неизвестной
d – свободный член

Стоит отметить, что а, b, с и d – известные числа.

Преобразования, которые можно совершать в кубических уравнениях:

Вынесение общего множителя за скобки.

Вынесение общего множителя за скобки можно сравнить с делением фруктов в обеих тарелках на одинаковые части и вынесением такой части в отдельную тарелку.

Алгоритм:

1. Разложить каждое слагаемое на множители.
2. Вынести за скобку множители, которые есть в обоих слагаемых.
3. Вынести скобку, как общий множитель.

Пример: 

 x³ — 2x² — 3x = x * x * x — 2 * x * x — 3 * x = x * (x² — 2x — 3)

Группировка

Алгоритм:

1. Объединить слагаемые в пары.
2. Вынести общий множитель из каждой скобки, чтобы получились одинаковые скобки.

Пример:

6x³ + 9x² + 8x + 12 = (6x³ + 9x²) + (8x + 12) = 3x² * (2x + 3) + 4 * (2x + 3) =
= (3x²+4) * (2x+3)

Рассмотрим решение кубического уравнения

4x + x³ = x² + 4

1. Перенесем все слагаемые в левую часть

4x + x³ — x² — 4 = 0

2. Заметим, что удобнее группировать 1 и 2 слагаемые и 3 и 4 слагаемые

(4x + x³) — (x² + 4) = 0

3. Вынесем общий множитель х из первой скобки 

x * (4 + x²) — (x² + 4) = 0

4. Вынесем ещё один общий множитель x² + 4 за скобки

(x — 1) * (4 + x²) = 0

5. Чтобы произведение было равно 0, один из множителей должен быть равен 0, запишем совокупность

6. Решим каждое уравнение отдельно

1. x — 1 = 0
   x = 1

2. 4 + x² = 0
   x² = -4
   Нет решений, так как x² ≥ 0 верно для любого х

Из этого следует, что у данного уравнения есть только одно решение x=1

Фактчек

• В линейном уравнении неизвестная находится в степени 1. Для решения такого уравнения в одной части уравнения нужно оставить только неизвестную, а в другой собрать все остальное.
• В кубическом уравнении неизвестная в квадрате, то есть в степени 2. Решать такое уравнение можно через дискриминант или по теореме Виета

D = b² — 4 ⋅ a ⋅ c
\(\large x_{1} = \frac{-b + \sqrt{D}}{2 ⋅ a}\)
\(\large x_{2} = \frac{-b — \sqrt{D}}{2 ⋅ a}\) 

или 

• В кубическом уравнении неизвестная находится в кубе, то есть в степени 3. Для решения такого уравнения используется вынесение общего множителя за скобки и способ группировки. 

Проверь себя

Задание 1.
Найдите корень уравнения (2x + 4) ⋅ 3 — 2x = 0

1. 3
2. 2
3. -2
4. -3

Задание 2.
Сколько корней будет у уравнения x² + x — 2 = 0?

1. Нет корней
2. Один корень
3. Два корня
4. Три корня

Задание 3.
Найдите корни уравнения x² + 4x — 5 = 0

1. 1 и 5
2. 1 и -5
3. 1 и 2
4. -1 и 2

Задание 4.
Найдите корни уравнения x² — 5x = 0

1. 0 и 5
2. 2 и 5
3. 25 и 5
4. 0 и 4

Задание 5.
Найдите корни уравнения 12x + 4 — 12x³ — 4x²=0

1. \(-\frac{1}{3}\)
2. -1 и 1
3. -1, \(-\frac{1}{3}\) и 1
4. -1, \(\frac{1}{3}\) и 1

Ответы: 1. — 4; 2. — 3; 3. — 2; 4. -1; 5. — 3

Свойства коэффициентов квадратного уравнения

Ключевые слова: Квадратный корень, Квадратные уравнения

Цели урока:

• Образовательные: формирование учебно-логических знаний, умений, навыков при решении квадратных уравнений разными методами через исследовательскую работу, обобщение и систематизацию опыта.
• Развивающие:
• способствовать развитию внимания, логического мышления, памяти;
• развитие обще учебных навыков, умения анализировать, сравнивать и делать выводы;
• Воспитательные: воспитание трудолюбия, взаимопомощи, культуры математической речи.

ЗАДАЧИ:

Образовательные:

• отработка навыков нахождения корней квадратного уравнения с помощью формул и теорем;
• формирование у учащихся основ разносторонних математических знаний;
• введение частных случаев решения квадратных уравнений.

Воспитательные:

• воспитание культуры умственного труда;
• воспитание культуры общения.

Развивающие:

• формирование умений и навыков учебной (практической и умственной) деятельности;
• развитие познавательных процессов учащихся (памяти, речи, мышления, внимания, воображения, восприятия).

Тип урока: комбинированный.

Ребята, сегодня на уроке мы вновь будем говорить о квадратных уравнениях. Ведь это очень важно, научиться грамотно, быстро и рационально решать квадратные уравнения. Ведь как говорил великий английский философ Герберт Спенсер: «Дороги не те знания, которые откладываются в мозгу, как жир, дороги те, которые превращаются в умственные мышцы!» (СЛАЙД 1)

Презентация

Результат вашей работы на уроке — ваша самооценка, выставленная в оценочном листе. Подпишите их.

1. Проверка выполнения домашнего задания

Дома вы должны были решить квадратные уравнения из сборника «3000 заданий для подготовки к ОГЭ» различными способами.

• Способом разложения на множители:
• Способом выделения квадрата двучлена:
  • по формулам корней квадратного уравнения
  • по формулам корней квадратного уравнения для четного второго коэффициента
  • по теореме Виета

Проверяем домашнее задание которое выводится на доску (СЛАЙД 2 — 3 ) Те у кого выполнены все уравнения верно, в оценочные листы ставят себе 5 баллов. Кто при решении использовал все 5 способов — добавляют еще 5 баллов, кто 4 способа — 4 балла и т.д…

2. Теперь перейдем к повторению опорных знаний

(СЛАЙД 4) устная работа:

1. Какие уравнения называются квадратными?
2. Сколько корней может иметь квадратное уравнение?
3. От чего зависит количество корней квадратного уравнения?
   
4. Если D > 0, то квадратное уравнение имеет…
   
5. Если D < 0, то уравнение …
   
6. Если D = 0, то уравнение….
   
7. Как найти D?
   
8. В каком случае квадратное уравнение называется приведенным?

3. Актуализация знаний

На прошлом уроке мы исследовали зависимость корней квадратного уравнения от его коэффициентов, получили приѐмы устного решения этих уравнений. (СЛАЙД 5)

Если а и с имеют противоположные знаки, то уравнение имеет действительные корни.

А именно:

Если с — положительное число корни имеют одинаковые знаки (в <0, то корни положительные; в>0, то корни отрицательные).

Если с — отрицательное число корни имеют противоположные знаки ( в>0, то корень больший по модулю

отрицательный).

Пишем в тетрадях сегодняшнее число и классная работа. Сейчас я вам предложу по повторенным понятиям выполнить математический диктант. На выполнение задания отводится очень короткое время. Вы записываете только ответы. (СЛАЙД 6)

1. Верно ли, что числа 15 и 7 являются корнями уравнения x² — 22x + 105 = 0? (да)
2. Определите знаки корней уравнения x² + 5x — 36 = 0. (корни имеют противоположные знаки, больший по модулю корень отрицательный)
3. Найдите устно корни уравнения x² — 9x + 20 = 0. (5; 4)
4. Составьте квадратное уравнение, корнями которого являются числа 2 и 0,3. (х² — 2,3х + 0,6)

В оценочных листах оцениваем правильность выполнения заданий. Каждое задание 1 балл.

4. Изучение нового материала

Сегодня мы продолжим исследование свойств коэффициентов квадратного уравнения, которые помогут нам быстро и, притом, устно находить корни уравнения.

5. Физкультминутка

Поморгали часто глазками. Покружили ими…

Разбейтесь на группы. Решите квадратные уравнения под №1 из ваших листов с практическими заданиями по формуле корней квадратных уравнений. Найдите теперь сумму коэффициентов. Какую закономерность можно заметить? (СЛАЙД 7)

1) 5x2— 8x + 3 = 0	x1 = 11 x2= 3/5	5 — 8 + 3 = 0
2) 6x2— 7x + 1 = 0	x1= 11 x2= 1/6	6 — 7 + 1 = 0
3) 2x2— 7x + 5 = 0	x1= 11 x2= 5/2	2 — 7 + 5 = 0

Какой вывод вы можете сделать?

Вывод: Если сумма коэффициентов квадратного уравнения равна 0, то:

1) один корень равен 1;

2) другой корень равен c/а.

Если а + в + с = 0, то х₁= 1, х₂= c/а.

Решите устно (уравнения спроецированы на экран).

(СЛАЙД 8)

1) x2+ 23x — 24 = 0	1; — 24
2) x2+ 7x — 8 = 0	1; — 8
3) x2+ 15x — 16 = 0	1; — 16

Решите квадратные уравнения, приведенные на ваших листах под №2 по формулам корней квадратных уравнений: (СЛАЙД 9)

1) 9x+11x2+ 2 = 0 9 + 2 = 11	x1= — 11 x2= -2/9
2) 4x2— x- 3 = 0 4 — 3 = — 1	x1= -11 x2= 3/4
3) 5x2— 4x- 9 = 0 5 — 9 = — 4	x1= — 11 x2 = 9/5

Найдите теперь сумму коэффициентов а и с. Какую закономерность можно заметить?

Вывод: Если сумма коэффициентов а и с равна коэффициенту в, то:

1) один корень равен —1;

2) другой корень равен —с/а

Если а + с = в, тох₁= -1, х₂= —с/а

Решите устно (уравнения спроецированы на экран). (СЛАЙД 10)

1) 11x2+ 27x + 16 = 0	-1; -16/11
2) x2— 7x — 8 = 0	-1; 8
3) 9x2+ 10x + 1 = 0	-1; -1/9

Продолжаем работать в группах. Самостоятельная работа на применение свойств коэффициентов квадратного уравнения, с последующей самопроверкой. Девочки 1 вариант, мальчики 2 вариант. Задания спроецированы на доске. (СЛАЙД 11) В лист самооценки заносится за каждое правильно выполненное задание 1 балл.

Вариант 1	Вариант 2
1) x2+ 15x — 16 = 0 2) 5x2+ x — 6 = 0 3) 2x2— x — 3 = 0 4) 4x2+ 7x +3 = 0	1) 7x2 — 9x + 2 = 0 2) 6x2 — 5x — 1 = 0 3) x2 — 9x — 10 = 0 4) 7x2 + x — 6= 0

5. Обобщение по теме. Домашнее задания

Сегодня на уроке мы познакомились еще с одними свойствами коэффициентов квадратного уравнения. Какова особенность сегодняшнего урока? ( Сами исследовали корни, находили закономерность, не работали по учебнику.) Домашнее задание носит познавательный интерес: найти на страницах сборника «3000 заданий для подготовки к ОГЭ» квадратные уравнения, решаемые методами, рассмотренными на уроке.

6. Рефлексия

Оцените свое участие в группах. Кто считает свою работу в группе активной, поставьте себе 5 баллов, а кто оценивает свою работу как пассивную? Поставьте себе 4.

Поставьте себе оценку за урок:

• 24-25 баллов «5»;
• 22-23 балла «4»;
• меньше 23 баллов «3».

(СЛАЙД 12) Спасибо за урок.

Лист самооценки

Квадратные уравнения: приведённые уравнения, формулы корней

• Приведённое квадратное уравнение
• Решение квадратных уравнений

Квадратное уравнение или уравнение второй степени с одним неизвестным — это уравнение, которое после преобразований может быть приведено к следующему виду:

ax² + bx + c = 0  — квадратное уравнение,

где  x  — это неизвестное, а  a,  b  и  c  — коэффициенты уравнения. В квадратных уравнениях  a  называется первым коэффициентом  (a ≠ 0),  b  называется вторым коэффициентом, а  c  называется известным или свободным членом.

Уравнение:

ax² + bx + c = 0

называется полным квадратным уравнением. Если один из коэффициентов  b  или  c  равен нулю, или нулю равны оба эти коэффициента, то уравнение представляют в виде неполного квадратного уравнения.

Приведённое квадратное уравнение

Полное квадратное уравнение можно привести к более удобному виду, разделив все его члены на  a,  то есть на первый коэффициент:

x2 +	b	x +	c	= 0.
	a		a

Затем можно избавиться от дробных коэффициентов, обозначив их буквами  p  и  q:

если	b	= p,  а	c	= q,
	a		a

то получится   x² + px + q = 0.

Уравнение  x² + px + q = 0  называется приведённым квадратным уравнением. Следовательно, любое квадратное уравнение, в котором первый коэффициент равен 1, можно назвать приведённым.

Например, уравнение:

x² + 10x — 5 = 0

является приведённым, а уравнение:

-3x² + 9x — 12 = 0

можно заменить приведённым уравнением, разделив все его члены на  -3:

x² — 3x + 4 = 0.

Решение квадратных уравнений

Чтобы решить квадратное уравнение, надо привести его к одному из следующих видов:

ax² + bx + c = 0;

ax² + 2kx + c = 0;

x² + px + q = 0.

Для каждого вида уравнения есть своя формула нахождения корней:

Вид уравнения	Формула корней
ax2 + bx + c = 0
ax2 + 2kx + c = 0
x2 + px + q = 0	или если коэффициент  p  нечётный

Обратите внимание на уравнение:

ax² + 2kx + c = 0

это преобразованное уравнение  ax² + bx + c = 0,  в котором коэффициент  b  — четный, что позволяет его заменить на вид  2k.   Поэтому формулу нахождения корней для этого уравнения можно упростить, подставив в неё  2k  вместо  b:

Пример 1. Решить уравнение:

3x² + 7x + 2 = 0.

Так как в уравнении второй коэффициент не является чётным числом, а первый коэффициент не равен единице, то искать корни будем по самой первой формуле, называемой общей формулой нахождения корней квадратного уравнения. Сначала определим, чему равны коэффициенты:

a = 3,  b = 7,  c = 2.

Теперь, для нахождения корней уравнения, просто подставим значения коэффициентов в формулу:

x1 =	-2	= —	1	,   x2 =	-12	= -2
	6		3		6

Ответ:  —	1	,  -2.
	3

Пример 2:

x² — 4x — 60 = 0.

Определим, чему равны коэффициенты:

a = 1,  b = -4,  c = -60.

Так как в уравнении второй коэффициент — чётное число, то будем использовать формулу для квадратных уравнений с чётным вторым коэффициентом:

x₁ = 2 + 8 = 10,   x₂ = 2 — 8 = -6

Ответ:  10,  -6.

Пример 3.

y² + 11y = y — 25.

Приведём уравнение к общему виду:

y² + 11y = y — 25;

y² + 11y — y + 25 = 0;

y² + 10y + 25 = 0.

Определим, чему равны коэффициенты:

a = 1,  p = 10,  q = 25.

Так как первый коэффициент равен  1,  то будем искать корни по формуле для приведённых уравнений с чётным вторым коэффициентом:

Ответ:  -5.

Пример 4.

x² — 7x + 6 = 0.

Определим, чему равны коэффициенты:

a = 1,  p = -7,  q = 6.

Так как первый коэффициент равен  1,  то будем искать корни по формуле для приведённых уравнений с нечётным вторым коэффициентом:

x₁ = (7 + 5) : 2 = 6,

x₂ = (7 — 5) : 2 = 1.

Ответ:  6,  1.

Когда квадратное число имеет действительные корни? (3 способа сказать) – JDM Educational

При работе с квадратными уравнениями корни (решения) могут быть вещественными или комплексными. Полезно знать, какие признаки искать, чтобы сказать, когда решения реальны.

Итак, когда квадратное число имеет действительные корни? Квадратное уравнение имеет действительные корни, если дискриминант положительный или нулевой (не отрицательный). С точки зрения алгебры это означает b ² >= 4ac. Визуально это означает, что график квадратичного уравнения (параболы) касается оси x хотя бы один раз.

Конечно, квадратное число, касающееся оси x только один раз в вершине, имеет один повторяющийся действительный корень вместо двух различных действительных корней.

В этой статье мы поговорим о том, как определить, что квадратное число имеет действительные решения. Мы также рассмотрим некоторые примеры, а также то, как написать квадратное уравнение, зная его действительные корни.

Начнем.

Когда квадратное число имеет действительные корни?

Есть несколько способов узнать, имеет ли квадратное уравнение действительные корни:

• Посмотрите на дискриминант – если он положительный или нулевой, то корни вещественные.
• Посмотрите на график – если парабола касается оси x, то корни вещественные.
• Посмотрите на коэффициенты – есть некоторые частные случаи, которые подскажут вам, когда существуют реальные решения квадратного уравнения (подробнее об этом далее в статье!)

квадратичная формула представлена ​​в моей статье здесь.)

Начнем с метода, использующего дискриминант.

Посмотрите на дискриминант

Первый способ определить, имеет ли квадратное число действительные корни, это посмотреть на дискриминант. Если дискриминант положительный или нулевой, то квадратное уравнение имеет действительные корни.

Дискриминантом является выражение b ² – 4ac под радикалом в квадратичной формуле. Его знак может сказать нам о характере решений соответствующего квадратного уравнения.

Помните, что для квадратного уравнения:

• AX ² + BX + C = 0

Дискриминант определяется по выражению:

• B ² — 4.

Дискриминантный знак в квадратной формуле.

Дискриминант — это выражение под знаком радикала в квадратной формуле.

Чтобы получить положительный или нулевой дискриминант, нам нужно:

• b ² – 4ac >= 0

или:

• B ² > = 4AC

Есть действительно два разных случая, когда квадратичный имеет реальные корни:

• Первый случай — это, когда дискриминант положительный 2 – 4ac > 0) – это дает нам два различных действительных корня.
• Второй случай, когда дискриминант равен нулю (b ² – 4ac = 0) – это дает нам один повторяющийся действительный корень.

Дискриминант положительный (два различных действительных корня)

Вот пример квадратного уравнения с двумя действительными корнями:

• 2x ² + 10x + 8 = 0

В этом случае a = 2, b = 10 и c = 8. This gives us:

• b ²
• = (10) ²
• = 100

and:

• 4ac
• = 4(2)( 8)
• = 64

Итак, б ² – 4ac > 0 (поскольку 100 – 64 = 36 > 0), и, следовательно, дискриминант положителен. Это означает, что квадратное число имеет два различных действительных корня.

Двумя действительными корнями являются -1 и -4. Вы можете увидеть это, разложив квадратное выражение на множители как 2(x + 1)(x + 4) = 0,

(Если хотите, вы можете проверить эти решения, используя квадратную формулу с a = 2, b = 10 и с = 8).

Дискриминант равен нулю (один повторяющийся действительный корень)

Вот один пример квадратного уравнения с одним повторяющимся действительным корнем:

• x ² + 4x + 4 = 0

В этом случае A = 1, B = 4 и C = 4. Это дает нам:

• B ²
• = (4) ²
• = 16

and

• 4ac
• = 4(1)(4)
• = 16

So, b ² – 4ac = 0 (поскольку 16 – 16 = 0), и, таким образом, дискриминант равен нулю. Это означает, что квадратное число имеет один повторяющийся действительный корень.

Повторяющийся действительный корень x = -2. Вы можете увидеть это, разложив x ² + 4x + 4 как (x + 2)(x + 2).

(Вы также можете использовать квадратную формулу с a = 1, b = 4 и c = 4, чтобы проверить это решение.)

Посмотрите на график

на его графике. Для любого квадратного уравнения график будет представлять собой параболу .

Помните, что одной из ключевых особенностей параболы является ее вершина. Вершина параболы похожа на «вершину горы» (для отрицательных значений а) или «дно долины» (для положительных значений а).

Если парабола касается оси x, то квадратное уравнение имеет действительные решения. Возможны два случая:

• Парабола дважды касается оси x (это дает нам два действительных корня)
• Парабола касается оси x один раз в вершине (это дает нам один повторяющийся действительный корень)

График квадратного касания оси X дважды (два действительных корня)

Как видите, график функции f(x) = x ² – 6x + 8 представляет собой параболу, которая дважды касается оси x , при x = 2 и x = 4. Это означает, что квадратное уравнение имеет два различных действительных корня (в этом случае дискриминант положительный).

Как вы можете видеть на графике выше, парабола касается оси x в двух разных местах. Это означает, что квадратное уравнение x ² – 6x + 8 имеет два действительных корня, x = 2 и x = 4 (то есть оба значения x, где пересекаются парабола и ось x).

Будьте осторожны: чтобы квадратное уравнение имело два действительных корня, его график должен коснуться оси x дважды .

Если график касается оси x один раз, то квадратное число имеет один повторяющийся действительный корень (см. случай ниже). Если график вообще не касается оси x, то у квадратичного уравнения нет действительных корней (вместо этого у него есть два различных комплексных корня).

График квадратного касания оси X один раз (один повторный действительный корень)

Как видите, график функции f(x) = x ² – 4x + 4 представляет собой параболу, вершина которой (дно долины) лежит на оси x в точке x = 2. Это означает, что квадратное уравнение имеет один повторяющийся (двойной) действительный корень. В этом случае дискриминант равен нулю.

Как вы можете видеть на графике выше, вершина (дно впадины) этой параболы лежит на оси x. Это означает квадратное уравнение x ² — 4x + 4 имеет одно действительное решение.

Будьте внимательны: чтобы квадратное уравнение имело одно решение, его график должен касаться оси x ровно один раз .

Если график дважды касается оси x, то он имеет два действительных решения.

Если график вообще не касается оси x, то он имеет два комплексных решения (и никаких действительных решений).

Посмотрите на коэффициенты

Вы также можете посмотреть на коэффициенты квадратного уравнения в стандартной форме, чтобы определить, есть ли у него действительные корни. Помните, что стандартная форма квадратного уравнения имеет ноль с одной стороны и члены в порядке убывания с другой: .

Когда коэффициент x

² равен 1 (a = 1)

В этом случае мы ищем b ² >= 4c. Если это так, то квадратное уравнение имеет действительные корни.

Например, квадратное уравнение x ² + 4x + 3 = 0 имеет a = 1, b = 4 и c = 3.

Это дает нам:

• B ²
• = 4 ²
• = 16

и

• 4AC
• = 4*1*3
• = 12

Тогда B ² > 4AC (с 16> 12), и так. действительные корни для этого квадратного: x = -1 и x = -3.

Когда Коэффициент x

² Не равно 1 (a не равно 1)

В этом случае разделите все квадратное уравнение на a. Тогда вы находитесь в первом случае, когда коэффициент при х ² равен 1.

Например, возьмем уравнение 3х ² + 24х + 48 = 0. Поскольку а = 3, разделим оба стороны на 3.

Это оставляет нам x ² + 8x + 16 = 0. Для этого нового уравнения a = 1, b = 8 и c = 16.

Тогда мы имеем:

• b ²
• = 8 ²
• = 64

and

• 4ac
• = 4*1*16
• = 64

Это означает, что b ² = 4ac, поэтому существует один повторяющийся действительный корень, который равен x = -4.

Когда коэффициент X равен 0 (b = 0)

В этом случае наш дискриминант упрощается до -4ac. Чтобы получить действительные корни, дискриминант должен быть положительным или равным нулю.

Это означает -4ac >= 0. Есть два случая для рассмотрения:

• Если a и c имеют противоположные знаки (один положительный, а другой отрицательный), то квадратное уравнение имеет действительные корни.
• Если a и c имеют одинаковые знаки (оба положительные или оба отрицательные), то квадратное уравнение имеет два комплексных корня.

Например, квадратное уравнение x ² – 4 = 0 имеет два действительных корня. В этом случае a = 1, b = 0 и c = -4.

Поскольку b = 0, а также a и c имеют противоположные знаки (a положительное, c отрицательное), мы знаем, что существуют действительные корни. На самом деле решения равны 2 и -2.

Вы можете проверить это с помощью квадратичной формулы или разложения квадратов: (x + 2)(x – 2) = 0.

Помните, что вы всегда можете использовать калькулятор, чтобы проверить решения Квадратное уравнение. Вы также можете использовать решатель квадратных уравнений, такой как этот от WolframAlpha.

Для калькулятора WolframAlpha помните, что:

• Квадратичный коэффициент (x ² коэффициент) означает A
• Линейный коэффициент (коэффициент x) означает B
• Примеры константы Средство Ca

16 Примеры квадратичного имущества с реальным средним значением CAROTS 9008

16 из квадратных уравнений.

Вот несколько примеров квадратных уравнений с действительными корнями. Посмотрите на них, чтобы увидеть, заметили ли вы шаблон , прежде чем читать дальше.

• x ² + x – 2 = 0 (решения: x = 1 и x = -2)
• x ² + 2x – 3 = 0 (решения: x = 1 и x = -3)
• x ² + 3x – 4 = 0 (решения: x = 1 и x = — 4)
• х ² + 4х – 5 = 0 (решения: х = 1 и х = -5)
• х ² + 5х – 6 = 0 (решения: х = 1 и х = -6)

Вы можете заметить, что коэффициенты x ² (значения a) равны 1. Это упрощает дискриминант до b ² – 4с.

Вы также можете заметить, что все коэффициенты x (значения b) являются целыми числами:

• 1, 2, 3, 4, 5

Вы также можете заметить, что постоянные члены (значения c) являются отрицательными целыми числами:

• -2, -3, -4, -5, -6

Это гарантирует, что дискриминант будет положительным (что дает нам два различных действительных корня для квадратного).

Последнее, на что вы могли обратить внимание, это то, что решения равны 1 и с (где с — постоянный член).

После того, как мы увидим шаблон, мы можем использовать его для создания квадратных уравнений с действительными корнями. Мы можем выбрать любое целое число n и составить квадратное число с действительными корнями 1 и –n.

Все, что нам нужно сделать, это FOIL (x – 1)(x + n), чтобы найти наш квадрат. Это будет выглядеть так:

• (x + 1)(x + n) = 0
• x ² + (n-1)x – n = 0

Например, допустим, мы выберите n = 10.  Тогда нам нужно будет FOIL (x – 1)(x + 10), что дает x ² + 9x – 10.

Тогда квадратное число x ² + 9x – 10 = 0 имеет два действительных корня: x = 1 и x = -10.

Мы также можем умножить квадратное уравнение на любое действительное число (кроме нуля), чтобы получить новое уравнение с теми же корнями. Например, если мы умножим x ² + 9x – 10 = 0 на 2, мы получим 2x ² + 18x – 20 = 0, что также имеет корни из 1 и -10.

Как написать квадратное уравнение с заданными действительными корнями?

Теперь пришло время подумать о работе в обратном направлении. Это означает, что нужно взять действительные числа и написать квадратное уравнение с этими числами в качестве его решений.

Это легко сделать. Более того, существует бесконечно много таких уравнений для заданного набора корней.

Допустим, мы хотим написать квадратное уравнение с двумя действительными решениями r и s. Все, что нам нужно сделать, это FOIL (x – r)(x – s), чтобы найти квадратное.

Это дало бы нам квадратное уравнение x ² – (r+s)x + rs.

Пример. Запись квадратного уравнения с заданными вещественными корнями

Допустим, мы хотим найти квадратное уравнение с действительными корнями 4 и 7.  Тогда у нас есть r = 4 и s = 7,

Уравнение будет кратным (x – r)(x – s) = 0. Подстановка r = 4 и s = 7 дает нам:

• (x – r)(x – s) = 0
• (x – 4)(x – 7) = 0

Использование FOIL в левой части дает нам x ² – 11x + 28 = 0. Мы можем взять любое кратное этому уравнению (например, мы могли бы умножить обе части на 2 без изменения решений x = 4 и x = 7).

Заключение

Теперь вы знаете, когда квадратное уравнение имеет действительные корни. Вы также знаете, на что обращать внимание с точки зрения дискриминанта, графика и коэффициентов.

Надеюсь, эта статья оказалась вам полезной. Если это так, пожалуйста, поделитесь ею с теми, кто может использовать эту информацию.

Вы можете узнать больше о других методах решения квадратичных уравнений в этом ресурсе Университета Ламара.

Вы можете узнать больше о квадратичных уравнениях в других моих статьях о квадратичных уравнениях без действительного решения и квадратичных уравнениях с одним действительным решением.

Вы также можете прочитать мою статью о том, когда использовать квадратное уравнение, или мою статью о том, как разложить квадратный бином на множители (вы можете использовать частный случай квадратной формулы).

В этой статье подробно рассказывается о том, как использовать квадратичную функцию для нахождения характера решений (действительных или комплексных) кубической функции.

Не забудьте подписаться на мой канал YouTube и получать обновления о новых математических видео!

Подпишитесь на наш канал на YouTube!

~Джонатон

Видео: Нахождение корней квадратного уравнения из графика

Стенограмма видео

В этом видео мы поговорим о поиске корней квадратного уравнения. В частности, мы рассмотрим, как найти их на графике. Прежде всего, мы должны помнить, что квадратное уравнение — это уравнение в форме 𝑦 равно 𝑎𝑥 в квадрате плюс 𝑏𝑥 плюс 𝑐. Иногда мы называем его полиномом второго порядка. Итак, у него есть член в квадрате 𝑥 — что-то, умноженное на 𝑥 в квадрате, то есть просто число, умноженное на 𝑥 в квадрате — у него есть член в 𝑥, то есть некоторое число, умноженное на 𝑥, и у него есть постоянный член, который является просто числом, которое может быть положительным или отрицательный.

Теперь вспомните множитель 𝑥, так что 𝑏 в нашем уравнении или постоянный член сам по себе, 𝑐 в нашем уравнении или даже оба могут на самом деле оказаться равными нулю. Так, например, у нас может быть что-то вроде пяти 𝑥 в квадрате плюс три 𝑥 плюс два. И в этом случае 𝑎-значение будет положительное пять, 𝑏-значение будет положительное три, а 𝑐-значение будет положительное два. Или у нас может быть такое уравнение, как 𝑦 равно двум 𝑥 в квадрате минус девять, и в этом случае 𝑎-значение будет равно двум, 𝑏-значение будет равно нулю — так что члена 𝑥 нет — и 𝑐 в этом случае отрицательное девять.

Другой пример: 𝑦 равно трем 𝑥 в квадрате плюс семь 𝑥. И в этом случае 𝑎-значение равно трем, 𝑏 будет положительным числом семь, а 𝑐 будет равно нулю. Таким образом, в конце нет постоянного термина.

И еще один пример: 𝑦 равно 𝑥 в квадрате, и в этом случае 𝑎-значение будет равно единице, 𝑏-значение будет равно нулю, а 𝑐-значение также равно нулю. Итак, это все примеры квадратных уравнений. И это нормально, что 𝑏 равно нулю; это нормально, что 𝑐 равно нулю. Но обратите внимание, что 𝑎 никогда не равно нулю в квадратном уравнении, потому что тогда оно не было бы квадратным; у нас не было бы члена в квадрате.

Так что же такое корень? И зачем нам его искать? Помните, что существует множество реальных ситуаций, которые можно смоделировать с помощью квадратных уравнений. И во многих случаях было бы очень полезно знать, что такое 𝑥-координата, когда 𝑦-координата равна нулю. Так, например, во сколько астероид упадет на землю? Когда в печи закончится топливо? Когда в химической реакции закончится катализатор? Или когда машина перестанет буксовать? Так что нахождение корней квадратного уравнения может быть очень полезным занятием. Таким образом, весь корень состоит в том, что такое 𝑥-координата, когда 𝑦-координата равна нулю. Другими словами, в какой точке эта кривая пересекает ось 𝑥?

Существует множество способов выяснить, что такое корни. Итак, есть несколько алгебраических способов, которые, вероятно, являются лучшими. Но в этом видео мы просто сконцентрируемся на считывании этих значений с графика, который нам дали. Итак, давайте посмотрим на некоторые примеры.

Правильный номер один, поэтому нам дан график 𝑦 равно 𝑥 в квадрате минус три 𝑥 минус четыре. И вопрос заключается в том, чтобы с помощью приведенного графика найти корни квадратного числа 𝑦 равно 𝑥 в квадрате минус три 𝑥 минус четыре. Что ж, это здорово, потому что квадратное число, корни которого мы пытаемся найти, — это то, для которого нам дан график. Итак, все, что нам нужно сделать, это посмотреть, где она пересекает 𝑥-ось, а затем нам просто нужно прочитать эти 𝑥-координаты. Таким образом, этот график пересекает ось 𝑥 в двух местах: в одном, когда 𝑥 равно отрицательной единице, и в другом, когда 𝑥 равно четырем. Таков наш ответ. Есть два ответа: 𝑥 равно отрицательной единице и 𝑥 равно четырем.

Итак, номер два, нам дан график, и вопрос гласит: используя данный график, найдите корни квадратного уравнения 𝑦 равно минусу 𝑥 в квадрате плюс 𝑥 плюс шесть. Итак, первое, что вы заметите, это то, что уравнение, показанное на графике, на первый взгляд выглядит немного иначе, чем уравнение, которое нам дали в вопросе. Но помните, что нам нужно посмотреть на коэффициент при квадрате 𝑥, коэффициент при 𝑥, а затем постоянный член. Итак, если мы сделаем это для вопроса, мы увидим, что 𝑎-значение отрицательное, 𝑏-значение равно единице, а 𝑐 равно шести. И хотя они находятся в другом порядке на графике, у нас все еще есть 𝑎-значение, равное единице, 𝑏-значение, равное единице, и 𝑐-значение, равное шести. Итак, у нас есть такое же уравнение. Таким образом, график соответствует уравнению в вопросе. Итак, чтобы найти корни, нам просто нужно выяснить, что такое 𝑥-координата, где график пересекает 𝑥-ось. Итак, мы видим, что кривая пересекает ось 𝑥 в двух местах: в одном месте 𝑥 равно отрицательным двум, а в другом — там, где 𝑥 равно положительным трем. Итак, это наше решение.

Итак, для третьего числа нам дан график, а затем вопрос гласит: используя показанный график, найдите корни уравнения 𝑦 равно 𝑥 в квадрате минус шесть 𝑥 плюс девять. Поэтому просто проверьте, соответствует ли уравнение, которое мы даем в вопросе, уравнению, которое мы даем на графике. Так что это просто вопрос чтения того, где это пересекает ось 𝑥. Теперь этот вопрос немного отличается от других, потому что на самом деле он не пересекает ось 𝑥 как таковую; он просто касается его в этом единственном месте в 𝑥 равно трем.

Теперь мы коснемся алгебраических решений этих вопросов в другом видео. Но давайте просто переставим 𝑦 равно 𝑥 в квадрате минус шесть 𝑥 плюс девять. И вы можете видеть, что если я умножу это, у меня будет 𝑦 равно 𝑥 минус три раза 𝑥 минус три. А определение корня — это 𝑥-значение, которое порождает 𝑦-координату нуля. Итак, если я поставлю 𝑥 минус трижды 𝑥 минус три, а затем положу 𝑦 равно нулю, мы увидим, что что-то, умноженное на что-то, или что-то, умноженное на себя, равно нулю. Теперь, чтобы это было правдой, по крайней мере одно из этих значений должно быть равно нулю: либо 𝑥 минус три равно нулю, либо 𝑥 минус три равно нулю. Таким образом, то же самое равно нулю, и каждый из них генерирует корень.

Тогда в первом случае очевидно, что 𝑥 равно трем, мы сделаем эту скобку равной нулю. И то же самое касается другого — содержимого другой скобки. Итак, у нас просто возникла ситуация, когда у нас есть два ответа, но они оказались одинаковыми. И мы называем это «повторяющимися корнями». Таким образом, в подобных ситуациях, когда график только касается оси 𝑥, ответ будет заключаться в том, что у нас есть повторяющиеся корни в 𝑥, равном трем.

Переходим к номеру четыре, поэтому нам дан график, а затем он говорит, что с помощью графика найдите корни 𝑦 равно отрицательному 𝑥 в квадрате плюс четыре 𝑥 уберите два. И это уравнение совпадает с уравнением графика, который нам дали. Так что это просто вопрос считывания 𝑥-координат точек, где он пересекает 𝑥-ось. Но сейчас мы сталкиваемся с небольшими трудностями. Во всех предыдущих вопросах делалась именно эта координатная точка — так что решения в целых числах, решения в целых числах для 𝑥. Но теперь у нас есть решение чуть выше нуля и пять десятых и решение чуть ниже трех целых пяти десятых. Так что я бы сказал, что это похоже на ноль целых шесть и три целых четыре десятых.

Таким образом, это подчеркивает большую ограниченность графического метода, поскольку мы можем получить только приблизительные решения. Мы не можем получить действительно очень точные решения для них, потому что мы считываем значения с графика. И у нас есть только масштаб графика; поэтому мы не можем получить действительно очень точные ответы. Если бы я сделал это алгебраически, фактические ответы будут такими: 𝑥 равно двум минус корень два и 𝑥 равно двум плюс корень два. Таким образом, с точными ответами я могу выбрать количество знаков после запятой. И я могу дать ответ сколь угодно точно. Читая график, мы, вероятно, начали бы с одного или двух знаков после запятой в зависимости от масштаба графика.

Теперь с номером пять нам дан график, и нам говорят использовать этот график, чтобы найти корни уравнения 𝑦 равно 𝑥 в квадрате минус восемь 𝑥 плюс восемнадцать. Таким образом, у нас есть одно и то же уравнение в каждом случае. Таким образом, мы должны просто видеть, где этот график пересекает 𝑥-ось, и считывать 𝑥-координаты. Теперь вспомним, что квадратичные кривые — это параболы. Так что это будет продолжаться бесконечно в том же направлении и бесконечно в том же направлении. Кривая поворачивается в этой точке здесь, но на самом деле она никогда полностью не касается или не достигает оси 𝑥. Таким образом, для этого конкретного графика или этого конкретного уравнения нет никаких корней.

Это означает, что для данного конкретного уравнения не имеет значения, на какое значение вы замените 𝑥. Вы никогда не придумаете число, которое будет генерировать 𝑦-координату нуля. Так что ответ может немного озадачить. Мы называем это «нет настоящих корней»; можно просто сказать, что нет корней. Но на самом деле, если мы изобретем совершенно новую систему счисления — комплексные числа или мнимые числа — можно использовать некоторые из этих комплексных или мнимых значений для 𝑥, что создаст 𝑦-координату нуля. Но это уже совсем другая история. Все, что вам нужно об этом думать, это ситуации, когда кривая не пересекает ось 𝑥. Мы просто говорим, что настоящих корней нет.

Итак, последний вопрос, который мы рассмотрим, — вот этот. Ближе к концу это становится немного сложнее, но мы побеспокоимся об этом, когда доберемся до этого. Итак, нам дан график 𝑦 равно 𝑥 в квадрате минус два 𝑥. И нам нужно, в части а, использовать этот график, чтобы найти корни 𝑦 равно 𝑥 в квадрате минус два 𝑥. Так что уравнения одинаковые. Так что нужно просто посмотреть на график и выяснить, где он пересекает 𝑥-ось, и посмотреть на эти 𝑥-координаты. Таким образом, ответы там 𝑥 равно нулю, а 𝑥 равно двум. Теперь, часть b, используйте график, чтобы решить, что 𝑥 в квадрате минус два 𝑥 равно единице. Теперь это не поиск корней как таковых, но мы пытаемся найти, какие 𝑥-координаты будут генерировать 𝑦-координату одного. Итак, когда мы искали корни, мы пытались выяснить, какие 𝑥-координаты порождают 𝑦-координату нуля. Но в данном случае мы ищем 𝑦-координату единицы. Итак, если я нарисую линию 𝑦, равную единице на моем графике, везде, где этот график пересекает 𝑦, будет равна единице, которая сгенерирует для меня мои 𝑥-координаты. Так что у нас это. Я нарисовал 𝑦 равно единице, и наш исходный график пересекает 𝑦 равно единице в этих двух точках. И если я отчитаю 𝑥-координаты в первом случае слева здесь, у меня минус ноль целых четыре десятых. И для этого правостороннего случая здесь это выглядит так, что 𝑥 равно двум целых четыре десятых. Итак, мы снова обнаружили некоторое ограничение использования графиков, потому что стопроцентно точные ответы были бы такими: 𝑥 — это один минус корень два, а 𝑥 — это один плюс корень два. Но, используя графики, то, что мы получили, было настолько близко, насколько это возможно.

Теперь перейдем к части c, все стало немного сложнее, потому что проблема в том, что уравнение, которое мы дали на графике 𝑦 равно 𝑥 в квадрате минус два 𝑥, не совпадает с уравнением, которое мы пытаемся решить здесь . У нас нет 𝑦 равно 𝑥 в квадрате минус два 𝑥. В левой части у нас есть 𝑦 равно 𝑥 в квадрате минус три 𝑥 плюс один. И приравняем 𝑦-координату к нулю. Итак, в идеале у нас есть квадратное число 𝑦, равное 𝑥 в квадрате минус три 𝑥 плюс один. И мы просто будем искать, где это пересекает ось 𝑥 и имеет 𝑦-координату нуля.

Итак, что нам нужно сделать, так это хорошо сказать, какие шаги нам нужно пройти, чтобы получить это-это выражение, похожее на выражение, которое мы получили для графика. Ну, мы могли бы сделать это в несколько разных этапов. Таким образом, чтобы получить от отрицательной тройки 𝑥 до отрицательной двойки 𝑥. Мне нужно добавить 𝑥. Итак, если я добавлю 𝑥 к обеим частям этого уравнения, у меня получится вот это. А теперь, если я вычту единицу из каждой части уравнения, я получу только 𝑥 в квадрате минус два 𝑥 в левой части. Теперь, как и в части b, нам нужно было изобразить 𝑦 равным 𝑥 в квадрате минус два 𝑥 и 𝑦 равным единице и посмотреть, где они пересекаются. Теперь я нарисую 𝑦 равно 𝑥 в квадрате минус два 𝑥 и 𝑦 равно 𝑥 минус один и посмотрю, где они пересекаются — другими словами, где их 𝑦-координаты будут равны. Итак, 𝑦 равно 𝑥 минус один. Я мог бы написать так: 𝑦 равно единице 𝑥 минус единица.

И если вы помните из уравнений прямых линий, тот, что стоит перед 𝑥 — множитель 𝑥 — говорит нам о наклоне этой прямой. А отрицательный говорит нам, где он пересекает ось 𝑦 — точку пересечения 𝑦. Итак, у меня есть отрицательный, где он пересекает ось 𝑦, а наклон равен единице. Поэтому каждый раз, когда я увеличиваю свою 𝑥-координату на единицу, моя 𝑦-координата также увеличивается на единицу. Так что это тоже будет в теме. Увеличьте мою 𝑥-координату на единицу, 𝑦-координата увеличится на единицу. Таким образом, я могу провести прямую линию 𝑦, равную 𝑥 минус единица, через эти точки. А затем мне нужно выяснить, где этот квадратичный график пересекает прямую линию. Так это здесь и здесь; это когда, хотя линия 𝑦 равна 𝑥, она имеет ту же 𝑦-координату, что и квадратичный график 𝑦 равен 𝑥 в квадрате минус два 𝑥.

Итак, теперь давайте прочитаем 𝑥-координаты, где они пересекаются. Таким образом, левая точка здесь имеет 𝑥-координату ноль целых четыре десятых, а правая точка имеет 𝑥-координату- выглядит как две целых шесть десятых. И если бы я сделал это алгебраически, фактические ответы будут такими: три минус корень пять больше двух или три плюс корень пять больше двух. И они довольно близки к нулю, четыре и две целых шесть десятых. Но опять же, это просто показывает ограничения ваших тренировок с использованием графика. Читая значения по графику, а не алгебраически, таких точных ответов не получить.

Итак, давайте подведем итоги. Корни квадратного уравнения — это 𝑥-координаты точек на графике, которые имеют 𝑦-координаты нуля, поэтому 𝑥-значения в уравнении, которые генерируют 𝑦-значение нуля, — другими словами, точки, где оно пересекает 𝑥-ось. Таким образом, на графике вы можете просто прочитать 𝑥-координаты с графика, где кривая пересекает 𝑥-ось. И это могут быть не целые числа; поэтому вы можете дать только приблизительные решения. И реальных решений может быть два или одно, а может и вовсе не быть. Так что удачи в поиске корней квадратных уравнений из графиков.

Построение квадратного уравнения с заданными корнями

Если α и β являются двумя корнями квадратного уравнения, то формула для построения квадратного уравнения: = 0

То есть

x ²   — (сумма корней)x + произведение корней = 0

Если квадратное уравнение задано в стандартной форме, мы можем найти сумму и произведение корней используя коэффициент x ² , x и постоянный член.

Рассмотрим квадратное уравнение стандартной формы приведенного выше квадратного уравнения.

Тогда формула для получения суммы и произведения корней квадратного уравнения:

Примечание:

Иррациональные корни квадратного уравнения встречаются в сопряженных парах.

То есть, если (m + √n) является корнем, то  (m — √n) является другим корнем того же уравнения квадратного уравнения.

Пример 1:

Составьте квадратное уравнение, корни которого равны 2 и 3.

Решение:

Сумма корней равна

= 2 + 3

= 5

02002 Произведение корней равно 90 x 3

= 6

Составление квадратного уравнения:

x ² — (сумма корней)x + произведение корней = 0

x ² — 5x + 6 = 0

3 90 :

Составьте квадратное уравнение, корни которого равны 1/4 и -1.

Решение:

Сумма корней:

= 1/4 + (-1)

= 1/4 — 1

= 1/4 — 4/4

= (1 — 4)/ 4

= -3/4

Произведение корней равно

= (1/4) x (-1)

= -1/4

Составление квадратного уравнения сумма корней)x + произведение корней = 0

x ²  — (-3/4)x + (-1/4) = 0

x ²  + (3/4)x — 1/4 = 0

Умножьте каждую сторону на 4.

4x ²  + 3x — 1 = 0

Пример 3 :

Составьте квадратное уравнение, корни которого равны 2/3 и 5/2.

Решение:

Сумма корней равна

= 2/3 + 5/2

Наименьшее общее умножение знаменателей 3 и 2 равно 6.

С помощью умножения каждый знаменатель равен 6.

Тогда

= 4/6 + 15/6

= (4 + 15)/6

= 19/6  

Произведение корней равно

= 2/3 x 5/2

= 5/3

Составление квадратного уравнения :

x ²  — (сумма корней)x + произведение корней = 0

x ²  — (19/6)x + 5/3 = 0

Умножьте каждую сторону на 6.

6x ²  — 19x + 10 = 0

0 2

Пример 0 0 3

квадратного уравнения (2 + √3), затем составьте уравнение, учитывая, что корни иррациональны.

Решение:

(2 + √3) — иррациональное число.

Мы уже знаем, что иррациональные корни квадратного уравнения встречаются в сопряженных парах.

То есть, если (2 + √3) является одним корнем квадратного уравнения, то (2 — √3) будет другим корнем того же уравнения.

Итак, (2 + √3) и (2 — √3) являются корнями искомого квадратного уравнения.

Сумма корней равна

= (2 + √3) + (2 — √3)

= 4

Произведение корней равно

= (2 +√3) (2 -√3)

= 2 ² -√3 ²

= 4 -3

= 1

Формирование квадратичного уравнения:

x ²  — (сумма корней)x + произведение корней = 0

x ²  — 4x + 1 = 0

Пример 5:

12 = 0, найдите квадратное уравнение, корни которого равны

(α + β) ² и (α — β) ²

Решение :

Дано : α и β корни x + β = -7/1

= -7

произведение корней = постоянный член / коэффициент x ²

αβ = 12/1

= 12

Квадратное уравнение с корнями (α + β)

6 2

 и (α — β) ² равно

x ² — [(α + β) ²  + (α — β) ² ]x + (α + β) ² (α — β) ²  = 0 —-(1)

Найдите значения (α + β) ² и (α — β) ² .

(α + β) ² = (-7) ²

(α + β) ²  = 49

(α — β) ^{0 6 0 β-9 +} ) = (0 7 0 9 ) 4αβ

(α — β) ² = (-7) ²  — 4(12)

(α — β) ² = 49 — 48

(α — 0 0 6) 9 0 0 6) 9 0 0 6)

Итак, искомое квадратное уравнение

(1)—-> x ²  — [49 + 1]x + 49 ⋅ 1 = 0

x ²  — 50x + 49 = 0

2 Пример 6 :

Если α и β корни x ²  + px + q = 0, найдите квадратное уравнение, корни которого равны

α/β и β/α

Решение:

Дано: β — корни x ²  + px + q = 0,

Тогда

сумма корней = -коэффициент x/коэффициент x ²

α + β = -p/1

α + β = -p

произведение корней = постоянный член/коэффициент x Квадратное уравнение с корнями α/β и β/α   равно

x ²  — (α/β + β/α)x + (α/β)(β/α) = 0

x ² — [α/β + β/α]x + 1 = 0 —-(1)

Найдите значение (α/β + β/α).

α/β + β/α = α ² /αβ + β ² /αβ

= (α ²  + β ² )/αβ

= [(α   + β) ² — 2αβ]/αβ

= (p ^2 90 — 20q квадратичное искомое) 3 уравнение

(1)—-> x ²  -[(p ²  — 2q)/q]x + 1 = 0

Умножьте каждую сторону на q.

qx ²  — (p ²  — 2q)x + q = 0

Пожалуйста, присылайте свои отзывы на [email protected]

Мы всегда ценим ваши отзывы.

©Все права защищены. onlinemath5all.com

Природа корней квадратного уравнения

В этом разделе мы рассмотрим корни квадратного уравнения.

То есть мы будем анализировать, являются ли корни квадратного уравнения равными или неравными, действительными или мнимыми, рациональными или иррациональными.

Чтобы исследовать корни квадратного уравнения, давайте рассмотрим общую форму квадратного уравнения.

ах ² + Ьх + с = 0

(здесь a, b и c — действительные и рациональные числа)

Чтобы узнать природу корней квадратного уравнения, мы будем использовать дискриминант b ²  — 4ac.

Потому что b ²  — 4ac различает природу корней.

Давайте посмотрим, как этот дискриминант b ² — 4ac можно использовать, чтобы узнать природу корней квадратного уравнения.

Примеры 1-5: Исследуйте природу корней квадратного уравнения.

Пример 1:

3x ² + 8x + 4 = 0

Решение:

Данное квадратичное уравнение в общей форме

AX ² + BX + C = 0

Тогда мы a = 3, b = 8 и c = 4.

Найдите значение дискриминанта b ² — 4ac.

B ² — 4AC = 8 ² — 4 (3) (4)

B ² — 4AC = 64 — 48

B ² — 4AC = 16

Здесь, b

0006 2  — 4ac > 0, а также полный квадрат.

Итак, корни вещественные, неравные и рациональные.

Пример 2:

2x ² — 3x — 1 = 0

Решение:

Данное квадратное уравнение в общем виде

AX ² + BX + C = 0

Тогда у нас есть a = 2, b = -3 и c = -1.

Найдите значение дискриминанта b ²  — 4ac.

б ²  — 4ac = (-3) ² — 4(2)(-1)

b ² — 4ac = 9 + 8

b ² — 4ac = 17

Здесь, b 0-

0 2 идеальный квадрат.

Итак, корни действительные, неравные и иррациональные.

Пример 3:

x ² — 16x + 64 = 0

Решение:

Данное квадратичное уравнение в общем виде

AX ² + BX + C = 0

Тогда мы имеем a = 1, b = -16 и c = 64,

Найти значение дискриминанта b ²  — 4ac.

B ² — 4AC = (-16) ² — 4 (1) (64)

B ² — 4AC = 256- 256

B ² — 4AC = 0

. корни вещественные, равные и рациональные.

Пример 4:

5x ² — 4x + 2 = 0

Решение:

Данное квадратичное уравнение в общем виде

AX ² + BX + C = 0

AX ² + BX + C = 0

0003

Тогда имеем a =  5, b  =  -4 и c  =  2.

Найдите значение дискриминанта b ²  — 4ac.

B ² — 4AC = (-4) ² — 4 (5) (2)

B ² — 4AC = 16- 40

B ² — 4AC = -24

здесь , b ²  — 4ac < 0. 

Итак, корни мнимые.

Пример 5: 

1/(x + 1) + 2/(x — 4) = 2

Решение:

Данное квадратное уравнение не имеет общей формы.

Сначала запишите данное квадратное уравнение в общем виде.

1/(x + 1) + 2/(x — 4) = 2

Сложите две дроби в правой части уравнения, используя перекрестное умножение.

[(x — 4) + 2(x + 1)]/[(x + 1)(x — 4)] = 2

(x — 4 + 2x + 2)/(x ²  — 3x — 4) = 2

(3x — 2)/(x ²  — 3x — 4) = 2

Умножьте каждую сторону на (x ²  — 3x — 4).

3x — 2 = 2(x ²  — 3x — 4)

3x — 2 = 2x ² — 6x — 8

2x ² — 9x — 6 = 0

Теперь квадратичное уравнение — общая форма

AX ² + Bx + C = 0

Тогда у нас есть a = 2, b = -9 и c = -6.

Найдите значение дискриминанта b ²  — 4ac.

B ² — 4AC = (-9) ² — 4 (2) (- 6)

B ² — 4AC = 81 + 48

B ² — 4AC = 129

здесь , б ²  — 4ac > 0, но не полный квадрат.

Итак, корни действительные, неравные и иррациональные.

Пример 6 :

x = 1 — 2y

4y = x ² + 3

Сколько упорядоченных пар (x, y) в плоскости xy являются решениями приведенной выше системы уравнений?

A) 0

B) 1

C) 2

D) Бесконечно много

Решение:

x = 1 — 2y —-(1)

9 0 0

0 0 0 —-(2)

(1) :

x = 1 — 2y

Добавьте 2y к обеим сторонам.

x + 2y = 1

Вычесть x с обеих сторон.

2y = 1 — x

Умножьте обе стороны на 2.

4y = 2 — 2x

Подставьте 4y = 2 — 2x в (2).

2 — 2x = x ² + 3

x ² + 2x+ 1 = 0

Сравнение AX ² + BX+ C = 0 и x ² + 2x+ 1 = 0,

a = 1, b = 2 и c = 1

Найдите значение дискриминанта b ²  — 4ач.

B ² — 4AC = 2 ² — 4 (1) (1)

B ² — 4AC = 4- 4

B ² — 4AC = 0

Здесь, B ²  — 4ac = 0. 

Итак, корни вещественные и равные. Это означает, что существует только одно действительное значение для x. Следовательно, у нас будет только одно действительное значение y.

Следовательно, только одна упорядоченная пара (x, y) в плоскости xy является решением данной системы уравнений.

Правильный ответ (В).

Пример 7 :

2x ²  + 8x — m ³ = 0

Если корни приведенного выше квадратного уравнения равны, то найдите значение m.

Решение:

Сравнение ax ²  + bx + c = 0 и 2x ²  + 8x — m ³  = 0,

 = 0,

7 m 0 0 8 и 0

Поскольку корни данного уравнения равны,

b ²  — 4ac = 0

8 ²  — 4(2)(-m ³ ) = 0

64 + 8m ³  = 0

Вычесть 64 с обеих сторон.

8m ³ = -64

Разделение обеих сторон на 8.

M ³ = -8

M ³ = (-2) ³

M = -2

Доброго. ваши отзывы на [email protected]

Мы всегда ценим ваши отзывы.

©Все права защищены. onlinemath5all.com

1.5: Квадратные уравнения с комплексными корнями

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

40893

• Ричард В. Беверидж
• Общественный колледж Клэтсопа

В разделе \(1.3,\) мы рассмотрели решение квадратных уравнений, имеющих два действительных корня. Это было связано с тем, что при вычислении корней для каждого уравнения часть квадратной формулы, имеющая квадратный корень (\(b^{2}-4 a c,\), часто называемая дискриминантом), всегда была положительным числом. 9{2}-4(1)(3)}}{2 * 1} \\
=\frac{6 \pm \sqrt{36-12}}{2} \\
=\frac{6 \pm \ sqrt{24}}{2} \\
=\frac{6 \pm 4.899}{2}
\end{массив}
\]
\begin{массив}{ll}
\приблизительно \frac{6+4.899 {2} & \приблизительно \frac{6-4.899}{2} \\
\приблизительно \frac{10.899}{2} & \приблизительно \frac{1.101}{2} \\
\приблизительно 5.449 & \приблизительно 0,551
\end{массив}

Когда мы прибавили и вычли квадратный корень из 24 из 6 в квадратной формуле, это дало два ответа, и они были действительными, потому что квадратный корень из 24 является действительным. 9{2}-4(1)(12)}}{2 * 1} \\
=\frac{6 \pm \sqrt{36-48}}{2} \\
=\frac{6 \pm \ sqrt{-12}}{2} \\
=\frac{6}{2} \pm \frac{6 \cdot 464 i}{2} \\
\приблизительно 3 \pm 1,732 i
\end{array }

Здесь дискриминант отрицателен, что приводит к двум комплекснозначным ответам. Если уравнение имеет действительные коэффициенты, комплексные корни всегда будут сопряженными парами. Комплексно-сопряженные числа имеют одну и ту же вещественную часть и имеют противоположные знаки в своих комплекснозначных (или мнимых) частях: \(a \pm b i\) 9{2}\)
11) \(\quad (x+5)(x-6)=(2 x-1)(x-4)\)
12) \(\quad (3 x-4)( х+2)=(2 х-5)(х+5)\)

Ответить

1) \(\quad x \приблизительно 1,758,-0,758\)
3) \(\quad x \приблизительно 0,344,-1,744\)
5) \(\quad x \приблизительно 0,1 \overline{6} \pm 0,373 i\)
7) \(\quad x \приблизительно-0,5 \pm 1,204 i\)
9) \(\quad x \приблизительно 0,286 \pm 0,881 i\)
11) \(\quad x \приблизительно 4 \pm 4,243 i\)

---

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или страница

   Автор

   Ричард В. Беверидж

   Лицензия

   CC BY-NC-SA

   Показать страницу TOC

   нет

2. Теги

   1. источник[1]-math-37238

Природа корней квадратного уравнения

Квадратные уравнения являются неотъемлемой частью алгебры в математике. Квадратные уравнения — это уравнения, содержащие хотя бы один член в квадратной форме или в квадрате. Квадратные уравнения также известны как уравнения второй степени. Стандартная форма квадратного уравнения ax² + bx + c = 0, где a, b и c — константы, или числовые коэффициенты, или действительные числа, и они не равны 0, а x — неизвестная переменная, значение которой будет обнаружено путем решения задачи. уравнение с использованием различных методов квадратного уравнения и двух степеней x означает квадрат на x, где природа корней может быть реальной, либо оцененной, либо предполагаемой.

Чем квадратные уравнения отличаются от квадратных полиномов?

Квадратный многочлен становится квадратным уравнением, когда многочлен приравнивается к 0. Например, квадратичный многочлен равен ax + bx² + c, а квадратное уравнение — это ax + bx² + c =0.

Методы, используемые для нахождения корней квадратных уравнений

Корни квадратного уравнения — это значение неизвестного фактора уравнения. Например, если ax + bx² + c = 0, то корнем квадратного уравнения будет значение x. Ниже приведены некоторые методы, которые можно использовать для нахождения корней квадратных уравнений: 

• Метод факторизации

• Метод квадратичных формул

• Завершение метода квадратов.

Графическое представление квадратного уравнения

Квадратные уравнения также могут быть представлены на графиках, а представление квадратных уравнений на графике известно как графическое представление квадратных уравнений. Корни квадратного уравнения — это точки, которые касаются оси x. Например, корни x² + 9будет 3 и -3.

Ниже приведены некоторые важные моменты, которые следует учитывать при графическом представлении квадратных уравнений:

• Если на графике квадратного уравнения ни одна точка не касается оси x, то следующее уравнение не имеет корней .

• Если график квадратного полиномиального уравнения касается оси x в двух разных точках, то это означает, что уравнения имеют действительные и различные корни.

• Если график квадратного полиномиального уравнения касается оси x, то это означает, что оно имеет действительные и равные корни.

Тип корней

Существует три типа корней:

Природа корней

Дискриминант представляет собой выражение под квадратным корнем. Дискриминант представлен как Δ. Δ — греческий символ буквы D.

Дискриминант определяет природу корней квадратного уравнения. Слово «природа» относится к типам чисел, к которым могут относиться корни, а именно к действительным, рациональным, иррациональным или мнимым и т. д. 

• Если Δ<0, то корни не вещественные и в графическом представлении кривая не пересекает ось абсцисс ни в одной точке.

• Если Δ=0, то корни вещественные и равные, а в графическом представлении кривая пересекается только в одной точке на оси x.

• Если ∆> 0, то корни либо рациональны, либо иррациональны, и в графическом представлении кривая пересекается в двух различных точках на оси x.

• Δ — квадрат рационального числа, тогда корни рациональны.

• Δ не является квадратом рационального числа, то корни иррациональны и могут быть выражены в десятичной форме.

Решенные примеры

1. Обсудите природу корней квадратного уравнения 2×2 – 8x +3 = 0

Решения: Здесь все коэффициенты рациональны. Дискриминант D для данного уравнения будет равен

D = b2 – 4ac = (-8)2- 4*2*3

=64-24

= 40 > 0

Как видим, дискриминант данного квадратного уравнения положительный, но не полный квадрат.

Следовательно, корни квадратного уравнения действительны, неравны и иррациональны.

2. Определите значение k, при котором квадратное выражение (x-k) (x-10) +1 =0 имеет целые корни.

Решение: данное квадратное уравнение можно переписать как

x2 – (10 + k) x +1 + 10k = 0

b2 – 4ac = 100 + k2 + 20k – 40k = k2 -100k + 96 = (k — 10)2 — 4

Квадратное уравнение будет иметь целочисленный корень, если значение дискриминанта > 0, D — полный квадрат, a=1, а b и c считаются целыми числами.