24:x=3 решить уравнение… -reshimne.ru
Новые вопросы
Ответы
X=24:3
x=8
Вот так вот))
24:x=3. x=24:3. x=8.
Похожие вопросы
Помогите со 2 вариантом. Срочно надо…
С одного участка собрали 1440 центнеров пшеницы, а с другого площадь которого на 12 га меньше 1080 см. Найдите площадь первого участка, если известно,что на первом участке собрали с каждого гектара на 2 ц больше чем на втором…
Произведение двух чисел в 6 раз больше первого числа найдите второе число
1-е число *….=произведение…
С краткой записью и с решением.
..
Семёновские мастера расписали 1600 матрёшек. Пятую часть всех матрёшек увезли на выставку, а остальные упоковали в коробки, по 20 матрёшек в каждую,и отправили на ярмарку. Сколько коробок с матрёшками отправили на ярмарку?
B вагоне 36 мест. по 4 в каждом купе. Укажите номер купе. в котором расположено место №2….
Математика
Литература
Алгебра
Русский язык
Геометрия
Английский язык
Химия
Физика
Биология
Другие предметы
История
Окружающий мир
География
Українська мова
Українська література
Қазақ тiлi
Беларуская мова
ИнформатикаЭкономика
Музыка
Право
Французский язык
Немецкий язык
МХК
ОБЖ
Психология
ГДЗ Ответы Математика 3 класс Богданович М В, Лишенко Г П 301 – 325 Задания 39 – 46 Страницы » Допомога учням
Другие задания смотри здесь.
..
Задание 301. Составь и реши уравнения.
1) Неизвестное число х увеличили в 9 раз и получили 72. Найди неизвестное число.
2) Неизвестное число уменьшили в 3 раза и получили 9. Найди неизвестное число.
3) К неизвестному числу прибавили 16 и получили 84. Найди неизвестное число.
Решение.
1) Обозначим неизвестное число буквой х. Составим уравнение:
х • 9 = 72
х = 72 : 9
х = 8
Ответ: неизвестное число равно 8.
2) Обозначим неизвестное число буквой х. Составим уравнение:
х : 3 = 9
х = 9 • 3
х = 27
Ответ: неизвестное число равно 27.
3) Обозначим неизвестное число буквой х. Составим уравнение:
х + 16 = 84
х = 84 – 16
х = 68
Ответ: неизвестное число равно 68.
Задание 302*. Из четырёх одинаковых квадратов составили один большой. Найди его периметр, если периметр маленького квадрата 8 см. Начерти большой и один маленький квадраты.
Решение.
8 : 4 = 2 (см) – сторона маленького квадрата.
2 + 2 = 4 (см) – сторона большого квадрата.
4 • 4 = 16 (см) – периметр большого квадрата.
Ответ: периметр большого квадрата 16 см.
Во сколько раз сумма периметров маленьких квадратов больше периметра большого квадрата?
Решение.
8 • 4 = 32 (см) – сумма периметров 4 маленьких квадратов.
32 : 16 = 2 (раза) – у столько раз сумма периметров маленьких квадратов больше периметра большого квадрата.
Ответ: у 2 раза.
Задание 303°.
9 • 4 + 9 • 6 = 36 + 54 = 90
9 • 8 – 4 = 72 – 4 = 68
(2 + 7) • 9 = 9 • 9 = 81
66 – 39 = 27
9 • 5 + 9 • 5 = 45 + 45 = 90
2 + 7 • 9 = 2 + 63 = 65
63 : 7 : 3 = 9 : 3 =3
18 + 81 = 99
Задание 304°. Две сестры и младший брат вместе слепили 24 вареника. Сёстры слепили по 9 вареников. Сколько вареников слепил брат?
Решение.
9 • 2 = 18 (в.) – вареников слепили две сестры вместе.
24 – 18 = 6 (в.) – вареников слепил брат.
Ответ: брат слепил 6 вареников.
Задание 305.
|
9 • 9 = 81 81 – 41 = 40 40 : 8 = 5 |
54 : 9 = 6 6 • 3 = 18 18 – 9 = 9 |
9 • 7 = 63
63 – 15 = 48 48 : 8 = 6 |
45 : 9 = 5 5 • 8 = 40 40 – 6 = 34 |
Задание 306. На какое число надо разделить 42, чтобы получить 7? Составь уравнение и реши его.
Решение.
Обозначим неизвестное число х. Составим уравнение.
42 : х = 7
х = 42 : 7
х = 6
Ответ: неизвестное число равно 6.
Задание 307. В магазин привезли 60 плееров. В течение 9 дней продавали по 6 плееров ежедневно.
Сколько плееров осталось продать?
Решение.
6 • 9 = 54 (п.) – плееров продали.
60 – 54 = 6 (п.) – плееров осталось продать.
Ответ: осталось продать 6 плееров.
Задание 308. В саду 36 слив, а груш — в 4 раза меньше. Яблонь в саду на 16 больше, чем слив и груш вместе. Сколько яблонь в саду?
Решение.
36 : 4 = 9 (деревьев) – груш в саду.
36 + 9 = 45 (д.) – слив и груш вместе в саду.
45 + 16 = 61 (д.) – яблонь в саду.
Ответ: в саду 61 яблоня.
Задание 309. Составь выражения и найди их значения.
1) Первое слагаемое 42, а второе — частное чисел 21 и 7.
2) Делимое 42, а делитель — разность чисел 30 и 24.
3) Найти разность произведений чисел 7 и 7 и 8 и 5; 8 и 7 и 4 и 5.
4) Найти сумму частных чисел 64 и 8 и 54 и 6; 48 и 8 и 24 и 8.
Решение.
1) 42 + (21 : 7) =42 + 3 =45
2) 42 : (30 – 24) = 42 : 6 = 7
3) (7 • 7) – (8 • 5) = 49 – 40 = 9
(8 • 7) – (4 • 5) = 56 – 20 = 36
4) (64 : 8) + (54 : 6) = 8 + 9 = 17
(48 : 8) + (24 : 8) = 6 + 3 = 9
Задание 310.
|
18 — х = 2 х = 18 – 2 х = 16 18 – 16 = 2 |
18 : х = 2 х = 18 : 2 х = 9 18 : 9 = 2 |
х : 2 = 9 х = 9 • 2 х = 18 18 : 2 = 9 |
х • 9 = 81 х = 81 : 9 х = 9 9 • 9 = 81 |
Задание 311*. Запиши три числа, каждое из которых делится на 2; на 3; на 2 и на 3.
Решение.
На 2 делятся парные числа: 2, 4, 6, …
На 3 делятся числа, сумма цифр которых делится на 3: 3, 9, 12, 15, …
На 2 и 3 делятся числа, которые делятся на 2 • 3 = 6: 6, 18, 24, …
Задание 312°. В двух корзинах было 20 груш. Когда из первой корзины взяли 4 груши, в обеих корзинах груш стало поровну.
Решение.
20 – 4 = 16 (г.) – груш стало поровну.
16 : 2 = 8 (г.) – груш было во второй корзине сначала.
8 + 4 = 12 (г.) – груш было в первой корзине сначала.
Ответ: сначала в первой корзине было 12 груш, во второй – 8 груш.
Задание 313.
42 : 7 + 17 = 6 + 17 = 23
56 – 42 : 7 = 56 – 6 = 50
20 + 9 • 5 = 20 + 45 = 65
24 – 9 : 3 = 24 – 3 = 21
(36 + 12) : 6 = 48 : 6 = 8
36 + 12 : 6 = 36 + 2 = 38
Задание 314. (Устно.) До Нового года осталось 8 недель и 4 дня. Сколько дней осталось до Нового года?
Решение.
7 • 8 = 56 (д.) – дней у восьми неделях.
56 + 4 = 60 (д.) – дней осталось до Нового года.
Ответ: до Нового года осталось 60 дней.
Задание 315. (Устно.) Рассмотри числовые данные и ответь на вопросы.
Масса овцы 35 кг, гуся 5 кг, утки 2 кг.
1) Какова масса овцы и двух таких гусей?
2) Во сколько раз масса овцы больше массы гуся и утки вместе?
3) На сколько килограмм масса гуся и утки вместе меньше массы овцы?
Решение.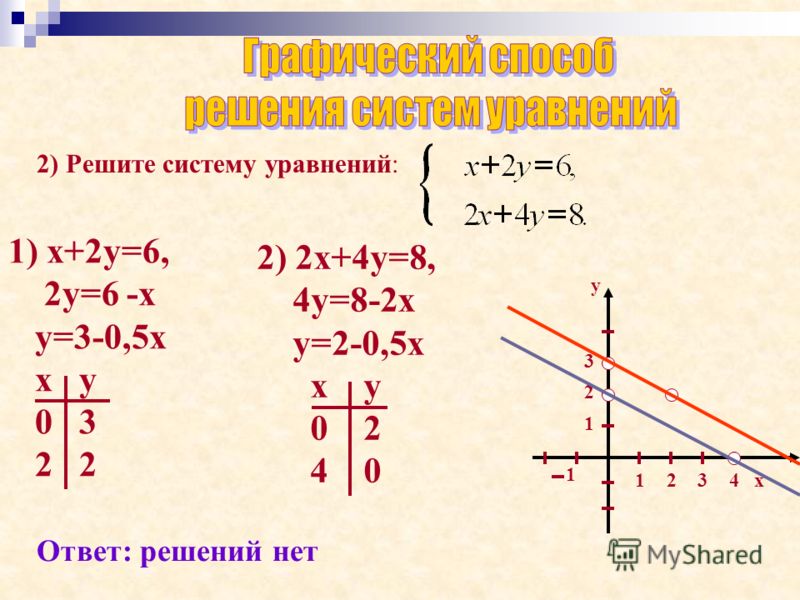
1) 35 + 5 • 2 = 45 (кг) – масса овцы и двух гусей.
2) 35 : (5 + 2) = 5 (раз) – во столько раз больше масса овцы, чем масса гуся и утки вместе.
3) 35 – (5 + 2) = 35 – 7 = 28 (кг) – на столько килограмм меньше масса гуся и утки вместе, чем масса овцы.
Задание 316. Составь задачу по выражению 36 + 36 : 4.
Масса овцы 36 кг, а масса индюка у 4 раза меньше. Какова масса овцы и индюка вместе?
Задание 317. Масса овцы 32 кг, а масса индейки — в 4 раза меньше. Какова масса девяти таких индеек?
Решение.
32 : 4 = 8 (кг) – масса индейки.
8 • 9 = 72 (кг) – масса 9 индеек.
Ответ: масса 9 индеек 72 кг.
Что тяжелее: девять таких индеек или две овцы и на сколько килограммов?
32 • 2 = 64 (кг) – масса двух овец.
72 – 64 = 8 (кг) – на столько килограмм больше масса индеек, чем овец.
Ответ: масса индеек тяжелее на 8 кг, чем масса овец.
Задание 318. На первом станке за 1 ч мастерица изготовила 4 м полотна, а на втором — на 3 м больше.
За сколько часов на втором станке она изготовит 56 м полотна, если будет работать с такой производительностью?
4 + 3 = 7 (м) – полотна изготовила на втором станке за час (производительность второго станка).
56 : 7 = 8 (часов) — время, за которое изготовит 56 м полотна на втором станке.
Ответ: на втором станке 56 м полотна мастерица изготовит за 8 часов.
На сколько метров полотна меньше за это время мастерица изготовила бы на первом станке?
1 способ.
7 – 4 = 3 (м) – на столько меньше полотна производит за час на первом станке.
3 • 8 = 24 (м) – на столько меньше полотна произведёт за 8 часов на первом станке.
2 способ.
4 • 8 = 32 (м) – полотна производит за 8 часов на первом станке.
7 • 8 = 56 (м) – полотна производит за 8 часов на втором станке.
56 – 32 = 24 (м) – на столько меньше полотна производит за 8 часов на первом станке, чем на втором станке.
Ответ: на первом станке мастерица за это время изготовила бы полотна на 24 м меньше, чем на втором станке.
Задание 319*. У Тани 25 орехов. Сколько орехов она должна отдать брату, чтобы у неё осталось на 9 орехов больше, чем будет у брата?
Решение.
25 – 9 = 16 (ор.) – орехов поровну у Тани и брата.
16 : 2 = 8 (ор.) – орехов должна отдать Таня брату.
Ответ: Тана должна отдать брату 8 орехов.
Задание 320.
|
Числа |
8 |
14 |
18 |
9 |
18 |
27 |
18 |
36 |
72 |
81 |
|
Найти |
половину |
треть |
девятую часть |
|||||||
Решение.
|
8 : 2 = 4 14 : 2 = 7 18 : 2 = 9 |
9 : 3 = 3 18 : 3 = 6 27 : 3 = 9 |
18 : 9 = 2 36 : 9 = 4 72 : 9 = 8 81 : 9 = 9 |
2) Найди треть 2 дм 4 см.
2 дм 4 см = 2 дм + 4 см = 2 • 1 дм + 4 см = 2 • 10 см + 4 см = 24 см
24 см : 3 = 8 см
Задание 321. За 9 кг кабачков заплатили 72 грн. Сколько стоят 5 кг таких кабачков?
Решение.
72 : 9 = 8 (грн) – цена кабачков.
8 • 5 = 40 (грн) – стоимость 5 кг кабачков.
Ответ: 5 кг таких кабачков стоят 40 грн.
Задание 322. (Устно.) 36 м уменьши в 9 раз; найди девятую часть 45 кг; найди, во сколько раз 9 меньше 72; реши уравнение х • 9 = 72.
Решение.
|
36 м : 9 = 4 м 45 кг : 9 = 5 кг 72 : 9 = 8 |
х • 9 = 72 х = 72 : 9 х = 8 8 • 9 = 72 |
Задание 323.
18 + 36 : 9 = 18 + 4 = 22
72 – 27 : 9 = 72 – 3 = 69
54 : (6 + 3) = 54 : 9 = 6
54 : 6 + 3 = 9 + 3 = 12
63 : 9 • 3 = 7 • 3 = 21
63 + 9 • 3 = 63 + 27 = 90
38 + 57 = 95
91 – 19 = 72
Задание 324. Тарас поймал а окуней, а Коля — b окуней. Запиши в виде выражений ответы на вопросы.
1) Сколько окуней поймали мальчики вместе?
2) На сколько больше окуней поймал Тарас?
3) Во сколько раз больше окуней поймал Тарас?
Решение.
1) а + b (ок.) – окуней поймали мальчики вместе.
2) а – b (ок.) – на столько больше окуней поймал Тарас, чем Коля.
3) а : b (раз) – во столько больше раз окуней поймал Тарас, чем Коля.
Задание 325. В группе туристов 36 мужчин и 27 женщин. Они сели в лодки, по 9 человек в каждую. Сколько было лодок? Реши задачу двумя способами.
Решение.
1-й способ: (□ + □) : □
36 + 27 = 63 (т.) – туристов всего.
63 : 9 = 7 (л.) – было лодок.
2-й способ: □ : □ + □ : □
36 : 9 = 4 (л.) – лодки с женщинами.
27 : 9 = 3 (л.) – лодки с мужчинами.
4 + 3 = 7 (л.) – было лодок.
Ответ: было 7 лодок.
Другие задания смотри здесь…
Урок алгебры в 10-м классе (занятие элективного курса) по теме «Методы решения уравнений высших степеней»
На занятии изучается методика решения уравнений высших степеней. Рассматриваются два метода: разложение на множители и замена переменной. Понижение степени уравнений с помощью деления многочленов по схеме Горнера и приведение различных уравнений к замене переменной. Дана историческая справка исследования уравнений высших степеней. Представлена презентация урока.
Метод разложения на множители.
Этот метод основан на применении теоремы Безу. Если число α является корнем многочлена P(x) степени n, то его можно представить в виде P(x) = (x — α)Q(x), где Q(x) — многочлен степени (n-1).
Теорема Безу: “Остаток от деления многочлена Р(х) на двучлен (x — α) равен P(α), т.е. значению многочлена при x = α” Таким образом, если известен хотя бы один корень уравнения Р(х)=0 степени n, то с помощью теоремы Безу можно свести задачу к решению уравнения степени (n-1), понизить степень уравнения. Теорема. Пусть несократимая дробь p/q является корнем уравнения a0xn + a1xn-1+ … + ax-1x+ an = 0 с целыми коэффициентами, тогда число p – является делителем свободного члена an, а q – делителем старшего коэффициента a0. У многочлена с целыми коэффициентами целые корни являются делителями свободного члена. Таким образом, зная корень многочлена, его легко разложить на множители, т.е. разделить P(x) на (x — α) “углом” или по схеме Горнера.
Схема Горнера
|
a0 |
a1 |
a2 |
. |
an-1 |
an |
α |
a0 |
b1 = α a0 + a1 |
b2 = α b1 + a2 |
… |
bn-1 = α bn-2 + an-1 |
0 |
..
(x — x1)(x — x2) … (a0x2 + bx + c) = 0, x1= α – корень многочлена.
Пример №1. x3 — 9x2 + 26x — 24 = 0 Решение. Выпишем делители свободного члена
p = ±1; ±2; ±3; ±4; ±6; ±8; ±12; ±24, R(2) = 0, x1= 2.
Понизим степень уравнения делением многочленов в столбик «углом»
x3 — 2x2
-7x2 + 26x
-7x2 + 14x
12x — 24
12x — 24
Разложим на множители (x — 2)(x2 — 7x + 12) = 0, x1 = 2, x2 = 3, x3 = 4.
Ответ: {2;3;4}
Решить самостоятельно.
Пример №2: x3 + 7x2 — 56x + 48 = 0 Ответ: {1;4;-12}
Пример №3: x3 — 5x2 — 2x + 16 = 0 Ответ:
Понижение степени по схеме Горнера.
Пример №4: x4 + 3x3 — 24x2 + 17x + 3 = 0
Решение. Найдем делители свободного члена p =±1; ±3, R(1) = 0, x1= 1.
|
1 |
3 |
-24 |
17 |
3 |
|
1 |
1 |
4 |
-20 |
-3 |
0 |
x1= 1 |
3 |
1 |
7 |
1 |
0 |
|
x2= 3 |
Разложим на множители (x — 1)(x — 3)(x2 + 7x + 1) = 0 Ответ:
Пример №5: x6 — x5 — 8x4 + 14x3 + x2 — 13x + 6 = 0
p = ±1; ±2; ±3; ±6
|
1 |
-1 |
-8 |
14 |
1 |
-13 |
6 |
|
1 |
1 |
0 |
-8 |
6 |
7 |
-6 |
0 |
x1= 1 |
-1 |
1 |
-1 |
-7 |
13 |
-6 |
0 |
|
x2= -1 |
2 |
1 |
1 |
-5 |
3 |
0 |
|
|
x2= 2 |
-3 |
1 |
-2 |
1 |
0 |
|
|
|
x2= -3 |
Разложим на множители (x — 1)(x + 1)(x — 2)(x + 3)(x2 — 2x + 1) = 0
(x — 1)(x + 1)(x — 2)(x + 3)(x — 1)3 = 0
Ответ: {±1; 2; -3}
Пример №6: 2х4– 7х3 – 3х2 + 5х – 1 = 0, p = ± 1,
|
2 |
-7 |
-3 |
5 |
-1 |
|
1 |
2 |
-5 |
-8 |
-3 |
-4 |
не корень |
-1 |
2 |
-9 |
6 |
-1 |
0 |
x1= -1 |
0,5 |
2 |
-8 |
2 |
0 |
|
x2= 0,5 |
(х + 1)(х – 0,5)(2х2 – 8х + 2) = 0
х2 – 4х + 1 = 0 D/4 = 4 – 1 = 3 x = 2 ±√3 Ответ: {1; 0,5; 2 ±√3}
Решить самостоятельно.
Пример №7: 2х4 + 17х3 – 17х2 — 8х + 6 = 0 Ответ: {1/2; 1; -5 ±√19}
Пример №8: х4 + 3х3 – 5х2 — 13х + 6 = 0 Ответ: {2; -3; -1 ±√2}
Замена переменной.
Пример №9:
1. Возвратные уравнения
a0xn + a1xn-1+ … + an-1x+ an = 0 – Возвратное симметричное, если a0 = an, a1 = an-1 и т.д.
1) Для нечетных возвратных многочленов справедлива теорема: “Всякий возвратный многочлен нечетной степени имеет корнем х = -1. Затем схема Горнера.
2) Возвратное уравнение 4-й степени aх4 + bх3 + cх2 + bx + a = 0, a ≠ 0. Делим на x2
Получим замену
Пример №10: 6х4 — 35х3 + 62х2 — 35x + 6 = 0
Делим на x2, получим
6t2 — 35t + 50 = 0 t1= 5/2; t2= 10/3
Решить самостоятельно.
Пример №11: 2х4 + 3х3 — 24х2 — 3x + 2 = 0 Ответ:
Пример №12: 12х4 — 16х3 — 11х2 — 16x + 12 = 0 Ответ: {2; 0,5}
2. Однородные уравнения.
a0xn + a1xn-1y + … + ax-1xyn-1+ anyn = 0 Делим на yn, x ≠ 0, y ≠ 0.
a0(x/y)n + a1(x/y)n-1 + … + an-1(x/y)+ an = 0, получим замену x/y = t
a0tn + a1tn-1 + … + an-1t+ an = 0
Пример №13: 2х4 + х2(x + 2) — 3(x + 2)2 = 0 Делим на (x + 2)2, получим
Решить самостоятельно.
Пример №14: (x — 1)4 + 9(x + 1)4 = 10(x2 — 1)2 Ответ: {-2; -0,5; 0}
3.
Уравнения (x + a)(x + b)(x + c)(x + d) = m, m ≠ 0.
Если выполняется одно из условий a + b = c + d, b + c = a + d, a + c = b + d, то выполняется замена переменной.
Пример №15: (x + 2)(x — 3)(x + 1)(x + 6) = -96; 2+1=-3+6
(x + 2)(x — 3)(x + 1)(x + 6) = -96, (x2 + 3x + 2)(x2 + 3x — 18) = -96
x2 + 3x = t, (t + 2)(t — 18) = -96, t2 — 16t + 60 = 0, t1=10, t2=6
Решить самостоятельно.
Пример №16: (x — 2)(x + 4)(x + 1)(x + 7) = 63
4. Уравнения приводим к замене
Решить самостоятельно.
Пример №18: Ответ: {0,5; 3,5}
5. Биномиальные уравнения
(x + a)n + (x + b)n = c, замена x = t — (a + b)/2, получим (t — p)n + (t + p)n = c.
Применяем формулу бинома Ньютона
Пример №19: (x + 6)4 + (x + 4)4 = 82, x = t — (6+4)/2 = t-5,
(t — 1)4 + (t + 1)4 = 82, t 4 + 4t3 + 6t2 + 4t + 1+ t4 — 4t3 + 6t2 — 4t + 1 = 82,
x1= -3, x2= -7. Ответ: {-3; -7}
Решить самостоятельно.
Пример №20: (x + 3)4 + (x + 5)4 = 16, Ответ: {3; -5}
Домашнее задание:
Пример №2: x3 + 7x2— 56x + 48 = 0 Ответ: {1; 4; -12}
Пример №3: x3 — 5x2— 2x + 16 = 0 Ответ:
Пример №7: 2x4 + 17x3 — 17x2— 8x + 6 = 0 Ответ: {1/2; 1; -5 ±√19}
Пример №8: x4 + 3x3 — 5x2— 13x + 6 = 0 Ответ: {2; -3; -1 ±√2}
Пример №11: 2x4 + 3x3 — 24x2— 38x + 2 = 0 Ответ:
Пример №12: 12x4 — 16x3 — 11x2— 16x + 12 = 0 Ответ: {2; 0,5}
Пример №14: (x — 1)4 + 9(x + 1)4 = 10(x2— 1)2 Ответ: {-2; -0,5; 0}
Пример №16: (x — 2)(x + 4)(x + 1)(x + 7) = 63
Пример №18:
Пример №20: (x + 3)4 + (x + 5)4 = 16, Ответ: {3; -5}
Историческая справка
Квадратные уравнения
1.
1. Индийский ученый Брахмагупта (VIIв) – правило решений квадратных уравнений.
1.2. После трудов Нидерландского математика А.Жирара (1595-1632г.), а также Декарта и Ньютона способ решений квадратных уравнений принял современный вид.
1.3. Ф. Виетт (1591г.) – зависимость корней от коэффициента.
Кубические уравнения х3+рх +q = 0
1.4. Сципион Даль Ферро (1465-1526г.) и его ученик Фиори.
1.5. Н. Тарталья (1499-1557г.) – не опубликовал своих трудов.
1.6. Д. Кардано (1501-1576г.), «Великое искусство, или о правилах алгебры» – узнал об открытии Тартальи.
Формула корней кубического уравнения (формула Кардано)
х3+х — 1 = 0
р=1 q= -1
Уравнения 3-й и 4-й степени
1.7. Ученик Кардано Л.Феррари (1522-1567г.) – метод решения уравнения 4й степени.
1.8. Р.Бомбелли (1530-1572г.) – полное исследование кубических уравнений.
1.
9. Ф.Виет (1540-1603г.) – полное изложение вопросов, связанных с решением уравнений 3й и 4й степени.
Уравнения 5-й степени
1.10. Норвежский математик Н. Абель (1802-1829г.) – доказал, что в общем случае корни уравнений 5й степени и более высоких степеней не могут быть выражены через радикалы.
1.11. Французский математик Э. Галуа (1811-1832г.) выделил класс алгебраических уравнений, которые разрешены в радикалах.
заказ решений на аукционе за минимальную цену с максимальным качеством
Предлагаю идею сайта-аукциона по выполнению домашних заданий. Он будет включать:
- решение задач по математике (сейчас доступен решебник Филиппова), физике, химии, экономике
- написание лабораторных, рефератов и курсовых
- выполнение заданий по литературе, русскому или иностранному языку.
Основное отличие от большинства сайтов, предлагающих выполнение работ на заказ – сайт рассчитан на две категории пользователей: заказчиков и решающих задания.
Причем, по желанию (чтобы заработать, увеличить свой рейтинг, получить решение сложной задачи) пользователи могут играть любую из этих ролей.
Объединение сервисов в одну систему
Основой для идеи послужили несколько работающих систем, объединение которых позволит сделать сервис для решения задач на заказ. Эти системы:
- Форум, где посетители обмениваются идеями и помогают друг другу
- Система bugtracking, где обнаруженные проблемы проходят путь от публикации до принятия в исполнение и решения
- Аукцион, где цена за товар или услугу определяется в результате торгов
- Система рейтингов, где участники могут оценивать ответы друг друга. Причем, чем больше рейтинг пользователя, тем более значимым становится его голос
Принцип работы
Для удобства и проведения аналогий с реальной жизнью назовем заказчиков студентами, а решающих задания – репетиторами.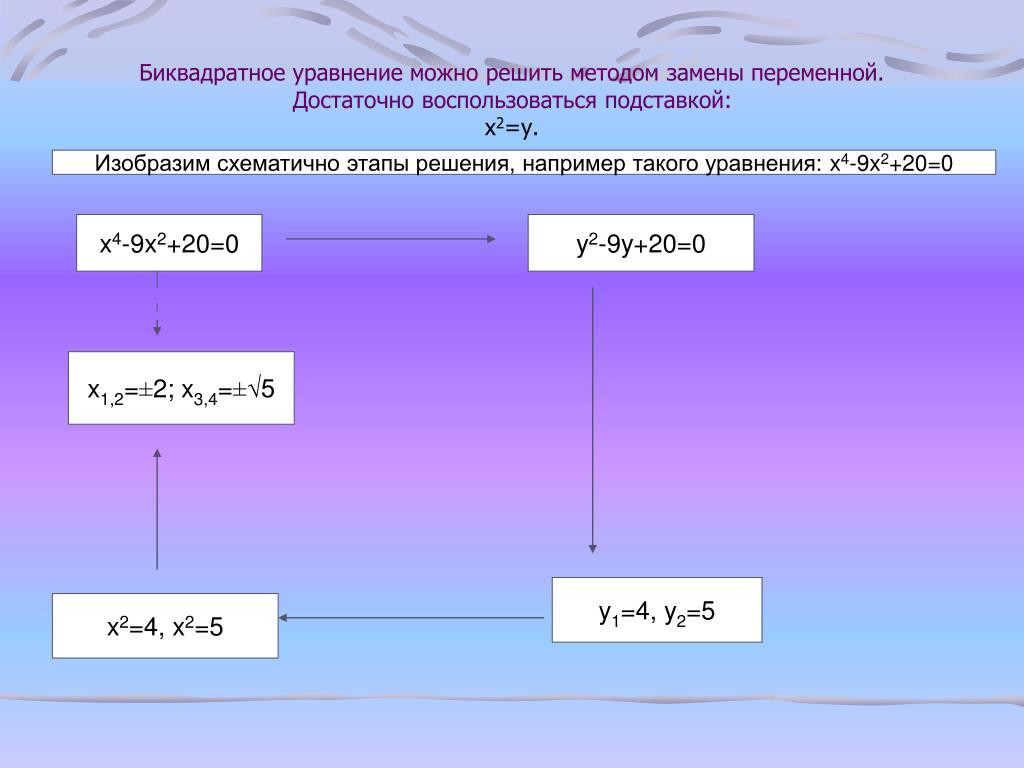
Итак, студенту необходимо решить несколько задач. Он заходит на сайт, выбирает раздел с соответствующей дисциплиной и создает новую тему (аналогия с форумом). Но при создании темы он также указывает стартовую (максимальную) цену, которую он готов заплатить за решение задач и крайний срок исполнения задания. Можно будет назначить и нулевую цену – если студенту нужно только бесплатное решение.
Как только тема создана, все пожелавшие подписаться на раздел репетиторы получают уведомление. Причем, условие получения уведомлений можно настроить. Например, уведомлять только о заказах со стартовой ценой более 500 р. и сроком решения не менее недели.
Заинтересовавшиеся репетиторы делают ставки. Причем студент (автор темы) видит ставки и может посмотреть информацию по каждому репетитору (его решения, рейтинг, дату начала участия в проекте). Когда студент посчитает нужным, он может остановить аукцион и назначить задание одному из репетиторов, сделавшему ставку (не обязательно самую низкую, т.
к. можно учитывать и другие факторы – см. выше).
Деньги блокируются на счете студента, и репетитор начинает решать задание. Он должен представить его к сроку, заданному изначально. Выполненное решение публикуется в свободном доступе и его может оценить как заказчик, так и другие репетиторы. На этих оценках и строится рейтинг. Если к решению нет претензий – деньги окончательно переводятся со счета студента на счет репетитора.
За счет чего будет развиваться сервис
Первое – положительная обратная связь. Чем больше условий задач и решений будет опубликовано на сайте, тем чаще его будут находить пользователи через поисковики, будет больше ссылок на готовые решения. Именно поэтому важно размещать решенные задачи в свободном доступе. Знаю это по опыту своего сайта exir.ru (ex irodov.nm.ru) – большая ссылочная база получена исключительно за счет благодарных пользователей.
Второе – удобный сервис для заказчиков и для желающих заработать на решениях.
Преимущества для заказчиков
Студентам и школьникам не нужно перебирать десятки сайтов для сравнения цен, а потом надеяться, что после оплаты они получат качественное решение (и, вообще, все не закончится перечислением денег). Заказчики создают аукцион на понижение цены и могут смотреть на рейтинги желающих решить задачи и ранее выполненные ими решения. Кроме того, деньги окончательно перечисляются исполнителю только после полного решения.
Преимущества для решающих задания
Не нужно создавать и продвигать свой сайт, размещать множество объявлений во всех доступных источниках информации. Заказчики сами придут к вам. Не нужно решать все присланные задания с целью поддержания репутации – можно выбирать те, которые будут интересны по уровню сложности, цене и срокам решения.
Преимущества для владельца сервиса
Если вы не понимаете, какую выгоду получит делающий вам какое-нибудь предложение – будьте осторожны! 🙂 У меня уже есть большой опыт работы с сайтом, предоставляющим бесплатные решения по физике.
И вариант с получением прибыли от размещения рекламы подходит и для нового сервиса. Кроме того, мне нравится помогать людям и довольно тяжело смотреть, как множество вопросов по задачам остаются на форуме без ответа. Предложенный аукцион решений сможет значительно сократить число вопросов без ответов.
В будущем возможен вариант и с получением некоторого небольшого процента от оплаты заказов. Но процент этот должен быть минимален и на начальном этапе он взиматься точно не будет.
Что необходимо для создания сервиса
- Самым важное сейчас – собрать команду, готовую принять участие в выполнении заданий. Если покупатели заходят в пустой магазин – они надолго забывают в него дорогу.
Поэтому я собираю предварительные заявки от посетителей, готовых заниматься решениями. Не нужно подписания никаких договоров о намерениях. Просто сообщите, на какие темы вы готовы решать задания, какой у вас опыт подобной работы (e-mail: [email protected]). Когда сервис заработает – я пришлю приглашение на регистрацию.
- Выбрать платежную систему.
- Сделать подходящий движок для сайта. Нужно решить – создавать его с нуля или изменить какой-нибудь существующий движок (например, форумный) с открытой лицензией.
- Привлечь посетителей. Учитывая посещаемость exir.ru и число публикуемых на форуме вопросов, думаю, это не будет большой проблемой.
ГДЗ по Геометрии для 9 класса Смирнов В.А., Туяков Е.А. на 5
ГДЗ по Геометрии для 9 класса Смирнов В.А., Туяков Е.А. на 5Часто ищут
- Русский язык 9 класс Рабочая тетрадь Академический школьный учебник
- Авторы: Загоровская О. В., Чаплыгина Э.Н
- Издательство: Просвещение 2014
- Алгебра 9 класс Дидактические материалы Алгоритм успеха
- Авторы: Мерзляк А.Г., Полонский В.Б., Якир М.С., Рабинович Е.М.
- Издательства: Просвещение, Вентана-граф 2017-2021
- Русский язык 9 класс
- Авторы: Рыбченкова Л. М., Александрова О.М., Загоровская О.В.
- Издательство: Просвещение 2015
- Биология 9 класс Живой организм
- Авторы: Сапин М.Р., Сонин Н.И.
- Издательство: Дрофа 2014
- Физика 9 класс Классический курс
- Авторы: Громов С. В., Родина Н.А., Белага В.В., Ломаченков И.А., Панебратцев Ю.А.
- Издательство: Просвещение 2018
- Русский язык 9 класс Школа 2100
- Авторы: Бунеев Р.Н., Бунеева Е.В., Барова Е.С.
- Издательство: Баласс 2016
- Русский язык 9 класс Алгоритм успеха
- Авторы: Шмелев А. Д., Флоренская С.Н., Митюрев С.Н.
- Издательство: Вентана-граф 2016
- Английский язык 9 класс Рабочая тетрадь Новый курс
- Авторы: Афанасьева О.В., Михеева И.В.
- Издательство: Дрофа 2017
- Алгебра 9 класс Рабочая тетрадь
- Авторы: Миндюк Н. Г., Шлыкова И.С.
- Издательство: Просвещение 2018
В., Чаплыгина Э.Н
М., Александрова О.М., Загоровская О.В.
В., Родина Н.А., Белага В.В., Ломаченков И.А., Панебратцев Ю.А.
Д., Флоренская С.Н., Митюрев С.Н.
Г., Шлыкова И.С.Калькулятор дробей
Этот калькулятор дробей выполняет базовые и расширенные операции с дробями, выражения с дробями в сочетании с целыми, десятичными и смешанными числами.
Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Калькулятор помогает найти значение из операций с несколькими дробями. Решайте задачи с двумя, тремя и более дробями и числами в одном выражении.
Правила выражений с дробями:
Дроби — для деления числителя на знаменатель используйте косую черту, т. е. для пятисотых введите 5/100 . Если вы используете смешанные числа, оставьте пробел между целой и дробной частями.
Смешанные числа (смешанные числа или дроби) сохраняют один пробел между целым числом и дробью
и используют косую черту для ввода дробей, например, 1 2/3 . Пример отрицательной смешанной дроби: -5 1/2 .
Поскольку косая черта является одновременно знаком дробной части и деления, используйте двоеточие (:) в качестве оператора деления дробей, т. е. 1/2 : 1/3 .
Decimals (десятичные числа) вводятся с десятичной точкой . и они автоматически конвертируются в дроби — т.
е. 1.45 .
Математические символы
| Символ | Название символа | Символ Значение | Пример |
|---|---|---|---|
| + | plus sign | addition | 1/2 + 1/3 |
| — | minus sign | subtraction | 1 1/2 — 2/3 |
| * | asterisk | multiplication | 2/3 * 3/4 |
| × | times sign | multiplication | 2/3 × 5/6 |
| : | division sign | division 91/2 • сложение дробей и смешанных чисел: 8/5 + 6 2/7 • деление целых чисел и дробей: 5 ÷ 1/2 • сложные дроби: 5/8 : 2 2/3 • десятичная дробь: 0,625 • Преобразование дроби в десятичную: 1/4 • Преобразование дроби в процент: 1/8 % • сравнение дробей: 1/4 2/3 • умножение дроби на целое число: 6 * 3/4 • квадратный корень дроби: sqrt(1/16) • уменьшение или упрощение дроби (упрощение) — деление числителя и знаменателя дроби на одно и то же ненулевое число — эквивалентная дробь: 4/22 • выражение со скобками: 1/3 * (1/2 — 3 3/8) • составная дробь: 3/4 от 5/7 • кратные дроби: 2/3 от 3/5 • разделить, чтобы найти частное: 3/5 ÷ 2/3 Калькулятор следует известным правилам для порядка операций .
еще математические задачи »
Слово «мульти» означает более двух или много. Вот почему решение многошаговых уравнений сложнее, чем одношаговых и двухшаговых уравнений, потому что они требуют больше шагов. Основная цель решения многошаговых уравнений, так же как и одношаговых и двухшаговых уравнений, состоит в том, чтобы изолировать неизвестную переменную в одной части уравнения, сохраняя константу или число в противоположной части. Однако правила хранения переменной отсутствуют. Все зависит от ваших предпочтений. «Стандартный» или обычный способ — расположить его с левой стороны. Но бывают случаи, когда имеет смысл оставить его в правой части уравнения. Поскольку мы имеем дело с уравнениями, нам нужно помнить, что любая операция, которую мы выполняем с одной стороны, должна быть применена и к другой, чтобы уравнение оставалось «сбалансированным». Эта концепция выполнения одной и той же операции с обеих сторон применяется к четырем арифметическим операциям, а именно: сложению, вычитанию, умножению и делению. Например, если мы добавляем 5 в левую часть уравнения, мы также должны добавить 5 в правую часть. Ключевые шаги, которые следует запомнить: Пример 1: Решите приведенное ниже многошаговое уравнение. Это типичная задача для многошаговых уравнений, где переменные присутствуют с обеих сторон. Обратите внимание, что в этом уравнении нет круглых скобок и одинаковых членов, которые можно было бы объединить с обеих сторон уравнения. Очевидно, что наш первый шаг — решить, где сохранить или изолировать неизвестную переменную x. Поскольку 7x «больше», чем 2x, мы могли бы оставить его слева. Это означает, что нам придется избавиться от 2x с правой стороны. Для этого нам нужно вычесть обе части уравнения на 2x, потому что противоположность +2x равна -2x. После этого приятно видеть только переменную x с левой стороны. Это означает, что мы должны переместить все константы в правую часть, исключив +3 в левой части. Противоположность +3 равна -3, поэтому мы вычтем обе стороны на 3. Последний шаг — выделить переменную x отдельно в левой части уравнения. Поскольку +5 — это умножение x, то его противоположная операция — деление на +5. Пример 2: Решите приведенное ниже многошаговое уравнение. Самым первым нашим шагом должно стать избавление от скобок путем применения распределительного свойства умножения вместо сложения. То есть умножьте -2 внутри каждого члена в скобках (5-4x). Теперь пришло время решить, где хранить неизвестную переменную x. Если вы решите оставить переменную слева, это прекрасно. Однако для практики попробуем держать его справа. Мы должны прийти к тем же ответам. Чтобы избавиться от -3x в левой части, мы добавляем обе стороны по 3x, так как противоположность -3x равна +3x. После того, как мы упростим, добавив обе части в 3 раза, мы получим это менее запутанное уравнение. Приятно видеть переменную x только справа. Итак, мы должны переместить все константы в левую часть. Очевидно, -10 справа нужно удалить. Противоположностью -10 является +10, поэтому мы добавим обе части по 10. Поскольку +11 — это умножение x, то его противоположная операция — деление на +11. Итак, мы собираемся разделить обе части на 11, и все готово! Пример 3: Решите приведенное ниже многошаговое уравнение. Наш первый шаг должен состоять в том, чтобы убрать круглые скобки в ОБЕИХ частях уравнения, применив свойство Распределение. Для левой стороны умножьте -4 внутри каждой скобки (4x-8), а для правой стороны умножьте +3 внутри скобки (-8x-1). Теперь, прежде чем мы даже решим, какую часть уравнения выделить переменную, похоже, нам нужно провести небольшую уборку дома. Нам нужно объединить одинаковые члены ( x ) в левой части уравнения. Опять же, не имеет значения, с какой стороны изолировать решаемую переменную. Скажем, мы решили оставить его слева. Это означает, что мы должны избавиться от -24x с правой стороны. Противоположностью -24x является +24x, поэтому мы собираемся добавить обе стороны в 24x. Далее мы должны переместить все константы в правую часть уравнения. Этот +32 слева должен исчезнуть! Противоположность +32 равна -32, поэтому мы вычтем обе части на 32. Последний шаг — выделить переменную x отдельно в левой части уравнения. Поскольку +5 — это умножение x, то его противоположная операция — деление на +5. Итак, делим обе части на 5 и готово! Пример 4: Решите уравнение 13x — 9x + 20 = 30 + 2, Пошаговое решение: 1) Объедините переменные в левой части уравнения. То есть 13х — 9х=4х. Кроме того, упростите константы в правой части, что дает нам 30+2=32. 2) Избавьтесь от 20 в левой части, вычтя 20 из обеих частей уравнения. 3) Чтобы найти x, разделите обе части на 4, чтобы получить x=3. Пример 5: Решите приведенное ниже уравнение. Пошаговое решение: 1) Соедините одинаковые термины с обеих сторон. 2) Вычтите 6y с обеих сторон, чтобы оставить переменную y только в левой части. 3) Добавьте 11 к обеим частям уравнения. 4) Наконец, разделите обе части на -10, чтобы получить решение. Пример 6: Решите приведенное ниже уравнение. Пошаговое решение: 1) Объедините аналогичные члены с переменной m и константами в обеих частях уравнения. 2) Добавьте 5 м к обеим частям уравнения. Он сохранит переменную слева и удалит переменную справа. 3) Добавьте 14 с обеих сторон. 4) Последний шаг — разделить одношаговое уравнение на -3, чтобы получить значение m. Пример 7: Решите уравнение 2\left( {x — 5} \right) = 5x + 23. Пошаговое решение: 1) Удалите скобки с левой стороны уравнения путем распределения числа вне круглых скобок в двучлен внутри. 2) На этот раз для удобства мы оставим переменную справа. Для этого мы вычтем 2x с обеих сторон уравнения. 3) Затем вычтите 23 из обеих частей уравнения. 4) Остается просто разделить обе части на коэффициент 3x, который равен 3, чтобы получить значение x. Пример 8: Решите приведенное ниже уравнение. Пошаговое решение: 1) Удалите две скобки с обеих сторон линейного уравнения, применив распределительное свойство умножения над сложением. 2) Объедините константы с обеих сторон. Это значительно очистит уравнение. 3) Добавьте 7h к обеим сторонам, чтобы оставить член с переменной слева и исключить член справа. 4) Добавьте 57 к обеим частям уравнения, чтобы константа осталась справа. 5) Разделите обе части на 22, чтобы получить окончательное решение. Вот и все! Вас также может заинтересовать: Решение одношаговых уравнений Одношаговое уравнение Практические задачи с ответами Решение двухэтапного уравнения линейные уравнениялинейные уравненияЛинейные уравнения Уравнение — это утверждение, в котором говорится, что два алгебраических выражения равны. 1. Тождества: ВСЕ замены переменной делают уравнение верным. Пример: x + 1 = 1 + x (верно для всех действительных чисел) Набор решений: { х | x — любое действительное число} Попробуйте этот пример: 2(1 x ) = 2 x + 2 2. Противоречия: НИКАКИЕ замены для переменной не делают уравнение верным. Пример: x + 1 = 2 + x (верно для НЕТ действительных чисел) Набор решений: Пустой набор { }=Æ . Попробуйте следующий пример: 2 x + 3 = 2( x + 1) + 3 3. Условные уравнения: НЕКОТОРЫЕ замены переменной делают уравнение верным. Пример: x + 1 = 3 (верно для одного действительного числа; только 2) Набор решений: { x | х = 2} Попробуйте следующий пример: 2( x 1) = x + 1
Уравнение называется линейным уравнением, если переменная, которую мы должны решить, не имеет степени и не входит в знаменатель дроби. Например, 2( x 5) 15 = 7 x 20 является линейным уравнением. При решении любого уравнения наша цель — найти значение, которое могло бы заменить переменную таким образом, чтобы уравнение осталось верным. Если мы заменим x на 7 в линейном уравнении выше, две части уравнения не будут равны друг другу: 2(7 5) 15 равно 11, а 7(7) 20 равно 29. Но если мы заменим x с 1 две части уравнения дадут нам один и тот же ответ: 2(1 5) 15 равно 27 и 7(-1) 20 также равно 27. Поэтому мы говорим, что 1 является решением нашего уравнения. Но как найти решение линейного уравнения? г. Думайте об уравнении как о шкале или балансе, выражения на каждой стороне равны, поэтому они уравновешивают друг друга. Если мы хотим, мы можем удвоить обе стороны, и они все равно будут сбалансированы, потому что мы увеличили их одинаково. Точно так же мы можем прибавить или вычесть одну и ту же сумму с обеих сторон, и они все равно будут равны. На самом деле две части уравнения будут равны независимо от того, какую операцию мы выполняем, пока она выполняется с обеими частями уравнения.
Помните, что наша цель при решении линейного уравнения — найти x (или любую другую используемую переменную). Это означает, что мы хотим манипулировать уравнением, пока не получим выражение, которое говорит: x = C (где C — число или выражение, в котором нет x ). В приведенном выше примере это выражение будет x = 1, .Давайте рассмотрим наше уравнение: Пример 1) Решить 2( х 5) 15 = 7 х 20 Первое, что нужно сделать, это попытаться максимально упростить каждую часть уравнения. Помните, что мы можем комбинировать члены, которые находятся на одной стороне уравнения, но не на противоположных сторонах . 2 х 10 15 = 7 х 20 2 х 25 = 7 х 20 Обратите внимание, что в приведенном выше выражении есть переменные с обеих сторон уравнения, и мы хотим получить x = C и C не могут иметь x с. 2 x 25 7 x = 7 x 20 7 x 5 х 25 = 20 Теперь нам нужно исключить 25 слева. И мы можем сделать это, добавив 25 к обеим частям этого уравнения. 5 х 25 + 25 = 20 + 25 5 х = 5 И, наконец, чтобы отменить 5, умноженное на x , мы можем разделить обе части этого уравнения на 5. г.Получаем x = 1, .ЧТО, ЕСЛИ НАШЕ УРАВНЕНИЕ ВКЛЮЧАЕТ Дроби? Пример 2) Хорошо начнем задачу так же, как и предыдущую, максимально распределив и упростив. (ЖК-дисплей 3, 5 и 20 равен 60) Теперь, поскольку это уравнение, и мы можем выполнять любые арифметические операции, пока мы делаем это с обеих сторон, мы можем попытаться исключить знаменатели. Мы достигаем этого, умножая обе части уравнения на общий знаменатель дробей в обеих частях уравнения. в данном случае 60, г.240 х 200 = 120 + 24 х 3 240 х 200 = 117 + 24 х Начнем с удаления xs в правой части путем вычитания 24 x . 240 x 200 24 x = 117 + 24 x 24 x 216 х 200 = 117 Затем удалите 200, добавив 200 с обеих сторон, 216 х 200 + 200 = 117 + 200 216 х = 317 А затем разделите на 216 с обеих сторон, чтобы отменить 216, умноженные на x. Итак, х = 317/216. ИНОГДА МОЖЕТ ПРИНИМАТЬСЯ В ЛИНЕЙНЫХ УРАВНЕНИЯХ, ВКЛЮЧАЮЩИХ БОЛЕЕ ОДНОЙ ПЕРЕМЕННОЙ:
Пример 3) Решите 4 в + 5 y = 2 t + 9 y для т . Поскольку мы решаем это уравнение для t , нам нужно убедиться, что в итоге мы получим t = C , где C является либо числом, либо, в данном случае, выражением, которое не имеет t s в этом. Итак, мы начинаем с исключения t s из правой части этого уравнения, вычитая 2 t из обеих частей. 4 в + 5 у 2 т = 2 т + 9 у 2 т 4 в + 5 у 2 т = 9 у Далее нам нужно исключить 5y из левой части (потому что в ней нет ts). Мы можем сделать это, вычитая 5 y с обеих сторон. 4 в + 5 у 2 т 5 у = 9 у 5 у 4 в 2 т = 4 у г. До этого момента мы действовали точно так же, как и в предыдущих задачах, но теперь у нас есть новая ситуация с левой стороны. У нас есть более одного t, и они не могут быть объединены. 2 т (2 a 1) = 4 у Теперь мы можем изолировать переменную t путем деления обеих сторон на 2 (2 a 1): Что после сокращения дает нам: С ограничением: Приложения и задачи WordQ1 Решить i 2x 5 17 ii 3y 2 1 iii 5p 4 29 iv 4a 3 27 v 2z 3 19 vi 7m 1 20 vii 24x 3 42 viii 4m 94 5 i…Перейти к Главная >
Селина Солюшнс
Класс 6
Математика
>
Глава 22. Вопрос 1 Упражнение 22(B) Q1) Решите: (i) 2x + 5 = 17 (ii) 3y — 2 = 1 (iii) 5p + 4 = 29 (iv) 4a — 3 = -27 (2 v) 2z + 3 = -19 (vi) 7m — 1 = 20 (vii) 2,4x — 3 = 4,2 (viii) 4m + 9,4 = 5 (ix) 6y + 4 = -4,4 Answer: Solution 1: (i) 2x + 5 = 17 2x = 17 — 5 2x = 12 x = 6 (ii) 3y — 2 = 1 3y = 1 + 2 3y = 3 y = 1 (iii) 5p + 4 = 29 5p = 29 — 4 5p = 25 p = 5 (iv) 4a — 3 = -27 4A 4A 4A 4A 4A 4A 4A 4A 4A 4A 4A 4A. = -27 + 3 4a = -24 a = -6 (v) 2z + 3 = -19 2z = -19 -3 2z = -22 9181 z = -11 981 (vi) 7m — 1 = 20 7m = 20 + 1 7m = 21 m = 3 (vii) 2,4x — 3 = 4,2 2,4x = 4,2 2,4x = 4,2×1 3 918 x = 3 (viii) 4m + 9,4 = 5 4m = 5 — 9,4 4m = -4,4 m = -1,1 (ix) 6y + 91 = -81,4 91 = -4 1,4 91 4. 6у = -8.4 у = -1.4 Стенограмма видео «привет
Добро пожаловать, чтобы вести обучение сегодня мы
собираюсь увидеть
как решать уравнения
2x первый 2x
плюс 5 равно 17
x плюс y равно 17
2x равно 17 минус 5
12 х равно 12 на
2 что 6.
хорошо, тогда мы идем с другим случаем
второй
второй 3y минус 2 равно 1.
3у равно 3
у равно 1
со следующим
5п плюс 4
равно 295р равно 25
p равно 5 напрямую
так что мы увидим следующий набор вопросов
следующий набор вопросов у нас 4 с минусом
3
равно минус 27 то же самое мы
должен
делай здесь
четвертый
4а минус 3 равно минус 27
4а равно плюс 3
будет минус 24
минус 24 а равно минус 24 на 4.
6 4 24 а равно минус 6
в следующем случае ты будешь бить
2 з плюс 3
равно минус 19
2z равно минус 19
минус 3
2 z равно
минус 22
z равно 22 на 2 равно 11.
это -11 нормально
тогда мы идем с другими случаями
другие вещи
7 м минус 1 равно 20
семь м равно
21 м равно
21 на семь
это m равно
три семь три двадцать один
тогда мы идем с другим случаем восемь семь
к одному
две целых четыре десятых в два целых четыре х
минус
три равно четырем точкам два
нормально это дается как
две точки
так что это небольшая ошибка в вопросе
сам
2,4
х в минус 3 это
4. Связанные вопросы Q2) Решите: (i) (ii) (iii) (iv) (v) (vi) Q3) Решите: (i) -8m — 2 = -10 (ii) 4x + 2x = 3 + 5 (iii) 4x — x + 5 = 8 (iv) 6x + 2 = 2x + 10 (v) 18 — ( 2а. Фейсбук WhatsApp Копировать ссылку Было ли это полезно? Упражнения Упражнение 22 (a) Упражнение 22 (b) Упражнение 22 (C) Упражнение 22 (D) РЕССИОНАЯ УПРАЖНЕНИЯ Главы Номер (консультант. Оценка Числа в Индии и международной системе (со сравнением) Разрядное значение Натуральные числа и целые числа (включая шаблоны) Отрицательные числа и целые числа Численная строка HCF и LCM Игра с числами Наборы ОТВЕТ Propororts (Включение Word Wress) 912 918 918 918 918 918 1018 101818 181818181818 гг. |
Наиболее распространенные мнемоники для запоминания этого порядка операций: 
А 
Какую часть составляют девочки?
Итак, мы собираемся разделить обе части на 5, и все готово!
Последний шаг — выделить переменную x отдельно в правой части уравнения.
Уравнения могут быть истинными или ложными. Мы определяем три типа уравнений на основе того, существуют ли замены для переменной, которые сделают уравнение верным.
Это факт, который мы собираемся использовать для решения линейного уравнения.
Итак, нам нужно исключить x с из одной части этого уравнения. На самом деле не имеет значения, с какой стороны, но ради согласованности я всегда буду стараться оставить x с левой стороны. Это означает, что я хочу убрать 7 x с правой стороны. Мы можем сделать это, вычитая 7 x из обеих частей уравнения. Вычитание 7 x отменяет 7 x в правой части, и, поскольку я собираюсь также вычесть его из левой части, равенство сохраняется.
Помните, что наша цель — оставить одну букву t с левой стороны. В подобных ситуациях мы можем разложить выражение на множители, и это позволит нам записать несколько терминов как один термин.
Простые (линейные) уравнения (включая текстовые задачи)
>
Упражнение 22(Б)
>
Вопрос 1
4 -4.0
2
2,4 х 2,4 х равно
4,2 т
так это вопрос задан неправильно давайте
проверить вопрос
сам вопрос 2.4
вопрос здесь 2,4 х равно 400
2,4 х равно 4,2
х равно 4,2 разделить на 2,4
это будет 42 разделить на
24.
42 разделить на
24
будет 1,75
вы можете сделать общий метод деления
и вы можете найти его
и проверяем со следующим последним
один последний второй последние два один
4 м равно
94 м плюс 9,4
тоже равно 5
5 4м
равно 5 минус 9,4
m равно я должен сделать это
9,4 минус 5.
четыре девять минус пять четыре четыре точки
четыре будет минус четыре целых четыре
к четырем будет
минус один балл один
хорошо, тогда мы делаем это еще один девятый
последний
у девятого шесть лет
плюс четыре равно минус 4,4
6y равно минус 4,4
минус 4 и 6y равно
минус четыре
y равно минус восемь целых четыре десятых
деленное на
шесть шесть пять шесть
два шесть четыре ноль двадцать четыре будет
минус один пункт шесть
Я надеюсь, вы понимаете это видео, если вы
есть какие-либо вопросы, вы можете поместить его в
поле для комментариев спасибо за просмотр
видео
..