Коэффициент ранговой корреляции Спирмена онлайн
Примеры решенийКоэффициент СпирменаКоэффициент Кендалла Коэффициент конкордацииКоэффициент контингенции Группировка данных Показатели вариации Доверительный интервал Различие средних
Назначение сервиса. С помощью данного онлайн-калькулятора производится:
- расчет коэффициента ранговой корреляции Спирмена;
- вычисление доверительного интервала для коэффициента и оценка его значимости;
- Шаг №1
- Шаг №2
- Видеоинструкция
Инструкция. Укажите количество данных (количество строк), нажмите Далее. Полученное решение сохраняется в файле Word (см пример нахождения коэффициента ранговой корреляции Спирмена). Также создается шаблон решения в Excel.
Количество строк
Укажите количество данных (количество строк), нажмите Далее. Полученное решение сохраняется в файле Word (см пример нахождения коэффициента ранговой корреляции Спирмена). Также создается шаблон решения в Excel.
Количество строк
Расчет коэффициента состоит из следующих этапов:
- Ранжирование признаков по возрастанию. Ранг – это порядковый номер. Если встречаются два одинаковых значения, им присваивают одинаковое значение ранга, равное среднему арифметическому рангов этих значений.
- Определение разности рангов каждой пары сопоставляемых значений, d = dx — dy.
- Возведение в квадрат разность di и нахождение общей суммы, ∑d2.

- Вычисление коэффициента корреляции рангов по формуле: где d2 – квадратов разностей между рангами; N – количество признаков, участвовавших в ранжировании.
Свойства коэффициента ранговой корреляции Спирмена
- Нормируемость. Коэффициент корреляции рангов может принимать значения от -1 до +1.
p = 1свидетельствует о возможном наличии прямой связи,p =-1свидетельствует о возможном наличии обратной связи. - Ограниченность. Для оценки данных необходима выборка от 5 до 40 наблюдений по каждой переменной. При большом количестве одинаковых рангов по сопоставляемым переменным коэффициент дает приближенные значения. При совпадении значений вносится поправка на одинаковые ранги. В этом случае формула имеет вид:
где d

- Независимость. Чтобы получить адекватный результат, необязательно наличие нормального закона распределения коррелируемых рядов.
Область применения. Коэффициент корреляции рангов используется для оценки качества связи между двумя совокупностями. Кроме этого, его статистическая значимость применяется при анализе данных на гетероскедастичность.
Пример. По выборке данных наблюдаемых переменных X и Y:
- составить ранговую таблицу;
- найти коэффициент ранговой корреляции Спирмена и проверить его значимость на уровне 2a
- оценить характер зависимости
Решение. Присвоим ранги признаку Y и фактору X.
| X | Y | ранг X, dx | ранг Y, dy |
| 28 | 21 | 1 | 1 |
| 30 | 25 | 2 | 2 |
| 36 | 29 | 4 | 3 |
| 40 | 31 | 5 | 4 |
| 30 | 32 | 3 | 5 |
| 46 | 34 | 6 | 6 |
| 56 | 35 | 8 | 7 |
| 54 | 38 | 7 | 8 |
| 60 | 39 | 10 | 9 |
| 56 | 41 | 9 | 10 |
| 60 | 42 | 11 | 11 |
| 68 | 44 | 12 | 12 |
| 70 | 46 | 13 | 13 |
| 76 | 50 | 14 | 14 |
Матрица рангов.

| ранг X, dx | ранг Y, dy | (dx — dy)2 |
| 1 | 1 | 0 |
| 2 | 2 | 0 |
| 4 | 3 | 1 |
| 5 | 4 | 1 |
| 3 | 5 | |
| 6 | 6 | 0 |
| 8 | 7 | 1 |
| 7 | 8 | 1 |
| 10 | 9 | 1 |
| 9 | 10 | 1 |
| 11 | 11 | 0 |
| 12 | 12 | 0 |
| 13 | 13 | 0 |
| 14 | 14 | 0 |
| 105 | 105 | 10 |
Проверка правильности составления матрицы на основе исчисления контрольной суммы:
Сумма по столбцам матрицы равны между собой и контрольной суммы, значит, матрица составлена правильно.

По формуле вычислим коэффициент ранговой корреляции Спирмена.
Связь между признаком Y и фактором X сильная и прямая
Значимость коэффициента ранговой корреляции Спирмена
Для того чтобы при уровне значимости α проверить нулевую гипотезу о равенстве нулю генерального коэффициента ранговой корреляции Спирмена при конкурирующей гипотезе Hi. p ≠ 0, надо вычислить критическую точку:
где n — объем выборки; ρ — выборочный коэффициент ранговой корреляции Спирмена: t(α, к) — критическая точка двусторонней критической области, которую находят по таблице критических точек распределения Стьюдента, по уровню значимости α и числу степеней свободы k = n-2.

По таблице Стьюдента находим t(α/2, k) = (0.1/2;12) = 1.782
Поскольку Tkp < ρ, то отклоняем гипотезу о равенстве 0 коэффициента ранговой корреляции Спирмена. Другими словами, коэффициент ранговой корреляции статистически — значим и ранговая корреляционная связь между оценками по двум тестам значимая.
Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Пример нахождения коэффициента ранговой корреляции Спирмена
На практике для определения тесноты связи двух признаков часто применяется коэффициент ранговой корреляции Спирмена (Р). Значения каждого признака ранжируются по степени возрастания (от 1 до n), затем определяется разница (d) между рангами, соответствующими одному наблюдению.Пример №1. Зависимость между объемом промышленной продукции и инвестициями в основной капитал по 10 областям одного из федеральных округов РФ в 2003 году характеризуется следующими данными.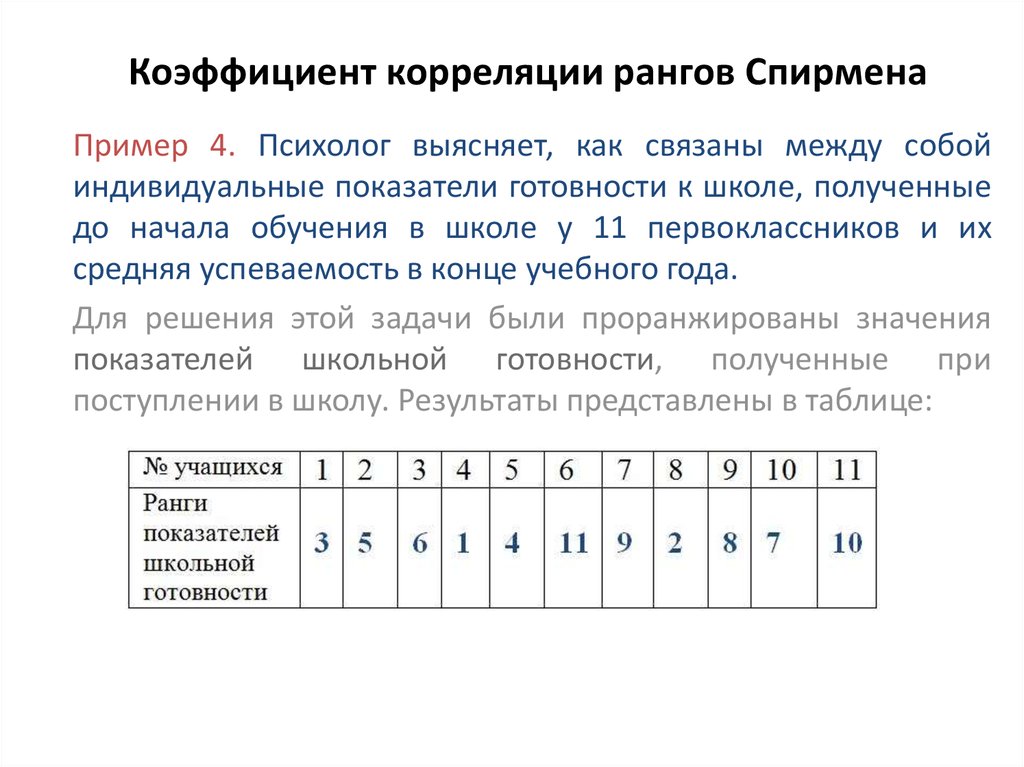
Вычислите ранговые коэффициенты корреляции Спирмена и Кендэла. Проверить их значимость при α=0,05. Сформулируйте вывод о зависимости между объемом промышленной продукции и инвестициями в основной капитал по рассматриваемым областям РФ.
Присвоим ранги признаку Y и фактору X. Найдем сумму разности квадратов d2.
Используя калькулятор, вычислим коэффициент ранговой корреляции Спирмена:
| X | Y | ранг X, dx | ранг Y, dy | (dx — dy)2 |
| 1.3 | 300 | 1 | 2 | 1 |
| 1.8 | 1335 | 2 | 12 | 100 |
| 2.4 | 250 | 3 | 1 | 4 |
| 3.4 | 946 | 4 | 8 | 16 |
4. 8 8 |
670 | 5 | 7 | 4 |
| 5.1 | 400 | 6 | 4 | 4 |
| 6.3 | 380 | 7 | 3 | 16 |
| 7.5 | 450 | 8 | 5 | 9 |
| 7.8 | 500 | 9 | 6 | 9 |
| 17.5 | 1582 | 10 | 16 | 36 |
| 18.3 | 1216 | 11 | 9 | 4 |
| 22.5 | 1435 | 12 | 14 | 4 |
| 24.9 | 1445 | 13 | 15 | 4 |
| 25.8 | 1820 | 14 | 19 | 25 |
28.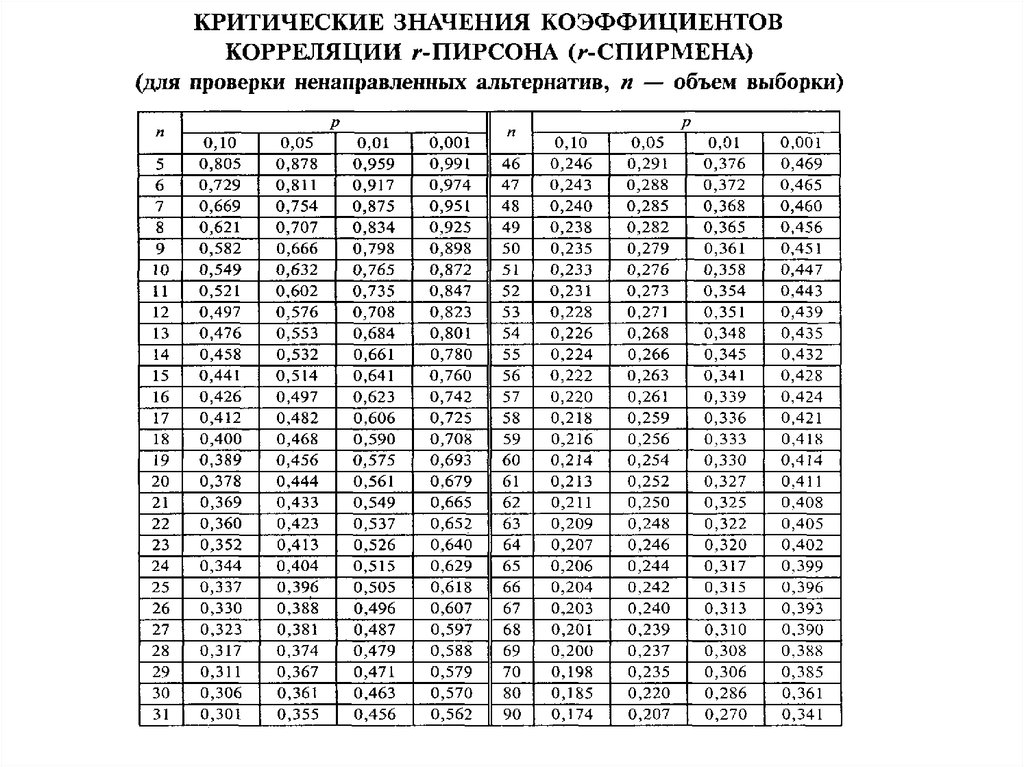 5 5 |
1246 | 15 | 10 | 25 |
| 33.4 | 1435 | 16 | 14 | 4 |
| 42.4 | 1800 | 17 | 18 | 1 |
| 45 | 1360 | 18 | 13 | 25 |
| 50.4 | 1256 | 19 | 11 | 64 |
| 54.8 | 1700 | 20 | 17 | 9 |
| 364 |
Связь между признаком Y фактором X сильная и прямая.
Оценка коэффициента ранговой корреляции Спирмена
Значимость коэффициента ранговой корреляции СпирменаПо таблице Стьюдента находим Tтабл.
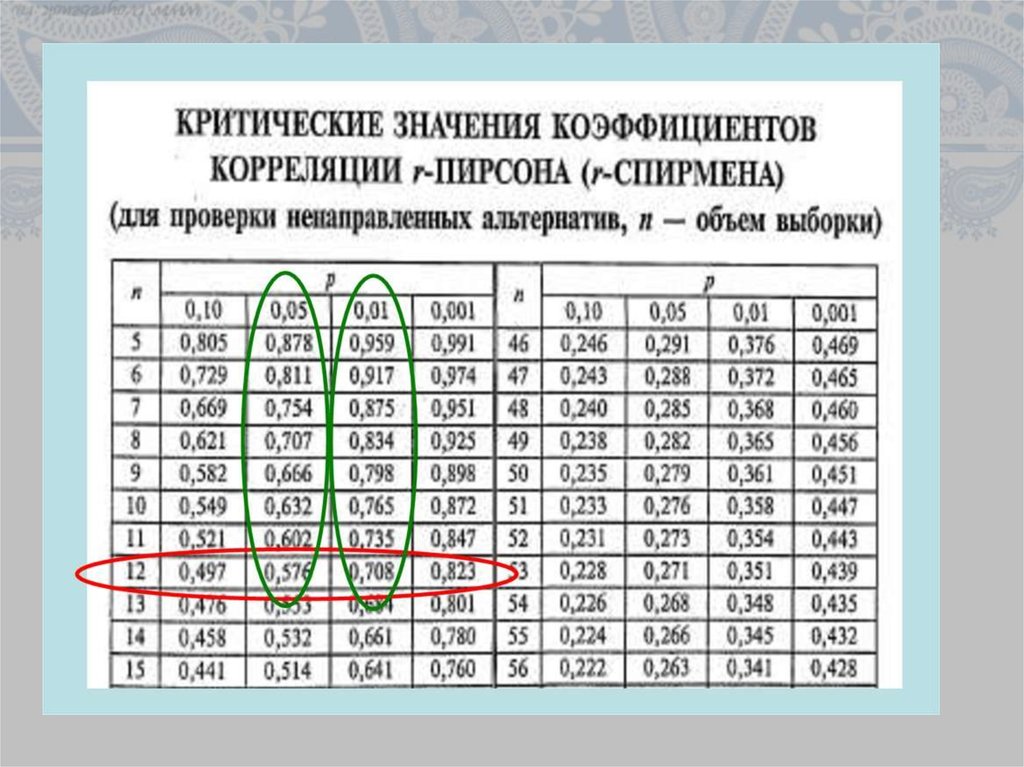
Tтабл = (18;0.05) = 1.734
Поскольку Tнабл > Tтабл , то отклоняем гипотезу о равенстве нулю коэффициента ранговой корреляции. Другими словами, коэффициента ранговой корреляции Спирмена статистически — значим.
Интервальная оценка для коэффициента ранговой корреляции (доверительный интервал)
Доверительный интервал для коэффициента ранговой корреляции Спирмена: p(0.5431;0.9095).
Перейти к онлайн решению своего примера
Пример №2. Исходные данные.
| 5 | 4 |
| 3 | 4 |
| 1 | 3 |
| 3 | 1 |
| 6 | 6 |
| 2 | 2 |
 Переформирование рангов производиться без изменения важности ранга, то есть между ранговыми номерами должны сохраниться соответствующие соотношения (больше, меньше или равно). Также не рекомендуется ставить ранг выше 1 и ниже значения равного количеству параметров (в данном случае n = 6). Переформирование рангов производится в табл.
Переформирование рангов производиться без изменения важности ранга, то есть между ранговыми номерами должны сохраниться соответствующие соотношения (больше, меньше или равно). Также не рекомендуется ставить ранг выше 1 и ниже значения равного количеству параметров (в данном случае n = 6). Переформирование рангов производится в табл.
| Номера мест в упорядоченном ряду | Расположение факторов по оценке эксперта | Новые ранги |
| 1 | 1 | 1 |
| 2 | 2 | 2 |
| 3 | 3 | 3.5 |
| 4 | 3 | 3.5 |
| 5 | 5 | 5 |
| 6 | 6 | 6 |
 Переформирование рангов производится в табл.
Переформирование рангов производится в табл.
| Номера мест в упорядоченном ряду | Расположение факторов по оценке эксперта | Новые ранги |
| 1 | 1 | 1 |
| 2 | 2 | 2 |
| 3 | 3 | 3 |
| 4 | 4 | 4.5 |
| 5 | 4 | 4.5 |
| 6 | 6 | 6 |
| ранг X, dx | ранг Y, dy | (dx — dy)2 |
| 5 | 4. 5 5 | 0.25 |
| 3.5 | 4.5 | 1 |
| 1 | 3 | 4 |
| 3.5 | 1 | 6.25 |
| 6 | 6 | 0 |
| 2 | 2 | 0 |
| 21 | 21 | 11.5 |
где
j — номера связок по порядку для признака х;
Аj — число одинаковых рангов в j-й связке по х;
k — номера связок по порядку для признака у;
Вk — число одинаковых рангов в k-й связке по у.
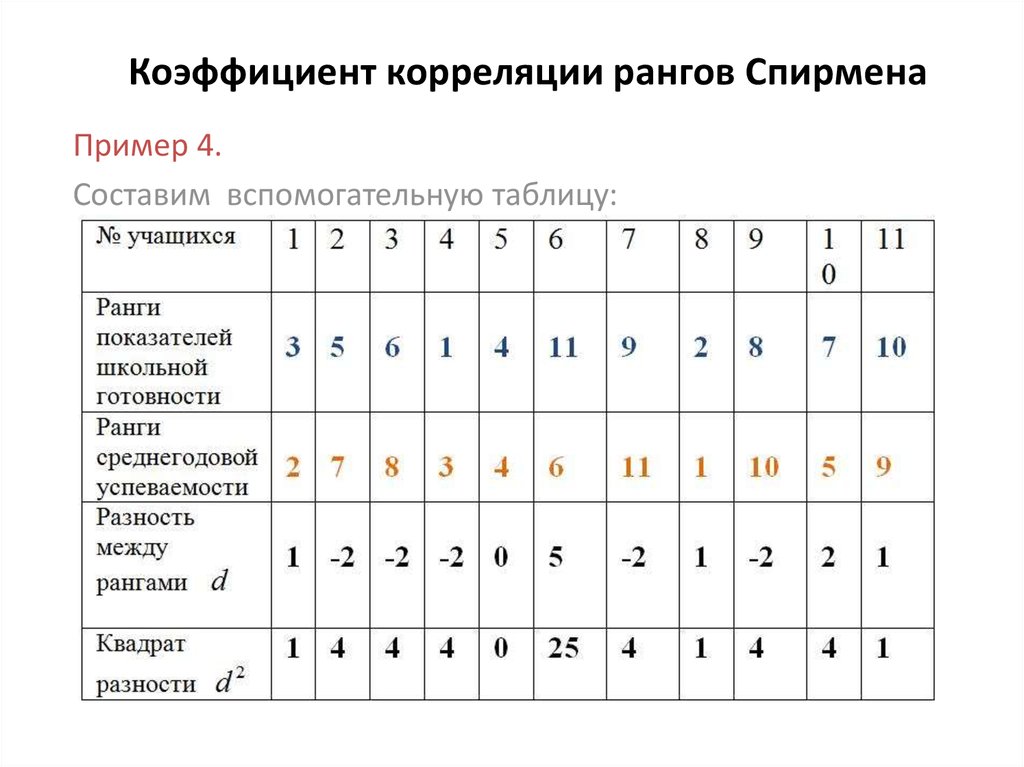
A = [(23-2)]/12 = 0.5
B = [(23-2)]/12 = 0.5
D = A + B = 0.5 + 0.5 = 1
Связь между признаком Y и фактором X умеренная и прямая.
Задание №1. Определите тесноту связи с помощью коэффициента корреляции рангов Спирмена между X и Y.
Скачать решение
Задание №2. С помощью коэффициента ранговой корреляции Спирмена определите, между мнениями каких политических деятелей по вопросу приоритетов мероприятий региональной политики в России наблюдается наибольшее совпадение.
Пример №2
Spearman’s Rank-Orrelation — руководство о том, когда ее использовать, что она делает и каковы предположения.
В этом руководстве рассказывается, когда следует использовать ранговую корреляцию Спирмена для анализа данных, какие допущения необходимо выполнить, как ее рассчитать и как ее представить. Если вы хотите узнать, как запустить корреляцию Спирмена в SPSS Statistics, перейдите к нашему руководству по корреляции Спирмена в SPSS Statistics.
Когда следует использовать ранговую корреляцию Спирмена?
Ранговая корреляция Спирмена является непараметрической версией корреляции Пирсона произведение-момент. Коэффициент корреляции Спирмена (ρ, также обозначаемый как r s ) измеряет силу и направление связи между двумя ранжированными переменными.
Каковы предположения теста?
Вам нужны две переменные: порядковые, интервальные или относительные (см. наше руководство по типам переменных, если вам нужны разъяснения). Хотя обычно вы надеетесь использовать корреляцию Пирсона произведение-момент для интервальных или относительных данных, корреляцию Спирмена можно использовать, когда допущения корреляции Пирсона заметно нарушаются. Однако корреляция Спирмена определяет силу и направление 9.0015 монотонная связь между вашими двумя переменными, а не сила и направление линейной зависимости между вашими двумя переменными, которую определяет корреляция Пирсона.
Что такое монотонная связь?
Монотонная связь — это связь, которая выполняет одно из следующих действий: (1) по мере увеличения значения одной переменной увеличивается и значение другой переменной; или (2) по мере увеличения значения одной переменной значение другой переменной уменьшается. Примеры монотонных и немонотонных зависимостей представлены на диаграмме ниже:
Примеры монотонных и немонотонных зависимостей представлены на диаграмме ниже:
Почему монотонные отношения важны для корреляции Спирмена?
Корреляция Спирмена измеряет силу и направление монотонной связи между двумя переменными. Монотонность «менее ограничительна», чем линейная зависимость. Например, на среднем изображении выше показана зависимость, которая является монотонной, но нелинейной.
Монотонная зависимость не является строго предположением о корреляции Спирмена. То есть вы можете запустить корреляцию Спирмена для немонотонного отношения, чтобы определить, существует ли монотонная составляющая к ассоциации. Однако обычно вы выбираете меру связи, такую как корреляция Спирмена, которая соответствует шаблону наблюдаемых данных. То есть, если диаграмма рассеяния показывает, что взаимосвязь между двумя вашими переменными выглядит монотонной, вы должны запустить корреляцию Спирмена, потому что она будет измерять силу и направление этой монотонной взаимосвязи. С другой стороны, если, например, связь кажется линейной (оценивается с помощью диаграммы рассеяния), вы должны запустить корреляцию Пирсона, потому что она будет измерять силу и направление любой линейной зависимости. Вы не всегда сможете визуально проверить, есть ли у вас монотонная зависимость, поэтому в этом случае вы все равно можете запустить корреляцию Спирмена.
С другой стороны, если, например, связь кажется линейной (оценивается с помощью диаграммы рассеяния), вы должны запустить корреляцию Пирсона, потому что она будет измерять силу и направление любой линейной зависимости. Вы не всегда сможете визуально проверить, есть ли у вас монотонная зависимость, поэтому в этом случае вы все равно можете запустить корреляцию Спирмена.
Как ранжировать данные?
В некоторых случаях ваши данные могут быть уже ранжированы, но часто вы обнаружите, что вам нужно ранжировать данные самостоятельно (или использовать SPSS Statistics, чтобы сделать это за вас). К счастью, ранжирование данных не является сложной задачей и легко выполняется путем обработки ваших данных в таблице. Рассмотрим следующий пример данных, касающихся оценок, полученных на экзамене по математике и английскому языку:
| Оценки | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Английский | 56 | 75 | 45 | 71 | 61 | 64 | 58 | 80 | 76 | 61 |
| Математика | 66 | 70 | 40 | 60 | 65 | 56 | 59 | 77 | 67 | 63 |
Процедура ранжирования этих результатов следующая:
Сначала создайте таблицу с четырьмя столбцами и пометьте их, как показано ниже: 037 Ранг (англ. )
)
Вам необходимо ранжировать баллы по математике и английскому языку отдельно.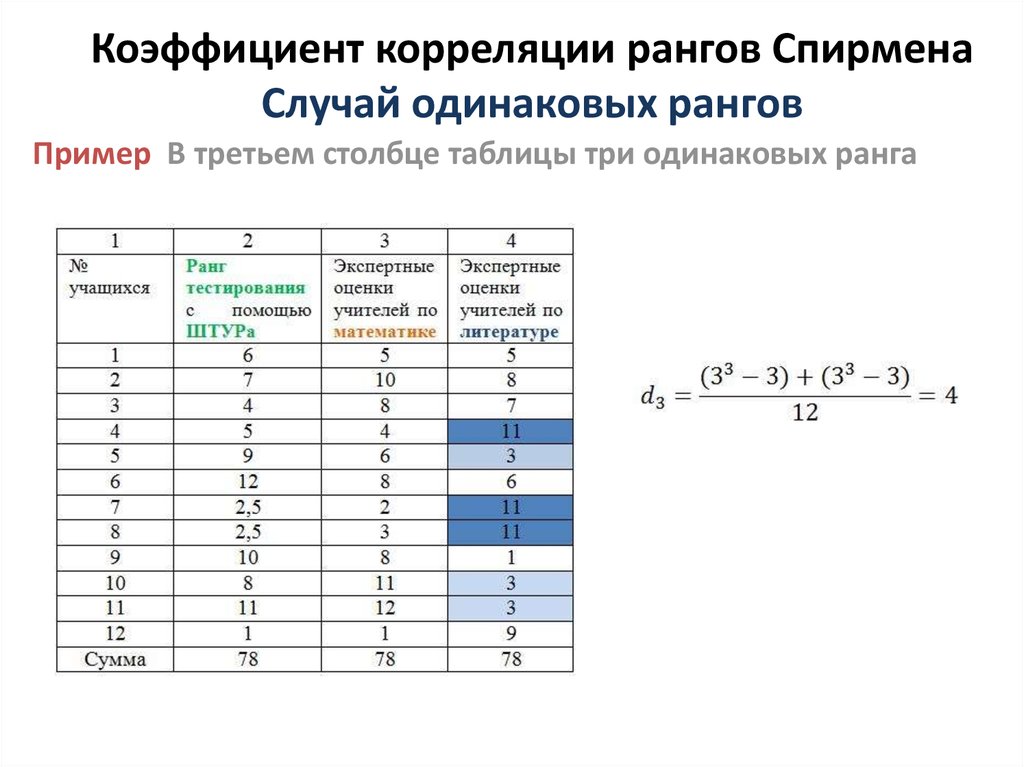 Оценка с самым высоким значением должна быть помечена как «1», а самая низкая оценка должна быть помечена как «10» (если в вашем наборе данных более 10 случаев, то самый низкий балл будет равен количеству случаев, которые у вас есть). Посмотрите внимательно на двух человек, которые набрали 61 балл на экзамене по английскому языку (выделены жирным шрифтом). Обратите внимание на их общий рейтинг 6,5. Это связано с тем, что, когда у вас есть два одинаковых значения в данных (называемых «связью»), вам нужно взять среднее значение рангов, которые они в противном случае занимали бы. Мы делаем это, потому что в этом примере у нас нет способа узнать, какой балл должен быть помещен в ранг 6, а какой — в ранг 7. Таким образом, вы заметите, что ранги 6 и 7 не существуют для английского языка. Эти два ранга были усреднены ((6 + 7)/2 = 6,5) и присвоены каждой из этих «равных» оценок.
Оценка с самым высоким значением должна быть помечена как «1», а самая низкая оценка должна быть помечена как «10» (если в вашем наборе данных более 10 случаев, то самый низкий балл будет равен количеству случаев, которые у вас есть). Посмотрите внимательно на двух человек, которые набрали 61 балл на экзамене по английскому языку (выделены жирным шрифтом). Обратите внимание на их общий рейтинг 6,5. Это связано с тем, что, когда у вас есть два одинаковых значения в данных (называемых «связью»), вам нужно взять среднее значение рангов, которые они в противном случае занимали бы. Мы делаем это, потому что в этом примере у нас нет способа узнать, какой балл должен быть помещен в ранг 6, а какой — в ранг 7. Таким образом, вы заметите, что ранги 6 и 7 не существуют для английского языка. Эти два ранга были усреднены ((6 + 7)/2 = 6,5) и присвоены каждой из этих «равных» оценок.
Каково определение ранговой корреляции Спирмена?
Существует два метода расчета корреляции Спирмена в зависимости от того, (1) ваши данные не имеют связанных рангов или (2) ваши данные имеют связанные ранги.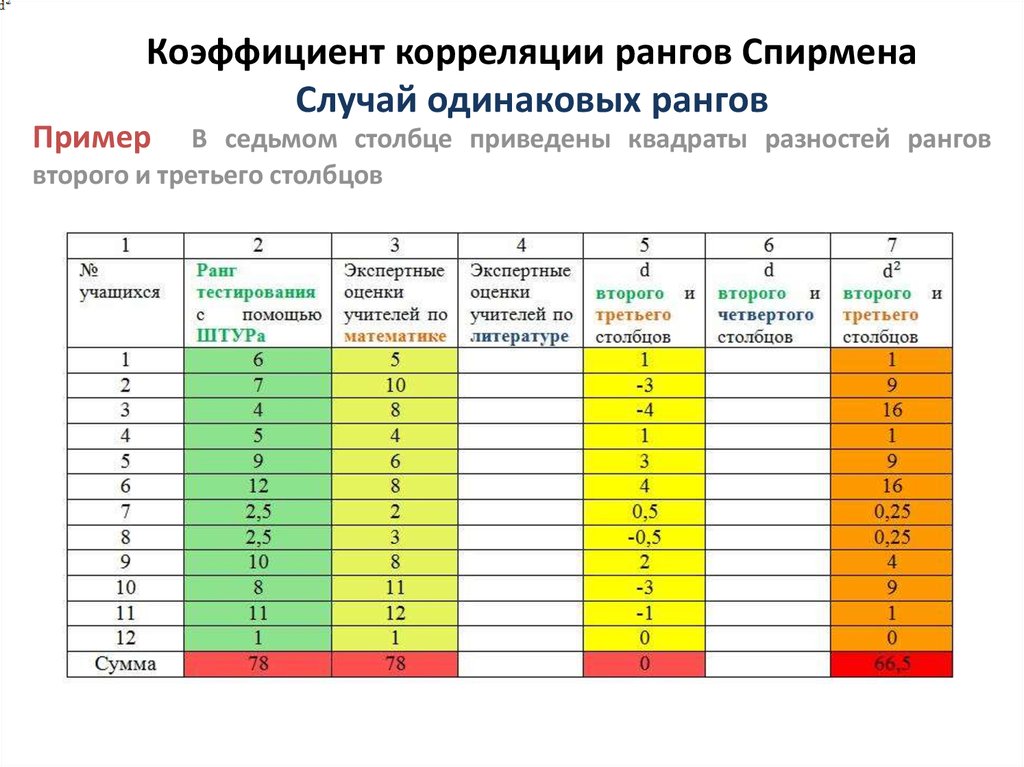 Формула для случая, когда нет одинаковых рангов:
Формула для случая, когда нет одинаковых рангов:
, где d i = разница в парных рангах и n = количество наблюдений. Формула для использования при равных рангах:
, где i = парный счет.
« предыдущая
1 2
следующая »
Главная О нас Свяжитесь с нами Условия использования Ценности и файлы cookie © 2018 Lund Research LtdКорреляция рангов Спирмена
переменные являются порядковыми переменными, вы все равно можете измерить силу и направление их связи, используя непараметрическую корреляционную статистику. Наиболее распространенным из них является ранговый коэффициент корреляции Спирмена, ρ, который учитывает ранги значений для двух переменных. Например, рассмотрим длину и вес выборки из пяти котят:
| Котенок | Длина (см) | Вес (г) |
| 1 | 7,8 | 245 |
| 2 | 8,2 | 321 |
| 3 | 7,5 | 260 |
| 4 | 9,0 | 405 |
| 5 | 8. 1 1 | 272 |
Ранги этих значений приведены в следующей таблице:
| Котенок | Длина Ранг | Вес Ранг |
| 1 | 2 | 1 |
| 2 | 4 | 4 |
| 3 | 1 | 2 |
| 4 | 5 | 5 |
| 5 | 3 | 3 |
Корреляция Спирмена эквивалентна вычислению коэффициента корреляции Пирсона для ранжированных данных. Таким образом, ρ всегда будет значением между -1 и 1. Чем дальше ρ от нуля, тем сильнее связь между двумя переменными. Знак ρ соответствует направлению зависимости. Если она положительна, то при увеличении одной переменной другая имеет тенденцию к увеличению. Если он отрицателен, то при увеличении одной переменной другая имеет тенденцию к уменьшению.
Возможно, вы захотите использовать корреляцию Спирмена, если ваши данные имеют нелинейную зависимость (например, экспоненциальную зависимость) или у вас есть один или несколько выбросов.


