Периметр и площадь. Почему дети в начальной школе путаются в том, что кажется взрослым очень простым
Нам, взрослым, некоторые вещи кажутся очевидными. Всем мы знаем, как вычислить периметр и площадь у фигуры, например. А вот для детей в началке это сложно. Как им помочь, рассказывает наш блогер, учитель начальных классов Ольга Катаева.
Родители по-разному относятся к вопросу выполнения домашнего задания. Некоторые помогают, корректируют, контролируют. Некоторые делают задания за ребёнка. А кто-то считает, что выполнение домашнего задания — ответственность ребёнка, и не вмешиваются.
Есть родители, которые предпочитают с детьми не заниматься совсем (это касается не только домашних заданий). Восхищают родители, которые занимаются со своими детьми, помогают им понять то, что решали в классе, разбирают ошибки в контрольных. А есть такие, которые не разбирают материал вместе с ребёнком, а требуют полного заучивания программы, не интересуясь, понял он что-то или нет.
Много раз объясняла родителям, что у детей начальных классов другое мышление
Они не могут думать абстрактными понятиями. Они не могут понять материал, заучив правило или формулу. Чтобы научиться говорить определениями и формулами, младшие школьники должны усвоить понятие на практике.
Они не могут понять материал, заучив правило или формулу. Чтобы научиться говорить определениями и формулами, младшие школьники должны усвоить понятие на практике.
В начальной школе есть совсем простые темы, а есть темы потруднее. Есть очень трудные. Одна из них — «Площадь и периметр». Взрослым, у которых логическое мышление уже сформировано, эта тема не кажется трудной, поэтому они с лёгкостью объясняют её дома детям, не придерживаясь рекомендаций и объяснений учителя. Родители помнят, как учили эту тему в школе. Правда, не в начальных классах, а в среднем звене и старшем — то есть тогда, когда начинает формироваться логическое и абстрактное мышление. Поэтому подросткам дают формулы.
Дети начальной школы часто путают понятия «площадь» и «периметр»
Объяснению и повторению этой темы уделяется не так уж много времени. Родители, видя двойки за контрольные с такими заданиями, пытаются по своему объяснить, как решать. Дают формулу на периметр: P=2а+2b, но не объясняют, что она обозначает.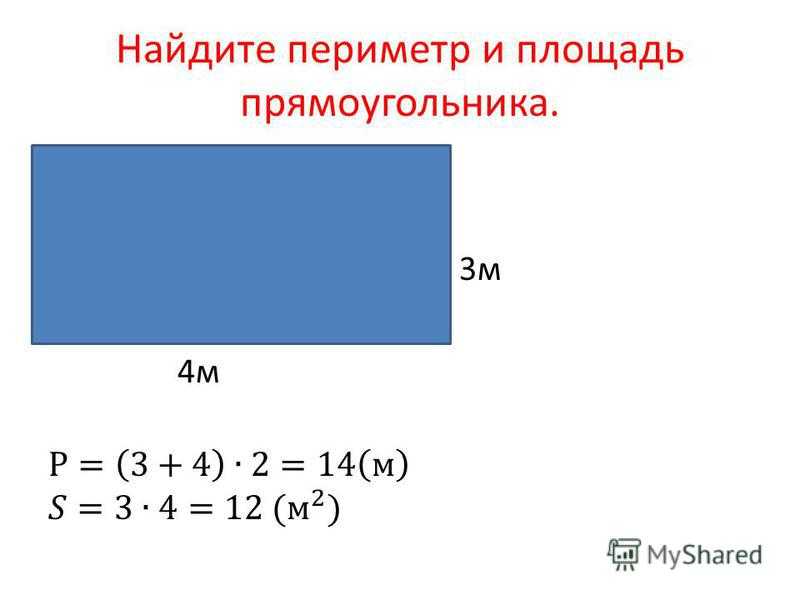
Вспомним формулу площади S=ab. И в той, и в другой формулах присутствует умножение — это первая причина, почему дети путаются (другие причины надо выяснять, это могут быть пространственно-конструктивные нарушения и др.).
Как можно объяснить эту тему, чтобы ребёнок ее понял? Обратимся к определению периметра: «Пери́метр — общая длина границы фигуры», или «Периметр — длина контура замкнутой плоской фигуры», или так: «Периметр — сумма длины всех сторон плоской геометрической фигуры». В начальной школе даётся такое определение: «Периметр — это сумма длин всех сторон фигуры». Важно понять, что периметр — это весь контур фигуры, то есть мы складываем вместе длины всех сторон.
Когда мы говорим о площади, мы говорим о «части плоскости, заключённой внутри замкнутой геометрической фигуры», о том, сколько места занимает фигура на плоскости. Площадь находят мерками, квадратиками (поэтому и единицы площади квадратные — так детям понятнее). Если фигура — прямоугольник, её делят на равные квадратики и считают их. Так можно делать с небольшими фигурами, которые помещаются в тетрадках.
Так можно делать с небольшими фигурами, которые помещаются в тетрадках.
Находить площадь «Красной площади», которая в Москве, так нельзя
Есть формула. Для нахождения площади больших фигур, прямоугольной формы, достаточно знать длину и ширину и перемножить их (можно ввести ассоциацию с таблицей Пифагора, которая тоже поделена на квадратики и значение произведения находят путём умножения чисел).
Вот оно — существенное отличие: периметр — сложение, площадь — умножение. Поэтому в период, когда идёт отработка этих понятий, не следует вводить формулу периметра прямоугольника с умножением. Если ученик поймёт суть понятия «периметр», он сможет найти периметр любого многоугольника. Если зациклить его на формуле для нахождения периметра прямоугольника, школьник не сможет перенести знание для нахождения периметра другой фигуры.
Не надо заучивать с детьми формулы и определения. Надо понимать возрастные особенности младших школьников и объяснять на понятном для них «языке» — через образы, ассоциации, через практику, через действование.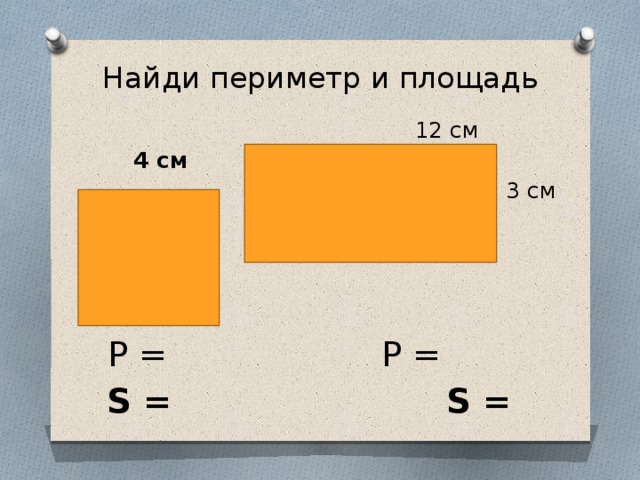
Удачи родителям, которые понимают своих детей и помогают им в нелёгкой учебной жизни.
Вы находитесь в разделе «Блоги». Мнение автора может не совпадать с позицией редакции.
Фото: Shutterstock / pupunkkop
Периметр и площадь. Периметр и площадь прямоугольника Нахождение периметра
Наверняка каждый из нас учил в школе такую важную составляющую геометрии, как периметр. Нахождение периметра просто необходимо для решения множества задач. О том, как найти периметр, расскажет наша статья.
Стоит помнить, что периметр любой фигуры это почти всегда сумма ее сторон. Давайте рассмотрим несколько разных геометрических фигур.
- Прямоугольник — это такой четырехугольник, у которого параллельные стороны равны попарно между собой. Если одна сторона X, а другая Y, то мы получим такую формулу для нахождения периметра этой фигуры:
P = 2(X+Y) = X+Y+X+Y = 2X+2Y.
Пример решения задачи:
Допустим, что сторона X = 5 см, сторона Y = 10 см.
 Значит, подставив эти значения в нашу формулу, мы получим — P = 2*5 см + 2* 10см = 30 см.
Значит, подставив эти значения в нашу формулу, мы получим — P = 2*5 см + 2* 10см = 30 см. - Трапеция — это четырехугольник, у которого две противоположные стороны параллельны, но не равны между собой. Периметр трапеции — это сумма всех четырех её сторон:
Пример решения задачи:
Допустим, что сторона X = 5 см, сторона Y = 10 см, сторона Z = 8 см, сторона W = 20 см. Значит, подставив эти значения в нашу формулу, мы получим — P = 5 см + 10 см + 8 см + 20 см = 43 см.
- Периметр круга (длину окружности) можно вычислить по формуле:
P = 2rπ = dπ, где r — это радиус круга, d — диаметр круга.
Пример решения задачи:
Допустим, что радиус r нашего круга равен 5 см, тогда диаметр d будет равен 2*5 см = 10 см. Известно, что π = 3,14. Значит, подставив эти значения в нашу формулу, мы получим — P = 2*5 см*3,14 = 31,4 см.
- Если Вам необходимо найти периметр треугольника, то Вы можете столкнуться с рядом проблем при этом, поскольку треугольники могут иметь очень разные формы.
 Например, есть острый, тупой, равнобедренный, прямоугольный или равносторонний треугольники. Хотя формула для всех видов треугольников такая:
Например, есть острый, тупой, равнобедренный, прямоугольный или равносторонний треугольники. Хотя формула для всех видов треугольников такая:P = X+Y+Z, где X, Y, Z — стороны фигуры.
Проблема в том, что при решении многих задач на нахождение периметра этой фигуры Вам не всегда будут известны длины всех сторон. Например, вместо информации о длине одной из сторон Вы можете иметь градус угла или длину высоты конкретного треугольника. Это существенно осложнит задачу, но не сделает ее решение нереальным. О том, как найти периметр треугольника, какой формы бы он не был можно прочитать » «.
- Периметр такой фигуры, как ромб находят также как и периметр квадрата, ведь ромб — это параллелограмм, который имеет равные стороны. Узнать, как найти периметр квадрата можно прочитав статью на нашем сайте » «.
Теперь Вы знаете, как найти сторону периметра той геометрической фигуры, какой Вам нужно!
На этом занятии мы познакомимся с новым понятием — периметр прямоугольника.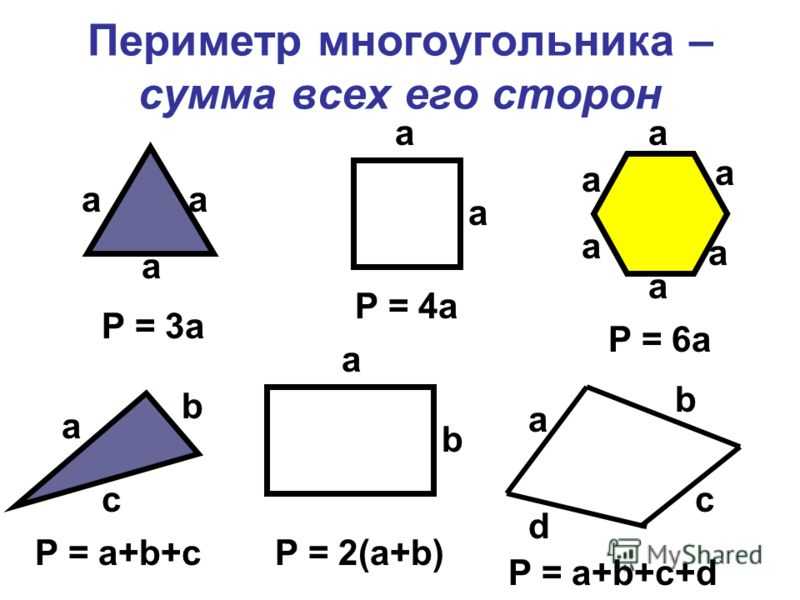
На данном уроке мы познакомимся с периметром прямоугольника и его вычислением.
Рассмотрим следующую геометрическую фигуру (рис. 1):
Рис. 1. Прямоугольник
Данная фигура — прямоугольник. Вспомним, какие отличительные особенности прямоугольника мы знаем.
Прямоугольник — это четырехугольник, у которого четыре прямых угла и стороны попарно равны.
Что в нашей жизни может иметь прямоугольную форму? Например, книга, крышка стола или земельный участок.
Рассмотрим следующую задачу:
Задача 1 (рис. 2)
Вокруг земельного участка строителям понадобилось поставить забор. Ширина этого участка — 5 метров, длина — 10 метров. Забор какой длины получится у строителей?
Рис. 2. Иллюстрация к задаче 1
Забор ставят по границам участка, поэтому, чтобы узнать длину забора, нужно знать длину каждой из сторон. У данного прямоугольника стороны равны: 5 метров, 10 метров, 5 метров, 10 метров. Составим выражение для подсчета длины забора: 5+10+5+10. Воспользуемся переместительным законом сложения: 5+10+5+10=5+5+10+10. В данном выражении есть суммы одинаковых слагаемых (5+5 и 10+10). Заменим суммы одинаковых слагаемых произведениями: 5+5+10+10=5·2+10·2. Теперь воспользуемся распределительным законом умножения относительно сложения: 5·2+10·2=(5+10)·2.
У данного прямоугольника стороны равны: 5 метров, 10 метров, 5 метров, 10 метров. Составим выражение для подсчета длины забора: 5+10+5+10. Воспользуемся переместительным законом сложения: 5+10+5+10=5+5+10+10. В данном выражении есть суммы одинаковых слагаемых (5+5 и 10+10). Заменим суммы одинаковых слагаемых произведениями: 5+5+10+10=5·2+10·2. Теперь воспользуемся распределительным законом умножения относительно сложения: 5·2+10·2=(5+10)·2.
Найдем значение выражения (5+10)·2. Сначала выполняем действие в скобках: 5+10=15. А затем повторяем число 15 два раза: 15·2=30.
Ответ: 30 метров.
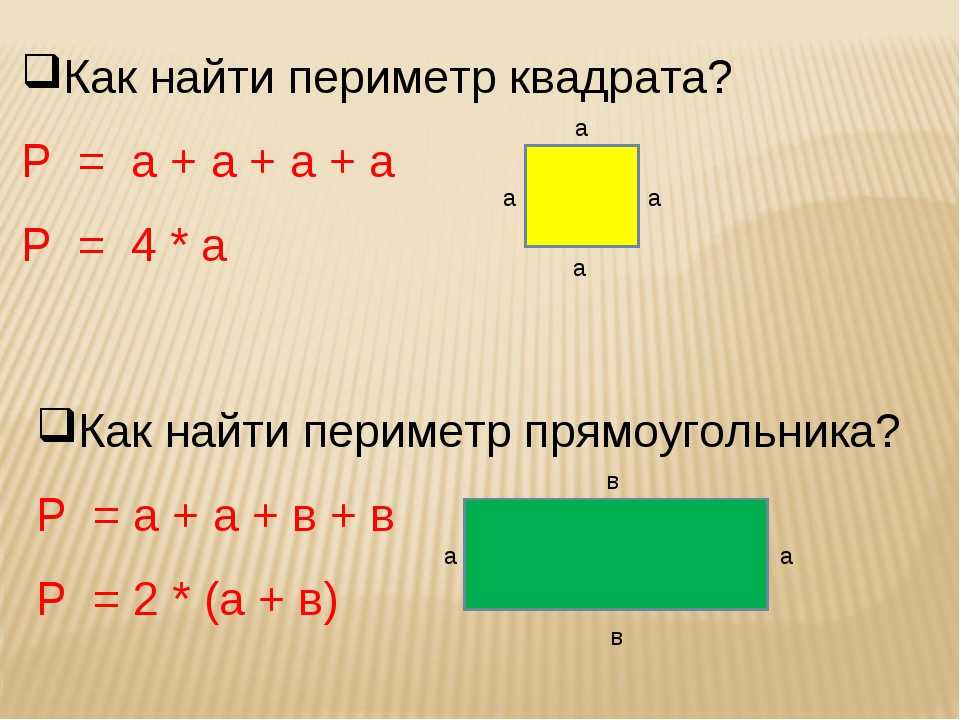
Периметр прямоугольника — сумма длин всех его сторон.
Воспользуемся формулой периметра прямоугольника и найдем периметр прямоугольника со сторонами 7 см и 3 см: (7+3)·2=20 (см).
Периметр любой фигуры измеряется в линейных единицах.
На данном уроке мы познакомились с периметром прямоугольника и формулой его вычисления.
Произведение числа и суммы чисел равно сумме произведений данного числа и каждого из слагаемых.
Если периметр — это сумма длин всех сторон фигуры, то полупериметр — сумма одной длины и одной ширины. Мы находим полупериметр, когда работаем по формуле нахождения периметра прямоугольника (когда мы выполняем первое действие в скобках — (a+b)).
Список литературы
- Александрова Э.И. Математика. 2 класс. — М.: Дрофа, 2004.
- Башмаков М.И., Нефёдова М.Г. Математика. 2 класс. — М.: Астрель, 2006.
- Дорофеев Г.В., Миракова Т.И. Математика. 2 класс. — М.: Просвещение, 2012.
- Festival.1september.ru ().
- Nsportal.ru ().
- Math-prosto.ru ().
Домашнее задание
- Найти периметр прямоугольника, у которого длина 13 метров, а ширина — 7 метров.

- Найти полупериметр прямоугольника, если его длина — 8 см, а ширина — 4 см.
- Найти периметр прямоугольника, если его полупериметр — 21 дм.
Не многие формулы из курса школьной математики мы применяем в повседневной жизни. Однако, есть такие уравнения, которые имеют применение, если не на регулярной основе, то время от времени. Одна из таких формул — вычисление периметра фигуры.
Что такое периметр?
Периметром называют суммарную длину всех сторон геометрической фигуры. Для его обозначения используется буква латинского алфавита «Р». Проще говоря, чтобы найти периметр, необходимо измерить длины всех сторон геометрической фигуры и сложить полученные значения. Длина вычисляется обычным измерительным прибором, таким как линейка, рулетка, сантиметровая лента и прочее.
Единицей измерения соответственно являются сантиметры, метры, миллиметры и другие меры длины. Длина стороны многоугольника вычисляется путем прикладывания измерительного прибора от одной вершины к другой.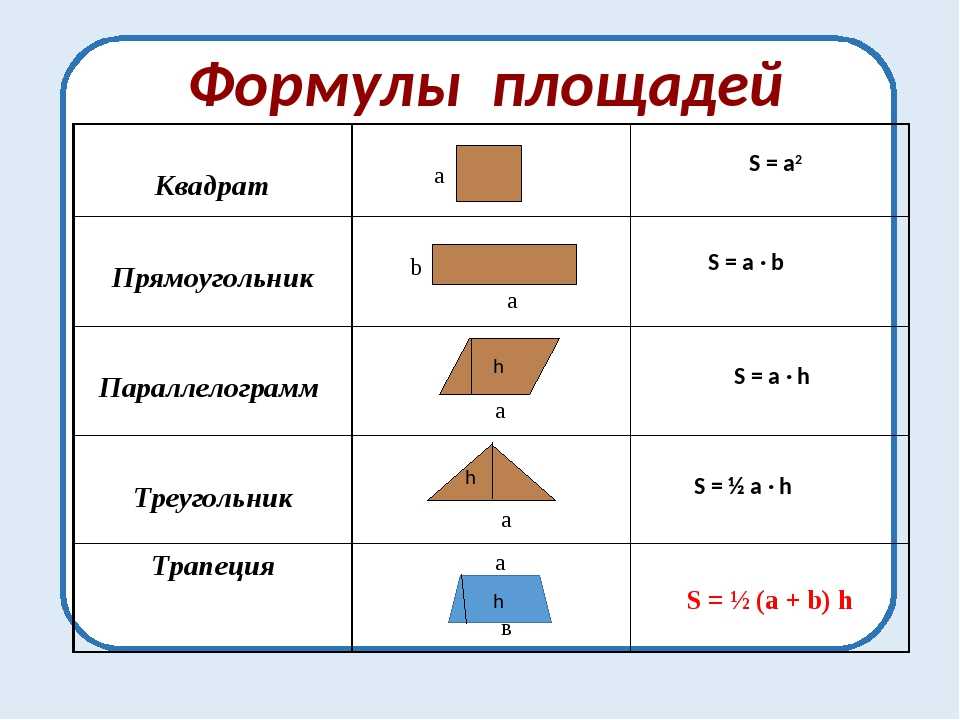 Начало шкалы деления прибора должно совпадать с одной из вершин. Второе числовое значение, на которое попадает другая вершина и является длиной стороны многоугольника. Таким же образом необходимо измерить все длины сторон фигуры и полученные значения сложить. Единицей измерения периметра является та же самая единица, которая используется для измерения стороны фигуры.
Начало шкалы деления прибора должно совпадать с одной из вершин. Второе числовое значение, на которое попадает другая вершина и является длиной стороны многоугольника. Таким же образом необходимо измерить все длины сторон фигуры и полученные значения сложить. Единицей измерения периметра является та же самая единица, которая используется для измерения стороны фигуры.
Прямоугольником следует называть геометрическую фигуру, которая состоит из четырех сторон разной длины и три угла у которой прямые. При построении такой фигуры на плоскости получается так, что стороны у нее будут попарно равны, но не равны все между собой. Что такое периметр прямоугольника? Это также суммарная длина всех длин фигуры. Но так как у прямоугольника по две стороны имеют одинаковое значение, то в вычислении периметра можно дважды сложить длины двух смежных сторон. Единицей измерения периметра прямоугольника также являются общепринятые единицы измерения.
Треугольником следует называть геометрическую фигуру, имеющую три угла (как разного значения, так и одинакового) и состоящую из отрезков, образованных от точек пересечения лучей, образующих углы. Треугольник имеет три стороны и три угла. В нем могут быть из трех равны две стороны. Такой треугольник следует считать равнобедренным. Бывают такие фигуры, в которых равны все три стороны между собой. Принято такие треугольники называть равносторонними.
Треугольник имеет три стороны и три угла. В нем могут быть из трех равны две стороны. Такой треугольник следует считать равнобедренным. Бывают такие фигуры, в которых равны все три стороны между собой. Принято такие треугольники называть равносторонними.
Что такое периметр треугольника? Его вычисление можно провести по аналогии с периметром четырехугольника. Равен периметр треугольника суммарной длине длин его сторон. Вычисление периметра треугольника, в котором две стороны равны — равнобедренного — упрощается умножением одной длины равных сторон на два. К полученному значению необходимо прибавить значение длины третьей стороны. Вычисление периметра треугольника с равными сторонами можно свести к простому вычислению произведения одной длины стороны треугольника на три.
Прикладное значение периметра
Вычисление периметра в повседневной жизни применяется во многих сферах, но чаще всего при выполнении строительных, геодезических, топографических, архитектурных, планировочных работах. Но перечисленным сферы применения вычисления периметра, конечно же, не ограничиваются.
Но перечисленным сферы применения вычисления периметра, конечно же, не ограничиваются.
Например, при выполнении геодезических и топографических работ очень часто возникает необходимость посчитать периметр границ определенного участка. Но на практике участки редко имеют правильную форму. Поэтому вычисление длины периметра происходит по формуле расчета суммы длин всех сторон участка.
Необходимость вычисления периметра участка очень часто обусловлена тем, что необходимо знать, какое количество материала потребуется для установки ограждений. Даже простой приусадебный участок нуждается в измерении периметра для того, чтобы грамотно обнести его забором.
Измерительные приборы на местности
Для вычисления периметра на местности невозможно использование простой ученической линейки. Поэтому специалисты используют специальные приборы. Конечно, самый простой и доступный вариант — это измерение длины границы участка шагами. Размер шага взрослого человека составляет примерно один метр.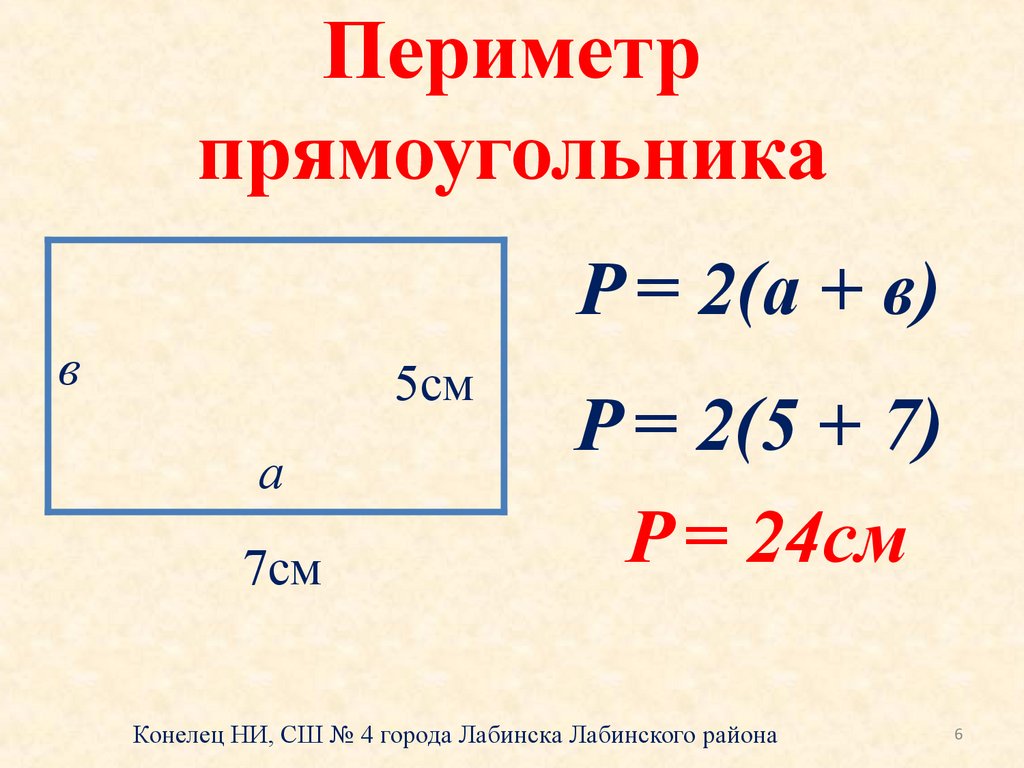 Иногда один метр и двадцать сантиметров. Но этот способ очень неточный и дает большую погрешность в измерении. Он подходит в том случае, если нет необходимости точного вычисления длины границы, а есть потребность просто прикинуть примерную длину.
Иногда один метр и двадцать сантиметров. Но этот способ очень неточный и дает большую погрешность в измерении. Он подходит в том случае, если нет необходимости точного вычисления длины границы, а есть потребность просто прикинуть примерную длину.
Для более точного вычисления длины сторон участка и, соответственно, периметра, существуют специальные приборы. В первую очередь, можно воспользоваться специальной металлической рулеткой или обычным проводом.
Также существуют специальные измерительные устройства, такие как дальномеры. Приборы бывают оптические, лазерные, световые, ультразвуковые. Следует помнить, что чем дальше дальномер способен измерять расстояние, тем выше у него погрешность. Такие приборы используются в геодезических и топографических съемках.
Прямоугольник обладает многими отличительными особенностями, исходя из которых, выработаны правила вычисления его различных числовых характеристик. Итак, прямоугольник:
Плоская геометрическая фигура;
Четырехугольник;
Фигура, у которой противоположные стороны равны и параллельны, все углы прямые.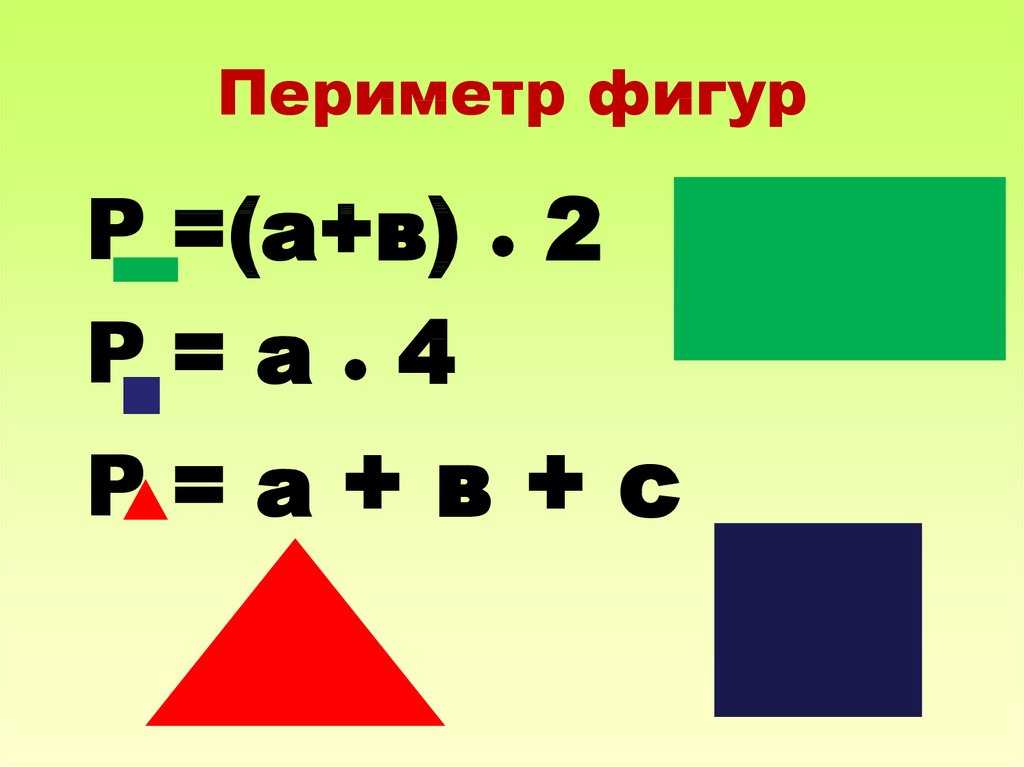
Периметр – это общая длина всех сторон фигуры.
Вычисление периметра прямоугольника — довольно простая задача.
Все, что вам нужно знать, это ширину и длину прямоугольника. Поскольку прямоугольник имеет две равные длины и две равные ширины, измеряется только одна сторона.
Периметр прямоугольника равен удвоенной сумме 2-х его сторон длины и ширины.
P = (a + b) 2, где a — длина прямоугольника, b — ширина прямоугольника.
Так же периметр прямоугольника можно найти при помощи суммы всех сторон.
P= a+a+b+b, где а– длина прямоугольника, b – ширина прямоугольника.
Периметр квадрата — это длина стороны квадрата, умноженная на 4.
P = a 4, где a — длина стороны квадрата.
Дополнение: Нахождение найти площади и периметра прямоугольников
В программе обучения за 3 класс предусмотрено изучение многоугольников и их особенностей. Для того чтобы понять, как найти периметр прямоугольника и площадь, разберемся, что подразумевается под этими понятиями.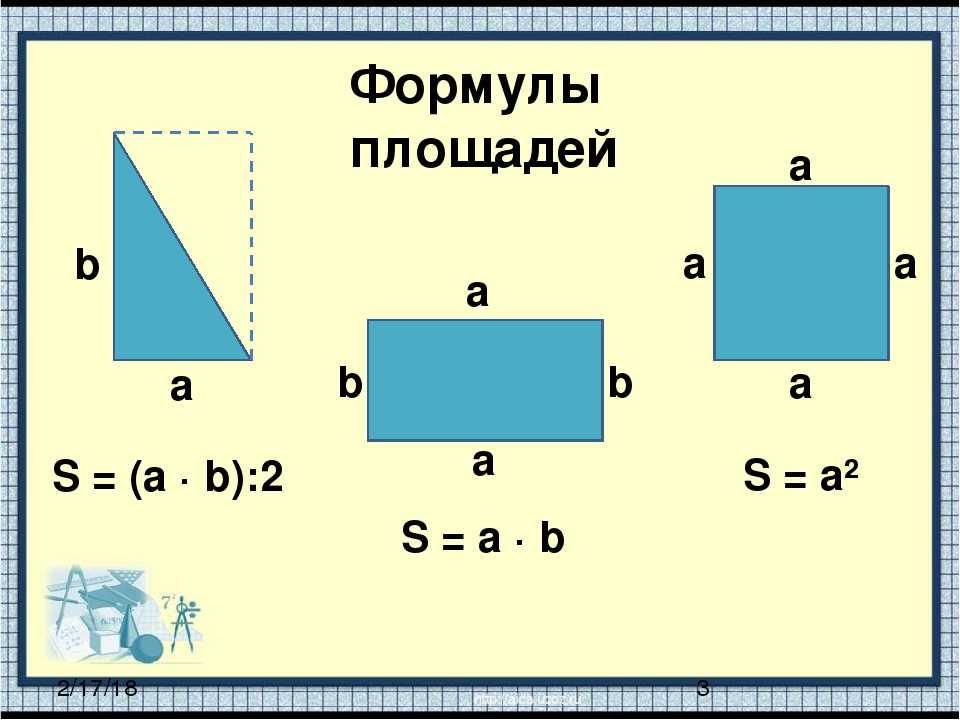
Основные понятия
Нахождение периметра и площади требует знания некоторых терминов. К ним относятся:
- Прямой угол. Образуется из 2 лучей, имеющих общее начало в виде точки. При знакомстве с фигурами (3 класс) прямой угол определяют с помощью угольника.
- Прямоугольник. Это четырехугольник, все углы которого являются прямыми. Его стороны называют длиной и шириной. Как известно, противоположные стороны этой фигуры равны.
- Квадрат. Является четырехугольником, все стороны которого равны.
При знакомстве с многоугольниками их вершины могут называться АВСД. В математике принято именовать точки на чертежах буквами латинского алфавита. В названии многоугольника перечисляют все вершины без пропусков, например, треугольник ABC.
Вычисление периметра
Периметр многоугольника — это сумма длин всех его сторон. Эта величина обозначается латинской буквой P. Уровень знаний для предложенных примеров — 3 класс.
Задача №1: «Начертите прямоугольник 3 см шириной и 4 см длиной с вершинами ABCD. Найдите периметр прямоугольника ABCD».
Найдите периметр прямоугольника ABCD».
Формула будет выглядеть так: P=AB+BC+CD+AD либо P=AB×2+BC×2.
Ответ: P=3+4+3+4=14 (см) либо P=3×2 + 4×2=14 (см).
Задача №2: «Как найти периметр прямоугольного треугольника ABC, если значения сторон равны 5, 4 и 3 см?».
Ответ: P=5+4+3=12 (см).
Задача №3: «Найдите периметр прямоугольника, одна сторона которого равна 7 см, а другая на 2 см длиннее».
Ответ: P=7+9+7+9=32 (см).
Задача №4: «Соревнования по плаванию проходили в бассейне, периметр которого составляет 120 м. Сколько метров проплыл участник соревнований, если ширина бассейна 10 м?».
В данной задаче стоит вопрос, как найти длину бассейна. Для решения найдите длины сторон прямоугольника. Ширина известна. Сумма длин двух неизвестных сторон должна составить 100 м. 120-10×2=100. Чтобы узнать расстояние, которое преодолел пловец, нужно разделить полученный результат на 2. 100:2=50.
Ответ: 50 (м).
Вычисление площади
Более сложной величиной является площадь фигуры.
Площадь квадрата со стороной 1 см равна 1 см². Квадратный дециметр обозначен как дм², а квадратный метр — м².
Области применения единиц измерения могут быть такими:
- В см² измеряют маленькие предметы, например фотографии, обложки учебников, листы бумаги.
- В дм² можно измерить географическую карту, оконное стекло, картину.
- Для измерения пола, квартиры, земельного участка используют м².
Если начертить прямоугольник 3 см длиной и 1 см шириной и разбить на квадраты со стороной 1 см, то в нем поместится 3 квадрата, а значит, его площадь составит 3 см². Если прямоугольник разбит на квадраты, найдем периметр прямоугольника также без затруднений. В данном случае он равен 8 см.
Другой способ посчитать количество квадратов, вмещающихся в фигуру, — это использование палетки. Начертим на кальке квадрат площадью 1 дм², что составляет 100 см². Поместим кальку на фигуру и посчитаем число квадратных сантиметров в одном ряду.
Способы сравнения площадей:
- На глаз. Иногда достаточно просто взглянуть на предметы, поскольку в некоторых случаях и невооруженным глазом видно, что одна фигура занимает больше места, как, например, учебник, лежащий на столе рядом с пеналом.
- Наложение. Если фигуры совпадают при наложении, их площади равны. Если же одна из них полностью помещается внутри второй, то ее площадь меньше. Места, занимаемые тетрадным листом и страницей из учебника, можно сравнить, наложив их друг на друга.
- По количеству мерок. Фигуры при наложении могут и не совпадать, однако иметь одинаковую площадь. Сравнить в этом случае можно, подсчитав количество квадратов, на которые разбита фигура.
- Числа. Сравниваются численные значения, измеренные одной и той же меркой, например, в м².
Пример №1: «Швея сшила детское одеяло из квадратных разноцветных лоскутков. Один лоскуток длиной 1 дм, в ряду по 5 штук. Сколько дециметров ленты понадобится швее для обработки краев одеяла, если известна площадь 50 дм²?».
Один лоскуток длиной 1 дм, в ряду по 5 штук. Сколько дециметров ленты понадобится швее для обработки краев одеяла, если известна площадь 50 дм²?».
Чтобы решить задачу, нужно ответить на вопрос, как найти длину прямоугольника. Далее найдем периметр прямоугольника, составленного из квадратов. Из задачи ясно, что ширина одеяла — 5 дм, вычисляем длину, разделив 50 на 5, и получаем 10 дм. Теперь найдите периметр прямоугольника со сторонами 5 и 10. P=5+5+10+10=30.
Ответ: 30 (м).
Пример №2: «На раскопках обнаружен участок, где могут находиться древние сокровища. Сколько территории придется исследовать ученым, если известен периметр 18 м и ширина прямоугольника 3 м?».
Определим длину участка, проделав 2 действия. 18-3×2=12. 12:2=6. Искомая территория будет также равна 18 м² (6×3=18).
Ответ: 18 (м²).
Таким образом, зная формулы, вычислить площадь и периметр не составит труда, а приведенные выше примеры помогут попрактиковаться в решении математических задач.
Содержимое:
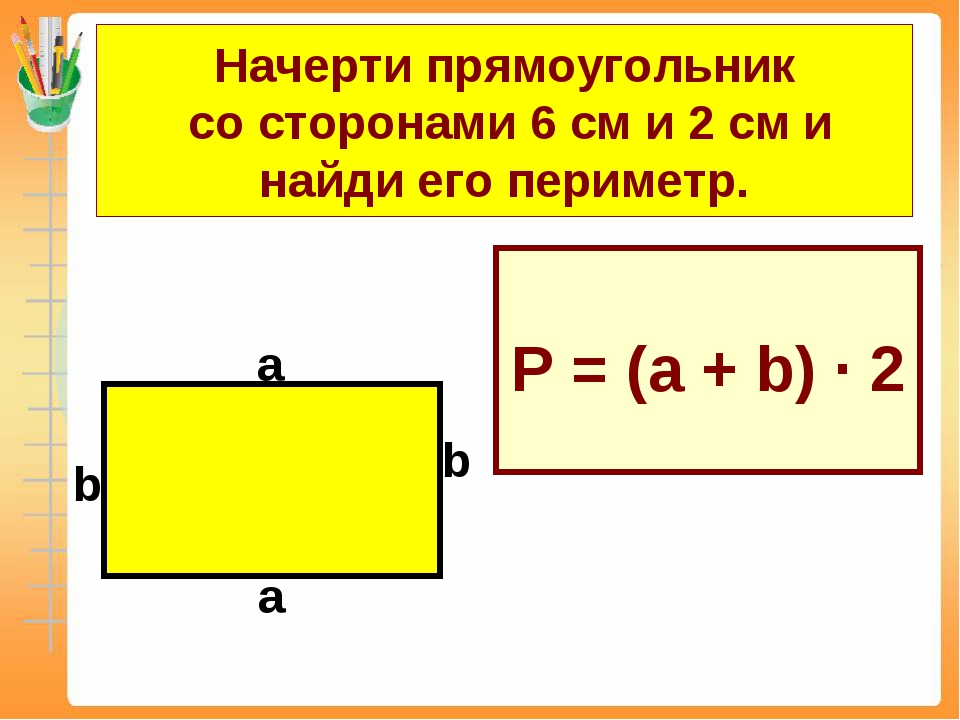
Вычисление периметра прямоугольника — довольно простая задача.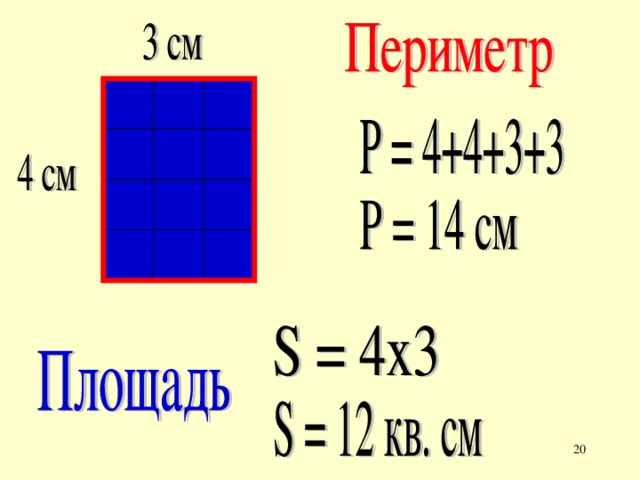 Все, что вам нужно знать, это ширину и длину прямоугольника. Если эти величины не даны, вам необходимо найти их. Эта статья расскажет, как это сделать.
Все, что вам нужно знать, это ширину и длину прямоугольника. Если эти величины не даны, вам необходимо найти их. Эта статья расскажет, как это сделать.
Шаги
1 Стандартный метод
- 1 Формула для вычисления периметра. Основная формула для вычисления периметра прямоугольника: P = 2 * (l + w) .
- Запомните: периметр – это общая длина всех сторон фигуры.
- В этой формуле P — «периметр», l — длина прямоугольника, w — ширина прямоугольника.
- У длины всегда большее значение, чем у ширины.
- Поскольку прямоугольник имеет две равные длины и две равные ширины, измеряется только одна сторона l (длина) и одна сторона w (ширина) (хотя у прямоугольника четыре стороны).
- Вы также можете записать формулу в виде: P = l + l + w + w
- 2 Найдите длину и ширину. В обычной математической задаче длина и ширина прямоугольника, как правило, даны. Если вы ищите периметр прямоугольника в реальной жизни, используйте линейку или рулетку, чтобы найти длину и ширину.

- Если вы вычисляете периметр прямоугольника в реальной жизни, используйте рулетку или мерную ленту, чтобы найти длину и ширину нужного участка. Если работы проводятся на открытом воздухе, измерьте все стороны, чтобы убедиться, что параллельные стороны действительно совпадают.
- Например: l = 14 см, w = 8 см
- 3 Сложите длину и ширину. Подставьте значения в формулу и сложите их.
- Обратите внимание, что в соответствии с порядком операций, математические выражения в скобках решаются в первую очередь.
- Например: P = 2 * (l + w) = 2 * (14 + 8) = 2 * (22)
- 4 Умножьте эту сумму на два (согласно формуле).
- Обратите внимание, что умножив сумму на два, вы учли две другие стороны прямоугольника. Складывая ширину и длину, вы складываете только две стороны фигуры. Поскольку две другие стороны прямоугольника равны двум сложенным, сумма просто умножается на два и таким образом находится общая сумма всех четырех сторон.

- Полученное число будет периметром прямоугольника.
- Например: P = 2 * (l + w) = 2 * (14 + 8) = 2 * (22) = 44 см
- Обратите внимание, что умножив сумму на два, вы учли две другие стороны прямоугольника. Складывая ширину и длину, вы складываете только две стороны фигуры. Поскольку две другие стороны прямоугольника равны двум сложенным, сумма просто умножается на два и таким образом находится общая сумма всех четырех сторон.
- 5 Альтернативный метод: сложите l + l + w + w . Вместо сложения двух сторон и умножения их на два, можно просто сложить все четыре стороны и найти периметр прямоугольника.
- Если вам тяжело дается понятие периметра, то данный метод как раз для вас.
- Например: P = l + l + w + w = 14 + 14 + 8 + 8 = 44 см
2 Вычисление периметра через площадь и одну сторону
- 1 Формула для площади прямоугольника. Если вам дана площадь прямоугольника, вы должны знать формулу для ее вычисления, чтобы найти недостающую информацию для вычисления периметра.
- Запомните: площадь фигуры — это значение общего пространства, которое ограничено сторонами фигуры.
- Формула для вычисления площади прямоугольника: A = l * w
- Формула для вычисления периметра прямоугольника: P = 2 * (l + w)
- В приведенных выше формулах А — «площадь», P — «периметр»,l — длина прямоугольника, w — ширина прямоугольника.

- 2 Разделите площадь на данную в задаче сторону, чтобы найти другую сторону.
- Так как для вычисления площади вам нужно умножить длину на ширину, то разделив площадь на ширину, вы получите длину. Аналогично, деление площади на длину даст вам ширину.
- Например: A = 112 см2, l = 14 см
- A = l * w
- 112 = 14 * w
- 112/14 = w
- 8 = w
- 3 Добавьте длину и ширину. Теперь, когда у вас есть значения длины и ширины, их можно подставить в формулу для вычисления периметра прямоугольника.
- Первым делом нужно сложить длину и ширину, поскольку данная часть уравнения заключена в скобки.
- Согласно порядку вычислений, первым выполняется действие, приведенное в скобках.
- 4 Умножьте сумму длины и ширины на два. После того как вы сложили длину и ширину прямоугольника, можно найти периметр, умножив полученное число на два. Это необходимо для добавления оставшихся двух сторон прямоугольника.

- Противоположные стороны прямоугольника равны, именно поэтому сумму длины и ширины нужно умножить на два.
- Одинакова как длина противоположных сторон, так и ширина.
- Например: Р = 2 * (14 + 8) = 2 * (22) = 44 см
3 Периметр прямоугольной фигуры
- 1 Запишите основную формулу для определения периметра. Периметр – это общая длина всех сторон фигуры.
- Прямоугольник имеет четыре стороны. Стороны, образующие длину, равны друг другу и стороны, образующие ширину, равны друг другу. Таким образом, периметр является суммой этих четырех сторон.
- Прямоугольная фигура. Рассмотрим фигуру формы «L». Такая фигура может быть разбита на два прямоугольника. Однако, при вычислении периметра фигуры такое разбиение на два прямоугольника не учитывается. Периметр рассматриваемой фигуры: , где S – стороны фигуры (смотрите рисунок).
- Каждая “s” – это отдельная сторона сложного прямоугольника.
- 2 В обычной математической задаче стороны фигуры, как правило, даны.
 Если вы ищите периметр прямоугольной фигуры в реальной жизни, используйте линейку или рулетку, чтобы найти ее стороны.
Если вы ищите периметр прямоугольной фигуры в реальной жизни, используйте линейку или рулетку, чтобы найти ее стороны.- Для объяснения введем следующие обозначения: L, W, l1, l2, w1, w2 . Прописные L и W l и w
- Таким образом, формула Р = S1 + S2 + S3 + S4 + S5 + S6 записывается в виде: (обе формулы, по сути, одинаковы, но используют разные переменные).
- Переменные “w” и “l” просто заменяют числа.
- Пример: L = 14 см, W = 10 см, l1 = 5 см, l2 = 9 см, w1 = 4 см, w2 = 6 см.
- Обратите внимание, что l1 +l2 =L . Аналогично, w 1 + w2 =W .
- 3 Сложите стороны.
- 48 см
4 Периметр прямоугольной фигуры (известны только некоторые стороны)
- 1 Проанализируйте данные вам значения сторон. Вы можете найти периметр прямоугольной фигуры, если вам даны по крайней мере одна полная длина или полная ширина и, по крайней мере, три неполные ширины и длины.

- Для «L»-образной прямоугольной фигуры используется формула P = L + W + l1 + l2 + w1 + w2
- В приведенной выше формуле: P – это периметр, прописные L и W обозначают полную длину и ширину фигуры. Строчные l и w обозначают неполную длину и ширину фигуры.
- Пример: L = 14 см, l1 = 5 см, w1 = 4 см, w2 = 6 см; Требуется найти: W, l2.
- 2 Используя данные значения сторон, найдите неизвестные стороны. Учтите, что l1 +l2 =L . Аналогично, w 1 + w2 =W .
- Например: L = l1 + l2; W = w1 + w2
- L = l1 + l2
- 14 = 5 + l2
- 14 – 5 = l2
- 9 = l2
- W = w1 + w2
- W = 4 + 6
- W = 10
- Например: L = l1 + l2; W = w1 + w2
- 3 Сложите стороны. Подставьте значения в формулу и вычислите периметр прямоугольной фигуры.
- P = L + W + l1 + l2 + w1 + w2 = 14 + 10 + 5 + 9 + 4 + 6 = 48 см
Что вам понадобится
- Карандаш
- Бумага
- Калькулятор (опционально)
- Линейка или рулетка (опционально)
Что такое площадь и периметр? Определение, формула, примеры, факты
Периметр двумерной фигуры – это общее расстояние вокруг соответствующей фигуры. Для фигур с прямыми сторонами, таких как треугольник, прямоугольник, квадрат или многоугольник; периметр это сумма длин всех сторон.
Для фигур с прямыми сторонами, таких как треугольник, прямоугольник, квадрат или многоугольник; периметр это сумма длин всех сторон.
Площадь двумерной фигуры — это пространство, ограниченное периметром данной фигуры. Чтобы вычислить площадь различных фигур, используйте разные формулы, основанные на количестве сторон и других характеристиках, таких как углы между сторонами.
Если все измерения выражены в сантиметрах, единицы измерения периметра и площади различных форм:
Понятия площади и периметра являются основой для понимания евклидовой геометрии и вычисления объема объемных фигур в трехмерном пространстве. пространство, такое как конусы, призма, сфера и цилиндр. Кроме того, мы используем эти формулы для вычисления площади и периметра четырехугольников и многоугольников, состоящих из сторон и кривых. Реальная полезность этой концепции в нескольких областях, таких как картографирование, архитектура и геодезия. Геометрическое представление фигур делается путем зарисовки расстояний и площадей для ясности понимания.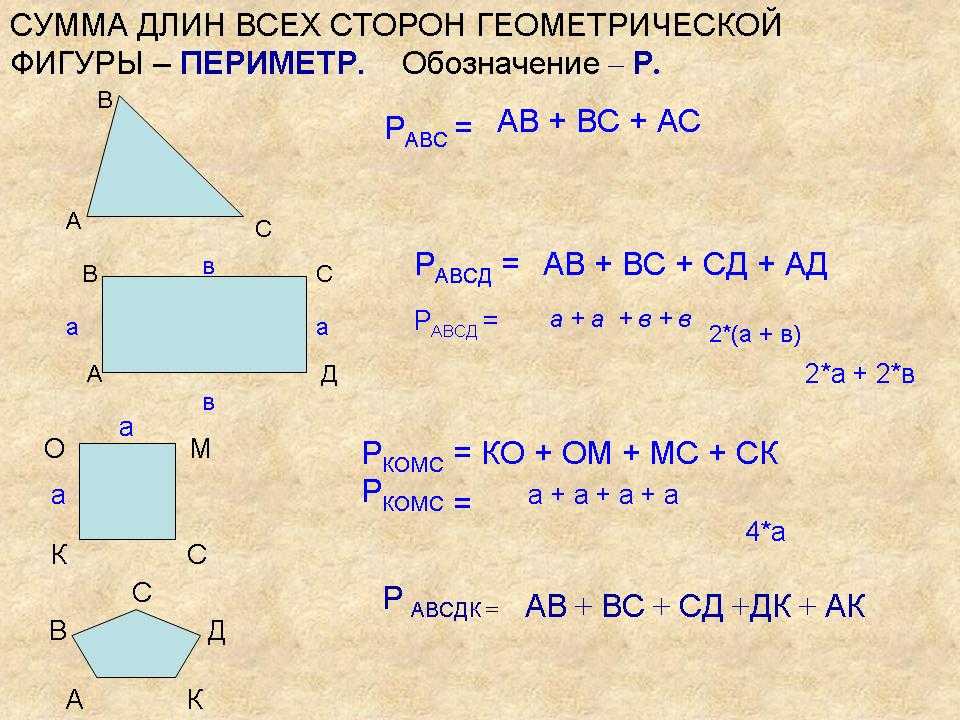
Трехмерные объекты, полученные из двухмерных форм и топографической съемки полей.
1 Площадь треугольника с основанием в 7 единиц равна 21 квадратной единице. Какова высота треугольника?2 единицы 3 единицы 4 единицы 6 единиц Правильный ответ: 6 единиц 2 Какова площадь треугольника с основанием 6 единиц и высотой 10 единиц?16 квадратных единиц 30 квадратных единиц 32 квадратных единиц 60 квадратных единиц Правильный ответ: 30 квадратных единиц 3 Если площадь квадрата 36 кв. см. Каков его периметр? см. Каков его периметр?9 см 12 см 18 см 24 см Правильный ответ: 24 см 4 Чему равен периметр правильного пятиугольника со стороной 8 см?32 см 40 см 64 см 80 см Правильный ответ: 40 см |
Как объяснить ребенку разницу между площадью и периметром?
Во-первых, площадь фигуры — это поверхность или плоское пространство, которое покрывает фигура, тогда как периметр фигуры представляет собой расстояние вокруг ее границы. Во-вторых, площадь измеряется в квадратных единицах, тогда как периметр измеряется в линейных единицах. Например, площадь квадрата длиной 3 см будет равна (3 см × 3 см) = 9квадратный см. Его периметр будет 4 × 3 см = 12 см.
Например, площадь квадрата длиной 3 см будет равна (3 см × 3 см) = 9квадратный см. Его периметр будет 4 × 3 см = 12 см.
Где мы используем площадь и периметр в реальной жизни?
Мы используем площадь и периметр для различных целей в нашей повседневной жизни. Например, покупая дом, мы должны знать его площадь, а покупая проволоку для ограждения сада, мы должны знать его периметр.
Периметр добавляет или умножает стороны фигуры?
Периметр — это мера границы формы. Чтобы найти периметр, нужно сложить длины всех сторон.
Дан набор фигур с одинаковой площадью, какая из фигур будет иметь самый короткий периметр?
Окружность будет иметь самый короткий периметр.
Периметр и площадь Класс 7 Формулы
Понятие периметра и площади фигур широко используется в нашей повседневной жизни. Учащиеся обычно сталкиваются с проблемами при проведении различия между ними, если им не ясна основная логика и концепция измерения. Следовательно, эта статья была создана, чтобы помочь учащимся понять формулы периметра и площади 7 класса, а также дать некоторые практические советы по их запоминанию.
Следовательно, эта статья была создана, чтобы помочь учащимся понять формулы периметра и площади 7 класса, а также дать некоторые практические советы по их запоминанию.
Список формул для периметра и площади класса 7
Ниже приведен список некоторых понятий и формул, связанных с периметром и площадью.
- Периметром замкнутой фигуры является общая длина ее границы, тогда как площадь — это занимаемое ею пространство.
- Периметр квадрата = 4 × сторона
- Периметр прямоугольника = 2 × (длина + ширина)
- Площадь квадрата = сторона × сторона
- Площадь прямоугольника = Длина × Ширина
- Площадь параллелограмма = Основание × Высота
- Площадь треугольника = 1/2 × основание × высота
- Расстояние вокруг круглой области называется ее окружностью.
- Длина окружности = πd, d — диаметр, а π = 22/7 или 3,14
- Площадь круга = πr 2 , где «r» — радиус круга.
Применение формул периметра и площади Класс 7
Площадь и периметр фигур широко используются в нашей повседневной жизни.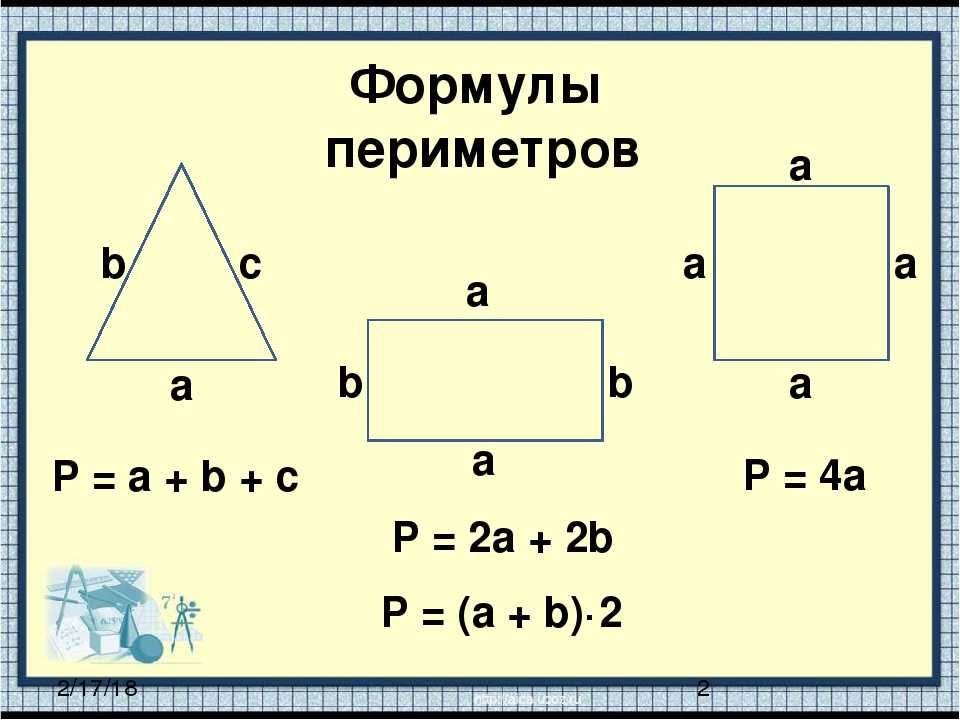 Несколько примеров приведены ниже.
Несколько примеров приведены ниже.
- Чтобы положить плитку на пол, нужно вычислить площадь пола и разделить ее на площадь одной плитки, чтобы узнать, сколько плиток потребуется, чтобы покрыть весь пол. Обычно плитка и пол комнаты имеют квадратную или прямоугольную форму, поэтому формулы площади квадрата и прямоугольника очень удобны.
- Чтобы поставить забор вокруг поля, нам нужно рассчитать периметр поля. В зависимости от того, имеет ли поле квадратную, прямоугольную или круглую форму, мы можем использовать формулы, чтобы узнать длину периметра, а затем рассчитать необходимое количество ограждений.
Советы по запоминанию формул периметра и площади класса 7
Формулы периметра и площади класса 7 являются основными вводными формулами, которые используются для понимания понятий, связанных с измерением. Следующие советы помогут учащимся легко выучить эти формулы:
- Один из лучших способов запомнить что-либо — записать это, так как мозг быстро обрабатывает это.
 Учащимся рекомендуется полностью записывать понятия и логику вместе с формулой, чтобы они имели для них смысл. Они должны прививать эту привычку каждый день, чтобы досконально понимать формулы.
Учащимся рекомендуется полностью записывать понятия и логику вместе с формулой, чтобы они имели для них смысл. Они должны прививать эту привычку каждый день, чтобы досконально понимать формулы. - После завершения письменной части учащиеся должны просмотреть все решенные примеры в своем учебнике, а затем попытаться решить их. Это познакомит их с различными вариантами использования формул. После решенных примеров они должны отработать как можно больше вопросов-упражнений. Это поможет им получить достаточную практику в использовании, а также в написании формул, что поможет им хорошо их запомнить.
- Учащиеся также могут установить изображения формул в качестве обоев на своих ноутбуках и мобильных устройствах. Это обеспечит быстрый пересмотр в течение дня.
Периметр и площадь класса 7 Формулы Примеры
Пример 1: Лара хочет оградить свой сад с трех сторон забором длиной 15 м, 10 м и 11 м. Найдите стоимость ограждения сада с трех сторон, если цена ограждения 120 руб.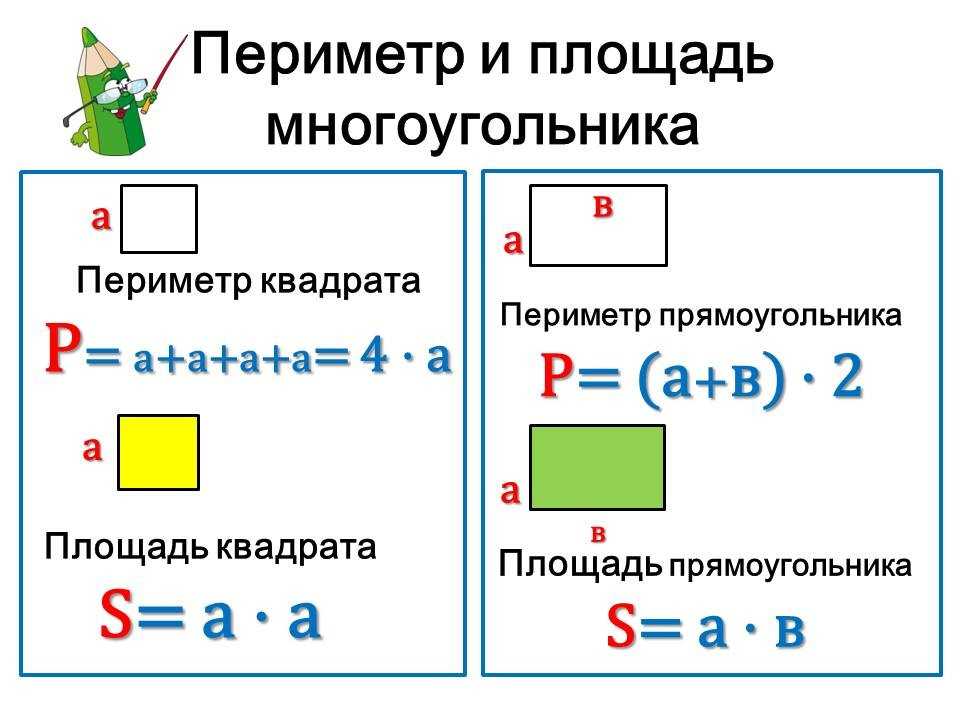 /м.
/м.
Решение: Общая стоимость ограждения = Скорость ограждения × общая длина требуемого ограждения
Требуемая общая длина ограждения = Периметр сада
Периметр сада = сумма трех сторон
= 15 + 10 +11
= 36 м
Общая стоимость ограждения = 120 × 36
= 4320 900 рупий 03
Пример 2 : Дверь размером 4 м × 2 м крепится к стене. с размерами 11 м × 11 м. Каковы будут общие трудозатраты на покраску стены, если затраты на покраску 1 м 2 стены составляют рупий. 2.50.
Решение: Общие трудозатраты = Скорость покраски × Площадь стены, подлежащей покраске
Площадь стены, подлежащей окраске = Площадь стены — Площадь двери
Площадь стены = 11 × 11 = 121 кв. м
Площадь двери = 4 × 2 = 8 кв. м
Площадь окрашивания = 121 — 8 = 113 квадратных метров
Общая стоимость покраски стены = 2,5 × 113
= рупий. 282.5
282.5
Учащиеся могут загрузить лист Math Formulas Class 7 для печати снизу:
Часто задаваемые вопросы по формулам периметра и площади 7 класса
Каковы важные формулы периметра и площади класса 7?
Важные формулы Периметра и Площади приведены ниже:
- Периметр замкнутой фигуры – это общая длина ее границы, а площадь – это занимаемое ею пространство.
- Периметр квадрата = 4 × сторона
- Периметр прямоугольника = 2 × (длина + ширина)
- Площадь квадрата = сторона × сторона
- Площадь прямоугольника = длина × ширина
- Площадь параллелограмма = основание × высота
- Площадь треугольника = 1/2 × основание × высота
- Расстояние вокруг круглой области называется ее окружностью.
- Длина окружности = πd, d — диаметр, а π = 22/7 или 3,14
Каковы основные формулы периметра и площади класса 7?
Основные формулы периметра и площади 7 класса помогают в вычислении площади и периметра квадратов, прямоугольников, кругов, треугольников, параллелограммов. Они обобщены в этой статье вместе с некоторыми практическими советами, чтобы запомнить их.
Они обобщены в этой статье вместе с некоторыми практическими советами, чтобы запомнить их.
Сколько формул содержится в формулах периметра и площади класса 7?
В этой статье приведены десять формул, связанных с периметром и площадью, которые помогают решить основные вопросы измерения. Знание этих формул необходимо, так как понятие измерения встречается в повседневной жизни.
Как я могу запомнить формулы периметра и площади класса 7?
Учащиеся могут легко запомнить формулы периметра и площади 7 класса с помощью следующих пунктов:
- Поскольку наш мозг легко обрабатывает рукописную информацию, запись формул является одним из лучших способов их запоминания.
- Как только учащиеся поймут логику формул, они должны просмотреть все решенные примеры в своем учебнике и попытаться решить их самостоятельно. Это откроет для них широкий спектр применений формул. После этого они должны попрактиковаться в решении задач, чтобы получить достаточно практики в решении задач.


 Значит, подставив эти значения в нашу формулу, мы получим — P = 2*5 см + 2* 10см = 30 см.
Значит, подставив эти значения в нашу формулу, мы получим — P = 2*5 см + 2* 10см = 30 см.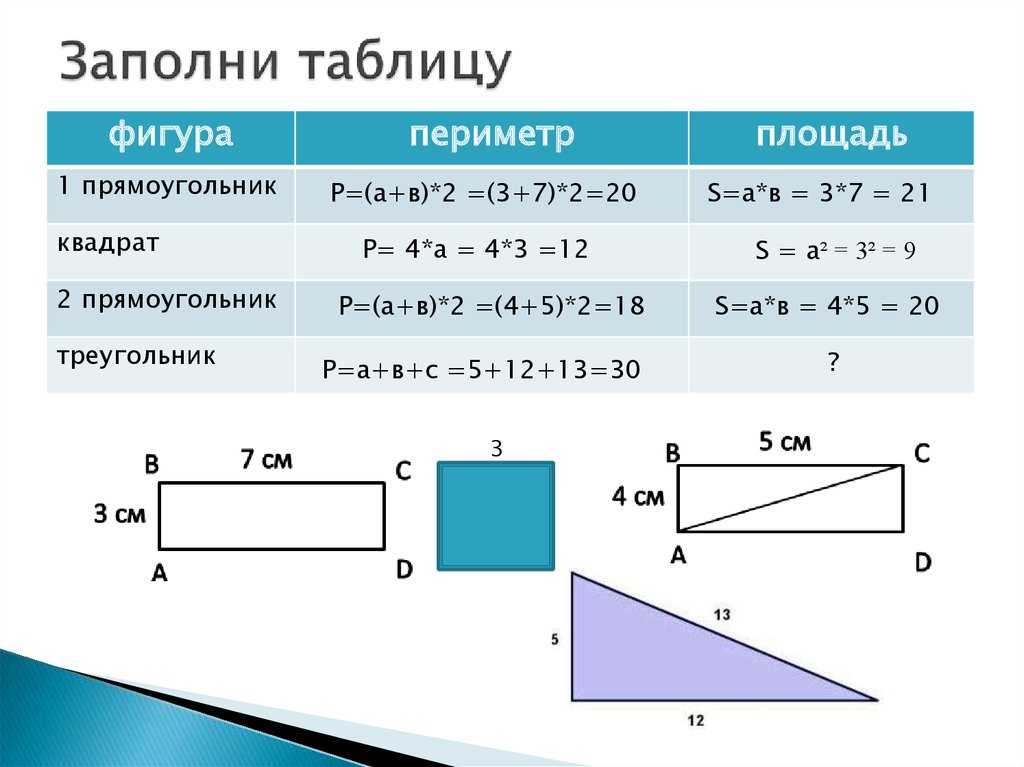 Например, есть острый, тупой, равнобедренный, прямоугольный или равносторонний треугольники. Хотя формула для всех видов треугольников такая:
Например, есть острый, тупой, равнобедренный, прямоугольный или равносторонний треугольники. Хотя формула для всех видов треугольников такая:




 Если вы ищите периметр прямоугольной фигуры в реальной жизни, используйте линейку или рулетку, чтобы найти ее стороны.
Если вы ищите периметр прямоугольной фигуры в реальной жизни, используйте линейку или рулетку, чтобы найти ее стороны.
 Учащимся рекомендуется полностью записывать понятия и логику вместе с формулой, чтобы они имели для них смысл. Они должны прививать эту привычку каждый день, чтобы досконально понимать формулы.
Учащимся рекомендуется полностью записывать понятия и логику вместе с формулой, чтобы они имели для них смысл. Они должны прививать эту привычку каждый день, чтобы досконально понимать формулы.