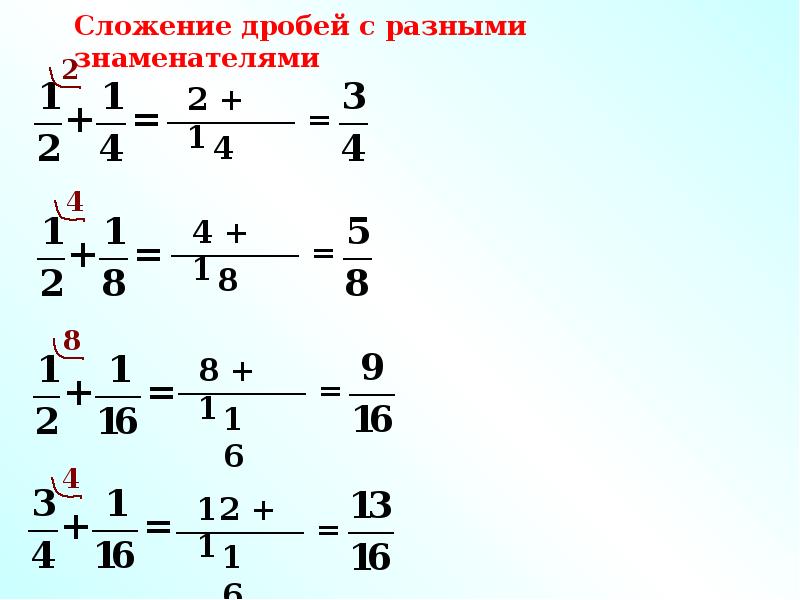
Как сложить простые дроби: § Сложение дробей с разными знаменателями. Как найти общий знаменатель

Содержание

§ Сложение дробей с разными знаменателями. Как найти общий знаменатель

Дроби. Числитель и знаменатель Сокращение дробей Сравнение дробей Смешанные числа. Выделить целую часть Сложение дробей. Общий знаменатель Вычитание дробей Умножение дробей Деление дробей Нахождение дроби от числа Нахождение целого по известной дроби

При сложении дробей могут встретиться разные случаи.

Сложение дробей с одинаковыми знаменателями

Такой случай наиболее простой. При сложении дробей с равными знаменателями складывают числители, а знаменатель оставляют тот же.

Пример.

C помощью букв это правило сложения можно записать так:

Запомните!

Записывая ответ, проверьте нельзя ли полученную дробь сократить.

Сложение дробей с разными знаменателями

Чтобы сложить дроби с разными знаменателями нужно воспользоваться следующими правилами.

Привести данные дроби к наименьшему общему знаменателю (НОЗ). Для этого найти наименьшее общее кратное знаменателей.

Пример. Сложить дроби.

Как найти общий знаменатель

Находим НОК (15, 18).

НОК (15, 18) = 3 · 2 · 3 · 5 = 90

Найти дополнительные множители для каждой дроби. Для этого наименьший общий знаменатель (НОК из пункта 1) делим по очереди на знаменатель каждой дроби.
Полученные числа и будут дополнительными множителями для каждой из дробей. Множители записываем над числителем дроби справа сверху.
90 : 15 = 6 — дополнительный множитель для дроби
.
90 : 18 = 5 — дополнительный множитель для дроби
.
Числитель и знаменатель каждой дроби умножаем на свой дополнительный множитель, пользуясь основным свойством дроби.
После умножения в знаменателях обеих дробей должен получиться наименьший общий знаменатель. Затем складываем дроби как дроби с одинаковыми знаменателями.
Проверяем полученную дробь.
- Eсли в результате получилась неправильная дробь, результат записываем в виде смешанного числа. Проверим нашу дробь.
  38 < 90
  У нас дробь правильная.
- Если в результате получилась сократимая дробь, необходимо выполнить сокращение.
Ещё раз весь пример целиком.

Сложение смешанных чисел

Сочетательное и переместитительное свойства сложения позволяют привести сложение смешанных чисел к сложению их целых частей и к сложению их дробных частей.

Чтобы сложить смешанные числа нужно.

Отдельно сложить их целые части.
Пример.
Складываем целые части.
Отдельно сложить дробные части.
Если у дробных частей знаменатели разные, то сначала приводим их к общему знаменателю, а затем складываем.
Сложить полученные результаты из пунктов 1 и 2.
Если при сложении дробных частей получилась неправильная дробь, то нужно выделить целую часть из этой дроби и прибавить к полученной в пункте 1 целой части.

Ещё один пример на сложение смешанных чисел.

Ваши комментарии

Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи «ВКонтакте».

Оставить комментарий:


Отправить

Как сложить обыкновенные дроби: с одинаковыми/разными знаменателями

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

MicroExcel. ru Математика Алгебра Сложение обыкновенных дробей

В данной публикации мы рассмотрим, каким образом можно сложить обыкновенные (простые) дроби с одинаковыми/разными знаменателями и смешанные дроби. Также разберем примеры решения задач для лучшего понимания и закрепления теоретического материала.

Сложение дробей
- С одинаковыми знаменателями
- С разными знаменателями
Сумма смешанных дробей
Примеры задач

Сложение дробей

С одинаковыми знаменателями

В данном случае все предельно просто. При сложении дробей с одинаковыми знаменателями суммируются числители, а знаменатель остается неизменным.

a/c

b/c

a+b/c

Примечание: полученную путем сложения новую дробь в некоторых случаях можно сократить.

С разными знаменателями

Для того, чтобы сложить дроби с разными знаменателями, выполняем следующие действия:

1. Приводим заданные дроби к наименьшему общему знаменателю.
2. Складываем полученные результаты как дроби с одинаковыми знаменателями.

Сумма смешанных дробей

Чтобы сложить смешанные дроби, необходимо отдельно просуммировать целые части, и отдельно дробные.

a/b

+ Y

c/d

= (X + Y) + (

a/b

c/d

)

Примечание: Если дробные части имеют разные знаменатели, значит их сперва нужно привести к наименьшему общему знаменателю, и только после этого складывать.

Примеры задач

Задание 1

Найдите сумму дробей

4/11

7/11

Решение

Т.к. у нас дроби с одинаковыми знаменателями, то:

4/11

7/11

4+7/11

11/11

Задание 2

Найдите сумму дробей

5/12

4/7

Решение

В данном случае нам сначала нужно привести дроби к наименьшему общему знаменателю.
Наименьшее общее кратное обоих знаменателей равняется 84, следовательно, дополнительный множитель для первой дроби – число 7, для второй – 12.

5/12

5⋅7/12⋅7

35/84

4/7

4⋅12/7⋅12

48/84

Таким образом, мы получили дроби с одинаковыми знаменателями, и теперь их можно сложить:

35/84

48/84

35+48/84

83/84

Задание 3

Найдите сумму дробей 2

6/13

и 5

3/13

Решение

Дробные части имеют один и тот же знаменатель, значит мы сразу же можем выполнить сложение:

6/13

+ 5

3/13

= 2 + 5 + (

6/13

3/13

) = 7 +

6+3/13

= 7

9/13

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

Как складывать дроби: 3 простых шага + 5 замечательных заданий

Возможно, ваши ученики знают, как обращаться с числителем и знаменателем, но готовы ли они к тому, что будет дальше? Внезапно пришло время научиться складывать дроби — и ваш класс запутался.

Чувствуете страх?

Вы не одиноки. Добавление дробей может показаться сложным, но это не обязательно.

Почему учащиеся испытывают трудности с дробями?

Дроби — особенно операции с дробями — сложный предмет для большинства учащихся. Проблемы с дробями могут снизить уверенность в математике и привести к математическому беспокойству, если учащиеся не получают достаточной поддержки по предмету.

Фракции — это борьба по нескольким причинам. Исследование показало, что самыми большими проблемами являются:

1. Понимание того, что означают числа

До дробей учащиеся привыкли работать с целыми числами : основные числа, представляющие целые суммы. Дроби знакомят учащихся с рациональными числами , которые имеют совершенно новый набор правил и закономерностей.

Значение дробей сбивает с толку, если сравнивать их с целыми числами. Целые числа выражаются только одним способом, в то время как дроби могут быть выражены разными способами и по-прежнему представляют одну и ту же сумму.

Например, число три можно представить только одним способом, но ²⁄₄ представляет то же количество, что и ½, 0,5 и 50%. Будучи студентом, это трудно уложить в голове.

2. Различные операции с целыми числами и дробями

Методы сложения, вычитания, умножения и деления целых чисел отличаются от тех же операций с дробями. Правила становятся гораздо более непредсказуемыми и запутанными. Многие студенты и учителя имеют ограниченное представление о том, как и почему используются эти методы.

Дроби сложнее представить с помощью визуальных средств или манипуляций, и правила их добавления труднее понять. Изучение того, как умножать и делить дроби, может еще больше запутать, так как учащиеся должны помнить различия между этими операциями. Это большая корректировка для студентов, которые уже знакомы с арифметикой целых чисел.

Типы дробей

Студенты должны сначала понять разницу между каждым типом дроби , чтобы успешно добавить их.

Начнем с основных компонентов дроби.

Дробь представляет части целого. Числитель (верхнее число) показывает количество деталей, которые у вас есть. Знаменатель (нижнее число) показывает общее количество частей, на которые делится целое.

На приведенном выше рисунке наш круг разделен на четыре части. Это означает, что четыре — наш знаменатель. Из этих четырех частей одна выделена. Это означает, что один — наш числитель. Итак, наша дробь равна ¼ или одной четверти.

Существуют три основные категории дробей: Правильные, неправильные и смешанные.

В дополнение к этому уравнения дробей будут разделены на две отдельные категории: те, в которых похожи на дроби , и те, в которых отличаются от дробей .

Базовые знания об этих типах помогут учащимся понять, что делать, когда они сталкиваются с вопросом о сложении дробей.

Теперь, когда вы знакомы с каждым типом дроби, вы можете приступить к сложению! Научите своих учеников приведенной ниже трехэтапной формуле, чтобы уверенно решать уравнения сложения дробей.

3 простых шага для сложения дробей

Сначала это может показаться пугающим, но сложение дробей может быть простым. Все, что вам нужно сделать, это выполнить три простых шага:

Шаг 1: Найдите общий знаменатель
Шаг 2: Сложите числители (с сохранением знаменателя)
Шаг 3: Упростите дробь

Давайте рассмотрим каждый шаг в немного более подробно.

Шаг 1: Найдите общий знаменатель

Если ваши два знаменателя уже совпадают, вы складываете дроби с как знаменатели . Фантастика! Это означает, что вы можете перейти ко второму шагу.

Если у вас разные знаменатели, вы складываете дроби с в отличие от знаменателей. При сложении разных дробей необходимо найти общий знаменатель , чтобы можно было сложить две дроби вместе.

Посмотрите видео ниже, чтобы понять , почему нам нужен общий знаменатель для сложения дробей.

Вы можете найти общий знаменатель, используя эквивалентных дробей : дроби, имеющие одинаковое значение. Например, ²⁄₄, ³⁄₆ и ⁴⁄₈ являются эквивалентными дробями, потому что все они могут быть уменьшены до ½.

Существует два основных метода нахождения общего знаменателя.

1) Метод общего знаменателя

В этом методе вы умножаете верхнюю и нижнюю часть каждой дроби на знаменатель другой. Например, рассмотрим следующее уравнение:

⅓ + ⅙

Наши дроби имеют два разных знаменателя: три и шесть. Нам нужно умножить числитель и знаменатель в ⅓ на шесть, а затем умножить числитель и знаменатель в ⅙ на три.
Когда мы это сделаем, наши новые дроби станут ⁶⁄₁₈ и ³⁄₁₈.

Две новые дроби имеют одинаковый знаменатель, так что теперь мы можем их сложить!

2) Метод наименьшего общего знаменателя

Этот метод включает нахождение наименьшего из всех общих знаменателей, а затем умножение исходных дробей для получения этого знаменателя.

Чтобы найти наименьший общий знаменатель, перечислите все числа, кратные числу, и найдите среди них наименьшее число, которое совпадает.

Например, используя то же уравнение, что и раньше — ⅓ + ⅙ — вы можете составить таблицу для определения наименьшего общего кратного.

Как видно из нашей таблицы, наименьшее число, кратное одному и тому же, равно шести.

Итак, для ⅓ числитель и знаменатель нужно умножить на два, чтобы получить ²⁄₆. Для ⅙ числа нужно умножить на единицу, чтобы дробь осталась прежней. И снова наши фракции готовы к добавлению!

Шаг 2: Сложите числители (сохраните знаменатель)

Этот шаг довольно прост. Сложите числители, чтобы сумма стала новым числителем, а знаменатель остался прежним.

Давайте воспользуемся нашим предыдущим примером:

⅓ + ⅙

Используя наше новое уравнение из метода общего знаменателя — ⁶⁄₁₈ + ³⁄₁₈ — нам нужно сложить шесть и три вместе. В знаменателе по-прежнему будет восемнадцать.

Шесть плюс три равно девяти, поэтому наш ответ ⁹⁄₁₈.

Шаг 3: Упростите дробь

Если ваша дробь содержит большие числа, вам может понадобиться упростить ее.

Упрощение включает в себя нахождение наименьшей возможной эквивалентной дроби. В нашем предыдущем уравнении наш ответ был ⁹⁄₁₈. Это число кажется немного большим, поэтому посмотрим, сможем ли мы упростить его до более простого числа.

Чтобы упростить дробь, вам нужен общий делитель : число, которое делится на оба числа поровну. Например, два — это общий делитель четырех и шести, потому что оба числа можно разделить на два.

Два самых простых метода упрощения дроби:

1) Метод проб и ошибок

Для этого метода просто продолжайте делить числитель и знаменатель на маленькие числа. Начните с двух, затем трех, четырех и так далее, пока не получите наименьший возможный ответ.

С нашим ответом ⁹⁄₁₈ мы можем продолжать делить на маленькие числа, пока не найдем то, которое работает.

Можно ли разделить девять и восемнадцать на два? Нет. Мы не можем разделить девять на два поровну.

Хорошо, попробуем другой номер.

Можно ли разделить девять и восемнадцать на три? Да! Когда мы делим оба числа на три, наша дробь становится ³⁄₆.

Теперь, когда у нас есть более простой ответ, пришло время посмотреть, сможем ли мы упростить его еще больше. И три, и шесть можно снова разделить на три, поэтому наш окончательный ответ — ½.

2) Найдите наибольший общий делитель (НОД)

НОД — это наибольшее число, которое делится на два или более чисел без остатка.

Этот метод похож на нахождение наименьшего общего знаменателя — вы найдете ответ, перечислив все возможные факторы.

Используя наш предыдущий пример с ⁹⁄₁₈, мы найдем и перечислим все делители каждого числа, начиная с единицы. После того, как вы перечислили все множители этого числа, все, что вам нужно сделать, это найти наибольшее число, повторяющееся в обоих списках.

В этом также поможет удобный стол.

Воспользуемся нашей таблицей, чтобы найти наибольшее число, общее для обоих чисел. В этом случае наибольший общий делитель для девяти и восемнадцати равен девяти. Теперь мы можем разделить оба числа на девять, чтобы получить уменьшенную дробь: ½.

Если объединить все три шага сложения дробей, получится следующее:

Сложение смешанных дробей

Вышеприведенные шаги отлично подходят для правильных и неправильных дробей, но как насчет сложения дробей с целыми числами?

Складывать смешанные дроби на самом деле очень просто: просто преобразуйте их в неправильные дроби, и вы готовы начать сложение!

Любую смешанную дробь можно превратить в неправильную. Например, 1 ¾ — это то же самое, что ⁷⁄₄.

Источник изображения: Central Bucks School District

Преобразование смешанных дробей в неправильные осуществляется в три этапа:

1. Умножьте целое число на знаменатель

Возьмем 1 ¾. Если мы умножим наше целое число (один) на наш знаменатель (четыре), мы получим четыре.

2. Добавьте это число к числителю

Наше новое число (четыре) плюс наш числитель (три) равно семи.

3. Напишите новый числитель над исходным знаменателем

Наш новый числитель (семь) по отношению к исходному знаменателю (четыре) равен ⁷⁄₄. Теперь вы можете сложить дробь!

Важность сложения дробей

Как учитель, вы, вероятно, хорошо знакомы с извечным вопросом, который задают ученики: «Зачем я вообще это делаю?»

В этом контексте это, безусловно, правильный вопрос. Почему сложение дробей так важно для изучения?

Во-первых, у этой арифметики есть множество реальных применений. Во многих случаях вам нужно будет найти общее количество частей целого, когда они объединены.

Вот несколько возможных примеров сложения дробей в реальной жизни:

Упражнения : Если вы пробежали ¼ мили в понедельник и ¾ мили во вторник, какое расстояние вы пробежали за оба дня?
Тайм-менеджмент : Если вы работаете 8 ½ часов в понедельник и 6 ¾ часов во вторник, сколько часов вы проработали в оба дня?
Кулинария/выпечка : Если вы добавите ½ стакана стружки молочного шоколада и ⅓ чашки стружки белого шоколада в тесто для печенья, каково общее количество стружки шоколада в вашем рецепте?

Если этого недостаточно, знание операций с дробями на самом деле очень важно для изучения более сложной математики и естественных наук, что в конечном итоге приводит к успеху во многих академических или карьерных сферах.

Недостаточное знание операций с дробями может привести к более слабым навыкам в более поздних математических и естественных науках. Одно исследование показало, что в Соединенных Штатах и Великобритании знание дробей учащимися начальных классов может предсказать общие математические способности в старшей школе.

Исследование навыков, технологий и методов управления на рабочем месте (STAMP) показало, что 68% работающих людей в возрасте 18 лет и старше используют дроби в своей повседневной работе. Это означает, что значительному количеству взрослых в Соединенных Штатах требуется твердое базовое знание дробей и их операций. Изучение этих навыков как можно раньше является ключом к успеху на многих рабочих местах.

5 Увлекательные занятия по сложению дробей

Теперь, когда вы знаете, чему научить своих учеников складывать дроби, давайте сосредоточимся на том, как. Вдохновитесь этими пятью увлекательными идеями занятий, которые дополнят ваши уроки сложения дробей.

1) Prodigy

Prodigy – это учебная платформа, ориентированная на учебную программу, с более чем 1 500 навыками, позволяющими детям практиковать математику. Используйте его, чтобы освоить все виды дробей, от базового понимания до более сложных операций, таких как сложение.

Prodigy отправляет игроков в захватывающее приключение, где они отвечают на математические вопросы, чтобы «сразиться» с другими персонажами. Платформа предназначена для того, чтобы вовлечь учащихся в игровой процесс, поэтому они действительно захотят, чтобы продолжала играть и, как результат, больше занималась математикой!

Платформа — отличный инструмент для дополнения уроков, домашних заданий и многого другого. Это также может помочь вам дифференцировать обучение и определить конкретные проблемные места, помогая каждому учащемуся добиться успеха в своем собственном темпе.

«Наш последний тест был на Fractions, и это был первый раз, когда я действительно убедился, что каждый день в Prodigy они отрабатывают эти конкретные навыки, и результаты теста очень хорошо отражали дополнительную практику, которую они получили! » — Жюстин Хилл учитель 3-го класса, центральные школы Восточного Сиракуз-Миноа

2) Игра с ударами сложение дробей претендовать на место в доске.
Вы можете найти множество игр на разные темы. В этом выпуске с добавлением дробей игроки должны бросать кости, чтобы найти соответствующее уравнение, а затем размещать свои игровые фишки на дроби, которая соответствует ответу.
Игрок, который первым соберет все свои фишки на доске, становится победителем!
4) Словесные задачи
Словесные задачи для уравнений дробей представляют собой реальные примеры вопросов, на которые отвечают учащиеся, помогая им понять цель таких вопросов.
Источник изображения: Teachers Pay Teachers
Карточки с задачами Word и рабочие листы — отличный способ задать эти вопросы. Если вы хотите, чтобы ваш класс был более вовлечен, вы можете использовать манипуляторы или даже самих учеников.
Например, «если три человека одеты в зеленое, а двое — в синее, какова доля в классе людей, одетых в зеленое или синее?»
4) Составители уравнений
В этом упражнении учащиеся рисуют или строят уравнения, чтобы визуализировать, как выглядит сложение дробей.
Источник изображения: Desert Designed
Предложите учащимся составить уравнения или использовать манипуляции, чтобы лучше понять, что на самом деле означает сложение дробей. Дробные полосы или шкала дробей — отличные варианты, чтобы сделать эту абстрактную концепцию более удобоваримой и конкретной.
Проверьте три типа дробей Примечания
5) Math mates
Эта активная игра поднимает учеников со своих мест, сотрудничая с одноклассниками и практикуя математику… все сразу!
У каждого ученика своя фракция. Игроки ходят по комнате, находят партнеров и работают вместе, чтобы сложить свои фракции.
Эта игра отлично подходит для отработки навыков, полученных в классе, и поощрения командной работы.
Заключительные мысли о добавлении дробей
Переход от базовых навыков дробей к сложению, безусловно, пугает, но добавление дробей можно упростить, выполнив три простых шага, описанных выше.
Используйте информацию из этого руководства, чтобы победить на следующем уроке математики и упростить сложение дробей для ваших учеников. Далее: вычитание, умножение и деление. О боже!
Создайте или войдите в свою учетную запись учителя на Prodigy – игровой платформе для обучения математике, ориентированной на учебную программу, с полезными инструментами как для преподавателей, так и для учащихся.
Сложение дробей
PGSG8gJWt1g
Дробь типа 3 4 говорит, что у нас есть 3 из 4 частей, на которые делится целое.
Чтобы сложить дроби, нужно выполнить три простых шага:
Шаг 1: Убедитесь, что нижние цифры (
0363 знаменатели ) совпадают с
Шаг 2: Сложите верхние числа (числители ), поместите этот ответ над знаменателем
Шаг 3. Упростите дробь (если возможно)
Пример:
1 4 + 1 4
Шаг 1 .
Нижние числа (знаменатели) уже одинаковы. Сразу переходите к шагу 2.
Шаг 2 . Сложите верхние числа и поставьте ответ над тем же знаменателем:
.
1 4 + 1 4 «=» 1 + 1 4 «=» 2 4
Шаг 3 . Упростите дробь:
2 4 «=» 1 2
На картинке это выглядит так:

1 4 + 1 4 = 2 4 = 1 2

. .. и вы видите, как 2 4 проще, как 1 2 ? (см. Эквивалентные дроби.)

Пример:
1 3 + 1 6
Шаг 1 : Нижние числа разные. Видите, как кусочки разного размера?
1 3 + 1 6 = ?

Нам нужно сделать их одинаковыми, прежде чем мы сможем продолжить, потому что мы не может добавить их вот так.
Число «6» в два раза больше, чем «3», поэтому, чтобы сделать нижние числа одинаковыми, мы можем умножить верхнюю и нижнюю часть первой дроби на 2 , например:
× 2
1 3   =   2 6
× 2
Важно: вы умножаете как верхнее, так и нижнее на одинаковую сумму,
, чтобы значение дроби осталось прежним
Теперь дроби имеют одинаковое нижнее число («6»), и наш вопрос выглядит так:
2 6 + 1 6

Нижние числа теперь одинаковы, поэтому мы можем перейти к шагу 2.

Шаг 2 : Сложите верхние числа и поместите их над одним знаменателем:
2 6 + 1 6 «=» 2 + 1 6 «=» 3 6
На картинке это выглядит так:
904:30 1 6
2 6 + = 3 6

Шаг 3 : Упростить дробь:
3 6 «=» 1 2

В графической форме весь ответ выглядит так:
2 6 + 1 6 = 3 6 = 1 2

С ручкой и бумагой
А вот как это сделать ручкой и бумагой (нажмите кнопку воспроизведения):

Играй!
Попробуйте сложить дроби.
Стихотворение, которое поможет вам вспомнить
♫ «Если вашей целью является сложение или вычитание,
Нижние числа должны быть одинаковыми!
♫ «Измените низ, используя умножение или деление,
Но то же самое нужно применить к верху,
♫ » И не забудьте упростить,
Пока не пришло время прощаться»
Пример:
1 3 + 1 5
Опять же, нижние цифры разные (ломтики разного размера)!
1 3 + 1 5 = ?

Но давайте попробуем разделить их на более мелкие, чтобы были одинаковыми :
5 15 + 3 15

Первая дробь: умножив верх и низ на 5, мы получили 5 15 :
× 5
1 3   =   5 15
× 5
Вторая дробь: умножив верх и низ на 3, мы получили 3 15 :
× 3
1 5   =   3 15
× 3
Нижние числа теперь одинаковы, поэтому мы можем добавить верхние числа:
5 15 + 3 15 = 8 15

Результат уже настолько прост, насколько это возможно, поэтому ответ:
1 3 + 1 5 «=» 8 15
Уравнивание знаменателей
Откуда в предыдущем примере мы узнали, что нужно разрезать их на ¹ / ₁₅ тысяч, чтобы знаменатели совпадали? Мы просто перемножили два знаменателя (3 × 5 = 15).
Прочитать о двух основных способах приведения знаменателей в соответствие можно здесь:
Метод общего знаменателя или
Метод наименьшего общего знаменателя
Они оба работают, используйте тот, который вам больше нравится!
Пример: Кексы
Вы хотите испечь и продать кексы:
Друг может предоставить ингредиенты, если вы им дадите ¹ / ₃ продаж
Прилавок на рынке стоит ¹ / ₄ продаж
Сколько это вообще?

Нам нужно добавить ¹ / ₃ и ¹ / ₄
1 3 + 1 4 = ? ?
Сначала сделайте нижние числа (знаменатели) одинаковыми.
Умножить верх и низ ¹ / ₃ на 4 :
1×4 3×4 + 1 900 38 4 = ? ?
И умножить верх и низ ¹ / ₄ на 3 :
1×4 3×4 + 1 ×3 4×3 = ? ?
Теперь делаем вычисления:
4 12 + 3 12 = 4+3 9003 8 12 = 7 12

Ответ: 7 12 сбываний идут в ингридиентах и ценах рынка.
No related posts.