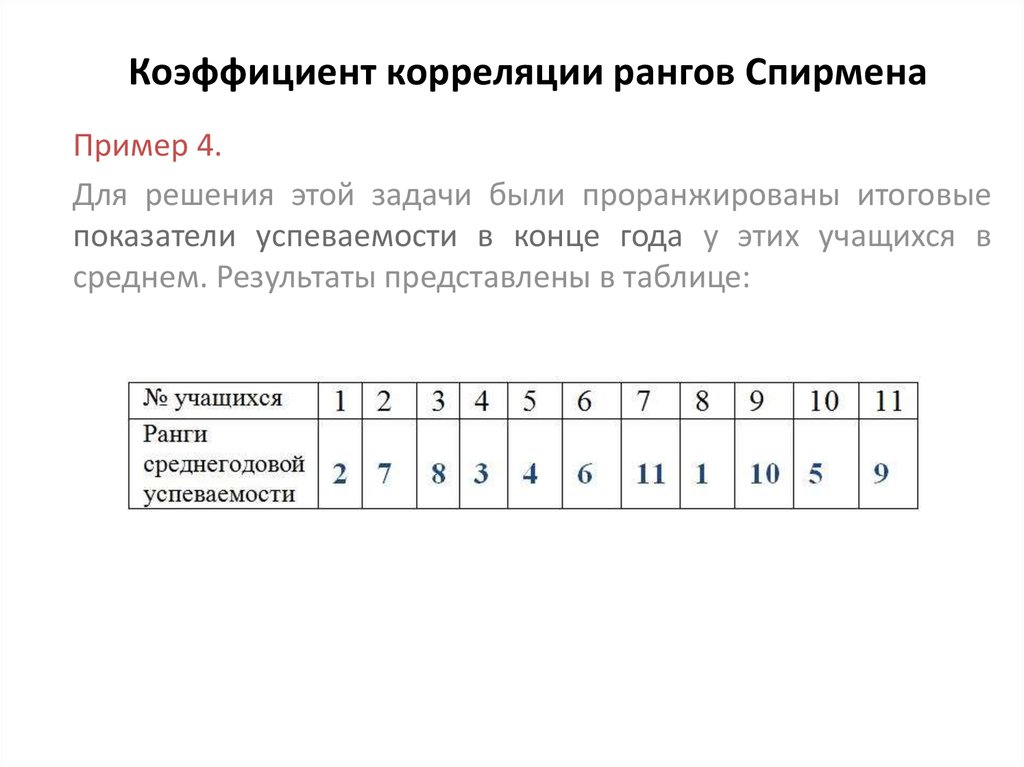
Пример нахождения коэффициента ранговой корреляции Спирмена
На практике для определения тесноты связи двух признаков часто применяется коэффициент ранговой корреляции Спирмена (Р). Значения каждого признака ранжируются по степени возрастания (от 1 до n), затем определяется разница (d) между рангами, соответствующими одному наблюдению.Пример №1. Зависимость между объемом промышленной продукции и инвестициями в основной капитал по 10 областям одного из федеральных округов РФ в 2003 году характеризуется следующими данными.
Вычислите ранговые коэффициенты корреляции Спирмена и Кендэла. Проверить их значимость при α=0,05. Сформулируйте вывод о зависимости между объемом промышленной продукции и инвестициями в основной капитал по рассматриваемым областям РФ.
Присвоим ранги признаку Y и фактору X. Найдем сумму разности квадратов d2.
Используя калькулятор, вычислим коэффициент ранговой корреляции Спирмена:
| X | Y | ранг X, dx | ранг Y, dy | (dx — dy)2 |
1. 3 |
300 | 1 | 2 | 1 |
| 1.8 | 1335 | 2 | 12 | 100 |
| 2.4 | 250 | 3 | 1 | 4 |
| 3.4 | 946 | 4 | 8 | 16 |
| 4.8 | 670 | 5 | 7 | 4 |
| 5.1 | 400 | 6 | 4 | 4 |
| 6.3 | 380 | 7 | 3 | 16 |
| 7.5 | 450 | 8 | 5 | 9 |
| 7.8 | 500 | 9 | 6 | 9 |
| 17.5 | 1582 | 10 | 16 | 36 |
18. 3 |
1216 | 11 | 9 | 4 |
| 22.5 | 1435 | 12 | 14 | 4 |
| 24.9 | 1445 | 13 | 15 | 4 |
| 25.8 | 1820 | 14 | 19 | 25 |
| 28.5 | 1246 | 15 | 10 | 25 |
| 33.4 | 1435 | 16 | 4 | |
| 42.4 | 1800 | 17 | 18 | 1 |
| 45 | 1360 | 18 | 13 | 25 |
| 50.4 | 1256 | 19 | 11 | 64 |
| 54.8 | 1700 | 20 | 17 | 9 |
| 364 |
Связь между признаком Y фактором X сильная и прямая.
Оценка коэффициента ранговой корреляции Спирмена
Значимость коэффициента ранговой корреляции СпирменаПо таблице Стьюдента находим Tтабл.
Tтабл = (18;0.05) = 1.734
Поскольку Tнабл > Tтабл , то отклоняем гипотезу о равенстве нулю коэффициента ранговой корреляции. Другими словами, коэффициента ранговой корреляции Спирмена статистически — значим. Интервальная оценка для коэффициента ранговой корреляции (доверительный интервал)
Доверительный интервал для коэффициента ранговой корреляции Спирмена: p(0.5431;0.9095).
Перейти к онлайн решению своего примера
Пример №2. Исходные данные.
| 5 | 4 |
| 3 | 4 |
| 1 | 3 |
| 3 | 1 |
| 6 | 6 |
| 2 | 2 |
| Номера мест в упорядоченном ряду | Расположение факторов по оценке эксперта | Новые ранги |
| 1 | 1 | 1 |
| 2 | 2 | 2 |
| 3 | 3 | 3.5 |
| 4 | 3 | 3.5 |
| 5 | 5 | 5 |
| 6 | 6 | 6 |
Переформирование рангов производится в табл.
| Номера мест в упорядоченном ряду | Расположение факторов по оценке эксперта | Новые ранги |
| 1 | 1 | 1 |
| 2 | 2 | 2 |
| 3 | 3 | 3 |
| 4 | 4 | 4.5 |
| 5 | 4 | 4.5 |
| 6 | 6 | 6 |
| ранг X, dx | ранг Y, dy | (dx — dy)2 |
| 5 | 4. 5 | 0.25 |
| 3.5 | 4.5 | 1 |
| 1 | 3 | 4 |
| 3.5 | 1 | 6.25 |
| 6 | 6 | 0 |
| 2 | 2 | 0 |
| 21 | 21 | 11.5 |
где
j — номера связок по порядку для признака х;
Аj — число одинаковых рангов в j-й связке по х;
k — номера связок по порядку для признака у;
Вk — число одинаковых рангов в k-й связке по у.
A = [(23-2)]/12 = 0.5
B = [(23-2)]/12 = 0.5
D = A + B = 0.5 + 0.5 = 1
Связь между признаком Y и фактором X умеренная и прямая.
Задание №1. Определите тесноту связи с помощью коэффициента корреляции рангов Спирмена между X и Y.
Задание №2. С помощью коэффициента ранговой корреляции Спирмена определите, между мнениями каких политических деятелей по вопросу приоритетов мероприятий региональной политики в России наблюдается наибольшее совпадение.
Пример №2
Коэффициент конкордации онлайн
Коэффициент конкордации является мерой согласованности мнений экспертов.,
где , Li — число связок (видов повторяющихся элементов) в оценках i-го эксперта, tl — количество элементов в l-й связке для i-го эксперта (количество повторяющихся элементов).
Если нет связанных рангов, то Ti равно нулю.
Назначение сервиса. С помощью онлайн-калькулятора производится расчет коэффициента конкордации, а также делается вывод о его значимости.
- Шаг №1
- Шаг №2
- Видеоинструкция
- Оформление Word
Инструкция. Укажите Число факторов и Число экспертов. Полученное решение сохраняется в файле Word.
Число факторов
Число экспертов
Пример. Шесть экспертов (n=6) ранжируют пять (m=5) элементов (X1, X2, …, X3) по их важности. Результаты сведены в таблицу. Определить суммарную ранжировку этих элементов и коэффициент конкордации. Проверить значимость коэффициента конкордации, если табличное значение χ20,01(4) для 1% уровня значимости и 4 степеней (k = n-1=5-1=4) свободны равно 13,277.
Таблица — Расчет коэффициента конкордации
| Эксперты ↓ Факторы→ | 1 | 2 | 3 | 4 | 5 | 6 | rj | di | d2 |
| 1 | 2 | 3 | 1 | 2 | 1 | 1 | 10 | -8 | 64 |
| 2 | 1 | 1 | 3 | 3 | 4 | 2 | 14 | -4 | 16 |
| 3 | 3 | 2 | 2 | 1 | 2 | 3 | 13 | -5 | 25 |
| 4 | 4 | 5 | 4 | 5 | 3 | 4 | 25 | 7 | 49 |
| 5 | 5 | 4 | 5 | 4 | 5 | 5 | 28 | 10 | 100 |
Анализ строки rj (суммы рангов, полученных элементом Xj от всех экспертов) показывает, что наименьшее значение эта сумма имеет для первого элемента.
Этому элементу приписывается ранг 1. Ранг 2 имеет 3-й элемент, ранг 3 имеет 2-й элемент, ранги 4 и 5 имеют 4-й и 5-й элементы соответственно.
Сумма рангов, проставленных всеми экспертами равна N·m·(m+1)/2 = 6·5·(5+1)/2=90. Если разделить это значение на количество ранжируемых элементов (6), получим среднее значение рангов, приходящихся на один элемент, равное 18. Вычтем это значение из суммы рангов, полученных элементом Xj от всех экспертов rj (см. строку dj табл.), возведем полученную разность в квадрат (см. строку d2 табл.) и просуммируем для всех элементов. В результате получим величину R(d2)=254. Максимально возможное значение этой величины равно:
Коэффициент конкордации W=254/360=0,71.
Значение χ2 = N·(m-l)·W=6·(5-l)·0,71=17,04, т.к. χ2> χ20,01 (χ 20,01(4) =13,27), следовательно, коэффициент значим, согласованность удовлетворительна.
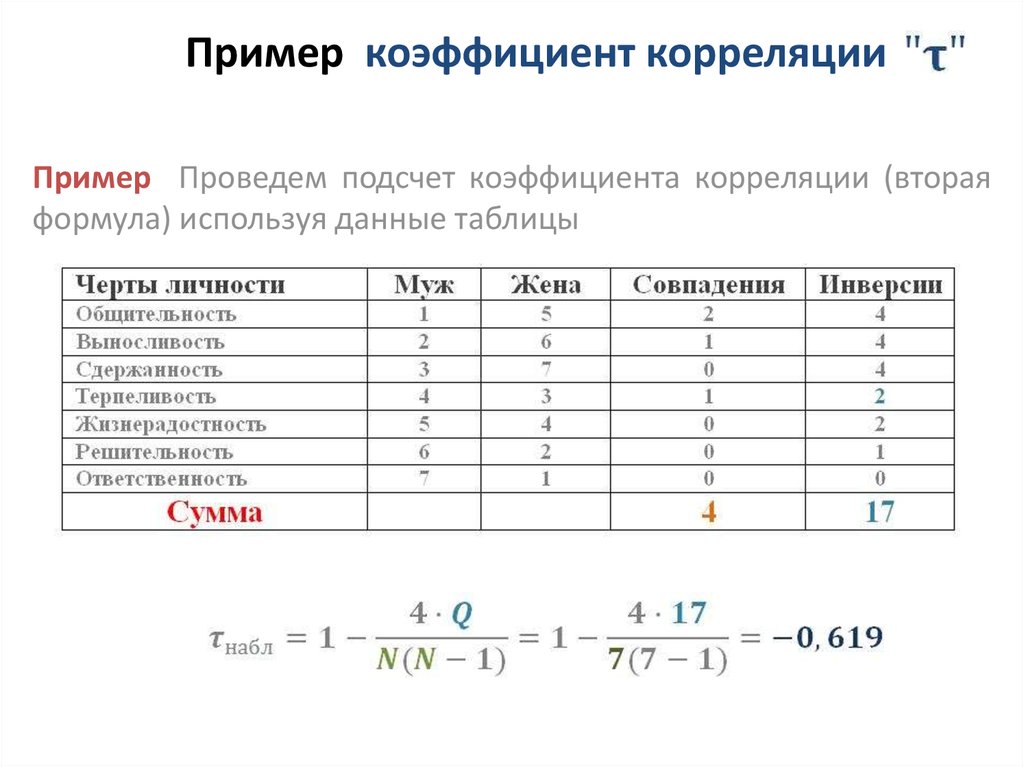
Пример №2.
Цель решения задачи: использование полученной информации для определения путей качественного совершенствования продукции, оценки технического уровня, конкурентоспособности холодильников на рынке, обоснования цен, надбавок (скидок) с цен с учетом технического уровня продукции, выявления новых секторов рынка холодильников.
Задание. Произвести экспертную оценку технических параметров холодильников по степени значимости их для потребителей.
Исходные данные
Технические параметры холодильников:
1. Объем камеры м3.
2. Количество камер шт.
3. Энергопотребление.
4. Наличие системы Hoy Frost.
5. Дизайн.
6. Бренд.
Число факторов n= 6
Число экспертов m= 4
- Решение
- Видео решение
Решение находим с помощью калькулятора.
Этап 1. Создание экспертной комиссии.
В экспертную группу вошло 4 эксперта.
Этап 2. Сбор мнений специалистов путем анкетного опроса.
Оценку степени значимости технических параметров холодильника для потребителей эксперты производят путем присвоения им рангового номера. Фактору, которому эксперт дает наивысшую оценку, присваивается ранг 1. Если эксперт признает несколько факторов равнозначными, то им присваивается одинаковый ранговый номер. На основе данных анкетного опроса составляется сводная матрица рангов.
Этап 3. Составление сводной матрицы рангов.
Таблица 1
Матрица рангов
| № п/п | Технические параметры холодильника | Единица измерения | Эксперты | |||
| 1 | 2 | 3 | 4 | |||
| 1 | Объем камеры (x1) | м3 | 3 | 4 | 5 | 4 |
| 2 | Бренд (x2) | - | 5 | 6 | 3 | 4 |
| 3 | Количество камер (x3) | Шт.
| 4 | 3 | 1 | 3 |
| 4 | Наличие систем Hoy Frost (x4) | - | 1 | 1 | 3 | 1 |
| 5 | Энергопотребление (x5) | Вт. | 6 | 5 | 6 | 6 |
| 6 | Дизайн (x6) | - | 2 | 2 | 2 | 2 |
Переформирование рангов производится в табл.
2, 3
Таблица 2
| Номера мест в упорядоченном ряду | 1 | 2 | 3 | 4 | 5 | 6 |
| Расположение факторов по оценке эксперта | 1(x3) | 2(x6) | 3(x2) | 3(x4) | 5(x1) | 6(x5) |
| Новые ранги | 1 | 2 | 3,5 | 3,5 | 5 | 6 |
Таблица 3
| Номера мест в упорядоченном ряду | 1 | 2 | 3 | 4 | 5 | 6 |
| Расположение факторов по оценке эксперта | 1(x4) | 2(x6) | 3(x3) | 4(x1) | 4(x2) | 6(x5) |
| Новые ранги | 1 | 2 | 3 | 4,5 | 4,5 | 6 |
4).
Матрица рангов
Таблица 4
| Эксперты Факторы | 1 | 2 | 3 | 4 | Сумма рангов | Δ | |
| x1 | 3 | 4 | 5 | 4,5 | 16,5 | 2,5 | 6,25 |
| x2 | 5 | 6 | 3,5 | 4,5 | 19 | 5 | 25 |
| x3 | 4 | 3 | 1 | 3 | 11 | -3 | 9 |
| x4 | 1 | 1 | 3,5 | 1 | 6,5 | -7,5 | 56,25 |
| x5 | 6 | 5 | 6 | 6 | 23 | 9 | 81 |
| x6 | 2 | 2 | 2 | 2 | 8 | -6 | 36 |
| Σ | 21 | 21 | 21 | 21 | 84 | S = 213,5 | |
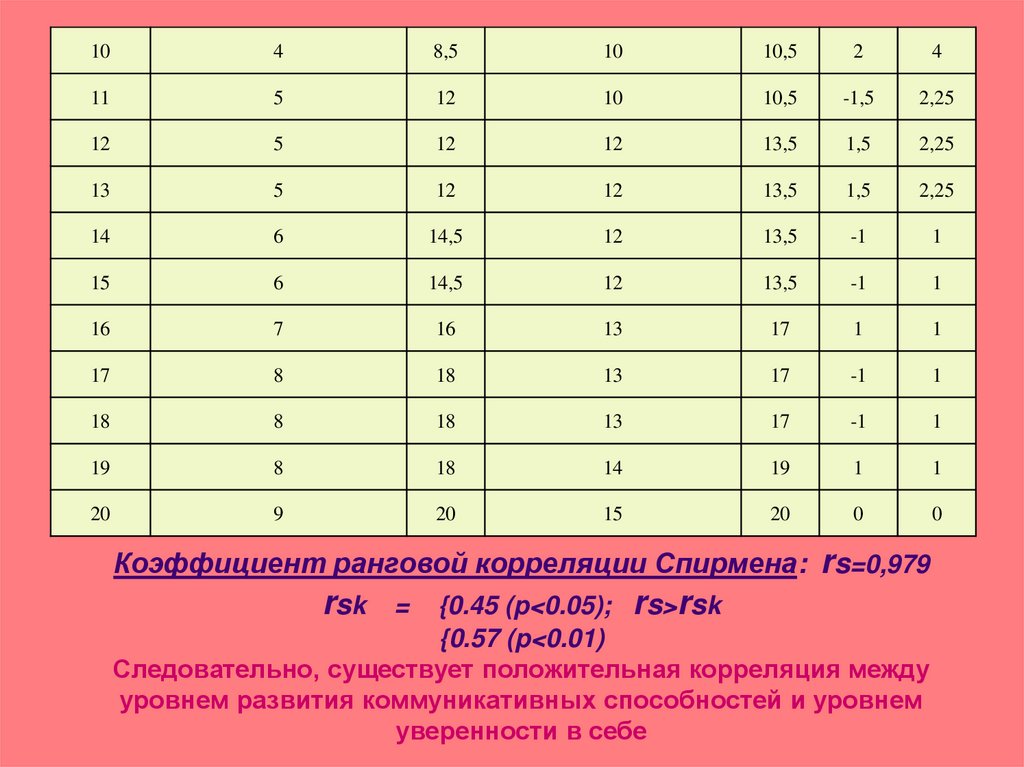
Проверка правильности составления матрицы на основе исчисления контрольной суммы:
.
Сумма по столбцам матрицы равны между собой и контрольной суммы, значит матрица составлена правильно.
Этап 4. Анализ значимости исследуемых факторов.
В данном примере факторы по значимости распределились следующим образом (табл. 5).
Таблица 5 — Расположение факторов по значимости
| Факторы | x4 | x6 | x3 | x1 | x2 | x5 |
| Сумма рангов | 6,5 | 8 | 11 | 16,5 | 19 | 23 |
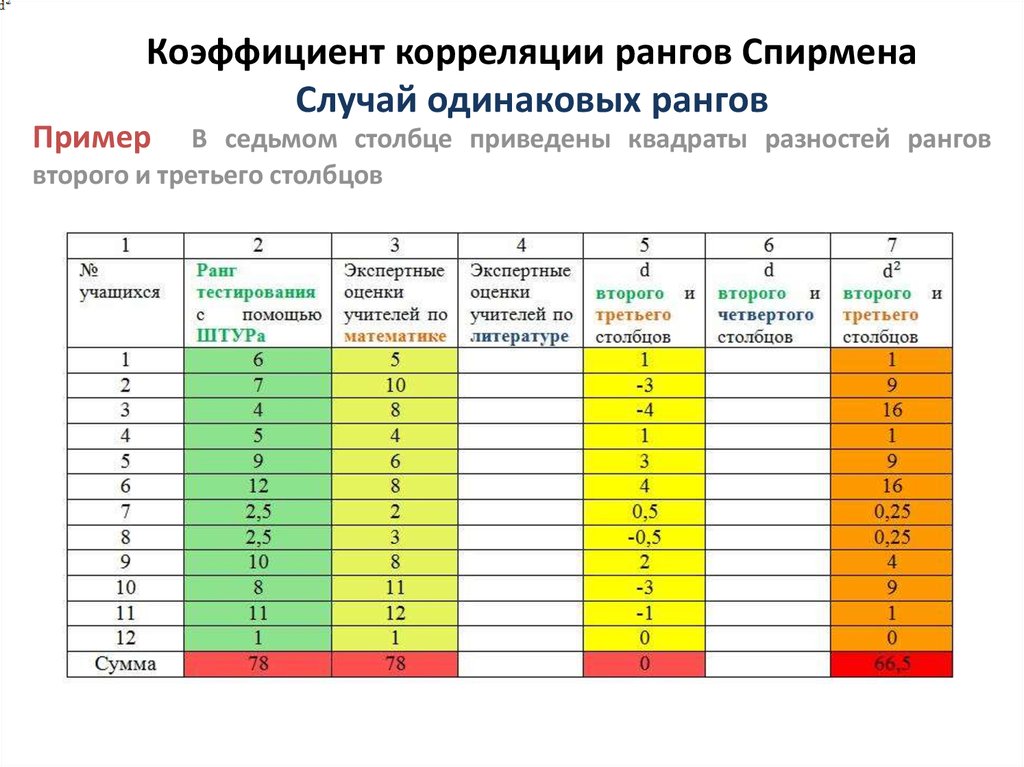
Рис. 1. Гистограмма и полигон распределения сумм рангов
Гистограмма (рис. 1) позволяет сделать следующие выводы:
1. Наибольшее значение для потребителей имеют фактор x4 (наличие систем Hoy Frost) и фактор x6 (дизайн).
2. Вторая группа по значимости включает в себя один фактор x3 (количество камер).
3. Третья группа включает в себя факторы x1 (объем камеры), x2 (бренд), x5 (энергопотребление).
Итак, важнейшими для потребителей являются следующие технические параметры холодильников: x4, x6, x3.
Этап 5. Оценка средней степени согласованности мнений всех экспертов.
Воспользуемся коэффициентом конкордации для случая, когда имеются связанные ранги (одинаковые значения рангов в оценках одного эксперта)
,
где , Li — число связок (видов повторяющихся элементов) в оценках i-го эксперта, tl — количество элементов в l-й связке для i-го эксперта (количество повторяющихся элементов).
S = 213,5 (см. табл. 6.4), n = 6, m = 4,
(в оценках 3-его эксперта одна связка, повторяется ранг «3,5» 2 раза),
, (в оценках 4-ого эксперта одна связка, повторяется ранг «4,5» 2 раза),
, (если нет связанных рангов, то Ti равно нулю)
.
W = 0.774 говорит о наличии высокой степени согласованности мнений экспертов. На высокую степень согласованности мнений экспертов указывает и полигон распределения сумм рангов (рис. 6.1). Ломанная и прямая линии близко расположены друг к другу.
Этап 6. Оценка значимости коэффициента конкордации.
Для этой цели исчислим критерий согласования Пирсона: , .
Вычисленный сравним с табличным значением для числа степеней свободы K = n-1 = 6-1 = 5 и при заданном уровне значимости α = 0,05.
Так как расчетный 15,471 > табличного = 11,07, то W = 0.744 — величина не случайная, а потому полученные результаты по оценке качественных свойств холодильников по степени их значимости для потребителей имеют смысл и могут использоваться в дальнейших исследованиях.
Этап 7. Подготовка решения экспертной комиссии.
Была поставлена задача выяснить, какие технические параметры холодильников в наибольшей степени интересуют потребителей.
В результате проведенного исследования на основе экспертных оценок выяснилось, что важнейшими качественными свойствами являются: наличие систем, дизайн и количество камер. Следовательно, качественное совершенствование холодильников должны идти по пути улучшения этих свойств (исходя из требований НТП).
Себестоимость, цены, доплата к ценам на изделия улучшенного качества и скидки с цен на холодильники должны строиться с учетом вышеперечисленных качественных свойств.
На основе получения суммы рангов (табл. 4) можно вычислить показатели весомости рассмотренных технических параметров холодильников для потребителя с тем, чтобы их можно было учитывать при оценке технического уровня холодильников. Для этого произведем следующие вычисления. Сначала по каждому параметру вычислим величины, обратные сумме рангов, то есть
; ;
; ; .
Это делается для того, чтобы привести в соответствие содержание сумм рангов коэффициентам весомости. Расположим полученные числа по мере убывания, сложим их, взвесим каждое число в полученной сумме, которую примем равной 1 (табл. 6).
Таблица 6
| Технические параметры | Величины, обратные сумме рангов | Коэффициенты весомости параметров |
| x4 x6 x3 x1 x2 x5 | 0,15
0,12 0,09 0,06 0,05 0,04 | 0,29
0,23 0,18 0,12 0,10 0,08 |
Коэффициент корреляции Спирмена — Voxco
ПОДЕЛИТЬСЯ СТАТЬЕЙ ПО
Содержание
Что такое коэффициент корреляции Спирмена?
Названный в честь Чарльза Спирмена и обозначаемый греческой буквой « ρ », коэффициент корреляции Спирмена представляет собой метод непараметрического анализа данных.
Это мера силы и направления статистической зависимости ранжирования между двумя переменными.
Это подходящая мера для использования, когда переменные измеряются по наименьшей порядковой шкале.
Преобразуйте процесс получения информации
Создайте действенный процесс сбора отзывов.
Подробнее
Допущения для коэффициента корреляции Спирмена
Корреляция Спирмена не предполагает никаких предположений о распределении данных, но основана на предположениях корреляции Пирсона.
Корреляции Пирсона — это статистическая мера силы линейной зависимости между переменными и ее предположениями, включающими:
- Уровень интервала или отношения
- Линейно связанный
- Двумерный нормально распределенный
Что касается коэффициента корреляции Спирмена, вы можете использовать его, если ваши данные не имеют вышеуказанных допущений.
Монотонная функция в коэффициенте корреляции Спирмена
Давайте сначала разберемся, что такое монотонная функция.
Монотонная функция, независимо от возрастания независимой переменной, никогда не возрастает и не убывает. График, показанный ниже, является лучшим представлением монотонной функции:
- Монотонно возрастающая – при увеличении переменной x переменная y никогда не уменьшается.
- Монотонно убывающая – при увеличении переменной x переменная y никогда не увеличивается.
- Немонотонность — по мере увеличения переменной x переменная y может увеличиваться или уменьшаться.
Загрузить набор инструментов для исследования рынка
Получить руководство по тенденциям в области исследования рынка, руководство по онлайн-опросам, руководство по гибким исследованиям рынка и шаблон 9 для исследования рынка 50003
Формула коэффициента корреляции Спирмена
Где,
n — количество точек данных двух переменных
di — разница в рангах i-го элемента ) может принимать значения от +1 до -1
Где,
- Значение ⍴ +1 означает идеальную связь ранга
- Значение ⍴ 0 означает отсутствие связи ранга
- Значение ⍴ -1 означает совершенную отрицательную связь между рангами.
Чем ближе значение ⍴ к 0, тем слабее связь между двумя рангами.
Перед вычислением коэффициента корреляции Спирмена важно ранжировать данные, просто чтобы заметить, что за увеличением одной переменной следует монотонная зависимость другой переменной.
Как рассчитать коэффициент корреляции Спирмена
Чтобы понять работу корреляции Спирмена, давайте рассмотрим пример и обсудим процесс шаг за шагом.
Пример: оценки учащихся по предметам Английский язык и Математика приведены в виде данных.
Шаг 1: Создайте таблицу для заданных данных Шаг 2: Ранжируйте два набора данных от высшего к низшему.В нашем случае высшая оценка будет оцениваться как «1» и так далее. Наименьшим оценкам будет присвоен самый низкий рейтинг. Это должно быть сделано как для оценок по английскому языку, так и по математике.
Шаг 3: Добавьте дополнительный столбец для «d», который обозначает разницу между рангами, и другой столбец, «d квадрат», который содержит квадрат «d».
Шаг 4: Добавьте значения «d-квадрата». В нашем случае ∑d = 12 Шаг 5: Подставьте значения в формулу коэффициента корреляции Спирмена. =1-(6*12)/(9(81-1))
=1-72/720
=1-01
=0,9
Ранговая корреляция Спирмена для наших данных равна 0,9
Как упоминалось выше, значение ⍴ приближается к +1, у них идеальная ассоциация рангов в данных.
Получить БЕСПЛАТНУЮ демоверсию
Узнайте, как Voxco может преобразовать ваши исследования в области опросов за 30 минут.
company
Select CountryAfghanistanAland IslandsAlbaniaAlgeriaAmerican SamoaAndorraAngolaAnguillaAntarcticaAntigua and BarbudaArgentinaArmeniaArubaAustraliaAustriaAzerbaijanBahamasBahrainBangladeshBarbadosBelarusBelauBelgiumBelizeBeninBermudaBhutanBoliviaBonaire, Saint Eustatius and SabaBosnia and HerzegovinaBotswanaBouvet IslandBrazilBritish Indian Ocean TerritoryBritish Virgin IslandsBruneiBulgariaBurkina FasoBurundiCambodiaCameroonCanadaCape VerdeCayman IslandsCentral African RepublicChadChileChinaChristmas IslandCocos (Keeling) IslandsColombiaComorosCongo (Brazzaville)Congo (Kinshasa)Cook IslandsCosta RicaCroatiaCubaCuraçaoCyprusCzech RepublicDenmarkDjiboutiDominicaDominican RepublicEcuadorEgyptEl SalvadorEquatorial GuineaEritreaEstoniaEthiopiaFalkland IslandsFaroe IslandsFijiFinlandFranceFrench ГвианаФранцузская ПолинезияФранцузские южные территорииГабонГамбияГрузияГерманияГанаГибралтарГрецияГренландияГренадаГваделупаГуамГватемалаГернсиГвинеяГвинея-БисауГайан aHaitiHeard Island and McDonald IslandsHondurasHong KongHungaryIcelandIndiaIndonesiaIranIraqIrelandIsle of ManIsraelItalyIvory CoastJamaicaJapanJerseyJordanKazakhstanKenyaKiribatiKosovoKuwaitKyrgyzstanLaosLatviaLebanonLesothoLiberiaLibyaLiechtensteinLithuaniaLuxembourgMacao S.
A.R., ChinaMacedoniaMadagascarMalawiMalaysiaMaldivesMaliMaltaMarshall IslandsMartiniqueMauritaniaMauritiusMayotteMexicoMicronesiaMoldovaMonacoMongoliaMontenegroMontserratMoroccoMozambiqueMyanmarNamibiaNauruNepalNetherlandsNew CaledoniaNew ZealandNicaraguaNigerNigeriaNiueNorfolk IslandNorth KoreaNorthern Mariana IslandsNorwayOmanPakistanPalestinian TerritoryPanamaPapua New GuineaParaguayPeruPhilippinesPitcairnPolandPortugalPuerto RicoQatarReunionRomaniaRussiaRwandaSão Tomé and PríncipeSaint BarthélemySaint HelenaSaint Kitts and NevisSaint LuciaSaint Martin (Dutch part)Saint Martin (French part)Saint Pierre and MiquelonSaint Vincent and the ГренадиныСамоаСан-МариноСаудовская АравияСенегалСербияСейшелыСьерра-ЛеонеСинг aporeSlovakiaSloveniaSolomon IslandsSomaliaSouth AfricaSouth Georgia/Sandwich IslandsSouth KoreaSouth SudanSpainSri LankaSudanSurinameSvalbard and Jan MayenSwazilandSwedenSwitzerlandSyriaTaiwanTajikistanTanzaniaThailandTimor-LesteTogoTokelauTongaTrinidad and TobagoTunisiaTurkeyTurkmenistanTurks and Caicos IslandsTuvaluUgandaUkraineUnited Arab EmiratesUnited Kingdom (UK)United States (US)United States (US) Minor Outlying IslandsUnited States (US) Virgin IslandsUruguayUzbekistanVanuatuVaticanVenezuelaVietnamWallis and FutunaWestern SaharaYemenZambiaZimbabwe
Предоставляя эту информацию, вы соглашаетесь с тем, что мы можем обрабатывать ваши персональные данные в соответствии с нашей Политикой конфиденциальности.
Исследуйте все типы вопросов опроса
, возможные на Voxco
Подробнее
Корреляция рангов Спирмена | Реальная статистика с использованием Excel
Когда данные распределены ненормально или когда наличие выбросов дает искаженную картину связи между двумя случайными величинами, ранговая корреляция Спирмена является непараметрическим критерием, который можно использовать вместо коэффициента корреляции Пирсона.
На этой веб-странице мы объясним основные понятия о корреляции Спирмена и о том, как ее рассчитать. Нажмите здесь, чтобы узнать, как выполнить проверку гипотез, чтобы определить, равна ли статистическая корреляция Спирмена нулю (т. е. определить, являются ли две выборки независимыми).
Определение 1 : Ранговая корреляция Спирмена (также называемая ро Спирмена ) представляет собой коэффициент корреляции Пирсона для рангов данных.
Пример 1 : В левой части рисунка 1 показана связь между IQ каждого подростка в выборке и количеством часов, которое они слушают рок-музыку в месяц.
Определите силу корреляции между IQ и рок-музыкой, используя как коэффициент корреляции Пирсона, так и ранговую корреляцию Спирмена. Сравните результаты. Рис. 1. Данные для примера 1 Например. ранг первой оценки IQ (ячейка A4 на рис. 1) равен =RANK.AVG(A4,A$4:A$13,1), поэтому мы помещаем эту формулу в ячейку C4. Если вы используете Excel 2007, вы должны использовать функцию реальной статистики RANK_AVG вместо RANK.AVG (как описано в ранжировании).
Теперь вычислим оба коэффициента корреляции следующим образом: видите, что на основе выборки нет большой корреляции между IQ и прослушиванием рок-музыки.
Наблюдение : При проведении анализа, если вы обнаружите наличие выбросов (например, с помощью гистограммы или диаграммы рассеивания), выполните следующие действия:
Рассчитайте коэффициент корреляции Пирсона для выборки с выбросами и без них. Если разница невелика, то можно быть уверенным, что выбросы не влияют на результаты. Вы также можете рассчитать ранговый коэффициент Спирмена.
Если это очень похоже на коэффициент корреляции Пирсона, это также хороший показатель того, что выбросы существенно не влияют на результаты.
Если есть явные различия, вам нужно быть осторожным в отношении того, как вы относитесь к выбросам.
Аналогичным образом, если вы проверите выборку данных для переменных x и y и увидите, что любая из них не является примерно нормальной (используя методы, описанные в Тестирование на нормальность и симметрию), вам потребуется использовать коэффициент Спирмена. а не Пирсона.
На рис. 2 показана диаграмма рассеяния для данных из примера 1. Мы видим, что данные довольно случайным образом разбросаны, хотя есть потенциальный выброс, когда число слушателей рэп-музыки достигает 45. Это дает некоторое свидетельство того, что ро Спирмена может быть лучше. выбор.
Рисунок 2 – Диаграмма рассеяния для данных из Примера 1 ,R1,1),RANK.AVG(R2,R2,1))
Для версий Excel до Excel 2010 следующая формула будет работать.