Y sin 1 x график функции: График y = f(x) = sin(1/x) (синус от (1 делить на х)) постройте график функции и изобразите его. Исследуйте данную функцию. [Есть ОТВЕТ!]

Содержание

Функция y = sin x, её график и свойства. Тригонометрия 8-11 класс смотреть онлайн видео от Математика от Баканчиковой в хорошем качестве.

12+

1 месяц назад

Математика от Баканчиковой135 подписчиков

Тригонометрия 8-11 класс. Какие свойства есть у функции y=sin x? Сегодня мы ответим на этот вопрос. Если Вы не видели наши предыдущие уроки по теме: «Функция y = sin x, график функции и способы задания функции» и серию уроков по теме «Свойства функции», то обязательно посмотрите их, тогда этот урок будет Вам очень понятен. По графику функции y=sin x мы подробно разберём почти все свойства этой функции: область определения, область значений, непрерывность, монотонность, наибольшее и наименьшее значения, ограниченность, выпуклость, нули функции, чётность, нечётность, периодичность, промежутки знакопостоянства. Подробный план урока и ссылки на предыдущие уроки Вы можете найти в описании под видео. 00:00 Начало видео. 00:20 Немного повторения. 01:29 Свойства функции y = sin x. 01:33 Область определения. 01:55 Область значений. 02:18 Непрерывность. 02:28 Монотонность. 04:30 Наибольшее и наименьшее значения. 04:49 Ограниченность. 05:18 Выпуклость. 06:11 Нули функции. 07:15 Чётность, нечётность. 07:36 Периодичность. 08:03 Промежутки знакопостоянства. 10:07 На следующем уроке … Если Вы впервые на нашем канале или не смотрели наши предыдущие уроки, то рекомендуем Вам посмотреть следующие видео: Числовые промежутки в неравенствах. Алгебра 9 класс. https://rutube.ru/video/0f2714959bde145fe9507ab7c0190ae8/ Способы задания функции. Примеры. https://rutube.ru/video/be19beb2a973ffbad226194f7e36e0f8/ Функция y = sin x, график функции и способы задания функции. Тригонометрия 8-11 класс. https://rutube.ru/video/f067b3cda83df006306963e40f30b5ab/ Чётность и нечётность тригонометрических функций. Тригонометрия 8-11 класса. https://rutube.ru/video/862e199545ac877d9adb674ac6115cbc/ Чётность функции. Определение чётной функции. Является ли чётной функция.

Свойства функции. Алгебра 7-11 класс. https://rutube.ru/video/00526d89c84dd14af604458fc65bca66/ Нечётность функции. Определение нечётной функции. Является ли нечётной функция. Свойства функции. Алгебра 7-11 класс. https://rutube.ru/video/77cdba840f3e6bc8a19371c6d65da264/ Определение синуса, косинуса, тангенса и котангенса на единичной окружности. Шпаргалка по тригонометрии. Алгебра 10 класс. https://rutube.ru/video/4a839b2f5c0a7656b8b41b6e5e67ddc4/ Все уроки по теме «Функция и её свойства» можно найти в плейлисте: https://rutube.ru/plst/57182 #свойствафункцииsin #свойствафункциисинус #областьопределения #областьзначений #непрерывность #монотонность #наибольшееинаименьшеезначения #ограниченность #выпуклость #нулифункции #чётность #нечётность #периодичность #промежуткизнакопостоянства #алгебратригонометрическиефункции #тригонометрическиефункцииалгебра10 #МатематикаОтБаканчиковой тригонометрия, алгебра тригонометрические функции, тригонометрические функции алгебра 10, свойства функции sin, свойства функции синус, область определения, область значений, непрерывность, монотонность, наибольшее и наименьшее значения, ограниченность, выпуклость, нули функции, чётность, нечётность, периодичность, промежутки знакопостоянства

Функция y=sinx.

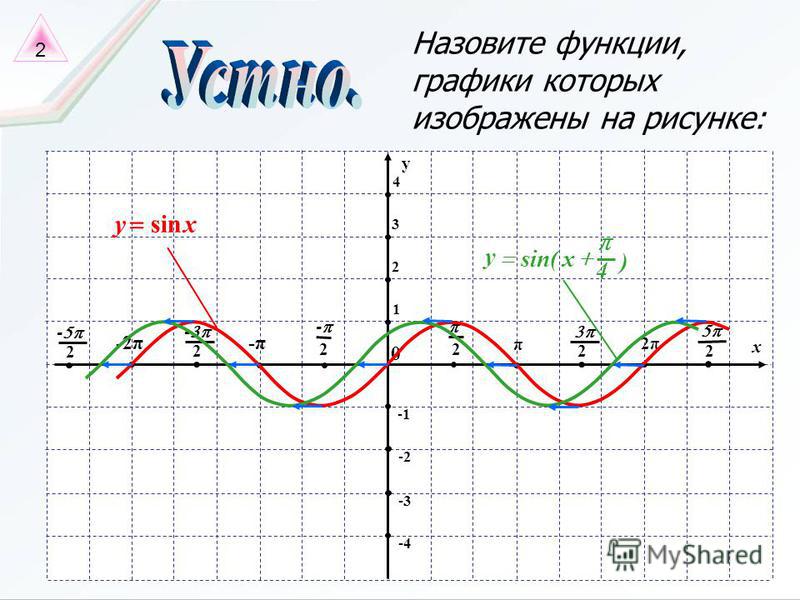Свойства. Преобразование графиков

Похожие презентации:

Функция y=sinx. Свойства. Преобразование графиков

Функция y=sinx, ее свойства и график

Тригонометрические функции y = sin x и y = cos x их свойства и графики

Функция y=sinx и её график

Тригонометрические функции y = sin x и y = cos x . Их свойства и графики

Преобразование графиков тригонометрических функций и их свойства

Свойства и график функции y=sinх

Тригонометрические функции, их свойства и графики

Функция y=sinx и ее свойства

Функции y = tgx и y = ctgx, их свойства и графики

Функция y=sinx
Свойства.
Преобразование
графиков.

2. Вспомним определение синуса и косинуса угла поворота:

2
sin
1
0
0
sin — ордината точки поворота
y
cos
x
1
cos — абсцисса точки поворота
(под «точкой поворота» следует понимать – «точку единичной
тригонометрической окружности, полученной при повороте на радиан от
начала отсчета»)
На оси абсцисс координатной плоскости Оху будем отмечать
точки, соответствующие различным углам поворота, а на
оси ординат – значения синусов этих углов.

6
5
4
2
y
y
3
1
2
1
1
0
0
1 x
x
0
1 2 3 4 5
2
6
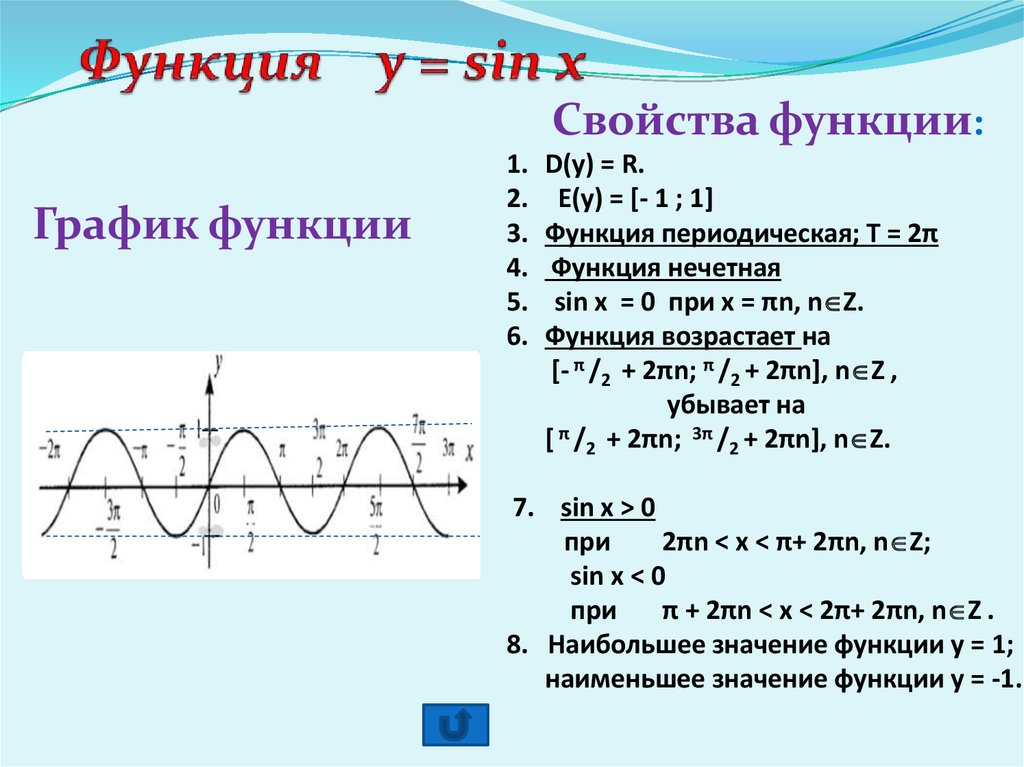
Получили график функции y=sinx на промежутке [0; ].

4. Построение графика функции y = sin x

y
2
1
0
0
-1
8
4
3 5 3 7
8 2 8 4 8
x
Теперь воспользуемся тем, что функция y=sinx является
нечетной, а, значит, график функции на промежутке [− ; 0]
можно получить из данного симметрией относительно
начала координат (или поворотом на 1800).
y
1
−
2
x
0
2
−1
Таким образом, мы получили график функции y=sinx на
промежутке [− ; ].
На практике, для построения графика функции у=sinx на промежутке [0; ], сначала
отмечают точки с координатами (0; 0), ( /6; 0,5), ( /2; 1), ( 5 /6; 0,5) и ( ; 0). Они
образуют своеобразную «арку», которая периодически (с периодом ) отображается
симметрично оси Ох.
y
1
5
6
2
3
2
2
3
2
1
2
6
0
1
6
2
2
5
6
2
−1
После этого используют свойство периодичности функции у=sinx.

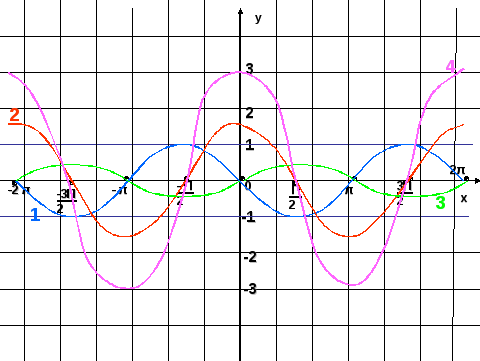Так как
наименьший положительный период функции y=sinx равен 2 , то
изображенный участок графика можно параллельно переносить влево и вправо
вдоль оси Ох на 2 n (n ) единичных отрезков.
График функции y=sinx называется синусоидой.
x

8. Заход Солнца

Дата
Время
Дата
Время
1.1
15.59
1.7
20.25
1.2
16.45
1.8
19.53
1.3
17.37
1.9
18.53
1.4
18.39
1.10
17.31
1.5
19.28
1.11
16.30
1.6
20.18
1.12
15.51

9. С помощью отрывного календаря нетрудно отметить момент захода Солнца на 1-е число каждого месяца и, соединив полученные точки

плавной линией, построить график,
взяв в качестве оси абсцисс среднее
время захода Солнца – 18ч

10. График захода Солнца

время
дата

11. Решение упражнений

y
y = sin x
2
2
т
3
2
1

-1
2
x
3
2
2
y
ED((yy))::yx R1; 1
x
1
2 3
2
2
-1
2
3
2
2
3
=2n ;n;n, n
xy = 0 x 2
2 nZ
22
22
yy 00
x 0;
y
x
1
2 3
2
2
-1
2
3
2
2
x
2 nx;2 n ;2 ;n0
x
y
y = sin x 2
x
1
2 3
2
2
-1
2
E ( y ) : y [1; 3]
3
2
2
y = sin x-1
y
x
1
2 3
2
2
-1
2
3
2
E ( y ) : y [ 2;0]
2
y
2
y = sin( x ) +1
3
x
1
2 3
2
2
-1
2
3
2
E ( y ) : y [0;2]
2
y = sin(x )
y
2
2
т
3
2
1
-1
2
x
3
2
2
y = sin(x 2 )
2
2
у
3
2
y
1
-1
2
x
3
2
2
y
y = sin(x )
3
2
2
т
3
2
1
-1
2
x
3
2
2
2 3
2
y
x
1
2
-1
2
x=0
sinx = x
3
2
2
y
Ø
2
2
3
2
1
-1
2
sin( x ) = ( x ) 1
6
3
т
2
x
3
2
2
y
Ø
2 3
2
x
1
2
-1
sinx >
2
3
2
x +1
2
y
y = sin x
y = x 1
x [0; )
x
1
2 3
2
2
-1
sinx <
у
2
3
2
x +1
2
2
1
sin(x
)<–
3
2
5
6
2
2
т
3
2
y
1
7
6
-1
2
x
3
2
2
y
I
I
3
2
2
I
I
-1
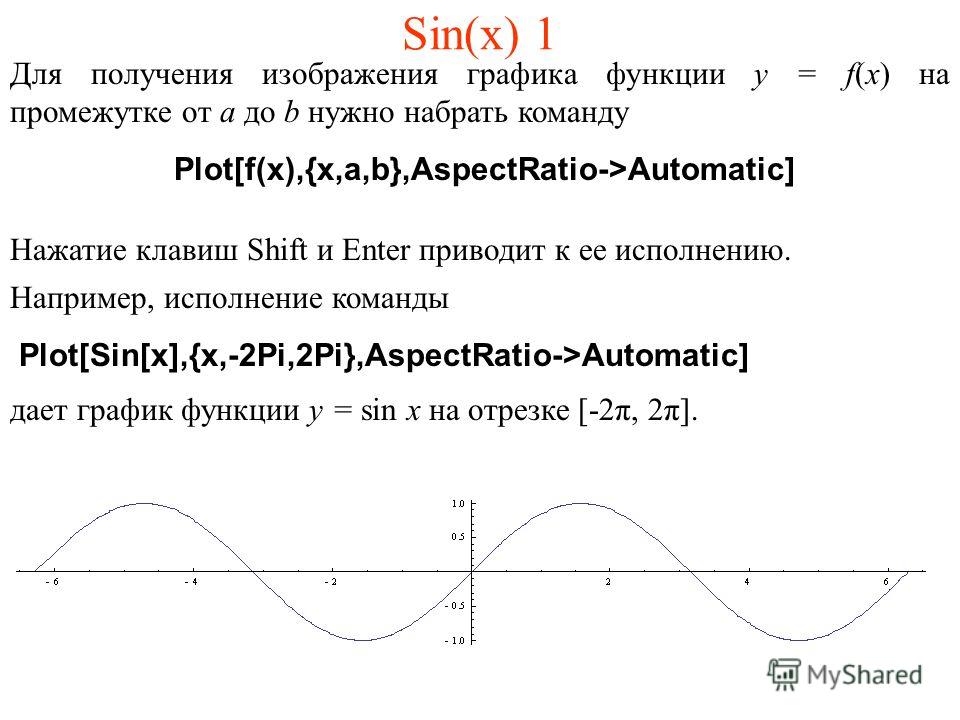
Найти область значений функции
Единичный отрезок – 1 клетка.

O
1
2
3
2
I
7
2
2
I
5
2
3
y = sin(x ) + 2
2
E( y ) : y [1;3]
3
I
x
Умение строить графики нам нужны при …
решении уравнений;

решении неравенств;
решении заданий, связанных с исследованием
свойств функций.
Рассмотрим графики функций, аналитическая запись
которых содержит знак абсолютной величины.
y = sin x
2 3
2
y
x
1
2
-1
2
3
2
2
y
y = sin x
2 3
2
x
1
2
-1
2
3
2
2

English Русский Правила

Мэтуэй | Популярные задачи

92) 9(3x) по отношению к x 92+1

1	Найти производную — d/dx	бревно натуральное х
2	Оценить интеграл	интеграл натурального логарифма x относительно x
3	Найти производную — d/dx
21	Оценить интеграл	интеграл от 0 до 1 кубического корня из 1+7x относительно x
22	Найти производную — d/dx	грех(2x)
23	Найти производную — d/dx
41	Оценить интеграл	интеграл от cos(2x) относительно x
42	Найти производную — d/dx	1/(корень квадратный из х)
43	Оценка интеграла 9бесконечность
45	Найти производную — d/dx	х/2
46	Найти производную — d/dx	-cos(x)
47	Найти производную — d/dx	грех(3x)
68	Оценить интеграл	интеграл от sin(x) по x
69	Найти производную — d/dx	угловой синус(х)
70	Оценить предел	ограничение, когда x приближается к 0 из (sin(x))/x 92 по отношению к х
85	Найти производную — d/dx	лог х
86	Найти производную — d/dx	арктан(х)
87	Найти производную — d/dx	бревно натуральное 5х92

График обратного синуса

Главная Алгебра II Тригонометрические функции Темы Обратные функции График функции обратного синуса

Темы

Введение

Темы
Right Angle Trigonometry
Pythagorean Theorem
Trigonometric Ratios
Reciprocal Trigonometric Functions
Co-functions
Special Triangles
The Unit Circle
Quadrants
Special Angles Larger Than 90º
Symmetry of Trigonometric Functions
Периодичность триггерных функций
Периодические функции
График синуса
График косинуса
Обратные функции
График функции арксинуса
График функции арккосинуса
Решение обратных тригонометрических уравнений
Тригонометрические тождества
Тождества суммы и разности

Примеры
Упражнения
Задачи Math Shack
Условия
Лучшее из Интернета
викторины
Раздаточный материал
Содержание

Обратные триггерные функции почти так же причудливы, как и их функциональные аналоги.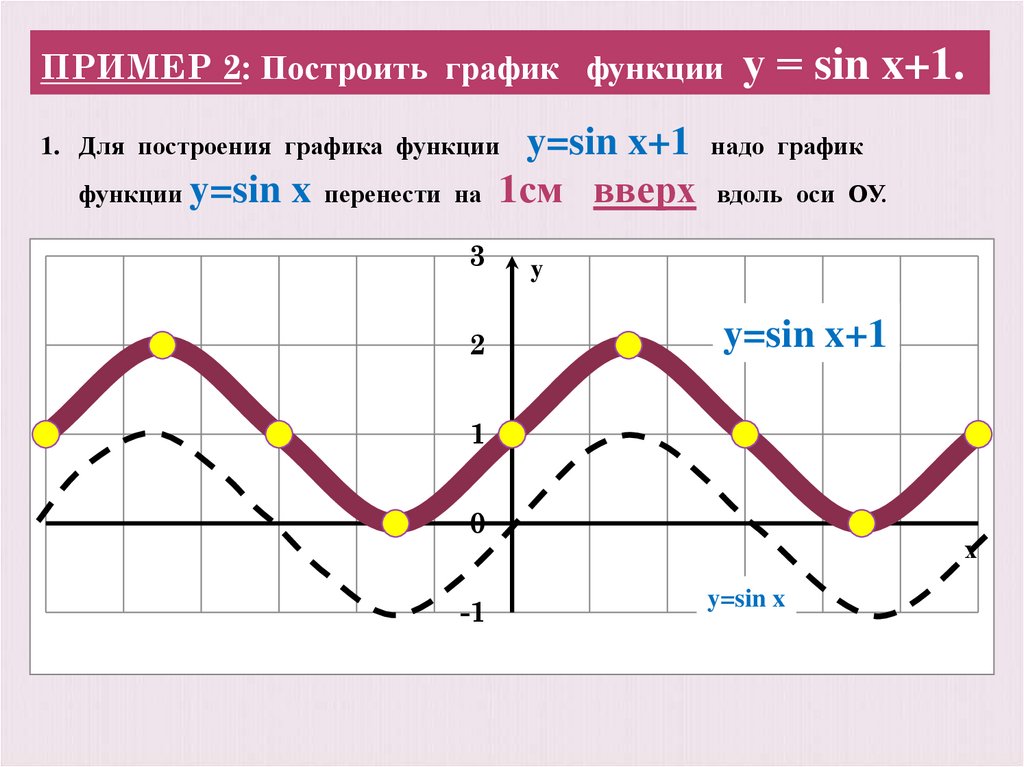 Они имеют тенденцию подниматься вверх по оси y . Они причудливы, потому что их нужно разрезать на кусочки, чтобы считать их функциями. Помните, что функции должны выдавать только одно значение х для каждого значения х . В противном случае они не пройдут тест вертикальной линии. облом.

Чтобы построить график обратной синусоидальной функции, нам сначала нужно ограничить или, проще говоря, выбрать часть нашего синусоидального графика для работы. Вот график y = sin x .

Далее мы ограничиваем область до [-90°, 90°]. В радианах это [- ^π ⁄ ₂ , ^π ⁄ ₂ ].

Чтобы найти график обратного синуса, нам нужно поменять местами переменные: x становится y , а y становится х . Вот график функции обратного синуса: y = sin ^-1 x (или y = arcsin x ):

Обратный синус1, 1 имеет область [-] и диапазон [- ^π ⁄ ₂ , ^π ⁄ ₂ ].