Кос х син х: Решите уравнение cos(x)=sin(x) (косинус от (х) равно синус от (х))

alexxlab / / Разное

«Помогите решить уравнение cos(cos(cos(cos x)))= sin(sin(sin(sin x)))?» — Яндекс Кью

Математика и математики

105060 участников сообщества

Анонимный вопрос  ·   ·

14,2 K

Andrei Novikov

Математика

кандидат физико-математических наук, математик, ис…  · 14 сент 2021

можно вообще доказать, что если косинусов и синусов больше, чем четыре (раз уж они на 4 повторениях уже не пересекаются), то решения не существует.)

Вообще отображения-то сжимают области значений вокруг точек, которые являются решениями x=sin(x) и cos(x)=x.

То есть вокруг точек 0 и примерно 0.74.)

2 оценили

  ·

185

Комментировать ответ…Комментировать…

Andrei Novikov

Математика

кандидат физико-математических наук, математик, ис.

..  · 14 сент 2021

весьма вероятно, вещественных корней здесь нет: 1) sin(x) и cos(x) имеют нзачения от [-1,1] 2) sin(sin(x)) имеют значения от [-sin(1),sin(1)] и cos(cos(x)) имеют нзачения от [cos(1),1] 3) sin(sin(sin(x))) имеют значения [-sin(si… Читать далее

2 оценили

  ·

4,9 K

Сергей Леонтьев

возражает

14 сент 2021

> там оценка, что-то вроде левая часть больше 0.65, правая — меньше 0.62/ Увы, ошибочка: [-0.67, 0.67] против… Читать дальше

Комментировать ответ…Комментировать…

Борис Державец

Data science

Openstack DevOps and IBM/Informix Certified DBA…  · 14 сент 2021

====================================================== UPDATE as of 22:45 MSK 15/09/2021 Python (NumPy && Matplotlib) решение одной относительно сложной математической задачи.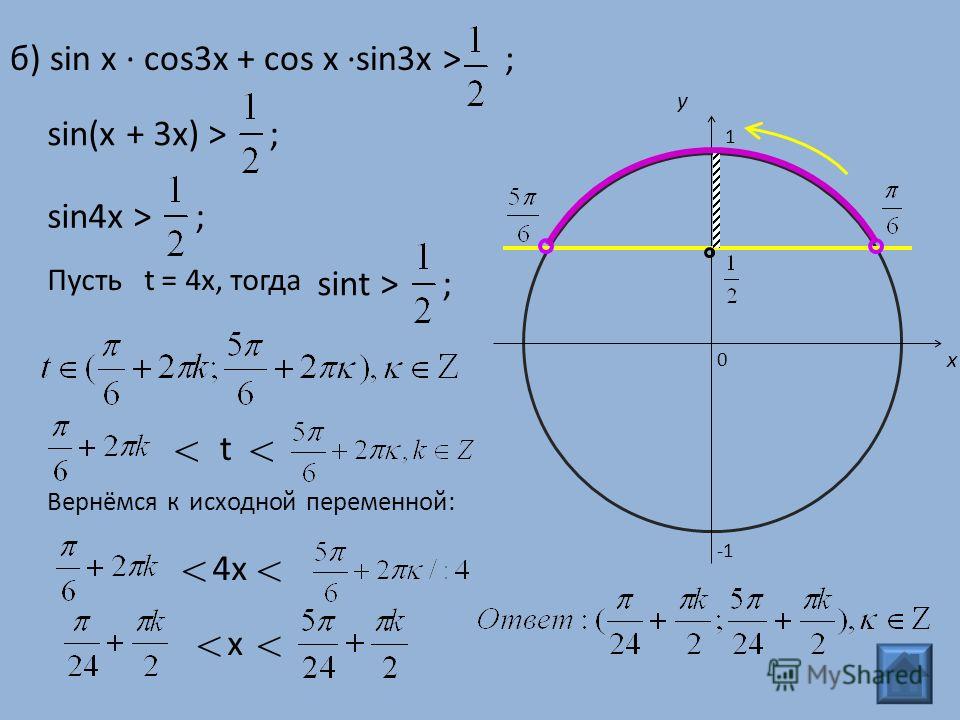

Сама задача состоит в том, чтобы найти все решения… Читать далее

2 оценили

  ·

267

Борис Державец

14 сент 2021

Solving one problem from YandexQ as of 14/09/2021 https://informatics-ege.blogspot.com/2021/09/solving-one-problem-… Читать дальше

Комментировать ответ…Комментировать…

Андрей Белов

библейская эволюция  · 14 сент 2021

Рассуждений много, но никто не предлагает решения. На кнопки и я могу нажимать. MaXima. Графики не дают пересечений, значит корней нет. Кто-нибудь может построить эти графики без программных методов? Без компьютера уже не обой… Читать далее

1 оценил

  ·

2,3 K

Andrei Novikov

15 сент 2021

Я дам решение в течение одной недели. Просто времени нет.

Комментировать ответ…Комментировать…

Вы знаете ответ на этот вопрос?

Поделитесь своим опытом и знаниями

Войти и ответить на вопрос

Курс высшей математики, Т.1

Курс высшей математики, Т.1
  

В.И.Смирнов Курс высшей математики, Т.1.: Изд-во «Наука». 1974. — 479 с.

Фундаментальный учебник по высшей математике, выдержавший более двадцати изданий, переведенный на множество языков мира, отличается, с одной стороны, систематичностью и строгостью изложения, а с другой – простым языком, подробными пояснениями и многочисленными примерами. Книга состоит из пяти томов. Тома третий и четвертый – каждый из двух частей.

Для студентов университетов и технических вузов.



Оглавление

ПРЕДИСЛОВИЕ К ВОСЬМОМУ ИЗДАНИЮ
ГЛАВА I. ФУНКЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ И ТЕОРИЯ ПРЕДЕЛОВ
1. Величина и ее измерение.
2. Число.
3. Величины постоянные и переменные.
4. Промежуток.
5. Понятие о функции.
6. Аналитический способ задания функциональной зависимости.
7. Неявные функции.
8. Табличный способ.
9. Графический способ изображения чисел.
10. Координаты.
11. График и уравнение кривой.
12. Линейная функция.
13. Приращение. Основное свойство линейной функции.
14. График равномерного движения.
15. Эмпирические формулы.
16. Парабола второй степени.
17. Парабола третьей степени.
18. Закон обратной пропорциональности.
19. Степенная функция.
20. Обратные функции.
21. Многозначность функции.
22. Показательная и логарифмическая функции.
23. Тригонометрические функции.
24. Обратные тригонометрические, или круговые, функции.
§ 2. ТЕОРИЯ ПРЕДЕЛОВ. НЕПРЕРЫВНЫЕ ФУНКЦИИ
25. Упорядоченное переменное.
26. Величины бесконечно малые.
27. Предел переменной величины.
28. Основные теоремы.
29. Величины бесконечно большие.
30. Монотонные переменные.
31. Признак Коши существования предела.
32. Одновременное изменение двух переменных величин, связанных функциональной зависимостью.
33. Примеры.
34. Непрерывность функции.
35. Свойства непрерывных функций.
36. Сравнение бесконечно малых и бесконечно больших величин.
37. Примеры.
38. Число е.
39. Недоказанные предложения.
40. Вещественные числа.
41. Действия над вещественными числами.
42. Точные границы числовых множеств. Признаки существования предела.
43. Свойства непрерывных функций.
44. Непрерывность элементарных функций.
ГЛАВА II. ПОНЯТИЕ О ПРОИЗВОДНОЙ И ЕГО ПРИЛОЖЕНИЯ
45. Понятие о производной.
46. Геометрическое значение производной.
47. Производные простейших функций.
48. Производные сложных и обратных функций.
49. Таблица производных и примеры.
50. Понятие о дифференциале.
51. Некоторые дифференциальные уравнения.
52. Оценка погрешностей.
§ 4. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ
53. Производные высших порядков.
54. Механическое значение второй производной.
55. Дифференциалы высших порядков.
56. Разности функций.
§ 5. ПРИЛОЖЕНИЕ ПОНЯТИЯ О ПРОИЗВОДНОЙ К ИЗУЧЕНИЮ ФУНКЦИЙ
57. Признаки возрастания и убывания функций.
58. Максимумы и минимумы функций.
59. Построение графиков.
60. Наибольшее и наименьшее значения функций.
61. Теорема Ферма.
62. Теорема Ролля.
63. Формула Лагранжа.
64. Формула Коши.
65. Раскрытие неопределенностей.
66. Различные виды неопределенностей.
§ 6. ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ
68. Частные производные и полный дифференциал функции двух независимых переменных.
69. Производные сложных и неявных функций.
§ 7. НЕКОТОРЫЕ ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ ПОНЯТИЯ О ПРОИЗВОДНЫХ
70. Дифференциал дуги.
71. Выпуклость, вогнутость и кривизна.
72. Асимптоты.
73. Построение графиков.
74. Параметрическое задание кривой.
75. Уравнение Ван-дер-Ваальса.
76. Особые точки кривых.
77. Элементы кривой.
78. Цепная линия.
79. Циклоида.
80. Эпициклоиды и гипоциклоиды.
81. Развертка круга.
82. Кривые в полярных координатах.
83. Спирали.
85. Овалы Кассини и лемниската.
ГЛАВА III. ПОНЯТИЕ ОБ ИНТЕГРАЛЕ И ЕГО ПРИЛОЖЕНИЯ
86. Понятие о неопределенном интеграле.
87. Определенный интеграл как предел суммы.
88. Связь определенного и неопределенного интегралов.
89. Свойства неопределенного интеграла.
90. Таблица простейших интегралов.
91. Правило интегрирования по частям.
92. Правило замены переменных. Примеры.
93. Примеры дифференциальных уравнений первого порядка.
§ 9. СВОЙСТВА ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
94. Основные свойства определенного интеграла.
95. Теорема о среднем.
96. Существование первообразной функции.

97. Разрыв подынтегральной функции.
98. Бесконечные пределы.
99. Замена переменной под знаком определенного интеграла.
100. Интегрирование по частям.
§ 10. ПРИЛОЖЕНИЯ ПОНЯТИЯ ОБ ОПРЕДЕЛЕННОМ ИНТЕГРАЛЕ
101. Вычисление площадей.
102. Площадь сектора.
103. Длина дуги.
104. Вычисление объемов тел по их поперечным сечениям.
105. Объем тела вращения.
106. Поверхность тела вращения.
107. Определение центров тяжести. Теоремы Гульдина.
108. Приближенное вычисление определенных интегралов; формулы прямоугольников и трапеций.
109. Формула касательных и формула Понселе.
110. Формула Симпсона.
111. Вычисление определенного интеграла с переменным верхним пределом.
112. Графические способы.
113. Площади быстро колеблющихся кривых.
§ 11. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ОБ ОПРЕДЕЛЕННОМ ИНТЕГРАЛЕ
115. Разбиение промежутка на части и образование различных сумм.
116. Интегрируемые функции.
117. Свойства интегрируемых функций.
ГЛАВА IV. РЯДЫ И ИХ ПРИЛОЖЕНИЯ К ПРИБЛИЖЕННЫМ ВЫЧИСЛЕНИЯМ
118. Понятие о бесконечном ряде.
119. Основные свойства бесконечных рядов.
120. Ряды с положительными членами. Признаки сходимости.
121. Признаки Коши и Даламбера.
122. Интегральный признак сходимости Коши.
123. Знакопеременные ряды.
124. Абсолютно сходящиеся ряды.
125. Общий признак сходимости.
§ 13. ФОРМУЛА ТЕЙЛОРА И ЕЕ ПРИЛОЖЕНИЯ
126. Формула Тейлора.
127. Различные виды формулы Тейлора.
128. Ряды Тейлора и Маклорена.
129. Разложение exp(x).
130. Разложение sin x и cos x.
131. Бином Ньютона.
132. Разложение log(1+x).
133. Разложение arctg x.
134. Приближенные формулы.
135. Максимумы, минимумы и точки перегиба.
136. Раскрытие неопределенностей.
§ 14. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ РЯДОВ
137. Свойства абсолютно сходящихся рядов.
138. Умножение абсолютно сходящихся рядов.
139. Признак Куммера.
140. Признак Гаусса.
141. Гипергеометрический ряд.
142. Двойные ряды.
143. Ряды с переменными членами. Равномерно сходящиеся ряды.
144. Равномерно сходящиеся последовательности функций.
145. Свойства равномерно сходящихся последовательностей.
146. Свойства равномерно сходящихся рядов.
147. Признаки равномерной сходимости.
148. Степенные ряды. Радиус сходимости.
149. Вторая теорема Абеля.
150. Дифференцирование и интегрирование степенного ряда.
ГЛАВА V. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
§ 15. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ФУНКЦИИ
152. О предельном переходе.
153. Частные производные и полный дифференциал первого порядка.
154. Однородные функции.
155. Частные производные высших порядков.
156. Дифференциалы высших порядков.
157. Неявные функции.
158. Пример.
159. Существование неявных функций.
160. Кривые в пространстве и поверхности.
§ 16. ФОРМУЛА ТЕЙЛОРА. МАКСИМУМЫ И МИНИМУМЫ ФУНКЦИИ ОТ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
161. Распространение формулы Тейлора на случай функции от нескольких независимых переменных.
162. Необходимые условия максимума и минимума функции.
163. Исследование максимума и минимума функции двух независимых переменных.
164. Примеры.
165. Дополнительные замечания о нахождении максимумов и минимумов функции.
166. Наибольшее и наименьшее значения функции.
167. Относительные максимумы и минимумы.
168. Дополнительные замечания.
169. Примеры.
ГЛАВА VI. КОМПЛЕКСНЫЕ ЧИСЛА, НАЧАЛА ВЫСШЕЙ АЛГЕБРЫ И ИНТЕГРИРОВАНИЕ ФУНКЦИЙ
170. Комплексные числа.
171. Сложение и вычитание комплексных чисел.
172. Умножение комплексных чисел.
173. Деление комплексных чисел.
174. Возвышение в степень.
175. Извлечение корня.
176. Показательная функция.
177. Тригонометрические и гиперболические функции.
178. Цепная линия.
179. Логарифмирование.
180. Синусоидальные величины и векторные диаграммы.
181. Примеры.
182. Кривые в комплексной форме.
183. Представление гармонического колебания в комплексной форме.
§ 18. ОСНОВНЫЕ СВОЙСТВА ЦЕЛЫХ МНОГОЧЛЕНОВ И ВЫЧИСЛЕНИЕ ИХ КОРНЕЙ
185. Разложение многочлена на множители.
186. Кратные корни.
187. Правило Горнера.
188. Общий наибольший делитель.
189. Вещественные многочлены.
190. Зависимость между корнями уравнения и его коэффициентами.
191. Уравнение третьей степени.
192. Решение кубического уравнения в тригонометрической форме.
193. Способ итерации.
194. Способ Ньютона.
195. Способ простого интерполирования.
§ 19. ИНТЕГРИРОВАНИЕ ФУНКЦИИ
196. Разложение рациональной дроби на простейшие.
197. Интегрирование рациональной дроби.
198. Интеграл от выражений, содержащих радикалы.
199. Интегралы вида…
200. Интегралы вида…
201. Интегралы вида…
3 6 Решить для ? cos(x)=1/2 7 Найти x sin(x)=-1/2 8 Преобразование градусов в радианы 225 9 Решить для ? cos(x)=(квадратный корень из 2)/2 10 Найти x cos(x)=(квадратный корень из 3)/2 11 Найти x sin(x)=(квадратный корень из 3)/2 92=9 14 Преобразование градусов в радианы 120 градусов 15 Преобразование градусов в радианы 180 16 Найти точное значение желтовато-коричневый(195) 92-4 38 Найти точное значение грех(255) 39 Оценить лог база 27 из 36 40 Преобразовать из радианов в градусы 2 шт. 92-3sin(x)+1=0 43 Найти x tan(x)+ квадратный корень из 3=0 44 Найти x sin(2x)+cos(x)=0 45 Упростить (1-cos(x))(1+cos(x)) 92=25 59 График f(x)=- натуральный логарифм x-1+3 60 Найдите значение с помощью единичного круга угловой синус(-1/2) 61 Найти домен квадратный корень из 36-4x^2 92=0 66 Найти x cos(2x)=(квадратный корень из 2)/2 67 График у=3 68 График f(x)=- логарифмическая база 3 x-1+3 92 71 Найти x квадратный корень из x+4+ квадратный корень из x-1=5 72 Решить для ? cos(2x)=-1/2 73 Найти x логарифмическая база x из 16=4 9х 75 Упростить (cos(x))/(1-sin(x))+(1-sin(x))/(cos(x)) 76 Упростить сек(х)sin(х) 77 Упростить кубический корень из 24 кубический корень из 18 92=0 96 Найти x 3x+2=(5x-11)/(8г) 97 Решить для ? sin(2x)=-1/2 98 Найти x (2x-1)/(x+2)=4/5 92+n-72)=1/(n+9)

Упрощенная методика моделирования устойчивости к электромагнитным помехам на жгутах кабелей с экранирующей оплеткой

Abstract   В этой статье предлагается эффективная методика упрощения многожильных проводников для моделирования электромагнитной невосприимчивости пучков кабелей в экранирующей оплетке в широком диапазоне частот. Сгруппировав дирижеров на основе знания Z -Смит, требуемое время расчета заметно сокращается, а сложность моделирования полностью экранирующих пучков кабелей значительно упрощается при хорошей точности. После краткого описания проблем помехоустойчивости в экранирующей конструкции подробно описана шестиэтапная процедура для получения геометрических характеристик уменьшенных кабельных жгутов. Численное моделирование проводится с использованием коммерческого программного обеспечения CST для проверки эффективности и преимуществ предлагаемого подхода. Исследование, рассматриваемое в этой статье, рассматривается как упрощенный метод моделирования электромагнитной невосприимчивости в экранирующей конструкции.
Ключевые слова: жгуты кабелей электромагнитная невосприимчивость плетеная защитная конструкция Численное моделирование
Получено: 17 февраля 2017 г.
Пересмотрено: 31 марта 2017 г.
Принятая рукопись онлайн:
ПАК: 41.20.-к (Прикладной классический электромагнетизм)
  41.20.Jб (распространение электромагнитных волн; распространение радиоволн)
  41.90.+э (Другие темы по электромагнетизму; электронная и ионная оптика)
Фонд: Проект поддержан Национальным фондом естественных наук Китая (грант № 51675086) и Национальным фондом предварительных исследований в области обороны Китая (грант № 6140758010116DZ02002).
Авторы, переписывающиеся:  Пинг-Ан Ду
Электронная почта: dupingan@uestc. edu.cn
Процитируйте эту статью: 

Пей Сяо (肖培), Пинг-Ань Ду (杜平安), Бао-Лин Ни (聂宝林), Дэн Рен (任丹) Упрощенная методика моделирования электромагнитной невосприимчивости на кабельных жгутах с экранирующей оплеткой 2017 г. Чин. физ. Б 26 094102

[1] Эго-Лемер С., Клинглер М., Лафон Ф., Коне Л. и Барановский С. 2012 IEEE Trans. Электромаг. Совместимость 54 1222
[2] Ren D, Du PA, Nie B N, Cao Z и Liu W K 2014 Acta Phys. Грех. 63 120701 (на китайском языке)
[3] Jiao C Q и Li Y Y 2015 Chin. физ. Б 24 104101
[4] Luo JW, Du PA, Ren D и Nie BL 2015 Acta Phys. Грех. 64 010701 (на китайском языке)
[5] Цао З., Ду П.А., Ни Б.Л., Рен Д. и Чжан К.Д. 2014 Acta Phys. Грех. 63 124102 (на китайском языке)
[6] Арианос С., Франкавилла М.А., Ригеро М. и Випиана 2014 IEEE Trans. Электромаг. Совместимость 56 844
[7] Ридель М. и Пармантье Дж. П. Международный симпозиум по электромагнитной совместимости 2014 г., 12-16 мая 2014 г., Токио, Япония, с. 21
[8] Xie H Y, Li Y, Qiao H L и Wang J G 2015 Chin. физ. Б 24 060501
[9] Джобава Р.Г., Геонджян А.Л., Хиппели Дж. и Чиковани Г. 2014 IEEE Trans. Электромаг. Совместимость 56 1420
[10] Baum CE, Liu TK и Tesche FM, 1978 Interaction Note 350 467547
[11] Wu Z J, Wang L F и Liao C L 2009 Acta Phys. Грех. 58 6146 (на китайском языке)
[12] Ван Дж. Р., Лю Ю. П. и Чжоу Х. Л., 2010 Acta Phys. Грех. 592948 (на китайском языке)
[13] Sun Y X, Zhuo Q K, Jiang Q H и Li Q 2015 Acta Phys. Грех. 64 44102 (на китайском языке)
[14] Ferrieres X, Parmantier JP, Bertuol S и Ruddle AR 2004 IEEE Trans. Электромаг. Совместимость 46 624
[15] Баутиста М.А.Э., Франкавилла М.А., Випиана Ф. и Векки Г. 2014 IEEE Trans. Антенны Распространение. 62 1523
[16] Li G, Hess G, Hoeckele R and Davidson 2015 IEEE Trans. Электромаг. Совместимость 57 827
[17] Андриё Г., Коне Л., Боке Ф. и Демулен Б. 2008 IEEE Trans. Электромаг. Совместимость 50 175
[18] Andrieu G, Reineix A, Bunlon X и Parmantier JP 2009 IEEE Trans. Электромаг. Совместимость 51 108
[19] Li Z, Shao Z J, Ding J и Niu Z Y 2011 IEEE Trans. Электромаг. Совместимость 53 1040
[20] Li Z, Liu L L, Yan J и Xu A W 2013 IEEE Trans. Электромаг. Совместимость 55 975
[21] Белхельфа С., Лефуили М. и Дрисси К.Е.К. 2015 IEEE Trans. Магн. 51 1
[22] Ридель М. и Пармантье Дж. П. Материалы семинара ЕКА по аэрокосмической электромагнитной совместимости, 2012 г., 21–23 мая 2012 г., Венеция, Италия, с. 1
[23] Чжэн И. Л., 2011 г. Анализ эквивалентной модели автомобильного жгута проводов и ее применение в моделировании электромагнитной совместимости (докторская диссертация) (Чунцин: Чунцинский университет) (на китайском языке)
[24] Пол С.

No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *

© 2015 - 2019 Муниципальное казённое общеобразовательное учреждение «Таловская средняя школа»

Карта сайта