Функция Лапласа — Энциклопедия по экономике
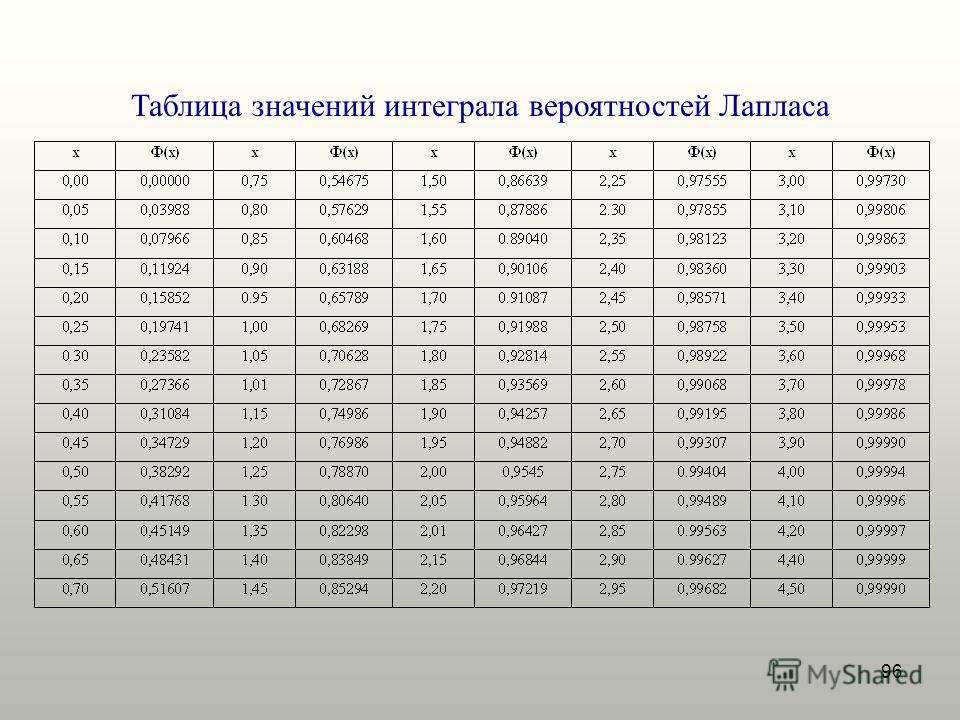
При нормальном распределении расчетные формулы для определения вероятности нахождения параметра х внутри поля допуска получаются с помощью нормированной функции Лапласа [c.152]Из таблицы значений функции Лапласа. следует, что [c.153]
Расчет вероятности наступления завершающего события в заданный срок обычно совершенно необходим, когда установленный директивный срок Гд оказывается меньше рассчитанного срока наступления завершающего события Тс. Предполагая, что значение 7″с подчиняется закону нормального распределения, можно рассчитать эту вероятность следующим образом. Аргумент нормальной функции распределения вероятностей (функции Лапласа) [c.235]
Найдя Ф(х) по таблице значений функции Лапласа (табл. 5.1), определяют вероятность наступления завершающего события в заданный срок. Считается что вероятность Рк должна находиться в пределах 0,35 [c.42]
Функция Лапласа — нечетная, т.е. Ф(— г) = — Ф(—z).
[c. 59]
59]
Доверительный интервал, доверительная вероятность и риск. Если случайная величина имеет нормальное распределение, то вероятность того, что ее значение появится в интервале (zo) около среднего значения зависит только от величины z, равной отношению отклонения Д от среднего значения и среднеквадратического отклонения z = Л/о. Интервал +Д называют доверительным интервалом, а соответствующую ему вероятность Р(г) — доверительной вероятностью, она равна при нормальном распределении функции Лапласа. Риск выхода за этот интервал R(z) = [1 — [c.59]
| Таблица 6.1 Значения интеграла вероятностей — функции Лапласа |
Принимаем, что плотность распределения смешанных случайных величин стремится к нормальному закону распределения. Предельную точку кривой нормального распределения выражаем через функцию Лапласа [c.91]
Затем, используя функцию Лапласа, определяют такое-значение А, при котором
[c.
Ф(х) — функция Лапласа, см. табл. 3.3 1), [c.139]
Функция Лапласа (интеграл вероятностей) [c.139]
Половина интеграла вероятности нормального распределения — функции Лапласа Ф(г) / 2 [c.344]
Подобно функции Лапласа уравнение (2.8) представляет собой квантиль-ное распределение энтропии нормированной нормально распределенной случайной величины на любом отрезке числовой оси. [c.24]
Допустим, произошло смещение центра группирования на величину Дг, тогда t = ta + At, t b=-tb+ ДЛ Используя разложение в ряд Тейлора функции Лапласа Ф(0, получим [c.54]
Эта функция, связанная с интегралом вероятности — функцией Лапласа (см. рис. 27) [c.77]
| Рис. 27. К определению функции Лапласа |
 53]
53]Напомним, Ф (и) = J e » I2 du — нормированная функция Лапласа. [c.156]
Таким образом, если задать величину t и использовать известную функцию Лапласа 0(t), можно определить доверительную вероятность Р = Ф (t), с которой выбор варианта, имеющего более высокую отдачу, будет лучшим (более эффективным). [c.98]
Предельное значение ожидаемой ошибки генеральной совокупности о может быть определено и другим образом — как верхняя граница доверительного интервала. Поскольку известна дисперсия D биномиального распределения, то доверительный интервал ожидаемой ошибки р может быть известным образом выражен через дисперсию и функцию Лапласа. Формула для подсчета доверительного интервала при этом получается громоздкой, но в [11] показано, что для п порядка сотен можно пользоваться удобной для практических расчетов приближенной формулой [c.93]
В. А. Щетина и др., 1988 Тс = среднеквадратическое отклонение интервала между поставками п — максимальное количество поставок в году ретроспективного периода [c.
 278]
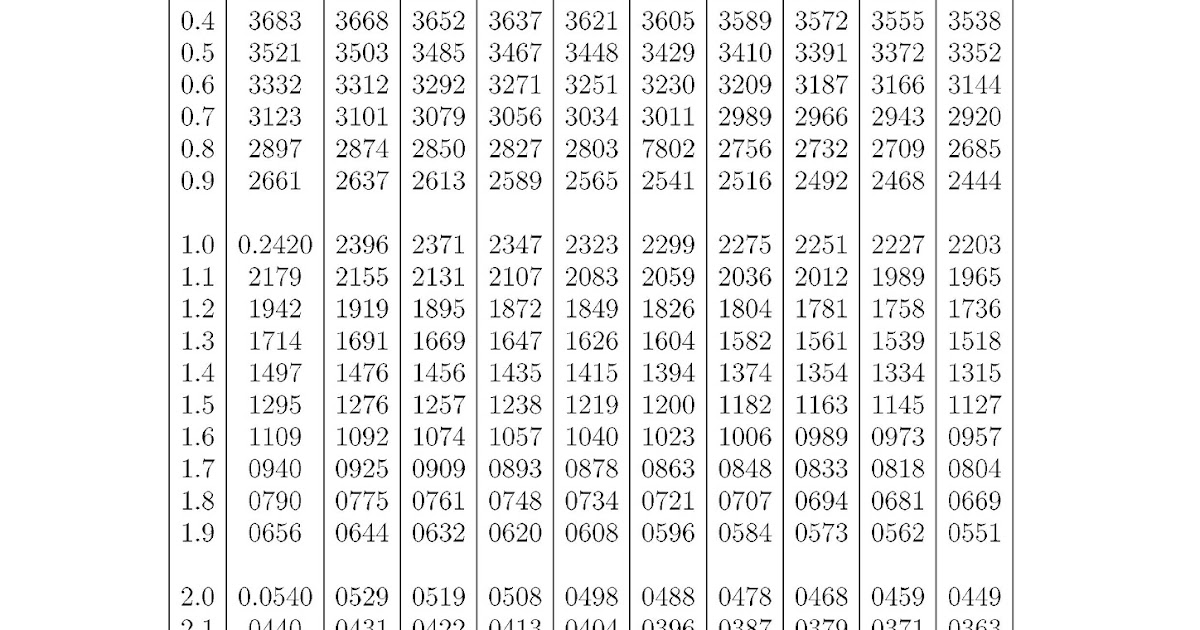
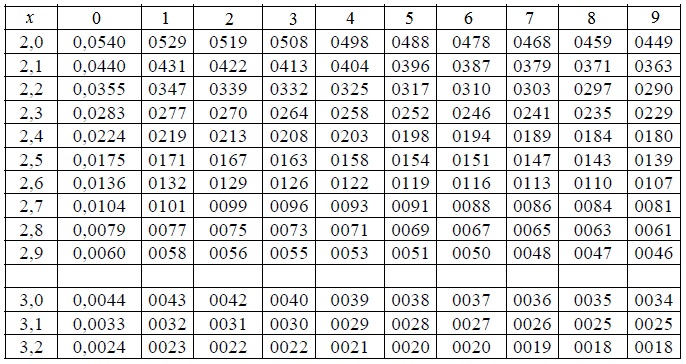
278]Для практических расчетов специально разработаны таблицы функций f(u), F(u) стандартизированного нормального распределения, однако чаще используется так называемая таблица значений функции Лапласа Ф(и) (Приложение 1). Функция Лапласа имеет вид [c.24]
Нормальное распределение используется при проверке различных гипотез в статистике (о величине математического ожидания при известной дисперсии, о равенстве математических ожиданий и т. д.). Подробная схема работы с таблицей значений функции Лапласа Ф(и) приведена в разделе 1.5.1. [c.26]
В левом столбце таблицы приведены значения СВ U с точностью до десятых, в верхней строке приведены сотые доли U (значения U в данном случае определяются с точностью до сотых). Значение Ф(и) определяется на пересечении соответствующих данному значению и строки и столбца (в данном случае Ф(и) дается с точностью до четвертого знака после запятой). Например, Ф(0.17) = 0.0675, т. е. P(0функцией распределения F(u) стандартизированной нормальной СВ представлена на рис.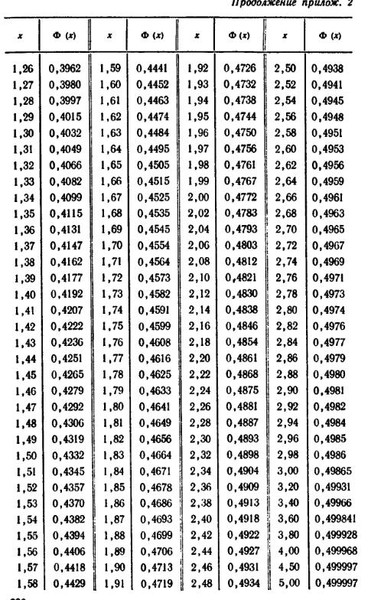 1.10.
[c.30]
1.10.
[c.30]
Приложение 1 Функция Лапласа (стандартизированное нормальное распределение) [c.335]
По значению t/ из графика на рис. 29 можно опред пить, с какой вероятностью отдельное значение результата измерения, подчиняющегося нормальному закону распределения вероятности, попадает в интервал V100 Uj. С вероятностью в два раза меньшей оно попадает в левую или правую половину этого интервала. Эта вероятность, как показано в разд. 3.3.4, определяется интегралом вероятности — функцией Лапласа L (tj), так что для повышения точности расчетов можно пользоваться не графиком, а таблицами функции Лапласа. Полученные из таблиц значения /. (т/) занесены в пятую графу табл. 11. [c.108]
Критерий Шарлье. Если число результатов наблюдений в ряду велико, то по теореме Бернулли число результатов, превышающих по абсолютному значению Кш И (х) будет и [ 1 — Ф (Кш)], где Ф (Кш) — значение нормированной функции Лапласа для Z — Кш. [c.77]
При проведении статистического анализа весьма часто использу ется таблица значений функции Лапласа (приложение 1)
[c. 30]
30]
Пусть в качестве альтернативной рассматривается гипотеза H[ m Ф m0. Тогда критические точки иа/2 и Ui a/2 = -ua/2 будут определяться по таблице функций Лапласа (приложение 1) из ус- [c.76]
При H М(Х) M(Y) по таблице функции Лапласа (прило- [c.81]
значение функции лапласа
Вы искали значение функции лапласа? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и значение функции лапласа таблица, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «значение функции лапласа».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни.
Решить задачу значение функции лапласа вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
DIFFYQS Преобразование Лапласа
Примечание: 1.5–2 лекции, §10.1 в [EP], §6.1 и части §6.2 в [BD]
Подраздел 6.1.1 Преобразование
В этой главе мы обсудим преобразование Лапласа 1 .
Преобразование Лапласа также позволяет лучше понять природу уравнений, с которыми мы имеем дело. Это можно рассматривать как преобразование между временной и частотной областью. Например, возьмем стандартное уравнение
.\begin{уравнение*} m x»(t) + c x'(t) + k x(t) = f(t) . \end{уравнение*}
Мы можем думать о \(t\) как о времени и \(f(t)\) как о входящем сигнале. Преобразование Лапласа преобразует уравнение из дифференциального уравнения во времени в алгебраическое (без производных) уравнение, где новая независимая переменная \(s\) — это частота.
Преобразование Лапласа преобразует уравнение из дифференциального уравнения во времени в алгебраическое (без производных) уравнение, где новая независимая переменная \(s\) — это частота.
Мы можем думать о преобразовании Лапласа как о черном ящике. Он ест функции и выплевывает функции в новую переменную. Мы пишем \(\mathcal{L} \bigl\{ f(t) \bigr\} = F(s)\) для преобразования Лапласа \(f(t)\text{.}\). напишите строчные буквы для функций во временной области и прописные буквы для функций в частотной области. Мы используем ту же букву, чтобы обозначить, что одна функция является преобразованием Лапласа другой. Например, \(F(s)\) является преобразованием Лапласа \(f(t)\text{.}\). Определим преобразование. 9{-st} f(t) \, dt . \end{уравнение*}
Заметим, что мы рассматриваем только \(t \geq 0\) в преобразовании. Конечно, если мы думаем о \(t\) как о времени, проблем нет, мы, как правило, заинтересованы в том, чтобы узнать, что произойдет в будущем (преобразование Лапласа — это то место, где безопасно игнорировать прошлое). {-sh}}{-s} — \frac{1}{-s} \right)
= \frac{1}{s} .
\end{уравнение*} 92} .
\конец{разделить}
\end{уравнение*}
{-sh}}{-s} — \frac{1}{-s} \right)
= \frac{1}{s} .
\end{уравнение*} 92} .
\конец{разделить}
\end{уравнение*}
Опять же, предел существует, только если \(s > 0\text{.}\)
Пример 6.1.4.
Общей функцией является функция единичного шага , которую иногда называют функцией Хевисайда 3 . Эта функция обычно задается как
\begin{уравнение*} и(т) = \begin{случаи} 0 & \текст{если} \; т < 0, \\ 1 & \текст{если} \; т \geq 0 . \end{случаи} \end{уравнение*}
Найдем преобразование Лапласа \(u(t-a)\text{,}\), где \(a \geq 0\) — некоторая константа. То есть функция, равная 0 для \(t < a\) и 1 для \(t \geq a\text{.}\) 9{-как}}{с}, \end{уравнение*}
, где, конечно, \(s > 0\) (и \(a \geq 0\), как мы уже говорили ранее).
Применяя аналогичные процедуры, мы можем вычислить преобразования многих элементарных функций. Многие базовые преобразования перечислены в таблице 6.1.
Таблица 6.1. Некоторые преобразования Лапласа (\(C\text{,}\) \(\omega\text{,}\) и \(a\) являются константами).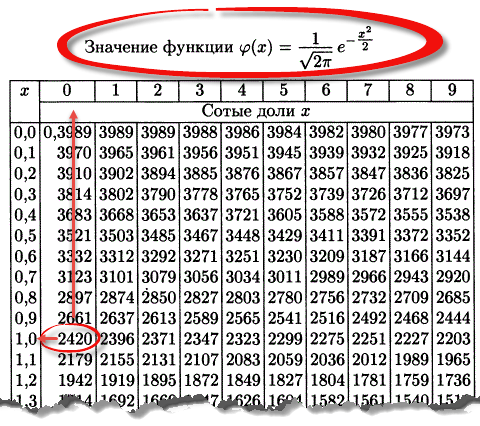
| \(ф(т)\) | \(\mathcal{L} \bigl\{ f(t) \bigr\}\) | \(\qquad\quad\) | \(f(t)\) 9{-st} f(t) \,dt =
C \mathcal{L} \bigl\{ f(t) \bigr\} .
\end{уравнение*} Таким образом, мы можем «вытащить» константу из преобразования. Точно так же у нас есть линейность. Поскольку линейность очень важна, мы сформулируем это как теорему. Теорема 6.1.1. Линейность преобразования Лапласа.Предположим, что \(A\text{,}\) \(B\text{,}\) и \(C\) являются константами, тогда \begin{уравнение*} \mybxbg{~~ \mathcal{L} \bigl\{ A f(t) + Bg(t) \bigr\} = A \mathcal{L} \bigl\{ f(t) \bigr\} + B \mathcal{L} \bigl\{g(t) \bigr\} , ~~} \end{уравнение*} и, в частности, \begin{уравнение*} \mathcal{L} \bigl\{ C f(t) \bigr\} = C \mathcal{L} \bigl\{ f(t) \bigr\} . \end{уравнение*} Упражнение 6.1.2. Проверьте теорему. То есть покажите, что \(\mathcal{L} \bigl\{ A f(t) + B g(t) \bigr\} =
A \mathcal{L} \bigl\{ f(t) \bigr\} +
B \mathcal{L} \bigl\{ g(t) \bigr\}\text{. Преобразование также существует для некоторых других функций, которые не имеют экспоненциального порядка, но это не будет иметь отношения к нам. Прежде чем говорить об уникальности, отметим, что для функций экспоненциального порядка мы получаем, что их преобразование Лапласа затухает на бесконечности: \begin{уравнение*} \lim_{s\to\infty} F(s) = 0 . \end{уравнение*} Теорема 6.1.3. Уникальность.Пусть \(f(t)\) и \(g(t)\) непрерывны и имеют экспоненциальный порядок. Предположим, что существует константа \(C\text{,}\) такая, что \(F(s) = G(s)\) для всех \(s > C\text{.}\). Тогда \(f( t) = g(t)\) для всех \(t \geq 0\text{.}\) Обе теоремы верны и для кусочно-непрерывных функций. Подраздел 6.1.3 Обратное преобразование Как мы уже говорили, преобразование Лапласа позволит нам преобразовать дифференциальное уравнение в алгебраическое уравнение. Как только мы решим алгебраическое уравнение в частотной области, мы захотим вернуться во временную область, поскольку это то, что нас интересует. Для данной функции \(F(s)\text{,}\) мы хотим найти функция \(f(t)\) такая, что \(\mathcal{L} \bigl\{ f(t) \bigr\} = F(s)\text{. В общем, мы хотим иметь возможность применять преобразование Лапласа к рациональным функциям, то есть к функциям вида \begin{уравнение*} \ гидроразрыв {F (с)} {G (с)} \end{уравнение*} , где \(F(s)\) и \(G(s)\) — многочлены. Поскольку обычно для рассматриваемых нами функций преобразование Лапласа стремится к нулю при \(s \to \infty\text{,}\), нетрудно видеть, что степень \(F(s)\) должна быть меньше, чем у \(G(s)\text{.}\) Такие рациональные функции называются 92+2s+2}\) Подобно уравнению Лапласа и лапласиану, преобразование Лапласа также названо в честь Пьера-Симона, маркиза де Лапласа 2 (1749–1827). Функция названа в честь английского математика, инженера и физика Оливера Хевисайда 4 (1850–1925). Только по стечению обстоятельств функция оказывается «тяжелой» с «одной стороны». ОДУ: преобразование ЛапласаПодраздел 3.1.1 ПреобразованиеВидео 3.1.1. Введение в преобразование Лапласа.В этом видео мы познакомимся с преобразованием Лапласа, которое принимает функции и выводит функцию другого типа. Это может показаться довольно странным и немного немотивированным, потому что доказательство того, что преобразования Лапласа полезны для нас, заключается в том, насколько они эффективны для решения дифференциальных уравнений. Одно преимущество произойдет сразу же: мы увидим, как преобразовывать очень прерывистые вещи, такие как ступенчатые функции и гамма-функция, в более разумные объекты. В этой главе мы обсудим преобразование Лапласа 1 . Преобразование Лапласа — очень эффективный метод решения некоторых задач ОДУ или УЧП. Подобно уравнению Лапласа и лапласиану, преобразование Лапласа также названо в честь Пьера-Симона, маркиза де Лапласа (1749–1827). Преобразование Лапласа также позволяет лучше понять природу уравнений, с которыми мы имеем дело. Это можно рассматривать как преобразование между временной и частотной областью. Например, возьмем стандартное уравнение .\begin{уравнение*} m x»(t) + c x'(t) + k x(t) = f(t) . \end{уравнение*} Мы можем думать о \(t\) как о времени и \(f(t)\) как о входящем сигнале. Мы можем думать о преобразовании Лапласа как о черном ящике. Он ест функции и выплевывает функции в новую переменную. Мы пишем \(\mathcal{L} \bigl\{ f(t) \bigr\} = F(s)\) для преобразования Лапласа \(f(t)\text{.}\). напишите строчные буквы для функций во временной области и прописные буквы для функций в частотной области. Мы используем ту же букву, чтобы обозначить, что одна функция является преобразованием Лапласа другой. Например, \(F(s)\) является преобразованием Лапласа \(f(t)\text{.}\). Определим преобразование. 9{-st} f(t) \, dt . \end{уравнение*} Заметим, что мы рассматриваем только \(t \geq 0\) в преобразовании. Конечно, если мы думаем о \(t\) как о времени, проблем нет, мы, как правило, заинтересованы в том, чтобы узнать, что произойдет в будущем (преобразование Лапласа — это то место, где безопасно игнорировать прошлое). Опять же, предел существует, только если \(s > 0\text{.}\) Пример 3.1.4.Общей функцией является функция единичного шага , которую иногда называют функцией Хевисайда 2 . Эта функция обычно задается как \begin{уравнение*} и(т) = \begin{случаи} 0 & \текст{если} \; т < 0, \\ 1 & \текст{если} \; т \geq 0 . \end{случаи} \end{уравнение*} Найдем преобразование Лапласа \(u(t-a)\text{,}\), где \(a \geq 0\) — некоторая константа. То есть функция, равная 0 для \(t < a\) и 1 для \(t \geq a\text{.}\) 9{-как}}{с}, \end{уравнение*} , где, конечно, \(s > 0\) (и \(a \geq 0\), как мы уже говорили ранее). Функция названа в честь английского математика, инженера и физика Оливера Хевисайда (1850–1925). Только по стечению обстоятельств функция оказывается «тяжелой» с «одной стороны». Применяя аналогичные процедуры, мы можем вычислить преобразования многих элементарных функций. | \(\frac{1}{s+a}\) |
Упражнение 3.1.1.
Проверьте таблицу 3.1.5.
Видео 3.1.2. Линейность, существование и инверсия преобразования Лапласа.
Преобразование Лапласа имеет множество свойств, благодаря которым оно ведет себя хорошо. В этом видео мы рассмотрим три важнейших из них: линейность, существование и инверсию.
Поскольку преобразование определяется интегралом, мы можем использовать свойства линейности интеграла. Например, предположим, что \(C\) является константой, тогда 9{-st} f(t) \,dt = C \mathcal{L} \bigl\{ f(t) \bigr\} . \end{уравнение*}
Таким образом, мы можем «вытащить» константу из преобразования. Точно так же у нас есть линейность. Поскольку линейность очень важна, мы сформулируем это как теорему.
Точно так же у нас есть линейность. Поскольку линейность очень важна, мы сформулируем это как теорему.
Теорема 3.1.1. Линейность преобразования Лапласа.
Предположим, что \(A\text{,}\) \(B\text{,}\) и \(C\) являются константами, тогда
\begin{уравнение*} \mybxbg{~~ \mathcal{L} \bigl\{ A f(t) + Bg(t) \bigr\} = A \mathcal{L} \bigl\{ f(t) \bigr\} + B \mathcal{L} \bigl\{g(t) \bigr\} , ~~} \end{уравнение*}
и, в частности,
\begin{уравнение*} \mathcal{L} \bigl\{ C f(t) \bigr\} = C \mathcal{L} \bigl\{ f(t) \bigr\} . \end{уравнение*}
Упражнение 3.1.2.
Проверьте теорему. То есть покажите, что \(\mathcal{L} \bigl\{ A f(t) + B g(t) \bigr\} = A \mathcal{L} \bigl\{ f(t) \bigr\} + B \mathcal{L} \bigl\{ g(t) \bigr\}\text{.}\)
Эти правила вместе с таблицей 3.1.5 позволяют легко найти преобразование Лапласа уже целого ряда функций. . Но будь осторожен. Распространенной ошибкой является мнение, что преобразование Лапласа произведения есть произведение преобразований. {ct}\) для всех \(t > 0\) (для простоты \( t_0 = 0\)). Пусть \(s > c\text{,}\) или, другими словами, \((c-s) < 0\text{.}\) По теореме сравнения из исчисления несобственный интеграл, определяющий \(\mathcal{L} \ bigl\{ f(t) \bigr\}\) существует, если существует следующий интеграл 9\infty = \frac{M}{cs} .
\end{уравнение*}
{ct}\) для всех \(t > 0\) (для простоты \( t_0 = 0\)). Пусть \(s > c\text{,}\) или, другими словами, \((c-s) < 0\text{.}\) По теореме сравнения из исчисления несобственный интеграл, определяющий \(\mathcal{L} \ bigl\{ f(t) \bigr\}\) существует, если существует следующий интеграл 9\infty = \frac{M}{cs} .
\end{уравнение*}
Преобразование также существует для некоторых других функций, которые не имеют экспоненциального порядка, но это не будет иметь отношения к нам. Прежде чем говорить об уникальности, отметим, что для функций экспоненциального порядка мы получаем, что их преобразование Лапласа затухает на бесконечности:
\begin{уравнение*} \lim_{s\to\infty} F(s) = 0 . \end{уравнение*}
Теорема 3.1.3. Уникальность.
Пусть \(f(t)\) и \(g(t)\) непрерывны и имеют экспоненциальный порядок. Предположим, что существует константа \(C\text{,}\) такая, что \(F(s) = G(s)\) для всех \(s > C\text{.}\). Тогда \(f( t) = g(t)\) для всех \(t \geq 0\text{.}\)
Обе теоремы верны и для кусочно-непрерывных функций. Напомним, что кусочно-непрерывная функция означает, что функция непрерывна, за исключением, возможно, дискретного набора точек, где она имеет скачкообразные разрывы, как функция Хевисайда. Уникальность, однако, не «видит» значений на разрывах. Таким образом, мы можем только заключить, что \(f(t) = g(t)\) вне разрывов. Например, единичная ступенчатая функция иногда определяется как \(u(0) = \nicefrac{1}{2}\text{.}\). Однако эта новая ступенчатая функция имеет то же самое преобразование Лапласа, что и мы. определено ранее, где \(u(0) = 1\text{.}\)
Напомним, что кусочно-непрерывная функция означает, что функция непрерывна, за исключением, возможно, дискретного набора точек, где она имеет скачкообразные разрывы, как функция Хевисайда. Уникальность, однако, не «видит» значений на разрывах. Таким образом, мы можем только заключить, что \(f(t) = g(t)\) вне разрывов. Например, единичная ступенчатая функция иногда определяется как \(u(0) = \nicefrac{1}{2}\text{.}\). Однако эта новая ступенчатая функция имеет то же самое преобразование Лапласа, что и мы. определено ранее, где \(u(0) = 1\text{.}\)
Подраздел 3.1.3 Обратное преобразование
Как мы уже говорили, преобразование Лапласа позволит нам преобразовать дифференциальное уравнение в алгебраическое уравнение. Как только мы решим алгебраическое уравнение в частотной области, мы захотим вернуться во временную область, поскольку это то, что нас интересует. Для данной функции \(F(s)\text{,}\) мы хотим найти функция \(f(t)\) такая, что \(\mathcal{L} \bigl\{ f(t) \bigr\} = F(s)\text{. t\sin(2t)\) для того же причины 9{-2t} \sin (2t) .
\end{уравнение*}
t\sin(2t)\) для того же причины 9{-2t} \sin (2t) .
\end{уравнение*}
Видео 3.1.4. Обратное преобразование Лапласа с повторяющимися факторами.
Видео 3.1.3 показало нам, как взять неприводимый квадратичный множитель и использовать завершение квадрата, чтобы записать его в форме, пригодной для выполнения обратных преобразований Лапласа. В этом видео мы покажем, как бороться с повторяющимися факторами.
В общем, мы хотим иметь возможность применять преобразование Лапласа к рациональным функциям, то есть к функциям вида
\begin{уравнение*} \ гидроразрыв {F (с)} {G (с)} \end{уравнение*}
, где \(F(s)\) и \(G(s)\) — многочлены. Поскольку обычно для рассматриваемых нами функций преобразование Лапласа стремится к нулю при \(s \to \infty\text{,}\), нетрудно видеть, что степень \(F(s)\) должно быть меньше, чем у \(G(s)\text{.}\) Такие рациональные функции называются правильными рациональными функциями , и мы всегда можем применить метод частичных дробей.

 {ct}\) для всех \(t > 0\) (для простоты \( t_0 = 0\)). Пусть \(s > c\text{,}\) или, другими словами, \((s-c) > 0\text{.}\) По теореме сравнения из исчисления несобственный интеграл, определяющий \(\mathcal{L} \ bigl\{ f(t) \bigr\}\) существует, если существует следующий интеграл 9\infty = \frac{M}{s-c} .
\end{уравнение*}
{ct}\) для всех \(t > 0\) (для простоты \( t_0 = 0\)). Пусть \(s > c\text{,}\) или, другими словами, \((s-c) > 0\text{.}\) По теореме сравнения из исчисления несобственный интеграл, определяющий \(\mathcal{L} \ bigl\{ f(t) \bigr\}\) существует, если существует следующий интеграл 9\infty = \frac{M}{s-c} .
\end{уравнение*}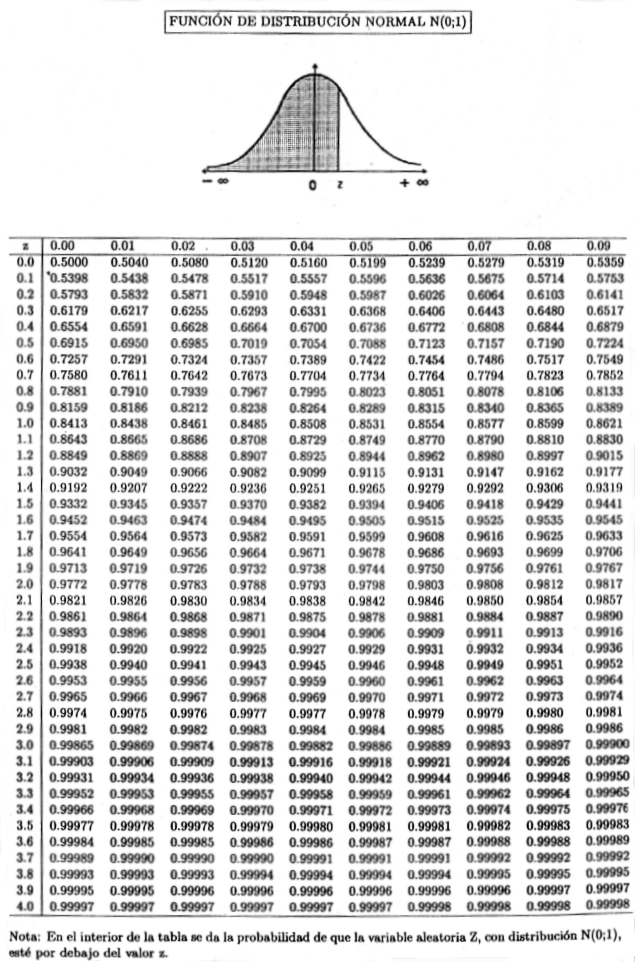 Напомним, что кусочно-непрерывная функция означает, что функция непрерывна, за исключением, возможно, дискретного набора точек, где она имеет скачкообразные разрывы, как функция Хевисайда. Уникальность, однако, не «видит» значений на разрывах. Таким образом, мы можем только заключить, что \(f(t) = g(t)\) вне разрывов. Например, единичная ступенчатая функция иногда определяется как \(u(0) = \nicefrac{1}{2}\text{.}\). Однако эта новая ступенчатая функция имеет то же самое преобразование Лапласа, что и мы. определено ранее, где \(u(0) = 1\text{.}\)
Напомним, что кусочно-непрерывная функция означает, что функция непрерывна, за исключением, возможно, дискретного набора точек, где она имеет скачкообразные разрывы, как функция Хевисайда. Уникальность, однако, не «видит» значений на разрывах. Таким образом, мы можем только заключить, что \(f(t) = g(t)\) вне разрывов. Например, единичная ступенчатая функция иногда определяется как \(u(0) = \nicefrac{1}{2}\text{.}\). Однако эта новая ступенчатая функция имеет то же самое преобразование Лапласа, что и мы. определено ранее, где \(u(0) = 1\text{.}\) {-т} .
\end{уравнение*} 9{-2t} \sin (2t) .
\end{equation*}
{-т} .
\end{уравнение*} 9{-2t} \sin (2t) .
\end{equation*}
 Преобразование берет дифференциальное уравнение и превращает его в алгебраическое уравнение. Если алгебраическое уравнение можно решить, применение обратного преобразования дает нам желаемое решение. Преобразование Лапласа также находит применение в анализе электрических цепей, ЯМР-спектроскопии, обработке сигналов и в других областях. Наконец, понимание преобразования Лапласа также поможет понять связанное с ним преобразование Фурье, которое, однако, требует большего понимания комплексных чисел. Мы не будем рассматривать преобразование Фурье.
Преобразование берет дифференциальное уравнение и превращает его в алгебраическое уравнение. Если алгебраическое уравнение можно решить, применение обратного преобразования дает нам желаемое решение. Преобразование Лапласа также находит применение в анализе электрических цепей, ЯМР-спектроскопии, обработке сигналов и в других областях. Наконец, понимание преобразования Лапласа также поможет понять связанное с ним преобразование Фурье, которое, однако, требует большего понимания комплексных чисел. Мы не будем рассматривать преобразование Фурье. Преобразование Лапласа преобразует уравнение из дифференциального уравнения во времени в алгебраическое (без производных) уравнение, где новая независимая переменная \(s\) — это частота.
Преобразование Лапласа преобразует уравнение из дифференциального уравнения во времени в алгебраическое (без производных) уравнение, где новая независимая переменная \(s\) — это частота. {-sh}}{-s} — \frac{1}{-s} \right)
= \frac{1}{s} .
\end{уравнение*} 92} .
\конец{разделить}
\end{уравнение*}
{-sh}}{-s} — \frac{1}{-s} \right)
= \frac{1}{s} .
\end{уравнение*} 92} .
\конец{разделить}
\end{уравнение*} Многие базовые преобразования перечислены в таблице 3.1.5.
Многие базовые преобразования перечислены в таблице 3.1.5.