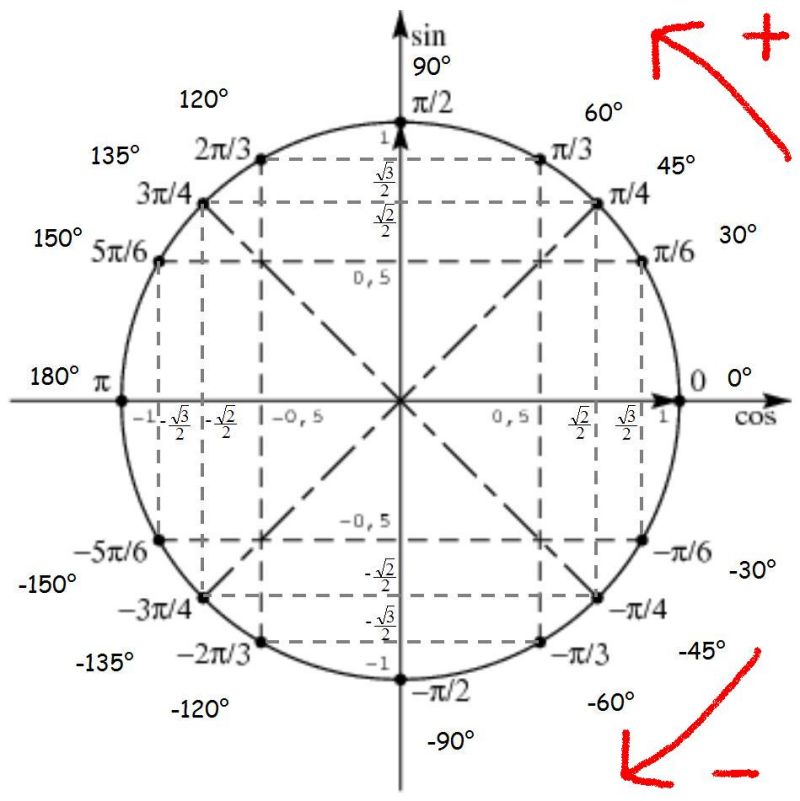
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктан(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | 92|||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктан(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт. )/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | тан(пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | соз(30) | |
| 47 | Найти точное значение | соз(60) | |
| 48 | Найти точное значение | ||
| 49 | Найти точное значение | соз(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | сек(60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найти точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | загар((5pi)/3) | ||
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 пи)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | угловой синус(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | КСК(45) | |
| 83 | Упростить | арктан(квадратный корень из 3) | |
| 84 | Найти точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найти точное значение | грех(150 градусов) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | загар((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найти точное значение | грех(пи/2) | |
| 91 | Найти точное значение | сек(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | угловой синус(0) | |
| 95 | Найти точное значение | грех(120 градусов) | |
| 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найти точное значение | соз(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
тригонометрия — Точные значения $\cos(2\pi/7)$ и $\sin(2\pi/7)$
спросил
Изменено 2 месяца назад
Просмотрено 20 тысяч раз
$\begingroup$
Каковы точные значения $\cos(2\pi/7)$ и $\sin(2\pi/7)$ и как их вычислить?
Я знаю, что $\cos(2\pi/7)$ и $\sin(2\pi/7)$ — действительная и мнимая части $e^{2\pi/7}$, но я не уверен, что это мне поможет.
.. 92 — \frac{1}{2}t — \frac{1}{8}$, которое неприводимо при $P(\alpha) = 0$. (Обратите внимание, что нецелочисленные коэффициенты $P(t)$ подразумевают, что $\alpha$ не является целым алгебраическим числом. В этом отношении величина $2\alpha$ ведет себя гораздо лучше, и часто бывает полезно работать с $2 \alpha$ вместо $\alpha$.) Чтобы увидеть, что вы получите, применяя формулу Кардано, обратитесь к другим ответам или просто погуглите: например, я быстро нашел эту страницу среди многих других (включая википедию), которая делает это. 9+$. (Обычно мы не сможем обойтись только повторным извлечением квадратных корней; этого может быть достаточно только тогда, когда общая функция Эйлера $\varphi(n)$ является, например, степенью $2$, поэтому даже когда $n = 7$.) С этой точки зрения применение кубической формулы является большой отговоркой, так как нет аналогичной формулы в степени $d > 4$: общий многочлен такой степени не может быть решен в радикалах… но круговые многочлены могут .
Чем ты вообще занимаешься? Ответ был известен Гауссу и включает в себя некоторую классическую алгебру — резольвенты , гауссовские периоды и т.
д. — это не очень хорошо помнят в наши дни. На самом деле я сам никогда не вникал в подробности. Но я какое-то время рыскал по сети в поисках приятного лечения, и в конце концов нашел эту статью Пола Гаррета. Я рекомендую его тем, кто хочет больше узнать об этой (насколько мне известно, не очень полезной, но интересной) классической проблеме: его заметки неизменно превосходны и обладают достоинством краткости (которой я восхищаюсь, особенно из-за отсутствия способности производить самому). 9{4}_{7}$$
$$t_{1} t_{2}=t_{1}+t_{3}$$
сходным образом
$$t_{1} t_{3}=t_{3}+t_{2}$$
$$t_{2} t_{3}=t_{2}+t_{1}$$
так
$$t_{1} t_{2}+t_{1} t_{3}+t_{2} t_{3}=-2$$
затем найдите $t_{1} t_{2} t_{3}$
$$t_{1} t_{2}=t_{1}+t_{3}$$
так как $t_1+t_2+t_3=-1$
$$t_{1} t_{2}=-1-t_{2}$$
$$t_{1} t_{2} t_{3}=\left(-1-t_{2}\right)t_{3}$$
$$t_{1} t_{2} t_{3}=-t_{3}-t_{2}t_{3}$$
$$t_{1} t_{2} t_{3}=-t_{3}-t_{2}-t_{1}$$
$$t_{1} t_{2} t_{3}=1$$
затем,
$$t_1 + t_2 + t_3 = -1$$
$$t_2 + t_3 = -1 -t_1$$
$$t_1 t_2 t_3 = 1$$
$$t_2 t_3 = \frac {1}{t_1} = t^{-1}_1$$
$$t_1 t_2 + t_1 t_3 + t_2 t_3 +2 = 0$$
$$t_1 ( t_2 + t_3 ) + t_2 t_3 +2 = 0$$
$$t_1 (-1 -t_1) + t^{-1}_1 +2 = 0$$
$$-t^2_1 -t_1 + 2 + t^{-1}_1 = 0$$
$$t^3_1 + t^2_1 -2t_1 -1 = 0$$
это утверждение также применимо к другим $t_k$
$$т^3+т^2-2-1=0$$
вернуться к утверждению, которое мы установили
$$t_{k}=2\cos\frac{2k\pi}{7}$$
корни кубического многочлена
$$т^3+т^2-2-1=0$$
есть корни косинуса, применяя резольвенту Лагранжа (если хотите посложнее) или формулу Тарталья,
$$2\cos\frac{2\pi}{7}=\frac{-1+\sqrt[3]{\frac{7}{2}\left(1+3\sqrt{-3}\ вправо)}+\sqrt[3]{\frac{7}{2}\left(1+3\sqrt{-3}\right)}}{3}$$ $ $ 2 \ cos \ frac {4 \ pi} {7} = \ frac {-1 + \ frac {- 1- \ sqrt {- 3}} {2} \ sqrt [3] {\ frac {7} {2 }\left(1+3\sqrt{-3}\right)}+\frac{-1+\sqrt{-3}}{2}\sqrt[3]{\frac{7}{2}\left (1+3\sqrt{-3}\справа)}}{3}$$ $ $ 2 \ cos \ frac {6 \ pi} {7} = \ frac {-1+ \ frac {- 1+ \ sqrt {- 3}} {2} \ sqrt [3] {\ frac {7} {2 }\left(1+3\sqrt{-3}\right)}+\frac{-1-\sqrt{-3}}{2}\sqrt[3]{\frac{7}{2}\left (1+3\sqrt{-3}\справа)}}{3}$$ и, заметьте $t_{k}=\zeta^{k}_{7}+\zeta^{-k}_{7}$ $t_{-k}=\zeta^{-k}_{7}+\zeta^{k}_{7}$ так $t_{1}=t_{1} т_{2}=т_{2} т_{3}=т_{3} т_{4}=т_{3} т_{5}=т_{2} т_{6}=т_{1}$ $$\zeta^{2k}_{7}-2+\zeta^{-2k}_{7}=-4\sin\frac{2k\pi}{7}$$ так $$t_{2k}-2=-4\sin\frac{2k\pi}{7}$$
$$\sqrt{t_{2k}-2}=2i\sin\frac{2k\pi}{7}$$
$$\sqrt{t_{2}-2}=2i\sin\frac {2\pi}{7}$$ $$\sqrt{t_{3}-2}=2i\sin\frac{4\pi}{7}$$ $$\sqrt{t_{1}-2}=2i\sin\frac{6\pi}{7}$$ замените каждый $t_{k}$ $$\sqrt{t_{2}-2}=\sqrt{\frac{-1+\frac{-1-\sqrt{-3}}{2}\sqrt[3]{\frac{7}{ 2}\left(1+3\sqrt{-3}\right)}+\frac{-1+\sqrt{-3}}{2}\sqrt[3]{\frac{7}{2}\ влево(1+3\sqrt{-3}\вправо)}}{3}-2}$$ $$\sqrt{t_{2}-2}=\sqrt{\frac{-7+\frac{-1-\sqrt{-3}}{2}\sqrt[3]{\frac{7}{ 2}\left(1+3\sqrt{-3}\right)}+\frac{-1+\sqrt{-3}}{2}\sqrt[3]{\frac{7}{2}\ влево(1+3\sqrt{-3}\вправо)}}{3}}$$ $ $ \ sqrt {t_ {2} -2} = \ sqrt {\ frac {3 \ left (-7+ \ frac {-1- \ sqrt {- 3}} {2} \ sqrt [3] {\ frac {7} {2}\left(1+3\sqrt{-3}\right)}+\frac{-1+\sqrt{-3}}{2}\sqrt[3]{\frac{7} {2}\влево(1+3\sqrt{-3}\вправо)}\вправо)}{9}}$$ $$\sqrt{t_{2}-2}=\frac{\sqrt{3\left(-7+\frac{-1-\sqrt{-3}}{2}\sqrt[3]{\frac {7} {2}\left(1+3\sqrt{-3}\right)}+\frac{-1+\sqrt{-3}}{2}\sqrt[3]{\frac{7} {2}\влево(1+3\sqrt{-3}\вправо)}\вправо)}}{3}$$ $$2i\sin\frac{2\pi}{7}=\frac{\sqrt{3\left(-7+\frac{-1-\sqrt{-3}}{2}\sqrt[3] {\ frac {7} {2} \ left (1 + 3 \ sqrt {- 3} \ right)} + \ frac {- 1 + \ sqrt {- 3}} {2} \ sqrt [3] {\ frac {7}{2}\влево(1+3\sqrt{-3}\вправо)}\вправо)}}{3}$$ так $$2\sin\frac{2\pi}{7}=\frac{\sqrt{-3\left(-7+\frac{-1-\sqrt{-3}}{2}\sqrt[3] {\ frac {7} {2} \ left (1 + 3 \ sqrt {- 3} \ right)} + \ frac {- 1 + \ sqrt {- 3}} {2} \ sqrt [3] {\ frac {7}{2}\влево(1+3\sqrt{-3}\вправо)}\вправо)}}{3}$$ $$2\sin\frac{4\pi}{7}=\frac{\sqrt{-3\left(-7+\frac{-1+\sqrt{-3}}{2}\sqrt[3] {\ frac {7} {2} \ left (1 + 3 \ sqrt {- 3} \ right)} + \ frac {- 1- \ sqrt {- 3}} {2} \ sqrt [3] {\ frac {7}{2}\влево(1+3\sqrt{-3}\вправо)}\вправо)}}{3}$$ $ $ 2 \ грех \ гидроразрыва {6 \ пи} {7} = \ гидроразрыва {\ sqrt {-3 \ влево (-7+ \ sqrt [3]] {\ гидроразрыва {7} {2} \ влево (1 + 3 \ sqrt{-3}\right)}+\sqrt[3]{\frac{7}{2}\left(1+3\sqrt{-3}\right)}\right)}}{3}$$ теперь мы закончили с
$$\cos\frac{2\pi}{7}=\frac{-1+\sqrt[3]{\frac{7}{2}\left(1+3\sqrt{-3}\ вправо)}+\sqrt[3]{\frac{7}{2}\left(1+3\sqrt{-3}\right)}}{6}$$
$$\cos\frac{4\pi}{7}=\frac{-1+\frac{-1-\sqrt{-3}}{2}\sqrt[3]{\frac{7}{2} }\left(1+3\sqrt{-3}\right)}+\frac{-1+\sqrt{-3}}{2}\sqrt[3]{\frac{7}{2}\left (1+3\sqrt{-3}\справа)}}{6}$$
$$\cos\frac{6\pi}{7}=\frac{-1+\frac{-1+\sqrt{-3}}{2}\sqrt[3]{\frac{7}{2} }\left(1+3\sqrt{-3}\right)}+\frac{-1-\sqrt{-3}}{2}\sqrt[3]{\frac{7}{2}\left (1+3\sqrt{-3}\справа)}}{6}$$
$$\sin\frac{2\pi}{7}=\frac{\sqrt{-3\left(-7+\frac{-1-\sqrt{-3}}{2}\sqrt[3] {\ frac {7} {2} \ left (1 + 3 \ sqrt {- 3} \ right)} + \ frac {- 1 + \ sqrt {- 3}} {2} \ sqrt [3] {\ frac {7}{2}\влево(1+3\sqrt{-3}\вправо)}\вправо)}}{6}$$
$$\sin\frac{4\pi}{7}=\frac{\sqrt{-3\left(-7+\frac{-1+\sqrt{-3}}{2}\sqrt[3] {\ frac {7} {2} \ left (1 + 3 \ sqrt {- 3} \ right)} + \ frac {- 1- \ sqrt {- 3}} {2} \ sqrt [3] {\ frac {7}{2}\влево(1+3\sqrt{-3}\вправо)}\вправо)}}{6}$$
$$\sin\frac{6\pi}{7}=\frac{\sqrt{-3\left(-7+\sqrt[3]{\frac{7}{2}\left(1+3\ sqrt {-3} \ right)} + \ sqrt [3] {\ frac {7} {2} \ left (1 + 3 \ sqrt {- 3} \ right)} \ right)}} {6} $ $ 9{-i\theta})$, вычисление квадрата и куба и поиск линейных соотношений, имея в виду, что $7$ $7$ корней из единицы дают в сумме ноль.
Затем вы можете использовать формулу Кардано для решения кубического. Я не знаю, рекомендую ли я на самом деле делать все это — я уверен, что вы получите беспорядок, хотя дискриминант будет идеальным квадратом, так что вы получите некоторое упрощение.
$\endgroup$
2
$\begingroup$ 9{1/3}/6 $$ — рассчитано Wolfram Alpha)
$\endgroup$
$\begingroup$
Вы уверены, что — это «точное» значение? Ну, это зависит от того, что вы подразумеваете под точным. Я хочу сказать, что я не думаю, что семиугольники можно построить с помощью линейки и циркуля, что означает, если я правильно помню, что синус и косинус не могут быть выражены в виде суммы дробей и квадратных корней дробей.
Я знаю, что $\cos\dfrac{2\pi}{17}$ — известное значение, возможно, вы это имели в виду.