12. Основные понятия
Основные понятия:
Скалярная величина; векторная величина; коллинеарные векторы; компланарные векторы; единичный вектор; сложение векторов; проекция вектора; линейная комбинация векторов; линейная зависимость векторов; базис; координаты вектора; базисные орты; правая система координат; направляющие косинусы; скалярное произведение; векторное произведение; смешанное произведение.
Понятие вектора широко применяется в экономике, математике, физике и других науках, при этом одинаково широко используется как алгебраическая концепция изложения векторного анализа, так и его геометрическая интерпретация, в рамках которой различаются величины двух видов: скалярные и векторные.
Скалярной величиной или скаляром называется величина, которая полностью определяется одним числом, выражающим отношение этой величины к соответствующей единице измерения, например, цена, количество проданного товара, стоимость и т. д.
Векторной величиной
 д.
д.Векторная величина графически обычно изображается как Связанный вектор или Направленный отрезок, т. е. отрезок прямой, у которого указано, какая из ограничивающих точек является его началом, а какая концом. Но в отличие от направленного отрезка, для описания которого необходимо указать начальную точку, длину и направление, Свободный вектор или просто Вектор представляет собой множество всех эквивалентных между собой связанных векторов и вполне характеризуется:
· направлением;
· длиной (модулем).
Для задания такого множества достаточно указать какой-либо один из связанных векторов этого множества – Представитель вектора, в качестве которого обычно выбирается связанный вектор с началом, совпадающим с началом координат.
Вектор обозначается одной маленькой буквой со стрелкой сверху, например, , или двумя буквами со стрелкой , где точка есть начало вектора (его точка приложения), а ‑ его конец.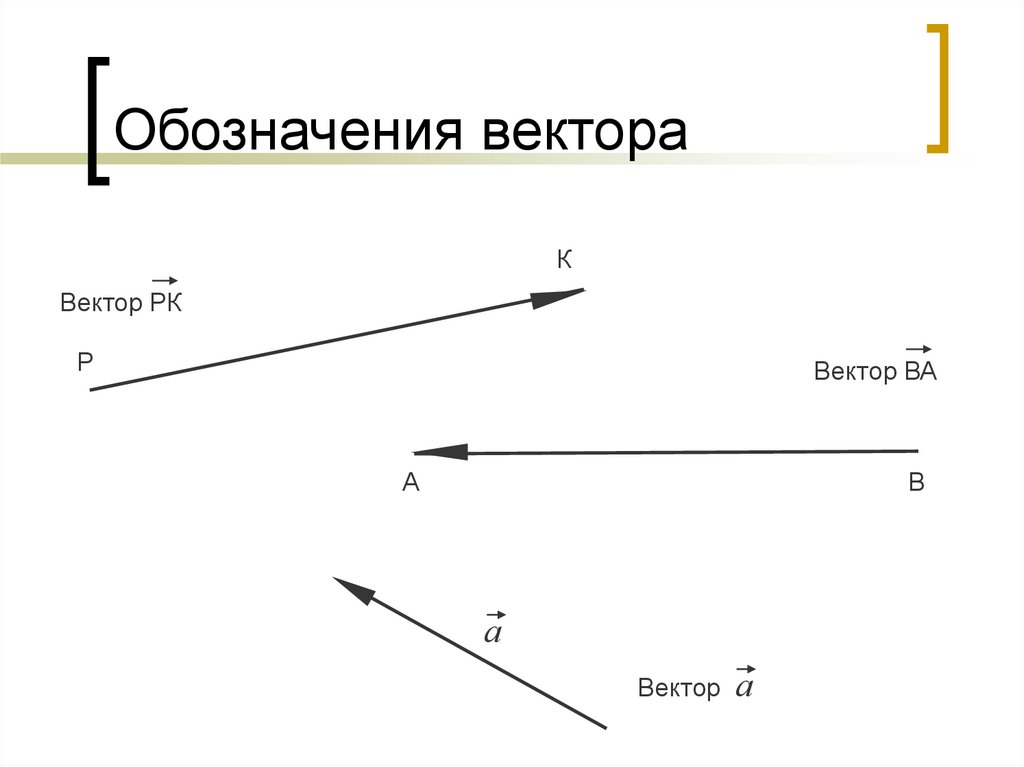
Длина вектора называется его Модулем, обозначается или и равна длине любого его представителя, т. е. расстоянию между начальной и конечной точками связного вектора . Вектор, длина которого равна нулю, называется Нуль-вектором и обозначается .
Два вектора называются равными, если:
1. равны их длины;
2. они параллельны;
3. они направлены в одну сторону.
Иными словами, равные векторы получаются один из другого параллельным переносом в пространстве.
Векторы называются Коллинеарными, если они расположены на одной или на параллельных прямых, и
Вектор, длина которого равна единице, называется Единичным вектором Или Ортом. Орт обозначатся .
| < Предыдущая | Следующая > |
|---|
Векторы. Основные понятия — презентация онлайн
1.
 В е к т о р ы. О с н о в н ы е п о н я т и я.a
В е к т о р ы. О с н о в н ы е п о н я т и я.aВектором
отрезок.
называется
направленный
Обозначают векторы символами a
или AB , где А- начало, а B-конец
направленного отрезка .
В
А
a
• Нулевым вектором (обозначается 0 )
называется вектор, начало и конец
которого совпадают.
• Расстояние между началом и концом
вектора называется его длиной, или
модулем или абсолютной величиной.
• Векторы называются коллинеарными,
если они расположены на одной прямой
или на параллельных прямых
• Векторы называются
компланарными, если они параллельны
одной плоскости.
• Векторы называются равными,
если они сонаправлены и имеют
равные длины.
• Два вектора, имеющие равные длины,
коллинеарные и противоположно
направленные, наз. противоположными.
• Вектор, длина которого равна 1,
называется единичным вектором или
ортом.
• Ортом вектора a называется
соноправленный ему вектор и
обозначается
a0
6.
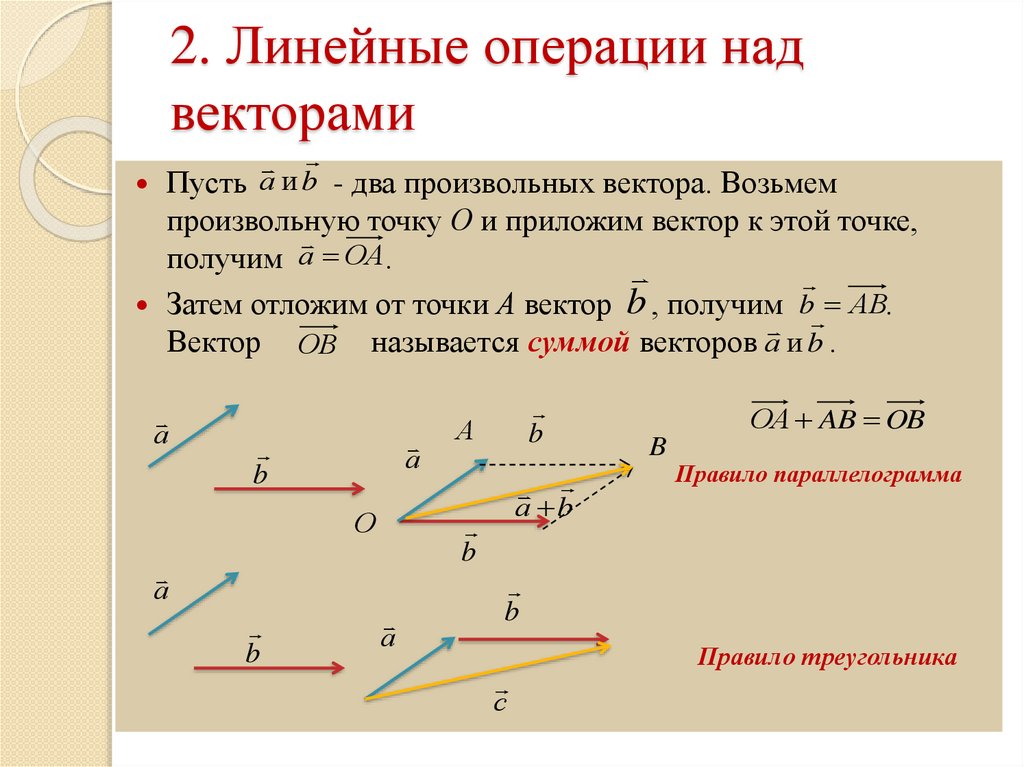
 Линейные операции над векторамиЛинейными операциями называют
Линейные операции над векторамиЛинейными операциями называютоперации сложения и вычитания
векторов и умножения вектора на
число.
8. Сложение векторов
c a bПравило треугольника.
c
b
a
c
9. Правило параллелограмма
ac
b
10. Сумма нескольких векторов
bc
a
a b c d
d
11. Вычитание векторов
ac
b
c a b
12. Свойства
a b b aa 0 a
a (b c) (a b) c
a ( a) 0
14. Умножение вектора на число
Произведением вектораaна
действительное число называется
b a
b
вектор
(обозначают
),
определяемый следующими условиями:
b a
1.
,
2. b a при
0 .
0и
b aпри
15. Умножение вектора на число
a1
b
2
3a
c
c
b
16. Свойства
( )a ( a) ( a)( )a a a
( a b) a b
1 a a
( 1) a a
• Отсюда вытекает условие коллинеарности
векторов: два ненулевых вектора
коллинеарны тогда и только тогда, когда
имеет место равенство
b a, 0.
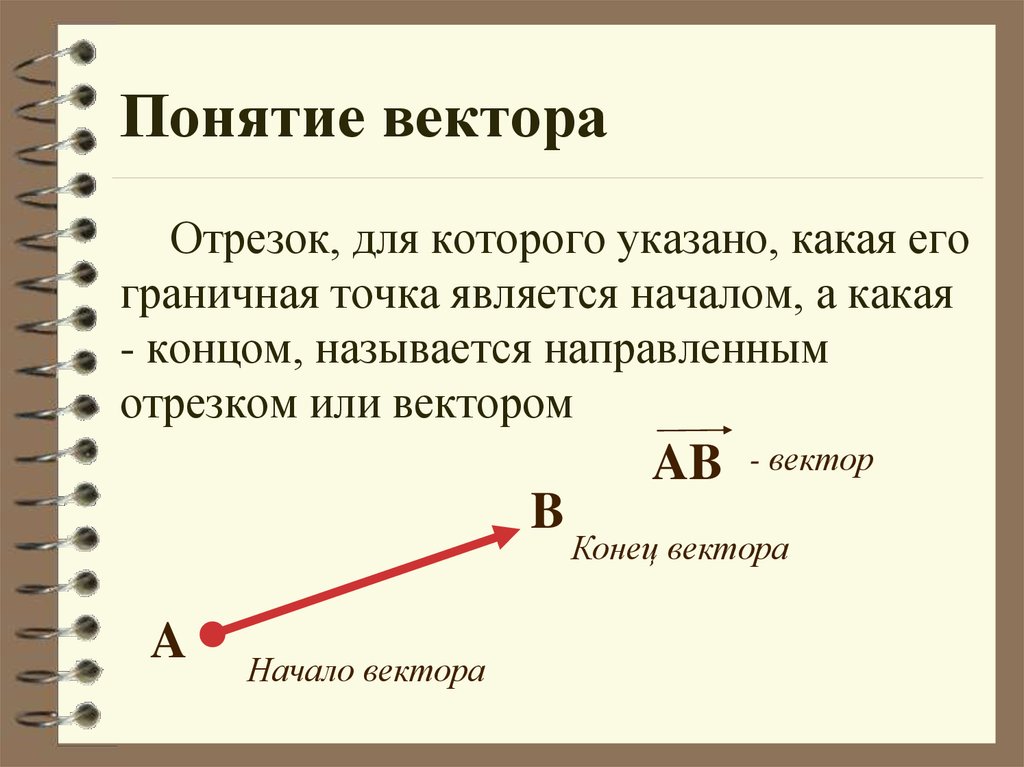
Если a 0 орт вектора a , то
a a a0
и тогда
a0
1
a
a
19. Пример
В треугольнике ABC сторона AB разделена на три равныечасти точками M и N.
Пусть CA a , CB b, выразить вектор
CM
через
a
b.
и
Решение
А
M
N
С
В
1
AM AB,
3
AB b a,
1
1
1
2
1
CM CM AM a b a a b a a b
3
3
3
3
3
21. Угол между двумя векторами
• Углом между векторами наз-сянаименьший угол 0 , на который
надо повернуть один из векторов до его
совпадения со вторым.
• Под углом между вектором и осью понимают
угол между вектором и единичным вектором,
расположенным на оси
a
l0
l
23. Проекция вектора на ось и составляющая вектора на оси
BA
l0
A1
)
B1
l
l
• Проекцией вектора AB на ось
называется разность x2 x1 между
координатами проекций конца и начала
вектора на эту ось.
Обозначается
прl AB .
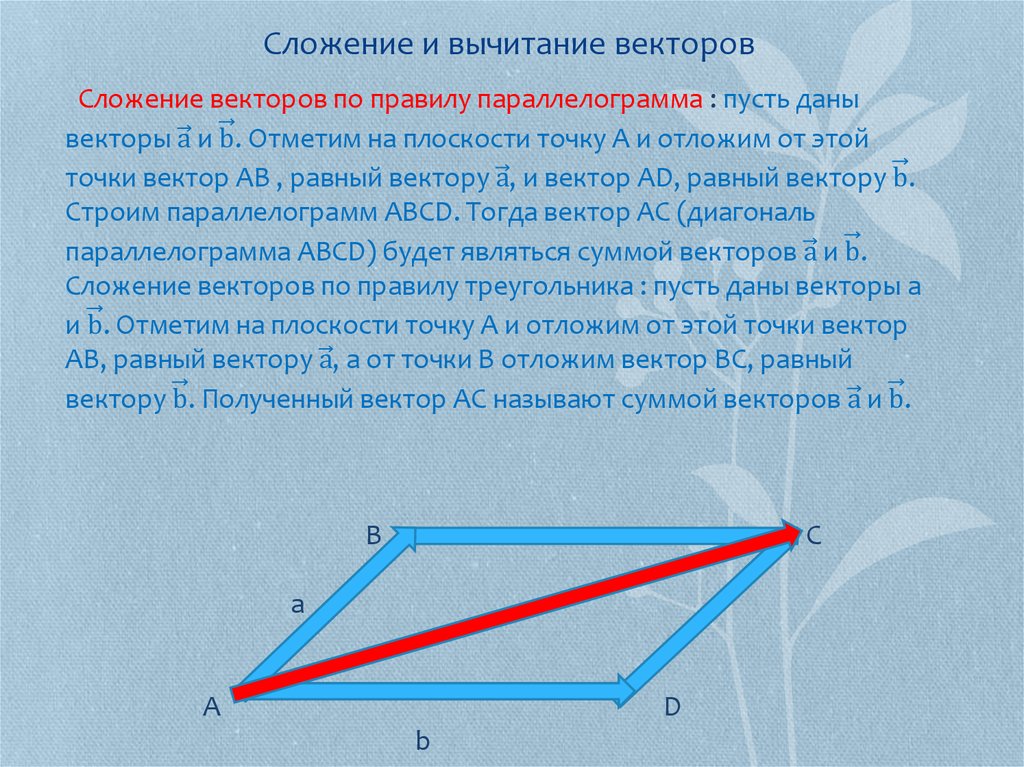
• Если — острый, то прl AB 0;
если — тупой, то прl AB 0;
если , то прl AB 0.
2
• Вектор A1 B1 наз. составляющей вектора
AB по оси l и обозначается
A1 B1 состl AB прl AB l0 x2 x1 l0
1) пр l AB АВ cos AB, l ;
3) пр a пр a.
2) прl a b прl a прl b;
l
l
29. Линейная зависимость векторов
• Векторыa1 , a2 ,…, an
наз-ся линейно
зависимыми, если существуют числа
1 , 2 ,…, n
не все равные 0, для
которых имеет место равенство
1 a1 2 a2 … n an 0 (*)
3
n
2
a1 a2 a3 … an
1
1
1
a1 2 a2 3 a3 … n an
2 a2 3 a3 … n an линейная
комбинация векторов
• Векторы
a1 , a2 ,…, an
наз-ся
линейно независимыми, если равенство
1 a1 2 a2 … n an 0
выполняется только при
1 2 … n 0
• Для того чтобы векторы были линейно
зависимы, необходимо и достаточно,
чтобы хотя бы один из этих векторов
можно было представить в виде
линейной комбинации остальных.
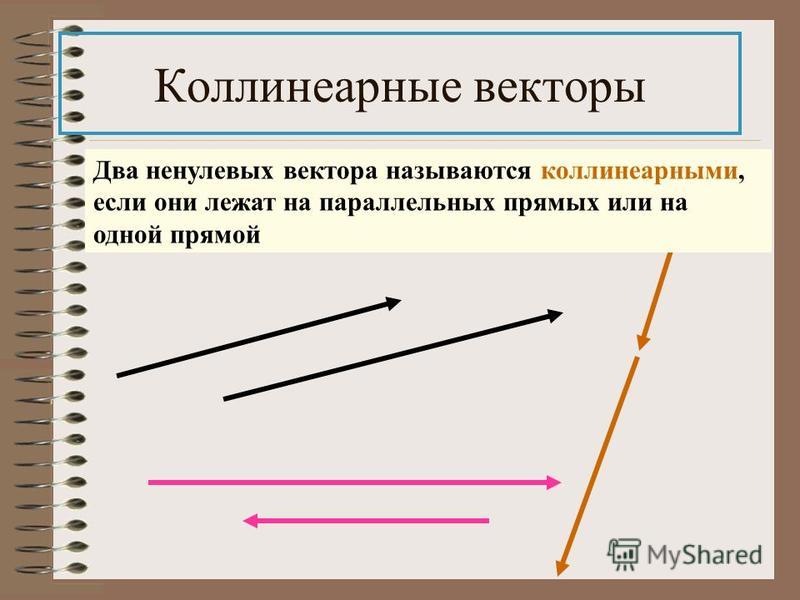
• Всякие три вектора на плоскости
линейно зависимы.
• Рассмотрим три вектора на плоскости
a, b, c
C
B1
B
A
D
D1
AC AB1 AD1
AB1 1 AB
AD1 2 AD
AC 1 AB 2 AD
• Для того чтобы два вектора были
линейно независимы, необходимо и
достаточно, чтобы они были
неколлинеарны.
• Для того чтобы три вектора в
пространстве были линейно
независимы, необходимо и достаточно,
чтобы они были некомпланарны.
• Максимальное число линейно
независимых векторов на плоскости
равно двум.
• Максимальное число линейно
независимых векторов в пространстве
равно трём.
38. Базис на плоскости и в пространстве
• Базисом на плоскости называютдва любых линейно независимых
вектора.
Т. Разложение любого вектора
на плоскости по базису b, c
является единственным
a
• Базисом в пространстве называют
три любых линейно независимых
вектора.
Т. Разложение любого вектора a
в пространстве по базису b, c, d
является единственным
41.
 Прямоугольный декартовый базисZ
Прямоугольный декартовый базисZi j k,
i j k 1.
i
k
Y
j
X
Z
k
A
a
Y
O
i
X
j
Z
D
A
k
i
X
B
Y
a
O
j
C
E
OA OB BE EA
OA OB OD OC
OB прox a i
прox a a x
OC прoy a j
прoy a a y
OD прoz a k
прoz a a z
a ax i a y j az k
46. Линейные операции над векторами в координатной форме
• Пустьa ax i a y j az k
b b x i b y j bz k
тогда:
1) a b (a x
2)
bx ) i ( a y b y ) j ( a z bz ) k
a a x i a y j a z k
ax a y az
3) a || b
bx b y bz
4)
a a a a
2
x
2
y
2
z
A x1 ; y1 ; z1
B x2 ; y 2 ; z 2
AB x2 x1 i y 2 y1 j z 2 z1 k
AB
x
x1 y 2 y1 z 2 z1
2
2
2
2
49. Направляющие косинусы
ZM
a
))
O
X
Y
• Пусть дан вектор
a ax i a y j az k
a x прox a a cos
a y прoy a a cos
a z прoz a a cos
ax
cos
a
cos
ay
a
az
cos
a
2
2
2
cos cos cos 1
54.
 Координаты единичного вектораa 0 cos , cos , cos ,
Координаты единичного вектораa 0 cos , cos , cos ,55. Пример
Найти косинусы углов, которые, вектор AB составляет сосями координат, если А (1,2,3) и В (2,4,5).
Решение.
AB 2 1;4 2;5 3 1;2;2 ,
AB 12 22 22 3,
тогда
1
2
2
cos , cos , cos
3
3
3
56. Деление отрезка в данном отношении
A2M
A1
A1 x1 ; y1 ; z1
A2 x2 ; y 2 ; z 2
M x; y; z
A1 M
MA2
x1 x 2
x
1
y1 y 2
y
1
z1 z 2
z
1
• Если
1,
т.е.
A1 M MA2
x
1 x2
x
2
y1 y2
y
2
z
1 z2
z
2
, то
61. Скалярное произведение векторов
Скалярным произведением векторовназывается
произведение
их
модулей на косинус угла между
ними.
a b a b cos
63. Условие перпендикулярности векторов
a b a b 0a b a прa b
a b b прb a
65. Проекция вектора на вектор
a bпрb a
b
66.
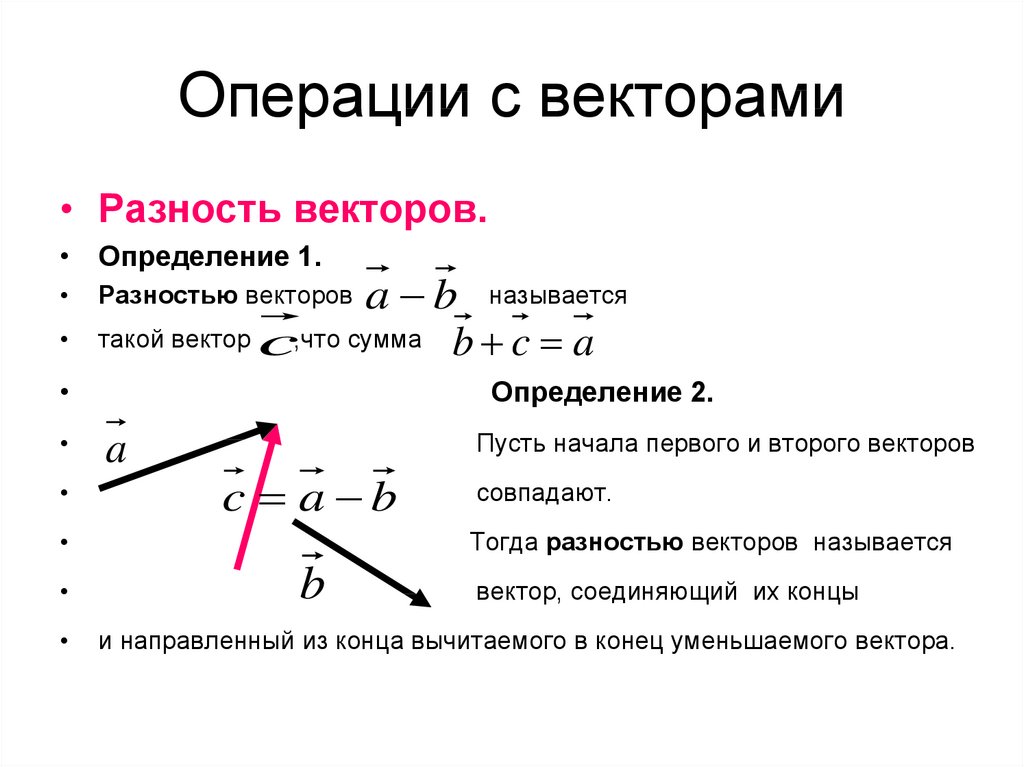 Угол между векторамиcos
Угол между векторамиcos a b
a b
x1 x2 y1 y 2 z1 z 2
.
2
x y z x y z2
2
1
2
1
2
1
2
2
2
2
67. Физический смысл скалярного произведения
Работа постоянной силы напрямолинейном участке пути равна
скалярному произведению вектора
силы на вектор перемещения.
68. Физический смысл скалярного произведения
Fl
A F l
69. Свойства скалярного произведения
1) a b b a2) (a b) ( a) b a ( b)
2
3) a a
a
2
a
2
• Пусть даны два вектора
a ax i a y j az k
b bx i b y j b z k
Найдем скалярное произведение этих
векторов
(ax i a y j az k ) (bx i by j bz k )
= a x bx
a y by az bz
2
2
i i i i 1
2
2
2
2
j j j j 1
k k k k 1
i j 0
j k 0
i k 0
73. Пример
Дан векторугол
c 2a 3b , причем a 4
между векторами
Найти модуль вектора
c.
a
и
b
равен
,
b 5
60 0.
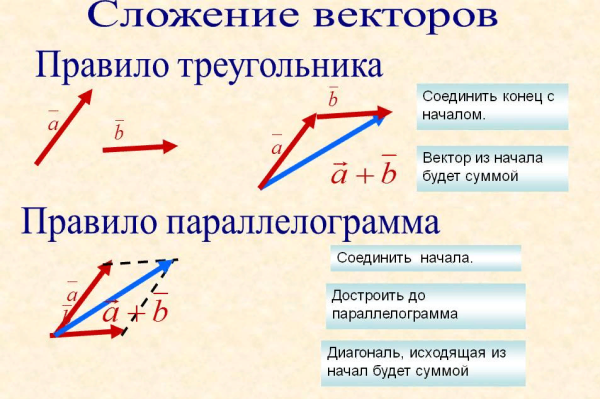
,
Решение
с
a a
2a 3b
2
2
с
2
2
4a 12a b 9b .
2
4 16
2
2
2
b b 5 25,
a b a b cos 4 5 cos 60
то
2
c
4 16 12 10 9 25
2
0
10,
409 .
75. Векторное произведение векторов
• Векторным произведением вектора aна вектор b наз. вектор c a b,
удовлетворяющий следующим условиям:
1)
2)
c a b sin
c
a
c
b
3)векторы образуют правую тройку
77. Понятие «правой» тройки векторов
a , b, cТройку векторов
называют правой, если
направление вектора c таково, что, смотря из его конца
вдоль вектора, кратчайший поворот от вектора
a
к вектору b будет виден против движения часовой
стрелки.
с
a , b, с
b
— правая тройка
a
78. Обозначение векторного произведения векторов
cc a b
b
a
79. Свойства векторного произведения
a b b aa b 0 a 0
или
b 0 или a b
a a 0
80.
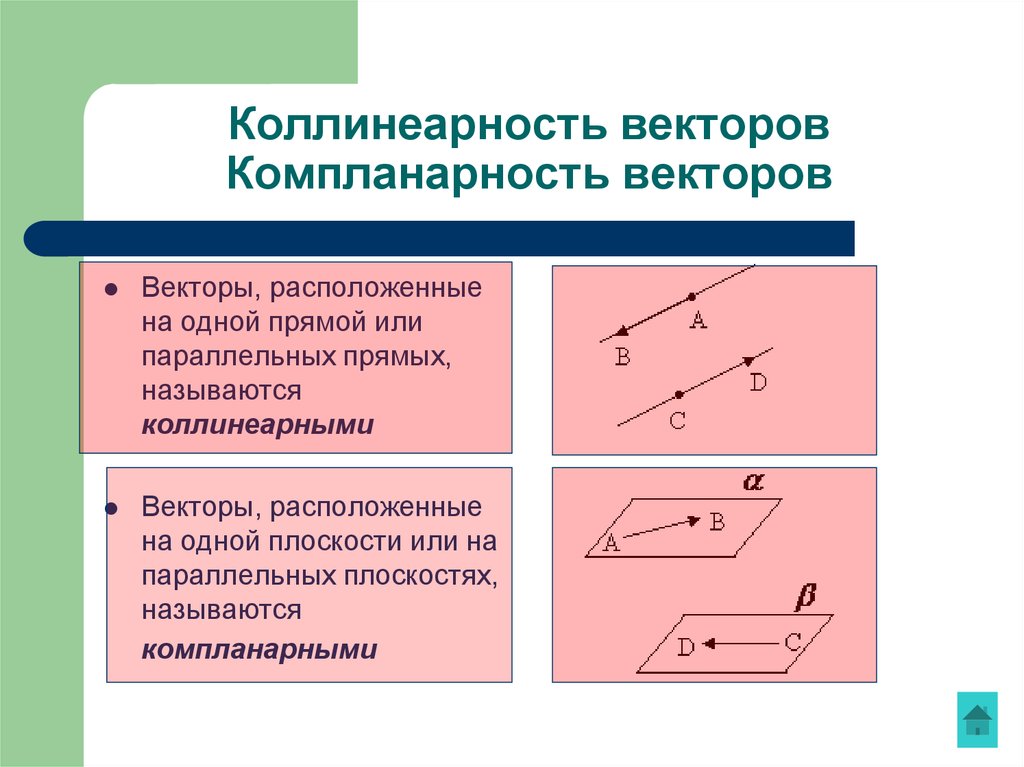 Свойства векторного произведения( a b) c a c b c
Свойства векторного произведения( a b) c a c b c( a b ) ( a ) b a ( b )
81. Физический смысл векторного произведения
FO
M
82. Физический смысл векторного произведения
Если F – сила, приложенная к точке М,то момент этой силы относительно точки
О равен векторному произведению
векторов F и OM .
83. Векторные произведения координатных векторов
kj
i
i j k,
j i k ,
k i j,
i k j,
j k i.
k j i.
a b ax i a y j az k bx i by j bz k
axbx i i axby i j axbz i k a ybx j i
a yby j j a ybz j k az bx k i az by k j
az bz k k
axby k axbz j a y bx k a y bz i az bx j az by i
a y bz az by i axbz az bx j axby a y bx k
ay
by
az
ax
i
bz
bx
ax
az
j
bx
bz
ay
k
by
86. Векторное произведение в координатной форме
ia b ax
bx
j
k
ay
az
by
bz
87. Пример
Найти векторное произведение векторовa 2i 3 j k ,
b 3i j 4k .
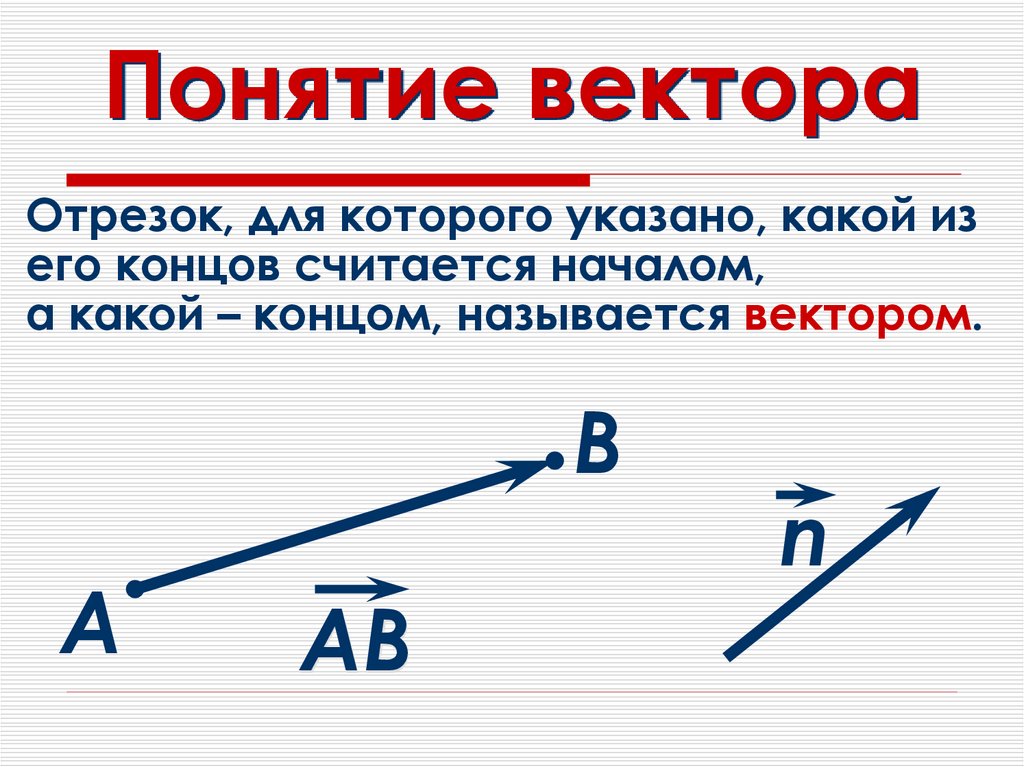
Решение
i
a b 2
k
3 1
1
i
1 4
3 1 4
2
1
3 4
j
3
j
2
3
3 1
k 13i 5 j 11k .
B
a
A
b
C
S a b sin
89. Площадь параллелограмма
S пар a b90. Площадь треугольника
1S a b
2
91. Пример
Найти2a 3b a 2b ,
если
Решение
a 2, b 1, 900.
2a 3b a 2b
2 a a 3 b a 4 a b 6 b b
7 b a 7 b a sin
7 1 2 sin 90 14.
0
92. Смешанное произведение
Смешанным произведением трёхвекторов называется произведение
вида :
( a b) c
a b
ay
by
az
ax
i
bz
bx
ax
az
j
bx
bz
ay
by
k
c cx i c y j cz k
ay
abc
by
az
ax
cx
bz
bx
ax
az
cy
bx
bz
ay
cz
by
94. Смешанное произведение
ax a y azabc b x b y b z
cx c y cz
95. Компланарные векторы
Три вектора называются компланарными, еслиони лежат в одной или параллельных плоскостях.

p
a
n
b
c
a, b, c компланарн ы,
m
m, n, p некомплана рны.
96. Условие компланарности трёх векторов
Еслиa, b, c
компланарны, то
ax
bx
ay
by
az
bz 0.
cx
cy
cz
Элементами определителя являются координаты
векторов
a , b, c
c
a
b
98. Объём параллелепипеда
V abc99. Объём тетраэдра
Vтет1
abc
6
Основные понятия векторов
Неподвижный вектор $$\overrightarrow{AB}$$ — это отрезок, определяемый началом $$A$$ и концом $$B$$.
Основные характеристики фиксированного вектора $$\overrightarrow{AB}$$ следующие:
- Угол фиксированного вектора $$\overrightarrow{AB}$$: определяется прямой линией который содержит $$\overrightarrow{AB}$$ и все его параллели.
- Направление фиксированного вектора $$\overrightarrow{AB}$$: определяет начало и конец данного вектора.
- Величина фиксированного вектора $$\overrightarrow{AB}$$: это длина отрезка $$AB$$.
 Он представлен $$|\overrightarrow{AB}|$$ и всегда является положительным числом или нулем.
Он представлен $$|\overrightarrow{AB}|$$ и всегда является положительным числом или нулем.
Например, есть улица с односторонним движением. На этой улице может быть даже две полосы, но обе полосы могут двигаться только в одном направлении.
Классы векторов
Два вектора эквивалентны, если они имеют одинаковую величину, угол и направление.
Векторы, представленные на следующем рисунке, эквивалентны.
Множество всех векторов, эквивалентных данному вектору $$\overrightarrow{AB}$$, называется свободным вектором. То есть свободные векторы имеют одинаковую величину, угол и направление.
Связанные векторы — это эквивалентные векторы, лежащие на одной прямой. А именно, есть фиксированные векторы, которые имеют одинаковую величину, угол и направление и лежат на одной прямой.
Обратные векторы имеют одинаковую величину и угол, но разные направления.
Векторы $$\vec{u}$$ и $$-\vec{u}$$ являются обратными, поскольку имеют одинаковую величину и угол, но разное направление.
Единичные векторы — это те, величина которых равна $$1$$, то есть $$|\vec{u}|=1$$.
Как определить вектор
Зная координаты начала координат $$A$$ и конечной точки $$B$$, можно определить компоненты вектора $$\overrightarrow{AB}$$, соединяющие $$A$$ и $$B$$, вычитая координаты начала координат из координат конца: $$$ \overrightarrow{AB}= (x_2,y_2)-(x_1,y_1)=(x_2-x_1, y_2-y_1)$$$ Где $$A$$ — это точка $$(x_1,y_1)$$, а $$B$$ — точка $$(x_2,y_2)$$. 92}=\sqrt{25}=5$$$
Основные понятия и соглашения, векторы, скаляры, операции над векторами, векторная алгебра, скалярное произведение, перекрестное произведение, тройное произведение
Основные понятия и соглашения, векторы, скаляры, операции по векторам, векторная алгебра, скалярное произведение, перекрестное произведение, тройное произведениеSolitaryRoad.com
Владелец сайта: Джеймс Миллер
[ Дом ] [ Вверх ] [ Информация ] [ Почта ]
ОСНОВНЫЕ ПОНЯТИЯ И УСЛОВНЫЕ ОБОЗНАЧЕНИЯ, ВЕКТОРЫ, СКАЛЯРЫ, ОПЕРАЦИИ НАД ВЕКТОРАМИ, ВЕКТОРНАЯ АЛГЕБРА, СКОРОСТНОЕ ПРОИЗВЕДЕНИЕ, ПЕРЕКРЕСТНОЕ ПРОИЗВЕДЕНИЕ, ТРОЙНОЕ ПРОИЗВЕДЕНИЕ
Векторный анализ связан с векторами и операциями с ними. Его происхождение лежит в
области физики. В области физики некоторые вещи, такие как температура, масса, длина, объем,
плотность, время, расстояние и скорость обладают только «величиной». Другие вещи, такие как сила, скорость
и ускорение обладают как величиной, так и направлением. Те вещи, которые обладают только
величины называются скалярными величинами; те, которые имеют как величину, так и направление
относятся к векторным величинам.
Его происхождение лежит в
области физики. В области физики некоторые вещи, такие как температура, масса, длина, объем,
плотность, время, расстояние и скорость обладают только «величиной». Другие вещи, такие как сила, скорость
и ускорение обладают как величиной, так и направлением. Те вещи, которые обладают только
величины называются скалярными величинами; те, которые имеют как величину, так и направление
относятся к векторным величинам.
Векторов. Вектор представляет собой «направленный отрезок линии» (т. е. стрелку), представляющий такую величину, как сила, скорость и т. д., которые обладают как величиной, так и направление. Направление количества задается направление стрелки и величина по длине стрелки. См. рис. 1. Точка O стрелки OP называется начальной точкой вектора, а точка P конечная точка или вершина.
● Два вектора считаются равными, если они имеют одинаковая величина и направление независимо от положения их начальных точек.
● Вектор, имеющий направление, противоположное направлению вектора A
но имеющие ту же величину обозначаются -А.
Нулевой вектор. Если точки O и P вектора OP на рис.1 совпадают, то вектор OP называется нулевой вектор, обозначаемый 0. Он имеет нулевую величину и не имеет определенного направления.
Сложение векторов. Для векторов определена операция сложения. Сумма двух векторы A и B — это вектор C, как показано на рис. 2а. Поместим начальную точку B в конечная точка A и C — это вектор, идущий от начальной точки A в конечную точку B. Мы напишите C = A + B.
● Разница (A — B) двух векторов A и B равна сумма А и (-В) т.е. А — В = А + (-В). вектор A — B — это вектор, идущий от вершины B к наконечник А. См. рис. 2б. Мы видим из рисунка, что В + (А — В) = А.
По умолчанию Скаляр. Число в отличие от вектора. Слово «скаляр» используется для
отличие от слова «вектор». Это принято в любом контексте, когда векторы и действительные числа
оба обсуждаются, чтобы называть действительные числа скалярами.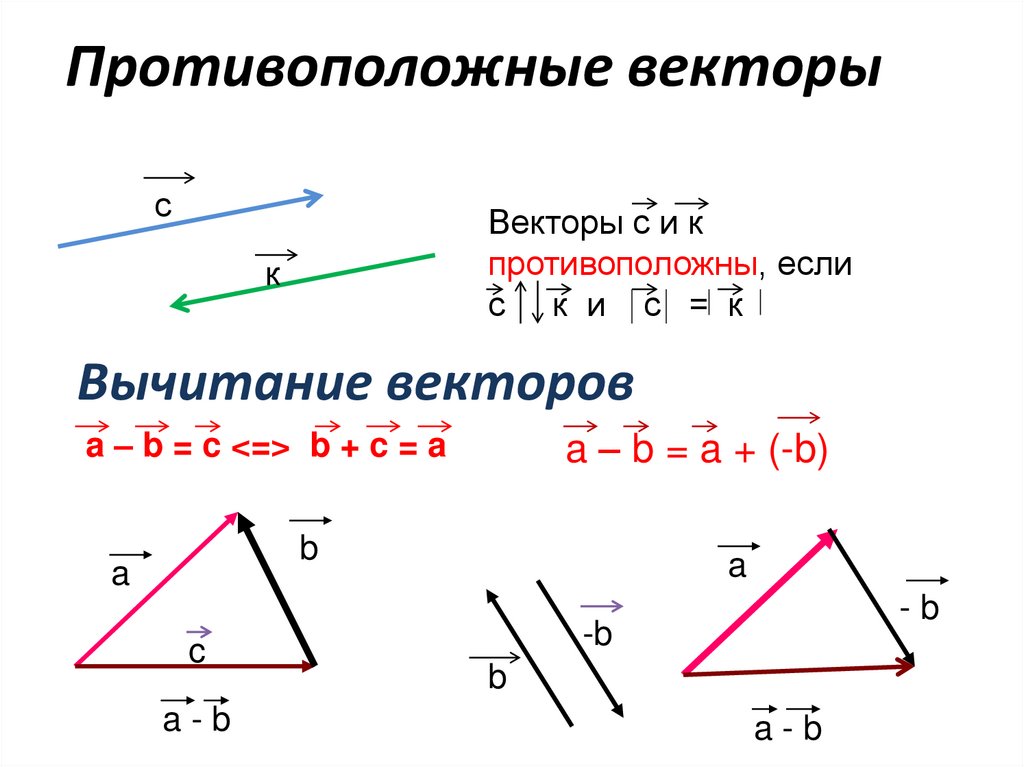
Произведение вектора A на скаляр m. Произведение вектора A на скаляр m равно вектор mA с величиной |m| раз больше величины A и с направлением, таким же, как или противоположен A, в зависимости от того, является ли m положительным или отрицательным. Если m = 0, mA является нулевым вектором.
Единичный вектор. Единичный вектор — это вектор, имеющий единичную величину, т. е. величину 1,
.
Аналитическое представление векторы. Пусть i, j и k — единичные векторы направленные вдоль положительных осей x, y и z правую декартову систему координат, как изображен на рис. 3. Пусть A — вектор, начальный точка находится в начале координат O и конечная точка находится в координатах (a 1 , 2 , 3 ). Затем вектор A может быть представлен как
(1) A = a 1 i + a 2 j + a 3 k .
См. рис. 4.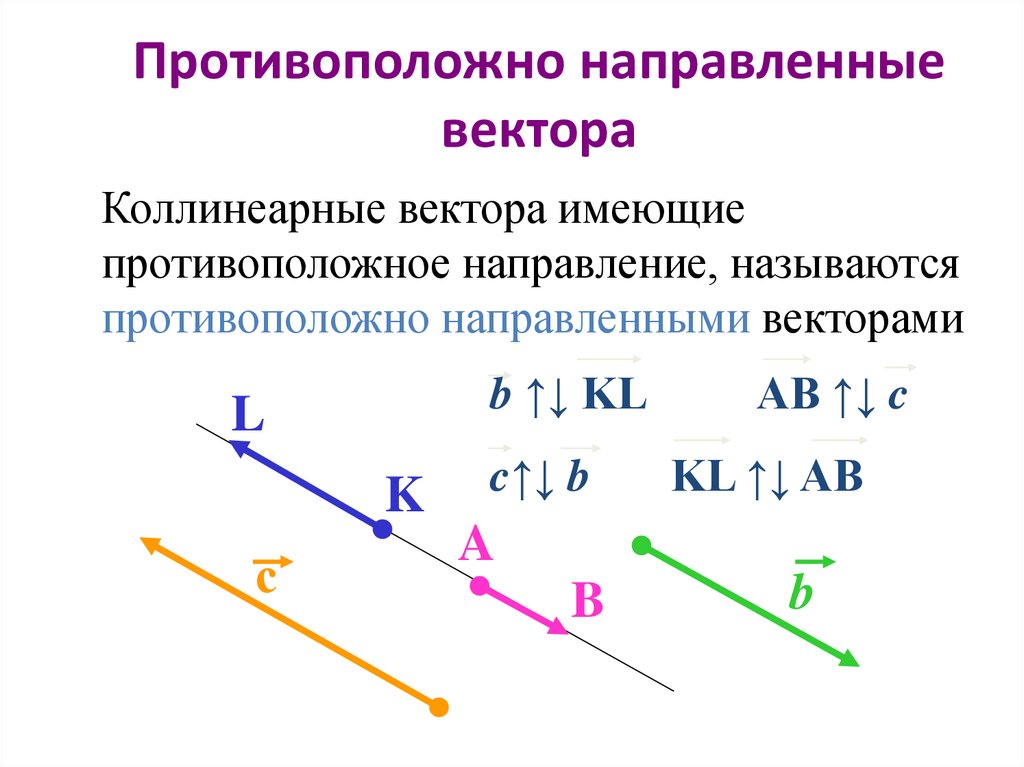 Векторы a 1 i, a 2 j и a 3 k равны
называемые векторами компонентов A в x, y
и z направлениях соответственно. 1 , 2 и 3 называется компонентами x, y и z матрицы A.
величина А равна
Векторы a 1 i, a 2 j и a 3 k равны
называемые векторами компонентов A в x, y
и z направлениях соответственно. 1 , 2 и 3 называется компонентами x, y и z матрицы A.
величина А равна
a 1 , a 2 и a 3 представляют величины проекции вектора A на оси x, y и z соответственно.
Любой вектор может быть представлен в форме (1) выше.
Второе представление вектора. Вектор также часто обозначается просто упорядоченная тройка, написанная вертикально или горизонтально, как в
или
A = (а 1 , а 2 , а 3 ),
упорядоченная тройка, состоящая из трех компонентов.
Сумма двух векторов, выраженная в аналитической форме, получается сложением соответствующих
компонентов, т.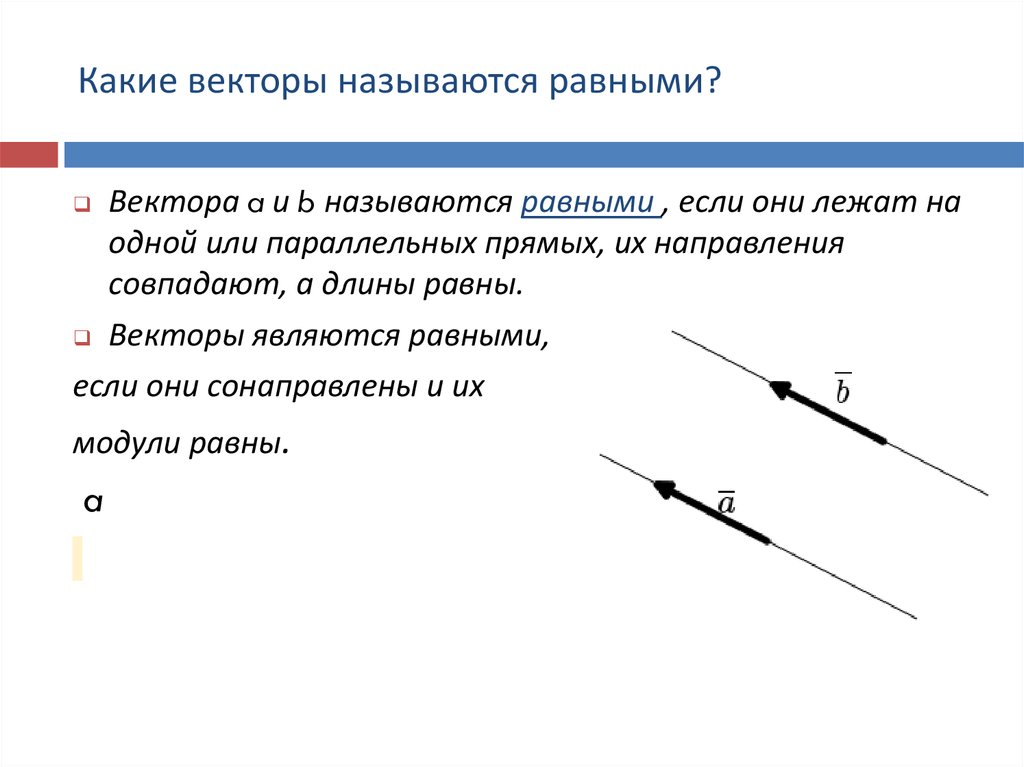
A + B = (a 1 + b 1 ) i + (a 2 + b 2 ) j + (a 3 + b 3 ) k
По умолчанию Абсолютное значение вектора. Числовая длина вектора; величина вектор. Абсолютное значение представляет собой квадратный корень из суммы квадратов компонентов вдоль оси. Абсолютное значение a i + b j + c k равно
.
Син. Числовое значение
Законы векторной алгебры. Если A, B и C — векторы, а m и n — скаляры, то
1. A + B = B + A Переместительный закон сложения
2. A + (B + C) = (A + B) + C Ассоциативный закон сложения
3. мА = Am
4. n(nA) = (mn)A
5. (м + н)А = мА + нА
6. m(A + B) = mA + mB
m(A + B) = mA + mB
7. A + 0 = A Аддитивная идентичность
8. A + (-A) = 0 Аддитивный обратный
Эти законы позволяют нам обращаться с векторными уравнениями так же, как с обычными алгебраическими уравнениями. Например, если A + B = C, то путем перестановки A = C — B.
В векторном анализе часто используется вектор положения или радиус-вектор.
Вектор положения (или радиус-вектор). Вектор положения — это вектор, который простирается от начало системы координат в некоторую точку (x, y, z) в пространстве, т.е. вектор
r = xi + yj + zk
или
r = (x, y, z)
По умолчанию Скалярное произведение. Скалярное произведение A∙B двух векторов A и B определяется как произведение
величин A и B и косинуса угла θ между ними, т.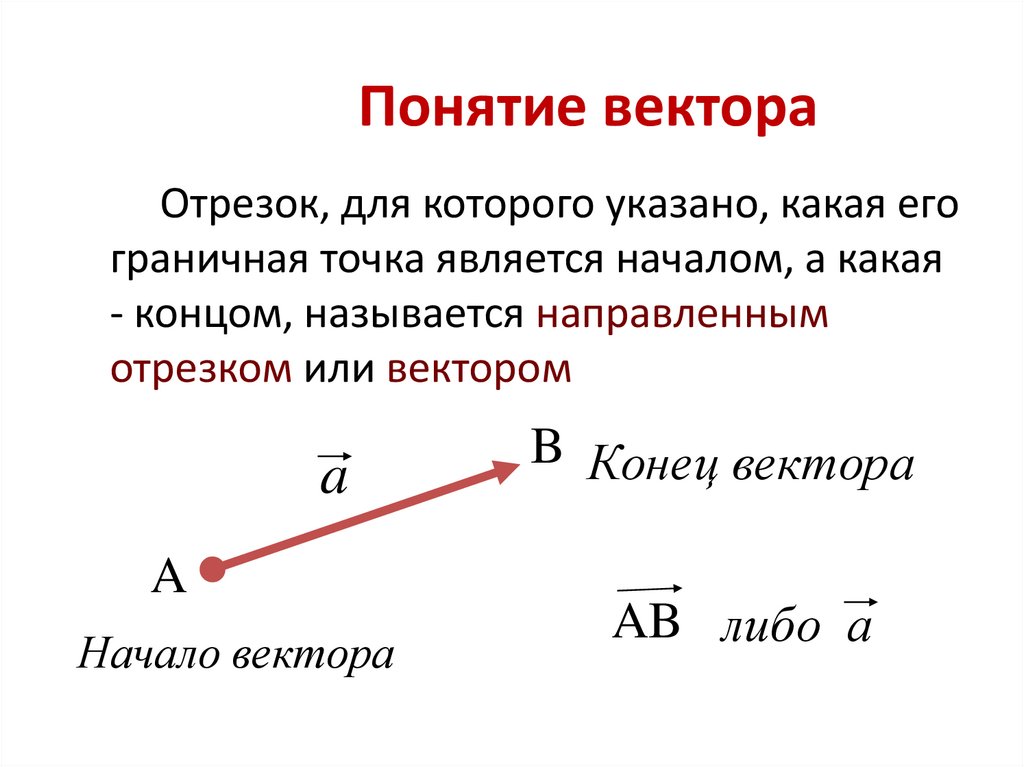 е.
е.
A∙B = |A| |Б| cos θ
Син. скалярное произведение, скалярное произведение, внутреннее произведение
Обратите внимание, что A∙B является скаляром, а не вектором.
● A∙B = a 1 b 1 + a 2 b 2 + a 3 b 3
где A = a 1 i + a 2 j + a 3 k и B = b 1 i + b 2 к + б 3 к
Длина вектора в виде скалярного произведения. Длина вектора X равна
.
Законы действительны для скалярных произведений:
1] A∙B = B∙A Закон
2] A∙(B + C) = A∙B + A∙C Левый распределительный закон
3] (A + B)∙C = A∙C + B∙C Правораспределительный закон
4] m(A∙B) = (mA)∙B = A∙(mB) = (A∙B)m где m — скаляр
5] i∙i = j∙j =k∙k = 1, i∙j = j∙k = k∙i = 0
6] Если A∙B = 0 и A и B не равны нулю
векторы, то А и В перпендикулярны.
По умолчанию Векторное (или перекрестное) произведение. векторное (или перекрестное) произведение A×B двух векторов A и B определяется как
A×B = |A| |Б| грех θ и
, где θ — угол от A до B, а u — единичный вектор, перпендикулярный плоскости A и B, и так направлено, что если вы согните пальцы правой руки в направлении, которое переводит А в Б, ваш большой палец указывает в направлении u (т. е. правый винт, завернутый в направлении u переводит А в В). См. рис. 5.
Если A = a 1 i + a 2 j + a 3 k и B = b 1 i + b 2 j + b 3 k , затем
= (A 2 B 3 — B 2 A 3 ) I + (A 3 B 1 — B 3 A 1 ) J + (A 1 B 1 ) J + (A 1 B B 1 ) (A 1 B 1 ) (A 1 A 1 ) (A 1 A 1 ) (A 1 A 1 ). 2 — б 1 а 2 ) к
2 — б 1 а 2 ) к
Правила действительны для перекрестных произведений:
1] A×B = — B×A
2] A×(B + C) = A×B + A×C Левый распределительный закон
3] (A + B)×C = A×C + B×C Правораспределительный закон
4] m(A×B) = (mA)×B = A×(mB) = (A×B)m , где m — скаляр
5] i×i = j×j =k×k = 0 i×j = j×k = k×i = 1
6] Если A×B = 0 и A и B ненулевые векторы, то A и B параллельны..
Тройные продукты. Умножение точек и векторных произведений трех векторов A, B и C производить значимые продукты следующих форм:
1) (A∙B)C
2) A∙(B×C) скалярное тройное произведение или коробочное произведение
3) A×(B×C) векторное тройное произведение
Скалярное тройное произведение A∙(B×C). Пусть А = а 1 i + a 2 j + a 3 k , B = b 1 i + b 2 j + b 3 k и C = c 1 i
+ с 2 к + с 3 к . Затем
Пусть А = а 1 i + a 2 j + a 3 k , B = b 1 i + b 2 j + b 3 k и C = c 1 i
+ с 2 к + с 3 к . Затем
, что равно объему параллелепипеда с ребрами А, В и С, или отрицательному значению этот объем, в зависимости от того, как A, B и C образуют или не образуют правовинтовую систему.
● A∙(B×C) = (A×B)∙C т. е. точку и крестик можно поменять местами без изменения Значение.
В скалярном тройном произведении A∙(B×C) скобки иногда опускают и записывают А∙В×С или А×В∙С . Иногда его обозначают просто [ABC]. Его еще называют коробкой. продукт.
Векторное тройное произведение. Произведение A×(B×C) называется векторным тройным произведением.
1] A×(B×C) = B(A∙C) – C(A∙B) = (A∙C)B – (A∙B)C
2] (A×B)×C = (A∙C)B — (B∙C)A
Обратите внимание, что
(A∙B)C А(Б∙С)
А×(В×С) (А×В)×С
Обобщенное тождество Лагранжа.
Для векторов A, B, C, D верно следующее
(A×B)∙(C×D) = (A∙C)(B∙D) — (A∙D)(B∙C)
Тождество Лагранжа.
(A×B)∙(A×B) = (A∙A)(B∙B) — (A∙B) 2
Еще от SolitaryRoad.com:
Путь Истины и Жизни
Божье послание миру
Иисус Христос и Его Учение
Мудрые слова
Путь просветления, мудрости и понимания
Путь истинного христианства
Америка, коррумпированная, развратная, бессовестная страна
О честности и ее отсутствии
Критерием христианства человека является то, что он есть
Кто попадет в рай?
Высшее лицо
О вере и делах
Девяносто пять процентов проблем, с которыми большинство людей пришли от личной глупости
Либерализм, социализм и современное государство всеобщего благосостояния
Желание причинить вред, мотив поведения
Учение это:
О современном интеллектуализме
О гомосексуализме
О самодостаточной загородной жизни, приусадебном хозяйстве
Принципы жизни
Тематические пословицы, поучения,
Цитаты. Общие поговорки. Альманах бедного Ричарда.
Общие поговорки. Альманах бедного Ричарда.
Америка сбилась с пути
Действительно большие грехи
Теория формирования характера
Моральное извращение
Ты то, что ты ешь
Люди как радиотюнеры — они выбирают и слушать одну длину волны и игнорировать остальные
Причина черт характера — по Аристотелю
Эти вещи идут вместе
Телевидение
Мы то, что мы едим — живем по дисциплине диеты
Избегание проблем и неприятностей в жизни
Роль привычки в формировании характера.
Истинный христианин
Что такое истинное христианство?
Личные качества истинного христианина
Что определяет характер человека?
Любовь к Богу и любовь к добродетели тесно связаны
Прогулка по одинокой дороге
Интеллектуальное неравенство между людьми и властью в хороших привычках
Инструменты сатаны. Тактика и Уловки, используемые Дьяволом.
О реакции на обиды
Настоящая христианская вера
Естественный путь – неестественный путь
Мудрость, Разум и Добродетель тесно связаны
Знание одно, мудрость другое
Мои взгляды на христианство в Америке
Самое главное в жизни это понимание
Оценка людей
Мы все примеры — хорошо это или плохо
Телевидение — духовный яд
Перводвигатель, который решает, «Кто мы есть»
Откуда берутся наши взгляды, взгляды и ценности?
Грех — дело серьезное.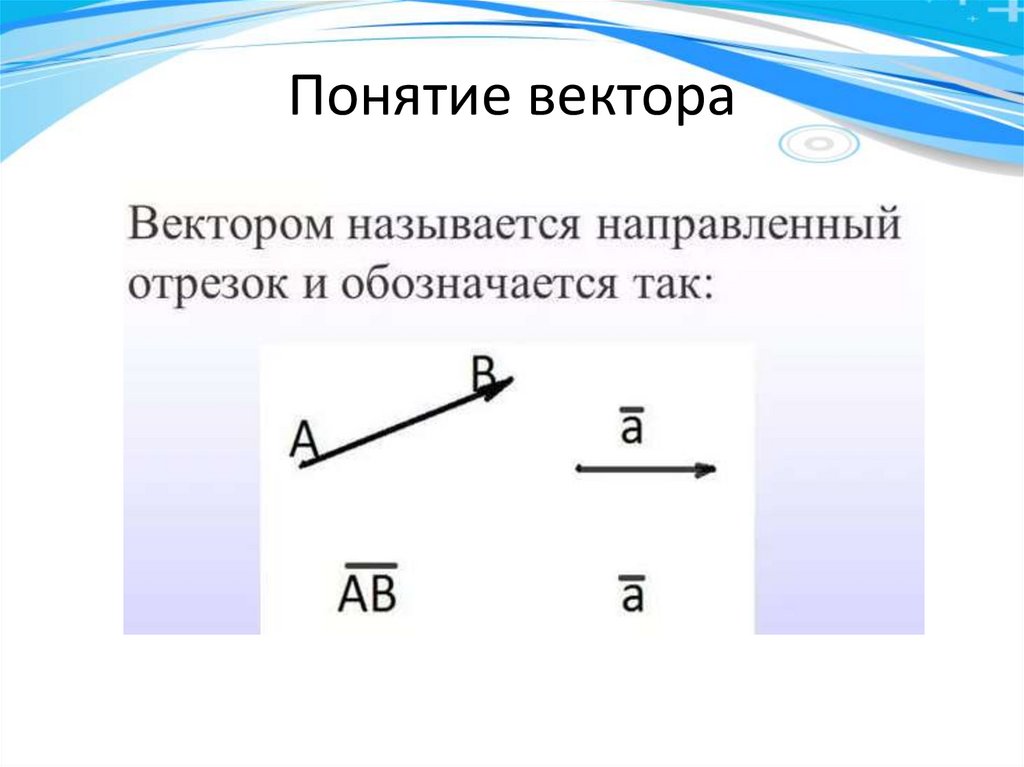

 Он представлен $$|\overrightarrow{AB}|$$ и всегда является положительным числом или нулем.
Он представлен $$|\overrightarrow{AB}|$$ и всегда является положительным числом или нулем.