2 синус в кубе х. Самые необходимые тригонометрические формулы
Формулы суммы и разности синусов и косинусов для двух углов α и β позволяют перейти от суммы указанных углов к произведению углов α + β 2 и α — β 2 . Сразу отметим, что не стоит путать формулы суммы и разности синусов и косинусов с формулами синусов и косинусов суммы и разности. Ниже мы перечислим эти формулы, приведем их вывод и покажем примеры применения для конкретных задач.
Формулы суммы и разности синусов и косинусов
Запишем, как выглядят формулы суммы и разности для синусов и для косинусов
Формулы суммы и разности для синусов
sin α + sin β = 2 sin α + β 2 cos α — β 2 sin α — sin β = 2 sin α — β 2 cos α + β 2
Формулы суммы и разности для косинусов
cos α + cos β = 2 cos α + β 2 cos α — β 2 cos α — cos β = — 2 sin α + β 2 cos α — β 2 , cos α — cos β = 2 sin α + β 2 · β — α 2
Данные формулы справедливы для любых углов α и β . Углы α + β 2 и α — β 2 называются соответственно полусуммой и полуразностью углов альфа и бета. Дадим формулировку для каждой формулы.
Дадим формулировку для каждой формулы.
Определения формул сумм и разности синусов и косинусов
Сумма синусов двух углов равна удвоенному произведению синуса полусуммы этих углов на косинус полуразности.
Разность синусов двух углов равна удвоенному произведению синуса полуразности этих углов на косинус полусуммы.
Сумма косинусов двух углов равна удвоенному произведению косинуса полусуммы и косинуса полуразности этих углов.
Разность косинусов двух углов равна удвоенному произведению синуса полусуммы на косинус полуразности этих углов, взятому с отрицательным знаком.
Вывод формул суммы и разности синусов и косинусов
Для вывода формул суммы и разности синуса и косинуса двух углов используются формулы сложения. Приведем их ниже
sin (α + β) = sin α · cos β + cos α · sin β sin (α — β) = sin α · cos β — cos α · sin β cos (α + β) = cos α · cos β — sin α · sin β cos (α — β) = cos α · cos β + sin α · sin β
Также представим сами углы в виде суммы полусумм и полуразностей.
α = α + β 2 + α — β 2 = α 2 + β 2 + α 2 — β 2 β = α + β 2 — α — β 2 = α 2 + β 2 — α 2 + β 2
Переходим непосредственно к выводу формул суммы и разности для sin и cos.
Вывод формулы суммы синусов
В сумме sin α + sin β заменим α и β на выражения для этих углов, приведенные выше. Получим
sin α + sin β = sin α + β 2 + α — β 2 + sin α + β 2 — α — β 2
Теперь к первому выражению применяем формулу сложения, а ко второму — формулу синуса разностей углов (см. формулы выше)
sin α + β 2 + α — β 2 = sin α + β 2 cos α — β 2 + cos α + β 2 sin α — β 2 sin α + β 2 — α — β 2 = sin α + β 2 cos α — β 2 — cos α + β 2 sin α — β 2 sin α + β 2 + α — β 2 + sin α + β 2 — α — β 2 = sin α + β 2 cos α — β 2 + cos α + β 2 sin α — β 2 + sin α + β 2 cos α — β 2 — cos α + β 2 sin α — β 2 Раскроем скобки, приведем подобные слагаемые и получим искомую формулу
Действия по выводу остальных формул аналогичны.
Вывод формулы разности синусов
sin α — sin β = sin α + β 2 + α — β 2 — sin α + β 2 — α — β 2 sin α + β 2 + α — β 2 — sin α + β 2 — α — β 2 = sin α + β 2 cos α — β 2 + cos α + β 2 sin α — β 2 — sin α + β 2 cos α — β 2 — cos α + β 2 sin α — β 2 = = 2 sin α — β 2 cos α + β 2
Вывод формулы суммы косинусов
cos α + cos β = cos α + β 2 + α — β 2 + cos α + β 2 — α — β 2 cos α + β 2 + α — β 2 + cos α + β 2 — α — β 2 = cos α + β 2 cos α — β 2 — sin α + β 2 sin α — β 2 + cos α + β 2 cos α — β 2 + sin α + β 2 sin α — β 2 = = 2 cos α + β 2 cos α — β 2
Вывод формулы разности косинусов
cos α — cos β = cos α + β 2 + α — β 2 — cos α + β 2 — α — β 2 cos α + β 2 + α — β 2 — cos α + β 2 — α — β 2 = cos α + β 2 cos α — β 2 — sin α + β 2 sin α — β 2 — cos α + β 2 cos α — β 2 + sin α + β 2 sin α — β 2 = = — 2 sin α + β 2 sin α — β 2
Примеры решения практических задач
Для начала, сделаем проверку одной из формул, подставив в нее конкретные значения углов. Пусть α = π 2 , β = π 6 . Вычислим значение суммы синусов этих углов. Сначала воспользуемся таблицей основных значений тригонометрических функций, а затем применим формулу для суммы синусов.
Пусть α = π 2 , β = π 6 . Вычислим значение суммы синусов этих углов. Сначала воспользуемся таблицей основных значений тригонометрических функций, а затем применим формулу для суммы синусов.
Пример 1. Проверка формулы суммы синусов двух углов
α = π 2 , β = π 6 sin π 2 + sin π 6 = 1 + 1 2 = 3 2 sin π 2 + sin π 6 = 2 sin π 2 + π 6 2 cos π 2 — π 6 2 = 2 sin π 3 cos π 6 = 2 · 3 2 · 3 2 = 3 2
Рассмотрим теперь случай, когда значения углов отличаются от основных значений, представленных в таблице. Пусть α = 165 ° , β = 75 ° . Вычислим значение разности синусов этих углов.
Пример 2. Применение формулы разности синусов
α = 165 ° , β = 75 ° sin α — sin β = sin 165 ° — sin 75 ° sin 165 — sin 75 = 2 · sin 165 ° — 75 ° 2 cos 165 ° + 75 ° 2 = = 2 · sin 45 ° · cos 120 ° = 2 · 2 2 · — 1 2 = 2 2
С помощью формул суммы и разности синусов и косинусов можно перейти от суммы или разности к произведению тригонометрических функций. Часто эти формулы называют формулами перехода от суммы к произведению. Формулы суммы и разности синусов и косинусов широко используются при решении тригонометрических уравнений и при преобразовании тригонометрических выражений.
Формулы суммы и разности синусов и косинусов широко используются при решении тригонометрических уравнений и при преобразовании тригонометрических выражений.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Соотношения между основными тригонометрическими функциями – синусом, косинусом, тангенсом и котангенсом — задаются тригонометрическими формулами . А так как связей между тригонометрическими функциями достаточно много, то этим объясняется и обилие тригонометрических формул. Одни формулы связывают тригонометрические функции одинакового угла, другие – функции кратного угла, третьи – позволяют понизить степень, четвертые – выразить все функции через тангенс половинного угла, и т.д.
В этой статье мы по порядку перечислим все основные тригонометрические формулы, которых достаточно для решения подавляющего большинства задач тригонометрии. Для удобства запоминания и использования будем группировать их по назначению, и заносить в таблицы.
Навигация по странице.
Основные тригонометрические тождества
Основные тригонометрические тождества задают связь между синусом, косинусом, тангенсом и котангенсом одного угла. Они вытекают из определения синуса, косинуса, тангенса и котангенса, а также понятия единичной окружности . Они позволяют выразить одну тригонометрическую функцию через любую другую.
Подробное описание этих формул тригонометрии, их вывод и примеры применения смотрите в статье .
Формулы приведения
Формулы приведения следуют из свойств синуса, косинуса, тангенса и котангенса , то есть, они отражают свойство периодичности тригонометрических функций, свойство симметричности, а также свойство сдвига на данный угол. Эти тригонометрические формулы позволяют от работы с произвольными углами переходить к работе с углами в пределах от нуля до 90 градусов.
Обоснование этих формул, мнемоническое правило для их запоминания и примеры их применения можно изучить в статье .
Формулы сложения
Тригонометрические формулы сложения показывают, как тригонометрические функции суммы или разности двух углов выражаются через тригонометрические функции этих углов. Эти формулы служат базой для вывода следующих ниже тригонометрических формул.
Формулы двойного, тройного и т.д. угла
Формулы двойного, тройного и т.д. угла (их еще называют формулами кратного угла) показывают, как тригонометрические функции двойных, тройных и т.д. углов () выражаются через тригонометрические функции одинарного угла . Их вывод базируется на формулах сложения.
Более детальная информация собрана в статье формулы двойного, тройного и т.д. угла .
Формулы половинного угла
Формулы половинного угла показывают, как тригонометрические функции половинного угла выражаются через косинус целого угла . Эти тригонометрические формулы следуют из формул двойного угла.
Их вывод и примеры применения можно посмотреть в статье .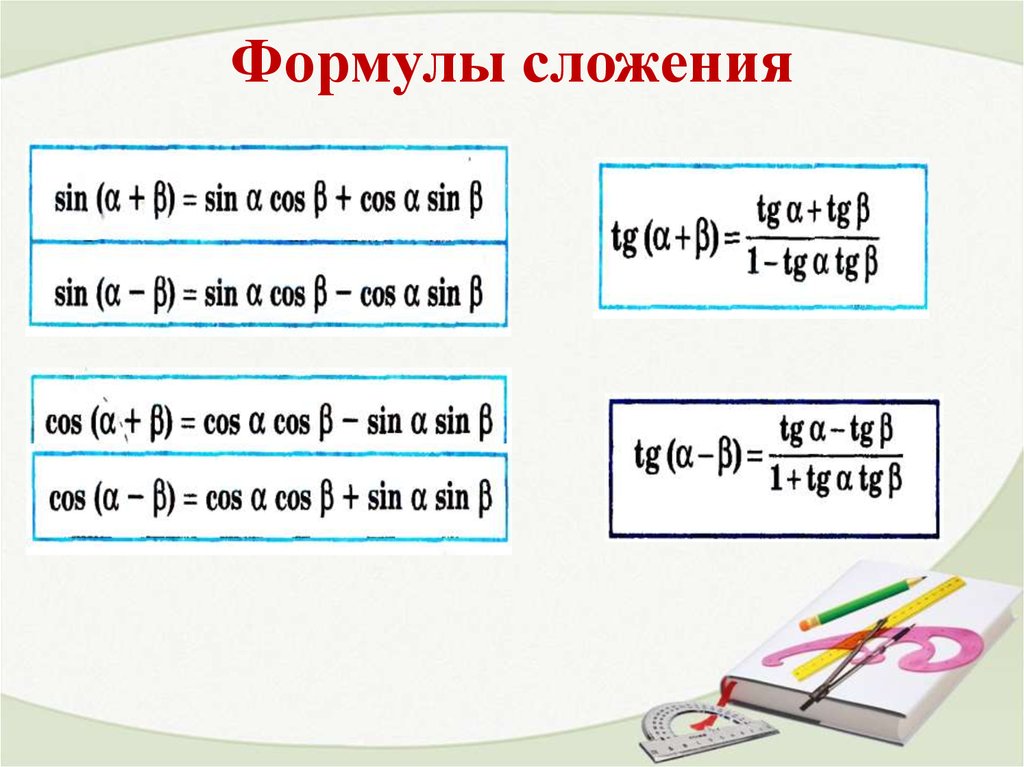
Формулы понижения степени
Тригонометрические формулы понижения степени призваны содействовать переходу от натуральных степеней тригонометрических функций к синусам и косинусам в первой степени, но кратных углов. Иными словами, они позволяют понижать степени тригонометрических функций до первой.
Формулы суммы и разности тригонометрических функций
Основное предназначение формул суммы и разности тригонометрических функций заключается в переходе к произведению функций, что очень полезно при упрощении тригонометрических выражений. Указанные формулы также широко используются при решении тригонометрических уравнений, так как позволяют раскладывать на множители сумму и разность синусов и косинусов.
Формулы произведения синусов, косинусов и синуса на косинус
Переход от произведения тригонометрических функций к сумме или разности осуществляется посредством формул произведения синусов, косинусов и синуса на косинус .
Универсальная тригонометрическая подстановка
Обзор основных формул тригонометрии завершаем формулами, выражающими тригонометрические функции через тангенс половинного угла. Такая замена получила название универсальной тригонометрической подстановки . Ее удобство заключается в том, что все тригонометрические функции выражаются через тангенс половинного угла рационально без корней.
Список литературы.
- Алгебра: Учеб. для 9 кл. сред. шк./Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова; Под ред. С. А. Теляковского.- М.: Просвещение, 1990.- 272 с.: ил.- ISBN 5-09-002727-7
- Башмаков М. И. Алгебра и начала анализа: Учеб. для 10-11 кл. сред. шк. — 3-е изд. — М.: Просвещение, 1993. — 351 с.: ил. — ISBN 5-09-004617-4.
- Алгебра и начала анализа: Учеб. для 10-11 кл. общеобразоват. учреждений / А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын и др.; Под ред. А. Н. Колмогорова.- 14-е изд.- М.: Просвещение, 2004.
 — 384 с.: ил.- ISBN 5-09-013651-3.
— 384 с.: ил.- ISBN 5-09-013651-3. - Гусев В. А., Мордкович А. Г. Математика (пособие для поступающих в техникумы): Учеб. пособие.- М.; Высш. шк., 1984.-351 с., ил.
Copyright by cleverstudents
Все права защищены.
Охраняется законом об авторском праве. Ни одну часть сайта , включая внутренние материалы и внешнее оформление, нельзя воспроизводить в какой-либо форме или использовать без предварительного письменного разрешения правообладателя.
Это последний и самый главный урок, необходимый для решения задач B11. Мы уже знаем, как переводить углы из радианной меры в градусную (см. урок «Радианная и градусная мера угла »), а также умеем определять знак тригонометрической функции, ориентируясь по координатным четвертям (см. урок «Знаки тригонометрических функций »).
Дело осталось за малым: вычислить значение самой функции — то самое число, которое записывается в ответ. Здесь на помощь приходит основное тригонометрическое тождество.
Основное тригонометрическое тождество.
Для любого угла α верно утверждение:
sin 2 α + cos 2 α = 1.
Эта формула связывает синус и косинус одного угла. Теперь, зная синус, мы легко найдем косинус — и наоборот. Достаточно извлечь квадратный корень:
Обратите внимание на знак «±» перед корнями. Дело в том, что из основного тригонометрического тождества непонятно, каким был исходный синус и косинус: положительным или отрицательным. Ведь возведение в квадрат — четная функция, которая «сжигает» все минусы (если они были).
Именно поэтому во всех задачах B11, которые встречаются в ЕГЭ по математике, обязательно есть дополнительные условия, которые помогают избавиться от неопределенности со знаками. Обычно это указание на координатную четверть, по которой можно определить знак.
Внимательный читатель наверняка спросит: «А как быть с тангенсом и котангенсом?» Напрямую вычислить эти функции из приведенных выше формул нельзя. Однако существуют важные следствия из основного тригонометрического тождества, которые уже содержат тангенсы и котангенсы. А именно:
А именно:
Важное следствие: для любого угла α можно переписать основное тригонометрическое тождество следующим образом:
Эти уравнения легко выводятся из основного тождества — достаточно разделить обе стороны на cos 2 α (для получения тангенса) или на sin 2 α (для котангенса).
Рассмотрим все это на конкретных примерах. Ниже приведены настоящие задачи B11, которые взяты из пробных вариантов ЕГЭ по математике 2012.
Нам известен косинус, но неизвестен синус. Основное тригонометрическое тождество (в «чистом» виде) связывает как раз эти функции, поэтому будем работать с ним. Имеем:
sin 2 α + cos 2 α = 1 ⇒ sin 2 α + 99/100 = 1 ⇒ sin 2 α = 1/100 ⇒ sin α = ±1/10 = ±0,1.
Для решения задачи осталось найти знак синуса. Поскольку угол α ∈ (π /2; π ), то в градусной мере это записывается так: α ∈ (90°; 180°).
Следовательно, угол α
лежит во II координатной четверти — все синусы там положительны. Поэтому sin α
= 0,1.
Поэтому sin α
= 0,1.
Итак, нам известен синус, а надо найти косинус. Обе эти функции есть в основном тригонометрическом тождестве. Подставляем:
sin 2 α + cos 2 α = 1 ⇒ 3/4 + cos 2 α = 1 ⇒ cos 2 α = 1/4 ⇒ cos α = ±1/2 = ±0,5.
Осталось разобраться со знаком перед дробью. Что выбрать: плюс или минус? По условию, угол α принадлежит промежутку (π 3π /2). Переведем углы из радианной меры в градусную — получим: α ∈ (180°; 270°).
Очевидно, это III координатная четверть, где все косинусы отрицательны. Поэтому cos α = −0,5.
Задача. Найдите tg α , если известно следующее:
Тангенс и косинус связаны уравнением, следующим из основного тригонометрического тождества:
Получаем: tg α = ±3. Знак тангенса определяем по углу α . Известно, что α ∈ (3π /2; 2π ). Переведем углы из радианной меры в градусную — получим α ∈ (270°; 360°).
Очевидно, это IV координатная четверть, где все тангенсы отрицательны. Поэтому tg α
= −3.
Поэтому tg α
= −3.
Задача. Найдите cos α , если известно следующее:
Снова известен синус и неизвестен косинус. Запишем основное тригонометрическое тождество:
sin 2 α + cos 2 α = 1 ⇒ 0,64 + cos 2 α = 1 ⇒ cos 2 α = 0,36 ⇒ cos α = ±0,6.
Знак определяем по углу. Имеем: α ∈ (3π /2; 2π ). Переведем углы из градусной меры в радианную: α ∈ (270°; 360°) — это IV координатная четверть, косинусы там положительны. Следовательно, cos α = 0,6.
Задача. Найдите sin α , если известно следующее:
Запишем формулу, которая следует из основного тригонометрического тождества и напрямую связывает синус и котангенс:
Отсюда получаем, что sin 2 α = 1/25, т.е. sin α = ±1/5 = ±0,2. Известно, что угол α ∈ (0; π /2). В градусной мере это записывается так: α ∈ (0°; 90°) — I координатная четверть.
Итак, угол находится в I координатной четверти — все тригонометрические функции там положительны, поэтому sin α
= 0,2.
При выполнении тригонометрических преобразований следуйте следующим советам:
- Не пытайтесь сразу придумать схему решения примера от начала до конца.
- Не пытайтесь преобразовывать сразу весь пример. Продвигайтесь вперёд маленькими шагами.
- Помните, что кроме тригонометрических формул в тригонометрии можно по-прежнему применять все справедливые алгебраические преобразования (вынесение за скобку, сокращение дробей, формулы сокращённого умножения и так далее).
- Верьте, что всё будет хорошо.
Основные тригонометрические формулы
Большинство формул в тригонометрии часто применяется как справа налево, так и слева направо, поэтому учить эти формулы нужно так хорошо, чтобы Вы легко смогли применить некоторую формулу в обоих направлениях. Запишем для начала определения тригонометрических функций. Пусть имеется прямоугольный треугольник:
Тогда, определение синуса:
Определение косинуса:
Определение тангенса:
Определение котангенса:
Основное тригонометрическое тождество:
Простейшие следствия из основного тригонометрического тождества:
Формулы двойного угла. Синус двойного угла:
Синус двойного угла:
Косинус двойного угла:
Тангенс двойного угла:
Котангенс двойного угла:
Дополнительные тригонометрические формулы
Тригонометрические формулы сложения. Синус суммы:
Синус разности:
Косинус суммы:
Косинус разности:
Тангенс суммы:
Тангенс разности:
Котангенс суммы:
Котангенс разности:
Тригонометрические формулы преобразования суммы в произведение. Сумма синусов:
Разность синусов:
Сумма косинусов:
Разность косинусов:
Сумма тангенсов:
Разность тангенсов:
Сумма котангенсов:
Разность котангенсов:
Тригонометрические формулы преобразования произведения в сумму. Произведение синусов:
Произведение синуса и косинуса:
Произведение косинусов:
Формулы понижения степени.
Формулы половинного угла.
Тригонометрические формулы приведения
Функцию косинус называют кофункцией функции синус и наоборот. Аналогично функции тангенс и котангенс являются кофункциями. Формулы приведения можно сформулировать в виде следующего правила:
- Если в формуле приведения угол вычитается (прибавляется) из 90 градусов или 270 градусов, то приводимая функция меняется на кофункцию;
- Если же в формуле приведения угол вычитается (прибавляется) из 180 градусов или 360 градусов, то название приводимой функции сохраняется;
- При этом перед приведенной функцией ставится тот знак, который имеет приводимая (т.е. исходная) функция в соответствующей четверти, если считать вычитаемый (прибавляемый) угол острым.
Формулы приведения задаются в виде таблицы:
По тригонометрической окружности легко определять табличные значения тригонометрических функций:
Тригонометрические уравнения
Для решения некоторого тригонометрического уравнения его нужно свести к одному из простейших тригонометрических уравнений, которые будут рассмотрены ниже. Для этого:
Для этого:
- Можно применять тригонометрические формулы приведенные выше. При этом не нужно пытаться преобразовать сразу весь пример, а нужно двигаться вперед маленькими шагами.
- Нужно не забывать о возможности преобразовать некоторое выражение и с помощью алгебраических методов, т.е. например, вынести что-нибудь за скобку или, наоборот, раскрыть скобки, сократить дробь, применить формулу сокращенного умножения , привести дроби к общему знаменателю и так далее.
- При решении тригонометрических уравнений можно применять метод группировки . При этом нужно помнить, что для того чтобы произведение нескольких множителей было равно нолю, достаточно чтобы любой из них был равен нолю, а остальные существовали .
- Применяя метод замены переменной , как обычно, уравнение после введения замены должно стать проще и не содержать первоначальной переменной. Также нужно не забыть выполнить обратную замену.
- Помните, что однородные уравнения часто встречаются и в тригонометрии.

- Раскрывая модули или решая иррациональные уравнения с тригонометрическими функциями нужно помнить и учитывать все тонкости решения соответствующих уравнений с обычными функциями.
- Помните про ОДЗ (в тригонометрических уравнениях ограничения на ОДЗ в основном сводятся к тому, что делить на ноль нельзя, но не забываем и о других ограничениях, особенно о положительности выражений в рациональных степенях и под корнями четных степеней). Также помните, что значения синуса и косинуса могут лежать только в пределах от минус единицы до плюс единицы включительно.
Главное, если не знаете, что делать, делайте хоть что-нибудь, при этом главное правильно использовать тригонометрические формулы. Если то, что Вы при этом получаете становиться все лучше и лучше, значит продолжайте решение, а если становиться хуже, значит вернитесь к началу и попробуйте применить другие формулы, так поступайте пока не наткнетесь на правильный ход решения.
Формулы решений простейших тригонометрических уравнений. Для синуса существует две равнозначные формы записи решения:
Для синуса существует две равнозначные формы записи решения:
Для остальных тригонометрических функций запись однозначна. Для косинуса:
Для тангенса:
Для котангенса:
Решение тригонометрических уравнений в некоторых частных случаях:
 Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным.
Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным.Успешное, старательное и ответственное выполнение этих трех пунктов, а также ответственная проработка итоговых тренировочных тестов , позволит Вам показать на ЦТ отличный результат, максимальный из того, на что Вы способны.
Нашли ошибку?
Если Вы, как Вам кажется, нашли ошибку в учебных материалах, то напишите, пожалуйста, о ней на электронную почту (). В письме укажите предмет (физика или математика), название либо номер темы или теста, номер задачи, или место в тексте (страницу) где по Вашему мнению есть ошибка. Также опишите в чем заключается предположительная ошибка. Ваше письмо не останется незамеченным, ошибка либо будет исправлена, либо Вам разъяснят почему это не ошибка.
Вывод тригонометрических тождеств (единичный круг)
В этом примере показано, как получить тригонометрические тождества, используя тригонометрические функции и геометрию единичного круга.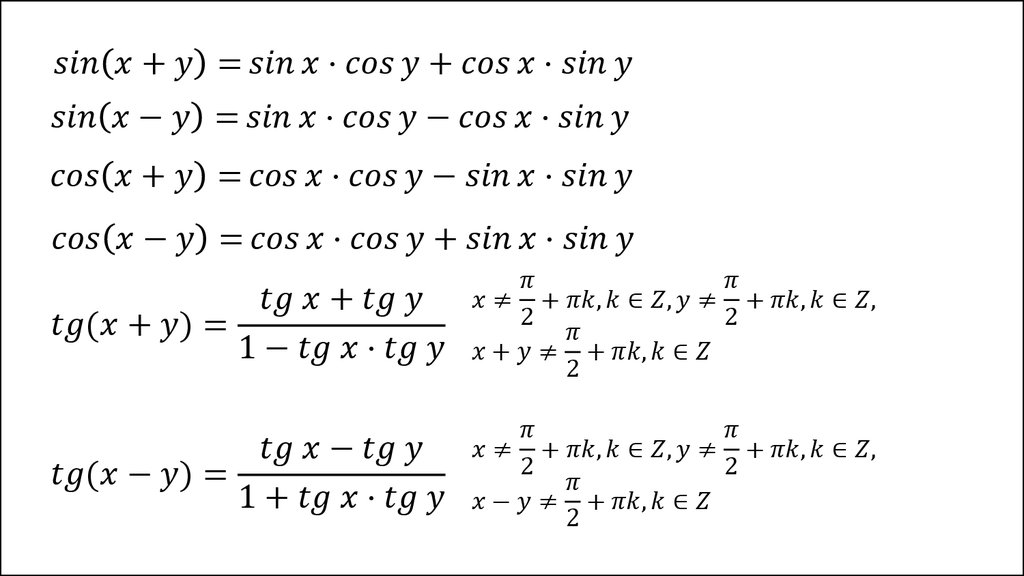 В этом примере показано, как:
В этом примере показано, как:
- Получение пифагорейского тождества (единичный круг)
- Получение суммы двух тождеств углов (единичная окружность)
- Получение разности тождеств двух углов (единичная окружность)
- Получение тождеств двойного угла (единичная окружность)
- Получение тождеств половинного угла (единичная окружность)
Получение пифагорейского тождества (единичный круг)
Тождество Пифагора связывает квадраты сторон прямоугольного треугольника на единичной окружности вместе. Однако может быть трудно понять, как квадраты сторон переводятся в геометрию прямоугольного треугольника на единичной окружности. В этом примере показаны шаги для нахождения отношения между длиной и квадратом длины и .
Шаги
Начните с прямоугольного треугольника на единичной окружности, как показано ниже, определяемой точкой . Обозначьте длины смежных и противолежащих сторон через угол треугольника.

Длины смежных и противоположных сторон можно найти, применяя определения функций синуса и косинуса.
Затем разделите прямоугольный треугольник на два подобных треугольника, проведя линию из угла прямоугольного треугольника перпендикулярно его гипотенузе. Это показано ниже:
Затем найдите длину смежной стороны, отмеченной переменной , первого подобного треугольника, показанного ниже:
Примените определение косинуса и затем подставьте длину in вместо гипотенузы и длину примыкающей стороны и затем решить для .
Повторите этот процесс, чтобы найти длину противоположной стороны второго подобного треугольника, помеченного переменной :
Примените определение синуса и затем подставьте длину in вместо гипотенузы и длину противоположной стороны и затем решить для .
Наконец, мы можем заметить, что гипотенуза прямоугольного треугольника длины может быть выражена как сумма длин, что дает нам тождество Пифагора:
Получение суммы двух тождеств углов (единичная окружность)
В этом примере выводится сумма двух тождеств углов с использованием определений окружности тригонометрических функций синуса и косинуса на единичной окружности.
шагов
Начните с рисования точки, соответствующей сумме двух углов (альфа) и (бета) на единичной окружности. Из определений окружности тригонометрических функций мы знаем, что горизонтальная координата этой точки равна , а вертикальная координата равна .
Это дает нам начальную установку для получения тождеств, где цель состоит в том, чтобы выразить и в терминах тригонометрии отдельных углов и .
Затем нарисуйте тригонометрию, связанную с углами и в виде двух прямоугольных треугольников, наложенных друг на друга. Я также нарисую длину поверх фигуры, чтобы освободить место для других выражений.
Ключевым моментом здесь является проведение вертикальной линии через правую угловую вершину прямоугольного треугольника, соответствующую углу . Это формирует два прямоугольных треугольника, которые подобны прямоугольному треугольнику, образованному углом . Вертикальные и горизонтальные компоненты точки, образованной к тому времени, могут быть представлены с помощью длин сторон этих двух прямоугольных треугольников.

Из единичного круга мы знаем, что примыкающая сторона прямоугольного треугольника, образованного равен , а противоположная сторона равна .
Поскольку теперь мы знаем гипотенузу этого первого подобного прямоугольного треугольника, мы можем найти соседние и противоположные стороны, используя определения окружности тригонометрических функций. Обратите внимание, вы также можете представить масштабирование смежной и противоположной сторон на значение .
Повторите тот же процесс, чтобы найти длины второго подобного прямоугольного треугольника. На этот раз длины сторон масштабируются на значение .
Наконец, приравняйте вертикальную и горизонтальную длины вместе, чтобы получить тождества.
Это приводит к сумме тождеств двух углов, показанных ниже.
Получение разности тождеств двух углов (единичная окружность)
ДЕЛО:
Получение тождеств двойных углов (единичная окружность)
Этот пример демонстрирует, как получить тождества двойного угла, используя теорему о вписанном угле на единичной окружности.
шагов
Начните рисовать единичный круг и разделите его на две равные части, нарисовав диаметр.
Нарисуйте еще одну точку по окружности окружности, которая образует угол, обозначенный как (альфа). Теорема о вписанном угле гарантирует, что этот треугольник всегда будет прямоугольным, даже если точка движется свободно.
Затем обратите внимание, что есть еще один пример теоремы о вписанном угле с углом, образованным точками .
Примените определения функций косинуса и синуса к показанной здесь точке, нарисовав прямоугольный треугольник.
Это дает нам начальную установку для вывода, потому что мы можем связать тригонометрию выражения и тригонометрию угла (альфа).
Найдите неизвестные длины прямоугольного треугольника
Примените определение функций косинуса и синуса, чтобы найти длины и . Обратите внимание, что гипотенуза имеет длину .
Поскольку это прямоугольный треугольник, мы можем найти длины его смежных и противоположных сторон, используя определения косинуса и синуса.
 Обратите внимание, поскольку гипотенуза будет иметь длину, они масштабируются с коэффициентом .
Обратите внимание, поскольку гипотенуза будет иметь длину, они масштабируются с коэффициентом .Обратите внимание, что есть еще один пример теоремы о вписанном угле, на этот раз с прямоугольным треугольником, связанным с центральным углом:
Затем мы можем применить определения синуса и косинуса, чтобы найти длины прямоугольного треугольника. Эти длины и есть то, что описывают тождества.
Заметьте, что треугольники и подобны треугольникам, потому что у них три одинаковых угла. Ниже показаны два выделенных треугольника с помеченными углами.
Поскольку треугольники подобны, отношения их соответствующих сторон равны, как показано в уравнении ниже:
Затем мы можем подставить длины в уравнение, которое связывает отношение смежных сторон вместе:
Используя приведенную выше диаграмму, которая иллюстрирует длины из предыдущих шагов, и решая выражение, получаем первое тождество:
Это дает нам двойной угол тождество синуса:
Затем мы можем подставить длины в уравнение, которое связывает отношение противоположных сторон вместе:
Используя приведенную выше диаграмму и найдя выражение: получаем второе тождество:
Это дает нам форму тождества косинуса двойного угла:
Чтобы получить значения синуса и косинуса, мы можем заменить тождество Пифагора на :
Это дает нам другую форму тождества двойного косинуса угла:
Наконец, чтобы получить последнюю форму тождества косинуса с двойным углом, мы можем изменить тождество Пифагора и заменить выражение косинуса.

Это дает нам последнюю форму тождества косинуса двойного угла:
Заключение
Получение тождеств половинных углов (единичная окружность)
ДЕЛО:
© 2023 Kurt Bruns
Тригонометрические тождества суммы к произведению
Основные тождества суммы к произведению для синуса и косинуса следующие:
\[\begin{align} \sin x+\sin y & =2\sin\left(\frac{x+y}{2}\right)\cos\left(\frac{x-y}{2}\right) \\ \cos x+\cos y &=2\cos\left(\frac{x+y}{2}\right)\cos\left(\frac{x-y}{2}\right). \конец{выравнивание}\]
Из этих идентичностей мы также можем сделать вывод о идентичности разницы с продуктом:
\[\begin{align} \sin x-\sin y & = 2\cos\left(\frac{x+y}{2}\right)\sin\left(\frac{x-y}{2}\right) \\ \cos x-\cos y &= -2\sin\left(\frac{x+y}{2}\right)\sin\left(\frac{x-y}{2}\right) \\&= 2 \sin\left(\frac{x+y}{2}\right)\sin\left(\frac{y-x}{2}\right) \end{align}\]
и сумма тангенсов и тождества разницы с произведением:
\[\begin{align}
\tan (x) + \tan (y) &= \tan(x+y)\big(1-\tan(x)\tan(y)\big)\\
\tan(x)-\tan(y)&=\tan(xy)\big(1+\tan(x)\tan(y)\big). \конец{выравнивание}\]
\конец{выравнивание}\]
Доказательство основного тождества суммы и произведения для синуса происходит следующим образом:
\[\begin{выравнивание} 2 \ sin \ left ({\ frac {\ alpha + \ beta} 2} \ right) \ cos \ left ({\ frac {\ alpha — \ beta} 2} \ right) & знак равно 2 \ гидроразрыва {\ грех \ влево ({\ гидроразрыва {\ альфа + \ бета} 2 + \ гидроразрыва {\ альфа — \ бета} 2} \ справа) + \ грех \ влево ({\ гидроразрыва {\ альфа + \beta} 2 — \frac {\alpha — \beta} 2}\right)} 2\\ &= \sin \left(\frac {2 \alpha} 2\right) + \sin \left(\frac {2 \beta} 2\right)\\ &= \sin\alpha + \sin\beta. \конец{выравнивание}\]
Доказательства для косинуса и тангенса аналогичны. \(_\квадрат\)
Упростить
\[\dfrac{\cos3x-\cos x}{\cos3x+\cos x}.\]
У нас есть
\[\begin{выравнивание} \frac{\cos3x-\cos x}{\cos3x+\cos x} &= \frac{-2\sin\left(\frac{3x+x}{2}\right)\sin\left(\frac{ 3x-x}{2}\right)}{2\cos\left(\frac{3x+x}{2}\right)\cos\left(\frac{3x-x}{2}\right)} \\ & = -\frac{2\sin2x\sin x}{2\cos2x\cos x} \\\\ & = -\tan2x\tan x.
\ _\квадрат \конец{выравнивание}\]
В треугольнике \(\треугольник ABC\) докажите, что
\[\sin A+\sin B+\sin C=4\cos\frac{A}{2}\cos\frac{B}{2}\cos\frac{C}{2}.\]
У нас есть
\[\begin{выравнивание} \sin A+\sin B+\sin C &=2\sin\left(\frac{A+B}{2}\right)\cos\left(\frac{A-B}{2}\right) +2\sin \frac{C}{2}\cos\frac{C}{2} \\ &= 2\cos\frac{C}{2}\cos\left(\frac{A-B}{2}\right) + 2\sin\frac{C}{2}\cos\frac{C}{2 } \\ & = 2\cos\frac{C}{2}\left(\cos\Big(\frac{A}{2}-\frac{B}{2}\Big)+\sin\frac{C}{ 2}\справа)\\ &= 2\cos\frac{C}{2}\left(\cos\Big(\frac{A}{2}-\frac{B}{2}\Big)+\cos\Big(\frac{ A}{2}+\frac{B}{2}\Big)\right) \\ &= 2\cos\frac{C}{2}\left(2\cos\frac{A}{2}\cos\frac{B}{2}\right) \\ &= 4\cos\frac{A}{2}\cos\frac{B}{2}\cos\frac{C}{2}.\ _\square \конец{выравнивание}\]
Найдите все решения в области \([-2\pi,2\pi]\) уравнения
\[\cos(4x) + \cos(2x) =0.\]
У нас есть
\[\begin{выравнивание} \cos(4x)+\cos(2x) &=0\\ 2\cos\left(\frac{4x+2x}{2}\right)\cos\left(\frac{4x-2x}{2}\right) &=0 \\ \cos(3x)\cos(x) &=0.
\\ \конец{выравнивание}\]
Для \(\cos(3x)=0,~x=\frac{4n\pi\pm\pi}{6}\ подразумевает x=-\frac{5\pi}{6},~-\frac{ \pi}{6},~\frac{\pi}{6},~\frac{5\pi}{6}.\)
Для \(\cos(x)=0,~x=2n\pi \pm\frac{\pi}{2}\ подразумевает x=-\frac{3\pi}{2},~-\frac{\pi}{2},~\frac{\pi}{2}, ~\frac{3\pi}{2}.\)Следовательно, решения равны \(x = -\frac{3\pi}{2},~-\frac{5\pi}{6},~-\frac{\pi}{2},~-\ frac{\pi}{6},~\frac{\pi}{6},~\frac{\pi}{2},~\frac{5\pi}{6},~\frac{3\pi {2}\). \(_\квадрат\)
Запишите \(\sin(x) + \sin(2x) + \sin(3x) + \sin(4x)\) как произведение тригонометрических функций.
У нас есть
\[\begin{align}
\sin(x)+ \sin(2x)+\sin(3x)+\sin(4x) &=\big(\sin(4x)+\sin(x)\big )+\большой(\sin(3x)+\sin(2x)\big)\\ & = 2\sin\left(\frac{4x+x}{2}\right)\cos\left(\frac{4x-x}{2}\right)+2\sin\left(\frac{3x +2x}{2}\справа)\cos\слева(\frac{3x-2x}{2}\справа)\\ &=2\sin\left(\frac{5x}{2}\right)\cos\left(\frac{3x}{2}\right)+2\sin\left(\frac{5x}{2} \справа)\cos\слева(\frac{x}{2}\справа)\\ &=2\sin\left(\frac{5x}{2}\right)\left(\cos\Big(\frac{3x}{2}\Big)+\cos\Big(\frac{x}{ 2}\большой)\правый)\\ &=2\sin\left(\frac{5x}{2}\right)\left(2\cos\left(\frac{\frac{3x}{2}+\frac{x}{2}}{ 2}\right)\cos\left(\frac{\frac{3x}{2}-\frac{x}{2}}{2}\right)\right)\\ &=2\sin\left(\frac{5x}{2}\right)\left(2\cos(x)\cos\Big(\frac{x}{2}\Big)\right)\\ &=4\sin\left(\frac{5x}{2}\right)\cos(x)\cos\left(\frac{x}{2}\right).

 — 384 с.: ил.- ISBN 5-09-013651-3.
— 384 с.: ил.- ISBN 5-09-013651-3.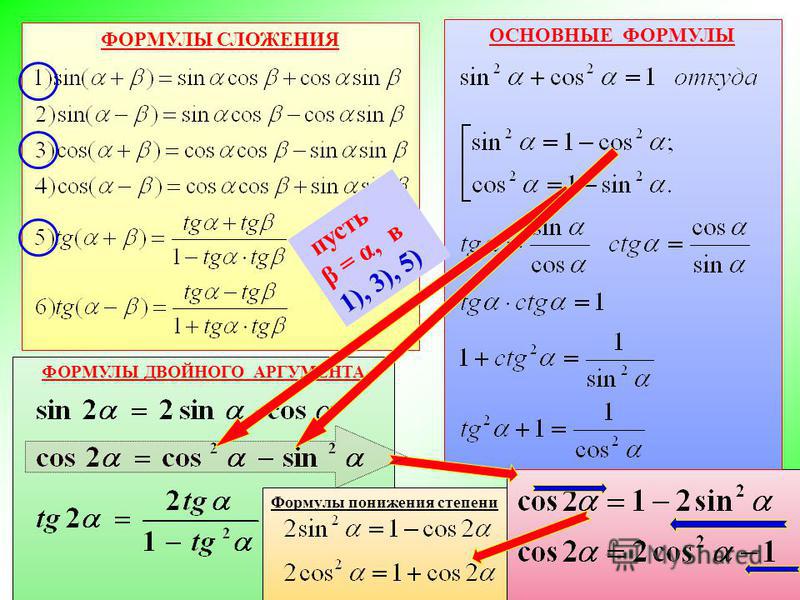 Для любого угла α
верно утверждение:
Для любого угла α
верно утверждение:


 Обратите внимание, поскольку гипотенуза будет иметь длину, они масштабируются с коэффициентом .
Обратите внимание, поскольку гипотенуза будет иметь длину, они масштабируются с коэффициентом .
 \ _\квадрат
\конец{выравнивание}\]
\ _\квадрат
\конец{выравнивание}\] \\
\конец{выравнивание}\]
\\
\конец{выравнивание}\]