Докажите тождество » задачи — страница 1
тождество »
Докажите тождество 1) (a+2)3(степень) -25(а+2) = (а+2)(а+7)(а-3)
2) a2 + 2 ab + b2 — c2 + 2cd -d2 = (a+b+c-d)(a+b-c+d)
Решение: Решение
1) (a+2)3(степень) -25(а+2) = (а+2)(а+7)(а-3)
Упростим левую часть тождества:
(a + 2)³ — 25*(a + 2) = (a + 2)*(a² + 4a + 4 — 25) =
= (a + 2)*(a² + 4a — 21)
a² + 4a — 21 = 0
a₁ = — 7
a₂ = 3
a² + 4a — 21 = (a + 7)*(a — 7)
(a + 2)*(a² + 4a — 21) = (a + 2)*(a + 7)*( a — 3)
(a + 2)*(a + 7)*( a — 3) = (a + 2)*(a + 7)*( a — 3)
доказано
2) a²+ 2 ab + b² — c² + 2cd -d² = (a+b+c-d)(a+b-c+d)
Упростим левую часть тождества:
a² + 2 ab + b² — c² + 2cd -d² = (a² + 2 ab + b²) -(c² — 2cd + d²) =
= (a + b)² — (c — d)² = (a+b+c-d)(a+b-c+d)
(a + b + c — d)*(a + b — c + d) = (a + b + c — d)*(a + b — c + d)
доказаноДокажите тождество an= a1+(n-1)d ( формула n-го члена арифметической прогрессии) методом математической индукции
Решение: При n=1 имеем a(1=a1+d*(1-1)=a(1), так что для n=1 формула верна.
Допустим теперь, что формула верна и для произвольного n=k:
a(k)=a1+d*(k-1) и перейдём теперь к n=k+1:a(k+1)=ak+d=a1+d*(k-1)+d=a1+d*k — формула верна и для n=k+1. А значит, она верна и для любого целого n. Действительно, из справедливости формулы при n=1 (а в этом мы убедились непосредственно) вытекает её справедливость для n=2; из справедливости для n=2 следует справедливость для n=3 и. т. д. Тождество доказано.
Докажите тождество:
sin альфа * cos 3 альфа — cos альфа * sin 3 альфа = cos (3П/2 — 2 альфа)
Решение: по формуле синуса разностиsin альфа * cos 3 альфа — cos альфа * sin 3 альфа =sin(альфа-3альфа)=sin(-2альфа)=
учитывая нечетность синуса -sin(2альфа)
по формуле приведения
cos(3П/2 — 2 альфа)=- sin( 2 альфа)
значит sin альфа * cos 3 альфа — cos альфа * sin 3 альфа = cos (3П/2 — 2 альфа)
Доказано
Докажите тождество:
sin 105° cos 105° = — 1/4
Решение: А вот попроще решение: $$ 105^{0}=60^{0}+45^{0} $$По формулам суммы аргументов получаем: $$ sin(60^0+45^0)*cos(60^0+45^0)= \\ =(sin60^0cos45^0+cos60^0sin45^0)*(cos60^0cos45^0-sin60^0sin45^0) $$
Подставляем известные значения синусов и косинусов:
$$ (\frac{\sqrt3}{2}\frac{\sqrt2}{2}+\frac{1}{2}\frac{\sqrt2}{2})(\frac{1}{2}\frac{\sqrt2}{2}-\frac{\sqrt3}{2}\frac{\sqrt2}{2})=\\=\frac{\sqrt2(\sqrt3+1)}{4}\frac{\sqrt2(1-\sqrt3)}{4}=\frac{2*(-2)}{16}=-\frac{1}{4} $$
докажите тождество (sin⁴α-cos⁴α)/(sin²α)+2ctg²α=1/(sin²α)
Решение: (sin⁴α-cos⁴α)/(sin²α)+2ctg²α=1/(sin²α)чтобы доказать какое-либо дождество надо одну из частей привести к другой.
 2(\frac{x}{2}-\frac{\pi}{8})= \\ =2\sqrt{2}(\frac{1+cos2\cdot (\frac{x}{2}-\frac{\pi}{8})}{2})= \\ =\sqrt{2}(1+cos(x-\frac{\pi}{4})) $$
2(\frac{x}{2}-\frac{\pi}{8})= \\ =2\sqrt{2}(\frac{1+cos2\cdot (\frac{x}{2}-\frac{\pi}{8})}{2})= \\ =\sqrt{2}(1+cos(x-\frac{\pi}{4})) $$Воспользуемся формулой 2. И упростим cos:
$$ \sqrt{2}(1+cos(x-\frac{\pi}{4}))= \\ =\sqrt{2}(1+cosx\cdot cos(\frac{\pi}{4})+sinx \cdot sin(\frac{\pi}{4}))= \\ =\sqrt{2}(1+cosx\cdot \frac{\sqrt{2}}{2}+sinx \cdot \frac{\sqrt{2}}{2}) \\ =\sqrt{2}+cosx+sinx $$
Получаем что левая часть равна правой части:
$$ sinx+cosx+\sqrt{2}=\sqrt{2}+cosx+sinx $$
Что и требовалось доказать
Докажите тождество: sin(45-альфа) / cos(45-альфа)=1
Тема: синус и косинус разности
Решение: sin(45-альфа) / cos(45-альфа)=1
sin45cosA-cos45sinA/cosAcos45+sin45sinA=cosA-sinA/cosA+sinA не равно 1
cos(45+фльфа)=cos45cosA-sin45cosA при таком знаменателе =1Докажите тождество:
1) 1-sin t / cos t=cos t / 1+sin t
2)sin t / 1-cos t=1+ cos t / sin t
Решение: Умножаем крест на крест
cos^2t=(1-sint)(1+sint)
cos^2t=1-sin^2t
cos^2t+sin^2t=1
1=1
2)(1+cost)(1-cost)=sin^2t
1-cos^t=sin^2t
1=sin^2t+cos^2t
1=1.
 2 a $$
2 a $$Доказано
в левой части выносим за скобки sin²a:
sin²a(sin²a+cos²a)=1-cos²a
в правой части применяем основное тригонометрическое тождество:
sin²a(sin²a+cos²a)=sin²a
sin²a сокращается
sin²a+cos²a=1, а это основное тригонометрическое тождество. ч. т. д
1 2 3 > >>
Украинцы смогут бесплатно получить энергосберегающие LED-лампы на Укрпочте — Минфин
С нового года каждый совершеннолетний украинец сможет на Укрпочте бесплатно получить 5 светодиодных ламп взамен старых ламп накаливания. Об этом сообщила министр экономики Украины Юлия Свириденко.
►Подписывайтесь на страницу «Минфина» в фейсбуке: главные финансовые новости
«Сейчас, чтобы снизить нагрузку на энергетическую инфраструктуру, нам приходится внедрять различные, в том числе нетрадиционные, меры по энергоэффективности. Простая замена старых лампочек на новые LED-лампы может сэкономить стране в пиковые часы до 1,5 гигаватта электроэнергии.
По ее словам, замену 30 млн лампочек профинансирует Европейский Союз. Правительство Украины работает над тем, чтобы все процедуры со стороны ЕС были завершены до конца года, и уже в январе программа стартовала.
Читайте: ЕС купит для Украины 30 миллионов светодиодных лампочек
Где можно обменять
Программа будет реализовываться через Укрпочту, а ее механизм будет максимально упрощен. Человеку, который решит воспользоваться программой, нужно предварительно оставить заявку, прийти в отделение Укрпочты и обменять 5 ламп старого образца на 5 новых светодиодных.
«Мы сделаем программу достаточно долгой для того, чтобы все граждане Украины, желающие заменить лампочки, могли воспользоваться этой возможностью», — отметила Юлия Свириденко.
Напомним
Ранее «Минфин» писал, что Европейский Союз собирается профинансировать приобретение около 30 млн светодиодных лампочек для Украины.
Источник: Минфин
Комментировать
Страницу просматривают 8 незарегистрированных посетителей.
Получайте одно письмо в день с самыми важными новостями.
E-mail введен некорректно
E-mail уже существует
введите E-mail адрес
- Не зарегистрированы на Минфине? Придумайте логин и пароль для управления подпиской. (Я уже зарегистрирован)
только латинские буквы и цифры
логин уже существует введите логин логин должен содержать 3-15 символовВведите пароль
√Проверка не пройдена
Проверка не пройдена
- 24.12.2022
- 17:08 Правительство выделило более 27 миллионов на компенсацию коммунальных расходов за размещение переселенцев
- 16:05 Фонд поддержки энергетики Украины уже собрал 155 миллионов евро
- 15:07 Инфляция в Японии достигла 40-летнего максимума
- 14:09 Объем строительных работ за первое полугодие упал в два раза — Госстат
- 12:00
Сохраняется существенный дефицит электроэнергии.
 В Укрэнерго рассказали, где самая сложная ситуация
В Укрэнерго рассказали, где самая сложная ситуация - 11:03 Конгресс США одобрил бюджет с пакетом помощи для Украины и союзников почти на $45 миллиардов
- 09:27 Нацбанк снизил продажу валюты на межбанке почти вдвое
- 09:02 В Киеве прекращают работу трамваи и троллейбусы из-за дефицита электроэнергии
- 23.12.2022
- 19:09 Кабмин может разрешить бизнесу импортировать электроэнергию для собственных нужд из Европы
- 18:27 МВФ разрешил НБУ провести эмиссию гривны еще на 50 миллиардов в случае необходимости
Все новости
Связаться с застройщиком
Ваше ФИО
Телефон
Согласен на передачу персональных данных
\\circ }Тогда общее решение $\alpha $ равно
1.$\phi $2.$2n\pi \pm \dfrac{\pi }{3},\forall n \in Z$
3.$(2n + 1)\dfrac{\pi }{2},\forall n \in Z$
4.$n\pi ,\forall n \in Z$
Ответ
Подтверждено
242,7 тыс. + просмотров
+ просмотров
Подсказка: Для такого вопроса мы подходим к решению, упрощая решение односторонних выражений, так как здесь мы упростим левую часть, используя некоторые тригонометрические формулы, такие как 9\circ } = — \dfrac{1}{2}$
$ \Rightarrow 2\cos 2\alpha \cos \alpha — 2 \times \dfrac{1}{2}\cos \alpha = \sqrt 3 $
При упрощении получаем,
$ \Rightarrow cos3\alpha + cos\alpha — \cos \alpha = \sqrt 3 $
Получаем, $cos3\alpha = \sqrt 3 $
Мы знаем, что функция косинуса может дать только ответ в $[ — 1,1]$
т.е. диапазон функции косинуса $[ — 1,1]$ и здесь он равен $\sqrt 3 $ что больше 1
Вариант (А) правильный
Примечание: В вопросах тригонометрических функций нашим приоритетом должно быть использование тригонометрических свойств над алгебраическими формулами, как в этом вопросе, если мы использовали формулу для суммы куба три члена вместо куба функции косинуса задача могла стать более сложной, поэтому попробуйте использовать тригонометрическую функцию, если это возможно.
Недавно обновленные страницы
Рассчитать изменение энтропии, связанное с преобразованием класса 11 химии JEE_Main
Закон, сформулированный доктором Нернстом, представляет собой Первый закон термодинамики Химический класс 11 JEE_Main
Для реакции при rm0rm0rmC и нормальном давлении Химический класс 11 JEE_Main
Двигатель, работающий между rm15rm0rm0rmC и rm2rm5rm0rmC Класс 11 2 Для химической реакции JEE03
rm2Clg to rmCrmlrm2rmg знаки химии класса 11 JEE_MainИзменение энтальпии для перехода жидкой воды класса 11 химии JEE_Main
Рассчитать изменение энтропии, связанное с конверсией химии класса 11 JEE_Main
Закон, сформулированный доктором Нернстом, представляет собой Первый закон термодинамики Химический класс 11 JEE_Main
Для реакции при rm0rm0rmC и нормальном давлении Химический класс 11 JEE_Main
Двигатель, работающий между rm15rm0rm0rmC и rm2rm5rm0rmC Класс 11 2 Для химической реакции JEE03
rm2Clg в rmCrmlrm2rmg признаки 11 класса химии JEE_Main
Изменение энтальпии перехода жидкой воды 11 класса химии JEE_Main
Сомнения в тренде
Найдите точное значение, учитывая условия Sin(alpha) = 3/5, 0
Тригонометрия
Риз Л.
В моей книге ответ равен 2√5/25, если вы используете формулу, пожалуйста, напишите ее, чтобы я знал, как вы получили определенные ответы. Используйте специальный треугольник со сторонами 3-4-5, пожалуйста и спасибо!
Подписаться
Еще
Отчет
1 ответ эксперта
Лучший Новейшие Самый старыйАвтор: Лучшие новыеСамые старые
Джейкоб К. ответил 22/12/21
Репетитор
4.9 (109)
Выпускник McGill для вечернего обучения математике и экстренной помощи
Посмотреть таких репетиторов
Смотрите таких репетиторов
Итак, мы начинаем с Sin(α)=3/5. Возвращаясь к триггеру прямоугольного треугольника, помните, что Sin определяется как противоположность/гипотенуза.
Поскольку я не могу нарисовать здесь картинку, я сделаю все возможное, чтобы объяснить, как я понимаю, как должен выглядеть треугольник
Прямоугольный треугольник с большим углом β наверху, меньшим углом α внизу и прямым углом. Гипотенуза треугольника имеет длину 5, а высота треугольника, она же сторона, противолежащая углу α, имеет длину 3. Сторона, примыкающая к углу α, она же сторона, противолежащая углу β, имеет длину 4.
Учитывая это, теперь мы можем написать вниз Sin, Cos и Tan для каждого угла, учитывая SOHCAHTOA
Sin(α)=противоположная/гипотенуза=3/5
Cos(α)=прилежащая/гипотенуза=4/5
Tan(α)=противоположный/прилегающий=3/4
Sin(β)=противоположный угол β/гипотенуза=4/5
Cos(β)=прилежащий к стороне угол β/гипотенуза=3/5
Tan(β) = сторона, противоположная β/сторона, примыкающая β = 4/3
Я записал все это, потому что есть формула для Sin(α+β), которая должна быть в вашем учебнике по тригонометрии. Формула сложения для Sin:
Формула сложения для Sin:
Sin(α+β)=Sin(α)Cos(β)+Cos(α)Sin(β)
Теперь мы просто подставляем это, используя то, что у нас есть выше
Sin( α+β)=(3/5)(3/5)+(4/5)(4/5)=9/25+16/25=25/25=1
Причина, по которой вы получаете 1 в этом случае, заключается в том, что в прямоугольном треугольнике сложение двух углов, которые не являются прямыми, даст вам 90 градусов, так как 90+90 =180 и все треугольники в сумме дают 180 градусов, а грех 90 градусов равен 1.
Можно ли дать больше контекста для проблемы, пожалуйста? Я хотел бы продолжить работу с вами, если бы у меня было больше информации о проблеме, чтобы увидеть, где ответы будут разными. Удачи!
Голосовать за 0 Понизить
Подробнее
Отчет
Все еще ищете помощи? Получите правильный ответ, быстро.
Задайте вопрос бесплатно
Получите бесплатный ответ на быстрый вопрос.


 2(\frac{x}{2}-\frac{\pi}{8})= \\ =2\sqrt{2}(\frac{1+cos2\cdot (\frac{x}{2}-\frac{\pi}{8})}{2})= \\ =\sqrt{2}(1+cos(x-\frac{\pi}{4})) $$
2(\frac{x}{2}-\frac{\pi}{8})= \\ =2\sqrt{2}(\frac{1+cos2\cdot (\frac{x}{2}-\frac{\pi}{8})}{2})= \\ =\sqrt{2}(1+cos(x-\frac{\pi}{4})) $$ 2 a $$
2 a $$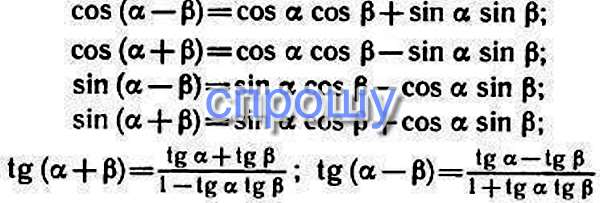 В Укрэнерго рассказали, где самая сложная ситуация
В Укрэнерго рассказали, где самая сложная ситуация