| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | cos(pi/4) | ||
| 9 | Найти точное значение | sin(45 град. ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) | |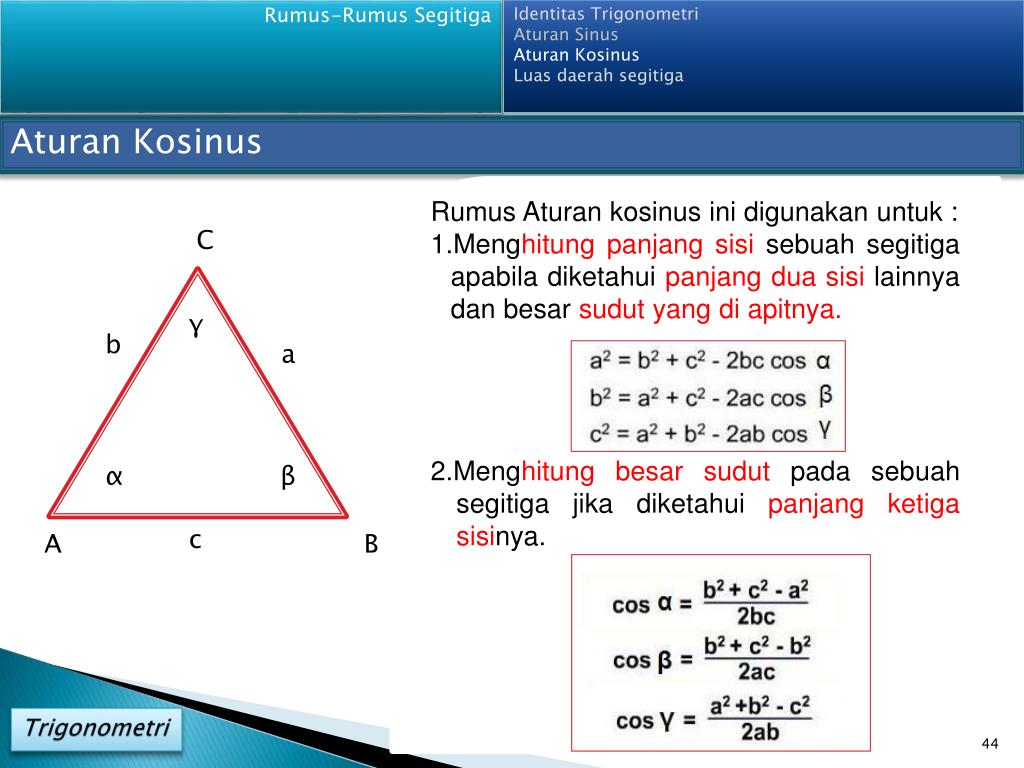
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) | |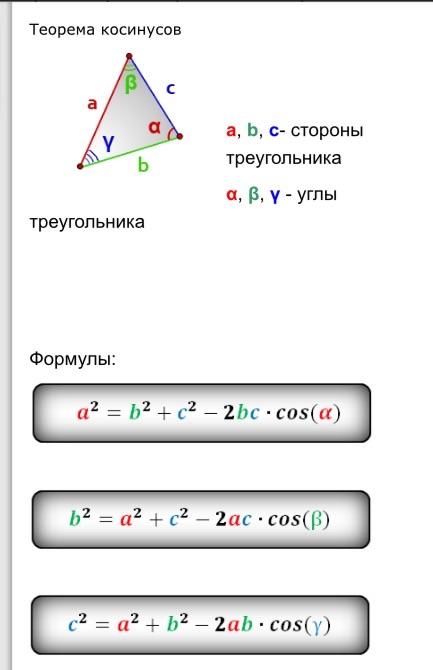
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | ||
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) | |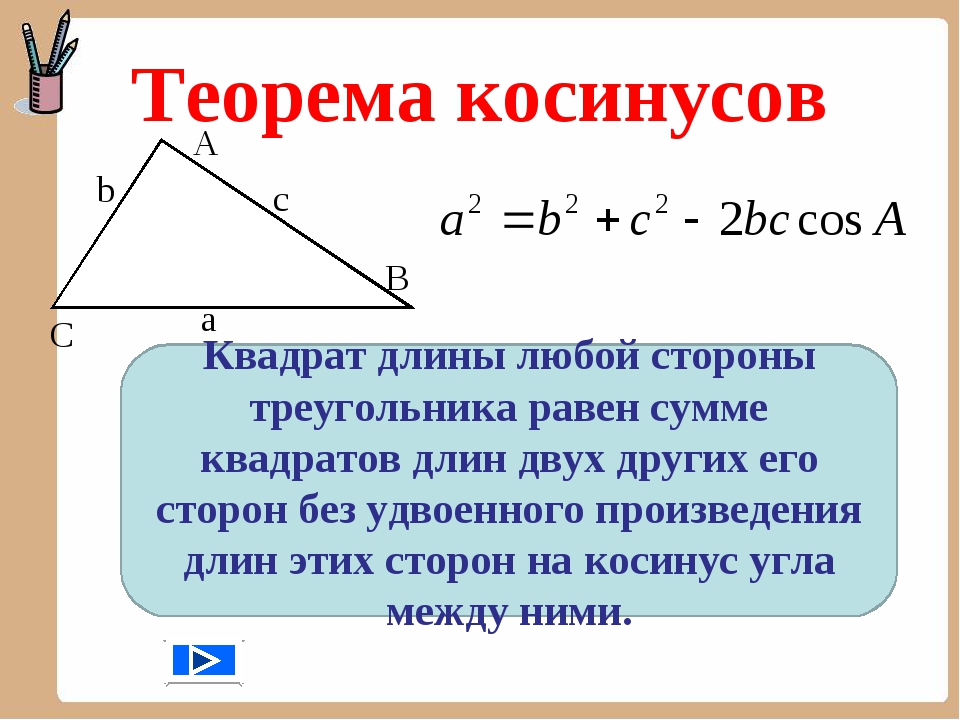
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град. ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
Косинус в кубе плюс косинус в квадрате
Автор Сфера закона На чтение 10 мин Просмотров 13 Опубликовано
Содержание
- Тригонометрические формулы.
- Формулы сложения.
- Формулы двойного угла.
- Формулы тройного угла.
- Формулы половинного угла.
- Косинус в кубе плюс косинус в квадрате
- Тригонометрические формулы. Их вывод
Тригонометрические формулы.
Тригонометрические формулы — это самые необходимые в тригонометрии формулы, необходимые для выражения тригонометрических функций, которые выполняются при любых значениях аргумента.
Формулы сложения.
sin (α + β) = sin α · cos β + sin β · cos α
sin (α — β) = sin α · cos β — sin β · cos α
cos (α + β) = cos α · cos β — sin α · sin β
cos (α — β) = cos α · cos β + sin α · sin β
tg (α + β) = (tg α + tg β) ÷ (1 — tg α · tg β)
tg (α — β) = (tg α — tg β) ÷ (1 + tg α · tg β)
ctg (α + β) = (ctg α · ctg β + 1) ÷ (ctg β — ctg α)
ctg (α — β) = (ctg α · ctg β — 1) ÷ (ctg β + ctg α)
Формулы двойного угла.
Формулы тройного угла.
ctg 3α = (3ctg α — ctg³ α) ÷ (1 — 3ctg² α)
Формулы половинного угла.
Синус половинного угла. Примечание: Знак перед корнем выбирается в зависимости от квадранта, в который попадает угол α/2 в левой части. Данное правило справедливо также для других формул, приведенных ниже.
Косинус половинного угла:
Тангенс половинного угла:
Котангенс половинного угла:
Выражение синуса через тангенс половинного угла:
Выражение косинуса через тангенс половинного угла:
Выражение тангенса через тангенс половинного угла:
Выражение котангенса через тангенс половинного угла:
Источник
Косинус в кубе плюс косинус в квадрате
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
а) Запишем уравнение в виде
Значит, или откуда или откуда или
б) С помощью числовой окружности отберем корни, принадлежащие отрезку Получим числа:
Ответ: а) б)
Приведем другое решение: поэтому уравнение можно преобразовать следующим образом:
Это решение приводит нас к альтернативной записи ответа пункта а).
Объединены корни двух уравнений и .
и
Их можно записать как
Серии решений данного уравнения и (где ) можно объединить в одну серию (где ).
Указанное обстоятельство легко видеть из того факта, что все соседние генерирующие решения точки на единичной тригонометрической окружности отстоят друг от друга на угол
Конечно, можно. Никто с этим и не спорит.
Здесь же в чистом виде ф-ла косинуса тройного угла (см. аналогию №500.346), поэтому простой и быстрый ответ П/6+Пk/3, kэZ
Здравствуйте! В дополнительном решении мы как раз отмечаем этот факт.
Теперь всё ок — благодарю! ps. Сайт отличный!
а) Решите уравнение:
б) Найдите все корни этого уравнения, принадлежащие отрезку
Левая часть уравнения имеет смысл при Выражение положительно при всех допустимых значениях
б) Корни, принадлежащие отрезку отберём с помощью единичной окружности. Получаем
Ответ: а) б)
непонятно почему не подходит х=п+2п?
Понятно почему не подходит (подставьте и проверьте).
Непонятно откуда Вы это взяли.
Непонятно вы объясняете. Почему корень х= П+2Пn не указан.
Разве мы не должны приравнивать вторую скобку к нулю?
Алина, в первой строке решения есть объяснение.
Но если очень хотите, то приравняйте. И при грамотном решении увидите, что вторая скобка корней не даёт
Все равно не понятно, объясните пожалуйста
Внизу есть ссылка «Помощь по заданию»
Почему это решение выпало?
И почему выпало решение x=pi/6+2pin?
Первого решения в этом уравнении нет вообще, а второе не входит в ОДЗ
Почему нет первого решения? sqrt(-cosx)+1=0
возводим обе части в квадрат
Потому, что так делать НЕЛЬЗЯ!
Корень НЕ МОЖЕТ равняться отрицательному числу
а) Решите уравнение
б) Укажите корни, принадлежащие отрезку
а) Сделаем замену получим квадратное уравнение корнями которого являются числа и Уравнение не имеет решений, а из уравнения находим корни или
б) Найдем корни, принадлежащие отрезку Решим неравенства:
откуда или
Соответствующие найденным значениям параметров корни: и
Ответ : а) б)
Источник
Тригонометрические формулы.
2\, \alpha>\\&\\ \cos\alpha\ne 0 & \sin\alpha\ne 0\\ \hline \end\]\(\blacktriangleright\) Формула вспомогательного аргумента: \[\begin\hline \text\\ \hline \\ \sin\alpha\pm \cos\alpha=\sqrt2\cdot \sin4\right)>\\\\ \sqrt3\sin\alpha\pm \cos\alpha=2\sin6\right)>\\\\ \sin\alpha\pm \sqrt3\cos\alpha=2\sin3\right)>\\\\ \hline \text\\ \hline\\ a\sin\alpha\pm b\cos\alpha=\sqrt\cdot \sin, \ \ \cos\phi=\dfrac a>, \ \sin\phi=\dfrac b>\\\\ \hline \end\]
Зная идею вывода формул, вы можете запомнить лишь несколько из них. Тогда остальные формулы вы всегда сможете быстро вывести.
Вывод всех основных тождеств был рассказан в предыдущем разделе “Введение в тригонометрию”.
\(\blacktriangleright\) Вывод формулы косинуса разности углов \(\cos=\cos\alpha\cos\beta+\sin\alpha\sin\beta\)
Рассмотрим тригонометрическую окружность и на ней углы \(\alpha\) и \(\beta\) . Пусть этим углам соответствуют точки \(A\) и \(B\) соответственно.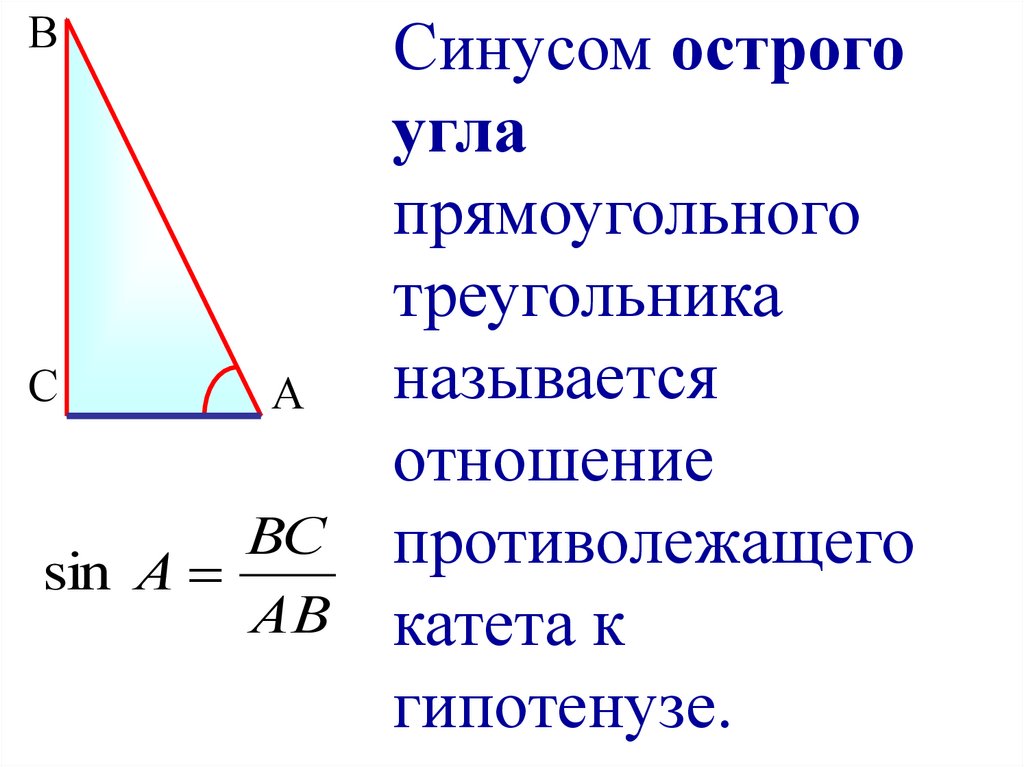
2\alpha=\dfrac2\)
Заметим, что в данных формулах степень синуса/косинуса равна \(2\) в левой части, а в правой части степень косинуса равна \(1\) .
\(\blacktriangleright\) Вывод формул произведения функций:
1) Сложим формулы косинуса суммы и косинуса разности двух углов:
Получим: \(\cos(\alpha+\beta)+\cos(\alpha-\beta)=2\cos\alpha\cos\beta \Rightarrow \cos\alpha\cos\beta=\dfrac12\Big(\cos(\alpha-\beta)+\cos(\alpha+\beta)\Big)\)
2) Если вычесть из формулы косинуса суммы косинус разности, то получим:
3) Сложим формулы синуса суммы и синуса разности двух углов:
\(\blacktriangleright\) Вывод формул суммы/разности функций:
Обозначим \(\alpha+\beta=x, \alpha-\beta=y\) . Тогда: \(\alpha=\dfrac2, \ \beta=\dfrac2\) . Подставим эти значения в предыдущие три формулы:
Получили формулу суммы косинусов.
Получили формулу разности косинусов.
Получили формулу суммы синусов.
4) Формулу разности синусов можно вывести из формулы суммы синусов:
Аналогично выводится формула суммы котангенсов.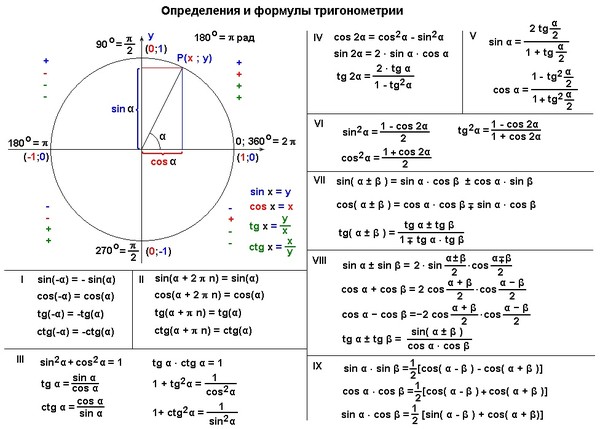
2=\dfrac=1\)
Таким образом, можно утверждать, что существует такой угол \(\phi\) , для которого, например, \(\cos \phi=a_1, \ \sin \phi=b_1\) . Тогда наше выражение примет вид:
\(\sqrt\,\big(\cos \phi \sin x+\sin \phi\cos x\big)=\sqrt\,\sin (x+\phi)\) (по формуле синуса суммы двух углов)
Значит, формула выглядит следующим образом: \[\,\sin (x+\phi),>> \quad \text \cos \phi=\dfrac a>\] Заметим, что мы могли бы, например, принять за \(\cos \phi=b_1, \ \sin \phi=a_1\) и тогда формула выглядела бы как \[a\sin x+b\cos x=\sqrt\,\cos (x-\phi)\]
\(\blacktriangleright\) Рассмотрим некоторые частные случаи формул вспомогательного угла:
\(a) \ \sin x\pm\cos x=\sqrt2\,\left(\dfrac1\sin x\pm\dfrac1\cos x\right)=\sqrt2\, \sin \left(x\pm\dfrac4\right)\)
\(b) \ \sqrt3\sin x\pm\cos x=2\left(\dfrac2\sin x\pm \dfrac12\cos x\right)=2\, \sin \left(x\pm\dfrac6\right)\)
\(c) \ \sin x\pm\sqrt3\cos x=2\left(\dfrac12\sin x\pm\dfrac2\cos x\right)=2\,\sin\left(x\pm\dfrac3\right)\)
Источник
Закон косинусов – формула, доказательство, определение
Закон косинусов связывает длины сторон треугольника с косинусом одного из его углов.
Используя тригонометрию, теперь мы можем получить значения расстояний и углов, которые невозможно измерить иначе. Закон косинусов находит применение при вычислении третьей стороны треугольника по двум сторонам и углу между ними, а также для вычисления углов треугольника, если нам известны все три стороны.
Треугольник состоит из 6 элементов (3 стороны + 3 угла). Давайте поймем закон формулы косинусов и его вывод, чтобы изучить взаимосвязь этих элементов с помощью функции косинуса.
| 1. | Что такое закон косинусов? |
| 2. | Формула закона косинусов |
| 3. | Доказательство закона косинусов |
| 4. | Нахождение недостающих сторон и углов |
| 5. | Часто задаваемые вопросы о законе косинусов |
Что такое закон косинусов?
Закон косинуса помогает установить зависимость между длинами сторон треугольника и косинусом его углов.
Закон косинусов в тригонометрии обобщает теорему Пифагора, применимую к прямоугольному треугольнику.
Закон косинусов: определение
Утверждение: Закон косинуса гласит, что квадрат любой стороны треугольника равен разности между суммой квадратов двух других сторон и удвоенным произведением других сторон. и угол косинуса между ними.
Пусть a, b и c — длины трех сторон треугольника, а A, B и C — три угла треугольника. Тогда закон косинуса гласит: a 2 = b 2 + c 2 − 2bc·cosA. Как сказано выше, закон косинусов в тригонометрии обобщает теорему Пифагора. Если вы подставите 90º вместо угла в одном из правил, что произойдет? Поскольку cos 90º = 0, остается теорема Пифагора.
Закон косинуса также известен как правило косинуса. Этот закон полезен для поиска недостающей информации в любом треугольнике. Например, если известны длины двух сторон треугольника и угол, заключенный между ними, это правило помогает найти третью сторону треугольника.
Давайте проверим различные формулы закона косинусов и метод нахождения этих недостающих параметров в следующих разделах.
Формула закона косинусов
Формулу закона косинусов можно использовать для нахождения недостающей стороны треугольника, если известны две его стороны и угол между ними, т. е. она используется в случае треугольника SAS. Мы знаем, что если A, B и C — вершины треугольника, то их противоположные стороны обозначаются строчными буквами a, b и c соответственно. Формула закона косинусов используется для:
- найти a, когда заданы b, c и A (или)
- найти b, когда даны a, c и B (или)
- найти c, когда заданы a, b и C (или)
- Найдите любой угол треугольника, если даны a, b и c.
Есть три закона косинусов и мы выбираем один из них для решения наших задач в зависимости от имеющихся данных.
A 2 = B 2 + C 2 — 2BC · COSA
B 2 = C 2 + A 2 — 2CA · COSB
C 2 2 — 2CA · COSB
C 2 2 — 2CA0054 = а 2 + b 2 — 2ab·cosC
Доказательство закона косинусов
Существует несколько способов доказать закон косинуса.
Докажем это с помощью тригонометрии. Рассмотрим следующий рисунок.
В ΔABM имеем
sin A = BM/AB = h/c
и,
cos A = AM/AB = r/c
Из уравнения (1) и (2) , получаем h = c(sin A) и r = c(cos A)
По теореме Пифагора в ΔBMC,
a 2 = h 2 + (b — r) 2
Подставим h = c(sin A) и r = c(cos A) в уравнение (3).
A 2 = (C (SINA)) 2 + (B — C (COSA)) 2
= C 2 SIN 2 A + B 2 + C 2 44 A + B 2 + C 2 444 A + B 2 + C 2 44 COS 2 A — 2BC · COSA
= C 2 (SIN 2 A + COS 2 A) + B 2 — 2BC0054 — 2bc·cosA
Следовательно, доказано.
Нахождение недостающей длины и углов с помощью закона косинусов
Как обсуждалось выше, закон косинусов можно использовать для вычисления недостающих параметров треугольника при наличии требуемых известных элементов.
Давайте рассмотрим следующие шаги, чтобы понять процесс нахождения недостающей стороны или угла треугольника с использованием закона косинуса.
- Шаг 1: Запишите полученные данные (длины сторон и меры углов) для треугольника и определите элемент для расчета.
- Шаг 2: Применение формулы косинуса,
a 2 = b 2 + c 2 — 2bc·cosA
б 2 = с 2 + а 2 — 2ca·cosB
с 2 = а 2 + b 2 — 2ab·cosC
где A, B и C — вершины треугольника, а их противоположные стороны представлены как a, b и c соответственно. - Шаг 3: Выразите полученный результат в подходящих единицах.
Рассмотрим несколько примеров, чтобы найти недостающую сторону и угол треугольника.
Пример: Посмотрите на рисунок ниже.
Нам нужно найти меру ∠A.
Мы будем использовать формулу
a 2 = b 2 + c 2 — 2bc.
cosA. Замените 10 на «а», 7 на «b» и 5 на «с».
10 2 = (7) 2 + (5) 2 — 2(5)(7)·cosA
70·cos A = -26
cos A = -13/35
A = 111,8º
В этом примере мы использовали закон уравнения косинуса, чтобы найти недостающий угол. Теперь давайте воспользуемся законом уравнения косинуса, чтобы найти недостающую сторону.
Пример: Две стороны треугольника равны 72 дюйма и 50 дюймов, а угол между ними равен 49º. Найдем недостающую сторону.
Решение:
Замените 72 на b, 50 на c и 49º на A.
Использование Закона Формулы Косинелей,
A 2 = B 2 + C 2 — 2BC · COSA
A 2 = (72) 2 + (50) 2 — 2) (72) (50) COS49º
A 2 = 5184 + 2500 — (7200) (0,656)
A 2 = 5184 + 2500 — 4723,2
A 2 = 2960,8
A 2 = 2960,8
A . Итак, недостающая длина стороны составляет 54,4 дюйма. Важные замечания по закону косинусов: Сложный вопрос: Паук запутался в своей паутине. Посмотрите на рисунок ниже. Сможете ли вы найти значение х? 
Часто задаваемые вопросы о законе косинусов
Что такое закон косинусов в тригонометрии?
Закон косинусов используется для нахождения недостающей стороны треугольника, когда известны две его стороны и угол между ними. Есть три закона косинусов и мы выбираем один из них для решения наших задач в зависимости от имеющихся данных.
- а 2 = b 2 + с 2 — 2bc·cosA
- b 2 = c 2 + a 2 — 2ca·cosB
- с 2 = а 2 + b 2 — 2ab·cosC
где A, B и C — вершины треугольника, а их противоположные стороны обозначены маленькими буквами a, b и c соответственно.
Для чего используется закон косинусов?
Закон косинусов можно использовать для нахождения неизвестных частей косоугольного треугольника (непрямоугольного треугольника), когда известны либо длины двух сторон и мера прилежащего к ним угла (SAS), либо длины даны три стороны (ССС).
Каковы возможные критерии закона косинусов?
Чтобы использовать закон косинусов, должны быть известны либо две стороны треугольника и мера прилежащего к ним угла (SAS), либо длина всех трех сторон треугольника (SSS).
Что такое формула закона косинусов?
Формула закона косинусов задается следующим образом:
где A, B и C — вершины треугольника, а их противоположные стороны представлены как a, b и c соответственно.
Как вывести формулу закона косинусов?
Существует несколько способов вывести закон формулы косинуса.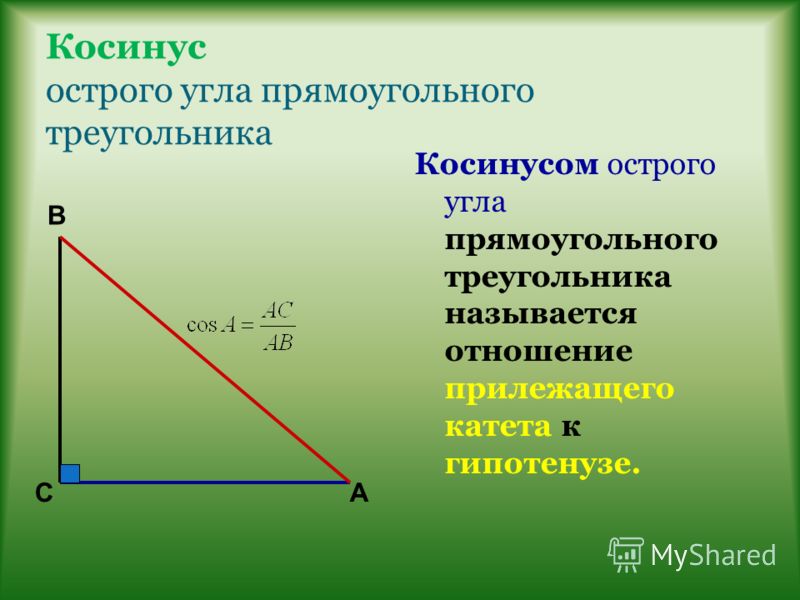
Некоторые из них даны как,
- Использование основных понятий тригонометрии.
- Использование векторной алгебры.
- Использование закона синуса.
- Использование координатной геометрии для определения расстояния между двумя точками координат.
Каково применение формулы закона косинусов?
Формула закона косинусов находит применение при нахождении недостающей стороны треугольника, когда известны две его стороны и угол между ними, т. е. она используется в случае треугольника SAS.
Как найти недостающую сторону или угол треугольника, используя закон косинусов?
Закон косинусов можно использовать, чтобы найти недостающую сторону или угол треугольника, применяя любую из следующих формул:
Здесь A, B и C — вершины треугольника, а их противоположные стороны обозначены буквами a, b и c соответственно.
Закон косинуса работает во всех треугольниках?
Да, закон косинусов применим ко всем треугольникам. Это справедливо как для прямоугольных, так и для косоугольных треугольников.
Кто изобрел закон косинусов?
Элементы Евклида способствовали открытию закона косинусов. Джамшид аль-Каши, персидский математик, был первым, кто в 15 веке в явном виде сформулировал закон косинусов.
Решение общих треугольников
Процесс решения треугольников можно разделить на несколько отдельных групп. Ниже приводится список этих категорий вместе с процедурой, которой необходимо следовать, чтобы найти недостающие части треугольника. Предполагается, что все три недостающие части должны быть найдены. Если необходимо определить только некоторые из неизвестных значений, может потребоваться модифицированный подход.
- SSS : Если известны три стороны треугольника, сначала используйте закон косинусов, чтобы найти один из углов. Обычно лучше всего сначала найти наибольший угол, противоположный самой длинной стороне. Затем с помощью закона синусов составите пропорцию, чтобы найти второй угол. Наконец, вычтите эти угловые измерения из 180 °, чтобы найти третий угол.
- Причина, по которой для нахождения наибольшего угла в треугольнике следует использовать закон косинусов, заключается в том, что если косинус положительный, то угол острый. Если косинус отрицательный, то угол тупой. Если косинус равен нулю, то угол прямой. Как только известен наибольший угол треугольника, два других угла должны быть острыми.
- Если наибольший угол находится не с помощью закона косинусов, а с помощью закона синусов, определение того, является ли угол острым или тупым, должно быть выполнено с использованием теоремы Пифагора или других средств, поскольку синус положителен для обоих острых углов. (первый квадрант) и тупые (второй квадрант) углы. Это добавляет дополнительный шаг к решению задачи.
- Если требуется размер только одного из углов, используйте закон косинусов. Закон косинусов можно использовать для нахождения всех недостающих углов, хотя решение с использованием закона косинусов обычно сложнее, чем решение с использованием закона синусов.
- SAS: Если известны две стороны и угол между ними треугольника, сначала используйте закон косинусов, чтобы найти третью сторону. Затем используйте закон синусов, чтобы найти меньший из двух оставшихся углов. Это угол напротив самой короткой или более короткой стороны, а не самой длинной стороны. Наконец, вычтите эти угловые измерения из 180 °, чтобы найти третий угол. Опять же, вы можете использовать закон косинусов, чтобы найти два недостающих угла, хотя решение с использованием закона косинусов обычно сложнее, чем решение с использованием закона синусов.
- ASA: Если известны два угла и прилежащая к ним сторона треугольника, сначала вычтите эти величины угла из 180°, чтобы найти третий угол. Затем используйте закон синусов, чтобы установить пропорции, чтобы найти длины двух недостающих сторон. Вы можете использовать закон косинусов, чтобы найти длину третьей стороны, но зачем беспокоиться, если вместо этого можно использовать закон синусов?
- AAS: Если известны два угла и сторона, не входящая в треугольник, сначала вычтите эти углы из 180°, чтобы найти третий угол. Затем используйте закон синусов, чтобы установить пропорции, чтобы найти длины двух недостающих сторон. Данная сторона лежит против одного из двух заданных углов. Если все, что нужно, это длина стороны, противоположной второму заданному углу, то используйте закон синусов для вычисления его значения.
- SSA: Это известно как неоднозначный случай . Если известны две стороны и не заключенный между ними угол треугольника, то существует шесть возможных конфигураций: две, если данный угол тупой или прямой, и четыре, если данный угол острый. Эти шесть возможностей показаны на рисунках 1 2 и 3 . На рисунках и h — высота, где h = a sin β, а β — острый угол.
Обычно лучше всего сначала найти наибольший угол, противоположный самой длинной стороне. Затем с помощью закона синусов составите пропорцию, чтобы найти второй угол. Наконец, вычтите эти угловые измерения из 180 °, чтобы найти третий угол.
Закон косинусов можно использовать для нахождения всех недостающих углов, хотя решение с использованием закона косинусов обычно сложнее, чем решение с использованием закона синусов.
Вы можете использовать закон косинусов, чтобы найти длину третьей стороны, но зачем беспокоиться, если вместо этого можно использовать закон синусов?
Рисунок 1
Два случая для SSA.
Рисунок 2
Рисунок 3
Два случая для SSA.
На рисунке 1(a) если b < h , то b не может достичь другой стороны треугольника, и никакое решение невозможно. Это происходит, когда б < а sin β.
На рисунке 1 (b) если b = h = a sin β, то образуется ровно один прямоугольный треугольник.
На рисунке 2 (a) если h < b < a , то есть a sin β < b , < a , то существуют два разных решения.
На рисунке 2 (b) если b = a , то существует только одно решение, а если b = a , то решение представляет собой равнобедренный треугольник.
Если угол β тупой или прямой, существуют следующие две возможности.
На рисунке 3 (а) если b > a , то возможно одно решение.
На рисунке 3 (b) если b ≤ a , то решения невозможны.
Пример 1: (SSS) Найдите разницу между наибольшим и наименьшим углами треугольника, если длины сторон равны 10, 19и 23, как показано на рис. 4 .
Рисунок 4
Чертеж для примера 1.
Во-первых, используйте закон косинусов, чтобы найти размер наибольшего угла (β), который противоположен самой длинной стороне (23).
Затем используйте закон синусов, чтобы найти размер наименьшего угла (α), который находится напротив самой короткой стороны (10).
Таким образом, разница между наибольшим и наименьшим углом равна
Пример 2: (SAS) Катеты равнобедренного треугольника имеют длину 28 и образуют угол 17° (рис.
5). Какова длина третьей стороны треугольника?
Рисунок 5
Чертеж для примера 2.
Это прямое применение закона косинусов.
Пример 3: (ASA) Найдите значение d на рис. 6 .
Рисунок 6
Чертеж для примера 3.
Сначала рассчитаем размеры углов α и β. Затем найдите значение a , используя закон синусов. Наконец, используйте определение синуса, чтобы найти значение d .
Наконец,
Пример 4: (AAS) Найдите значение x на рис. 7 .
Рисунок 7
Чертеж для примера 4.
Сначала вычислите величину угла α. Затем используйте закон синусов, чтобы вычислить значение x .
Пример 5: (SSA) Одна сторона треугольника длиной 20 образует угол 42° со второй стороной треугольника (8).