Фото алгебра: «Алгебра» — Яндекс Кью — Таловская средняя школа

Содержание

ГДЗ Алгебра Макарычев 8 класс Топ

Авторы:Макарычев, Миндюк, Нешков

Изд-во:Просвещение 2016-2021

Вид УМК:учебник

Найди ответ по номеру задания

1234567891011121314151617181920

2122232425262728293031323334353637383940

4142434445464748495051525354555657585960

6162636465666768697071727374757677787980

81828384858687888990919293949596979899100

101102103104105106107108109110111112113114115116117118119120

121122123124125126127128129130131132133134135136137138139140

141142143144145146147148149150151152153154155156157158159160

161162163164165166167168169170171172173174175176177178179180

181182183184185186187188189190191192193194195196197198199200

201202203204205206207208209210211212213214215216217218219220

221222223224225226227228229230231232233234235236237238239240

241242243244245246247248249250251252253254255256257258259260

261262263264265266267268269270271272273274275276277278279280

281282283284285286287288289290291292293294295296297298299300

301302303304305306307308309310311312313314315316317318319320

321322323324325326327328329330331332333334335336337338339340

341342343344345346347348349350351352353354355356357358359360

361362363364365366367368369370371372373374375376377378379380

381382383384385386387388389390391392393394395396397398399400

401402403404405406407408409410411 (н)411 (с)412413414415416417418419

420421422423424425426427428429430431432433434435436437438439

440441442443444445446447448449450451452453454455456457458459

460461462463464465466467468469470471472473474475476477478479

480481482483484485486487488489490491492493494495496497498499

500501502503504505506507508509510511512513514515516517518519

520521522523524525526527528529530531532533534535536537538539

540541542543544545546547548549550551552553554555556557558559

560561562563564565566567568569570571572573574575576577578579

580581582583584585586587588589590591592593594595596597598599

600601602603604605606607608609610611612613614615616617618619

620621622623624625626627628629630631632633634635636637638639

640641642643644645646647648649650651652653654655656657658659

660661662663664665666667668669670671672673674675676677678679

680681682683684685686687688689690691692693694695696697698699

700701702703704705706707708709710711712713714715716717718719

720721722723724725726727728729730731732733734735736737738739

740741742743744745746747748749750751752753754755756757758759

760761762763764765766767768769770771772773774775776777778779

780781782783784785786787788789790791792793794795796797798799

800801802803804805806807808809810811812813814815816817818819

820821822823824825826827828829830831832833834835836837838839

840841842843844845846847848849850851852853854855856857858859

860861862863864865866867868869870871872873874875876877878879

880881882883884885886887888889890891892893894895896897898899

900901902903904905906907908909910911912913914915916917918919

920921922923924925926927928929930931932933934935936937938939

940941942943944945946947948949950951952953954955956957958959

960961962963964965966967968969970971972973974975976977978979

980981982983984985986987988989990991992993994995996997998999

10001001100210031004100510061007100810091010101110121013101410151016101710181019

10201021102210231024102510261027102810291030103110321033103410351036103710381039

10401041104210431044104510461047104810491050105110521053105410551056105710581059

10601061106210631064106510661067106810691070107110721073107410751076107710781079

10801081108210831084108510861087108810891090109110921093109410951096109710981099

11001101110211031104110511061107110811091110111111121113111411151116111711181119

11201121112211231124112511261127112811291130113111321133113411351136113711381139

11401141114211431144114511461147114811491150115111521153

Топовые ГДЗ по другим предметам

org/Book»>Учебник
Учебник
Учебник
Учебник
Учебник
Учебник
Контурные
Учебник
Учебник

Подробные решения по алгебре за 8 класс авторы Макарычев, Миндюк, Нешков

Чтобы успеть своевременно и качественно подготовиться к экзамену, который предстоит в следующем, выпускном классе, многие восьмиклассники приступают к самостоятельному изучению предмета. В этом им сможет помочь гдз по алгебре за 8 класс Макарычев — в том случае, если грамотно и эффективно организовать занятия. Желательно запланировать на них не менее часа в день, занимаясь ежедневно. И стараться не допускать длительных, превышающих 10-14 дней, пропусков в подготовке. В противном случае это может привести к забыванию значительной части изученной информации. А последующее форсированное наверстывание материала вызовет усталость и спад интереса к изучаемому предмету.

Кто и почему использует сборники с ответами в процессе обучения?

Среди тех, кто часто или даже на постоянной основе применяет правильные решения по алгебре 8 класс Макарычева — такие категории пользователей:

готовящиеся к экзаменам девяти- и одиннадцатиклассники. Выпускники используют ресурс для того, чтобы вспомнить материал восьмого класса по дисциплине. А также — узнать, как следует грамотно оформлять ответы и решения в соответствии с изменениями требований регламентов Стандартов образования;
подростки, часто пропускающие занятия в школе по причине поездок на состязания, конкурсные мероприятия — научные, творческие и спортивные. С помощью этого источника они восполняют пробелы в знаниях, допущенные из-за пропусков объяснений учителя;
дети, переведенные на семейную, дистанционную, домашнюю форму обучения. В этом случае материал становится альтернативой или существенным дополнением к объяснениям темы педагогом;

сами предметники, для которых решебник становится оптимальным помощником, если требуется быстро проверить большое количество сданных учениками работ. Поскольку у учителя много работы (планирование, отчетность и пр.), которую надо выполнить срочно, они нередко обращаются к ресурсу, чтобы решить свои первоочередные задачи, не рискуя качеством проверки;
родители восьмиклассников — для оценки знаний своего ребенка, не внедряясь в темы и разделы курса дисциплины.

Явные плюсы применения онлайн справочника по алгебре за 8 класс (автор Макарычев)

Хотя и сегодня не все согласны с тем, что еуроки ГДЗ — полезный и нужный ресурс, его сторонники обращают внимание на такие плюсы этой информации:

её доступность для всех, круглосуточно;
минимум времени, которое потребуется, чтобы найти и применить нужное решение;
экономическая выгода, возможность заменить такой работой дорогостоящую репетиторскую помощь;
актуальность представленных данных.

Изучая сборники готовых ответов, разрабатывая и внедряя собственные схемы работы с ним, восьмиклассники учатся планировать, ценить свое время, оперативно находить и применять информацию. Это пригодится подросткам и в настоящем, и в будущем, не только в школе, но и впоследствии, после ее окончания.

Нормали и обратное транспонирование, часть 1: внешняя алгебра / Хабр

Есть такой загадочный факт о линейных преобразованиях: некоторые из них, а именно неоднородное масштабирование и сдвиг, по какой-то причине различают «обычные» векторы и нормали. Когда мы преобразуем «обычный» вектор матрицей, то нормали почему-то нужно преобразовывать обратной транспонированной матрицей. Как это понять?

С помощью нехитрых выкладок можно убедиться, что обратная транспонированная матрица сохраняет перпендикулярность нормалей к своим касательным плоскостям. В какой-то степени этого доказательства достаточно, но оно упускает более глубокую и интересную историю о стоящей за всем этим геометрии.

Эту историю я и хочу поведать в нескольких следующих статьях.

Вот небольшая затравка, прежде чем мы закопаемся в самую суть статьи. Рассмотрим старое доброе однородное масштабирование (один коэффициент по всем осям). Трудно придумать более безобидное преобразование — это всего лишь умножение всех векторов на одно и то же число.

Но при ближайшем рассмотрении здесь происходит что-то не совсем тривиальное. Некоторые величины несут с собой физические «размерности» или «единицы», такие как длины, площади и объёмы. При масштабировании эти величины изменяются в соответствии со своими единицами. Некоторые значения вообще «безразмерны» и не меняются при масштабировании.

В качестве примера давайте перечислим всевозможные поведения единиц при масштабировании в трёхмерном пространстве. Обозначим масштабный множитель как . Тогда:

Безразмерные числа не меняются, иными словами они умножаются на .
Длины умножаются на .
Площади умножаются на .
Объёмы умножаются на .
Но это ещё не всё: есть так же плотности, которые изменяются как обратные к масштабному коэффициенту величины:
Линейные плотности умножаются на .
Плотности по площади умножаются на .
Объёмные плотности умножаются на .
Плотности могут выражать вещи вроде количества текселей на длину, или геометрической вероятности, или количества частиц в объёме. Если 3D-модель масштабируется в сторону увеличения, а размер текстуры не изменяется, тогда плотность текселей на ней уменьшается , и так далее.

Получается, даже ограничившись однородным масштабом и рассмотрев скалярные (не векторные) значения, мы уже наблюдаем следующий феномен: различные значения, которые выглядят структурно одинаковыми (все они являются скалярами), оказывается ведут себя по разному будучи преобразованными, из-за различных единиц которые они несут в себе. А именно, они соответствуют различным степеням длины от -3 до 3. Величина, соответствующая -ой степени длины, масштабируется как .

(Можно было бы придумать величины со степенями масштабирования и более, или даже с дробными степенями. Но оставим их за рамками рассмотрения, потому что у них нет хорошей геометрической интерпретации в 3D.)

Окей, может это чем-то и похоже на различие обычных векторов и нормалей. Но как это работает для векторных величин? Как на всю эту картину влияет неоднородное масштабирование? И где тут появляется обратное транспонирование? Чтобы понять это по-настоящему, нам придётся ещё дальше продвинуться в математику.

Отныне и до конца нам понадобится внешняя алгебра, или алгебра Грассмана. Так как с ними скорее всего знакомы не все читатели, я изложу краткое введение в тему. Для более глубокого понимания обратитесь к этой лекции Эрика Лэнгиела, или к нескольким первым главам книги Дорста Geometric Algebra for Computer Science. В сети есть великое множество других материалов.

Внешняя алгебра — это расширение линейной алгебры, которое действует не только над векторами, но и над некими геометрическими сущностями высших порядков, которые называются бивекторами,

тривекторами и так далее. В общем случае эти объекты называются -векторы, где — внешняя степень или размерность объекта. Они подчиняются тем же правилам, что и векторы — их можно складывать и умножать на скаляры. Но геометрический смысл у них другой.

Мы часто представляем себе вектор как абстрактную стрелку — у неё есть направление в пространстве (в котором указывает стрелка) и абсолютная величина, представляемая длиной стрелки. Бивектор во многом такой же, но он плоский, а не линейный. Он представляется не стрелкой, а абстрактным участком плоской поверхности.

Как и у векторов, у бивекторов тоже есть направление в том смысле, что плоскость может быть обращена к различным направлениям в пространстве. Ещё у них есть абсолютная величина, геометрически представимая как площадь участка плоскости. Чего у них нет, так это концепции

формы на плоскости. Визуализируя бивектор как часть плоскости, вы можете представлять его как квадрат, круг, параллелограмм или любую другую сколь угодно замысловатую фигуру соответствующей площади.

Аналогично, тривекторы — это трёхмерные векторные величины, представляющие участок пространства, а не плоскости или стрелку. Опять же, у них нет определённой формы, а есть только абсолютное значение, которое теперь является объёмом, а не площадью или длиной.

В трёхмерном пространстве у тривекторов нет направления в полезном смысле слова. Иными словами, у них есть единственное возможное направление, которое параллельно пространству. Тем не менее, у тривекторов есть два противоположных направления, которые мы можем назвать «положительным» и «отрицательным», или «правосторонним» и «левосторонним». Это похоже на то, как вектор может указывать влево или вправо на одномерной прямой, и при желании мы можем назвать эти направления положительным и отрицательным.

В пространствах бо́льших размерностей тривекторы так же могут иметь много разных направлений, как векторы и бивекторы. Кроме того, там могут быть квадвекторы и -векторы более высоких степеней. Нам же будет достаточно трёх измерений.

Базисные -векторы

Бивекторы и тривекторы можно разложить на компоненты в базисе, так же как это делается с обычными векторами. Координатная запись вектора , означает, что может быть представлен как линейная комбинация базисных векторов:

Базисные векторы , , определяют направление и масштаб осей , , . Точно так же бивектор можно представить линейной комбинацией базисных бивекторов:

Здесь — это бивектор единичной площади, ориентированный вдоль плоскости . и можно представить по аналогии. Базисные бивекторы соответствуют не осям координат, а плоскостям, натянутым на

пары осей. Так определяются «координаты бивектора» , с помощью которых мы можем обозначить или соорудить любой бивектор в пространстве.

Случай тривектора менее интересен:

Как мы заметили выше, у тривектора в 3D есть только одно возможное направление, потому у него только один базисный элемент: единичный тривектор «вдоль» пространства . Все остальные тривекторы — это произведения на скаляр.

Внешнее произведение

Итак, внешняя алгебра содержит различные векторообразные объекты разных степеней: обычные векторы (степень 1), бивекторы (степень 2) и тривекторы (степень 3). Скалярам можно приписать степень 0. Наконец, чтобы объекты разных степеней могли взаимодействовать, внешняя алгебра определяет операцию под названием внешнее произведение, обозначаемое через . Оно даёт возможность сконструировать бивектор, перемножая два вектора, например:

В общем случае можно перемножить два любых вектора и получить бивектор, лежащий в плоскости, определяемой этими векторами. Абсолютным значением бивектора будет площадь параллелограмма, построенного на этих векторах (как у векторного произведения).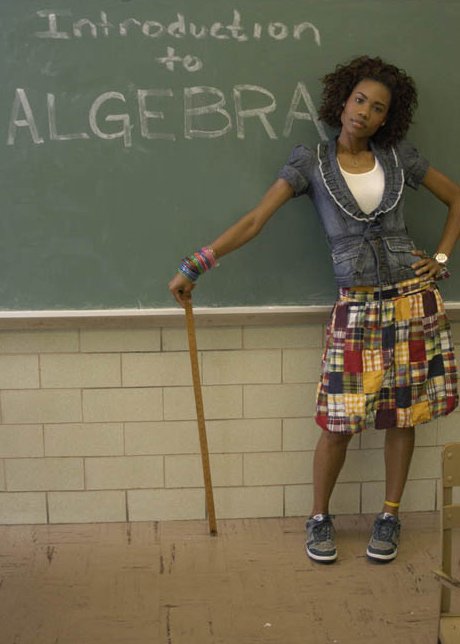

Заметим, что бивектор не «запоминает» на каких конкретно двух векторах он построен. Любые два вектора в той же плоскости, определяющие параллелограмм той же плоскости и ориентации, породят такой же бивектор. Бивектор может быть разложен на векторы, но не единственным способом.

Так же можно перемножить три вектора, или бивектор с вектором, чтобы получить тривектор.

Такое произведение равнозначно «скалярному смешанному произведению», которое даёт тривектор, представляющий ориентированный объём параллелепипеда, натянутого на три вектора.

Внешнее произведение подчиняется большинству известных правил умножения, например ассоциативности и дистрибутивному закону. Умножение на скаляр с ним тоже сочетается. Для скаляра получаем:

Но внешнее произведение двух векторов антикоммутативно, снова как и векторное произведение. Для векторов имеем:

Из этого следует несколько выводов. Во-первых, внешнее произведение любого вектора на себя равно нулю: . Более того, внешнее произведение набора линейно зависимых векторов тоже равно нулю. Например, когда и коллинеарны. В случае трёх векторов, когда копланарны.

Это так же объясняет почему степени выше 3 не существуют в трёхмерном пространстве. Внешнее произведение четырёх трёхмерных векторов всегда равно нулю, потому что в трёхмерном пространстве не может быть четырёх линейно независимых векторов.

Ранее я заявлял, что абсолютное значение вектора можно представлять как длину, значение бивектора — как площадь, а тривектора — как объём. Но что управляет именно таким сопоставлением единиц величинам?

Выше мы видели, что длины, площади и объёмы ведут себя по-разному при масштабировании. Равномерное масштабирование трёхмерного пространства с коэффициентом отмасштабирует длины, площади и объёмы как соответственно. Теперь у нас есть аппарат, показывающий что векторы, бивекторы и тривекторы ведут себя точно так же.

К вектору можно применить масштаб, умножив его на подходящую матрицу:

Вектор как единое целое, его компоненты , и его скалярное абсолютное значение, умножаются на коэффициент при масштабировании, поэтому мы может назвать его длиной, и в этом не будет противоречия.

Что насчёт бивекторов? Чтобы увидеть как они ведут себя при масштабировании (или любом другом линейном преобразовании), обратимся к внешнему произведению. В трёхмерном пространстве любой бивектор можно разложить на внешнее произведение двух векторов. Мы умеем преобразовывать векторы, а значит можем преобразовать бивектор, преобразовав составляющие его векторы и взяв внешнее произведение результатов:

Во как! Так как бивектор состоит из двух сомножителей, каждый из которых масштабируется на , бивектор обретает коэффициент , который делает его площадью.

Тривекторы тоже можно преобразовать, раскладывая на векторы. Теперь неудивительно, что три вектор-сомножителя придают тривектору коэффициент . Приведём выкладки для полноты:

Бивекторы и неравномерный масштаб

Теперь наконец мы можем вернуться к исходному вопросу. Что усложнится, если мы применим неравномерное масштабирование?

Чтобы понять это, давайте рассмотрим пример. Будем масштабировать в 3 раза по оси , оставляя остальные оси неизменными. Получится матрица вида:

На обычных векторах её действие очевидно: компонента умножается на 3, а компоненты не изменяются. В общем случае матрица изменяет как длину, так и направление вектора в зависимости от изначального направления: векторы, близкие к оси растягиваются сильнее, а близкие к плоскости — слабее.

Как такое преобразование повлияет на бивектор? Для начала давайте зайдём со стороны геометрии. Бивектор обозначает участок плоскости с заданными площадью и направлением, в которое направлена «лицевая» сторона. При растяжении такого участка вдоль оси мы ожидаем, что и направление и площадь изменятся. Но различные бивекторы изменятся по разному: на бивектор, близкий к плоскости , растяжение повлияет меньше, а бивектор, чья плоскость близка к , будет растянут сильнее.

Окей, вернёмся к алгебре. Как было показано выше, любой бивектор можно разложить на базисные бивекторы, выровненные по осям:

Чтобы применить масштабирование к бивектору, нужно лишь применить его к базисным бивекторам. Для этого разложим их на базисные векторы и применим к ним:

Это соответствует геометрической интуиции: не изменился, а и обрели множетель 3, потому что их плоскости включают ось .

Таким образом, вот общий эффект применения к бивектору :

Теперь, как и в случае с вектором, можно выписать преобразование бивектора в виде компонент, к котором применяется матрица:

Это то же самое преобразование, которое мы только что вывели, записанное в другой нотации. Обратите внимание на одно различие: матрица в этом выражении не совпадает с матрицей исходного преобразования.

Заметим однако забавное совпадение: обратная транспонированная пропорциональна матрице из предыдущей формулы:

К чему бы это?

Присоединённая матрица

Фактически, матрица преобразования для бивектора — это присоединённая матрица к .

Она пропорциональна обратной транспонированной матрице с коэффициентом . (Обратную к матрицу можно получить транспонированием присоёдинённой матрицы, разделив её на ). Присоединённая матрица определена даже когда необратима. Это хорошее свойство, потому что мы можем преобразовывать вектор необратимой матрицей, и должна быть возможность проделать то же самое с бивектором!

Давайте получше поймём почему присоединённая матрица — это то, что нужно. Введём понятие алгебраического дополнения.

У каждого элемента квадратной матрицы есть алгебраическое дополнение. Вычисляется алгебраическое дополнение элемента на -ой строке и -ом столбце следующим образом:

Возьмём исходную матрицу и вычеркнем строку и столбец . Останется подматрица размером .
Вычислим определитель этой подматрицы.
Умножим определитель на , то есть изменим его знак если нечётно. Это и есть алгебраическое дополнение!

Теперь склеим алгебраические дополнения обратно в матрицу , в результате чего получится присоединённая матрица.

Но как так получилось, что эта конструкция работает в преобразовании бивектора? Посмотрим на первый компонент бивектора . Этот член представляет компонент плоскости , а потому на него влияют только преобразования, которые применяет к осям и . В рецепте приготовления алгебраического дополнения матрицы тоже использзуется подматрица , которая определяет что делает с осями и . Далее мы берём её определитель, который есть ни что иное, как коэффициент масштабирования плоскости !

Из-за того, что мы выбрали бивекторный базис именно в таком порядке, каждый элемент присоединённой матрицы автоматически вычисляет детерминант, который определяет как масштабирует площади в соответствующей плоскости. Или, для внедиагональных элементов, как отображает площади из одной координатной плоскости в другую. Другими словами, алгебраические дополнения оказались в точности теми коэффициентами, которыми преобразуются компоненты бивектора.

(Между почим, знаковый множитель с третьего шага нужен чтобы разрешить некоторые проблемы упорядоченности. Без него у нас был бы базисный элемент вместо . Последний базисный элемент предпочитается по общепринятому соглашению. )

Несмотря на сфокусированность нашего повествования на трёхмерном случае, замечу, что в размерности присоединённая матрица преобразует -векторы в подходящем базисе. Фактически, для преобразования -векторов понадобится матрица -ых миноров, то есть определителей подматрицы с вычеркнутыми строками и столбцами.

В этом месте я должен сделать небольшое признание. На протяжении последних нескольких абзацев я прятал кое что в рукаве. Трюк вот в чём: бивекторы изоморфны обычным векторам в 3D. Фактически, компоненты бивектора в стандартном базисе — это компоненты нормали к плоскости бивектора с точностью до нормализации!

Давайте посмотрим как так получается. Ранее мы видели, что внешнее произведение набора линейно зависимых векторов равно нулю. Это значит, что плоскость бивектора может быть задана уравнением:

Любой вектор , лежащий в плоскости бивектора удовлетворяет этому уравнению потому что он образует линейно зависимый набор с двумя векторами, на которые натянута плоскость. Или, с другой стороны, тривектор, образованный и будет иметь нулевой объём.

Разложим это уравнение в стандартных векторном и бивекторном базисах и упростим:

Поясню на случай если шаги не очень понятны. Во второй строке я распределил внешнее произведение по всем членам базиса, большинство из которых уничтожились, потому что в них во внешнем произведении участвовало по две копии одной оси (например, ). В третьей строке я перегруппировал оси всех тривекторов к единому виду , что вполне законно, если мы отслеживаем изменения знака. Здесь во всех случаях было чётное количество изменений знака. Наконец, я вынес и сократил на него.

Теперь последняя строка выглядит как скалярное произведение векторов и ! Другими словами, она выглядит как обычное уравнение плоскости с вектором нормали .

Отсюда видно, что бивекторные координаты в базисе так же являются координатами нормали к плоскости в стандартном векторном базисе . Более того, внешнее произведение вектора на бивектор идентично скалярному произведению на соответствующий вектор нормали. Формально это применение звезды Ходжа, которая в трёхмерном случае взаимозаменяет бивекторы и их нормали. Подробнее об этом поговорим в будущих статьях.

Мы увидели, что векторы нормали в трёхмерном случае можно в какой-то мере представлять себе как бивекторы из внешней алгебры. Так же мы поняли геометрически почему присоединённая матрица — это правильный инструмент для преобразования бивектора. Это отвечает на наш исходный вопрос (почему некоторые преобразования различают обычные векторы и нормали) более удовлетворительно чем «алгебра так устроена».

Тем не менее, от нас ускользнуло ещё несколько вопросов. Я сказал, что бивекторы «изоморфны» векторам нормали, имея ввиду что между ними есть соотношение один к одному. Но какое именно соотношение? Вдобавок, почему мы закончили на присоединённой матрице, а не на обратной транспонированной? Они пропорциональны между собой, и обычно на практике не важно какую именно использовать, потому что нам не важны длины нормалей (обычно мы их всё равно нормализуем). Но мне бы всё ещё хотелось понять корни этого несоответствия.

Ещё вопрос: в затравке вначале статьи нам встретились единицы как с положительными, так и с отрицательными степенями масштаба, от -3 до 3. Теперь мы увидели, что внешние -векторы масштабируются как стпень от 0 до 3. Но что насчёт векторных единиц с отрицательными степенями масштаба? Существуют ли они? Если да, то что они такое?

В следующей серии мы зароемся ещё глубже и усложним нашу геометрическую историю ещё сильнее.