Таблица косинусов углов, вычислить косинус угла
Угол
Косинусом острого угла считается отношение величины прилежащего катета к величине гипотенузы. Прилежащим является катет, расположенный на одной из сторон угла.
cos (A) = в / с
где в — прилежащий катет;
с — гипотенуза.
Рассчитать косинус угла
cos (°) =
Таблица косинусов 1° — 180°
|
|
|
Таблица косинусов 180° — 360°
|
|
|
Синус 30 градусов, sin 30
Автор Admin На чтение 4 мин Просмотров 2.9к. Опубликовано
Синус 30 градусов равняется одной второй или ноль целых пять десятых.
sin 30° = 1/2 или sin 30° = 0,5
В радианной мере измерения углов синусу 30 градусов соответствует синус π/6:
sin 30° = sin π/6
Как это ни странно, но справедливо и обратное равенство, которое утверждает, что синус π/6 (синус пи на 6) равняется синусу 30 градусов:
sin π/6 . sin 30°
sin 30°
Равняется синус пи / 6 так же одной второй или ноль целых пять десятых.
sin π/6 = 1/2 или sin π/6 = 0,5
Это было для блондинок. Для брюнеток и лысых академиков математических наук можно записать всё это в общем виде, пусть распутывают:
sin 30° = sinπ/6 = 1/2 = 0,5
Для полного счастья здесь явно не хватает картинки синуса 30 градусов. А вот и она:
Надеюсь, первую часть задачи я решил и мне удалось объяснить блондинкам, чему равен синус тридцати градусов. Теперь нужно решить вторую половину задачи, с которой не в состоянии справиться даже вся академия математических наук, вместе взятая. Нужно в Интернете найти блондинок, которые ищут синус 30 градусов. Попробую вооружиться логикой блондинок и перечислю ниже поисковые запросы, которые блондинки могут вводить в поисковые системы при поиске ответа на вопрос: чему равен синус 30 градусов? И так, поисковые запросы, разбавленные моими комментариями, дабы поисковые системы не отлучили мое творение от блондинок.
Синус — это математики сверяют свои знания с Интернетом.
Синус, косинус — появилось начальство математиков, чтобы проверить, как математики сверили свои знания.
Синус угла — это очкастые ботаники, будущие Билы Гейтсы, чешут свои умные репы и пытаются вспомнить школьный курс математики.
Синус градусов — шустрые школьники мимоходом забрасывают свой вопрос, что бы побыстрее разделаться с этой бякой и продолжить игру.
Таблица синусов, тангенсов — добросовестные школьники и добропорядочные брюнетки соскребли все свои познания в тригонометрии и пытаются сверить их с Интернетом.
Значение синуса — математики, после долгих блужданий по сайтам с блондинками, наконец-то поняли, как лучше сформулировать поисковый запрос.
Значения косинусов и синусов — математики вдруг вспомнили, что не синусом единым живет тригонометрия.
Синус чему равен? — а вот и первые признаки присутствия блондинок в Интернете с их подкупающей непосредственностью общения, даже с компьютером.
Синусы и косинусы углов. Таблица значений синусов. Синус угла равен — это мамы пытаются проверить, как их чада сделали уроки.
Как найти синус? — это уже типичный вопрос растерянной блондинки.
Синус острого угла. Синус и косинус 30 — мамы с трудом, но уже начинают понимать, что требуется найти в задаче.
Синус числа — бедные мамы, они даже не подозревают, что углы можно измерять радианами.
Синус альфа — мамы вспомнили, какой буквой когда-то в школе они сами обозначали углы.
Калькулятор синусов — на помощь беспомощным мамам приходят умные папы.
Как найти синус угла? — умные папы нашли калькулятор синуса, теперь нужно узнать, как же этой штукой пользоваться.
Геометрия синус, косинус. Скачать таблицу синусов. Значения синусов углов — это чада оторвались от своих виртуальных игр и пытаются доказать умным папам, что папы не правильно нажимают на кнопочки калькулятора, потому что синус угла не может равняться трем банкам пива. Вычисления синуса — математики-теоретики пытаются слямзить результаты работы математиков-прикладников.
Вычисления синуса — математики-теоретики пытаются слямзить результаты работы математиков-прикладников.
Вычислить синус — это математики-прикладники тырят результаты работы своих коллег.
Синус бесконечности — это уже физики пытаются проверить расчеты математиков.
Нахождение синуса — блондинки пытаются узнать, где живут синусы.
Тригонометрический синус — все с удивлением обнаружили, что синусы бывают не только в математике.
Сколько синус 30 — ноль целых пять десятых.
Скольки равен sin 30 — стольки же, ноль пять.
Сколько будет синус 30? — вопрос, конечно, интересный…
ышт 30 — можно и так, только лучше переключаться на английский язык.
Таблица sin альфа 30градусов — здесь не совсем таблица, но и сину, с и 30 градусов точно есть.
Числа из которых синусы натуральные — математики, блондинка задала вопрос. Есть варианты ответов? Честь мундира поставлена на кон.
Кто может объяснить, почему синус 30 градусов равен 1/2? — ну, вундеркинды, блондинка задала вопрос. Кто осмелится ответить?
Кто осмелится ответить?
синус какого угла равен одной второй? — Синус тридцати градусов. Это если просто. Если по математической науке — тогда нужно добавлять периодичность этой тригонометрической функции.
Значение cos 30 — Расчет, тригонометрическая таблица и часто задаваемые вопросы
- Математика
- Значение cos 30
Какова важность и актуальность cos 30?
Что такое тригонометрические отношения?
Тригонометрические соотношения — это соотношения сторон треугольника, взятых одновременно по две. Эти соотношения дают отношение одной стороны треугольника к другой. Чтобы тригонометрические отношения были допустимы, один из углов треугольника должен быть прямым. Если мы предположим, что угол отсчета по горизонтали противоположен прямому углу, то горизонтальное сечение или ось x прямого угла называется основанием треугольника, а вертикальная сторона или ось y известна как соседняя сторона. Отрезок, соединяющий концы обеих стрелок, называется гипотенузой.
Отрезок, соединяющий концы обеих стрелок, называется гипотенузой.
Отношение прилежащей стороны к гипотенузе называется синусом (обычно -sin)
Отношение основания к гипотенузе называется косинусом (обычно -cos)
Отношение прилежащей стороны к основанию равно называется тангенсом (обычно тангенсом)
[Изображение будет загружено в ближайшее время]
Представление Cos 30°:
Когда берется отношение основания исходного угла к гипотенузе, это дает нам значение косинуса отношения под этим конкретным углом. Когда этот угол равен 30°, тогда значение называется cos 30. Значение cos 30 равно значению sin 60, поскольку они дополняют друг друга в треугольнике. Следовательно, значение sin 30 можно использовать и с cos 60, учитывая эту закономерность, мы можем заключить, что sin (90-х) = cos х; где x может быть любым углом.
Производная Cos 30°:
Чтобы получить значение cos 30°, давайте посмотрим на образовавшийся треугольник и проанализируем его.
Если рассматривать углы, то один из углов всегда равен 90°, а два других угла остаются дополняющими друг друга. Если мы должны взять значение cos 30°, это означает, что один из углов равен 30°, а значит, другой угол равен 180° — (90° + 30°), что равно 60°. Теперь, используя свойство прямоугольного треугольника с одним углом 30°, мы можем видеть, что длина гипотенузы в два раза больше, чем длина прилежащего катета, вдвое меньше длины гипотенузы.
Пусть гипотенуза равна x; тогда соседняя сторона имеет значение x/2.
Используя теорему Пифагора гипотенуза² = основание² + смежная² x² = adj²+(x/2)²
Что равно,
x² — (x/2)² =adj²
Упрощая, получаем,
( ¾ )x² =adj²
Отсюда значение adj²/x² = ¾ ;
Что дает нам adj/x = \[\sqrt{3}\]/2
И поскольку мы знаем, что отношение смежных с гипотенузой равно косинусу, следовательно, значение cos 30° равно \[\sqrt{3 }\]/2
Забавные факты:
Еще один способ запомнить значение cos 30° — запомнить его дробное значение π/6 , как оно обозначается в круговой системе или системе координат.
Примеры задач:
Решение. Мы знаем, что значение cos 30° равно \[\sqrt{3}\]/2; Следовательно, мы можем использовать это для вычисления смежной стороны треугольника, т.е. кврт{3}\]/2 = 6\[\кварт{3}\]
Следовательно, одна сторона равна 6\[\sqrt{3}\],
Теперь, по теореме Пифагора, гипотенуза = смежная²+основание²
12² = (6\[\sqrt{3}\])²+ основание² → 12²-(6\[\sqrt{3}\])² = основание²
база = \[\sqrt{144-108}\] = \[\sqrt{36}\] = 6 ;
Следовательно, две стороны равны 6 и 6 \[\sqrt{3}\].
Задача 2: Реактивный самолет во время испытаний летит со скоростью 1,5 Маха, как только взлетает. Между тем, он преодолевает расстояние в 2000 метров после того, как оказался рядом с вами. Теперь вам нужно посмотреть под углом 30°, чтобы увидеть самолет и вычислить высоту самолета.
Решение: Поскольку вы смотрите на него под углом 30°, это означает, что угол возвышения по отношению к земле составляет 30°. Поскольку высота выступает в качестве смежной стороны прямоугольного треугольника, мы можем вычислить высоту с помощью тригонометрии.
Поскольку высота выступает в качестве смежной стороны прямоугольного треугольника, мы можем вычислить высоту с помощью тригонометрии.
Cos Cos 30° = \[\frac{adjacent}{гипотенуза}\] = \[\frac{altitude}{2000}\]
\[\sqrt{3}\]/2 = \[\frac {altitude}{2000}\] ⇒altitude 1000\[\sqrt{3}\]
Отсюда видно, что самолет достиг высоты 1000\[\sqrt{3}\]м
Решение: Чтобы вычислить расстояние от лестницы до стены, нам нужно сначала найти прямоугольный треугольник, одна из сторон которого является путем пожарного. Путь образует примыкание к лестнице, тогда как сама лестница является гипотенузой, а стена вместе с ней выступает в качестве основания. Следовательно, теперь мы можем применить тригонометрию для вычисления смежных.
Используя cos 30° = \[\sqrt{3}\]/2
\[\sqrt{3}\]/2 = \[\frac{adjacent}{гипотенуза}\] = \[\frac{ соседний {20}\]сосед = 20\[\sqrt{3}\]/2 = 10\[\sqrt{3}\]
Следовательно, пожарный должен пройти расстояние 10\[\sqrt{3}\]м до добраться до ступеньки лестницы.
Дата последнего обновления: 29 мая 2023
•
Всего просмотров: 328.8k
•
Просмотров сегодня: 5.86k
Недавно обновленные страницы
90 094 LCM 3 и 4, и как найти наименьшее общее кратноеЧто такое простые проценты? — Пример, формула, решенные примеры и часто задаваемые вопросы
Линейные графики — определение, решенные примеры и практические задачи
Числа в словах
Дробь в процентах
Теорема Коши о среднем значении: введение, история и решенные примеры
НОК 3 и 4 и как найти наименьшее общее кратное
Что такое простые проценты? — Пример, формула, решенные примеры и часто задаваемые вопросы
Линейные графики — определение, решенные примеры и практические задачи
Числа в словах
Доля в процентах
Теорема Коши о среднем значении: введение, история и примеры решений
Актуальные темы
Таблица косинусов | Кубенс
Таблица косинусов значений косинусов углов, записанных в таблице от 0° до 360°.
С помощью таблицы косинусов можно произвести расчет, даже если под рукой не окажется научного калькулятора.
Чтобы найти косинус искомого угла, достаточно воспользоваться таблицей.
Таблица косинусов в радианах
| α | 0 | №6 | №4 | №3 | №2 | № | 3π2 | 2π |
| потому что α |
Таблица косинусов — Наровне таблица синусов изучается в начале тригонометрии. Без понимания таблицы косинусов будет очень сложно изучать тригонометрию и применять тригонометрические формулы.
Тригонометрические функции имеют большое практическое значение в геометрии. По сути это только показатели отношения различных сторон прямоугольного треугольника друг к другу, они могут помочь в решении большинства задач, результат которых сводится к решениям прямоугольных треугольников.
Одной из основных тригонометрических функций является косинус. Поэтому в этой таблице косинусов можно найти любое значение косинуса.
Таблица косинусов углов от 0° до 180°
| cos(0°) = 1 cos(1 градус) = 0,999848 cos(2°) = 0,999391 cos(3°) = 0,99863 cos(4°) = 0,997564 cos(5° ) = 0,996195 cos(6°) = 0,994522 cos(7°) = 0,992546 cos(8°) = 0,9 cos(9°) = 0,987688 cos(10°) = 0,98480 8 cos(11°) = 0,981627 cos(12°) = 0,978148 cos(13°) = 0,97437 cos(14°) = 0,970296 cos(15°) = 0,965926 cos(16°) = 0,9612 62 cos(17°) = 0,956305 cos(18°) = 0,951057 cos(19°) = 0,945519 cos(20°) = 0,939693 cos(21°) = 0,93358 cos(22°) = 0,927184 cos(23°) = 0,920505 9 0214 cos(24°) = 0,913545 cos(25°) = 0, 8 cos(26°) = 0,898794 cos(27°) = 0,891007 cos(28°) = 0,882948 cos(29°) = 0,87462 cos(30°) = 0,866025 соз( 31°) = 0,857167 cos(32°) = 0,848048 cos(33°) = 0,838671 cos(34°) = 0,829038 cos(35°) = 0,819152 cos(36°) = 0,809017 cos(37° ) = 0,798636 cos(38°) = 0,788011 cos(39°) = 0,777146 cos(40°) = 0,766044 cos(41°) = 0,75471 cos(42°) = 0,743145 cos(43°) = 0,731354 cos( 44°) = 0,71934 cos (45°) = 0,707107 | cos(46°) = 0,694658 cos(47°) = 0,681998 cos(48°) = 0,669131 cos(49°) = 0,656059 cos(50°) = 0,642788 co s(51°) = 0,62932 cos (52°) = 0,615661 cos(53°) = 0,601815 cos(54°) = 0,587785 cos(55°) = 0,573576 cos(56°) = 0,559193 cos(57°) = 0,544639 соз(58 °) = 0,529919 cos(59°) = 0,515038 cos(60°) = 0,5 cos(61°) = 0,48481 cos(62°) = 0,469472 cos(63°) = 0,453 99 cos(64°) = 0,438371 cos(65°) = 0,422618 cos(66°) = 0,406737 cos(67°) = 0,390731 cos(68°) = 0,374607 cos(69°) = 0,3583 68 cos(70°) = 0,34202 cos(71°) = 0,325568 cos(72°) = 0,309017 cos(73°) = 0,292372 cos(74°) = 0,275637 cos(75°) = 0,258819 cos(76°) = 0,241922 соз( 77°) = 0,224951 cos(78°) = 0,207912 cos(79°) = 0,190809 cos(80°) = 0,173648 cos(81°) = 0,156434 cos(82°) = 0,139173 902 14 cos(83°) = 0,121869 cos(84°) = 0,104528 cos(85°) = 0,087156 cos(86°) = 0,069756 cos(87°) = 0,052336 cos(88°) = 0,034899 cos(89°) = 0,017452 cos (90°) = 0 | cos(91°) = -0,017452 cos(92°) = -0,034899 cos(93°) = -0,052336 cos(94°) = -0,069756 cos(95°) = -0,087156 co с(96°) = -0,104528 cos(97°) = -0,121869 cos(98°) = -0,139173 cos(99°) = -0,156434 cos(100°) = -0,173648 cos(101°) = — 0,190809 cos(102°) = -0,207912 cos(103°) = -0,224951 cos(104°) = -0,241922 cos(105°) = -0,258819 cos(106°) = -0 .  275637 275637 cos(107 °) = -0,292372 cos(108°) = -0,309017 cos(109°) = -0,325568 cos(110°) = -0,34202 cos(111°) = -0,358368 cos(112°) = -0,374607 cos(113°) = -0,390731 cos(114°) = -0,406737 cos(115°) = -0,422618 cos(116°) = -0,438371 cos(117°) = -0,45399 cos(118°) = -0,469472 cos(119°) = -0,48481 9021 4 cos(120 °) = -0,5 cos(121°) = -0,515038 cos(122°) = -0,529919 cos(123°) = -0,544639 cos(124°) = -0,559193 cos(125°) ) = — 0,573576 cos(126°) = -0,587785 cos(127°) = -0,601815 cos(128°) = -0,615661 cos(129°) = -0,62932 cos(130°) = -0. 642788 потому(131 °) = -0,656059 cos(132°) = -0,669131 cos(133°) = -0,681998 cos(134°) = -0,694658 cos(135°) = -0,707107 | cos(136°) = -0,71934 cos(137°) = -0,731354 cos(138°) = -0,743145 cos(139°) = -0,75471 cos(140°) = -0,766044 902 14 cos(141° ) = -0,777146 cos(142°) = -0,788011 cos(143°) = -0,798636 cos(144°) = -0,809017 cos(145°) = -0,819152 cos(146°) = -0,829038 cos(147°) = -0,838671 cos(148°) = -0,848048 cos(149°) = -0,857167 cos(150°) = -0,866025 cos(151°) = -0,87462 cos(152°) = -0,882948 cos(153°) = -0,891007 cos(154°) = -0,898794 cos(155°) = -0, 8 902 14 cos(156° ) = -0,913545 cos(157°) = -0,920505 cos(158°) = -0,927184 cos(159°) = -0,93358 cos(160°) = -0,939693 cos(161°) = -0,945519 cos(162°) = -0,951057 cos(163°) = -0,956305 cos(164°) = -0,961262 cos(165°) = -0,965926 cos(166°) = -0,970296 cos (167°) = -0,97437 cos(168°) = -0,978148 cos(169°) = -0,981627 cos(170°) = -0,984808 cos(171°) = -0,987688 cos(172°) = -0,9 cos(173°) = -0,992546 90 214 cos(174° ) = -0,994522 cos(175°) = -0,996195 cos(176°) = -0,997564 cos(177°) = -0,99863 cos(178°) = -0,999391 cos(179°) = -0,999848 cos(180°) = -1 |
Cos 0 (косинус нуля)
равно (равно единице)
1 косинус (мера косинуса)
равно
3 косинус (косинус трех)
равно
косинус 90 (косинус 90 градусов)
= 0 (равно нулю)
косинус 30 (косинус 30 градусов)
равно
45 косинус (косинус 45 градусов)
равен
Косинус 60 (косинус 60 градусов)
равен
Таблица косинусов углов от 181° до 360°
902 08cos(182°) = -0,999391
cos(183°) = -0,99863
cos(184°) = -0,997564
cos(185°) = -0,996195
cos(186°) = -0,994522
cos(187°) = -0,992546
cos(188°) = -0,990 268
потому что(189 °) = -0,987688
cos(190°) = -0,984808
cos(191°) = -0,981627
cos(192°) = -0,978148
cos(193°) = -0,97437
cos(194°) = -0,970296
cos(195°) = -0,965926
cos(196°) = -0,961262
cos(197°) = -0,956305
cos(198°) = -0,951057
cos(199°) = -0,945519 9 0214 cos(200° ) = -0,939693
cos(201°) = -0,93358
cos(202°) = -0,927184
cos(203°) = -0,920505
cos(204°) = -0,913545
cos(205°) = -0,
8
cos(206°) = -0,898 794
потому(207 °) = -0,891007
cos(208°) = -0,882948
cos(209°) = -0,87462
cos(210°) = -0,866025
cos(211°) = -0,857167
cos(212°) = -0,848048
cos(213°) = -0,838671
cos(214°) = -0,829038
cos(215°) = -0,819152
cos(216°) = -0,809017
cos(217°) = -0,798636 9 0214 cos(218° ) = -0,788011
cos(219°) = -0,777146
cos(220°) = -0,766044
cos(221°) = -0,75471
cos(222°) = -0,743145
cos(223°) = -0,731354
cos(224°) = -0,71934 9021 4 cos(225° ) = -0,707107
cos(227°) = -0,681998
cos(228°) = -0,669131
cos(229°) = -0,656059
cos(230°) = -0,642788 9 0214 cos(231° ) = -0,62932
cos(232°) = -0,615661
cos(233°) = -0,601815
cos(234°) = -0,587785
cos(235°) = -0,573576
cos(236°) = -0,559193
cos(237°) = -0,544639
cos(238°) = -0,529919
cos(239°) = -0,515038
cos(240°) = -0,5
cos(241°) = -0,48481
cos(242°) = -0,46 9472
потому( 243°) = -0,45399
cos(244°) = -0,438371
cos(245°) = -0,422618
cos(246°) = -0,406737
cos(247°) = -0,390731
cos(24) 8°) = — 0,374607
cos(249°) = -0,358368
cos(250°) = -0,34202
cos(251°) = -0,325568
cos(252°) = -0,309017
cos(253°) = -0.


 9994
9994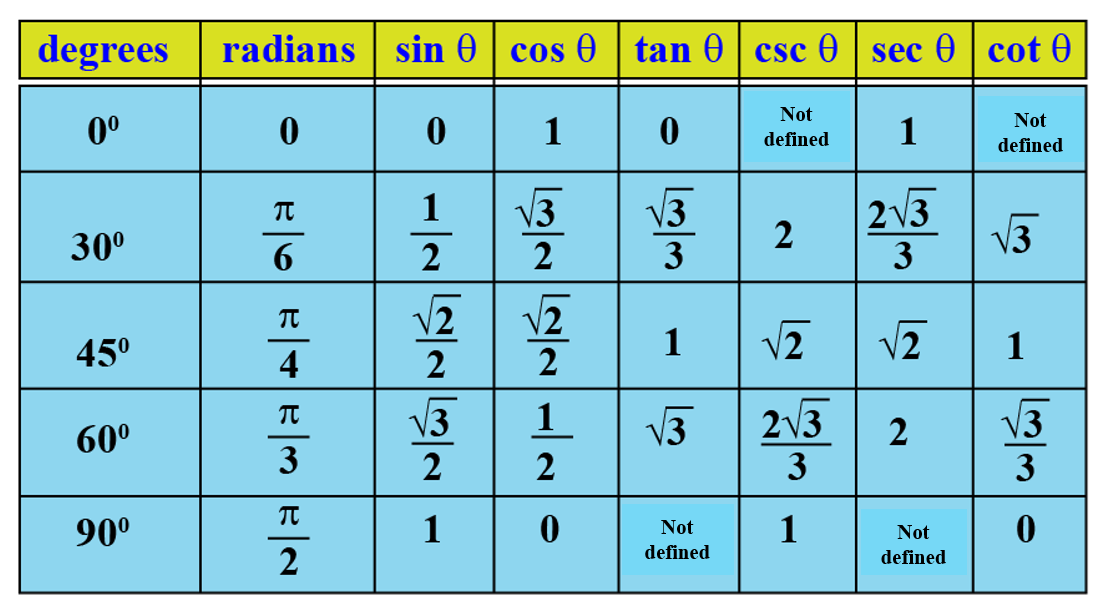 9063
9063 6691
6691 3584
3584 0349
0349 4067
4067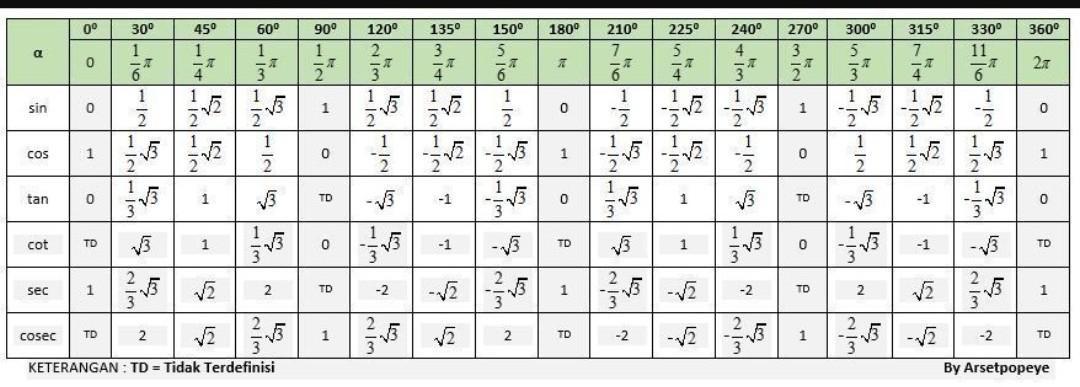 6947
6947 9135
9135 9994
9994
 788
788 5
5 1736
1736 225
225 5592
5592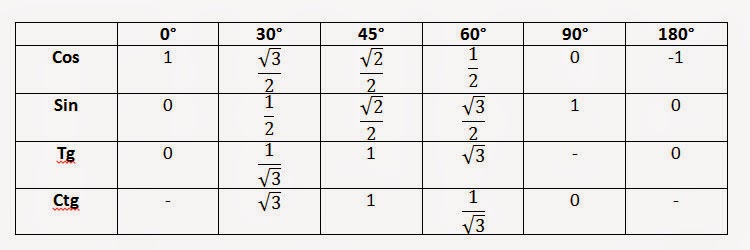 8387
8387 9848
9848