| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | cos(pi/4) | ||
| 9 | Найти точное значение | sin(45 град. ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) | |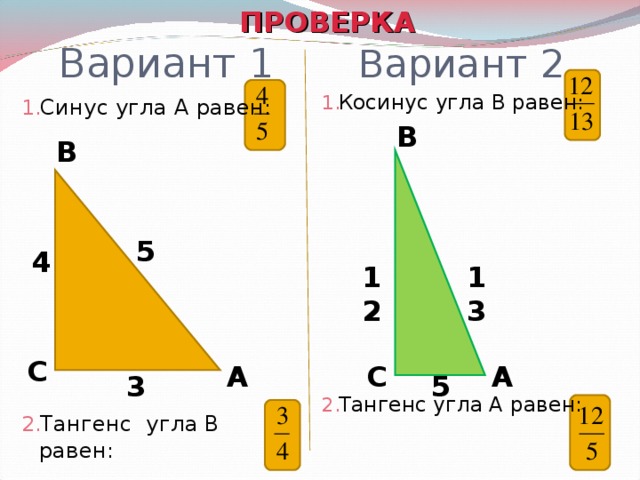
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) | |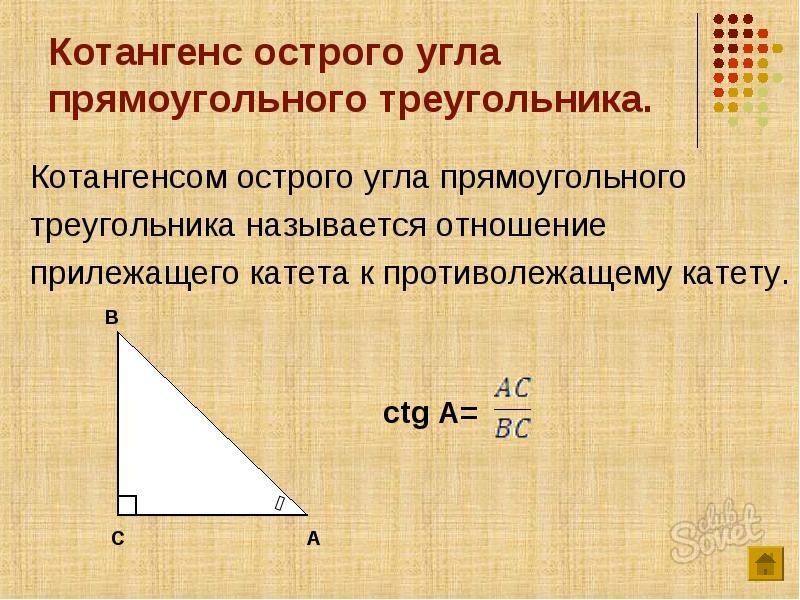
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) | |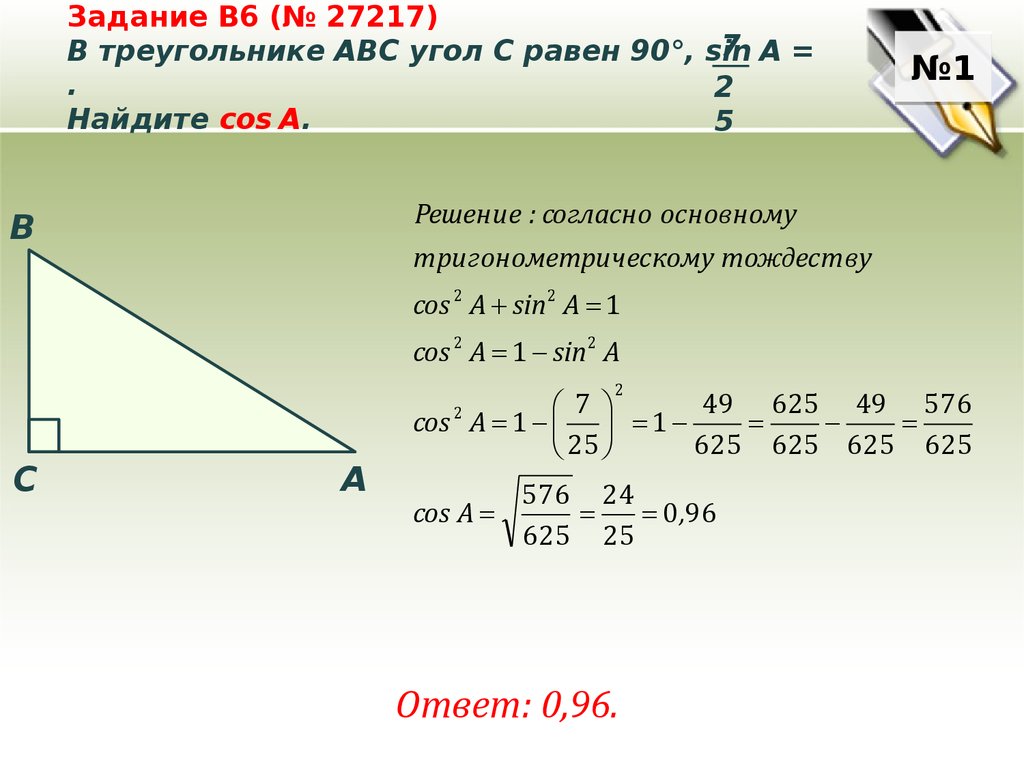
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) | |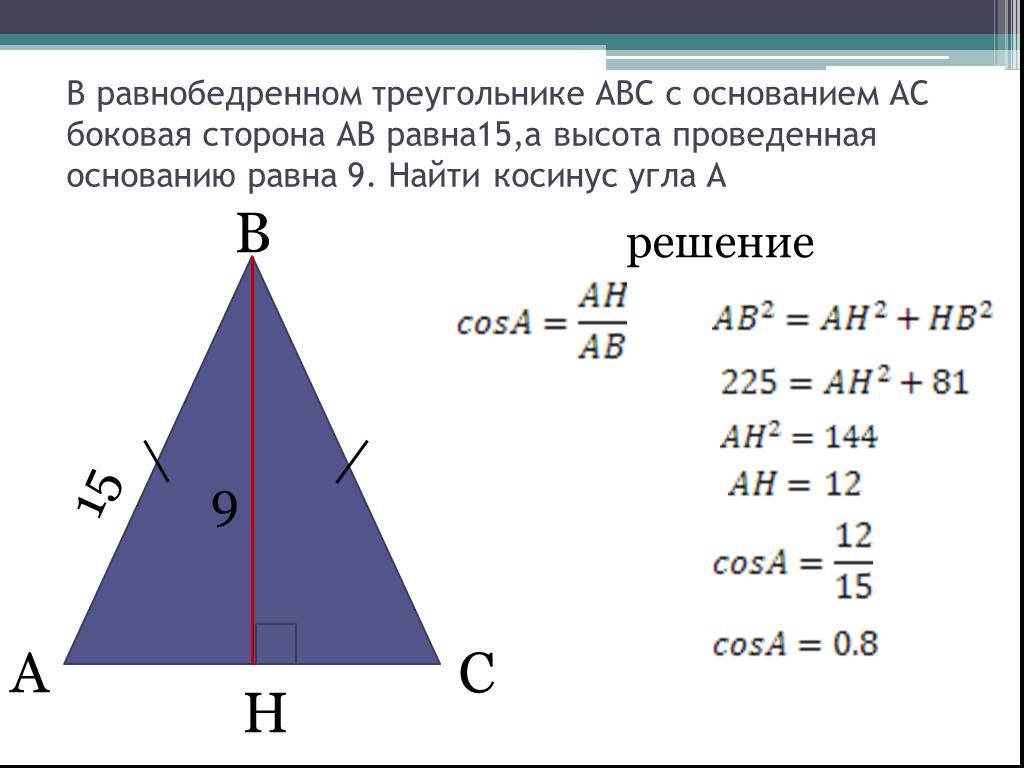
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | ||
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) | |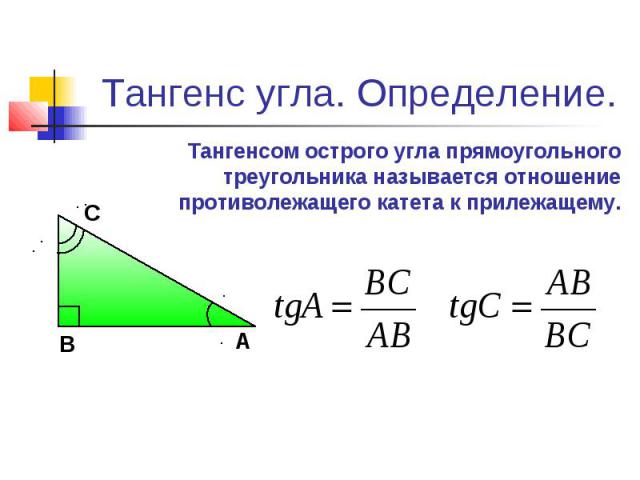
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| Найти точное значение | sin((4pi)/3) | ||
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | ||
| 95 | Найти точное значение | sin(120 град. ) | |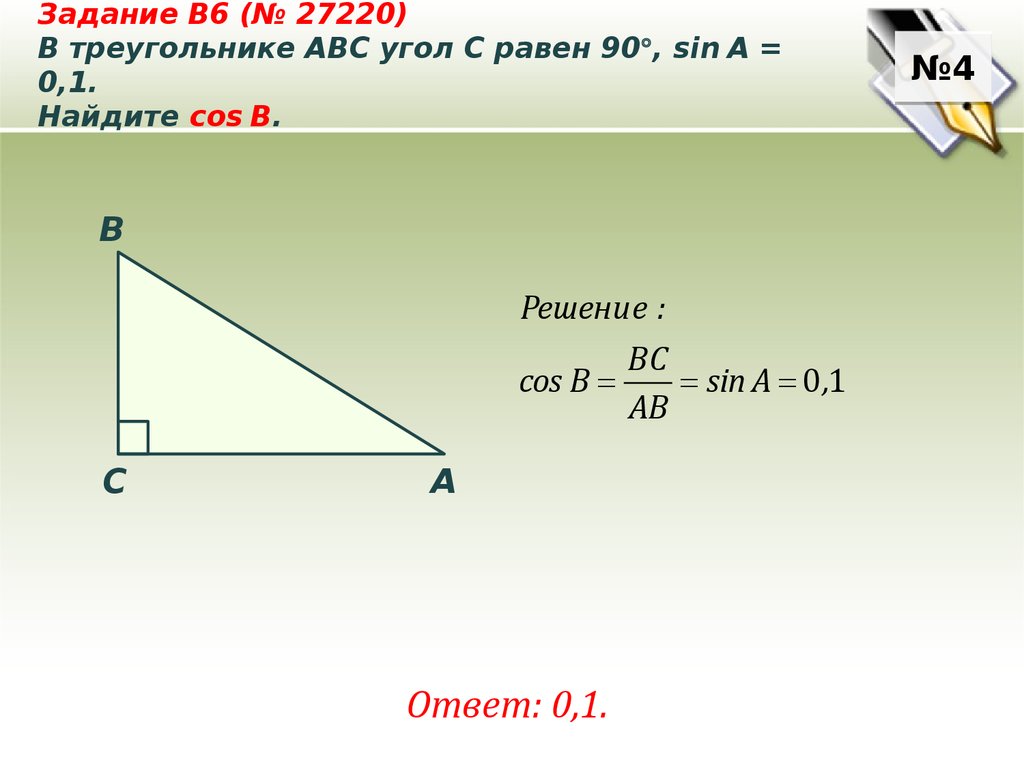
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
А.В. Погорелов. Геометрия. 8 класс. § 7. Контрольные вопросы, ответы — Решебник
Страница 1 из 2
Вопрос 1. Дайте определение косинуса острого угла прямоугольного треугольника.
Ответ.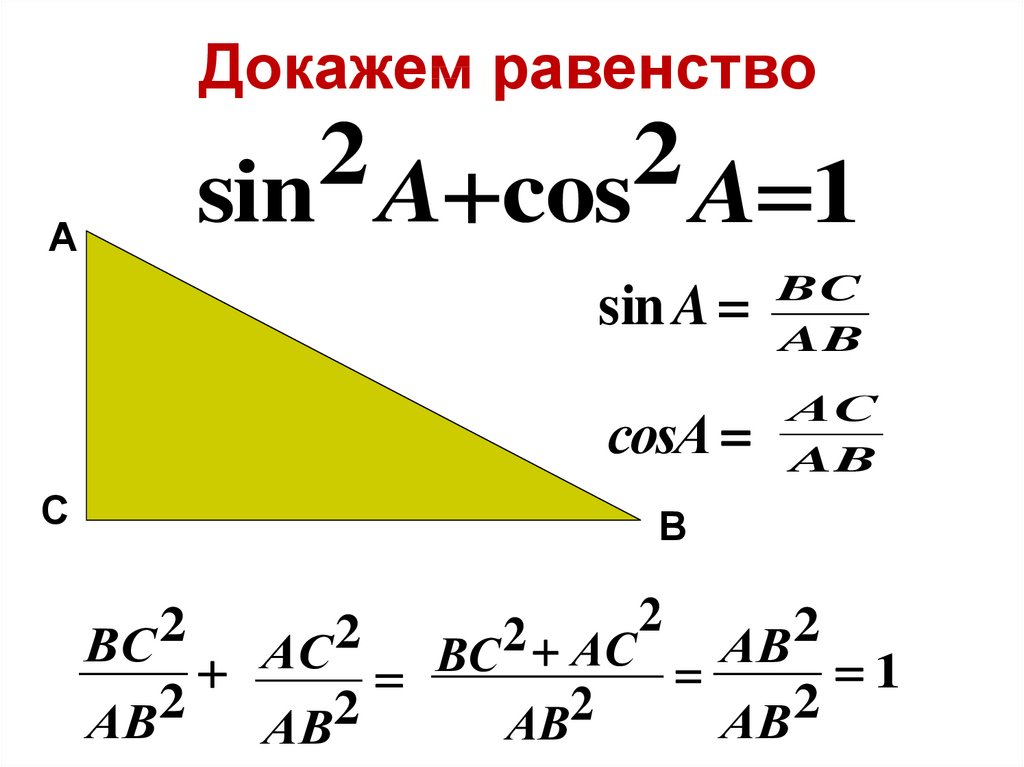
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
Косинус угла \(\alpha\) обозначается так: \(\cos \alpha\). На рисунке 147 показан прямоугольный треугольник ABC с углом A, равным \(\alpha\). Косинус угла \(\alpha\) равен отношению катета AC, прилежащего к этому углу, к гипотенузе AB, т.е.
\(\cos \alpha = \frac{AC}{AB}\).
Рис. 147
Вопрос 2. Докажите, что косинус угла зависит только от градусной меры угла и не зависит от расположения и размеров треугольника.
Ответ. Теорема 7.1. Косинус угла зависит только от градусной меры угла и не зависит от расположения и размеров треугольника.
Доказательство. Пусть ABC и A’B’C’ — два прямоугольных треугольника с одним и тем же углом при вершинах A и A’, равным \(\alpha\) (рис. 148).
Требуется доказать, что\(\frac{A’C’}{A’B’} = \frac{AC}{AB}\).
Рис. 148
Построим треугольник AB1C1, равный треугольнику A’B’C’, как показано на рисунке 148. Так прямые BC и B1C1 перпендикулярны прямой AC, то они параллельны. По теореме о пропорциональных отрезках
\(\frac{AC1}{AB1} = \frac{AC}{AB}\).
А так как по построению AC1 = A’C’, AB1 = A’B’, то
\(\frac{A’C’}{A’B’} = \frac{AC}{AB}\).
Теорема доказана.
Вопрос 3. Докажите теорему Пифагора.
Ответ. Теорема 7.2 (теорема Пифагора). В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Доказательство.Пусть ABC – данный прямоугольный треугольник с прямым углом C. Проведём высоту CD из вершины прямого угла C (рис. 149).
Рис. 149
По определению косинуса угла \(\cos A = \frac{AD}{AC} = \frac{AC}{AB}\).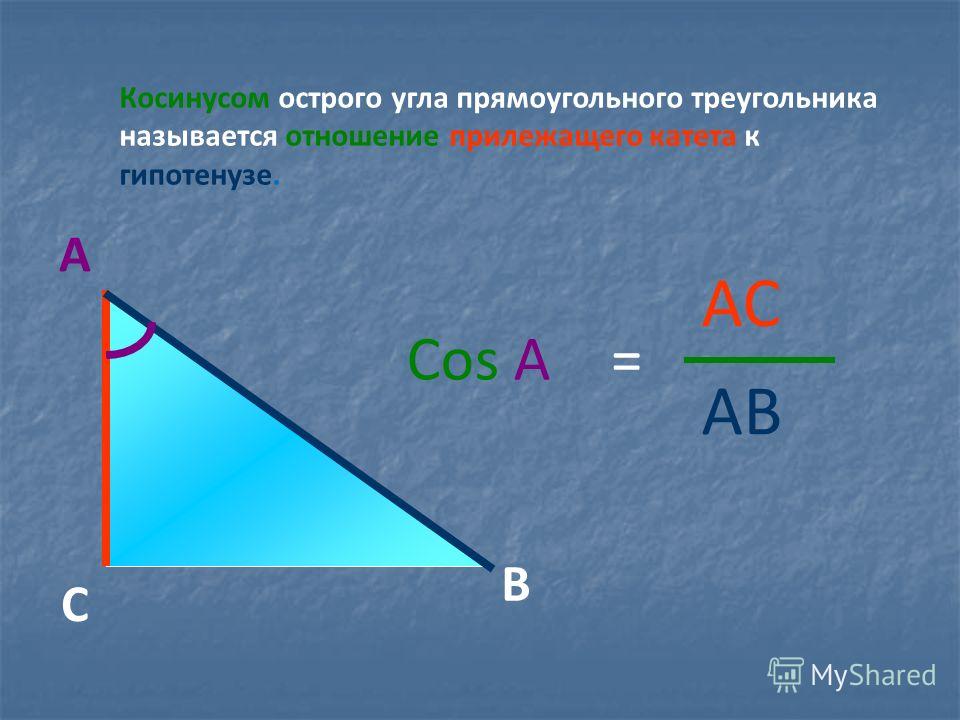
2\), т.е. \(AC < AB\) и \(BC < AB\). Так как AC и BC – катеты, а AB – гипотенуза, то из этого следует, что в любом прямоугольном треугольнике гипотенуза больше любого из катетов. Также следует отметить, что в любом прямоугольном треугольнике любой из катетов меньше гипотенузы.
Вопрос 5. Докажите, что \(\cos\alpha<1\) для острого угла \(\alpha\).
Ответ. Если бы в прямоугольном треугольнике гипотенуза была бы равна одному из катетов, то \(\cos\alpha = 1\) (если любое число разделить на это же число, то получим 1). Но это невозможно, так как в любом прямоугольном треугольнике гипотенуза не равна катетам (она больше любого из катетов). Значит, в прямоугольном треугольнике \(\cos\alpha \neq 1\).
Если бы в прямоугольном треугольнике катеты были бы больше гипотенузы, то \(\cos\alpha > 1\) (если большее число разделить на меньшее, то мы получим смешанное число, значение которого больше 1). Но это также невозможно.
Так как в любом прямоугольном треугольнике катеты меньше гипотенузы, то это значит, что \(\cos\alpha < 1\) (если разделить меньшее число на большее, то мы получим обыкновенную дробь, значение которой меньше 1).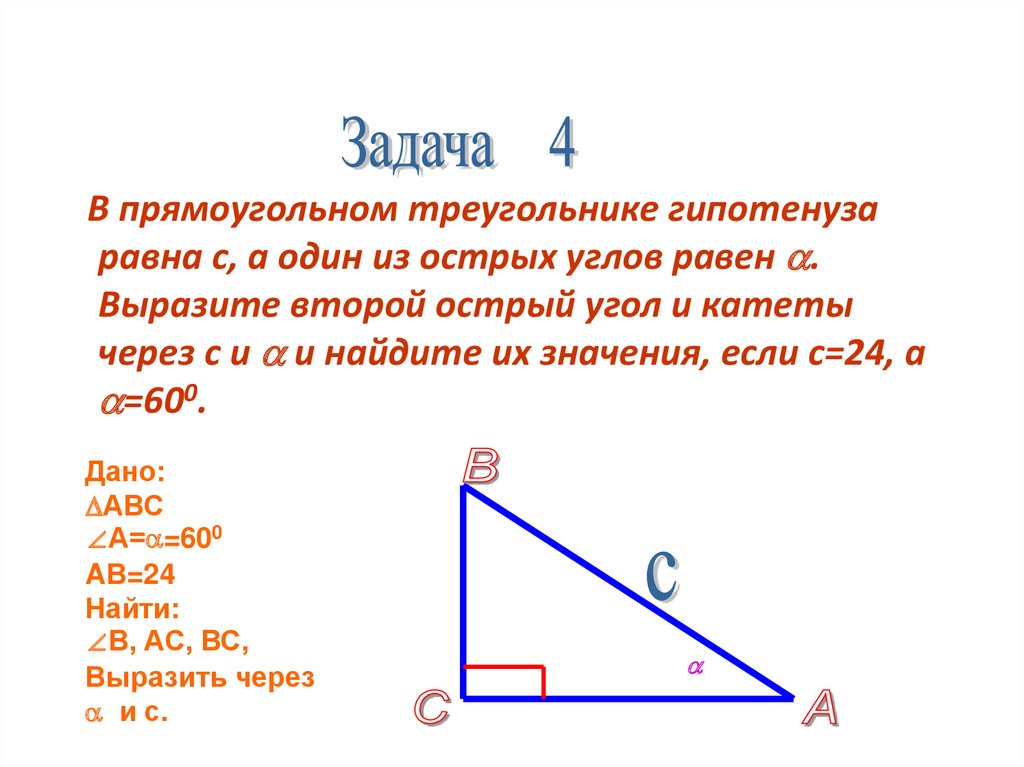
2\), т.е. \(AB < BC\). Значит, любая наклонная больше перпендикуляра.
Из решения задачи 29 к §3 следует, что если две какие-либо наклонные и перпендикуляры равны, то проекции тоже равны. Значит, равные наклонные имеют равные проекции.
Если AB не будет изменяться, то значение BC будет зависеть от значения AC, т.е. чем больше AC, тем больше BC. Значит, из двух наклонных больше та, у которой проекция больше.
Вопрос 7. Докажите неравенство треугольника.
Ответ. Теорема 7.3 (неравенство треугольника). Каковы бы ни были три точки, расстояние между любыми двумя из этих точек не больше суммы расстояний от них до третьей точки.
Это значит, что каждое из этих расстояний меньше или равно суммы двух других.
Доказательство. Пусть A,B,C – три данные точки. Если две точки из трёх или все три точки совпадают, то утверждение теоремы очевидно.
Если все точки различны и лежат на одной прямой, то одна из них лежит между двумя другими, например B.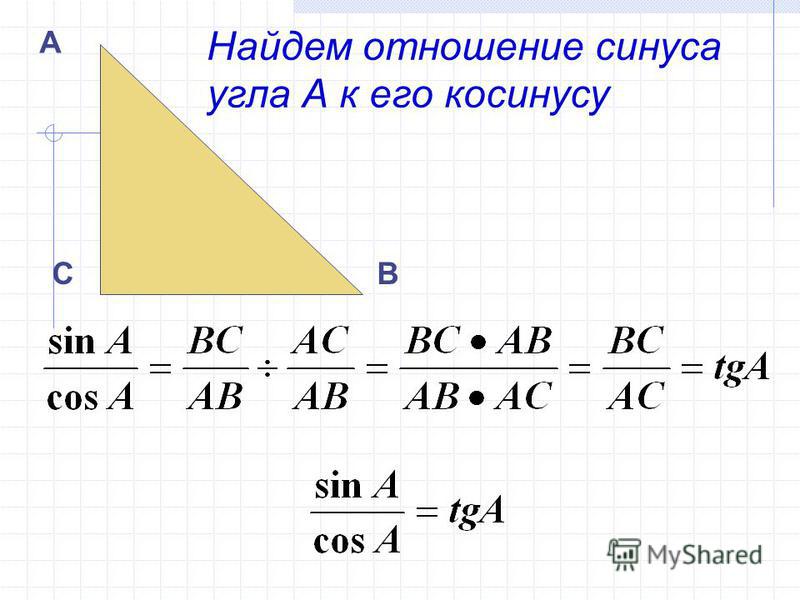
В этом случае AB + BC = AC. Отсюда видно, что каждое из трёх расстояний не больше суммы двух других.
Рис. 154
Допустим теперь, что точки не лежат на одной прямой (рис. 154). Докажем, что \(AB < AC + BC\). Опустим перпендикуляр CD на прямую AB. По доказанному \(AB \leq AD + BD\). И так как \(AD < AC\) и \(BD < BC\), то \(AB < AC + BC\). Теорема доказана.
Вопрос 8. Докажите, что в треугольнике каждая сторона меньше суммы двух других сторон.
Ответ. Требуется доказать следующую теорему:
Каков бы ни был треугольник, каждая его сторона меньше суммы двух других сторон.
Доказательство. Пусть ABC –данный треугольник. Как мы знаем, треугольник состоит из точек, не лежащих на одной прямой (рис. 154, б). Докажем, что \(AB < AC + BC\). Опустим перпендикуляр CD на прямую AB. По доказанному \(AB \leq AD + BD\). И так как \(AD < AC\) и \(BD < BC\), то \(AB < AC + BC\). Теорема доказана.
Вопрос 9.
2 \alpha}\).
Так как \(\cos \alpha\) зависит только от величины угла, то и \(\sin \alpha\) зависит только от величины угла.
По определению
\(tg \alpha = \frac{BC}{AC}\).
Разделим числитель и знаменатель на AB:
\(tg \alpha = \frac{BC}{AB} : \frac{AC}{AB} = \frac{sin \alpha}{cos \alpha}\).
Отсюда видно, что и \(tg \alpha\) зависит только от величины угла.
Вопрос 10. Как выражается катет прямоугольного треугольника через гипотенузу и острый угол, через острый угол и другой катет?
Ответ. Из определения \(\sin \alpha\), \(\cos \alpha\) и \(tg \alpha\) получаем следующие правила:
Катет прямоугольного треугольника через гипотенузу и острый угол выражается данным образом:
Катет, противолежащий углу \(\alpha\), равен произведению гипотенузы на \(\sin \alpha\).
Катет, прилежащий углу \(\alpha\), равен произведению гипотенузы на \(\cos \alpha\).
Катет прямоугольного треугольника через острый угол и другой катет выражается следующим образом:
Катет, противолежащий углу \(\alpha\), равен произведению второго катета на \(tg \alpha\).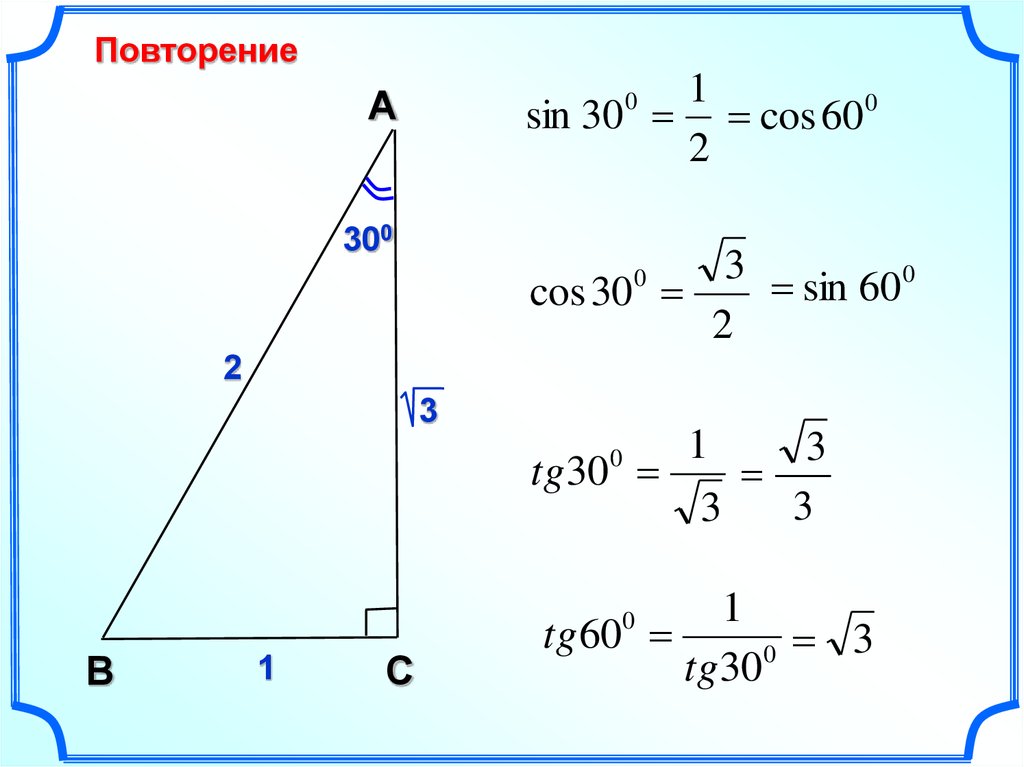
- Вперед
Вопрос Видео: Использование коэффициента синуса для нахождения косинуса угла
Стенограмма видео
Найдите cos 𝜃 при заданном sin 𝜃 равно отрицательному трем на пять, где 𝜃 больше или равно 270 градусам, но меньше 360 градусов.
Чтобы начать решать эту проблему, я на самом деле собираюсь использовать небольшое вспомогательное средство памяти, как вы, возможно, видели, это SOH CAH TOA. И мы на самом деле собираемся посмотреть на первую часть. Итак, потому что на самом деле это говорит нам о том, что синус угла или синус 𝜃 равен обратному делению на гипотенузу. Так это в прямоугольном треугольнике. Это говорит нам о том, что фактические значения, которые у вас были бы, то есть синус 𝜃, равен обратному делению на гипотенузу.
Таким образом, мы можем сказать, что если синус 𝜃 равен минус три больше пяти, это будет означать, что наша противоположность будет равна трем, а наша гипотенуза будет равна пяти.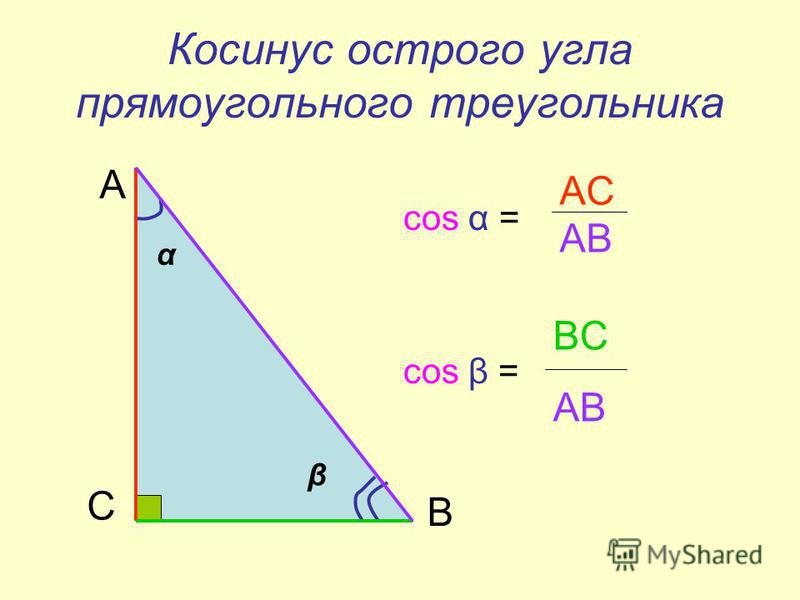
Также следует учитывать отрицательный знак. Но мы рассмотрим это немного позже в решении.
А теперь нарисуйте небольшой набросок, чтобы показать, что говорит нам это значение. Итак, если у нас есть прямоугольный треугольник, мы можем видеть, что противоположность равна трем, а гипотенузе — пять. Но что мы можем сделать, чтобы найти соседнее? На самом деле мы можем использовать теорему Пифагора, потому что мы можем сказать, что А будет равно квадратному корню из пяти в квадрате, потому что это квадрат нашей гипотенузы минус три в квадрате, потому что это одна из наших более коротких сторон в квадрате. И мы получаем это из переставленной версии 𝑎 в квадрате плюс 𝑏 в квадрате равно 𝑐 в квадрате, где 𝑎 в квадрате равно 𝑐 в квадрате минус 𝑏 в квадрате, где 𝑐 — гипотенуза.
Хорошо, отлично! Итак, мы можем решить это и найти A. Таким образом, мы получаем, что A равно корню из 16. Следовательно, A равно четырем. Причина, по которой мы хотели найти соседнюю сторону, заключается в том, что это вторая часть нашего SOH CAH TOA.
Это CAH, потому что мы пытаемся найти cos. Итак, мы хотим использовать CAH, который говорит нам, что косинус 𝜃 или любого угла равен соседнему по гипотенузе.
Хорошо, но теперь мы можем использовать это, потому что у нас есть соседний, который мы только что нашли. И мы уже знаем гипотенузу. Итак, мы можем сказать, что потому cos 𝜃 равно A над H. Итак, мы можем сказать, что потому cos 𝜃 равно четырем пятым. Но является ли это окончательным ответом? Итак, я хочу снова обратить ваше внимание на отрицательный знак, который мы рассмотрели ранее. sin 𝜃 был равен отрицательным трем пятым. Следовательно, может ли cos 𝜃 быть равным четырем пятым или отрицательным четырем пятым?
И мы немного взглянем на диаграмму cos, чтобы понять, какой из них является ответом. Итак, я нарисовал набросок диаграммы cos. И то, что это на самом деле говорит нам, является чем-то действительно важным. Он говорит нам, где наши синус, косинус или тангенс угла положительны, а где они будут отрицательными.
А буква А обозначает все. Таким образом, мы можем сказать, что все значения от нуля до 90 градусов будут положительными. Мы можем сказать, что значения от 90 до 180 будут положительными только тогда, когда это грех 𝜃. Мы можем сказать, что между 180 и 270 градусами синус будет положительным, если он касательный 𝜃. И мы можем сказать, что только cos 𝜃 будет положительным между 270 и 360 градусами.
Ну, если мы посмотрим на первоначальный вопрос, мы увидим, что на самом деле нас интересует именно этот последний участок, от 270 до 360 градусов. Итак, из диаграммы cos мы можем видеть, что на самом деле в этом секторе, косинус 𝜃 будет положительным. И на самом деле мы сказали, что грех 𝜃 был равен минус три больше пяти? Что ж, да, это было бы правильно, потому что диаграмма cos была бы только верхней левой частью, где sin 𝜃 был бы положительным. Таким образом, мы можем сказать, что cos 𝜃 равно четырем пятым.
Объяснение тригонометрических соотношений: cos — Интерактивная математика
Тригонометрия исследует отношения между сторонами треугольника, точнее, прямоугольного треугольника.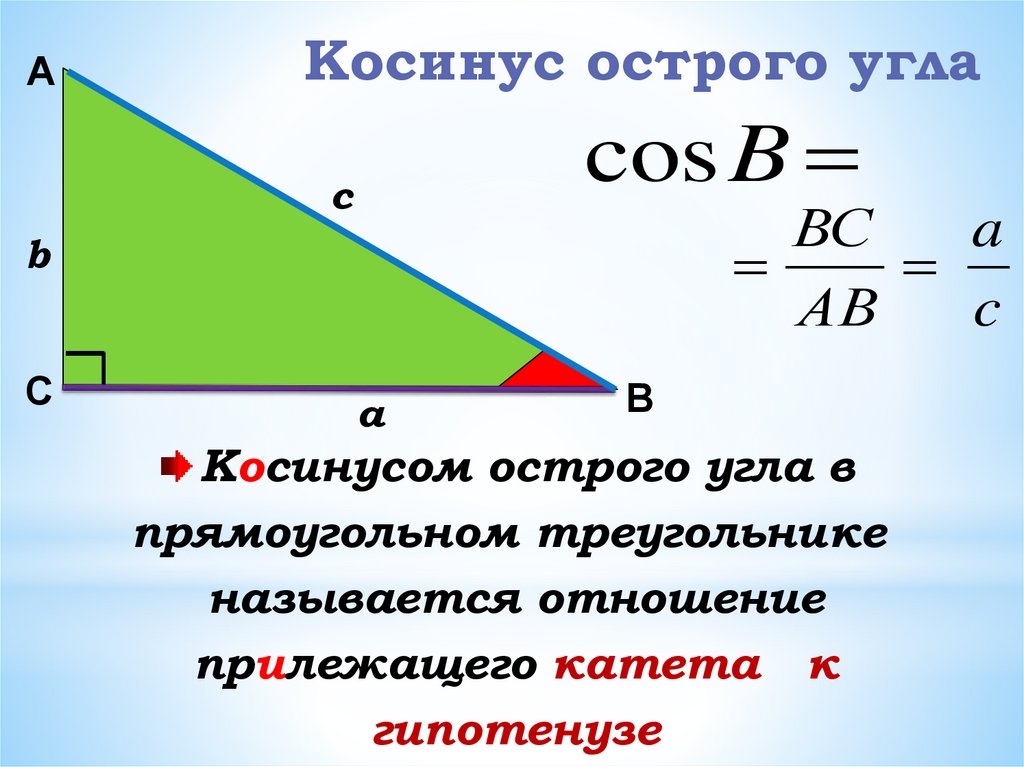
Прямоугольный треугольник имеет угол 90°. Уравнения и соотношения, описывающие отношения между сторонами треугольника и его углами, являются тригонометрическими функциями. В этой конкретной статье мы собираемся объяснить одно конкретное соотношение: «cos» или косинус. Но прежде чем мы углубимся в косинус, давайте взглянем на другие соотношения в тригонометрии.
Основные тригонометрические функции
Когда мы определяем тригонометрические отношения, давайте определим прямоугольный треугольник с одним из углов, названным x. Этот угол равен 90°. Вы определяете стороны треугольника как a, b, и c , где a — это сторона, прилегающая к x , а b — это сторона, противоположная x . c это гипотенуза или сторона, противолежащая прямому углу. Существует шесть основных тригонометрических функций.
- Sin x – отношение противолежащего катета к гипотенузе.
-
sin x = (противоположное) / (гипотенуза) = b / c
-
- Cos x – отношение прилежащего катета к гипотенузе.
-
cos x = (смежный) / (гипотенуза) = a / c
-
- Желто-коричневый x это сторона, противоположная соседней стороне.
-
tan x = (напротив) / (смежно) = b / a - Если вы сделаете
(b / c) / (a / c), , вы получитеb/a, что равно tan x. Таким образом, tan x можно выразить как отношение sin к cos.тангенс x = sin x / cos x.
-
- Cosec x является обратной величиной sin x .
-
csc x = 1 / sin x
-
- Sec x , является обратной величиной cos x.
-
сек х = 1 / cos х
-
- Детская кроватка x является обратной величиной tan x
-
кроватка x = 1 / коричневая x
-
Из шести основных тригонометрических функций вас в основном будут интересовать sin, cos и tan.
Функция косинуса
Вы можете определить функцию косинуса, используя прямоугольный треугольник, как описано выше. Однако вы можете использовать косинус в нескольких других приложениях.
Определение косинуса с помощью дифференциальных уравнений
Косинус можно использовать в дифференциальных уравнениях. Cos и sin — это две дифференцируемые триггерные функции, между которыми существует особое отношение.
cos x = ( d / dx ) sin x и
-sin x = ( d / dx ) cos x
Приведенные выше определения полезны при решении дифференциальных уравнений. Оба приведенных выше выражения являются решениями дифференциального уравнения:
y” + y = 0
Расширение серии Power
Тригонометрические функции также определяются с помощью степенных рядов. Применяя ряд Тейлора к косинусу, можно получить другое определение.
cos x = 1 – ( x2 / 2!) + ( x4 / 4!) – ( x6 / 6!) ….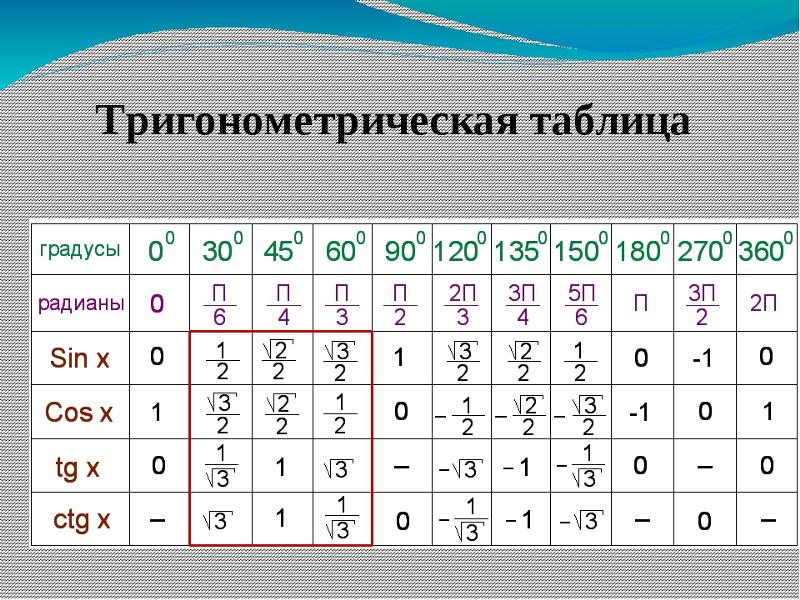
.
Экспоненциальное выражение с использованием формулы Эйлера
Эйлер связал синус и косинус функции по выражению:
ejx = cos x + j sin x
e-jx = cos x – j sinx
j в приведенных выше выражениях относится к мнимой единице, которая эквивалентна квадратному корню из (-1). Выражение или отношение Эйлера верно для всех комплексных значений. Это означает, что формула верна для всех действительных значений x .
Если мы добавим приведенные выше уравнения, мы можем найти краткое выражение для cos x в комплексной области как: реальный, вы можете записать выражение как:
cos x = Re( ejx )
Значения косинуса в четырех квадрантах окружности
Поскольку полный круг равен 360°, вы можете выразить косинус в различных частях круга, начиная с 0° до 360°. В первом квадранте окружности, углах от 0° до 90°, значение cos положительно. Во втором квадранте с диапазоном углов от 90° до 180° значение cos отрицательно.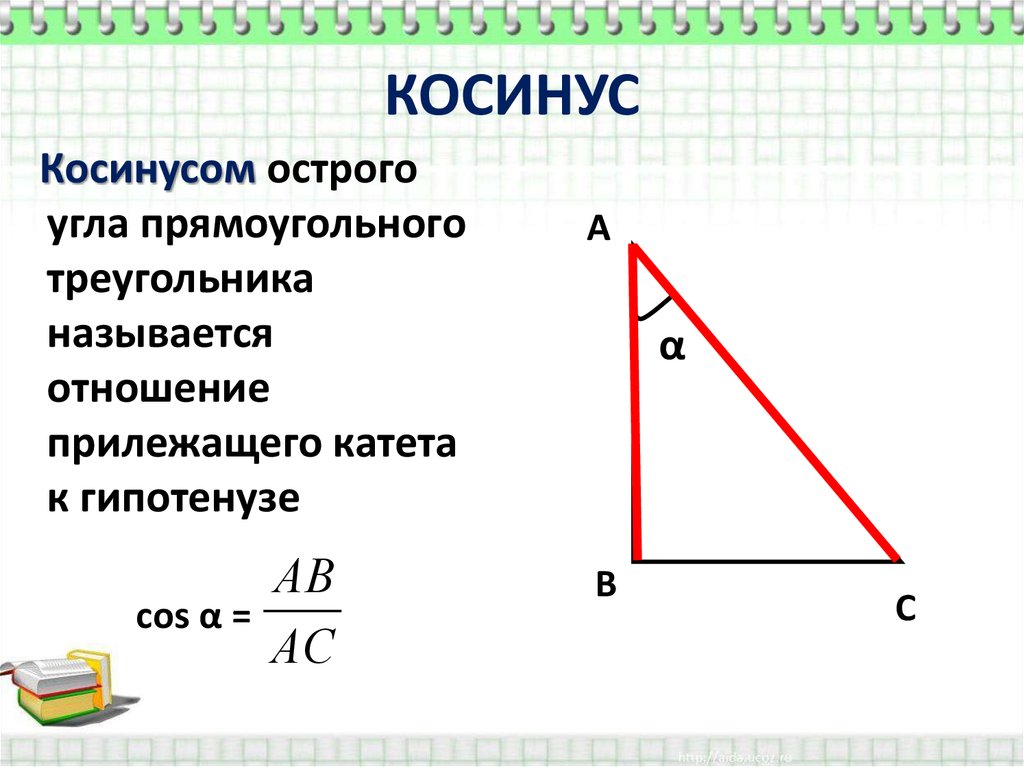
В третьем квадранте с диапазоном углов от 180° до 270° значение cos остается отрицательным. В четвертом квадранте в диапазоне углов от 270° до 360° значение cos положительно.
Примеры использования косинусов
Прежде чем я продолжу, позвольте мне ввести тригонометрическое тождество. Тригонометрические тождества — это отношения между тригонометрическими функциями, которые верны при любых условиях. Одно из них cos2 x + sin2 x = 1 . Давайте рассмотрим несколько примеров и применим это тригонометрическое тождество.
Пример 1
Гребень прямоугольного треугольника равен 0,866. Найдите косинус угла.
Приняв наше тригонометрическое тождество, мы можем изменить выражение.
cos2 x = 1 – sin2 x
cos x = (1 – sin2 x )1/2
Так как мы знаем значение выражение.
cos x = ( 1 – sin2 x )1/2
cos x = (1 – 0,8662 )1/2
cos x = 0,5
Длина гипотенузы AC равна 5 см, а сторона BC равна 3 см. Найдите угол при С.Чтобы освежить вашу память, косинус угла равен смежному/гипотенузе . Пусть угол C равен x .
cos x = 3/5
x = cos-1 (3/5)
x = 53 °
Угол при C равен 53°.
Выражение cos-1 означает обратный косинус. Это обратная функция cos. Если косинус угла равен x , то исходный угол равен cos-1 x . 90,5 = 60°
- 660°
- 234°
- -60°
660° больше, чем круг, который равен 360°. Но поскольку угол — это градус поворота, это означает, что точка прошла полный круг, а затем еще несколько. Полный круг не будет учитываться, так как угол интереса — это величина, на которую он повернулся от начальной точки до конечной точки.
Итак, cos 660° = cos ( 660 – 360 )° = cos 300°
Поскольку 300° попадает в четвертый квадрант, это означает, что значение cos положительно.