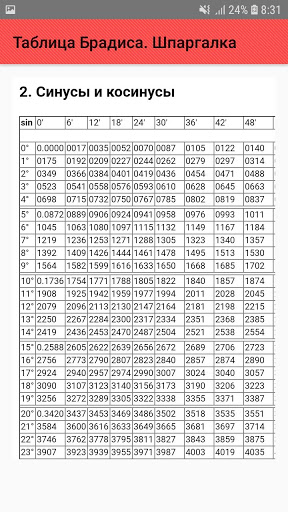
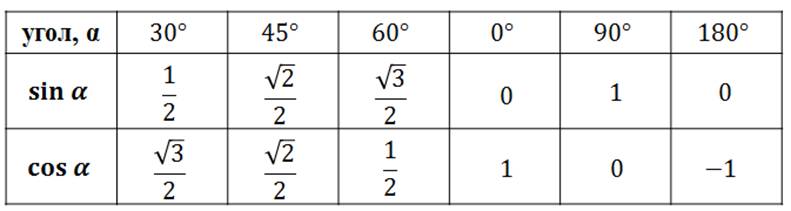
Таблица Брадиса для синуса и косинуса
| sin | 0′ | 6′ | 12′ | 18′ | 24′ | 30′ | 36′ | 42′ | 48′ | 54′ | 60′ | cos | 1′ | 2′ | 3′ |
| 0.0000 | 90° | ||||||||||||||
| 0° | 0.0000 | 0017 | 0035 | 0052 | 0070 | 0087 | 0105 | 0122 | 0140 | 0157 | 0175 | 89° | 3 | 6 | 9 |
| 1° | 0175 | 0192 | 0209 | 0227 | 0244 | 0262 | 0279 | 0297 | 0314 | 0332 | 0349 | 88° | 3 | 6 | 9 |
| 2° | 0349 | 0366 | 0384 | 0401 | 0419 | 0436 | 0454 | 0471 | 0488 | 0506 | 0523 | 87° | 3 | 6 | 9 |
| 3° | 0523 | 0541 | 0558 | 0576 | 0593 | 0610 | 0628 | 0645 | 0663 | 0680 | 0698 | 86° | 3 | 6 | 9 |
| 4° | 0698 | 0715 | 0732 | 0750 | 0767 | 0785 | 0802 | 0819 | 0837 | 0854 | 0. 0872 0872 | 85° | 3 | 6 | 9 |
| 5° | 0.0872 | 0889 | 0906 | 0924 | 0941 | 0958 | 0976 | 0993 | 1011 | 1028 | 1045 | 84° | 3 | 6 | 9 |
| 6° | 1045 | 1063 | 1080 | 1097 | 1115 | 1132 | 1149 | 1167 | 1184 | 1201 | 1219 | 83° | 3 | 6 | 9 |
| 7° | 1219 | 1236 | 1253 | 1271 | 1288 | 1305 | 1323 | 1340 | 1357 | 1374 | 1392 | 82° | 3 | 6 | 9 |
| 8° | 1392 | 1409 | 1426 | 1444 | 1461 | 1478 | 1495 | 1513 | 1530 | 1547 | 1564 | 81° | 3 | 6 | 9 |
| 9° | 1564 | 1582 | 1599 | 1616 | 1633 | 1650 | 1668 | 1685 | 1702 | 1719 | 0.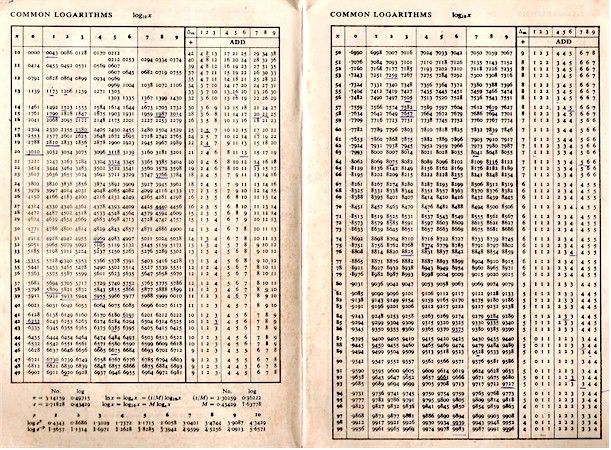 1736 1736 | 80° | 3 | 6 | 9 |
| 10° | 0.1736 | 1754 | 1771 | 1788 | 1805 | 1822 | 1840 | 1857 | 1874 | 1891 | 1908 | 79° | 3 | 6 | 9 |
| 11° | 1908 | 1925 | 1942 | 1959 | 1977 | 1994 | 2011 | 2028 | 2045 | 2062 | 2079 | 78° | 3 | 6 | 9 |
| 12° | 2079 | 2096 | 2113 | 2130 | 2147 | 2164 | 2181 | 2198 | 2215 | 2233 | 2250 | 77° | 3 | 6 | 9 |
| 13° | 2250 | 2267 | 2284 | 2300 | 2317 | 2334 | 2351 | 2368 | 2385 | 2402 | 2419 | 76° | 3 | 6 | 8 |
| 14° | 2419 | 2436 | 2453 | 2470 | 2487 | 2504 | 2521 | 2538 | 2554 | 2571 | 0. 2588 2588 | 75° | 3 | 6 | 8 |
| 15° | 0.2588 | 2605 | 2622 | 2639 | 2656 | 2672 | 2689 | 2706 | 2723 | 2740 | 2756 | 74° | 3 | 6 | 8 |
| 16° | 2756 | 2773 | 2790 | 2807 | 2823 | 2840 | 2857 | 2874 | 2890 | 2907 | 2924 | 73° | 3 | 6 | 8 |
| 17° | 2924 | 2940 | 2957 | 2974 | 2990 | 3007 | 3024 | 3040 | 3057 | 3074 | 3090 | 72° | 3 | 6 | 8 |
| 18° | 3090 | 3107 | 3123 | 3140 | 3156 | 3173 | 3190 | 3206 | 3223 | 3239 | 3256 | 71° | 3 | 6 | 8 |
| 19° | 3256 | 3272 | 3289 | 3305 | 3322 | 3338 | 3355 | 3371 | 3387 | 3404 | 0. 3420 3420 | 70° | 3 | 5 | 8 |
| 20° | 0.3420 | 3437 | 3453 | 3469 | 3486 | 3502 | 3518 | 3535 | 3551 | 3567 | 3584 | 69° | 3 | 5 | 8 |
| 21° | 3584 | 3600 | 3616 | 3633 | 3649 | 3665 | 3681 | 3697 | 3714 | 3730 | 3746 | 68° | 3 | 5 | 8 |
| 22° | 3746 | 3762 | 3778 | 3795 | 3811 | 3827 | 3843 | 3859 | 3875 | 3891 | 3907 | 67° | 3 | 5 | 8 |
| 23° | 3907 | 3923 | 3939 | 3955 | 3971 | 3987 | 4003 | 4019 | 4035 | 4051 | 4067 | 66° | 3 | 5 | 8 |
| 24° | 4067 | 4083 | 4099 | 4115 | 4131 | 4147 | 4163 | 4179 | 4195 | 4210 | 0. 4226 4226 | 65° | 3 | 5 | 8 |
| 25° | 0.4226 | 4242 | 4258 | 4274 | 4289 | 4305 | 4321 | 4337 | 4352 | 4368 | 4384 | 64° | 3 | 5 | 8 |
| 26° | 4384 | 4399 | 4415 | 4431 | 4446 | 4462 | 4478 | 4493 | 4509 | 4524 | 4540 | 63° | 3 | 5 | 8 |
| 27° | 4540 | 4555 | 4571 | 4586 | 4602 | 4617 | 4633 | 4648 | 4664 | 4679 | 4695 | 62° | 3 | 5 | 8 |
| 28° | 4695 | 4710 | 4726 | 4741 | 4756 | 4772 | 4787 | 4802 | 4818 | 4833 | 4848 | 61° | 3 | 5 | 8 |
| 29° | 4848 | 4863 | 4879 | 4894 | 4909 | 4924 | 4939 | 4955 | 4970 | 4985 | 0. 5000 5000 | 60° | 3 | 5 | 8 |
| 30° | 0.5000 | 5015 | 5030 | 5045 | 5060 | 5075 | 5090 | 5105 | 5120 | 5135 | 5150 | 59° | 3 | 5 | 8 |
| 31° | 5150 | 5165 | 5180 | 5195 | 5210 | 5225 | 5240 | 5255 | 5270 | 5284 | 5299 | 58° | 2 | 5 | 7 |
| 32° | 5299 | 5314 | 5329 | 5344 | 5358 | 5373 | 5388 | 5402 | 5417 | 5432 | 5446 | 57° | 2 | 5 | 7 |
| 33° | 5446 | 5461 | 5476 | 5490 | 5505 | 5519 | 5534 | 5548 | 5563 | 5577 | 5592 | 56° | 2 | 5 | 7 |
| 34° | 5592 | 5606 | 5621 | 5635 | 5650 | 5664 | 5678 | 5693 | 5707 | 5721 | 0. 5736 5736 | 55° | 2 | 5 | 7 |
| 0.5736 | 5750 | 5764 | 5779 | 5793 | 5807 | 5821 | 5835 | 5850 | 5864 | 0.5878 | 54° | 2 | 5 | 7 | |
| 36° | 5878 | 5892 | 5906 | 5920 | 5934 | 5948 | 5962 | 5976 | 5990 | 6004 | 6018 | 53° | 2 | 5 | 7 |
| 37° | 6018 | 6032 | 6046 | 6060 | 6074 | 6088 | 6101 | 6115 | 6129 | 6143 | 6157 | 52° | 2 | 5 | 7 |
| 38° | 6157 | 6170 | 6184 | 6198 | 6211 | 6225 | 6239 | 6252 | 6266 | 6280 | 6293 | 51° | 2 | 5 | 7 |
| 39° | 6293 | 6307 | 6320 | 6334 | 6347 | 6361 | 6374 | 6388 | 6401 | 6414 | 0. 6428 6428 | 50° | 2 | 4 | 7 |
| 40° | 0.6428 | 6441 | 6455 | 6468 | 6481 | 6494 | 6508 | 6521 | 6534 | 6547 | 6561 | 49° | 2 | 4 | 7 |
| 41° | 6561 | 6574 | 6587 | 6600 | 6613 | 6626 | 6639 | 6652 | 6665 | 6678 | 6691 | 48° | 2 | 4 | 7 |
| 42° | 6691 | 6704 | 6717 | 6730 | 6743 | 6756 | 6769 | 6782 | 6794 | 6807 | 6820 | 47° | 2 | 4 | 6 |
| 43° | 6820 | 6833 | 6845 | 6858 | 6871 | 6884 | 6896 | 8909 | 6921 | 6934 | 6947 | 46° | 2 | 4 | 6 |
| 44° | 6947 | 6959 | 6972 | 6984 | 6997 | 7009 | 7022 | 7034 | 7046 | 7059 | 0. 7071 7071 | 45° | 2 | 4 | 6 |
| 45° | 0.7071 | 7083 | 7096 | 7108 | 7120 | 7133 | 7145 | 7157 | 7169 | 7181 | 7193 | 44° | 2 | 4 | 6 |
| 46° | 7193 | 7206 | 7218 | 7230 | 7242 | 7254 | 7266 | 7278 | 7290 | 7302 | 7314 | 43° | 2 | 4 | 6 |
| 47° | 7314 | 7325 | 7337 | 7349 | 7361 | 7373 | 7385 | 7396 | 7408 | 7420 | 7431 | 42° | 2 | 4 | 6 |
| 48° | 7431 | 7443 | 7455 | 7466 | 7478 | 7490 | 7501 | 7513 | 7524 | 7536 | 7547 | 41° | 2 | 4 | 6 |
| 49° | 7547 | 7559 | 7570 | 7581 | 7593 | 7604 | 7615 | 7627 | 7638 | 7649 | 0. 7660 7660 | 40° | 2 | 4 | 6 |
| 50° | 0.7660 | 7672 | 7683 | 7694 | 7705 | 7716 | 7727 | 7738 | 7749 | 7760 | 7771 | 39° | 2 | 4 | 6 |
| 51° | 7771 | 7782 | 7793 | 7804 | 7815 | 7826 | 7837 | 7848 | 7859 | 7869 | 7880 | 38° | 2 | 4 | 5 |
| 52° | 7880 | 7891 | 7902 | 7912 | 7923 | 7934 | 7944 | 7955 | 7965 | 7976 | 7986 | 37° | 2 | 4 | 5 |
| 53° | 7986 | 7997 | 8007 | 8018 | 8028 | 8039 | 8049 | 8059 | 8070 | 8080 | 8090 | 36° | 2 | 3 | 5 |
| 54° | 8090 | 8100 | 8111 | 8121 | 8131 | 8141 | 8151 | 8161 | 8171 | 8181 | 0. 8192 8192 | 35° | 2 | 3 | 5 |
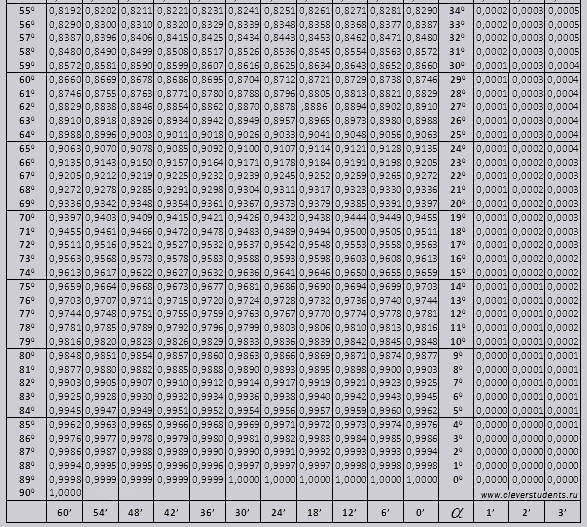
| 55° | 0.8192 | 8202 | 8211 | 8221 | 8231 | 8241 | 8251 | 8261 | 8271 | 8281 | 8290 | 34° | 2 | 3 | 5 |
| 56° | 8290 | 8300 | 8310 | 8320 | 8329 | 8339 | 8348 | 8358 | 8368 | 8377 | 8387 | 33° | 2 | 3 | 5 |
| 57° | 8387 | 8396 | 8406 | 8415 | 8425 | 8434 | 8443 | 8453 | 8462 | 8471 | 8480 | 32° | 2 | 3 | 5 |
| 58° | 8480 | 8490 | 8499 | 8508 | 8517 | 8526 | 8536 | 8545 | 8554 | 8563 | 8572 | 31° | 2 | 3 | 5 |
| 59° | 8572 | 8581 | 8590 | 8599 | 8607 | 8616 | 8625 | 8634 | 8643 | 8652 | 0. 8660 8660 | 30° | 1 | 3 | 4 |
| 60° | 0.8660 | 8669 | 8678 | 8686 | 8695 | 8704 | 8712 | 8721 | 8729 | 8738 | 8746 | 29° | 1 | 3 | 4 |
| 61° | 8746 | 8755 | 8763 | 8771 | 8780 | 8788 | 8796 | 8805 | 8813 | 8821 | 8829 | 28° | 1 | 3 | 4 |
| 62° | 8829 | 8838 | 8846 | 8854 | 8862 | 8870 | 8878 | 8886 | 8894 | 8902 | 8910 | 27° | 1 | 3 | 4 |
| 63° | 8910 | 8918 | 8926 | 8934 | 8942 | 8949 | 8957 | 8965 | 8973 | 8980 | 8988 | 26° | 1 | 3 | 4 |
| 64° | 8988 | 8996 | 9003 | 9011 | 9018 | 9026 | 9033 | 9041 | 9048 | 9056 | 0. 9063 9063 | 25° | 1 | 3 | 4 |
| 65° | 0.9063 | 9070 | 9078 | 9085 | 9092 | 9100 | 9107 | 9114 | 9121 | 9128 | 9135 | 24° | 1 | 2 | 4 |
| 66° | 9135 | 9143 | 9150 | 9157 | 9164 | 9171 | 9178 | 9184 | 9191 | 9198 | 9205 | 23° | 1 | 2 | 3 |
| 67° | 9205 | 9212 | 9219 | 9225 | 9232 | 9239 | 9245 | 9252 | 9259 | 9256 | 9272 | 22° | 1 | 2 | 3 |
| 68° | 9272 | 9278 | 9285 | 9291 | 9298 | 9304 | 9311 | 9317 | 9323 | 9330 | 9336 | 21° | 1 | 2 | 3 |
| 69° | 9336 | 9342 | 9348 | 9354 | 9361 | 9367 | 9373 | 9379 | 9383 | 9391 | 0.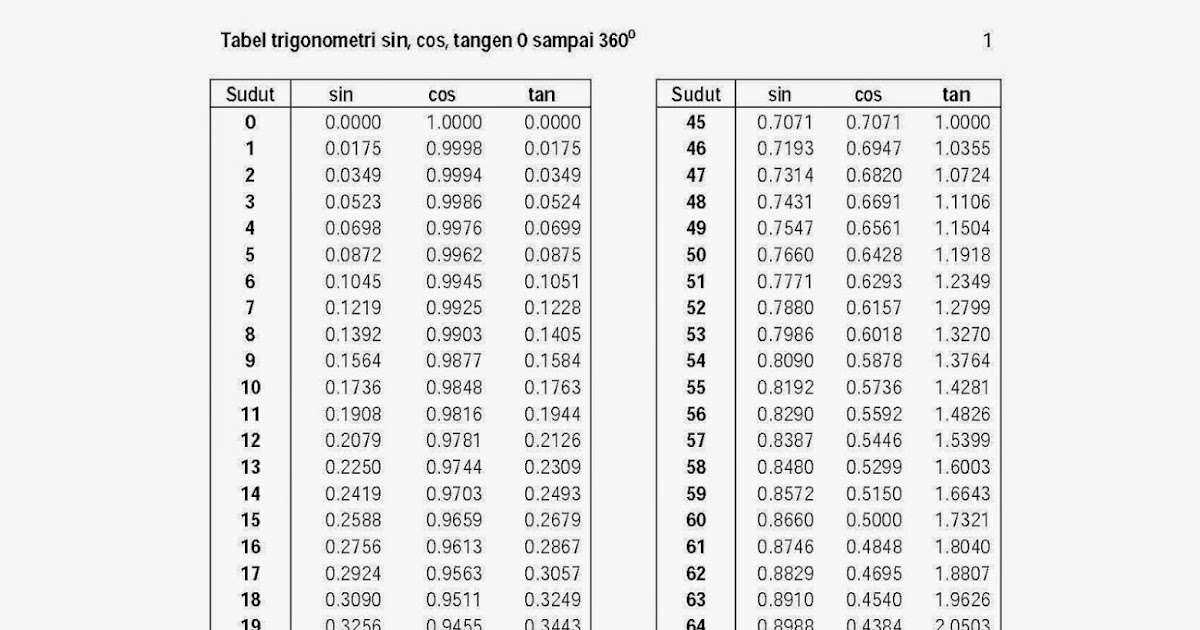 9397 9397 | 20° | 1 | 2 | 3 |
| 70° | 9397 | 9403 | 9409 | 9415 | 9421 | 9426 | 9432 | 9438 | 9444 | 9449 | 0.9455 | 19° | 1 | 2 | 3 |
| 71° | 9455 | 9461 | 9466 | 9472 | 9478 | 9483 | 9489 | 9494 | 9500 | 9505 | 9511 | 18° | 1 | 2 | 3 |
| 72° | 9511 | 9516 | 9521 | 9527 | 9532 | 9537 | 9542 | 9548 | 9553 | 9558 | 9563 | 17° | 1 | 2 | 3 |
| 73° | 9563 | 9568 | 9573 | 9578 | 9583 | 9588 | 9593 | 9598 | 9603 | 9608 | 9613 | 16° | 1 | 2 | 2 |
| 74° | 9613 | 9617 | 9622 | 9627 | 9632 | 9636 | 9641 | 9646 | 9650 | 9655 | 0. 9659 9659 | 15° | 1 | 2 | 2 |
| 75° | 9659 | 9664 | 9668 | 9673 | 9677 | 9681 | 9686 | 9690 | 9694 | 9699 | 9703 | 14° | 1 | 1 | 2 |
| 76° | 9703 | 9707 | 9711 | 9715 | 9720 | 9724 | 9728 | 9732 | 9736 | 9740 | 9744 | 13° | 1 | 1 | 2 |
| 77° | 9744 | 9748 | 9751 | 9755 | 9759 | 9763 | 9767 | 9770 | 9774 | 9778 | 9781 | 12° | 1 | 1 | 2 |
| 78° | 9781 | 9785 | 9789 | 9792 | 9796 | 9799 | 9803 | 9806 | 9810 | 9813 | 9816 | 11° | 1 | 1 | 2 |
| 79° | 9816 | 9820 | 9823 | 9826 | 9829 | 9833 | 9836 | 9839 | 9842 | 9845 | 0.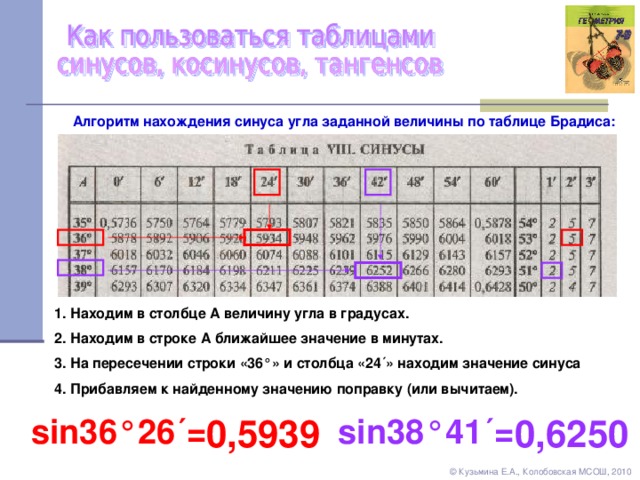 9848 9848 | 10° | 1 | 1 | 2 |
| 80° | 0.9848 | 9851 | 9854 | 9857 | 9860 | 9863 | 9866 | 9869 | 9871 | 9874 | 9877 | 9° | 0 | 1 | 1 |
| 81° | 9877 | 9880 | 9882 | 9885 | 9888 | 9890 | 9893 | 9895 | 9898 | 9900 | 9903 | 8° | 0 | 1 | 1 |
| 82° | 9903 | 9905 | 9907 | 9910 | 9912 | 9914 | 9917 | 9919 | 9921 | 9923 | 9925 | 7° | 0 | 1 | 1 |
| 83° | 9925 | 9928 | 9930 | 9932 | 9934 | 9936 | 9938 | 9940 | 9942 | 9943 | 9945 | 6° | 0 | 1 | 1 |
| 84° | 9945 | 9947 | 9949 | 9951 | 9952 | 9954 | 9956 | 9957 | 9959 | 9960 | 9962 | 5° | 0 | 1 | 1 |
| 85° | 9962 | 9963 | 9965 | 9966 | 9968 | 9969 | 9971 | 9972 | 9973 | 9974 | 9976 | 4° | 0 | 0 | 1 |
| 86° | 9976 | 9977 | 9978 | 9979 | 9980 | 9981 | 9982 | 9983 | 9984 | 9985 | 9986 | 3° | 0 | 0 | 0 |
| 87° | 9986 | 9987 | 9988 | 9989 | 9990 | 9990 | 9991 | 9992 | 9993 | 9993 | 9994 | 2° | 0 | 0 | 0 |
| 88° | 9994 | 9995 | 9995 | 9996 | 9996 | 9997 | 9997 | 9997 | 9998 | 9998 | 0. 9998 9998 | 1° | 0 | 0 | 0 |
| 89° | 9998 | 9999 | 9999 | 9999 | 9999 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0° | 0 | 0 | 0 |
| 90° | 1.0000 | ||||||||||||||
| sin | 60′ | 54′ | 48′ | 42′ | 36′ | 30′ | 24′ | 18′ | 12′ | 6′ | 0′ | cos | 1′ | 2′ | 3′ |
Статистика
| Табличка на двери |
Таблица Брадиса для синуса и косинуса
Таблица Брадиса для синуса и косинуса
| sin | 0` | 6` | 12` | 18` | 24` | 30` | 36` | 42` | 48` | 54` | 60` | cos | 1` | 2` | 3` |
0. 0000 0000 | 90° | ||||||||||||||
| 0° | 0.0000 | 0017 | 0035 | 0052 | 0070 | 0087 | 0105 | 0122 | 0140 | 0157 | 0175 | 89° | 3 | 6 | 9 |
| 1° | 0175 | 0192 | 0209 | 0227 | 0244 | 0262 | 0279 | 0297 | 0314 | 0332 | 0349 | 88° | 3 | 6 | 9 |
| 2° | 0349 | 0366 | 0384 | 0401 | 0419 | 0436 | 0454 | 0471 | 0488 | 0506 | 0523 | 87° | 3 | 6 | 9 |
| 3° | 0523 | 0541 | 0558 | 0576 | 0593 | 0610 | 0628 | 0645 | 0663 | 0680 | 0698 | 86° | 3 | 6 | 9 |
| 4° | 0698 | 0715 | 0732 | 0750 | 0767 | 0785 | 0802 | 0819 | 0837 | 0854 | 0. 0872 0872 | 85° | 3 | 6 | 9 |
| 5° | 0.0872 | 0889 | 0906 | 0924 | 0941 | 0958 | 0976 | 0993 | 1011 | 1028 | 1045 | 84° | 3 | 6 | 9 |
| 6° | 1045 | 1063 | 1080 | 1097 | 1115 | 1132 | 1149 | 1167 | 1184 | 1201 | 1219 | 83° | 3 | 6 | 9 |
| 7° | 1219 | 1236 | 1253 | 1271 | 1288 | 1305 | 1323 | 1340 | 1357 | 1374 | 1392 | 82° | 3 | 6 | 9 |
| 8° | 1392 | 1409 | 1426 | 1444 | 1461 | 1478 | 1495 | 1513 | 1530 | 1547 | 1564 | 81° | 3 | 6 | 9 |
| 9° | 1564 | 1582 | 1599 | 1616 | 1633 | 1650 | 1668 | 1685 | 1702 | 1719 | 0.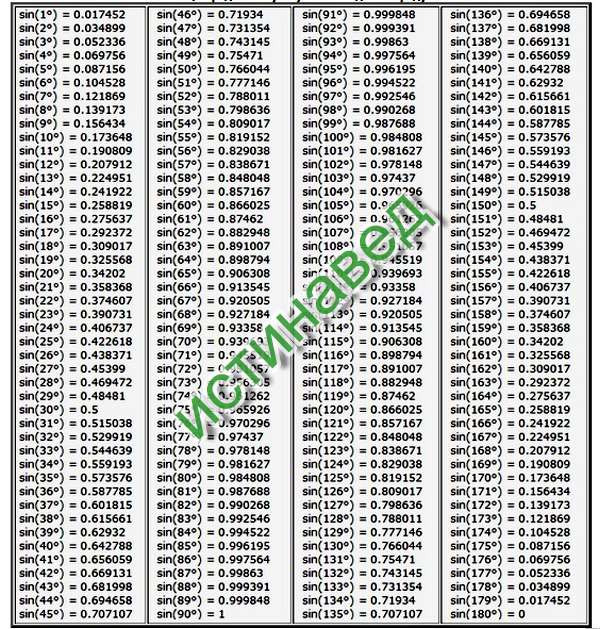 1736 1736 | 80° | 3 | 6 | 9 |
| 10° | 0.1736 | 1754 | 1771 | 1788 | 1805 | 1822 | 1840 | 1857 | 1874 | 1891 | 1908 | 79° | 3 | 6 | 9 |
| 11° | 1908 | 1925 | 1942 | 1959 | 1977 | 1994 | 2011 | 2028 | 2045 | 2062 | 2079 | 78° | 3 | 6 | 9 |
| 12° | 2079 | 2096 | 2113 | 2130 | 2147 | 2164 | 2181 | 2198 | 2215 | 2233 | 2250 | 77° | 3 | 6 | 9 |
| 13° | 2250 | 2267 | 2284 | 2300 | 2317 | 2334 | 2351 | 2368 | 2385 | 2402 | 2419 | 76° | 3 | 6 | 8 |
| 14° | 2419 | 2436 | 2453 | 2470 | 2487 | 2504 | 2521 | 2538 | 2554 | 2571 | 0. 2588 2588 | 75° | 3 | 6 | 8 |
| 15° | 0.2588 | 2605 | 2622 | 2639 | 2656 | 2672 | 2689 | 2706 | 2723 | 2740 | 2756 | 74° | 3 | 6 | 8 |
| 16° | 2756 | 2773 | 2790 | 2807 | 2823 | 2840 | 2857 | 2874 | 2890 | 2907 | 2924 | 73° | 3 | 6 | 8 |
| 17° | 2924 | 2940 | 2957 | 2974 | 2990 | 3007 | 3024 | 3040 | 3057 | 3074 | 3090 | 72° | 3 | 6 | 8 |
| 18° | 3090 | 3107 | 3123 | 3140 | 3156 | 3173 | 3190 | 3206 | 3223 | 3239 | 3256 | 71° | 3 | 6 | 8 |
| 19° | 3256 | 3272 | 3289 | 3305 | 3322 | 3338 | 3355 | 3371 | 3387 | 3404 | 0.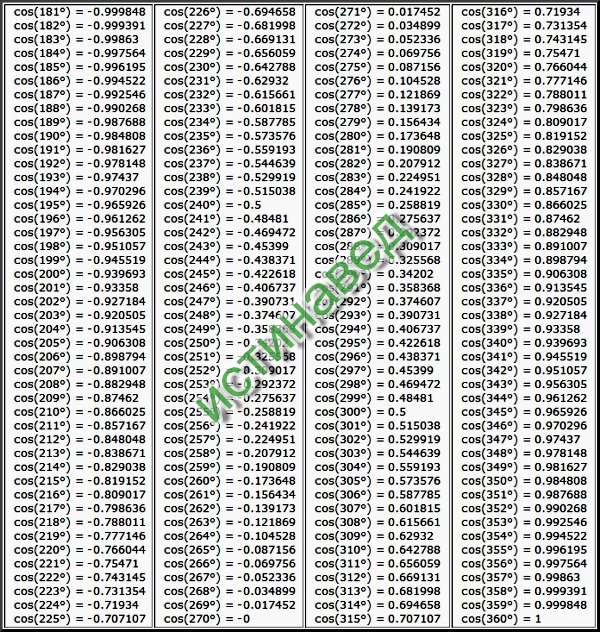 3420 3420 | 70° | 3 | 5 | 8 |
| 20° | 0.3420 | 3437 | 3453 | 3469 | 3486 | 3502 | 3518 | 3535 | 3551 | 3567 | 3584 | 69° | 3 | 5 | 8 |
| 21° | 3584 | 3600 | 3616 | 3633 | 3649 | 3665 | 3681 | 3697 | 3714 | 3730 | 3746 | 68° | 3 | 5 | 8 |
| 22° | 3746 | 3762 | 3778 | 3795 | 3811 | 3827 | 3843 | 3859 | 3875 | 3891 | 3907 | 67° | 3 | 5 | 8 |
| 23° | 3907 | 3923 | 3939 | 3955 | 3971 | 3987 | 4003 | 4019 | 4035 | 4051 | 4067 | 66° | 3 | 5 | 8 |
| 24° | 4067 | 4083 | 4099 | 4115 | 4131 | 4147 | 4163 | 4179 | 4195 | 4210 | 0. 4226 4226 | 65° | 3 | 5 | 8 |
| 25° | 0.4226 | 4242 | 4258 | 4274 | 4289 | 4305 | 4321 | 4337 | 4352 | 4368 | 4384 | 64° | 3 | 5 | 8 |
| 26° | 4384 | 4399 | 4415 | 4431 | 4446 | 4462 | 4478 | 4493 | 4509 | 4524 | 4540 | 63° | 3 | 5 | 8 |
| 27° | 4540 | 4555 | 4571 | 4586 | 4602 | 4617 | 4633 | 4648 | 4664 | 4679 | 4695 | 62° | 3 | 5 | 8 |
| 28° | 4695 | 4710 | 4726 | 4741 | 4756 | 4772 | 4787 | 4802 | 4818 | 4833 | 4848 | 61° | 3 | 5 | 8 |
| 29° | 4848 | 4863 | 4879 | 4894 | 4909 | 4924 | 4939 | 4955 | 4970 | 4985 | 0. 5000 5000 | 60° | 3 | 5 | 8 |
| 30° | 0.5000 | 5015 | 5030 | 5045 | 5060 | 5075 | 5090 | 5105 | 5120 | 5135 | 5150 | 59° | 3 | 5 | 8 |
| 31° | 5150 | 5165 | 5180 | 5195 | 5210 | 5225 | 5240 | 5255 | 5270 | 5284 | 5299 | 58° | 2 | 5 | 7 |
| 32° | 5299 | 5314 | 5329 | 5344 | 5358 | 5373 | 5388 | 5402 | 5417 | 5432 | 5446 | 57° | 2 | 5 | 7 |
| 33° | 5446 | 5461 | 5476 | 5490 | 5505 | 5519 | 5534 | 5548 | 5563 | 5577 | 5592 | 56° | 2 | 5 | 7 |
| 34° | 5592 | 5606 | 5621 | 5635 | 5650 | 5664 | 5678 | 5693 | 5707 | 5721 | 0. 5736 5736 | 55° | 2 | 5 | 7 |
| 35° | 0.5736 | 5750 | 5764 | 5779 | 5793 | 5807 | 5821 | 5835 | 5850 | 5864 | 0.5878 | 54° | 2 | 5 | 7 |
| 36° | 5878 | 5892 | 5906 | 5920 | 5934 | 5948 | 5962 | 5976 | 5990 | 6004 | 6018 | 53° | 2 | 5 | 7 |
| 37° | 6018 | 6032 | 6046 | 6060 | 6074 | 6088 | 6101 | 6115 | 6129 | 6143 | 6157 | 52° | 2 | 5 | 7 |
| 38° | 6157 | 6170 | 6184 | 6198 | 6211 | 6225 | 6239 | 6252 | 6266 | 6280 | 6293 | 51° | 2 | 5 | 7 |
| 39° | 6293 | 6307 | 6320 | 6334 | 6347 | 6361 | 6374 | 6388 | 6401 | 6414 | 0.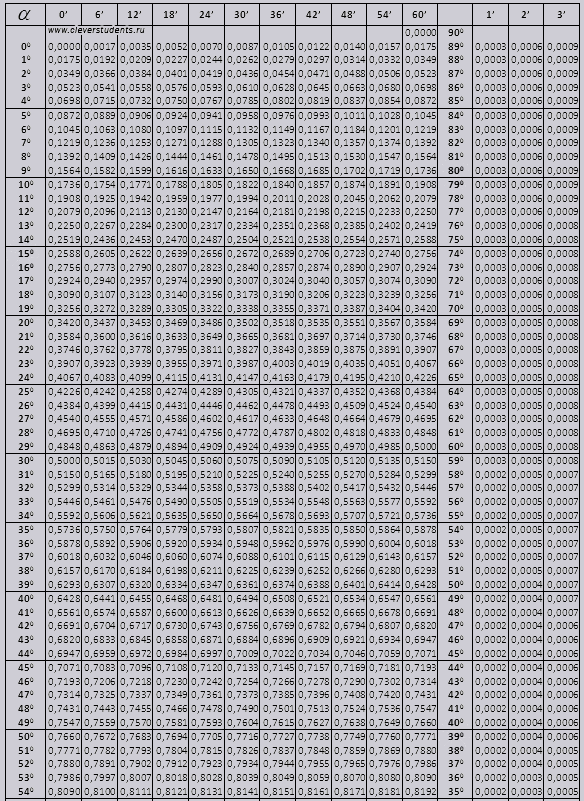 6428 6428 | 50° | 2 | 4 | 7 |
| 40° | 0.6428 | 6441 | 6455 | 6468 | 6481 | 6494 | 6508 | 6521 | 6534 | 6547 | 6561 | 49° | 2 | 4 | 7 |
| 41° | 6561 | 6574 | 6587 | 6600 | 6613 | 6626 | 6639 | 6652 | 6665 | 6678 | 6691 | 48° | 2 | 4 | 7 |
| 42° | 6691 | 6704 | 6717 | 6730 | 6743 | 6756 | 6769 | 6782 | 6794 | 6807 | 6820 | 47° | 2 | 4 | 6 |
| 43° | 6820 | 6833 | 6845 | 6858 | 6871 | 6884 | 6896 | 8909 | 6921 | 6934 | 6947 | 46° | 2 | 4 | 6 |
| 44° | 6947 | 6959 | 6972 | 6984 | 6997 | 7009 | 7022 | 7034 | 7046 | 7059 | 0.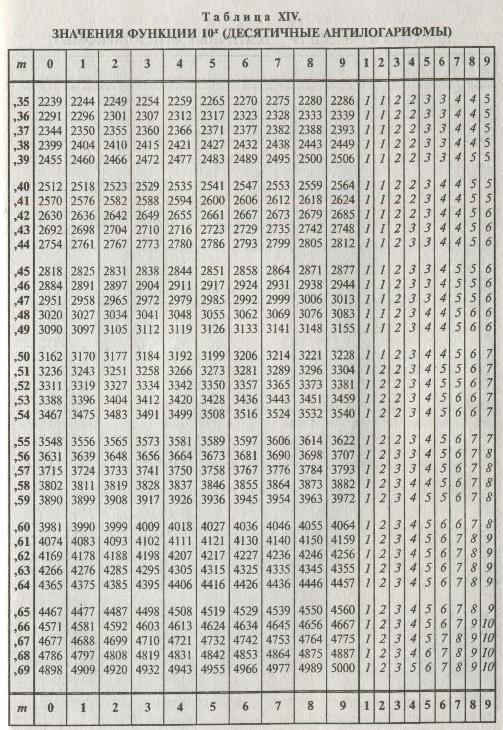 7071 7071 | 45° | 2 | 4 | 6 |
| 45° | 0.7071 | 7083 | 7096 | 7108 | 7120 | 7133 | 7145 | 7157 | 7169 | 7181 | 7193 | 44° | 2 | 4 | 6 |
| 46° | 7193 | 7206 | 7218 | 7230 | 7242 | 7254 | 7266 | 7278 | 7290 | 7302 | 7314 | 43° | 2 | 4 | 6 |
| 47° | 7314 | 7325 | 7337 | 7349 | 7361 | 7373 | 7385 | 7396 | 7408 | 7420 | 7431 | 42° | 2 | 4 | 6 |
| 48° | 7431 | 7443 | 7455 | 7466 | 7478 | 7490 | 7501 | 7513 | 7524 | 7536 | 7547 | 41° | 2 | 4 | 6 |
| 49° | 7547 | 7559 | 7570 | 7581 | 7593 | 7604 | 7615 | 7627 | 7638 | 7649 | 0. 7660 7660 | 40° | 2 | 4 | 6 |
| 50° | 0.7660 | 7672 | 7683 | 7694 | 7705 | 7716 | 7727 | 7738 | 7749 | 7760 | 7771 | 39° | 2 | 4 | 6 |
| 51° | 7771 | 7782 | 7793 | 7804 | 7815 | 7826 | 7837 | 7848 | 7859 | 7869 | 7880 | 38° | 2 | 4 | 5 |
| 52° | 7880 | 7891 | 7902 | 7912 | 7923 | 7934 | 7944 | 7955 | 7965 | 7976 | 7986 | 37° | 2 | 4 | 5 |
| 53° | 7986 | 7997 | 8007 | 8018 | 8028 | 8039 | 8049 | 8059 | 8070 | 8080 | 8090 | 36° | 2 | 3 | 5 |
| 54° | 8090 | 8100 | 8111 | 8121 | 8131 | 8141 | 8151 | 8161 | 8171 | 8181 | 0. 8192 8192 | 35° | 2 | 3 | 5 |
| 55° | 0.8192 | 8202 | 8211 | 8221 | 8231 | 8241 | 8251 | 8261 | 8271 | 8281 | 8290 | 34° | 2 | 3 | 5 |
| 56° | 8290 | 8300 | 8310 | 8320 | 8329 | 8339 | 8348 | 8358 | 8368 | 8377 | 8387 | 33° | 2 | 3 | 5 |
| 57° | 8387 | 8396 | 8406 | 8415 | 8425 | 8434 | 8443 | 8453 | 8462 | 8471 | 8480 | 32° | 2 | 3 | 5 |
| 58° | 8480 | 8490 | 8499 | 8508 | 8517 | 8526 | 8536 | 8545 | 8554 | 8563 | 8572 | 31° | 2 | 3 | 5 |
| 59° | 8572 | 8581 | 8590 | 8599 | 8607 | 8616 | 8625 | 8634 | 8643 | 8652 | 0.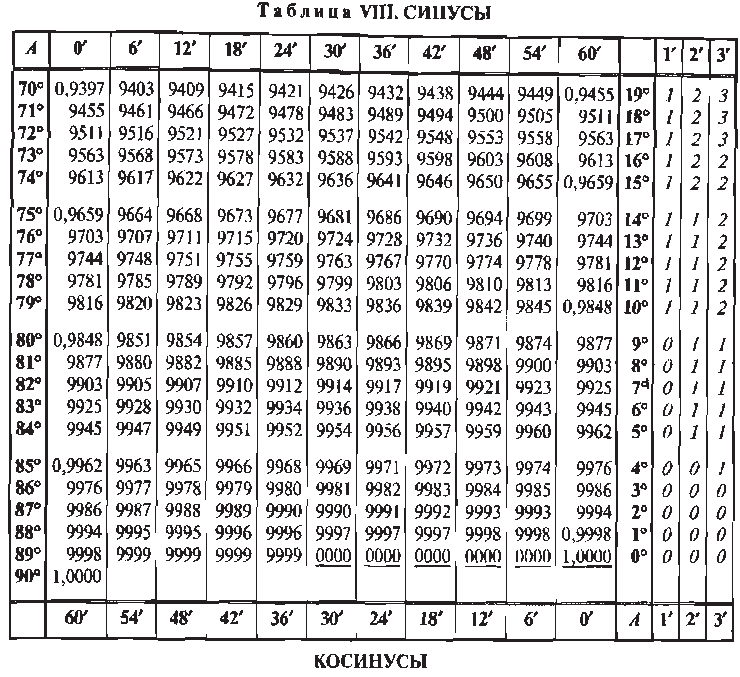 8660 8660 | 30° | 1 | 3 | 4 |
| 60° | 0.8660 | 8669 | 8678 | 8686 | 8695 | 8704 | 8712 | 8721 | 8729 | 8738 | 8746 | 29° | 1 | 3 | 4 |
| 61° | 8746 | 8755 | 8763 | 8771 | 8780 | 8788 | 8796 | 8805 | 8813 | 8821 | 8829 | 28° | 1 | 3 | 4 |
| 62° | 8829 | 8838 | 8846 | 8854 | 8862 | 8870 | 8878 | 8886 | 8894 | 8902 | 8910 | 27° | 1 | 3 | 4 |
| 63° | 8910 | 8918 | 8926 | 8934 | 8942 | 8949 | 8957 | 8965 | 8973 | 8980 | 8988 | 26° | 1 | 3 | 4 |
| 64° | 8988 | 8996 | 9003 | 9011 | 9018 | 9026 | 9033 | 9041 | 9048 | 9056 | 0.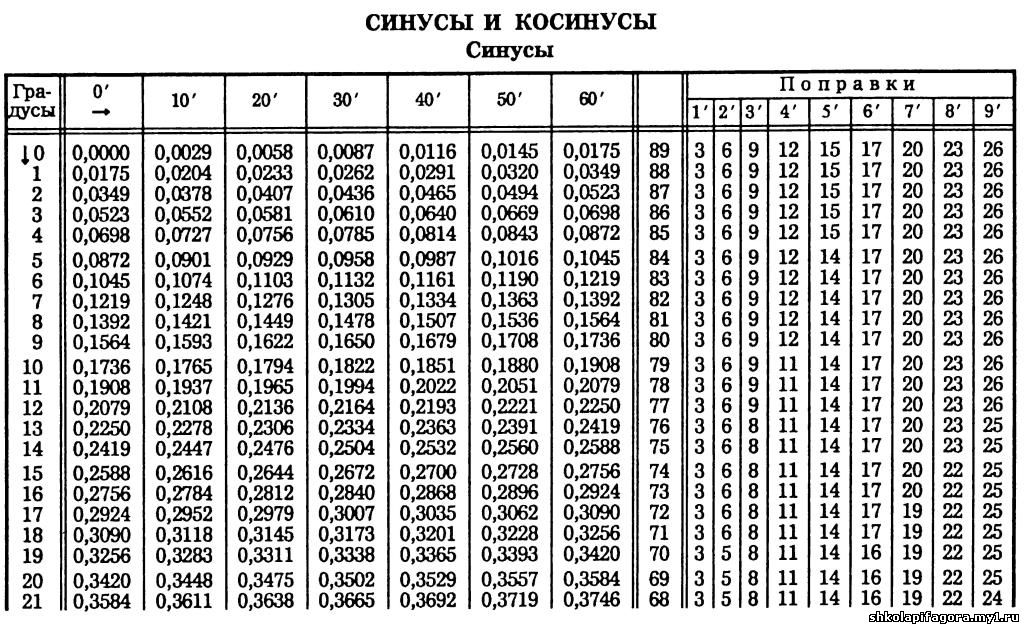 9063 9063 | 25° | 1 | 3 | 4 |
| 65° | 0.9063 | 9070 | 9078 | 9085 | 9092 | 9100 | 9107 | 9114 | 9121 | 9128 | 9135 | 24° | 1 | 2 | 4 |
| 66° | 9135 | 9143 | 9150 | 9157 | 9164 | 9171 | 9178 | 9184 | 9191 | 9198 | 9205 | 23° | 1 | 2 | 3 |
| 67° | 9205 | 9212 | 9219 | 9225 | 9232 | 9239 | 9245 | 9252 | 9259 | 9256 | 9272 | 22° | 1 | 2 | 3 |
| 68° | 9272 | 9278 | 9285 | 9291 | 9298 | 9304 | 9311 | 9317 | 9323 | 9330 | 9336 | 21° | 1 | 2 | 3 |
| 69° | 9336 | 9342 | 9348 | 9354 | 9361 | 9367 | 9373 | 9379 | 9383 | 9391 | 0. 9397 9397 | 20° | 1 | 2 | 3 |
| 70° | 9397 | 9403 | 9409 | 9415 | 9421 | 9426 | 9432 | 9438 | 9444 | 9449 | 0.9455 | 19° | 1 | 2 | 3 |
| 71° | 9455 | 9461 | 9466 | 9472 | 9478 | 9483 | 9489 | 9494 | 9500 | 9505 | 9511 | 18° | 1 | 2 | 3 |
| 72° | 9511 | 9516 | 9521 | 9527 | 9532 | 9537 | 9542 | 9548 | 9553 | 9558 | 9563 | 17° | 1 | 2 | 3 |
| 73° | 9563 | 9568 | 9573 | 9578 | 9583 | 9588 | 9593 | 9598 | 9603 | 9608 | 9613 | 16° | 1 | 2 | 2 |
| 74° | 9613 | 9617 | 9622 | 9627 | 9632 | 9636 | 9641 | 9646 | 9650 | 9655 | 0.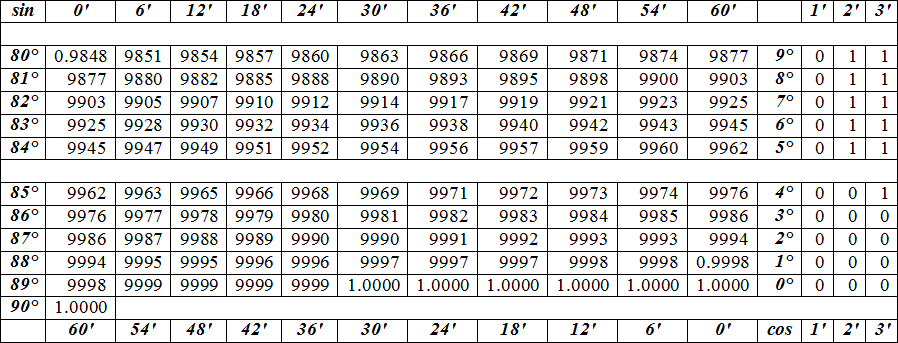 9659 9659 | 15° | 1 | 2 | 2 |
| 75° | 9659 | 9664 | 9668 | 9673 | 9677 | 9681 | 9686 | 9690 | 9694 | 9699 | 9703 | 14° | 1 | 1 | 2 |
| 76° | 9703 | 9707 | 9711 | 9715 | 9720 | 9724 | 9728 | 9732 | 9736 | 9740 | 9744 | 13° | 1 | 1 | 2 |
| 77° | 9744 | 9748 | 9751 | 9755 | 9759 | 9763 | 9767 | 9770 | 9774 | 9778 | 9781 | 12° | 1 | 1 | 2 |
| 78° | 9781 | 9785 | 9789 | 9792 | 9796 | 9799 | 9803 | 9806 | 9810 | 9813 | 9816 | 11° | 1 | 1 | 2 |
| 79° | 9816 | 9820 | 9823 | 9826 | 9829 | 9833 | 9836 | 9839 | 9842 | 9845 | 0.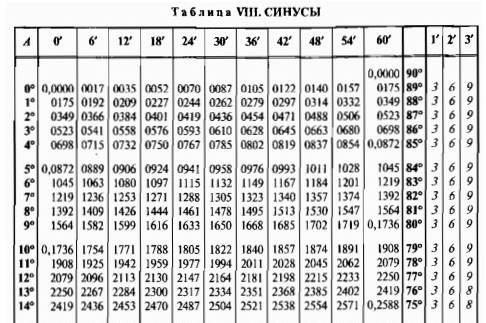 9848 9848 | 10° | 1 | 1 | 2 |
| 80° | 0.9848 | 9851 | 9854 | 9857 | 9860 | 9863 | 9866 | 9869 | 9871 | 9874 | 9877 | 9° | 0 | 1 | 1 |
| 81° | 9877 | 9880 | 9882 | 9885 | 9888 | 9890 | 9893 | 9895 | 9898 | 9900 | 9903 | 8° | 0 | 1 | 1 |
| 82° | 9903 | 9905 | 9907 | 9910 | 9912 | 9914 | 9917 | 9919 | 9921 | 9923 | 9925 | 7° | 0 | 1 | 1 |
| 83° | 9925 | 9928 | 9930 | 9932 | 9934 | 9936 | 9938 | 9940 | 9942 | 9943 | 9945 | 6° | 0 | 1 | 1 |
| 84° | 9945 | 9947 | 9949 | 9951 | 9952 | 9954 | 9956 | 9957 | 9959 | 9960 | 9962 | 5° | 0 | 1 | 1 |
| 85° | 9962 | 9963 | 9965 | 9966 | 9968 | 9969 | 9971 | 9972 | 9973 | 9974 | 9976 | 4° | 0 | 0 | 1 |
| 86° | 9976 | 9977 | 9978 | 9979 | 9980 | 9981 | 9982 | 9983 | 9984 | 9985 | 9986 | 3° | 0 | 0 | 0 |
| 87° | 9986 | 9987 | 9988 | 9989 | 9990 | 9990 | 9991 | 9992 | 9993 | 9993 | 9994 | 2° | 0 | 0 | 0 |
| 88° | 9994 | 9995 | 9995 | 9996 | 9996 | 9997 | 9997 | 9997 | 9998 | 9998 | 0.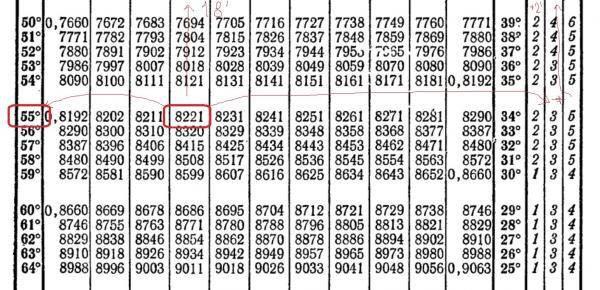 9998 9998 | 1° | 0 | 0 | 0 |
| 89° | 9998 | 9999 | 9999 | 9999 | 9999 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0° | 0 | 0 | 0 |
| 90° | 1.0000 | ||||||||||||||
| sin | 60` | 54` | 48` | 42` | 36` | 30` | 24` | 18` | 12` | 6` | 0` | cos | 1` | 2` | 3` |
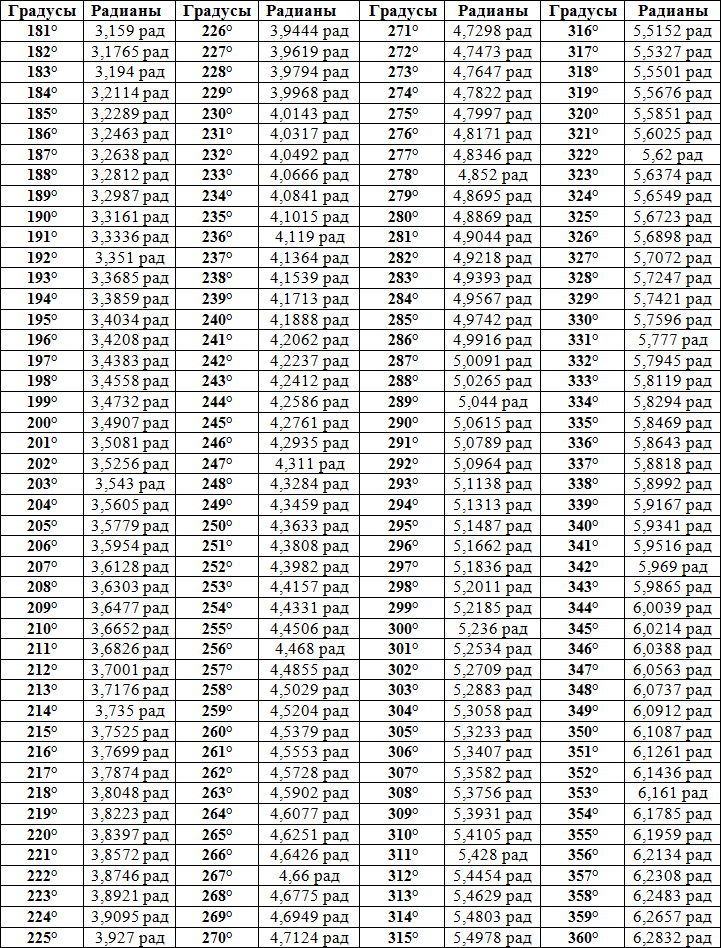
Таблица Брадиса для тангенса и котангенса
| tg | 0` | 6` | 12` | 18` | 24` | 30` | 36` | 42` | 48` | 54` | 60` | ctg | 1` | 2` | 3` |
| 0 | 90° | ||||||||||||||
| 0° | 0,000 | 0017 | 0035 | 0052 | 0070 | 0087 | 0105 | 0122 | 0140 | 0157 | 0175 | 89° | 3 | 6 | 9 |
| 1° | 0175 | 0192 | 0209 | 0227 | 0244 | 0262 | 0279 | 0297 | 0314 | 0332 | 0349 | 88° | 3 | 6 | 9 |
| 2° | 0349 | 0367 | 0384 | 0402 | 0419 | 0437 | 0454 | 0472 | 0489 | 0507 | 0524 | 87° | 3 | 6 | 9 |
| 3° | 0524 | 0542 | 0559 | 0577 | 0594 | 0612 | 0629 | 0647 | 0664 | 0682 | 0699 | 86° | 3 | 6 | 9 |
| 4° | 0699 | 0717 | 0734 | 0752 | 0769 | 0787 | 0805 | 0822 | 0840 | 0857 | 0,0875 | 85° | 3 | 6 | 9 |
| 5° | 0,0875 | 0892 | 0910 | 0928 | 0945 | 0963 | 0981 | 0998 | 1016 | 1033 | 1051 | 84° | 3 | 6 | 9 |
| 6° | 1051 | 1069 | 1086 | 1104 | 1122 | 1139 | 1157 | 1175 | 1192 | 1210 | 1228 | 83° | 3 | 6 | 9 |
| 7° | 1228 | 1246 | 1263 | 1281 | 1299 | 1317 | 1334 | 1352 | 1370 | 1388 | 1405 | 82° | 3 | 6 | 9 |
| 8° | 1405 | 1423 | 1441 | 1459 | 1477 | 1495 | 1512 | 1530 | 1548 | 1566 | 1584 | 81° | 3 | 6 | 9 |
| 9° | 1584 | 1602 | 1620 | 1638 | 1655 | 1673 | 1691 | 1709 | 1727 | 1745 | 0,1763 | 80° | 3 | 6 | 9 |
| 10° | 0,1763 | 1781 | 1799 | 1817 | 1835 | 1853 | 1871 | 1890 | 1908 | 1926 | 1944 | 79° | 3 | 6 | 9 |
| 11° | 1944 | 1962 | 1980 | 1998 | 2016 | 2035 | 2053 | 2071 | 2089 | 2107 | 2126 | 78° | 3 | 6 | 9 |
| 12° | 2126 | 2144 | 2162 | 2180 | 2199 | 2217 | 2235 | 2254 | 2272 | 2290 | 2309 | 77° | 3 | 6 | 9 |
| 13° | 2309 | 2327 | 2345 | 2364 | 2382 | 2401 | 2419 | 2438 | 2456 | 2475 | 2493 | 76° | 3 | 6 | 9 |
| 14° | 2493 | 2512 | 2530 | 2549 | 2568 | 2586 | 2605 | 2623 | 2642 | 2661 | 0,2679 | 75° | 3 | 6 | 9 |
| 15° | 0,2679 | 2698 | 2717 | 2736 | 2754 | 2773 | 2792 | 2811 | 2830 | 2849 | 2867 | 74° | 3 | 6 | 9 |
| 16° | 2867 | 2886 | 2905 | 2924 | 2943 | 2962 | 2981 | 3000 | 3019 | 3038 | 3057 | 73° | 3 | 6 | 9 |
| 17° | 3057 | 3076 | 3096 | 3115 | 3134 | 3153 | 3172 | 3191 | 3211 | 3230 | 3249 | 72° | 3 | 6 | 10 |
| 18° | 3249 | 3269 | 3288 | 3307 | 3327 | 3346 | 3365 | 3385 | 3404 | 3424 | 3443 | 71° | 3 | 6 | 10 |
| 19° | 3443 | 3463 | 3482 | 3502 | 3522 | 3541 | 3561 | 3581 | 3600 | 3620 | 0,3640 | 70° | 3 | 7 | 10 |
| 20° | 0,3640 | 3659 | 3679 | 3699 | 3719 | 3739 | 3759 | 3779 | 3799 | 3819 | 3839 | 69° | 3 | 7 | 10 |
| 21° | 3839 | 3859 | 3879 | 3899 | 3919 | 3939 | 3959 | 3979 | 4000 | 4020 | 4040 | 68° | 3 | 7 | 10 |
| 22° | 4040 | 4061 | 4081 | 4101 | 4122 | 4142 | 4163 | 4183 | 4204 | 4224 | 4245 | 67° | 3 | 7 | 10 |
| 23° | 4245 | 4265 | 4286 | 4307 | 4327 | 4348 | 4369 | 4390 | 4411 | 4431 | 4452 | 66° | 3 | 7 | 10 |
| 24° | 4452 | 4473 | 4494 | 4515 | 4536 | 4557 | 4578 | 4599 | 4621 | 4642 | 0,4663 | 65° | 4 | 7 | 11 |
| 25° | 0,4663 | 4684 | 4706 | 4727 | 4748 | 4770 | 4791 | 4813 | 4834 | 4856 | 4877 | 64° | 4 | 7 | 11 |
| 26° | 4877 | 4899 | 4921 | 4942 | 4964 | 4986 | 5008 | 5029 | 5051 | 5073 | 5095 | 63° | 4 | 7 | 11 |
| 27° | 5095 | 5117 | 5139 | 5161 | 5184 | 5206 | 5228 | 5250 | 5272 | 5295 | 5317 | 62° | 4 | 7 | 11 |
| 28° | 5317 | 5340 | 5362 | 5384 | 5407 | 5430 | 5452 | 5475 | 5498 | 5520 | 5543 | 61° | 4 | 8 | 11 |
| 29° | 5543 | 5566 | 5589 | 5612 | 5635 | 5658 | 5681 | 5704 | 5727 | 5750 | 0,5774 | 60° | 4 | 8 | 12 |
| 30° | 0,5774 | 5797 | 5820 | 5844 | 5867 | 5890 | 5914 | 5938 | 5961 | 5985 | 6009 | 59° | 4 | 8 | 12 |
| 31° | 6009 | 6032 | 6056 | 6080 | 6104 | 6128 | 6152 | 6176 | 6200 | 6224 | 6249 | 58° | 4 | 8 | 12 |
| 32° | 6249 | 6273 | 6297 | 6322 | 6346 | 6371 | 6395 | 6420 | 6445 | 6469 | 6494 | 57° | 4 | 8 | 12 |
| 33° | 6494 | 6519 | 6544 | 6569 | 6594 | 6619 | 6644 | 6669 | 6694 | 6720 | 6745 | 56° | 4 | 8 | 13 |
| 34° | 6745 | 6771 | 6796 | 6822 | 6847 | 6873 | 6899 | 6924 | 6950 | 6976 | 0,7002 | 55° | 4 | 9 | 13 |
| 35° | 0,7002 | 7028 | 7054 | 7080 | 7107 | 7133 | 7159 | 7186 | 7212 | 7239 | 7265 | 54° | 4 | 8 | 13 |
| 36° | 7265 | 7292 | 7319 | 7346 | 7373 | 7400 | 7427 | 7454 | 7481 | 7508 | 7536 | 53° | 5 | 9 | 14° |
| 37° | 7536 | 7563 | 7590 | 7618 | 7646 | 7673 | 7701 | 7729 | 7757 | 7785 | 7813 | 52° | 5 | 9 | 14 |
| 38° | 7813 | 7841 | 7869 | 7898 | 7926 | 7954 | 7983 | 8012 | 8040 | 8069 | 8098 | 51° | 5 | 9 | 14 |
| 39° | 8098 | 8127 | 8156 | 8185 | 8214 | 8243 | 8273 | 8302 | 8332 | 8361 | 0,8391 | 50° | 5 | 10 | 15 |
| 40° | 0,8391 | 8421 | 8451 | 8481 | 8511 | 8541 | 8571 | 8601 | 8632 | 8662 | 0,8693 | 49° | 5 | 10 | 15 |
| 41° | 8693 | 8724 | 8754 | 8785 | 8816 | 8847 | 8878 | 8910 | 8941 | 8972 | 9004 | 48° | 5 | 10 | 16 |
| 42° | 9004 | 9036 | 9067 | 9099 | 9131 | 9163 | 9195 | 9228 | 9260 | 9293 | 9325 | 47° | 6 | 11 | 16 |
| 43° | 9325 | 9358 | 9391 | 9424 | 9457 | 9490 | 9523 | 9556 | 9590 | 9623 | 0,9657 | 46° | 6 | 11 | 17 |
| 44° | 9657 | 9691 | 9725 | 9759 | 9793 | 9827 | 9861 | 9896 | 9930 | 9965 | 1,0000 | 45° | 6 | 11 | 17 |
| 45° | 1,0000 | 0035 | 0070 | 0105 | 0141 | 0176 | 0212 | 0247 | 0283 | 0319 | 0355 | 44° | 6 | 12 | 18 |
| 46° | 0355 | 0392 | 0428 | 0464 | 0501 | 0538 | 0575 | 0612 | 0649 | 0686 | 0724 | 43° | 6 | 12 | 18 |
| 47° | 0724 | 0761 | 0799 | 0837 | 0875 | 0913 | 0951 | 0990 | 1028 | 1067 | 1106 | 42° | 6 | 13 | 19 |
| 48° | 1106 | 1145 | 1184 | 1224 | 1263 | 1303 | 1343 | 1383 | 1423 | 1463 | 1504 | 41° | 7 | 13 | 20 |
| 49° | 1504 | 1544 | 1585 | 1626 | 1667 | 1708 | 1750 | 1792 | 1833 | 1875 | 1,1918 | 40° | 7 | 14 | 21 |
| 50° | 1,1918 | 1960 | 2002 | 2045 | 2088 | 2131 | 2174 | 2218 | 2261 | 2305 | 2349 | 39° | 7 | 14 | 22 |
| 51° | 2349 | 2393 | 2437 | 2482 | 2527 | 2572 | 2617 | 2662 | 2708 | 2753 | 2799 | 38° | 8 | 15 | 23 |
| 52° | 2799 | 2846 | 2892 | 2938 | 2985 | 3032 | 3079 | 3127 | 3175 | 3222 | 3270 | 37° | 8 | 16 | 24 |
| 53° | 3270 | 3319 | 3367 | 3416 | 3465 | 3514 | 3564 | 3613 | 3663 | 3713 | 3764 | 36° | 8 | 16 | 25 |
| 54° | 3764 | 3814 | 3865 | 3916 | 3968 | 4019 | 4071 | 4124 | 4176 | 4229 | 1,4281 | 35° | 9 | 17 | 26 |
| 55° | 1,4281 | 4335 | 4388 | 4442 | 4496 | 4550 | 4605 | 4659 | 4715 | 4770 | 4826 | 34° | 9 | 18 | 27 |
| 56° | 4826 | 4882 | 4938 | 4994 | 5051 | 5108 | 5166 | 5224 | 5282 | 5340 | 5399 | 33° | 10 | 19 | 29 |
| 57° | 5399 | 5458 | 5517 | 5577 | 5637 | 5697 | 5757 | 5818 | 5880 | 5941 | 6003 | 32° | 10 | 20 | 30 |
| 58° | 6003 | 6066 | 6128 | 6191 | 6255 | 6319 | 6383 | 6447 | 6512 | 6577 | 6643 | 31° | 11 | 21 | 32 |
| 59° | 6643 | 6709 | 6775 | 6842 | 6909 | 6977 | 7045 | 7113 | 7182 | 7251 | 1,7321 | 30° | 11 | 23 | 34 |
| 60° | 1,732 | 1,739 | 1,746 | 1,753 | 1,760 | 1,767 | 1,775 | 1,782 | 1,789 | 1,797 | 1,804 | 29° | 1 | 2 | 4 |
| 61° | 1,804 | 1,811 | 1,819 | 1,827 | 1,834 | 1,842 | 1,849 | 1,857 | 1,865 | 1,873 | 1,881 | 28° | 1 | 3 | 4 |
| 62° | 1,881 | 1,889 | 1,897 | 1,905 | 1,913 | 1,921 | 1,929 | 1,937 | 1,946 | 1,954 | 1,963 | 27° | 1 | 3 | 4 |
| 63° | 1,963 | 1,971 | 1,980 | 1,988 | 1,997 | 2,006 | 2,014 | 2,023 | 2,032 | 2,041 | 2,05 | 26° | 1 | 3 | 4 |
| 64° | 2,050 | 2,059 | 2,069 | 2,078 | 2,087 | 2,097 | 2,106 | 2,116 | 2,125 | 2,135 | 2,145 | 25° | 2 | 3 | 5 |
| 65° | 2,145 | 2,154 | 2,164 | 2,174 | 2,184 | 2,194 | 2,204 | 2,215 | 2,225 | 2,236 | 2,246 | 24° | 2 | 3 | 5 |
| 66° | 2,246 | 2,257 | 2,267 | 2,278 | 2,289 | 2,3 | 2,311 | 2,322 | 2,333 | 2,344 | 2,356 | 23° | 2 | 4 | 5 |
| 67° | 2,356 | 2,367 | 2,379 | 2,391 | 2,402 | 2,414 | 2,426 | 2,438 | 2,450 | 2,463 | 2,475 | 22° | 2 | 4 | 6 |
| 68° | 2,475 | 2,488 | 2,5 | 2,513 | 2,526 | 2,539 | 2,552 | 2,565 | 2,578 | 2,592 | 2,605 | 21° | 2 | 4 | 6 |
| 69° | 2,605 | 2,619 | 2,633 | 2,646 | 2,66 | 2,675 | 2,689 | 2,703 | 2,718 | 2,733 | 2,747 | 20° | 2 | 5 | 7 |
| 70° | 2,747 | 2,762 | 2,778 | 2,793 | 2,808 | 2,824 | 2,840 | 2,856 | 2,872 | 2,888 | 2,904 | 19° | 3 | 5 | 8 |
| 71° | 2,904 | 2,921 | 2,937 | 2,954 | 2,971 | 2,989 | 3,006 | 3,024 | 3,042 | 3,06 | 3,078 | 18° | 3 | 6 | 9 |
| 72° | 3,078 | 3,096 | 3,115 | 3,133 | 3,152 | 3,172 | 3,191 | 3,211 | 3,230 | 3,251 | 3,271 | 17° | 3 | 6 | 10 |
| 73° | 3,271 | 3,291 | 3,312 | 3,333 | 3,354 | 3,376 | 3 | 7 | 10 | ||||||
| 3,398 | 3,42 | 3,442 | 3,465 | 3,487 | 16° | 4 | 7 | 11 | |||||||
| 74° | 3,487 | 3,511 | 3,534 | 3,558 | 3,582 | 3,606 | 4 | 8 | 12 | ||||||
| 3,630 | 3,655 | 3,681 | 3,706 | 3,732 | 15° | 4 | 8 | 13 | |||||||
| 75° | 3,732 | 3,758 | 3,785 | 3,812 | 3,839 | 3,867 | 4 | 9 | 13 | ||||||
| 3,895 | 3,923 | 3,952 | 3,981 | 4,011 | 14° | 5 | 10 | 14 | |||||||
| tg | 60` | 54` | 48` | 42` | 36` | 30` | 24` | 18` | 12` | 6` | 0` | ctg | 1` | 2` | 3` |
Понравилась статья? Оставьте комментарий или поделитесь статьей со своими друзьями в социальных сетях.
Источник: http://www.rtiopt64.ru/blog/tablica bradisa dlja sinusa i kosinusa/2016-06-23-401
Данный материал является частной записью члена сообщества Club.CNews.
Редакция CNews не несет ответственности за его содержание.
Том Брэди Жена А. Курс ведьмы
TiktokЗагрузка
для вас
после
Thecosmicrx
Madi Murphy 🪐 Космический Baddie
Не обращайте внимания мужчины #OverwatchMe #andGO #witchtok
1,5 тыс. лайков, 46 комментариев. Видео TikTok от Мади Мерфи 🪐 Cosmic Baddie (@thecosmicrx): «Не обращай внимания на мою изголовье, я только что проснулась, раздосадованная невежеством магглов-гетеросексуалов #OverwatchMe #andGO #witchtok». Бегущий по лезвию 2049.
13,8 тыс. просмотров|
Blade Runner 2049 — Synthwave Goose
Anniesright
Annie
#Stitch с @leta_bitchknok .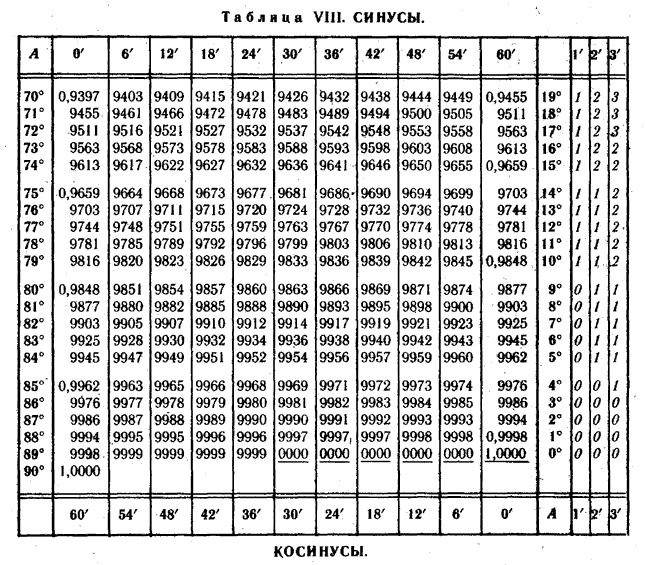 Видео TikTok от Annie (@anniesright): «#stitch with @leta_bitchknow, я устрою вечеринки по просмотру этих игр — давайте посмотрим, как работает волшебство». Cool Kids (наша ускоренная версия).
Видео TikTok от Annie (@anniesright): «#stitch with @leta_bitchknow, я устрою вечеринки по просмотру этих игр — давайте посмотрим, как работает волшебство». Cool Kids (наша ускоренная версия).
308,6 тыс. просмотров|
Cool Kids (our sped up version) — Echosmith
glamourlys
Alyssa Michelle
Reply to @michaelamosley #greenscreenvideo #tombrady #spiritualtiktok #affirmations
638.1K Likes, 6.7 К Комментарии. Видео TikTok от Алиссы Мишель (@glamourlys): «Ответить @michaelamosley #greenscreenvideo #tombrady #spiritualtiktok #аффирмации». Объясняя мое последнее видео «Жена Тома Брэди — ведьма». оригинальный звук.
4,9 млн просмотров|
original sound — Alyssa Michelle
gettingwitchywitit
Dylan
#greenscreen #fyp #witch #witchtok #supermodel #nfl #hiddengem #realizations
120. 5 K лайков, 925 комментариев. Видео TikTok от Дилана (@gettingwitchywitit): «#greenscreen #fyp #witch #witchtok #supermodel #nfl #hiddengem #realizations». Знаменитые ведьмы
Часть 3 | Жизель Бундхен | она же «Жена Тома Брэди». оригинальный звук.
5 K лайков, 925 комментариев. Видео TikTok от Дилана (@gettingwitchywitit): «#greenscreen #fyp #witch #witchtok #supermodel #nfl #hiddengem #realizations». Знаменитые ведьмы
Часть 3 | Жизель Бундхен | она же «Жена Тома Брэди». оригинальный звук.
577,1 тыс. просмотров|
оригинальный звук — Dylan
prestigespeaks
Ricky Prestige Leverett Jr.
Том Брэди говорит, что его жена — ведьма. #LawOfintention #SpirItualTiktok #Spirituality #Metaphysics #Metaphysical #Tombrady #PlayOffs #Witchtok #WOKE 9000 3 4.93. Видео TikTok от Ricky Prestige Leverett Jr. (@prestigespeaks): «Том Брэди говорит, что его жена — ведьма. Он спросил, есть ли у Тома суеверия. | Это может объяснить его успешную карьеру в НФЛ |
Закон Намерения и Желания гласит, что каждому намерению и желанию присущ механизм их выполнения.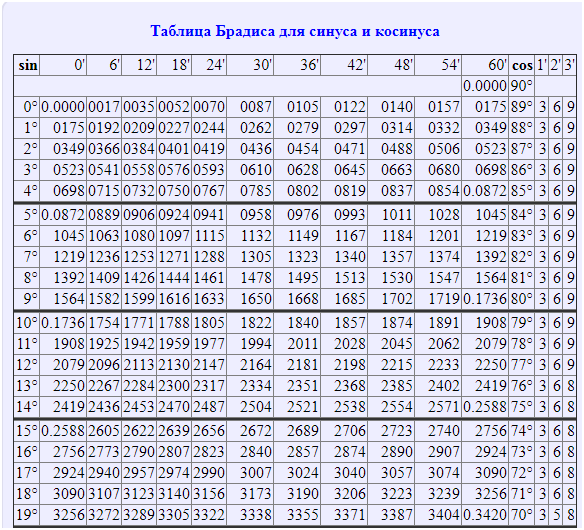 | …. Ленивое воскресенье.
| …. Ленивое воскресенье.
72 тыс. просмотров|
Lazy Sunday — Office Sound Studio
PDIMOCK
PDIMOCK
Рассказывая Джиму о жене Тома Брэди # #RealNews # #Witch # #tombrady
Tiktok Video от PDIMOCK (PDIMOCK). Джим о жене Тома Брэди ##realnews##witch##tombrady». Новости Тома Брэди. оригинальный звук.
862 просмотра|
оригинальный звук — Pdimock
thebronxstarseed
The Bronx Starseed
Отвечая на @abigailvaldez07 #greenscreenvideo да, он сделал это. Если это не последствия ваших собственных действий. #Tombrady Жена #GiselleWitch #Witch #Bruja #Football #SpiritualTiktok #SpiRitual #Spiritual #BRUJATOK #SPIRITAULITY . Видео TikTok от The Bronx Starseed (@thebronxstarseed): «Отвечая @abigailvaldez07 #greenscreenvideo, да, он это сделал. Если это не последствия ваших собственных действий. #tombrady wife #gisellewitch #witch #bruja #футбол #spiritualtiktok #духовность #духовность #бруяток». оригинальный звук.
Видео TikTok от The Bronx Starseed (@thebronxstarseed): «Отвечая @abigailvaldez07 #greenscreenvideo, да, он это сделал. Если это не последствия ваших собственных действий. #tombrady wife #gisellewitch #witch #bruja #футбол #spiritualtiktok #духовность #духовность #бруяток». оригинальный звук.
31 тыс. просмотров|
оригинальный звук — The Bronx Starseed
borotheluckylibra
The Hood Guru ✨
Жена ТОМА БРЭЙДИСА Жизель Бундхен действительно ведьма??? 🤔🤔🤔 #Astrology #natalchart #scorpiomoon #astrologypost #zodiacpost #taurusseason #scorpiofullmoon #astrologylove #synastryastrology
49.4K Likes, 986 Comments. Видео TikTok от The Hood Guru ✨ (@borotheluckylibra): «Жена ТОМА БРЭЙДИСА Жизель Бюндхен действительно ведьма??? ПОДТВЕРЖДЕНИЕ, ЧТО ЖЕНА ТОМА БРЭЙДИСА — ВЕДЬМА 🧙🏼♀️🧙🏼♀️🧙🏼♀️ | Смотрите до конца! .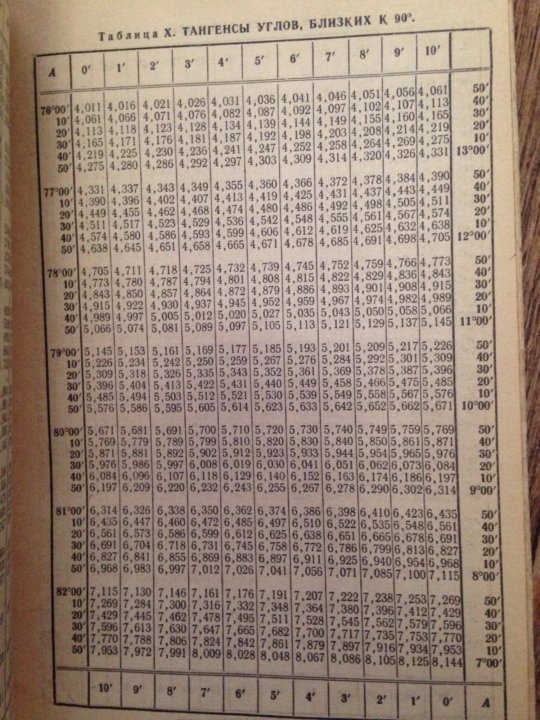 оригинальный звук.
оригинальный звук.
342,2 тыс. просмотров|
оригинальный звук — The Hood Guru ✨
История гонок Мэтью Брэди на road-results.com
Гонки Возраст: 29 • Категория: 2 Найдите этого гонщика на crossresults.com
|
| 27 марта | Кольцевая гонка Гошена | Мужская B | Гонки в пятой зоне | 9 | 37 | 349,05 | ||
| 14 июня | Критерий долины голубей | СМ П-12 | COS Гонки | 13 | 18 | 127,86 | ||
| 17 июля | Bannock Street Criterium, в память о Майке Нилдсе | Мужчины SM P-12 | COS Гонки | 18 | 22 | 174,72 | ||
| 14 августа | Colorado Road Champs PB от Criterium Bikes, SportsCorp, Black Swift, S | Мужчины SM P-12 | 16 | 22 | 174,38 |
Точки, выделенные жирным шрифтом , считаются текущими точками.
Очки, выделенные курсивом , игнорируются, потому что это была ваша вторая гонка в тот день.
Зеленые очки — это лучших пяти гонок из ваших последних десяти гоночных дней (в течение 12 месяцев) — среднее значение этих очков — это ваши текущие очки.
* — Очки улучшения делают некоторые предположения о том, какой категории была гонка (разные категории имеют разные минимальные требования к гонщикам и структуру очков). Очки основаны на информации, найденной здесь. Как и любые другие метаданные на этом сайте, эта информация должна использоваться как руководство, а не окончательный источник — по вопросам обновления обращайтесь к местному представителю USA Cycling. Очки обновления, сделанные более трех лет назад, выделены курсивом и исключаются из расчетов.
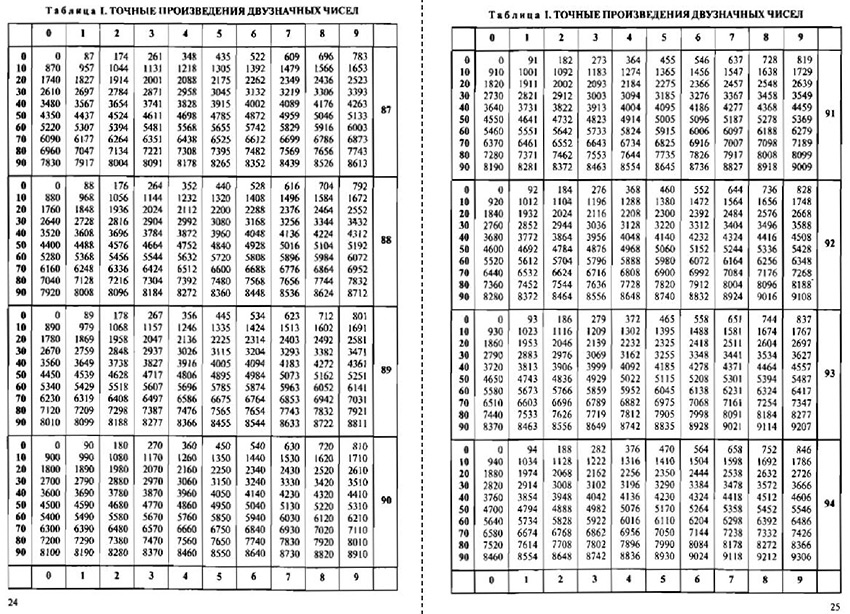
[PDF] Сжатие изображения сенсорного уровня на основе квантованного косинусного преобразования
- title={Сжатие изображения на сенсорном уровне на основе квантованного косинусного преобразования},
автор = {Никос Пицианис, Дэвид Дж.
 Брэди и Сяобай Сан},
booktitle={Защита SPIE + коммерческая разведка},
год = {2005}
}
Брэди и Сяобай Сан},
booktitle={Защита SPIE + коммерческая разведка},
год = {2005}
} Мы представляем новый подход к кодированию со сжатием на сенсорном уровне для интегрированной системы обработки изображений. Сжатие на физическом уровне уменьшает соотношение измерений и пикселей, а также объем данных для хранения и передачи, не мешая оценке или анализу изображения. Мы вводим конкретную схему компрессионного кодирования, основанную на квантованном косинусном преобразовании (ККП) и соответствующей схеме восстановления изображения. QCT ограничен троичным набором {-1,0,1} для экономических…
Посмотреть на SPIE
disp.duke.edu
Датчики изображения сжатия
В этом документе описывается стратегия обнаружения сжатия, разработанная в рамках Инициативы Compressive Optical MONTAGE Photography, и демонстрируется, что система может достигать сжатия до 50 % с обычными эталонными изображениями. .
Сжатие изображений для представления и кодирования видео
- М.
 Вакин, Дж. Ласка, Ричард Баранюк
Вакин, Дж. Ласка, Ричард Баранюк Информатика
- 2006
В этой статье предлагаются алгоритмы и оборудование для поддержки новой теории сжатия изображений, основанной на новой цифровой фото/видеокамере, которая напрямую получает случайные проекции светового поля без предварительного сбора пикселей/вокселей.
Новая архитектура видеокамеры со сжатием, использующая сжатие в оптической области
- Д. Тахар, Дж. Ласка, Ричард Баранюк
Информатика
Электронная обработка изображений
- 2006
Разработана новая архитектура камеры, в которой используется матрица цифровых микрозеркал для выполнения оптических расчетов линейных проекций изображения на псевдослучайные двоичные шаблоны, которые можно адаптировать для изображения на длинах волн, которые в настоящее время невозможны для обычных формирователей изображения на ПЗС и КМОП.
 .
.Архитектура для сжатия изображений
В этой статье предлагаются алгоритмы и оборудование для поддержки новой теории сжатия изображений, основанной на новой цифровой фото/видеокамере, которая напрямую получает случайные проекции сигнала без предварительного сбора пикселей/вокселей.
Спектрометры с компрессионной визуализацией с использованием кодированных апертур
В этой работе предлагается условная конструкция системы, которая сильно недоопределена, но все же обратима в вычислительном отношении и опирается на недавно разработанные концепции компрессионного зондирования.
Видеодатчики сжатия с использованием многоканальных формирователей изображения.
- M. Shankar, N. Pitsianis, D. Brady
Информатика
Прикладная оптика
- 2010
Стратегии дискретизации, а также связанные с ними алгоритмы реконструкции могут быть обсуждены и обсуждены.
 аппаратное обеспечение считывания в фокальной плоскости, что приводит к резкому сокращению полосы пропускания данных и вычислительной сложности.
аппаратное обеспечение считывания в фокальной плоскости, что приводит к резкому сокращению полосы пропускания данных и вычислительной сложности.Многоканальные схемы дискретизации для оптических систем формирования изображений.
- А. Портной, Н. Пицианис, Сяобай Сун, Д. Брейди
Физика
Прикладная оптика
- 2008
цель состоит в том, чтобы разработать ультратонкий формирователь изображений без ущерба для разрешения изображения.
Тонкие цифровые системы обработки изображений, использующие кодирование в фокальной плоскости
- Портной А., Пицианис Н., Колсте Р.
Физика
Электронная визуализация
- 2006
Использование кодирования фокальной плоскости для получения невырожденных данных более высоких частот между субапертурами системы визуализации показана обычная фокальная плоскость грубой выборки.

Распределенная визуализация с использованием массива компрессионных камер
- J. Ke, P. Shankar, M. Neifeld
Информатика
- 2009
Сжатие на физическом интерфейсе
В этой статье основное внимание уделяется недавнему прогрессу в физическом сжатии выборки в рамках Аналогово-информационной (A-to-I) и множественной оптической неизбыточной апертуры Агентства перспективных исследований Министерства обороны…
ПОКАЗАНЫ 1-10 ИЗ 11 ССЫЛОК
СОРТИРОВАТЬ ПОРелевантности Наиболее влиятельные документыНедавность
Изображение кодированной апертуры: анализ пространства Фурье.
- К. Ньюджент
Физика
Прикладная оптика
- 1987
Делается вывод, что трехмерная информация с разрешением, превышающим установленные здесь пределы, может быть получена только путем экстраполяции данных на большие углы обзора путем вывода теоремы выборки для кодированных апертур.

Изображение с кодированной апертурой: прогнозируемая производительность равномерно избыточных массивов.
- Э. Фенимор
Физика
Прикладная оптика
- 1978
Разработано общее выражение для отношения сигнал/шум (SNR) для URA в зависимости от типа отображаемого объекта и конструктивных параметров апертуры.
On The Multiplex Advantage Of Coded Source/Aperture Photon Imaging
- R. F. Wagner, David G. Brown, C. Metz
Physics
Other Conferences
- 1981
The vague concept of «resolution» of апертура детектора (или распределение источников в проходящем изображении) количественно определяется с точки зрения элементарной задачи распознавания сигналов и оказывается в 15 раз более эффективной, чем простая открытая апертура или источник той же площади для задач различения, когда объекты точечный.

Визуализация с масками с кодированной апертурой.
- G. Skinner
Physics
- 1984
Scanning optical reconstruction of coded aperture images
- G. Indebetouw, W. P. Shing
Physics
- 1982
A scanning optical technique is described и используется для восстановления изображений кодированных апертур, полученных с помощью четырех различных типов матриц. Демонстрируются возможности и преимущества методики…
Обратные задачи рентгеновской и гамма-астрономической визуализации
- Г. Скиннер, Т. Понман
Физика
- 1995
Получение изображений с помощью зеркал затруднено при высоких энергиях разработка рентгеновскими и гамма-астрономами множества альтернативных подходов к формированию изображений. Большинство из них…
Новая концепция рентгеновских микроскопов с маской формирования изображения с кодированной апертурой
- М.
 Мацуока, Йошики Комура Йошики Комура
Мацуока, Йошики Комура Йошики Комура Физика
- 1995
Мы предлагаем новую концепцию рентгеновских микроскопов с маской изображения с кодированной апертурой. При этом используются рентгеновские изображения через множество точечных отверстий, но не требуются ни отражательные, ни дифракционные свойства…
Апертурные маски с геометрическим кодированием.
- A. Gourlay, J. Stephen
Физика
Прикладная оптика
- 1983
Предлагаются три новых конструкции маски с кодированной апертурой. Эти маски обладают многими ценными свойствами, которыми обладают равномерно избыточные массивы, и, кроме того, имеют простую геометрическую конструкцию и мало…
Эталонная структурная томография.
- Д. Брэди, Н. Пицианис, Сяобай Сунь
Геология
Журнал Оптического общества Америки. A, Оптика, наука об изображении и зрение
- 2004
Эта работа иллюстрирует использование RST для получения многомерных изображений на основе геометрической модели излучения и знакомит с основными понятиями RST.

- М.

 М. Брадиса, и покажем, как использовать эти таблицы при нахождении значений тригонометрических функций.
М. Брадиса, и покажем, как использовать эти таблицы при нахождении значений тригонометрических функций. , ил.
, ил.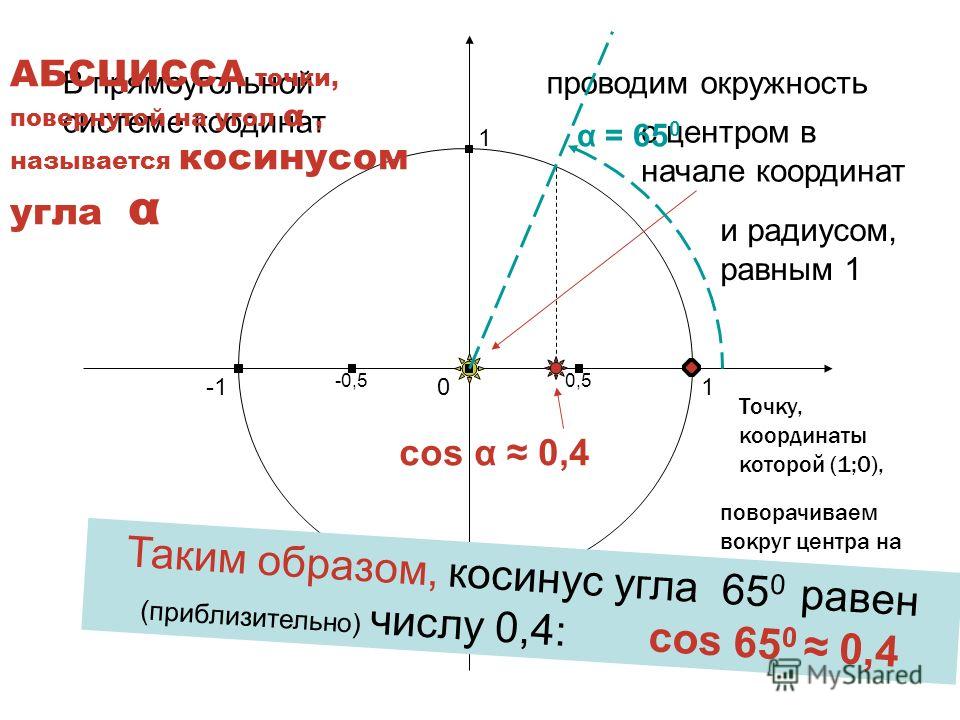 )
)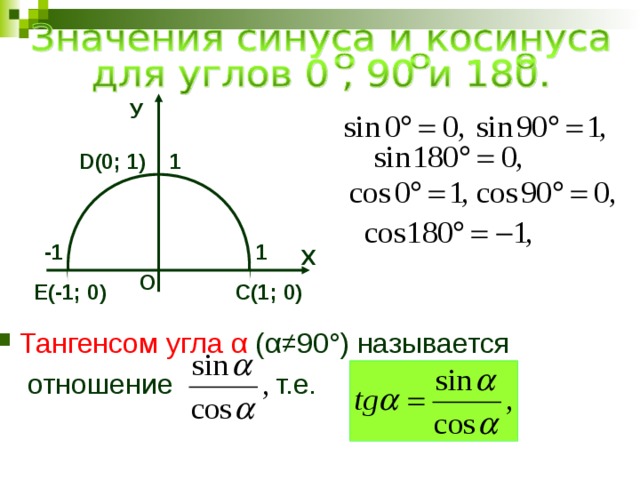 Значения функции 10* (десятичные антилогарифмы) 68
Значения функции 10* (десятичные антилогарифмы) 68 Вот как она звучит:
Вот как она звучит: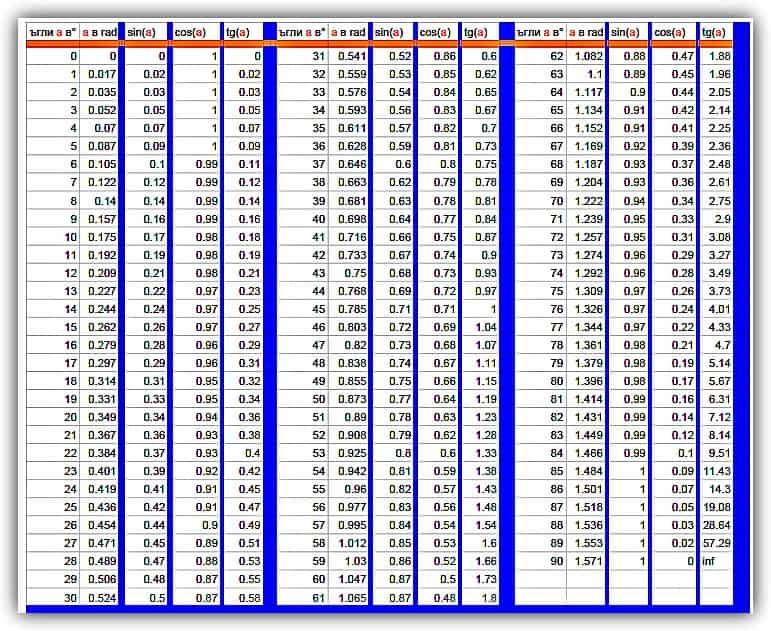



 ..
..

 Мы не будем рассматривать каждый шаг под микроскопом, это мы уже сделали. Посмотрим на результат.
Мы не будем рассматривать каждый шаг под микроскопом, это мы уже сделали. Посмотрим на результат.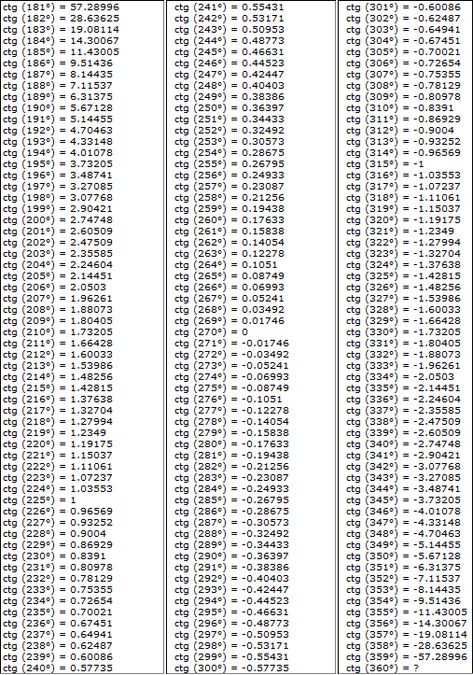
 И математики нас этому постоянно учат. Вот пример.
И математики нас этому постоянно учат. Вот пример. Получим:
Получим:  Но в данной таблице возможно узнать сколько составит тангенс от угла в 1020 градусов, он = -√3 Проверим 1020 0 = 300 0 +360 0 *2. Найдем по таблице.
Но в данной таблице возможно узнать сколько составит тангенс от угла в 1020 градусов, он = -√3 Проверим 1020 0 = 300 0 +360 0 *2. Найдем по таблице. Берем за основу 42 и воспользуемся добавочными столбцами в правой стороне, берем 2 поправку и добавляем к 0,3040 + 0,0006 получаем 0,3046.
Берем за основу 42 и воспользуемся добавочными столбцами в правой стороне, берем 2 поправку и добавляем к 0,3040 + 0,0006 получаем 0,3046.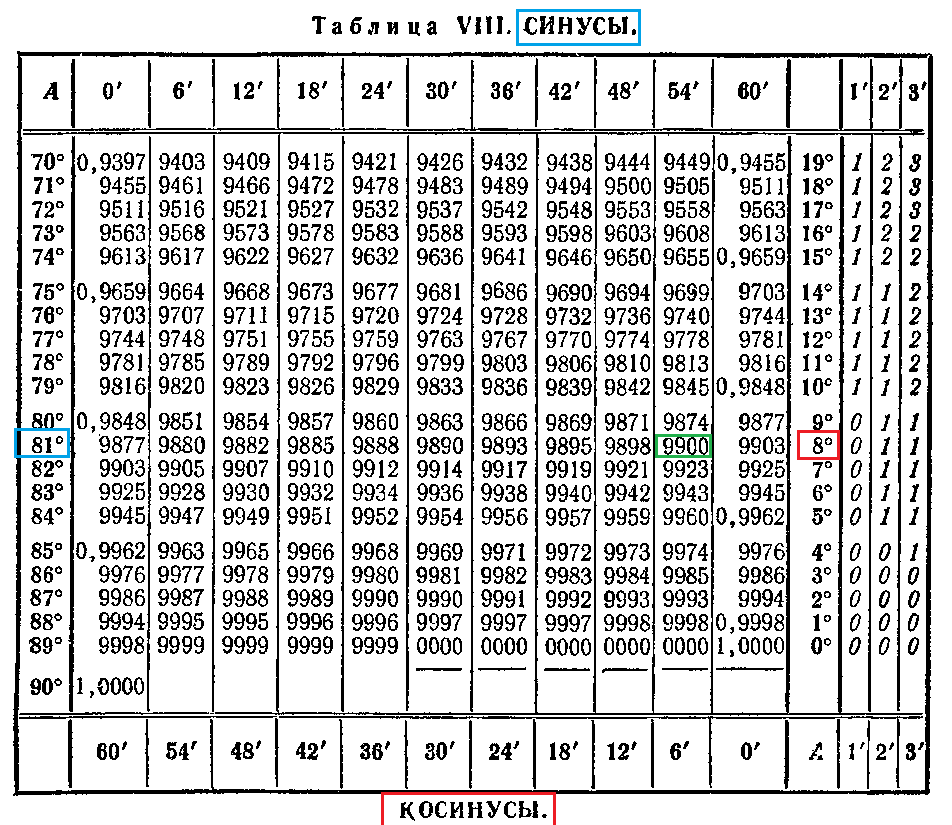 Брэди и Сяобай Сан},
booktitle={Защита SPIE + коммерческая разведка},
год = {2005}
}
Брэди и Сяобай Сан},
booktitle={Защита SPIE + коммерческая разведка},
год = {2005}
}  Вакин, Дж. Ласка, Ричард Баранюк
Вакин, Дж. Ласка, Ричард Баранюк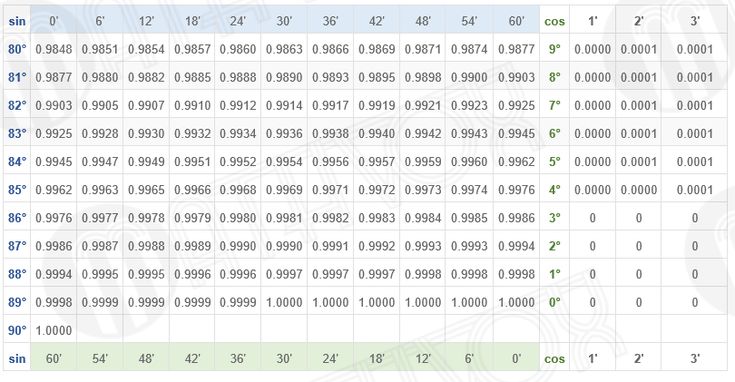 .
. аппаратное обеспечение считывания в фокальной плоскости, что приводит к резкому сокращению полосы пропускания данных и вычислительной сложности.
аппаратное обеспечение считывания в фокальной плоскости, что приводит к резкому сокращению полосы пропускания данных и вычислительной сложности.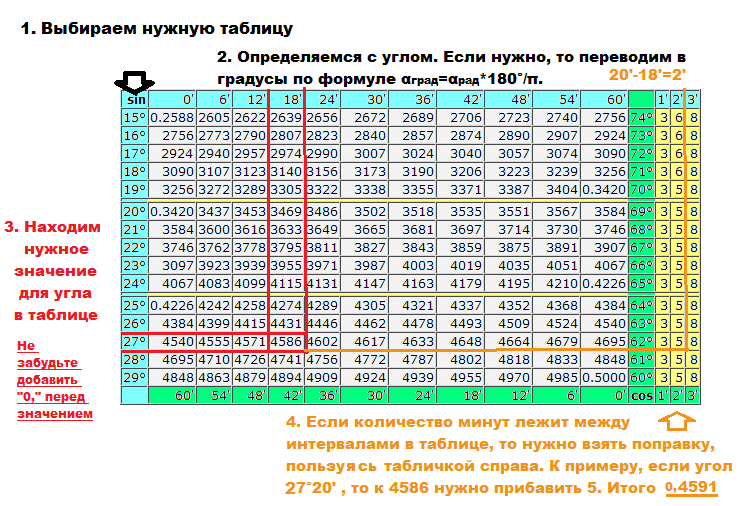


 Мацуока, Йошики Комура Йошики Комура
Мацуока, Йошики Комура Йошики Комура