Бесплатные видеоуроки от проекта «Инфоурок»
Большая коллекция из 3243 видеоурока по 20 предметам и различным темам
УченикВероника
УчительЕвгения Вадимовна
Отличный учитель, который всегда вовлекает ученика в процесс, и сам проявляет заинтересованность в успехах ученика. Интересно слушать и работать!
УченикВероника
УчительДарья Максимовна
Дарья Максимовна замечательный, отзывчивый педагог!Обьясняет простым и доступным язык любую сложную тему- это большой плюс!! Спасибо большое моему репетитору, так как я уверена, что ОГЭ сдам на отлично !!
УченикДарья
УчительЕлизавета Владимировна
Очень качественные и продуктивные занятия. Занимаюсь не долго, но уже чувствуется прогресс. Очень милый и добрый преподаватель. Всё понятно объясняет. Мне, очень нравится заниматься математикой с Елизаветой Владимировной.
УченикКарина
УчительАндрей Юрьевич
Мне понравилось заниматься с Андреем Юрьевичем. Впервые встречаю репетитора, который прежде учить языку, рассказывает про его истоки – географию, культуру, историю. Мне очень откликается такой подход. Видно, что преподаватель с большим опытом. Я очень довольна первым занятием! Буду продолжать заниматься с данным преподавателем.
Мне очень откликается такой подход. Видно, что преподаватель с большим опытом. Я очень довольна первым занятием! Буду продолжать заниматься с данным преподавателем.
УченикМия
УчительТатьяна Александровна
Ответственная, настойчивая, харизматичная, пунктуальная, высокий уровень проф подготовки, терпеливая. Наша девочка довольна, проявляет явный интерес к урокам и продвинулась в изучаемой теме. Большое спасибо вам и преподавателю Татьяне Александровне.
УченикАлёна
УчительЕлена Петровна
Прекрасный преподаватель. После восьми занятий английский стал намного лучше, многое узнала. Все понятно в объяснении, уроки на позитиве. Благодарна за работу. Искренне рекомендую.
УченикКатя
УчительЕлена Александровна
Все понравилось приятно работать с учителем. Как по мне лучше чем Елена Александровна я еще не видела учителя по русскому языку.
УченикДиана
УчительДиана Михайловна
У Дианы Михайловны занимаются английским языком две дочери: Есения и Ксения. Девочкам очень нравится преподаватель и наполнение уроков, материал преподносится в очень интересной форме, а все объяснения понятны и доступны. Девочки уже показали успехи в изучении английского языка в школе.
Девочкам очень нравится преподаватель и наполнение уроков, материал преподносится в очень интересной форме, а все объяснения понятны и доступны. Девочки уже показали успехи в изучении английского языка в школе.
УченикДмитрий
УчительСветлана Анатольевна
Дмитрий прошел со Светланой Анатольевной 4 занятия и уже виден прогресс! Мальчик по натуре немного застенчивый, поначалу был немногословен, но уже хорошо разговаривает на уроках, что говорит о профессионализме педагога.
УченикАрина
УчительИрина Сергеевна
Спасибо огромное. Очень рады, что нашли этот ресурс для занятий. Ирина Сергеевна объясняет все быстро, понятно и динамично. Всего за несколько занятий наверстали упущенное по химии и прошли дальше. Обязательно будем обращаться в дальнейшем.
УченикЕлизавета
УчительРимма Николаевна
У Елизаветы есть успехи, занимается с удовольствием и заинтересованностью. Римма Николаевна очень интересно преподносит материал. Очень нравится учитель, занимаемся с удовольствием.
УченикАртём
УчительНина Ивановна
Нам понравилась Нина Ивановна, хороший человек и прекрасный педагог. Очень ответственная, трудолюбивая и толковая. Сразу нашла подход к ученику. Доходчиво объяснит любую тему. Преподаватель, в отличии от многих репетиторов не просто отбывает время, а действительно помогает.
УченикЭдуард
УчительЖанна Сергеевна
Замечательный педагог, нашла подход с первых занятий. Все очень доходчиво и понятно объясняет. Ребенку очень нравится, просит дополнительные часы для занятий.
УченикЛюдмила
УчительРита Ивановна
Добрый день! Рита Ивановна очень профессионально оценила все пробелы моего сына и нам бы хотелось продолжить с ней обучение! Занятия очень хорошие, учитель понятно все объясняет, всем рекомендую.
УченикСветлана
УчительОльга Олеговна
Спасибо Ольге Олеговне за проведённый урок в праздничный день. Здоровья, процветания, побольше радостных событий в жизни, благополучия, успехов и удачи в таком не лёгком и таком нужном труде!!! Спасибо за урок, всё понравилось!
УченикИрина
УчительТатьяна Николаевна
Очень грамотный педагог, хорошо подходит к вопросам с которыми обращаемся, подход к ребенку очень понравился, буквально на 5-8 урок у ребенка был уже прогресс и теперь любит математику. На урок математики приходим с удовольствием, подтянули свои недочеты, решаем быстро примеры, а главное сами. Спасибо за знания!
На урок математики приходим с удовольствием, подтянули свои недочеты, решаем быстро примеры, а главное сами. Спасибо за знания!
УченикПолина
УчительСветлана Михайловна
Светлана Михайловна очень хороший учитель, за урок мы разбираем много вопросов и обсуждаем правила русского языка в каждом конкретном примере. Занимаюсь с удовольствием!
УченикМария
УчительДарья Александровна
Замечательный, приятный и внимательный преподаватель. Ребенок сначала засмущался от непривычного формата урока, но Дарья Александровна, в итоге, смогла завоевать внимание и доверие дочери. Обязательно будем продолжать обучение! Спасибо!
УченикАнтон
УчительСветлана Васильевна
Репетитор быстро оценила проблемы, порекомендовала способы восполнения пробелов. Продолжим заниматься дальше, так как Светлана Васильевна доступно объясняет материал, и все сразу становится понятным. Классный репетитор, советую!
УченикСофия
УчительГалина Михайловна
Добрый день! Галина Михайловна — замечательный педагог! Мне все было очень понятно и вообще было приятно общаться! Была непонятна тема : ,, Не /ни с глаголами ,,. После того, как Галина Михайловна объяснила, все трудности были сняты. Огромное спасибо !!! 🙏
После того, как Галина Михайловна объяснила, все трудности были сняты. Огромное спасибо !!! 🙏
УченикЛеонид
УчительЕлена Александровна
На уроке педагог работала по индивидуальной программе, выявила пробелы в знаниях и все доходчиво разъяснила. Сложные темы, объяснили легко и понятно, сыну все очень понравилось!
УченикГалина
УчительТамара Иосифовна
Замечательный педагог и очень доброжелательный человек!!! Тамара Иосифовна очень доходчиво объяснила непонятные для меня моменты, причем из разных тем, за один урок!!! Урок проходил в спокойной и дружественной обстановке. Спасибо большое!!! Очень понравилось!!!
УченикМария
УчительВладимир Григорьевич
Спасибо большое, Вы лучший преподаватель по информатике. Как хорошо, что есть такая замечательная платформа. Спасибо всем, кто ее организовал и Вам лично. Всем друзьям и знакомым буду рекомендавать! онлайн-уроки.
УченикОльга
УчительИрина Ивановна
Очень понравился урок! Ирина Ивановна с первых минут расположил к себе ребёнка так, что даже мой непоседливый и не очень настроенный на учебу пятиклассник увлекся так, что не заметил, как пролетели 45мин. Спасибо! С удовольствием продолжим занятия!
Спасибо! С удовольствием продолжим занятия!
УченикФёдор
УчительНаталия Анатольевна
Как родитель могу сказать, что самое важное — это расположить к себе ребенка. Уже после первого занятия с Наталией Анатольевной я увидела желание заниматься в глазах своей дочери. Занятие проходило очень комфортно. Понравилось, как построена программа проверочного урока.
УченикПолина
УчительМарина Михайловна
Мне очень понравилось вводное занятие, спасибо большое. За пол часа Марина Михайловна с помощью разговора поняла все мои слабые места и помогла многие из них подправить и понять. Я хочу заниматься с ней и далее.
УченикАйсултан
УчительГалина Дмитриевна
Здравствуйте! У нас был пробный урок с Галиной Дмитриевной по математике. Занимались именно логическими задачами. Учитель имеет очень хороший подход к детям и у нее есть своя отработанная хорошая методика. Хорошо объясняет, приятная. Спасибо!
УченикВиктор
УчительЮлия Анатольевна
Спасибо большое учитель объясняет очень хорошо там где ты что либо не поймёшь педагог тебе всё объяснит как раз педагог сказала повторить всё то что мне говорил предыдущий репетитор СПАСИБО БОЛЬШОЕ !!!
УченикМаксим
УчительАлёна Юрьевна
Благодарим за интересное и познавательное занятие! Преподаватель четко и внимательно ведет занятие, обращает внимание на моменты, которые необходимо доработать. Профессионально! Приятно общаться.
Профессионально! Приятно общаться.
УченикАлександр
УчительАнастасия Сергеевна
Добрый день! Мы безумно рады, что нам посчастливилось найти такого замечательного и удивительного педагога, как Анастасия Сергеевна! Она очень интересно проводит урок, ребёнок безумно рад. Сразу чувствуется, что человек талантливый. С нетерпением ждём новый урок.
УченикЕкатерина
УчительСергей Васильевич
Спасибо за урок! Занятие очень понравилось, Сергей Васильевич все понятно и интересно обьясняет, во время урока была доброжелательная атмосфера. Также учитель посоветовал некоторые книги и способы подготовки к экзамену. Спасибо!!!
УченикКарина
УчительГулез Гаджимурадовна
Нравятся все педагоги с которыми мы занмаемся, все обладают высоким уровнем профессионализма,используют интересные и современные методы и технологии обучения. Имеет хороший уровень научно-методической подготовки. Ребенок занимается с большим интересом. Будем заниматься с Вами до окончания школы, сейчас мы в 4 классе)
УченикФеона
УчительНаталия Михайловна
За 45 минут узнала и поняла больше, чем за полгода в школе. Учитель объясняет очень понятно, доходчиво, выше школьного уровня. Однозначно этот урок не последний. С Уважением, Феона.
Учитель объясняет очень понятно, доходчиво, выше школьного уровня. Однозначно этот урок не последний. С Уважением, Феона.
УченикЕкатерина
УчительНаталья Васильевна
Спасибо, Наталья Васильевна! Профессионально, четко, по делу. Педагог очень терпеливая, спокойная, уверенная. Занятие очень понравилось и ребенку и мне, маме.
УченикМаксим
УчительАлександр Александрович
Спасибо большое Александру Александровичу. Очень быстро нашел подход к ребёнку , а так же увлек математикой! Ребёнку было комфортно общаться. Надеемся встретиться на следующих занятиях.
УченикМарина
УчительНиколай Васильевич
Николай Васильевич помог за короткий срок восполнить пробелы в знаниях, за что очень благодарны! Уроки очень интересные! Будем обращаться еще к нему.
УченикМарина
УчительАлександр Сергеевич
Занятия ребенку с Александром Сергеевичем очень нравятся. Все схватывает, доволен уроками. С репетитором нашли общий язык. Мы очень благодарны Александру Сергеевичу! Хороший педагог. Спасибо.
Спасибо.
УченикЕлизавета
УчительАлёна Игоревна
Дети понимают всё, абсолютно. В школе не понимают ничего, а с Вашими репетиторами понимают всё. Сдвиги очень большие. Алёна Игоревна хороший педагог. Все занятия результативные.
УченикДжу Уван Ми
УчительГалина Михайловна
Плохо знаю русский язык, и постоянно делаю многие ошибки в тексте и в работе. Только благодаря достуным объяснениям учителя я мог самостоятельно находить ошибки. Большое спасибо за Вашу работу и сердечные помощи в изучении русского языка!
УченикРоман
УчительИрина Алексеевна
Мой сын занимался с Ириной Алексеевной, очень понравилось, всё спокойно и понятно было показано, рассказано. Очень профессионально и качественно выстроены занятия, учитель доброжелателен, ребенку интересно заниматься.
УченикЖеня
УчительОльга Сергеевна
Ольга Сергеевна — профессинал своего дела. Высококвалифицированный педагог. По английскому нужно было именно аудирование и речь, 100% подобрали репетитора по нашему запросу. Педагог строгий — то, что нужно моему ребёнку. Мы очень довольны!
Педагог строгий — то, что нужно моему ребёнку. Мы очень довольны!
УченикНикита
УчительСарвар Шодиевич
До этого никогда не занимался у репетиторов, думал что буду сидеть ничего не понимать и всё время уйдёт зря. Однако Сарвар Шодиевич очень понятно объясняет, не подчёркивает ваши «незнания» и до упора старается всё разъяснить. Могу с уверенностью посоветовать этого репетитора каждому, кто хочет разобраться в алгебре и геометрии.
УченикВиктор
УчительЮлия Анатольевна
Спасибо большое учитель объясняет очень хорошо там где ты что либо не поймёшь педагог тебе всё объяснит как раз педагог сказала повторить всё то что мне говорил предыдущий репетитор СПАСИБО БОЛЬШОЕ !!!
УченикЭльмира
УчительЛюдмила Евгеньевна
Выражаю благодарность центру где есть такие сильные и ответственные учителя. Отдельная благодарность Людмиле Евгеньевне за опыт за знания.
УченикДарья
УчительОльга Александровна
Ольга Александровна отлично объясняет темы, с ребенком нашла общий язык моментально. Дочь занимается с удовольствием, пробелы подтянули за пару уроков. Спасибо Вам большое!
Дочь занимается с удовольствием, пробелы подтянули за пару уроков. Спасибо Вам большое!
УченикОлеся
УчительГузалия Робертовна
Сыну очень понравилось заниматься с Гузалией Робертовной. Очень внимательный и доброжелательный педагог, который сразу видит слабые стороны. Всячески поощряет ребёнка и помогает поднять самооценку. Большое спасибо!
УченикДарья
УчительМария Никитична
Нравится, как преподает Мария Никитична (по программе школы + присутствует игровая минутка, ученице на занятиях не бывает скучно) Уровень знаний повысили до 5-ки, значительно расширили словарный запас. Все устраивает, рекомендует знакомым и в целом рада, что такая платформа существует.
УченикОлеся
УчительДаниил Станиславович
Спасибо. Урок понравился. Даниил Станиславович заинтересовал английским языком. Составили предположительные темы для занятий после новогодних праздников
УченикГеоргий
УчительЕкатерина Станиславовна
Грамотный, добрый, располагающий к себе педагог. С ребёнком Екатерина Станиславовна установила хороший контакт. Преподносит информацию очень доступно. Занятие проходит разнообразно, в том числе в игровой форме. Рекомендуем 5+
С ребёнком Екатерина Станиславовна установила хороший контакт. Преподносит информацию очень доступно. Занятие проходит разнообразно, в том числе в игровой форме. Рекомендуем 5+
УченикНиколя
УчительАлла Валентиновна
Алла Валентиновна отличный преподаватель! Выявила все пробелы в знаниях Константина по русскому языку и работает над их устранением. Также помогает в работе над текущими темами урока. Уже прошли несколько занятий и продолжаем заниматься. нашла общий язык с сыном. Все нравится. Хотим заниматься дальше!
УченикПолина
УчительСветлана Григорьевна
Светлана Григорьевна просто супер учитель!!!! Все очень понятно и хорошо объясняет, прохожу с ней темы по географии 6 класса. На уроке с ней очень интересно. Уже 2 урока — одно удовольствие!!!
УченикНаталья
УчительСергей Александрович
Классный репетитор, все темы разбираются на 5+, будем обязательно продолжать обучение, также рекомендуем всем ученикам!
УченикМаксим
УчительНадежда Викторовна
Замечательный педагог, с которым нравится заниматься. Максим готовится к сдаче ОГЭ по русскому языку и занимается с репетитором с начала ноября прошлого года. За это время успели повторить пройденный материал и изучить несколько тем нового материала. Надежда Викторовна объясняет материал в доступной форме. Максим продолжит с ней занятия.
Максим готовится к сдаче ОГЭ по русскому языку и занимается с репетитором с начала ноября прошлого года. За это время успели повторить пройденный материал и изучить несколько тем нового материала. Надежда Викторовна объясняет материал в доступной форме. Максим продолжит с ней занятия.
УченикАлександра
УчительИрина Борисовна
Отличный репетитор ! Ирина Борисовна обьясняет сложные темы простым и доступным языком ! Сердечно благодарю педагога за грамотность и профессионализм !!!!
УченикФеона
УчительЯнина Александровна
Преподаватель компетентный, объясняет понятно, выше школьного уровня. Быстро заполняет пробелы в знаниях. Будем сотрудничать. С Уважением, Феона.
УченикМадина
УчительМария Анатольевна
Очень чётко и понятно объяснила Мария Анатольевна. Спасибо вам. Не смотря первый раз, пробную занятия, она прям очень понравилась дочке и естественно мне💐. В дальнейшем обязательно будем заниматься с ней и подниматься.
УченикВероника
УчительЕвгения Вадимовна
Отличный учитель, который всегда вовлекает ученика в процесс, и сам проявляет заинтересованность в успехах ученика. Интересно слушать и работать!
Интересно слушать и работать!
УченикВероника
УчительДарья Максимовна
Дарья Максимовна замечательный, отзывчивый педагог!Обьясняет простым и доступным язык любую сложную тему- это большой плюс!! Спасибо большое моему репетитору, так как я уверена, что ОГЭ сдам на отлично !!
УченикДарья
УчительЕлизавета Владимировна
Очень качественные и продуктивные занятия. Занимаюсь не долго, но уже чувствуется прогресс. Очень милый и добрый преподаватель. Всё понятно объясняет. Мне, очень нравится заниматься математикой с Елизаветой Владимировной.
УченикКарина
УчительАндрей Юрьевич
Мне понравилось заниматься с Андреем Юрьевичем. Впервые встречаю репетитора, который прежде учить языку, рассказывает про его истоки – географию, культуру, историю. Мне очень откликается такой подход. Видно, что преподаватель с большим опытом. Я очень довольна первым занятием! Буду продолжать заниматься с данным преподавателем.
Урок геометрии «Синус, косинус, тангенс острого угла прямоугольного треугольника»
ГОСУДАРСТВЕННОЕ
ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
«ПЕРЕВАЛЬСКАЯ ГИМНАЗИЯ № 1»
Синус, косинус и тангенс острого угла прямоугольного треугольника
Разработка урока по геометрии (8 класс)
Разработала и провела
учитель математики
Купцова Ирина Николаевна
2020
Тема урока.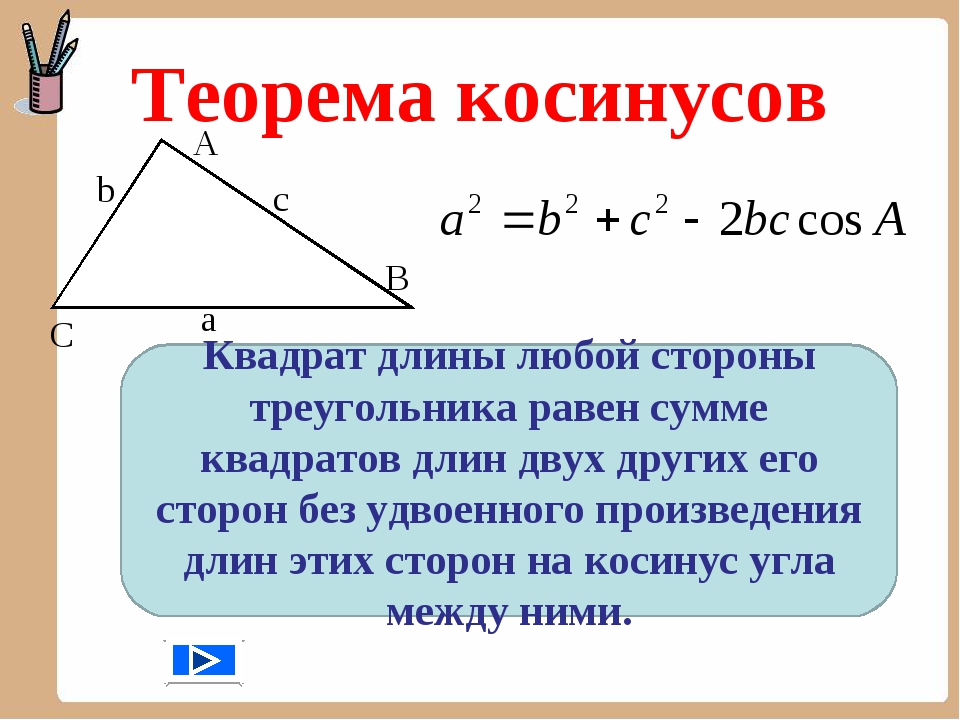 Синус, косинус, тангенс острого угла прямоугольного треугольника
Синус, косинус, тангенс острого угла прямоугольного треугольника
Цели урока: ввести понятие синуса, косинуса и тангенса острого угла прямоугольного треугольника, изучить основное тригонометрическое тождество и научить применять изученный материал к решению задач; развивать мыслительную деятельность, формировать умение чётко и ясно излагать свои мысли; способствовать выявлению и раскрытию способностей учащихся; воспитывать познавательную активность учащихся; прививать самостоятельность и любознательность
Тип урока: урок усвоения новых знаний
Методы: объяснительно – иллюстративный, эвристический, репродуктивный
Формы работы: фронтальная, индивидуальная, парная
Методическое обеспечение: учебник, дидактический материал, Интернет – ресурс
Ход урока
1.Организационный момент
Учитель. Каким должно быть настроение, чтобы урок получился удачным?
Предполагаемый ответ учащихся: настроение должно быть хорошим, деловым.
Учитель: я желаю вам до конца урока сохранить хорошее деловое настроение.
Учащиеся: спасибо!
Учитель: начинаем наш урок!
2.Актуализация опорных знаний
а) проверка домашнего задания
Учитель отвечает на вопросы учащихся, если они возникли. Если нет вопросов, фронтально проверяем решение домашней задачи.
Задача № 572 д
Учитель задает вопросы, учащиеся отвечают.
Решение
Учитель. Какие отрезки известны?
Учащиеся. Катет и гипотенуза
Учитель. Какой отрезок мы можем найти, зная катет и гипотенузу?
Учащиеся. Второй катет
Учитель. Какую теорему применяем?
Учащиеся. Теорему Пифагора. Учащийся читает формулу b= ,затем говорит чему равно b.
Какие следующие элементы треугольника найдем?
Учащийся. Проекции катетов на гипотенузу. Записывает на доске формулы: ac = ; bc= . Читаем ответы.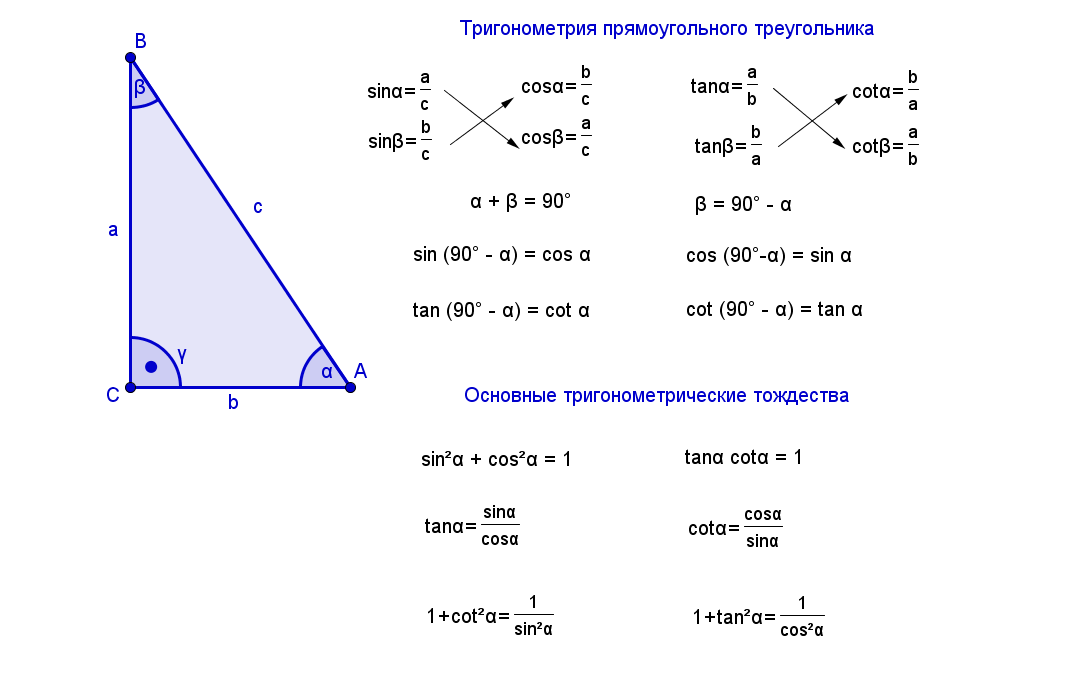
Учитель. Как найти высоту прямоугольного треугольника?
Учащиеся. По формуле h = . Читаем ответ.
Учитель. Молодцы! Продолжим урок
3.Мотивация учебной деятельности, сообщение темы, целей урока
Учитель. Математика – наука древняя, интересная и полезная. Сегодня мы с вами в очередной раз убедимся в этом. Очень хочется, чтобы каждый из вас сделал для себя хотя бы небольшое, но открытие. Великий ученый, математик Лейбниц сказал: «Кто хочет ограничиться настоящим, без знания прошлого, тот его никогда не поймет…». Поэтому и нам с вами для успешной работы нужно повторить изученный материал о прямоугольном треугольнике
Б) проверка ранее изученного материала в форме тестов с последующей проверкой и самооценкой
1. К каким треугольникам можно применить теорему Пифагора?
А) к любым;
Б) к прямоугольным;
В) к равнобедренным;
Г) не знаю.
2. Верно ли, что в прямоугольном треугольнике любой из катетов меньше гипотенузы?
А) нет;
Б) не знаю;
В) да.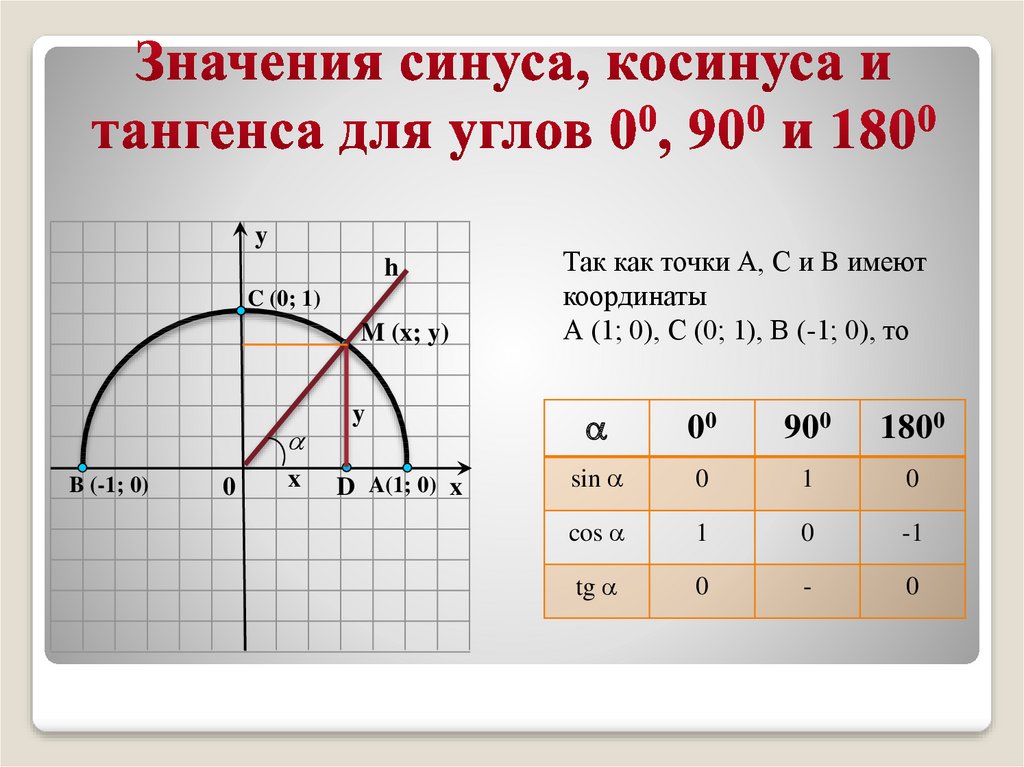
3. В прямоугольном треугольнике квадрат гипотенузы равен…
А) сумме катетов;
Б) квадрату катета;
В) сумме квадратов катетов;
Г) не знаю.
4.Чему равна гипотенуза прямоугольного треугольника, катеты которого равны
6 см и 8 см?
А) 10 см;
Б) 14 см;
В) 2 см;
Г) 12 см.
5.Гипотенуза прямоугольного треугольника равна 5 см, катет 3 см. Найти длину второго катета.
А) 5 см;
Б) 4 см;
В) 6 см;
Г) 8 см.
6.Какой из треугольников с указанными сторонами – прямоугольный?
А) 2; 5; 4.
Б) 10; 10; 10.
В) 12; 9; 15.
Г) нет правильного ответа
Ключ: 1Б; 2В; 3 В; 4А; 5 Б; 6В
Учитель. Сегодня на уроке мы продолжим изучать прямоугольный треугольник. Запишите тему урока «Синус, косинус, тангенс острого угла прямоугольного треугольника»
4.Изложение нового материала
1.Введем понятие катета и противолежащего угла, катета и прилежащего угла
В
С А
Учитель. В треугольнике АВС – катеты АС и ВС, гипотенуза АВ.
В треугольнике АВС – катеты АС и ВС, гипотенуза АВ.
Катет ВС является противолежащим углу А и прилежащим к углу В.
Катет АС является противолежащим углу В, прилежащим углу А.
2.Определение синуса, косинуса, тангенса острого угла прямоугольного треугольника
Учитель.
Отношение =
Отношение =
Отношение = tg A.
Учащиеся записывают формулы в тетрадь.
Затем работают с учебником ( изучают правила)
3.Отработка изученного материала (решение задач по готовым чертежам)
Задача № 1
A
2 5
B 3 C
Найти , , tg C.
Решение
; ; tg C =
Задача № 2
C
3
A 2 B
Найти
Решение
. Найдем сначала AC по теореме Пифагора.
AC = ; AC = =
Значит, .
5.Минутка отдыха
Учитель. Продолжим работу
4.Определение тангенса угла
Учитель. Тангенсом острого угла прямоугольного треугольника называется отношение синуса этого угла к косинусу этого угла.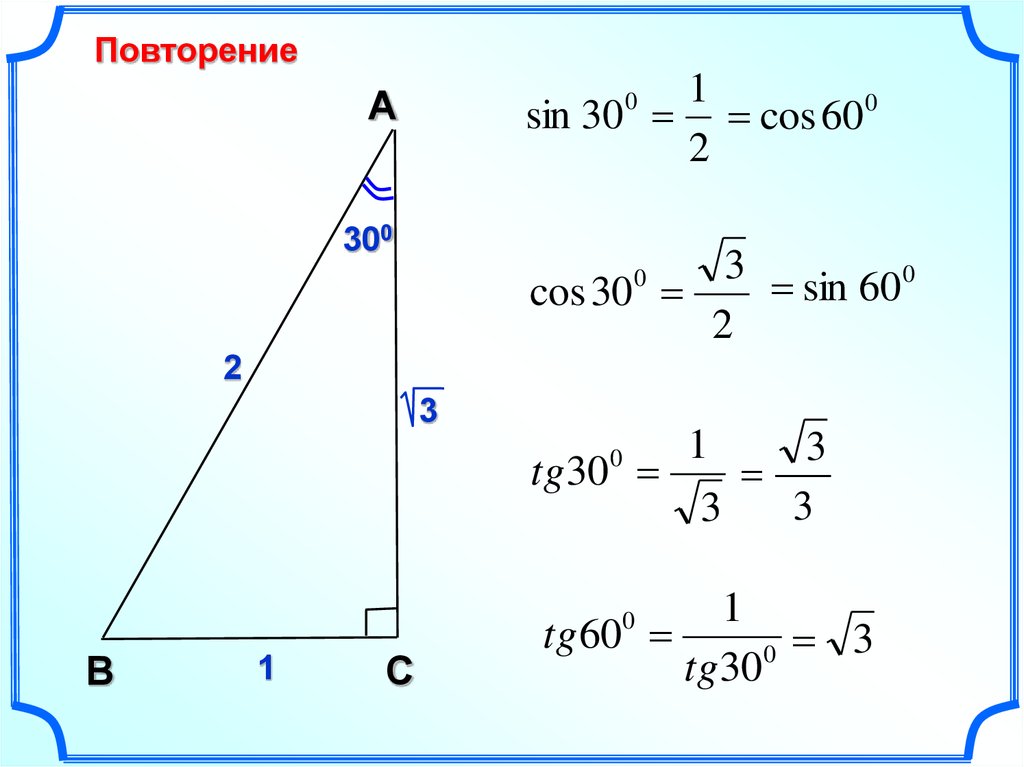
Учащиеся записывают формулу
tg α =
5.Записываем в тетрадь утверждение, что синус, косинус и тангенс острого угла прямоугольного треугольника зависят только от градусной меры угла и не зависят от размера треугольника
6.Изучение основного тригонометрического тождества
Записываем в тетрадь
+ = 1
7.Учитель.
Рассмотрим пример применения основного тригонометрического тождества
Задача
Дано: .
Найти: tg
Решение ( коллективно – фронтальный опрос)
По формулам = и tg = получим
= ; tg
6.Закрепление изученного материала
Решить № 591 а – коллективно
A
17
C 8 B
Учащиеся с помощью учителя записывают формулы
; ; tgA =
Учитель. Какой отрезок неизвестен в этих равенствах?
Учащиеся. АС.
Учитель. Как его найти?
Учащиеся. По теореме Пифагора
Учитель. Записываем формулу для нахождения АС = .
Вычисляем AC = = 15, тогда = ; ; tg A = .
Учитель. Найти и tg B – самостоятельно – работа в парах
Проверяем решение чтением ответов
7.Рефлексия учебной деятельности
Вопросы к учащимся
1.Что называется синусом, косинусом, тангенсом острого угла прямоугольного треугольника?
2.Какое равенство называют основным тригонометрическим тождеством?
Записать формулу, выражающую тангенс угла через синус и косинус.
4.Объяснить, почему синус, косинус и тангенс острого угла зависит от градусной меры угла и не зависит от размеров треугольника?
8.Подведение итогов урока
Выставление оценок с комментариями
9.Домашнее задание: изучить п. 69, решить № 591 (б), подготовить историческую справку о синусе, косинусе и тангенсе острого угла прямоугольного треугольника
Учитель. Поаплодируйте себе ( учащиеся аплодируют)
Учитель. Урок окончен. Спасибо за урок !
Литература
1. Атанасян Л.С. Геометрия 7 – 9. – М. Просвещение, 2014 – 382 с.
Атанасян Л.С. Геометрия 7 – 9. – М. Просвещение, 2014 – 382 с.
2. Зив Б.Г.,В.М.Мейлер и др. Дидактические материалы по геометрии для 8 класса. – М. Просвещение,2010 – 158 с.
3.Атанасян Л.С., Бутузов В.Ф. Изучение геометрии в 7 – 9 классах. – М. Просвещение, 2010 – 365 с.
4.Гаврилова Н.Ф. Поурочные разработки по геометрии 8 класс. – М.: Просвещение, 2019 – 414 с.
геометрия — Обобщение следствия закона косинуса
Задай вопрос
спросил
Изменено 1 год, 7 месяцев назад
Просмотрено 121 раз
$\begingroup$
Существует прямое следствие закона косинуса, утверждающего, что при фиксировании двух сторон треугольника и увеличении третьей увеличивается угол при вершине, противоположный третьей стороне.
Пусть $a,b,c$ и $a’,b’,c$ будут сторонами двух треугольников, а $\gamma$ и $\gamma’$ равны угол при вершине противоположен стороне $c$ (которая имеет одинаковую длину в обоих треугольниках). Если $a+b \leq a’+b’$, то $\gamma \geq \gamma’$.
Проще говоря, если сумма длин смежных сторон угла увеличивается (а противоположная длина остается неизменной), то этот угол уменьшается. В идеале это должно выполняться не только на плоскости, но и в любом пространстве, где выполняется закон косинуса, в частности, я имею в виду сферу и гиперболическое пространство.
Мне трудно это доказать, но моя интуиция подсказывает мне, что это должно быть правдой (я ничего не нашел в Интернете, хотя, по общему признанию, я не знаю, как это искать). Интуитивно, поскольку $c \leq a+b \leq a’+b’$, обход через $A$ «ближе» к кратчайшему соединению из $C$ в $D$, чем обход через $B$, поэтому $A$ ближе к отрезку $CD$, чем $B$.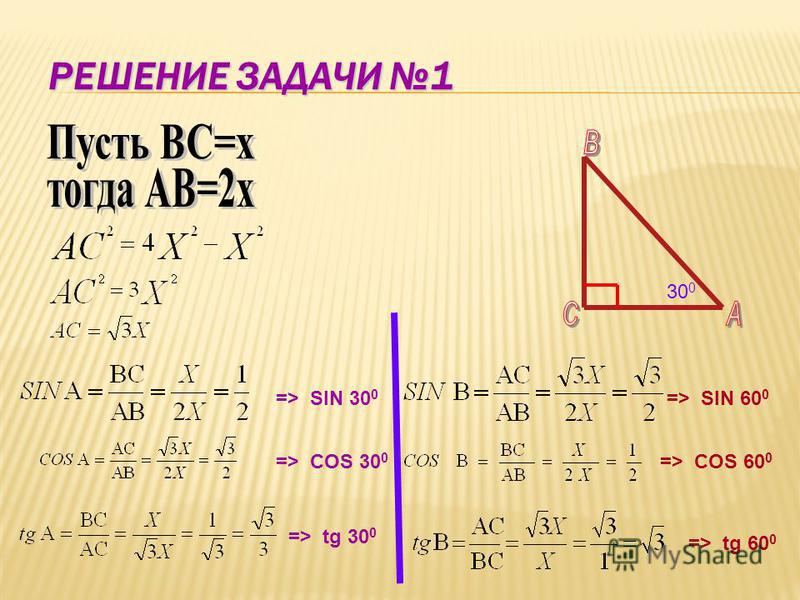
Буду благодарен за любую дополнительную информацию!
- геометрия
- тригонометрия
- евклидова геометрия
- монотонные функции
- метрическая геометрия
$\endgroup$
1
$\begingroup$
Из теоремы о внешнем угле треугольника \begin{align}\gamma =\gamma»+\alpha’=(\gamma’+\alpha)+\alpha’ \,(\alpha\geq0,\alpha’ \geq0)\end{выравнивание}
\begin{align}\gamma > \gamma’\, (\alpha \neq0)\end{align}
\begin{align}\gamma = \gamma’ \,(\alpha=\alpha’=0 )\конец{выравнивание}
$\endgroup$
1
$\begingroup$
Дан $\треугольник ABC$ с «вершиной» $C$ .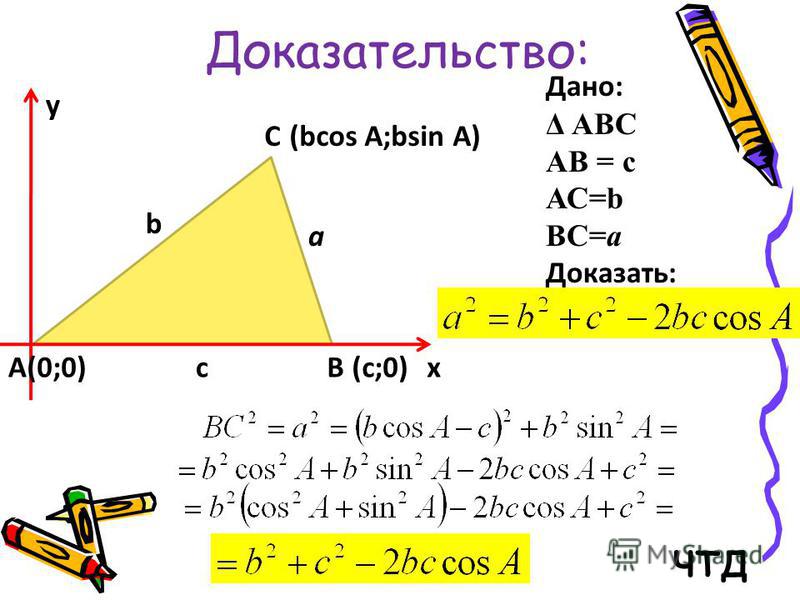 ..
..
- Как следствие теоремы о вписанном угле, множество точек $C’$ (по одну сторону от $\overline{ AB}$ как $C$), такой, что $\угол AC’B>\угол ACB$ ограничен дугой окружности $ACB$.
- С другой стороны, множество точек $C’$ таких, что $|AC’|+|BC’|<|AC|+|BC|$, ограничено эллипсом, проходящим через $C$ с фокусами $A$ и $Б$.
Круговая область с «большим углом» никогда полностью не покрывает эллиптическую область с «меньшей суммой сторон», поэтому гипотеза неверна: меньшая сумма сторон не означает больший угол. $\square$
Примечание. Когда $C$ является конечной точкой малой оси эллипса (то есть, когда $\треугольник ABC$ равнобедренный с вершиной $C$), «меньшая сумма- область сторон» покрывает область «большего угла»; так что в данном случае обратная гипотеза верна: больший угол подразумевает меньшую сумму сторон. Но, как правило, то, как сравниваются углы, не зависит от того, как сравниваются суммы сторон.
$\endgroup$
8
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
Интуиция для закона косинусов – BetterExplained
Закон косинусов представлен в виде геометрического результата, который связывает части треугольника:
Хотя это и правда, здесь действует более глубокий принцип.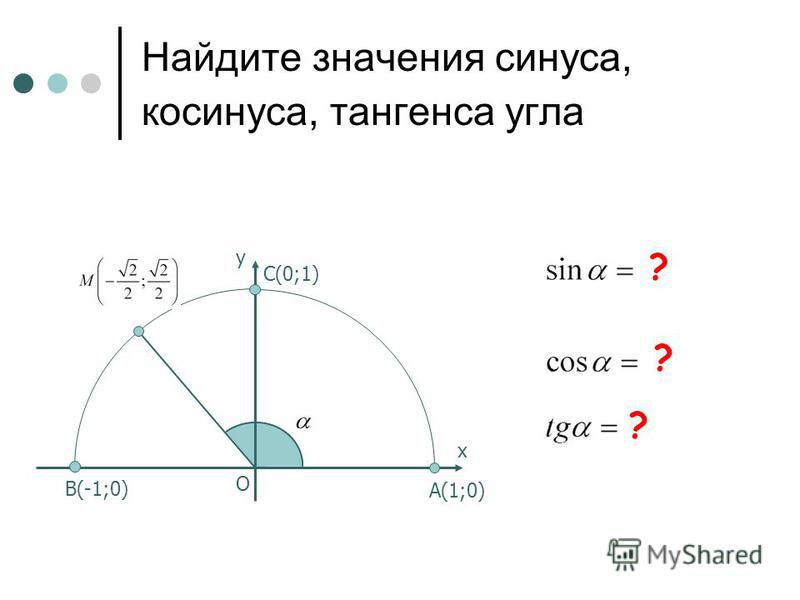
Закон взаимодействий: Целое основано на частях и взаимодействии между ними.
Формулировка «Закон косинусов» заставляет задуматься о механике формулы, а не о ее значении. Частью моей стратегии обучения является преобразование идей в осмысленные. 92$ расширяется, когда компоненты не полностью выстроены. Мы рассматриваем геометрические линии как члены алгебраического расширения.
Аналогия: Помощник повара
Представьте себе ресторан с единственным шеф-поваром Алисой. Она перегружена работой, поэтому Боба нанимают к ней помощником (су-шефом).
Основываясь на текущей производительности Алисы и производительности Боба в его интервью, что происходит, когда они работают вместе?
Конечно, новый результат должен быть их совместными усилиями:
Ха! Офисные работники повсюду закатывают глаза. Вы не можете просто предположить, что люди вносят одинаковый вклад, когда они собраны вместе: есть взаимодействия, которые необходимо учитывать.
Помимо индивидуального вклада, эти двое могут замедлять друг друга ( Куда ты опять положил венчик? ) или находить способы работать вместе ( Я все равно чищу морковь, возьми немного моей. ) .
В системе с несколькими частями начните с отдельных вкладов, а затем спросите, будет ли их взаимодействие:
- Помогайте друг другу
- Делать друг другу больно
- Игнорировать друг друга
Исходная идея о том, что «Всего = Алиса + Боб», в более общем виде выражается так:
Изучение сценария
Нам нужно отделить список участников (Алиса, Боб) от результата их взаимодействия.
Возьмем числа 5 и 3. Запишем их так:
- Части = (5, 3)
, и мы почти уверены, что их комбинация дает 8. Но есть ли другой способ получить такой вывод? 92$. Результат режима взаимодействия говорит, что система выдаст 64, если взаимодействует сама с собой.
Одно предостережение: при переходе к интерактивному представлению мы записали $(5 + 3)(5 + 3)$, но мы не можем с самого начала упростить $(5 + 3) = 8$. Мы используем сложение для учета, пока умножение не сможет объединить части.
Мы используем сложение для учета, пока умножение не сможет объединить части.
О, еще одно предостережение: почему мы можем просто добавить взаимодействия, но не части? Отличный вопрос. Отдельные части могут указывать в разных измерениях и не выстраиваться в одном масштабе. Взаимодействующие части превращаются в 92 + 3x = 15$ требует системного подхода.
Закон косинусов представляет собой систематический подход к работе с частями:
- Список частей
- Получить каждое взаимодействие как область
- Добавить, чтобы найти общий вклад
- Преобразование в эквивалентную «единую часть»
Последний шаг часто подразумевается. После того, как мы объединили беспорядок взаимодействий, нам нужна
Закон косинусов дает нам способ найти Чарли.
Что делать с косинусом?
Когда две части взаимодействуют друг с другом, они могут помочь, навредить или игнорировать друг друга:
- Идеальное выравнивание означает, что они помогают на 100% (5 и 3)
- Идеальная несоосность означает, что они больны на 100% (5 и -3)
- Частичное выравнивание или неправильное выравнивание означает, что они помогают или вредят в процентах
- Отсутствие выравнивания означает, что они игнорируют друг друга
Как измерить выравнивание? С косинусом.
Используя нашу аналогию с триггером, косинус равен процентам угла, который движется вдоль земли.
Угол 0 градусов точно следует за землей (100%), а вертикальное движение вообще не следует за ней (0%). Другие углы являются частью промежуточного значения.
Если части нашей системы можно записать в виде путей, и мы знаем, что угол между ними равен тета ($\theta$), то мы можем измерить перекрытие с помощью косинуса. Один путь действует как земля, а другой — это путь, по которому мы идем:
Когда пути идеально выровнены, используется их полная сила ($ab$ и $ba$). Фактор взаимодействия $\cos(\theta)$ изменяет эту силу, чтобы показать, что они на самом деле работают вместе.
Итак, наша мешанина взаимодействий становится:
Фу! И это закон косинусов: собирайте каждое взаимодействие, учитывайте выравнивание и упрощайте его до одной части. (Формула обычно записывается без квадратного корня, но обычно нужно $c$, а не $c^2$.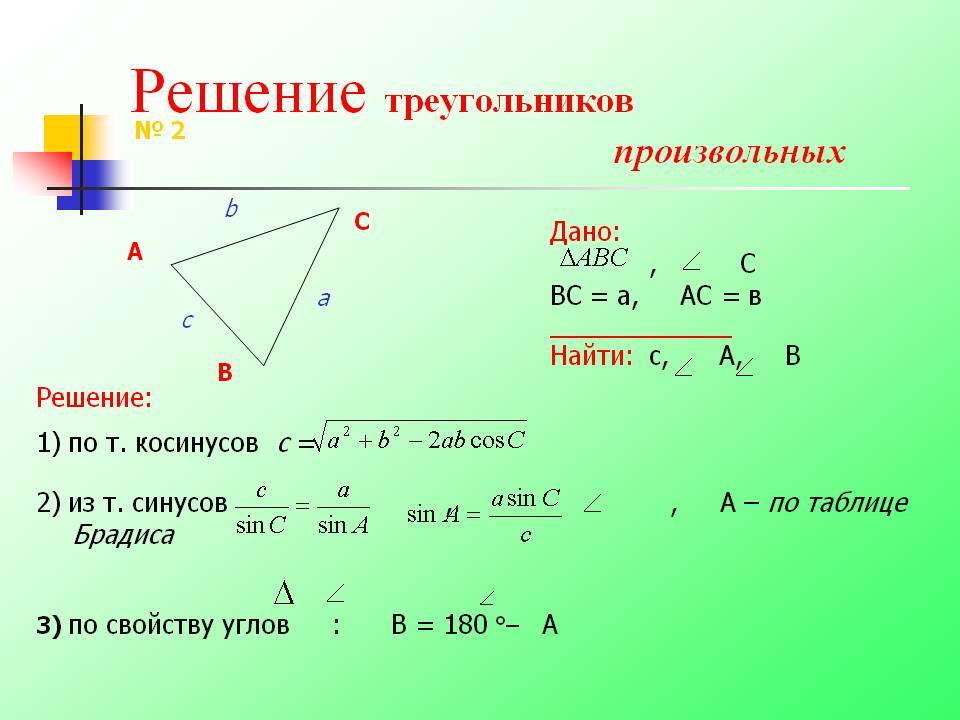
Почему закон косинусов часто пишется с отрицательным знаком? Итак, предполагается, что в типичном треугольнике маленький внутренний угол $C$ означает, что стороны выровнены отрицательно, а тета ($\theta$) — это внешний взгляд на их выравнивание:
Аналогично , большой внутренний угол означает, что стороны выровнены положительно и будут помогать друг другу. Как правило, небольшой угол означает, что вы движетесь в одном и том же направлении, но эта внутренняя/внешняя разница означает, что мы меняем знак.
Лично я не запоминаю, положительный или отрицательный знак: я думаю о том, будут ли части помогать или вредить друг другу в сценарии, и делать взаимодействие положительным или отрицательным. Не будьте рабом формулы.
Быстрая практическая задача
Допустим, у моего треугольника сторона $a = 10$, а сторона $b = 20$. Чему равна сторона $c$, если угол между $a$ и $b$ равен:
45 градусов на линии
Здесь нам нужен закон косинусов. $a$ и $b$ указывают частично в одном направлении. Переходим в режим взаимодействия, чтобы добраться до общего, комбинируемого юнита (площади): 92 = 400$
$a$ и $b$ указывают частично в одном направлении. Переходим в режим взаимодействия, чтобы добраться до общего, комбинируемого юнита (площади): 92 = 400$
Суммарные взаимодействия:
и эквивалент одной стороны (с):
70 градусов смещения
Опять же, нам нужен закон косинусов. Мы видим, что углы дерутся друг с другом, поэтому взаимодействие будет отрицательным:
Наша интуиция подсказывает, что это расположение должно быть на меньше на , чем предыдущее (поскольку стороны не работают вместе), и это так.
Полное совмещение или несоосность
Когда наш «треугольник» имеет угол 0 градусов (или 180), все части лежат ровно. Здесь части одного размера и могут рассматриваться как обычные числа:
- Полностью выровнены: 10 + 20 = 30
- Полностью смещено: 10 – 20 = -10 (указывает в направлении B).
 92 – 2ab\cos(\theta) = 100 + 400 + 400\cos(180) = 100$, что означает $c = \sqrt{100} = 10$ (указывая назад).
92 – 2ab\cos(\theta) = 100 + 400 + 400\cos(180) = 100$, что означает $c = \sqrt{100} = 10$ (указывая назад).
Опять же, мы не должны роботизированно следовать формуле: иметь примерное представление о том, что должно получиться в результате, и продумывать расчеты. («Общее взаимодействие таково, поэтому индивидуальная сторона будет такой…»).
Размышление о взаимодействиях — это одна из интерпретаций: в следующий раз мы будем рассматривать это как закон проекций.
Счастливая математика.
Приложение: Теорема Пифагора
Закон косинусов напоминает теорему Пифагора, не так ли?
Теперь вы можете догадаться почему. Теорема Пифагора — это частный случай нулевого взаимодействия , которое происходит, когда стороны находятся под прямым углом. В конце концов, угол 90 градусов является вертикальным и имеет 0% перекрытия с землей.
Закон косинусов принимает вид:
Если мы знаем, что части не будут взаимодействовать, мы можем игнорировать эффекты взаимодействия.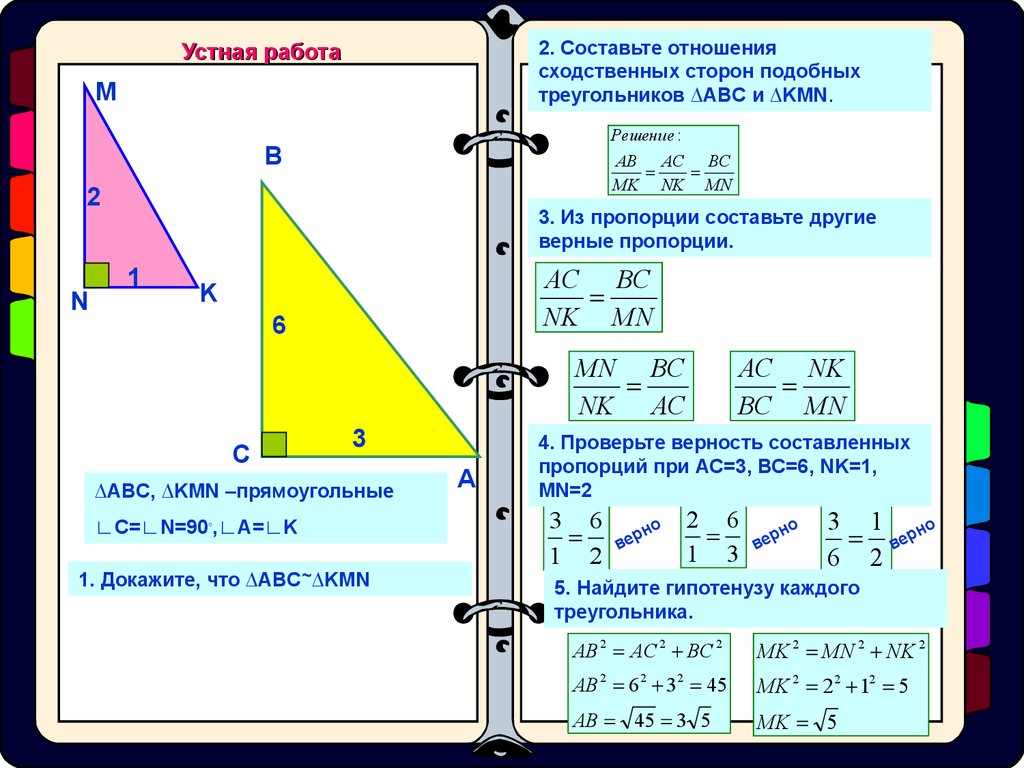

 92 – 2ab\cos(\theta) = 100 + 400 + 400\cos(180) = 100$, что означает $c = \sqrt{100} = 10$ (указывая назад).
92 – 2ab\cos(\theta) = 100 + 400 + 400\cos(180) = 100$, что означает $c = \sqrt{100} = 10$ (указывая назад).