Формулы синуса и косинуса суммы и разности аргументов — урок. Алгебра, 10 класс.
Перед тем как начать подробное ознакомление с формулами преобразования тригонометрических выражений, поясним, для чего вообще нужны преобразования тригонометрических выражений.
Дело в том, что очень часто тригонометрические выражения даже самого «устрашающего» вида после несложных преобразований довольно легко приводятся к выражениям с табличным значением аргумента — таким, например, как: 30°(π6),45°(π4),60°(π3)… или к таким выражениям, решение которых найти гораздо проще, чем решение исходного тригонометрического выражения.
В этом и заключается основная цель преобразования тригонометрических выражений — привести заданное выражение к такому виду, чтобы найти его решение было проще.
Формул преобразования тригонометрических выражений несколько. Основными и наиболее важными считаются формулы синуса и косинуса суммы аргументов, так как из них легко выводятся остальные формулы тригонометрии.
Доказательство самих формул синуса и косинуса суммы аргументов технически довольно сложно, и оно не входит в базовый курс обучения.
Примечание. Для краткости и упрощения в дальнейшем исключим слово «аргументов» из названий формул — это общепринятая практика — и, говоря о формулах синуса или косинуса суммы (разности), будем понимать, что это формулы синуса или косинуса суммы (разности) аргументов этих функций.
Формула синуса суммы: sin(x+y)=sinx⋅cosy+cosx⋅siny. (1)
Формула косинуса суммы: cos(x+y)=cosx⋅cosy−sinx⋅siny. (2)
Рассмотрим теперь выражение sin(x−y) в таком виде: sin(x+(−y)) — и воспользуемся формулой синуса суммы (1): sin(x+(−y))=sinx⋅cos(−y)+cosx⋅sin(−y).
Теперь вспомним о свойстве чётности функции косинус: cos(−y)=cosy —
и свойстве нечётности функции синус: sin(−y)=−siny.
Тогда:
sin(x+(−y))=sinx⋅cos(−y)+cosx⋅sin(−y)=sinx⋅cosy−cosx⋅siny.
Формула синуса разности: sin(x−y)=sinx⋅cosy−cosx⋅siny. (3)
Аналогично, представив cos(x−y) в виде cos(x+(−y)), воспользуемся формулой косинуса суммы (2),и свойствами чётности функции косинус cos(−y)=cosy,
и нечётности функции синус sin(−y)=−siny.
Тогда получим:
cos(x+(−y))=cosx⋅cos(−y)−sinx⋅sin(−y)=cosx⋅cosy+sinx⋅siny.
Формула косинуса разности: cos(x−y)=cosx⋅cosy+sinx⋅siny. (4)
Формулы тригонометрии
Взаимосвязь основных тригонометрических функций, каких как косинус и синус, тангенс и котангенс — называется формулы тригонометрии. Из-за того что взаимосвязей очень большое количество, соответственно и формул не меньше. Часть формул объединяет тригонометрические функции в зависимости от угла, который может быть либо кратным, либо одинаковым. Так же может выражаться от тангенса половинного угла. Так же через понижение степени.
Так же может выражаться от тангенса половинного угла. Так же через понижение степени.
Мы разберем самые основные из тригонометрических формул. С помощью которых можно решить большинство тригонометрических заданий. Для большего удобства объединим их по значению, по таблицам.
Начнем с тригонометрических тождеств.
Основы в тригонометрических тождествах определяют взаимосвязь косинуса и синуса, тангенса и котангенса в одном угле. И выходят из их определения и единичной окружности. Дают возможность выделить через любую функцию другую.
Далее рассмотрим тригонометрические формулы приведения.
Они вытекают из свойств синусов, косинусов, котангенсов и тангенсов. Тем самым выражают такие свойства функции как: периодичность, симметричность и сдвиг к рассматриваемому углу. так же дают возможность работать с углами в радиусе до 90 градусов и произвольные углы.
Формулы на сложение.
Из данных формул видно что функции на сумму или разность от 2 углов выводятся из их же тригонометрических функций.
 Так же являются основой для формул двойных, тройных и других углов.
Так же являются основой для формул двойных, тройных и других углов.Формула для двойных, тройных и других углов.
Из них видно что тригонометрическая функция двойного, тройного или какого то ни было угла выводится из т.ф. одинарных углов. Так же как и одинарные, двойные, тройные и т.д. существуют и половинные углы
Из формул половинного угла видно, что он выходит из косинуса угла целого.
Так же существуют методы понижения степени выглядят они как:
С помощью их использования возможно понизить функцию до первой степени. Взаимодействуя с натуральными степенями функций переводить до синусов и косинусов только кратных углов, в первую степень.
Сумма и разность в тригонометрической функции.
Помогают упростить тригонометрическое выражение, и разложить на множители синусы и косинусы.
Произведение синуса, косинуса, и одно на другое.

Метод универсальной тригонометрической подстановки.
Такая подстановка удобна тем, что функции получаются без корней.
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
Основное Тригонометрическое Тождество — Доказательство
Связь между sin и cos одного угла
Вы уже наверняка знаете, что тождественный — это равный.
Основные тригонометрические тождества — это равенства, которые устанавливают связь между синусом, косинусом, тангенсом и котангенсом одного угла. Это значит, что любую из этих функций можно найти, если известна другая функция.
Ключ к сердцу тригонометрии — основное тригонометрическое тождество. Запомните и полюбите его, чтобы отношения с тригонометрией сложились самым наилучшим образом:
Из основного тождества вытекают равенства тангенса и котангенса, поэтому оно — ключевое.
Равенство tg2α + 1 = 1/cos2α и равенство 1 + сtg2α + 1 = 1/sin2α выводят из основного тождества, разделив обе части на sin2α и cos2α.
В результате деления получаем:
Поэтому основному тригонометрическому тождеству уделяется максимум внимания. Но какая же «метрия» может обойтись без доказательств. Видите тождество — доказывайте, не раздумывая.
sin2α + cos2α = 1Сумма квадратов синуса и косинуса одного угла тождественно равна единице.
Чтобы доказать тождество, обратимся к теме единичной окружности.
Единичная окружность — это окружность с центром в начале прямоугольной декартовой системы координат. Радиус единичной окружности равен единице.
Докажем тождество sin2α + cos2α = 1
- Итак, нам известны координаты точки A (1; 0).

- Если развернуть точку A на угол α, то точка A становится на место точки A1.
- По определениям:
- Синус угла (sin α) — это отношение противолежащего катета к гипотенузе.
- Косинус угла (cos α) — это отношение прилежащего катета к гипотенузе.
- Опускаем перпендикулярную прямую A1B на x0 из точки A1.
Образовался прямоугольный треугольник OA1B.
|A1B| = |у|
|OB| = |x|.
- Гипотенуза OA1 имеет значение, равное радиусу единичной окружности.
|OA1| = 1.
- Применяя полученное выражение, записываем равенство по теореме Пифагора, поскольку получившийся угол — прямой:
|A1B| 2 + |OB|2 = |OA1|2.
- Записываем в виде: |y|2 + |x|2 = 12.

Это значит, что y2 + x2 = 1.
sin угла α = y
cos угла α = x - Вставляем данные угла вместо координат точек:
OB = cos α
A1B = sin α
A1O = 1 - Получаем основное тригонометрическое тождество: sin2α + cos2α = 1.
Что и требовалось доказать.
Основное тригонометрическое тождество связывает синус угла и косинус угла. Зная одно, вы легко можете найти другое. Нужно лишь извлечь квадратный корень по формулам:
- sin α = ±
- cos α = ±
Как видите, перед корнем может стоять и минус, и плюс. Основное тригонометрическое тождество не дает понять, положительным или отрицательным был исходный синус/косинус угла.
Как правило, в задачках с подобными формулами уже есть условия, которые помогают определиться со знаком. Обычно такое условие — указание на координатную четверть. Таким образом без труда можно определить, какой знак нам требуется.
Чтобы ребенок еще лучше учился в школе, запишите его на уроки математики в Skysmart. Наши преподаватели понятно объяснят что угодно — от дробей до синусов — и ответят на вопросы, которые бывает неловко задать перед всем классом.
Вместо скучных параграфов ребенка ждут интерактивные упражнения с мгновенной автоматической проверкой и онлайн-доска, где можно рисовать и чертить вместе с преподавателем.
Тангенс и котангенс через синус и косинус
Немного вводных:
- Синус угла — это ордината y.
- Косинус угла — это абсцисса x.
- Тангенс угла — это отношение ординаты к абсциссе.
- Котангенс угла — это отношение абсциссы к ординате.
Из всего этого множества красивых, но не сильно понятных слов, можно сделать вывод о зависимости одного от другого. Такая связь помогает отдельно преобразовывать нужные величины.
- tg α =
- ctg α =
Исходя из определений:
Это позволяет сделать вывод, что тригонометрические тождества
задаются sin и cos углов.
Отсюда следует, что тангенс угла — это отношение синуса угла к косинусу. А котангенс угла — это отношение косинуса к синусу.
Отдельно стоит обратить внимание на то, что тригонометрические тождества
верны для всех углов α, значения которых вписываются в диапазон.
- Например, выражение применимо для любого угла α, не равного + π + z, где z — это любое целое число. В противном случае, в знаменателе будет стоять 0.
Выражение
применимо для любого угла α, не равного π * z, где z — это любое целое число.
Связь между тангенсом и котангенсом
Уж насколько очевидной кажется связь между ранее рассмотренными тождествами, настолько еще более наглядна связь между тангенсом и котангенсом одного угла.
- Тождество записывается в следующем виде:
tg α * ctg α = 1.
Такое тождество применимо и справедливо при любых углах α, значение которых не равняются π/2 * z, где z — это любое целое число.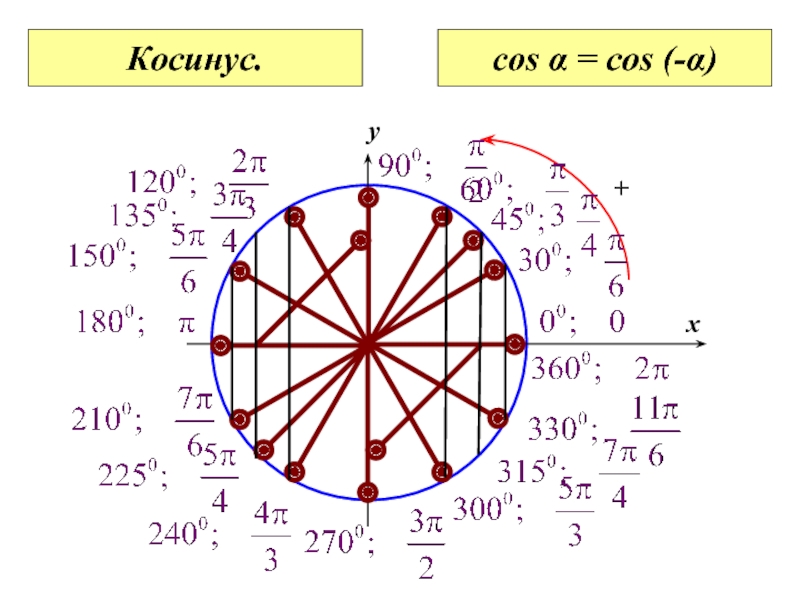 В противном случае, функции не будут определены.
В противном случае, функции не будут определены.
Как и любое другое, данное тригонометрическое тождество подлежит доказательству. Доказывать его очень просто.
tg α * ctg α = 1.
- По определению:
tg α = y/x
ctg α = x/y
- Отсюда следует, что tg α * ctg α = y/x * x/y = 1
- Преобразовываем выражение, подставляем и ,
получаем:
Получается, что тангенс и котангенс одного угла, при котором они имеют смысл — это взаимно обратные числа.
Если числа a и b взаимно обратные — это значит, что число a — это число, обратное числу b, а число b — это число, обратное числу a. Кроме того, это значит, что числу a обратно число b, а числу b обратно число a. Короче, и так, и эдак.
Какие, какие числа?🤯
Взаимно обратные числа — это два числа, произведение которых равно 1.
Если в голове вашего ребенка бурлит тригонометрическая каша, и все формулы смешались в один нераспутываемый клубок — записывайтесь на бесплатный вводный урок математики в онлайн-школу Skysmart.
Наши преподаватели помогут навести в голове порядок и разложить все знания по полочкам. На уроках вас ждут интересные задачки и располагающая атмосфера, в которой совсем не страшно задавать вопросы и получать от занятий — максимум.
Тангенс и косинус, котангенс и синус
Все тождества выше позволяют сделать вывод, что тангенс угла связан с косинусом угла, а котангенс угла — с синусом.
Эта связь становится очевидна, если взглянуть на тождества:
- tg2α + 1 =
Сумма квадрата тангенса угла и единицы равна числу, обратному квадрату косинуса этого угла.
- 1 + ctg2α =
Сумма единицы и квадрата котангенса угла равна числу, обратному квадрату синуса этого угла.
Вывести оба этих тождества можно из основного тригонометрического тождества:
sin2α + cos2α = 1.
- Для этого нужно поделить обе части тождества на cos2α, где косинус не равен нулю.

- В результате деления получаем формулу tg2α + 1 =
- Если обе части основного тригонометрического тождества sin2α + cos2α = 1 разделить на sin2α, где синус не равен нулю, то получим тождество:
1 + ctg2α = . - Отсюда можно сделать вывод, что тригонометрическое тождество tg2α + 1 = применимо для любого угла α, не равного + π + z, где z — это любое целое число.
- А тригонометрическое тождество 1 + ctg2α = применимо для любого угла, не равного π * z, где z — это любое целое число.
Хорошо бы выучить все формулы и запомнить формулировки тождеств наизусть. Чтобы это сделать, сохраняйте себе табличку с основными формулами.
Основные тригонометрические тождества
1 | sin2α + cos2α = 1 |
2 | |
3 | |
4 | tgα * ctgα = 1 |
5 | tg2α + 1 = |
6 | 1 + ctg2α = |
Чтобы тратить еще меньше времени на решение задач, сохраняйте таблицу значений тригонометрических функции углов, которые чаще всего встречаются в задачах.
Примеры решения задач
Разберем пару задачек, для решения которых нужно знать основные тождества. Рассмотрите внимательно предложенные решения и потренируйтесь самостоятельно.
Задачка 1. Найдите cos α, tg α, ctg α при условии, что sin α = 12/13.
Как решаем:
- Чтобы решить задачу, необходимы следующие тригонометрические тождества:
- Выражаем cos α из тригонометрической единицы:
- Далее подставляем значения sin α:
- Вычисляем:
- Нам известны значения sin α и cos α, поэтому можно легко найти тангенс, используя формулу:
- Таким же образом, используя формулу, вычисляем значение котангенса:
Ответ:
Задачка 2. Найдите значение cos α,
если:
Как решаем:
- Чтобы решить задачу, необходимы следующие тригонометрические тождества:
- Выражаем cos α из тригонометрической единицы:
- Далее подставляем значения sin α:
- Вычисляем:
- То же самое проделываем со вторым значение sin α
Подставляем значения sin α:
- Вычисляем:
Ответ:
Как видите, задачи решаются достаточно просто, нужно лишь верно применять формулы основных тождеств.
Алгебра любит практику — как можно больше практики. Чтобы натренироваться в решении задачек и накачать математический бицепс, записывайте вашего ребенка на бесплатный вводный урок математики в онлайн-школу Skysmart.
У нас есть все для эффективных и веселых занятий: опытные преподаватели, интересные задачки, интерактивный формат и внушительная порция вдохновения и поддержки!
Формулы приведения [Love Soft]
Формулы приведения — сокращенное название формул, которые позволяют привести синусы и косинусы к соответствующим значениям синусов и косинусов острых углов (т.е. от 0 до 90 градусов).
Формулы приведения косинуса
Формулы приведения синуса
Формулы приведения тригонометрических функций
Мнемоническое правило
Подготовительный шаг: аргумент исходной функции представляется в виде
$\pm \alpha + 2\pi z$ или $\pi/2 \pm \alpha + 2\pi z$ или $\pi \pm \alpha + 2\pi z$ или $3\pi/2 \pm \alpha + 2\pi z$,
причем угол должен быть от 0 до 90 градусов (острый). Это замечание про угол альфа очень важно, так как для других углов мнемоническое правило может приводить к неверным результатам.
Это замечание про угол альфа очень важно, так как для других углов мнемоническое правило может приводить к неверным результатам.
При приведении функции от аргумента вида kp/2 ± α, где k – целое число, к функции от аргумента α:
Дальше определяется знак, который имеет исходная функция. Функция в правой части записываемой формулы приведения будет иметь такой же знак как и приводимая функция.
название функции сохраняется для 1-го и 3-го случая (нечетный квадрант), и меняется на «дополнительное» (кофункцию), для 2-го и 4-го случая (четный квадрант) [синус на косинус, косинус на синус, тангенс на котангенс, котангенс на тангенс]
Например, при приведении ctg (α – p/2) убеждаемся, что α – p/2 при 0 < α < p/2 лежит в четвертом квадранте, где котангенс отрицателен, и, по второму правилу, меняем название функции: ctg (α – p/2) = –tg α.
Задача
Используя мнемоническое правило, приведите $\sin 777^\circ$ к тригонометрическим функциям острого угла. \circ$.
\circ$.
Правило лошади
Если мы откладываем угол от вертикальной оси, лошадь говорит «да» (киваем головой вдоль оси OY) и приводимая функция меняет своё название: синус на косинус, косинус на синус, тангенс на котангенс, котангенс на тангенс.
Если мы откладываем угол от горизонтальной оси, лошадь говорит «нет» (киваем головой вдоль оси OХ) и приводимая функция не меняет название.
Знак правой части равенства совпадает со знаком приводимой функции, стоящей в левой части равенства.
Пример
sin(120) = sin(90+30) = [лошадь говорит да] = cos(30) = $\frac {\sqrt 3} 2 $
или
sin(120) = sin(180-60) = [лошадь говорит нет] = sin(60) = $\frac {\sqrt 3} 2 $
Новоселов — таблица
Формулы приведения в особом доказательстве не нуждаются.
Формулы первой строки выражают свойства четности и нечетности тригонометрических функций, прочие же формулы вытекают из теорем сложения для косинуса и синуса.
В последнем столбце дано геометрическое пояснение формул приведения для острого угла α (равные треугольники заштрихованы).
Формулы четвёртой и восьмой строк легко вывести также и геометрически. Если к углу α прибавить π, т. е. половину полного оборота, то подвижной радиус займёт диаметрально противоположное положение. Абсцисса х и ордината у конца подвижного радиуса, т. е. косинус и синус угла, изменят знаки (не изменяя абсолютной величины) на противоположные, а их отношения не изменятся.
Формулы приведения показывают, что в практических вычислениях достаточно знать значения тригонометрических функций лишь острых углов (и даже не больших 45°).
Обоснование:
Пример. Вычислить cos(-1000°)
mat/trig/sin-cos-privedenie.txt · Последние изменения: 2020/09/23 22:28 — kc
Тригонометрические формулы
1.
 Зависимости между функциями одного аргумента:
Зависимости между функциями одного аргумента:2. Значения тригонометрических функций:
| α° | 0 | 30 | 45 | 60 | 90 | 180 | 270 | 360 |
|---|---|---|---|---|---|---|---|---|
| sin(α) | 0 | 12 | 22 | 32 | 1 | 0 | -1 | 0 |
| cos(α) | 1 | 32 | 22 | 12 | 0 | -1 | 0 | 1 |
| tg(α) | 0 | 13 | 1 | 3 | − | 0 | − | 0 |
| ctg(α) | − | 3 | 1 | 13 | 0 | − | 0 | − |
3.
 Четность или нечетность:
Четность или нечетность:4. Знаки в четвертях:
| Триг. функция | Четверть | |||
|---|---|---|---|---|
| I | II | III | IV | |
| sin(α) | + | + | − | − |
| cos(α) | + | − | − | + |
| tg(α) | + | − | + | − |
| ctg(α) | + | − | + | − |
5.
 Формулы приведения:
Формулы приведения:| β = | 90 ± α | 180 ± α | 270 ± α | 360 ± α |
|---|---|---|---|---|
| sin(β) | cos(α) | ∓sin(α) | −cos(α) | ±sin(α) |
| cos(β) | ∓sin(α) | −cos(α) | ±sin(α) | cos(α) |
| tg(β) | ∓ctg(α) | ±tg(α) | ∓ctg(α) | ±tg(α) |
| ctg(β) | ∓tg(α) | ±ctg(α) | ∓tg(α) | ∓ctg(α) |
6.
 Решение тригонометрических уравнений:
Решение тригонометрических уравнений:sin(x) = a ⇔ x = (-1)n arcsin(a) + n π, n = 0, 1 … ∈ Z
cos(x) = a ⇔ x = ± arccos(a) + 2 n π, n = 0, 1 … ∈ Z
tg(x) = a ⇔ x = arctg(a) + n π, n = 0, 1 … ∈ Z
7. Формулы суммы и разности:
sinαβsinαcosβcosαsinβ sinαβsinαcosβcosαsinβ cosαβcosαcosβsinαsinβ cosαβcosαcosβsinαsinβ8. Формулы двойного угла:
9. Формулы тройного угла:
10. Формулы преобразования суммы и разности:
а) Преобразование суммы и разности одинаковых триг. функций с разными углами:
Преобразования для синуса:
sinαsinβ2sinαβ2cosαβ2 sinαsinβ2sinαβ2cosαβ2Преобразования для косинуса:
cosαcosβ2cosαβ2cosαβ2 cosαcosβ2sinαβ2sinαβ2Преобразования для тангенса:
tgαtgβsinαβcosαcosβ tgαtgβsinαβcosαcosβПреобразования для котангенса:
ctgαctgβsinβαsinαsinβ ctgαctgβsinβαsinαsinβб) Преобразование суммы и разности разных триг.
 функций с разными углами: sinαcosβ2sinαβ2π4cosαβ2π4
sinαcosβ2sinαβ2π4cosαβ2π4
функций с разными углами: sinαcosβ2sinαβ2π4cosαβ2π4
sinαcosβ2sinαβ2π4cosαβ2π4в) Специфические формулы:
AsinαBcosαA2B2sinαarctgBA sinαsin2α…sinnαsin12n1αsinnα2sinα2 cosαcos2α…cosnαcos12n1αsinnα2sinα211. Формулы преобразования произведения:
sinαsinβcosαβcosαβ2 sinαcosβsinαβsinαβ2 cosαcosβcosαβcosαβ212. Формулы понижения степени:
13. Выражение тригонометрических функций через тангенс половинного угла:
ttgα2sinα1cosα1cosαsinα1cosα1cosα
Тригонометрические и геометрические преобразования, sin(A + B), sin(A
Коэффициенты для суммы углов
Как демонстрируют различные примеры, иногда нам нужны значения углов, отличных от 0, 30, 45, 60 и 90 градусов. В этой главе вы должны научиться двум вещам:
В этой главе вы должны научиться двум вещам:
1. sin(A + B) не является равным sinA + sinB. В этом случае не срабатывает простое раскрытие скобок, как в алгебре.
2. Формулу, по которой вычисляется sin(A + B).
Во-первых, покажем, что раскрытие скобок не «срабатывает». Пусть A = 30 градусов и B = 45 градусов. Sin30 равен 0.5. Sin45 равен 0.7071. Складывая, получим 1.2071.
Вы знаете, что ни синус, ни косинус не может быть больше 1. Почему? Потому что в дробях, по которым они вычисляются, гипотенуза выступает в качестве знаменателя. Самое большее значение мы получим, если числитель равен знаменателю. Синус или косинус не может быть больше 1, и поэтому значение 1,2071 не верно.
Нахождение синуса, косинуса или тангенса полного угла (A + B)
Нахождение sin(A + B)
Самый простой способ найти sin (A + B) — используя геометрическое построение, показанное на рисунке. Большой угол (A + B), состоит из двух маленьких, А и В. Рисунок (1) показывает, что противоположная сторона состоит из двух частей. Нижняя часть, разделенная линией между углами (2), есть синус А. Линия между двумя углами, разделенная гипотенузой (3), есть косинус B. Умножаем их. Средняя линия и в числителе, и в
знаменателе, поэтому они сокращаются, оставляя нижнюю часть противоположной стороны над гипотенузой (4).
Нижняя часть, разделенная линией между углами (2), есть синус А. Линия между двумя углами, разделенная гипотенузой (3), есть косинус B. Умножаем их. Средняя линия и в числителе, и в
знаменателе, поэтому они сокращаются, оставляя нижнюю часть противоположной стороны над гипотенузой (4).
Обратите внимание на маленький прямоугольный треугольник (5). Затененный угол есть A, потому что линия на его верхней части параллельна линии в основании. Подобные прямоугольные треугольники с углом А показывают, что верхний угол, отмеченный А также равен оригинальному углу А. Верхняя часть противоположной (6) над длинной, заштрихованный треугольник является соs А. Противоположный над основной гипотенузой (7) есть синус. Поскольку стороны с пометкой «противоположные» (7) и в числителе и знаменателе, когда cos и sin перемножаются, cosAsinB есть верхняя часть оригинального противоположного — для (A + B) — разделенные основной гипотенузой (8).
Теперь, сложим это все вместе (9). Sin(A + B) есть две части противоположного — все разделенные гипотенузой (9). Записывая это в тригонометрическую форму: sin(A + B) = sin A cos B + cos A sin B.
Записывая это в тригонометрическую форму: sin(A + B) = sin A cos B + cos A sin B.
Нахождение cos(A + B)
Очень похожая конструкция находит формулу для косинуса угла созданного двумя углами, сложенными вместе.
Используя ту же самую конструкцию (1), обратите внимание, что смежная сторона является полной линией основания (для соs A), c частью, которая вычитается справа. Каждая часть должна использовать тот же знаменатель, гипотенузу (A + B) треугольника.
Полная линия основания, разделенная линией между углами A и E есть cosA (2). Эта разделяющая линия, деленная гипотенузой (A + B) треугольника, есть cos B (3). Поэтому, полная линия основания, деленная гипотенузой есть произведение cosAcosB (4).
Теперь, небольшая часть, которая должна быть вычтена. Заштрихованная часть (5) представляет sinA, который умножается заштрихованной частью (6) есть sin E, который есть другой частью и , которая нам нужна (7). Вычитание дает соs (А + В) (8), поэтому формула, которая нам нужна:
cos(A + B) = cos A cos B — sin A sin B
Нахождение tan(A + B)
Полный геометрический вывод формулы для tg (A + B) является сложным. Проще всего вывести его из двух формул, которые мы уже сделали. В любом угле, тангенс равен синус, деленному на косинус. Используя тот факт, tan (A + B) = sin(A + B)/соs(A + B). Это выражение можно расширить к виду:
Проще всего вывести его из двух формул, которые мы уже сделали. В любом угле, тангенс равен синус, деленному на косинус. Используя тот факт, tan (A + B) = sin(A + B)/соs(A + B). Это выражение можно расширить к виду:
tan(A + B) = [sin A cos B + cos A sin B]/[cos A cos B — sin A sin B]
Разделив верхнюю и нижнюю часть на cos A cos B, что превращает все члены в тангенсы, получаем:
tan(A + B) = [tan A + tan B]/[1 — tan A tan B]
Коэффициенты для 75 градусов
Покажем коэффициенты синуса, косинуса и тангенса, подставляя в формулу суммы, и потом упрощая результат к своей простейшей форме, прежде чем находить суммы. После внесения основных замен в каждом конкретном случае, примерная работа в заштрихованной части, чтобы показать, как результат сводится к простейшей форме для оценки.
Если вы используете ваш карманный калькулятор для оценки, скорей всего, не имеет значения или вы упрщаете выражения сначала или просто пропускаете его! Все зависит от калькулятора: некоторые вычисля. т разницу, некоторые нет!
т разницу, некоторые нет!
Коэффициенты углов, больших, чем 90 градусов
До сих пор рассматривалось соотношение острых углов (между 0 и 90 градусами). Другие треугольники с тупым углом (более 90 градусов) и до 180 градусов могут появиться в последующих задачах. Для упрощения классификации углов по размеру, они делятся на сектора (квадранты).
Квадрант есть четвертой частью круга. Так как круг делится на 360 градусов, квадранты имеют по 90 градусов. 0-90 градусов это первый квадрант, 90-180 — второй, 180-270 — третий и 270-360 — четвертый.
Используя линии, обозначающие границы квадранта, 0 или 360 это горизонталь направо, 90 — вертикально вверх, 180 — горизонталь слева и 270 сверху вниз. Теперь, используем этот метод для построения графиков.
Большие углы определяется вектором вращения, начиная с нуля и вращением против часовой стрелки. Горизонтальные элементы х: положительные справа, отрицательные слева. Вертикальные элементы у: положительные вверх, отрицательные вниз. Вращающийся вектор является р. Таким образом, синус угла есть y/r, косинус х/r, и тангенс у/х. Вектор r — всегда положителен. Таким образом, знак отношения может быть вычислен для различных секторов.
Вращающийся вектор является р. Таким образом, синус угла есть y/r, косинус х/r, и тангенс у/х. Вектор r — всегда положителен. Таким образом, знак отношения может быть вычислен для различных секторов.
Здесь приведены знаки для трех отношений в четырех квадрантах.
Кроме того, как эквивалентный угол в первой четверти «переключается» когда вектор переходит из одного квадранта в другой. В первой четверти, стороны определены в соотношениях для синуса, косинуса и тангенса. При перемещении к большим углам в остальных секторах, противоположная сторона всегда есть вертикальная (у). То, что называется смежное, всегда есть горизонталью (х). Гипотенуза это всегда вращающийся вектор (r). Вы можете видеть картину как изменяются тригонометрические соотношения для углов.
Отношения в четырех квадрантах
Отношения для различных углов
Теперь у вас есть два пути получить формулы для различных углов. Во-первых, используя геометрическую конструкцию, такую, которая, например, была использована для суммы углов, реверсивную так, что (A — B) есть угол B вычитающийся из угла A.
В рассуждениях, аналогичных тем, которые были использованы для суммы углов, здесь представлены несколько сокращенные формулы для синуса и косинуса:
sin(A — B) = sin A cos B — cos A sin B
and
cos(A — B) = cos A cos B + sin A sin B
Геометрическая конструкция
Формулы суммы и разницы
Второй способ нахождения формулы для разницы углов использует уже полученную формулу суммы, но делает B отрицательным. Из нашего исследования знаков для различных секторов, отрицательные углы с 1-го квадранта будут в 4 квадранте. Проводя эту подстановку, получим тот же результат, который был получен геометрически в предыдущем разделе.
Поиск формулы тангенса проходит тем же методом, или заменой синуса и косинуса в формулах или более непосредственно, превращая tg(-B) = — tg B. В любом случае вы получите:
tan(A — B) = [tan A — tan B]/[1 + tan A tan B]
Отношения с помощью четырех секторов
Вы можете вывести несколько отношений с формулами суммы и разности. Вы уже сделали соотношение для 75 градусов. Теперь можно выполнить то же для 15 градусов. Эти формулы дают соотношения для углов в 15 градусов интервалы через четыре квадранта. Построив их на 360 градусов, вы можете увидеть, как эти три соотношения изменяются, когда вектор проходит через четыре квадранта.
Вы уже сделали соотношение для 75 градусов. Теперь можно выполнить то же для 15 градусов. Эти формулы дают соотношения для углов в 15 градусов интервалы через четыре квадранта. Построив их на 360 градусов, вы можете увидеть, как эти три соотношения изменяются, когда вектор проходит через четыре квадранта.
«Волна» синуса и косинуса колеблется вверх и вниз между +1 и -1. Обратите внимание, что «волны» смещены на 90 градусов друг относительно друга. Этот факт станет важным позже.
Кривая тангенса начинается, как синусоида, но вскоре она стремится достичь бесконечности на 90 градусах. Двигаясь » вне видимости» в положительном направлении, она «приходит» с отрицательного направления с другой стороны на 90 градусах. Проходя через точку в 180 градусов, функция тангенса повторяет то, что она «делала» проходя 0 или 360 градусов. На 270 градусах она повторяет то же, было на 90 градусах.
Пифагор в тригонометрии
Формула часто может быть упрощена, так как были найдены выводы формулы тангенса от формул синуса и косинуса, а также изменение ее членов одного отношения к другому отношению, использeущеuj другие члены. При этом, теорема Пифагора, выраженная в тригонометрическом соотношении, очень удобна.
При этом, теорема Пифагора, выраженная в тригонометрическом соотношении, очень удобна.
Предположим, что прямоугольный треугольник имеет гипотенузу длиной 1. Тогда одна из сторон будет иметь длину sinA, а другая — cosA. Отсюда, согласно теореме Пифагора: cos2 A + sin2 A = 1. Это выражение всегда истинно для любого значения A.
Немного о том, как это было записано. Cos2 A означает (cos A)2. Если вы написали это как cos A2, уравнение будет означать что-то другое. A есть число в нескольких угловых значениях, которое представляет угол. A2 было бы то же самое число, возведенное в квадрат. Его значение зависело бы от использованного числового значения, поэтому это не очень хороший член для использования. Это означает квадрат синуса ли косинуса, не сам угол. Формула Пифагора может быть выражена иначе. Например, две другие формы:
cos2 A = 1 — sin2 A, и sin2 = 1 — cos2 A.
Умножение углов
Формулы сумм, вместе с теоремой Пифагора, используются для углов, которые в 2, 3 или больше раз кратны любым оригинальным углам. Здесь приводятся формулы для 2А и 3А.
Формула суммы работает, когда оба угла одинаковые или различны: sin(A + B) или sin(A + A). Однако, sin(A + A) в действительности sin 2A. Поэтому, sin 2A есть sin A cos A + cos A sin A. Оба члена выражения есть одним и тем же произведением, записанным в разном порядке, так что это выражение может быть упрощено до sin 2A = 2 sin A cos A.
Подобным образом, cos 2A = cos A cos A — sin A sin A, что также может быть записано как: cos 2A = cos2 A — sin2 A. Используя теорему Пифагора, изменяем это к виду: cos 2A = 2cos2 A — 1. Наконец, tg 2A = 2 tg A/[1 — tg2 A].
Теперь тройной угол (3А) используется, чтобы показать, как получены следующие кратные углы. В основном, это так же просто, как запись 3A = 2 + A и повторного применения формулы суммы. Но тогда, чтобы получить в результате формулу в работающем виде, необходимо заменить часть 2А, на выражения с простым углом А.
Но тогда, чтобы получить в результате формулу в работающем виде, необходимо заменить часть 2А, на выражения с простым углом А.
На рисунках внизу вы можете видеть, что с каждым разом вычисления становятся сложнее.
УМНОЖЕНИЕ УГЛОВ Производные от формул суммы
УМНОЖЕНИЕ УГЛОВ Соотношения для 3A
Свойства равнобедренного треугольника
Вы уже видели, что прямоугольный треугольник является полезным строительным блоком для других фигур. Равнобедренный треугольник имеет несколько различных видов использования. Дело в том, что его использование основывается на том, что равнобедренный треугольник имеет две равные стороны и два равные углы между основанием и боковыми равными сторонами. Перпендикуляр из третьего угла на третью сторону делит ее пополам. Таким образом весь треугольник делится на два равных прямоугольных треугольника.
Любой треугольник, за исключением прямоугольного треугольника, можно разделить на три прилегающих равнобедренных треугольника, разделив каждую сторону на две равные части и построить перпендикуляры из точек разделения. Там, где любые два из этих перпендикуляров встречаются, если линии тянутся к углам исходного треугольника, три линии должны быть равны, потому что две из них образуют стороны равностороннего треугольника. Таким образом, перпендикуляр с третьей стороны исходного треугольника должен также встретиться в одной точке.
Там, где любые два из этих перпендикуляров встречаются, если линии тянутся к углам исходного треугольника, три линии должны быть равны, потому что две из них образуют стороны равностороннего треугольника. Таким образом, перпендикуляр с третьей стороны исходного треугольника должен также встретиться в одной точке.
Это утверждение справедливо, как мы покажем здесь, независимо от того, является ли исходный треугольник острым или тупым. Разница с тупым прямоугольным треугольником в том, что место встречи перпендикуляров лежит снаружи исходного треугольника, а не внутри.
Что происходит в прямоугольном треугольнике? Перпендикуляры от средней точки гипотенузы другой стороны будут делить пополам эти две стороны — вы получаете два из трех! Место встречи находится гипотенузе.
Углы в окружности
Основное свойство окружности это то, что ее центр находится на одинаковом расстоянии от любой точки окружности. Это расстояние есть радиусом окружности.
Если вы нарисуете любой треугольник внутри круга, перпендикуляры из средней точки его сторон встретятся в центре окружности а радиусы из углов треугольника делят его на три равнобедренных треугольника
Теперь, если вы назовете равные пары углов в каждом равнобедренном треугольнике A, A, B, B, C, C, вы обнаружите, что исходный треугольник имеет один угол A+B, один угол B+C, и один угол A+ C. Три угла в сумме дают 2A + 2B + 2С, а это как известно равно 180 градусов.
Три угла в сумме дают 2A + 2B + 2С, а это как известно равно 180 градусов.
В любом равнобедренном треугольнике угол при вершине равен 180 градусов минус удвоенный угол при основании. Поэтому, согласно предыдущего пункта, 180 — 2A должен быть такой же, как и 2B + 2С, например.
Рассмотрим угол правый нижний угол, опирающийся на окружность. Угол в центре равен 2B + 2С. Углом, опирающийся на окружность равен B + C. Вы видите, что для любого сегмента круга, угол в центре всегда в два раза больше угла, опирающегося на окружность.
Утверждение выше приводит к интересным фактам об углах в окружностях. Вместо определения углов со стороной треугольника, используют дугу (часть окружности) круга. Часть окружности, которая определяется углом в центре называется хордой окружности.
Угол в центре в два раза больше чем угол на окружности
Любой угол, касающийся окружности, используя хорду как ограничение угла, равен половине угла в центре. Таким образом, все углы в круге, с основанием на той же хорде, должны быть равны. Предположим, что хорда имеет угол 120 градусов. Угол на окружности будет равен 60 градусам.
Предположим, что хорда имеет угол 120 градусов. Угол на окружности будет равен 60 градусам.
Особый случай представляет собой полукруг (точный полукруг). Угол в центре представляет собой прямую линию (180 градусов). Каждый угол в полукруге равен 90 градусам (прямой угол). Любой треугольник в полукруге является прямоугольным треугольником.
Определения
Выше мы часто использовали углы, которые дополняют углы до прямого угла (90 градусов) или до двух прямых углов (180 градусов). Когда два угла образовывают угол 180 градусов (два прямых угла), они называются дополнительными. Если два угла добавить до 90 градусов (один прямой угол), их называют комплементарными
Вопросы и задачи
1. Синус угла А равен 0,8 и синус угла B равен 0.6. Из различных зависимостей, полученных до сих пор, найдите следующее: тангенс А, тангенс B, синус (A + B), косинус (A + B), синус (A — B), косинус (A — B), тангенс (А + B) и тангенс (A — B) без использования таблиц или тригонометрических клавиш калькулятора.
2.На экваторе Земля имеет радиус 4000 км. Углы вокруг экватора измеряется в меридианах долготы, с линией с севера на юг проходящей через Гринвич (Англия), в качестве нулевого отсчета. Два места используются для наблюдения за луной: первое это Кения, на экваторе 37,5 к востоку от Гринвича, а другой является Суматра, на экваторе к востоку 100,5. Как далеко друг от друга эти два места, если расстояние измерять мнимой прямой, проходящей через Землю?
3.Если бы наблюдения были сделаны горизонтально от точки наблюдения в вопросе 2 (к востоку от первой, к западу от второй), под каким углом была бы линия пересечения наблюдений?
4.В определенное время, точно синхронизированное в обоих местах, наблюдается спутник. В Кении, высота линии визирования с центром на спутнике составляет 58 градусов выше горизонтали на восток. На Суматре, высота составляет 58 градусов выше горизонтали на запад. Как далеко находится спутник? Используйте расстояние между точками рассчитанное в вопросе 2.
5. Косинус определенного угла в два раза больше синуса того же угла. Чему равен тангенс этого угла? Не используйте таблицы или калькулятор для ответа на этот вопрос.
6. Синус определенного угла равен именно 0.28. Найдите косинус и тангенс этого угла. Не используйте таблицы или калькулятор для ответа на этот вопрос.
7. Синус определенного угла равен 0.6. Найдите синус углов, больших чем заданный в два и три раза.
8. Найдите синус и косинус угла, большего ровно в два раза чем угол из вопроса 7.
9. Используя 15 градусов, как единичный угол, и формулы для отношения 2А и 3А найдите значения синусов 30 и 45 градусов.
10. Используя 30 градусов, как единичный угол, найти значения синусов 60 и 90 градусов.
11. Используя 45 градусов, как единичный угол, найдите значения тангенсов 60 и 90 градусов.
12. Используя 60 градусов, как единичный угол, найдите значения косинусов 120 и 180 градусов.
13. Используя 90 градусов, как единичный угол, найдите значения косинусов 180 и 270 градусов.
14. Используя формулы тангенса для умножения углов и таблицы, найдите тангенсы утроенных углов в 29, 31, 59 и 61 градусов. Посчитайте изменения знака между утроенным углом 29 и 31 градусов и между 59 и 61 градусов.
15. Синус угла составляет 0,96. Найдите синус и косинус удвоенного угла.
16. Задача сводится к алгебраической выражению вида 8cos2 A + cos A = 3. Решите для косинуса А, и укажите, в каком квадранте будет угол, представляющий каждое решение придет. Приведите приближенные значения из таблицы или используя калькулятор.
Тригонометрические формулы
Тригонометрические формулы и их вывод. Мы знаем, что их много и что их нужно учить, что эту информацию очень сложно запомнить и её периодически требуется повторять. Так, верно! Ниже представлен вывод этих формул, думаю, пригодится. Если запомнить принципы вывода, то когда будет необходимо — вы всегда «вспомните» нужную формулу. В любом случае информация будет полезна — кому-то проще выучить, кому-то вывести.
Сначала сами формулы, это ещё не все, будет продолжение.
Основное тригонометрическое тождество, его запомнить нетрудно – формула «красивая»:
Откуда взялась? Посмотрите, здесь всё подробно описано.
Из неё следуют:
*Простые алгебраические преобразования.
Так же из неё получаем две другие необходимые формулы путём деления на квадрат синуса и квадрат косинуса:
Формулы тангенса и котангенса. Их проще выучить:
Что дальше? Разберём некоторые группы формул! Рассмотрим эскиз:
Теорема! Косинус разности двух углов равен произведению косинусов этих углов сложенному с произведением синусов:
Доказательство:
Рассмотрим единичную окружность с углами α и β, которые образованы векторами
И положительным направлением оси ох. Угол между векторами равен:
Выразим скалярное произведение векторов по формуле:
Следовательно
Так как векторы имеют длину равную единице, а именно:
Теперь вычислим это же скалярное произведение по формуле:
Так как
Мы получили, что
Следовательно
Что и требовалось доказать!
Косинус суммы >>
Сумму α + β представляем как разность α–(–β) и подставляем a формулу для косинуса разности:
Так функция косинуса чётная а функция синуса нечётная
Значит
Синус суммы >>
Воспользуемся одной из формул приведения:
Теперь по формуле косинуса разности (1):
Получили
Синус разности >>
*Функция косинуса чётная, функция синуса нечётная
Следовательно
Получили группу формул:
Тангенс суммы >>
Используя формулу тангенса делим формулу (3) на (2):
Далее разделим числитель и знаменатель на cosα∙cosβ, получим:
Получили
Тангенс разности >>
Используя формулу тангенса делим формулу (4) на (1):
Также разделим числитель и знаменатель на cosα∙cosβ, получим:
Получили
Котангенс суммы >>
Используя формулу котангенса делим формулу (2) на (3):
Далее разделим числитель и знаменатель на sinα∙sinβ, получим:
Получили
Котангенс разности >>
Используя формулу котангенса делим формулу (1) на (4):
Далее разделим числитель и знаменатель на sinα∙sinβ, получим:
Получили
Пожалуйста, ещё группа:
Синус двойного угла >>
Используем формулу (3) — синуса суммы:
Косинус двойного угла >>
Используем формулу (2) — косинуса суммы:
Если из основного тригонометрического тождества выразим:
И подставим в (10), то получим:
Если выразим:
И подставим в (10), то получим:
Тангенс двойного угла >>
Используем формулу (5):
Котангенс двойного угла >>
Используем формулу (7):
Можем выделить группу формул:
Преобразование произведения тригонометрических функций в сумму и разность.
Возьмём формулы синуса суммы и синуса разности:
Сложим их почленно, то есть правую и левую части:
Возьмём формулы косинуса суммы и косинуса разности:
Сложим их почленно, то есть правую и левую части:
Теперь из cos (α–β) вычтем cos (α+β):
Получим:
Вот и ещё одна группа формул готова:
К этой статье будет дополнение-продолжение, разобрали ещё не всё, не пропустите! Успеха вам!
Скачать материал в формате PDF
С уважением, Александр Крутицких
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Функции синуса и косинуса
Синус и косинус: свойства Синусоидальная функция имеет ряд свойств, которые
результат из периодических и нечетных .
Функция косинуса имеет ряд свойств, которые
в результате периодических и даже .
Читателю не следует запоминать большинство следующих уравнений; еще,
читатель должен иметь возможность мгновенно получить их
от понимания характеристик функции.
Функции синуса и косинуса периодические с периодом 2р. Это означает, что
sin (q) = sin (q + 2p)
cos (q) = cos (q + 2p)
или, в более общем смысле,sin (q) = sin (q + 2pk)
cos (q) = cos (q + 2pk),
где k Î целые числа. Функция синуса — , нечетное ; следовательно,
sin (-q) = -sin (q)
Функция косинуса равна даже ; следовательно,
cos (-q) = cos (q)
Формула:
sin (x + y) = sin (x) cos (y) + cos (x) sin (y)
Тогда легко выводится из , чтоsin (x — y) = sin (x) cos (y) — cos (x) sin (y)
Или, в более общем смысле,sin (x y) = sin (x) cos (y) cos (x) sin (y)
cos (x + y) = cos (x) cos (y) — sin (x) sin (y)
Тогда легко вывести , чтоcos (x — y) = cos (x) cos (y) + sin (x) sin (y)
Или, в более общем смысле,cos (x y) = cos (x) cos (y) (- / +) sin (x) sin (y)
Из приведенного выше синусоидального уравнения мы можем вывести, что
sin (2x) = 2sin (x) cos (x)
Из приведенного выше уравнения косинуса мы можем вывести, чтоcos (2x) = cos 2 (x) — sin 2 (x)
(Обозначение sin 2 (x) эквивалентно (sin (x)) 2 . Предупреждение: sin -1 (x) означает arcsin (x), а не мультипликативный обратный
греха (х).)
Предупреждение: sin -1 (x) означает arcsin (x), а не мультипликативный обратный
греха (х).) Наблюдая за графиками синуса и косинуса, мы можем выразить
функция синуса через косинус и наоборот:
sin (x) = cos (90 ° — x)
и функция косинуса через синус:cos (x) = sin (90 ° — x)
Такая триггерная функция (f), обладающая свойствомf (q) = g (дополнение (q))
называется кофункцией функции g, отсюда и названия «синус» и « co синус».» Пифагорейская идентичность,
sin 2 (x) + cos 2 (x) = 1,
дает альтернативное выражение
для синуса через косинус и наоборот
sin 2 (x) = 1 — cos 2 (x)
cos 2 (x) = 1 — sin 2 (x)
Закон синусов связывает различные стороны и углы произвольного (не обязательно прямого) треугольника:
sin (A) / a = sin (B) / b = sin (C) / c = 2r.
где A, B и C — углы, противоположные сторонам a, b и c соответственно. Кроме того, r — радиус
круг, описанный в этом треугольнике.
Кроме того, r — радиус
круг, описанный в этом треугольнике.Закон косинусов связывает все три стороны и один из углов. произвольного (не обязательно прямого) треугольника:
c 2 = a 2 + b 2 — 2ab cos (C).
где A, B и C — углы, противоположные сторонам a, b и c соответственно. Его можно рассматривать как обобщенную форму теоремы Пифагора. Предупреждение : будьте осторожны при решении для одной из сторон, примыкающих к интересующему углу, поскольку часто будет два треугольника, удовлетворяющих данным условиям. Это можно понять из геометрии. Треугольник, определяемый SAS (сторона-угол-сторона) уникален, поэтому любой треугольник с ему должны соответствовать те же параметры SAS. Определенный треугольник by SSA, однако, не всегда уникален, и два треугольника с одни и те же параметры SSA могут совпадать, а могут и не совпадать.тригонометрических идентичностей | Безграничная алгебра
Закон синуса
По закону синусов можно найти неизвестные углы и стороны в любом треугольнике.
Цели обучения
Используйте закон синусов для решения задач с треугольниками любой конфигурации, а также для преобразования тригонометрических выражений
Основные выводы
Ключевые моменты
- Закон синусов используется для определения размеров всех трех углов и всех трех сторон треугольника.
- Закон синусов гласит, что следующие пропорции равны: [латекс] \ displaystyle {\ frac {\ sin \ alpha} {a} = \ frac {\ sin \ beta} {b} = \ frac {\ sin \ gamma } {c}} [/ latex], где [latex] \ alpha, \ beta, [/ latex] и [latex] \ gamma [/ latex] — углы, а [latex] a [/ latex], [latex] b [/ latex] и [latex] c [/ latex] — длины противоположных сторон, соответственно.{\ circ} [/ latex] угол, а любой другой треугольник — наклонный. Решить наклонный треугольник означает найти измерения всех трех углов и всех трех сторон.
Закон синусов гласит, что:
[латекс] \ displaystyle {\ frac {\ sin \ alpha} {a} = \ frac {\ sin \ beta} {b} = \ frac {\ sin \ gamma} {c}} [/ latex]
где [latex] \ alpha, \ beta, [/ latex] и [latex] \ gamma [/ latex] — углы, а [latex] a [/ latex], [latex] b [/ latex] и [latex] c [/ latex] — длины противоположных им сторон соответственно.

Наклонный треугольник: Стороны этого наклонного треугольника обозначены буквами a, b и c, а соответствующие им углы обозначены [latex] \ alpha [/ latex], [latex] \ beta [/ latex] и [латекс] \ гамма [/ латекс].
Обратите внимание на стандартный способ маркировки треугольников: угол [латекс] \ альфа [/ латекс] (альфа) — это противоположная сторона [латекс] а [/ латекс]; угол [латекс] \ бета [/ латекс] (бета) противоположная сторона [латекс] b [/ латекс]; и угол [латекс] \ гамма [/ латекс] (гамма) является противоположной стороной [латекс] c [/ латекс].
Чтобы решить наклонный треугольник, используйте любую пару применимых соотношений из формулы закона синусов. При расчете углов и сторон обязательно доведите точные значения до окончательного ответа.
Пример
Решите треугольник, показанный на рисунке, округляя окончательные ответы до ближайшей десятой.
Наклонный треугольник с неизвестными сторонами и углами: В этом треугольнике [латекс] \ альфа = 50 \ градус [/ латекс], [латекс] \ гамма = 30 \ градус [/ латекс] и [латекс] a = 10 [/латекс].
 {\ circ} \ quad \ quad \ quad c \ приблизительно 6.5 [/ латекс]
{\ circ} \ quad \ quad \ quad c \ приблизительно 6.5 [/ латекс]Закон косинусов
Закон косинусов можно использовать для определения углов и сторон треугольника в случаях, когда другие законы не применяются.
Цели обучения
Используйте закон косинусов для решения задач с треугольниками любой конфигурации, а также для преобразования тригонометрических выражений
Основные выводы
Ключевые моменты
- Закон косинусов можно использовать для определения углов и сторон треугольника в тех случаях, когда закон синусов не может быть применен, например, для треугольников с неизвестными углами.2 [/ latex], где [latex] c [/ latex] — это гипотенуза, а [latex] a [/ latex] и [latex] b [/ latex] — длины двух других сторон.
Использование закона косинусов
В некоторых случаях у нас может не быть достаточно информации, чтобы применить закон синусов, чтобы найти неизвестные углы и стороны в треугольнике.
 Например, рассмотрим треугольник, у которого известны все три стороны, но неизвестны значения углов. В таких случаях недостаточно информации для использования закона синуса. Закон косинусов полезен для: 1) вычисления третьей стороны треугольника, когда известны две стороны и их внутренний угол, и 2) вычисления углов треугольника, если известны только три стороны.
Например, рассмотрим треугольник, у которого известны все три стороны, но неизвестны значения углов. В таких случаях недостаточно информации для использования закона синуса. Закон косинусов полезен для: 1) вычисления третьей стороны треугольника, когда известны две стороны и их внутренний угол, и 2) вычисления углов треугольника, если известны только три стороны.Закон косинусов определяет соотношение между измерениями углов и длинами сторон наклонных треугольников. Три формулы составляют Закон косинусов. На первый взгляд формулы могут показаться сложными, потому что они включают много переменных. Однако, как только схема будет понята, с законом косинусов легче работать, чем со многими формулами на этом математическом уровне.
Закон косинусов гласит, что квадрат любой стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение двух других сторон и косинус включенного угла.2 — 2ab \ cos \ gamma \ end {align} [/ latex]
Наклонный треугольник (без прямого угла): Наклонный треугольник с углами [латекс] \ альфа [/ латекс], [латекс] \ бета [/ латекс] и [латекс] \ гамма [/ латекс] и наоборот.
 соответствующие стороны [латекс] a [/ латекс], [латекс] b [/ латекс] и [латекс] c [/ латекс].
соответствующие стороны [латекс] a [/ латекс], [латекс] b [/ латекс] и [латекс] c [/ латекс].Для определения размера отсутствующей стороны требуется соответствующая величина противоположного угла. При решении для угла нужны длины всех сторон. Обратите внимание, что каждую формулу закона косинусов можно переставить, чтобы найти угол.2 & = 244 — 120 \ sqrt {3} \\ b & = \ sqrt {244 — 120 \ sqrt {3}} \\ b & \ приблизительно 6.0 \ end {align}} [/ latex]
Обратите внимание, что теперь у нас достаточно информации, чтобы мы могли использовать закон синусов для определения неизвестных углов [латекс] \ альфа [/ латекс] и [латекс] \ гамма [/ латекс] в треугольнике.
Пифагорейские тождества
Тождества Пифагора полезны для упрощения выражений с помощью тригонометрических функций.
Цели обучения
Соедините тригонометрические функции с теоремой Пифагора, чтобы вывести тождества Пифагора.
Основные выводы
Ключевые моменты
- Тождества Пифагора выводятся из теоремы Пифагора и описывают взаимосвязь между синусом и косинусом на единичной окружности.
 2 [/ латекс]
2 [/ латекс]Для треугольника, нарисованного внутри единичного круга, длина гипотенузы треугольника равна радиусу круга, который равен [латекс] 1 [/ латекс]. Длины сторон треугольника составляют [латекс] x [/ латекс] и [латекс] y [/ латекс].
Тождество Пифагора на единичной окружности: Для треугольника, нарисованного внутри единичной окружности, длина гипотенузы равна радиусу окружности. Стороны треугольника имеют длины [латекс] x [/ латекс] и [латекс] y [/ латекс].2 т = 1 [/ латекс]
, что верно для любого действительного числа [латекс] т [/ латекс].
Мы можем использовать тождество Пифагора, чтобы найти косинус угла, если мы знаем синус, или наоборот. Однако, поскольку уравнение дает два решения, нам необходимо дополнительное знание угла, чтобы выбрать решение с правильным знаком. Если мы знаем, в каком квадранте находится угол, мы можем легко выбрать правильное решение.
Дополнительные тождества могут быть получены из тождества Пифагора [латекс] \ cos ^ 2 t + \ sin ^ 2 t = 1 [/ latex].
 2 т [/ латекс] упрощается до [латекс] 5 [/ латекс].
2 т [/ латекс] упрощается до [латекс] 5 [/ латекс].Формулы сложения и вычитания углов
Тригонометрические выражения можно упростить, используя специальные углы и набор формул для сложения и вычитания углов.
Цели обучения
Упростите тригонометрические выражения с помощью формул сложения и вычитания углов.
Основные выводы
Ключевые моменты
- Формулы для сложения и вычитания углов в тригонометрических выражениях позволяют нам найти синус, косинус или тангенс
данного угла, если мы можем разбить его
на сумму или разность двух специальных углов. - Формулы для косинуса: [латекс] \ cos (\ alpha + \ beta) = \ cos \ alpha \ cos \ beta — \ sin \ alpha \ sin \ beta [/ latex] и [latex] \ cos (\ alpha — \ beta) = \ cos \ alpha \ cos \ beta + \ sin \ alpha \ sin \ beta [/ latex].
- Формулы для синуса: [latex] \ sin (\ alpha + \ beta) = \ sin \ alpha \ cos \ beta + \ cos \ alpha \ sin \ beta [/ latex] и [latex] \ sin (\ alpha — \ beta) = \ sin \ alpha \ cos \ beta — \ cos \ alpha \ sin \ beta [/ latex].

- Формулы касательной: [латекс] \ displaystyle {\ tan (\ alpha + \ beta) = \ frac {\ tan \ alpha + \ tan \ beta} {1 — \ tan \ alpha \ tan \ beta}} [ / latex] и [latex] \ displaystyle {\ tan (\ alpha — \ beta) = \ frac {\ tan \ alpha — \ tan \ beta} {1 + \ tan \ alpha \ tan \ beta}} [/ latex] .2} [/ латекс].
Получение формул сложения и вычитания углов
Часто бывает проще найти точное значение синуса, косинуса или тангенса угла, если мы можем переписать данный угол в терминах двух углов, для которых известны тригонометрические значения. Мы можем использовать специальные углы, которые мы можем просмотреть в единичном круге, показанном ниже.
Единичная окружность: Единичная окружность со значениями синуса и косинуса, отображаемыми для специальных углов.
Существуют формулы для сложения и вычитания углов в каждой из тригонометрических функций.Они позволяют нам найти тригонометрическую функцию данного угла, если мы можем разбить ее на сумму или разность двух особых углов.

Чтобы увидеть, как выводятся эти формулы, мы можем разместить точки на диаграмме единичного круга. Предположим, что угол, для которого мы хотим найти тригонометрическую функцию, — это угол, образованный точкой [латекс] A [/ латекс], которая измеряет угол [латекс] \ альфа — \ бета [/ латекс]. Угол, образованный [латексом] A [/ латексом] и точкой [латекс] B [/ латексом] на положительной оси [латекса] x [/ латекса], такой же, как угол, образованный между двумя особыми углами, которые обозначается [латекс] P [/ латекс] и [латекс] Q [/ латекс].Точка [latex] P [/ latex] находится под углом [latex] \ alpha [/ latex] к положительной оси [latex] x [/ latex] – с координатами [latex] (\ cos \ alpha, \ sin \ alpha) [/ latex], а точка [latex] Q [/ latex] находится под углом [latex] \ beta [/ latex] от положительной оси [latex] x [/ latex] – с координатами [ латекс] (\ соз \ бета, \ грех \ бета) [/ латекс]. Углы равны, поэтому расстояние между точками [латекс] P [/ латекс] и [латекс] Q [/ латекс] такое же, как и между точками [латекс] A [/ латекс] и [латекс] B [/ латекс ].
 2} [/ латекс]
2} [/ латекс]можно вывести ряд соотношений между углами. Мы можем вывести следующие шесть формул.
Формулы для косинуса:
[латекс] \ begin {align} \ cos (\ alpha + \ beta) & = \ cos \ alpha \ cos \ beta — \ sin \ alpha \ sin \ beta \\ \ cos (\ alpha — \ beta) & = \ cos \ alpha \ cos \ beta + \ sin \ alpha \ sin \ beta \ end {align} [/ latex]
Формулы для синуса:
[латекс] \ begin {align} \ sin (\ alpha + \ beta) & = \ sin \ alpha \ cos \ beta + \ cos \ alpha \ sin \ beta \\ \ sin (\ alpha — \ beta) & = \ sin \ alpha \ cos \ beta — \ cos \ alpha \ sin \ beta \ end {align} [/ latex]
Формулы тангенса:
[латекс] \ displaystyle {\ begin {align} \ tan (\ alpha + \ beta) & = \ frac {\ tan \ alpha + \ tan \ beta} {1 — \ tan \ alpha \ tan \ beta} \\ \ tan (\ alpha — \ beta) & = \ frac {\ tan \ alpha — \ tan \ beta} {1 + \ tan \ alpha \ tan \ beta} \ end {align}} [/ latex]
[latex] [/ latex] Они полезны для поиска углов, которые могут быть получены путем сложения или вычитания специальных углов.
 {\ circ} [/ латекс]. Можно найти тригонометрические функции любого такого угла.
{\ circ} [/ латекс]. Можно найти тригонометрические функции любого такого угла.Пример
Используя формулу косинуса разности двух углов, найдите точное значение [latex] \ displaystyle {\ cos {\ left (\ frac {5 \ pi} {4} — \ frac {\ pi} {6 } \ right)}} [/ латекс].
Примените формулу [латекс] \ cos (\ alpha — \ beta) = \ cos \ alpha \ cos \ beta + \ sin \ alpha \ sin \ beta [/ latex]:
[латекс] \ displaystyle {\ cos {\ left (\ frac {5 \ pi} {4} — \ frac {\ pi} {6} \ right)} = \ cos {\ left (\ frac {5 \ pi } {4} \ right)} \ cos {\ left (\ frac {\ pi} {6} \ right)} + \ sin {\ left (\ frac {5 \ pi} {4} \ right)} \ sin {\ left (\ frac {\ pi} {6} \ right)}} [/ латекс]
Подставьте значения тригонометрических функций из единичной окружности:
[латекс] \ displaystyle {\ cos {\ left (\ frac {5 \ pi} {4} — \ frac {\ pi} {6} \ right)} = \ left (- \ frac {\ sqrt {2} } {2} \ right) \ left (\ frac {\ sqrt {3}} {2} \ right) + \ left (- \ frac {\ sqrt {2}} {2} \ right) \ left (\ frac {1} {2} \ right)} [/ латекс]
Упростить:
[латекс] \ displaystyle {\ begin {align} \ cos {\ left (\ frac {5 \ pi} {4} — \ frac {\ pi} {6} \ right)} & = — \ frac {\ sqrt {6}} {4} — \ frac {\ sqrt {2}} {4} \\ \ cos {\ left (\ frac {5 \ pi} {4} — \ frac {\ pi} {6} \ right )} & = — \ frac {\ sqrt {6} — \ sqrt {2}} {4} \ end {align}} [/ latex]
Пример
Найдите точное значение [латекс] \ sin (15 ^ {\ circ}) [/ latex].
 {\ circ} \ right)} = \ frac {\ sqrt {6} — \ sqrt {2}} {4}} [/ латекс]
{\ circ} \ right)} = \ frac {\ sqrt {6} — \ sqrt {2}} {4}} [/ латекс]Формулы двойных и половинных углов
Тригонометрические выражения можно упростить, применив формулы двойного и половинного угла.
Цели обучения
Упростите тригонометрические выражения с помощью формул двойного и половинного угла
Основные выводы
Ключевые моменты
- Формулы двойного угла являются частным случаем формул суммы, где [latex] \ alpha = \ beta [/ latex].Они полезны, когда мы хотим найти тригонометрическую функцию угла, который вдвое больше специального угла.
- Формулы половинного угла также являются частным случаем и полезны, когда мы хотим найти тригонометрическую функцию угла [latex] \ theta [/ latex], который составляет половину особого угла [latex] \ alpha [/ latex ] (Другими словами, [латекс] \ displaystyle {\ theta = \ frac {\ alpha} {2}} [/ latex]).
- Хотя каждая формула полуугла имеет знак [латекс] \ pm [/ латекс], знак, который применяется в каждом случае, зависит от квадранта, в который попадает угол, и правил применения знаков к тригонометрическим функциям.

Формулы двойного угла
В предыдущей концепции мы использовали формулы сложения и вычитания для тригонометрических функций. Теперь мы еще раз посмотрим на те же формулы. Формулы двойного угла являются частным случаем формул суммы, где [latex] \ alpha = \ beta [/ latex]. Другими словами, они позволяют нам найти тригонометрическую функцию угла, который вдвое больше специального угла. В таких случаях можно выводить формулы для нахождения синуса, косинуса и тангенса, и эти формулы полезны для упрощения тригонометрических выражений.
Вывод формулы двойного угла для синуса начинается с формулы суммы, которая была введена ранее: [latex] \ sin (\ alpha + \ beta) = \ sin \ alpha \ cos \ beta + \ cos \ alpha \ sin \ beta [ /латекс].
Если мы допустим [latex] \ alpha = \ beta = \ theta [/ latex], то имеем:
[латекс] \ Displaystyle {\ begin {align} \ sin (\ theta + \ theta) & = \ sin \ theta \ cos \ theta + \ cos \ theta \ sin \ theta \\ \ sin (2 \ theta) & = 2 \ sin \ theta \ cos \ theta \ end {align}} [/ latex]
Формула двойного угла для косинуса может быть получена аналогично:
[латекс] \ cos (2 \ theta) = \ cos ^ 2 \ theta — \ sin ^ 2 \ theta [/ latex]
Обратите внимание, что мы можем применить тождества Пифагора, чтобы получить еще два варианта формулы косинуса:
[латекс] \ displaystyle {\ begin {align} \ cos {\ left (2 \ theta \ right)} & = \ cos ^ 2 \ theta — \ sin ^ 2 \ theta \\ & = \ left (1- \ sin ^ 2 \ theta \ right) — \ sin ^ 2 \ theta \\ & = 1-2 \ sin ^ 2 \ theta \ end {align}} [/ latex]
[латекс] \ Displaystyle {\ begin {align} \ cos {\ left (2 \ theta \ right)} & = \ cos ^ 2 \ theta — \ sin ^ 2 \ theta \\ & = \ cos ^ 2 \ theta — \ left (1- \ cos ^ 2 \ theta \ right) \\ & = 2 \ cos ^ 2 \ theta -1 \ end {align}} [/ latex]
Аналогичным образом, чтобы вывести формулу двойного угла для касательной, замена [latex] \ alpha = \ beta = \ theta [/ latex] в формуле суммы дает
[латекс] \ displaystyle {\ begin {align} \ tan {\ left (\ alpha + \ beta \ right)} & = \ frac {\ tan \ alpha + \ tan \ beta} {1 — \ tan \ alpha \ tan \ beta} \\ \ tan {\ left (\ theta + \ theta \ right)} & = \ frac {\ tan \ theta + \ tan \ theta} {1 — \ tan \ theta \ tan \ theta} \\ \ tan {\ left (2 \ theta \ right)} & = \ frac {2 \ tan \ theta} {1 — \ tan ^ 2 \ theta} \ end {align}} [/ latex]
Формулы двойного угла резюмируются следующим образом:
- [латекс] \ sin {\ left (2 \ theta \ right)} = 2 \ sin \ theta \ cos \ theta [/ latex]
- [латекс] \ cos {\ left (2 \ theta \ right)} = \ cos ^ 2 \ theta — \ sin ^ 2 \ theta [/ latex]
- [латекс] \ cos {\ left (2 \ theta \ right)} = 1-2 \ sin ^ 2 \ theta [/ latex]
- [латекс] \ cos {\ left (2 \ theta \ right)} = 2 \ cos ^ 2 \ theta -1 [/ latex]
- [латекс] \ displaystyle {\ tan {\ left (2 \ theta \ right)} = \ frac {2 \ tan \ theta} {1 — \ tan ^ 2 \ theta}} [/ латекс]
Пример
Найдите [латекс] \ sin (60 ^ {\ circ}) [/ latex] с помощью функции [latex] \ sin (30 ^ {\ circ}) [/ latex].
 {\ circ} \ right)} & = 2 \ left (\ frac {\ sqrt {3}} {4} \ right) \\ & = \ frac {\ sqrt {3}} {2} \ end {align} } [/ latex]
{\ circ} \ right)} & = 2 \ left (\ frac {\ sqrt {3}} {4} \ right) \\ & = \ frac {\ sqrt {3}} {2} \ end {align} } [/ latex]Формулы полуугловых
Формулы полуугла
могут быть получены из формул двойного угла. Они полезны для нахождения тригонометрической функции угла [латекс] \ theta [/ latex], который составляет половину особого угла [латекс] \ альфа [/ латекс] (другими словами, [латекс] \ displaystyle {\ theta = \ frac {\ alpha} {2}} [/ latex]). Формулы половинного угла следующие:- [латекс] \ displaystyle {\ sin {\ left (\ frac {\ alpha} {2} \ right)} = \ pm \ sqrt {\ frac {1- \ cos \ alpha} {2}}} [/ латекс]
- [латекс] \ displaystyle {\ cos {\ left (\ frac {\ alpha} {2} \ right)} = \ pm \ sqrt {\ frac {1+ \ cos \ alpha} {2}}} [/ latex ]
- [латекс] \ displaystyle {\ tan {\ left (\ frac {\ alpha} {2} \ right)} = \ pm \ sqrt {\ frac {1 — \ cos \ alpha} {1 + \ cos \ alpha} }} [/ latex]
- [латекс] \ displaystyle {\ tan {\ left (\ frac {\ alpha} {2} \ right)} = \ frac {\ sin \ alpha} {1 + \ cos \ alpha}} [/ latex]
- [латекс] \ displaystyle {\ tan {\ left (\ frac {\ alpha} {2} \ right)} = \ frac {1 — \ cos \ alpha} {\ sin \ alpha}} [/ latex]
Хотя некоторые формулы имеют знак [латекс] \ pm [/ latex], применяется только один знак.
 {\ circ}) [/ latex], следовательно, положительный.
{\ circ}) [/ latex], следовательно, положительный.Тождества тригонометрической симметрии
Тождества тригонометрической симметрии основаны на принципах четных и нечетных функций, которые можно наблюдать на их графиках.
Цели обучения
Объясните тождества тригонометрической симметрии, используя графики тригонометрических функций
Основные выводы
Ключевые моменты
- Тригонометрические функции бывают четными или нечетными, что означает, что они симметричны относительно оси [latex] y [/ latex] или начала координат соответственно.
- Четные тригонометрические функции — это косинус и секанс, а нечетные тригонометрические функции — это синус, косеканс, тангенс и котангенс.
- Определения четных и нечетных функций можно использовать для получения тождеств симметрии, соответствующих каждой из шести тригонометрических функций.
- Тождества симметрии могут использоваться для нахождения тригонометрических функций отрицательных значений.

Ключевые термины
- нечетная функция : Непрерывный набор точек [latex] \ left (x, f (x) \ right) [/ latex], для которых [latex] f (-x) = -f (x) [/ latex ], и есть симметрия относительно начала координат.
- четная функция : Непрерывный набор точек [latex] \ left (x, f (x) \ right) [/ latex], для которых [latex] f (-x) = f (x) [/ latex], и есть симметрия относительно оси [латекс] y [/ латекс].
Симметрия в тригонометрических функциях
Мы уже обсуждали четные и нечетные функции. Напомним, что четные функции симметричны относительно оси [latex] y [/ latex], а нечетные функции симметричны относительно начала координат, [latex] (0, 0) [/ latex]. Напомним, что косинус является четной функцией, потому что он симметричен относительно оси [latex] y [/ latex].С другой стороны, синус и тангенс являются нечетными функциями, потому что они симметричны относительно начала координат.
Теперь мы рассмотрим каждую из тригонометрических функций и их совместные функции (секанс, косеканс и котангенс) и заметим симметрию на их графиках.
 Эта симметрия используется для получения определенных идентичностей.
Эта симметрия используется для получения определенных идентичностей.Симметрия вокруг оси [latex] y [/ latex]: косинус и секанс являются четными функциями с симметрией относительно оси [latex] y [/ latex].
Функции косинуса и секанса симметричны относительно оси y.Графики, симметричные относительно оси [latex] y [/ latex], представляют четные функции. Для четных функций любые две точки с противоположными значениями [latex] x [/ latex] имеют одинаковое значение функции. Математически это выражается как [латекс] f (-x) = f (x) [/ latex] для всех [latex] x [/ latex] в домене [latex] f [/ latex].
Симметрия относительно начала координат : синус, косеканс, тангенс и котангенс являются нечетными функциями и симметричны относительно начала координат.
Функции синуса, косеканса, тангенса и котангенса симметричны относительно начала координат.Графы, симметричные относительно начала координат, представляют нечетные функции. Для нечетных функций любые две точки с противоположными значениями [latex] x [/ latex] также имеют противоположные значения [latex] y [/ latex].
 Математически это выражается как [латекс] f (-x) = -f (x) [/ latex] для всех [latex] x [/ latex] в домене [latex] f [/ latex].
Математически это выражается как [латекс] f (-x) = -f (x) [/ latex] для всех [latex] x [/ latex] в домене [latex] f [/ latex].Тождества симметрии
Мы можем применить определения для четных и нечетных функций, чтобы вывести тождества симметрии, соответствующие каждой из наших шести тригонометрических функций.Следующие тождества симметрии полезны при нахождении тригонометрической функции отрицательного значения.
Обратите внимание, что только два тригонометрических тождества являются четными функциями: косинус и секанс. Для этих функций мы применяем [latex] f (-x) = f (x) [/ latex], чтобы найти следующие идентификаторы:
[латекс] \ begin {align} \ cos (-x) & = \ cos x \\ \ sec (-x) & = \ sec x \ end {align} [/ latex]
Для нечетных тригонометрических функций мы применяем [latex] f (-x) = -f (x) [/ latex] и находим следующие тождества:
[латекс] \ begin {align} \ sin (-x) & = — \ sin x \\ \ csc (-x) & = — \ csc x \\ \ tan (-x) & = — \ tan x \ \ \ cot (-x) & = — \ cot x \ end {align} [/ latex]
Пример
Найдите синус, косинус и тангенс [latex] \ displaystyle {\ theta = — \ frac {5 \ pi} {6}} [/ latex].

Во-первых, мы можем определить, что абсолютное значение [latex] \ theta [/ latex] является особым углом, [latex] \ displaystyle {\ frac {5 \ pi} {6}} [/ latex]. Из единичного круга мы знаем, что [латекс] \ displaystyle {\ cos {\ left (\ frac {5 \ pi} {6} \ right)} = — \ frac {\ sqrt {3}} {2}} [/ латекс] и [латекс] \ displaystyle {\ sin {\ left (\ frac {5 \ pi} {6} \ right)} = \ frac {1} {2}} [/ latex].
Используя эти значения из единичного круга, мы можем вычислить [латекс] \ displaystyle {\ tan {\ left (\ frac {5 \ pi} {6} \ right)}} [/ latex]:
[латекс] \ displaystyle {\ begin {align} \ tan {\ left (\ frac {5 \ pi} {6} \ right)} & = \ frac {\ sin {\ left (\ frac {5 \ pi} {6} \ right)}} {\ cos {\ left (\ frac {5 \ pi} {6} \ right)}} \\ & = \ frac {\ frac {1} {2}} {- \ frac {\ sqrt {3}} {2}} \\ & = \ left (\ frac {1} {2} \ right) \ cdot \ left (- \ frac {2} {\ sqrt {3}} \ right) \\ & = — \ frac {1} {\ sqrt {3}} \ end {align}} [/ latex]
Теперь, когда мы знаем синус, косинус и тангенс [latex] \ displaystyle {\ frac {5 \ pi} {6}} [/ latex], мы можем применить тождества симметрии, чтобы найти функции [latex] \ displaystyle {- \ frac {5 \ pi} {6}} [/ latex].

Применяя тождество симметрии для косинуса, получаем:
[латекс] \ displaystyle {\ begin {align} \ cos {\ left (- \ frac {5 \ pi} {6} \ right)} & = \ cos {\ left (\ frac {5 \ pi} {6 } \ right)} \\ & = — \ frac {\ sqrt {3}} {2} \ end {align}} [/ latex]
Применяя тождество для синуса, получаем:
[латекс] \ displaystyle {\ begin {align} \ sin {\ left (- \ frac {5 \ pi} {6} \ right)} & = — \ sin {\ left (\ frac {5 \ pi} { 6} \ right)} \\ & = — \ frac {1} {2} \ end {align}} [/ latex]
Наконец, применив тождество для касательной, мы имеем:
[латекс] \ displaystyle {\ begin {align} \ tan {\ left (- \ frac {5 \ pi} {6} \ right)} & = — \ tan {\ left (\ frac {5 \ pi} { 6} \ right)} \\ & = — \ left (- \ frac {1} {\ sqrt {3}} \ right) \\ & = \ frac {1} {\ sqrt {3}} \ end {align }} [/ latex]
Формула тригонометрии — [Sin, Cos, Tan, Cot, Sec и Cosec]
Формула тригонометрии : Тригонометрия — это хорошо известное имя в геометрической области математики, которое актуально в этой области с давних времен, а также применяется практически во многих случаях.

На простом языке тригонометрию можно определить как ту ветвь алгебры, которая связана с треугольником. В этом разделе мы в основном изучаем взаимосвязь между углами и длиной стороны данного треугольника. При таком подробном изучении треугольника формируется несколько типов уравнений, которые, следовательно, решаются для упрощения взаимосвязи между длинами сторон и углов такого треугольника.
Тригонометрия считается одним из старейших компонентов алгебры, существующей примерно с 3 века.Существуют практические применения тригонометрии в нескольких контекстах, таких как астрономия, геодезия, оптика или периодические функции.
Формулы тригонометрии
Что ж, будь то алгебра или геометрия, обе эти области математики основаны на научных вычислениях уравнений, и мы должны выучить различные формулы, чтобы их было легко вычислить.
Как мы знаем, в тригонометрии мы в основном измеряем разные стороны треугольника, из которых формируются несколько уравнений.
 Далее формулы тригонометрии составлены в соответствии с различными отношениями, используемыми в области, такими как синус, тангенс, косинус и т. Д. Таким образом, в основном есть номера формул, которые обычно используются в тригонометрии для измерения сторон треугольника. .
Далее формулы тригонометрии составлены в соответствии с различными отношениями, используемыми в области, такими как синус, тангенс, косинус и т. Д. Таким образом, в основном есть номера формул, которые обычно используются в тригонометрии для измерения сторон треугольника. .Здесь мы приводим список различных типов формул тригонометрии.
Основная формула тригонометрии
2. Sin Cos Tan на 0, 30, 45, 60 градусов
3.Пифагорейские тождества
4. Знак греха, Cos, Tan в разных квадрантах
A dd– S ugar – T o –C оферта
5. Радианы
1 градус = 60 минут
Пример: 1 ° = 60 ′1 минута = 60 секунд
Пример: 1 ′ = 60 дюймов6. Отрицательные углы [четно-нечетные отождествления]
Sin (-x) = — Sin x
Cos (-x) = Cos x
Tan (-x) = — Tan x
Cot (-x) = — Cot x
Sec (-x) = Sec x
Cosec (-x) = — Cosec x7.
 Значение Sin, Cos, Tan повторяется после 2𝛑
Значение Sin, Cos, Tan повторяется после 2𝛑Sin (2𝛑 + x) = Sin x
Cos (2𝛑 + x) = Cos x
Tan (2𝛑 + x) = Tan x8. Идентификация периодичности — углы смещения на 𝛑 / 2, 𝛑, 3𝛑 / 2
9. Идентификаторы суммы углов и разностей
10. Формула двойного угла
11. Формула тройного угла
12. Идентичность половинных углов
13. Сумма идентичностей
14.Идентификационные данные продукта
15. Закон греха
Здесь,
- ABC — вершины треугольника ABC.
- Место, противоположное углу A, — это a. то есть BC
- Место, противоположное углу B, равно b. т.е. AC
- Место, противоположное углу C, равно c. т.е. AB
16. Закон косинуса
17. Обратная тригонометрическая функция
Если Sin θ = x
, затем поместите Sin на правую сторону
Таким образом, вы можете видеть, что Sin — это угол.
 То же, что и обратная функция для всех функций Trignomentry, — это угол.
То же, что и обратная функция для всех функций Trignomentry, — это угол.18. Область и диапазон функций обратной тригонометрии
19. Формула обратной тригонометрии
20. Подстановка обратной тригонометрии
Как и любой другой раздел математики, формулы тригонометрии не менее важны, поскольку без этих формул вы не можете использовать значения треугольников для целей измерения. Эти формулы упрощают стороны треугольника, так что вы можете легко измерить все его стороны.
Мы призываем всех ученых понять эти формулы, а затем легко применять их для решения различных типов задач тригонометрии.
Тригонометрических и геометрических преобразований, Sin (A + B), Sin (A
Список всех тригонометрических тождеств (формул)
Коэффициенты суммирования углов
Как показали примеры, иногда нам нужны углы, отличные от 0, 30, 45, 60 и 90 градусов. В этой главе вам нужно узнать две вещи:
1. Sin (A + B) не равно sin A + sin B .Это не похоже на удаление скобок в алгебре.
Sin (A + B) не равно sin A + sin B .Это не похоже на удаление скобок в алгебре.
2. Формула того, чему равен sin (A + B).Во-первых, чтобы показать, что удаление скобок «не работает». Здесь: сделайте A 30 градусов и B 45 градусов.
Грех 30 равен 0,5. Sin 45 равен 0,7071. Если сложить два, получится 1,2071.
Вы знаете, что никакой синус (или косинус) не может быть больше 1. Почему? знаменателем этого отношения является гипотенуза. Максимум, что может быть в числителе, равно знаменателю. Синус или косинус никогда не могут быть больше 1, поэтому значение 1.2071, должно быть, ошибается.
Требуемый синус, косинус или тангенс полного угла (A + B)
В поисках греха (A + B)
Самый простой способ найти sin (A + B) — это геометрическая конструкция, показанная здесь. Большой угол (A + B) состоит из двух меньших, A и B. Конструкция (1) показывает, что противоположная сторона состоит из двух частей.
 Нижняя часть, разделенная линией между углами (2), есть sin A. Линия между двумя углами, разделенная гипотенузой (3), есть cos B.Умножьте два вместе. Средняя линия находится как в числителе, так и в знаменателе, поэтому каждая из них отменяет и оставляет нижнюю часть противоположной точки над гипотенузой (4).
Нижняя часть, разделенная линией между углами (2), есть sin A. Линия между двумя углами, разделенная гипотенузой (3), есть cos B.Умножьте два вместе. Средняя линия находится как в числителе, так и в знаменателе, поэтому каждая из них отменяет и оставляет нижнюю часть противоположной точки над гипотенузой (4). Обратите внимание на маленький прямоугольный треугольник (5). Заштрихованный угол — A, потому что линия на его верхней стороне параллельна базовой линии. Подобные прямоугольные треугольники с углом A показывают, что верхний угол, отмеченный A, также равен исходному A. Верхняя часть противоположного (6), над самым длинным из этого заштрихованного треугольника, равна cos A.Противоположностью главной гипотенузы (7) является sin B. Поскольку сторона, отмеченная «противоположная» (7), присутствует как в числителе, так и в знаменателе, когда cos A и sin B умножаются вместе, cos A sin B является верхней частью исходная противоположность — для (A + B) — деленная на главную гипотенузу (8).

Теперь соберите все вместе (9). Sin (A + B) — это две противоположные части, разделенные гипотенузой (9). Помещаем это в его триггерную форму:
sin (A + B) = sin A cos B + cos A sin B
Нахождение cos (A + B)
Очень похожая конструкция находит формулу для косинуса угла, образованного двумя сложенными углами.
Используя ту же конструкцию (1), обратите внимание, что смежная сторона является полной базовой линией (для cos A), с вычтенной частью справа. Каждая часть должна использовать один и тот же знаменатель — гипотенузу треугольника (A + B).
Полная базовая линия, разделенная линией раздела между углами A и E, равна cos A (2). Эта разделительная линия, разделенная гипотенузой треугольника (A + B), есть cos B (3). Таким образом, полная базовая линия, деленная на гипотенузу, представляет собой произведение cos A cos B (4).
Теперь небольшая часть, которую нужно вычесть. Заштрихованная часть (5) представляет sin A, который, умноженный на заштрихованную часть (6), равен sin E, что дает другой необходимый вам кусок (7).
 Вычитание дает cos (A + B) (8), поэтому нам нужна формула:
Вычитание дает cos (A + B) (8), поэтому нам нужна формула:cos (A + B) = cos A cos B — sin A sin B
В поисках загара (A + B)
Полный геометрический вывод формулы для tan (A + B) сложен. Самый простой способ — вывести его из двух формул, которые вы уже сделали.При любом угле тангенс равен синусу, деленному на косинус. Используя этот факт, tan (A + B) = sin (A + B) / cos (A + B). Так оно и есть, но вы можете расширить это до:
$ \ tan (A + B) = \ frac {\ sin \ A \ cos \ B + \ cos \ A \ \ sin \ B} {\ cos \ A \ cos \ B — \ sin \ A \ \ sin \ B} $
Разделим верхнюю и нижнюю части на cos A cos B, что превратит все члены в касательные, получив:
$ \ tan (A + B) = \ frac {\ tan \ A + \ tan \ B} {1 — \ tan \ A \ \ tan \ B} $
Передаточное число для 75 градусов
Покажите соотношения для синуса, косинуса и тангенса, подставив их в формулу суммы, а затем уменьшив результат до его простейшей формы, прежде чем оценивать шумы.
 После внесения основных замен в каждом случае черновая работа заключается в закрашивании — чтобы показать, как результат сводится к простейшей форме для оценки.
После внесения основных замен в каждом случае черновая работа заключается в закрашивании — чтобы показать, как результат сводится к простейшей форме для оценки.
Если вы используете свой карманный калькулятор для оценки, вероятно, не будет никакой разницы, упростите вы сначала выражения или просто пройдетесь по ним! Все зависит от калькулятора: некоторые имеют значение, некоторые — нет!
Соотношение углов больше 90 градусов
До сих пор учитывались отношения острых углов (от 0 до 90 градусов).Другие треугольники с тупыми углами (более 90 градусов) могут быть более 180 градусов в более поздних задачах. Чтобы упростить классификацию углов по размеру, они разделены на квадранты.
Квадрант — это четверть круга. Поскольку круг обычно делится на 360 градусов, квадранты называются сегментами с углом 90 градусов. 0-90 градусов — это 1-й квадрант, 90-180 — 2-й, 180-270 — 3-й и 270-360 — 4-й.
Рисование линиями для представления границ квадранта: 0 или 360 по горизонтали вправо, 90 по вертикали, 180 по горизонтали влево и 270 по вертикали.
 Теперь воспользуйтесь этим методом для построения графиков.
Теперь воспользуйтесь этим методом для построения графиков.Постепенно большие углы определяются вращающимся вектором, начинающимся с нуля и вращающимся против часовой стрелки. Горизонтальные элементы — это x: положительный справа, отрицательный слева. Вертикальные элементы — y. положительный вверх, отрицательный вниз. Вращающийся вектор — r. Итак, синус угла равен y / r, косинус x / r и тангенс y / x. Вектор r всегда положителен. Итак, знаком соотношений могут быть цифры для различных квадрантов.
Здесь знаки трех соотношений сведены в таблицу для четырех квадрантов.Также как эквивалентный угол в первом квадранте «переключается», когда вектор переходит от одного квадранта к другому. В первом квадранте стороны были определены в соотношениях для синуса, косинуса и тангенса. По мере того, как вы переходите к большим углам в оставшихся квадрантах, противоположная сторона всегда будет вертикальной (y). То, что называлось смежным, всегда является горизонтальным (x). Гипотенуза — это всегда вращающийся вектор (r).
 Вы начнете видеть закономерность в изменении этих тригонометрических соотношений углов.
Вы начнете видеть закономерность в изменении этих тригонометрических соотношений углов.Соотношения в четырех квадрантах
Передаточные числа для разностных углов
Теперь у вас есть два способа получить формулы для разностных углов. Во-первых, используйте геометрическую конструкцию, такую как та, которая использовалась для суммирования углов, изменив ее так, чтобы (A — B) был углом B, вычтенным из угла A.
В рассуждениях, аналогичных тем, которые использовались для суммирования углов, здесь представлены несколько сокращенно формулы синуса и косинуса:
sin (A — B) = sin A cos B — cos A sin B
а также
cos (A — B) = cos A cos B + sin A sin B
Геометрическая конструкция
Формулы суммы и разности
Второй метод нахождения формулы для разностных углов использует уже полученную формулу суммы, но делает B отрицательным.Из нашего исследования знаков для различных квадрантов, отрицательные углы от 1-го квадранта будут в 4-м квадранте.
 Выполнение этой замены дает те же результаты, которые геометрически были получены в предыдущем разделе.
Выполнение этой замены дает те же результаты, которые геометрически были получены в предыдущем разделе.Для нахождения формулы тангенса используется тот же метод, либо путем подстановки в формулы синуса и косинуса, либо, более напрямую, путем определения tan (-B) = — tan B. В любом случае вы получите:
$ \ tan (A — B) = \ frac {\ tan \ A — \ tan \ B} {1 + \ tan \ A \ \ tan \ B} $
Соотношения по четырем квадрантам
Вы можете вывести еще несколько соотношений с помощью формул суммы и разности.Вы уже сделали передаточные числа на 75 градусов. Теперь сделайте это на 15 градусов. Эти формулы дают соотношения для углов с 15-градусным интервалом в четырех квадрантах. Нанося их на полные 360 градусов, вы можете увидеть, как меняются три соотношения, когда вектор проходит через четыре квадранта.
И синус, и косинус «колеблются» вверх и вниз между +1 и -1. Обратите внимание, что «волны» смещены одна относительно другой на 90 градусов. Этот факт станет важным позже.

Касательная начинается как синусоида, но быстро поднимается вверх, достигая бесконечности под углом 90 градусов.Выходя за пределы шкалы в положительном направлении, он «появляется» из отрицательного направления по другую сторону 90 градусов. Проходя через точку 180 градусов, касательная кривая дублирует то, что она делает, проходя через 0 или 360 (в зависимости от того, как вы ее видите). При 270 градусах он повторяет то же самое, что и при 90 градусах.
Пифагор в тригонометрии
Формулу часто можно упростить, как это было обнаружено путем получения касательных формул из формул синуса и косинуса и изменения ее с членов, использующих одно отношение, на члены, использующие другое отношение.При этом очень удобна теорема Пифагора, выраженная в тригонометрических соотношениях.
Предположим, что в прямоугольном треугольнике длина гипотенузы равна 1 единице. Тогда одна из других сторон будет иметь длину sin A, а другая — cos A. Из этого теорема Пифагора показывает, что: cos 2 A + sin 2 A = 1.
 Это утверждение всегда верно, поскольку любое значение A.
Это утверждение всегда верно, поскольку любое значение A.Немного о том, как это написано. Cos 2 A означает (cos A) 2 .Если бы вы написали это cos A 2 , уравнение означало бы что-то другое. A — это число в некоторых угловых обозначениях, обозначающее угол. 2 будет тем же числом в квадрате. Его значение будет зависеть от используемой угловой записи, так что это не лучший термин для использования. Имеется в виду синус или косинус угла в квадрате, а не сам угол.
Формулу Пифагора можно транспонировать. Например, две другие формы:
cos 2 A = 1 — sin 2 A и sin 2 = 1 — cos 2 A.Несколько углов
Формулы суммы, наряду с теоремой Пифагора, используются для углов, которые равны 2, 3 или более точному кратному любому исходному углу. Здесь приведены формулы для 2A и 3A. Тот же метод используется далее в частях 3 и 4 этой книги.
Формула суммы работает независимо от того, одинаковые или разные углы: sin (A + B) или sin (A + A).
 Однако грех (А + А) на самом деле грех 2А. Итак, sin 2A — это sin A cos A + cos A sin A. Они оба являются одним и тем же произведением в противоположном порядке, поэтому это утверждение можно упростить до sin 2A = 2 sin A cos A.2 австралийских доллара
Однако грех (А + А) на самом деле грех 2А. Итак, sin 2A — это sin A cos A + cos A sin A. Они оба являются одним и тем же произведением в противоположном порядке, поэтому это утверждение можно упростить до sin 2A = 2 sin A cos A.2 австралийских доллараТеперь тройной угол (3A) используется только для того, чтобы показать, как получаются дальнейшие кратные.
По сути, это так же просто, как написать 3A = 2A + A и повторно применить формулы суммы. Но затем, чтобы получить результирующую формулу в работоспособной форме, вам нужно заменить часть 2A, чтобы получить все в терминах соотношений для простого угла A.
Пройдите свой путь по трем показанным здесь производным. Вы можете видеть, что при 4 А и более все усложняется (в частях 3 и 4 этой книги).
НЕСКОЛЬКО УГЛОВ, полученных из формул суммы
МНОЖЕСТВЕННЫЕ УГЛЫ Передаточные числа для 3A
Свойства равнобедренного треугольника
Вы уже видели, что прямоугольный треугольник — полезный строительный блок для других фигур.
 Равнобедренный треугольник используется несколько иначе. Но факт, на котором основано это использование, состоит в том, что равнобедренный треугольник имеет две равные стороны и два равных угла, противоположных этим двум сторонам. Перпендикуляр от третьего угла (не одного из равных) к третьей стороне (не одной из равных) делит эту третью сторону пополам.То есть он делит его на две равные части, превращая весь треугольник в зеркальные прямоугольные треугольники.
Равнобедренный треугольник используется несколько иначе. Но факт, на котором основано это использование, состоит в том, что равнобедренный треугольник имеет две равные стороны и два равных угла, противоположных этим двум сторонам. Перпендикуляр от третьего угла (не одного из равных) к третьей стороне (не одной из равных) делит эту третью сторону пополам.То есть он делит его на две равные части, превращая весь треугольник в зеркальные прямоугольные треугольники.В случае равнобедренных треугольников любой треугольник, кроме прямоугольного, можно разделить на три смежных равнобедренных треугольника, разделив каждую сторону на две равные части и возведя перпендикуляры из точек деления пополам. Там, где встречаются любые два из этих пополам перпендикуляров, если линии проводят к углам исходного треугольника, эти три линии должны быть равны, потому что две из них образуют стороны равнобедренного треугольника.Итак, перпендикуляр с третьей стороны исходного треугольника также должен пересекаться в той же точке.

Это утверждение верно, как мы показываем здесь, независимо от того, является ли исходный треугольник острым или тупым. Разница с треугольником с тупым углом заключается в том, что точка встречи находится за пределами исходного треугольника, а не внутри.
Что делает прямоугольный треугольник? Перпендикуляры от середины гипотенузы к двум другим сторонам разделят эти две стороны пополам — вы получите две из трех! Точка встречи находится на гипотенузе.
Углы по окружности
Основное свойство круга — то, что его центр находится на равном расстоянии от каждой точки на его окружности. Это равное расстояние и есть радиус круга.
Если вы нарисуете какой-либо треугольник внутри круга, перпендикуляры из средних точек его стороны встретятся в центре круга, а радиусы углов треугольника разделят его на три равнобедренных треугольника.
Теперь, если вы назовете равные пары углов в каждом равнобедренном треугольнике, A, A, B, B, C, C, вы обнаружите, что исходный треугольник имеет один угол A + B, один угол B + C и один угол A.
 + С.Сумма трех углов составляет 2A + 2B + 2C. Это, знаете ли, в сумме составляет 180 градусов.
+ С.Сумма трех углов составляет 2A + 2B + 2C. Это, знаете ли, в сумме составляет 180 градусов.В любом равнобедренном треугольнике угол при вершине равен 180 градусам минус удвоенный угол основания. Из-за факта, выведенного в предыдущем абзаце, например, 180 — 2A должно быть таким же, как 2B + 2C.
Рассмотрим углы, противоположные той части круга, против которой сидит верхняя левая сторона треугольника. Угол в центре равен 2B + 2C, как только что было вычислено. Угол на окружности B + C.»Вы обнаружите, что для любого сегмента круга угол в центре всегда в два раза больше угла на окружности.
Приведенное выше доказательство приводит к интересному факту об углах в окружностях. Вместо того, чтобы определять углы со стороной треугольника, используйте дугу (часть окружности) круга. Важен угол, соответствующий дуге в центре. Часть окружности круга, которая определяется углом в центре, называется хордой круга.
Угол в центре в два раза больше угла на окружностиЛюбой угол, касающийся окружности с использованием этой хорды в качестве завершения линий, ограничивающих угол, должен составлять лишь половину угла в центре.
 Таким образом, все углы в окружности, основанной на одной и той же хорде, должны быть равны. Предположим, что хорда имеет угол 120 градусов. Углы на окружности будут ровно 60 градусов.
Таким образом, все углы в окружности, основанной на одной и той же хорде, должны быть равны. Предположим, что хорда имеет угол 120 градусов. Углы на окружности будут ровно 60 градусов.Частный случай — полукруг (точный полукруг).Угол в центре — прямая линия (180 градусов). Каждый угол на окружности полукруга составляет ровно 90 градусов (прямой угол). Любой треугольник в полукруге — это прямоугольный треугольник.
Определения
Выше мы часто использовали углы, которые в сумме составляют либо прямой угол (90 градусов), либо два прямых угла (180 градусов). Когда два угла в сумме составляют 180 градусов (два прямых угла), они называются дополнительными . Когда два угла в сумме составляют 90 градусов (один прямой угол), они называются дополнительными .
Вопросы и проблемы
1. Синус угла A равен 0,8, а синус угла B равен 0,6. Из различных соотношений, полученных на данный момент, найдите следующее: tan A, tan B, sin (A + B), cos (A + B), sin (A — B), cos (A — B), tan (A + B) и tan (A — B), без использования таблиц или триггерных кнопок калькулятора.

2. На экваторе Земля имеет радиус 4000 миль. Углы вокруг экватора измеряются в меридианах долготы с линией с севера на юг, проходящей через Гринвич, Англия, в качестве нулевой точки отсчета.Два места используются для наблюдения за луной: одно — гора. Кения, на экваторе в 37,5 км к востоку от Гринвича; другая — Суматра, на экваторе, в 100,5 м восточной долготы. Насколько далеко друг от друга находятся эти два места, если измерять воображаемую прямую линию, проходящую через Землю?
3. Если прицелы производились горизонтально из точек наблюдения, упомянутых в вопросе 2 (к востоку от первой, к западу от второй), под каким углом пересекались бы линии обзора?
4. В определенное время, точно синхронизированное в обоих местах, наблюдается спутник.В Кении угол обзора спутника с центром на 58 градусов выше горизонтали в восточном направлении. На Суматре высота 58 градусов над горизонтом в западном направлении. Как далеко находится спутник? Используйте расстояние между точками, вычисленное в вопросе 2.

5. Косинус определенного угла ровно в два раза больше синуса того же угла. Каков тангенс этого угла? Для этого вопроса не нужны ни таблицы, ни калькулятор.
6. Синус определенного угла равен нулю.28. Найдите косинус и тангенс без таблиц или триггерных функций на вашем калькуляторе.
7. Синус определенного угла равен 0,6. Найдите синус двойного этого угла и тройного этого угла.
8. Найдите синус и косинус угла, ровно вдвое больше, чем в вопросе 7.
9. Используя 15 градусов как единичный угол и формулы для соотношений 2A и?> A, найдите значения синусов 30 и 45 градусов.
10. Используя 30 градусов в качестве единицы угла, найдите значения для синусов 60 и 90 градусов.
11. Используя 45 градусов как единичный угол, найдите значения для касательных 90 и 135 градусов.
12. Используя 60 градусов в качестве единицы угла, найдите значения косинусов 120 и 180 градусов.
13. Используя 90 градусов в качестве единицы угла, найдите значения косинусов 180 и 270 градусов.

14. Используя формулы касательных для множественных углов и таблицы, найдите тангенсы для трех, умноженных на 29, 31, 59 и 61 градус. Учтите изменения знака между 29 и 31 градусом и между 59 и 61 градусом.
15. Синус угла 0,96. Найдите синус и косинус для удвоенного угла.
16. Задача приводит к алгебраическому выражению в форме 8cos 2 A + cos A = 3. Решите для cos A и укажите, в каком квадранте будет угол, представляющий каждое решение. Приведите приблизительные значения из таблиц или вашего калькулятора.
Тригонометрия
Тригонометрические тождества (формулы)Исчисление — «Теорема синусов и косинусов» — формулы для суммы и разности
Я где-то читал, что функции синуса и косинуса полностью описываются этой теоремой:
- $ \ sin (0) = 0, \ cos (0) = 1 $
- $ \ sin (a-b) = \ sin (a) \ cos (b) — \ sin (b) \ cos (a) $
- $ \ cos (a-b) = \ cos (a) \ cos (b) + \ sin (a) \ sin (b) $
- Существует na $ r> 0 $ такое, что:
$$ 0 <\ sin (x)
С помощью этой теоремы мы можем доказать такие вещи, как:
$ \ sin ^ 2 (x) + \ cos ^ 2 (x) = 1 $
, выполнив$ \ cos (aa) = \ cos (a) \ cos (a) + \ sin (a) \ грех (а) $$ \ sin (-x) = — \ sin (x) $
, выполнив$ \ sin (0-x) = \ sin (0) \ cos (x) — \ sin (x) \ cos (0 ) $- $ \ cos (a + b) = \ cos (a) \ cos (b) — \ sin (a) \ sin (b) $
, выполнив$ \ cos (a — (- b)) = \ cos (a) \ cos (-b) + \ sin (a) \ sin (-b) $
- $ \ sin (a + b) = \ sin (a) \ cos (b) + \ sin (b) \ cos (a) $
$ \ sin (a — (- b)) = \ sin (a) \ cos (-b) — \ sin (-b) \ cos (a) $, выполнив
И другие тригонометрические тождества, которые также вытекают из того, что я уже сделал.

Проблема в том, что существует множество определений для функции синуса и косинуса. Начнем с классического определения:
Классическое определение
Синус
Функцияопределяется как отношение между противоположной стороной угла и гипотенузой этого прямоугольного треугольника.Функция косинуса
определяется как отношение между смежной стороной угла и гипотенузой этого прямоугольного треугольника.Тангенс
Функцияопределяется как отношение между функцией синуса и функцией косинуса(с $ \ cos (x) \ neq 0) $Другие тригонометрические тождества могут быть доказаны геометрически для угла , меньшего или равного $ \ frac {\ pi} {2} rad $ , потому что это прямоугольный треугольник. Итак, мы не можем доказать $ \ sin (ab) $ геометрически, а затем доказать $ \ sin (a + b) $ аналитически, как это сделал я, потому что мы предположили отрицательное значение $ b $, то, что геометрически не определено в прямоугольном треугольнике.
 .2 (x) = 1 $ можно доказать с помощью простой теоремы Пифагора в треугольнике с гипотенузой 1.
.2 (x) = 1 $ можно доказать с помощью простой теоремы Пифагора в треугольнике с гипотенузой 1.Формулы суммы и разности синусов и косинусов могут быть доказаны геометрически, как на этих изображениях, которые я нашел в этом ответе:
Определение единичного круга
Представьте себе круг с центром в декартовой плоскости, затем:
Функция
sineдля $ x \ in R, x> 0 $ может быть определена как позиция $ y $ точки окружности, где угол останавливается, если мы перемещаем на против часовой стрелки на внутри окружности.Косинус
Мы можем дать такое же определение для отрицательных углов, поэтому для $ x \ in R, x <0 $ справедливо то же самое, но мы знаем, что движется на по часовой стрелке.

Функция тангенса
(с $ \ cos (x) \ neq 0) $Затем мы можем определить эти функции для всех действительных чисел, поскольку, когда мы перемещаемся по на $ 2 \ pi $, мы возвращаемся в исходную точку.{2н-1} $$
Здесь, в том же вопросе, есть аналитическое доказательство тригонометрических тождеств для этих сумм.
Какое определение для исчисления лучше всего?
Ну, в исчислении мы используем тригонометрические функции МНОГОЕ: в интегральных подстановках, в рядах, рядах Тейлора (как те, которые я показал сейчас), производных, проверках сходимости (например, онде Эйлера в базовой задаче) и других вещах ...
Все определения, которые я вижу, в некотором роде круговые или недостаточно строгие, чтобы заставить меня чувствовать себя хорошо, принимая некоторые производные или интегральную замену, потому что меня всегда волнует область этих вещей.
 Поэтому я хочу дать ему очень четкое определение и уметь использовать все тригонометрические тождества.
Поэтому я хочу дать ему очень четкое определение и уметь использовать все тригонометрические тождества.Я видел много геометрических доказательств $ \ sin (ab) $, $ \ sin (a + b) $, $ \ cos (ab) $, $ \ cos (a + b) $ с использованием прямоугольного треугольника и затем внезапно человек начинает использовать эту формулу для всех действительных чисел. Мне нужно полное определение тригонометрических функций, которое работает периодически и для всех вещественных чисел. Определение ряда Тейлора кажется хорошим, но они генерируются с использованием тригонометрических тождеств, которые еще не доказаны (если принять это определение).
ps: Я знаю, что использовал некоторые примитивные слова в некоторых определениях, например, « путешествия », поэтому я допустил их в с акцентом на , но я надеюсь, что вы, ребята, понимаете. И извините за длинный пост, но мне нужно было это сделать, потому что я никогда не видел полного определения ни в одной книге. Спасибо.
Формулы произведения и суммы
Формулы произведения и суммы Формулы произведения и суммыИз формул сложения мы выводим следующие тригонометрические формулы (или тождества)
Замечание.
 Очевидно, что третья формула и четвертая эквивалентны (используйте свойство, чтобы увидеть это).
Очевидно, что третья формула и четвертая эквивалентны (используйте свойство, чтобы увидеть это).Приведенные выше формулы важны всякий раз, когда возникает необходимость преобразовать произведение синуса и косинуса в сумму. Это очень полезная идея в технике интеграции.
Пример. Выразите произведение как сумму тригонометрических функций.
Ответ. У нас есть
который дает
Обратите внимание, что приведенные выше формулы могут использоваться для преобразования суммы в продукт через тождества
Пример. Express как продукт.
Ответ. У нас есть
Обратите внимание, что мы использовали.
Пример. Проверить формулу
Ответ. У нас есть
а также
Следовательно
что ясно подразумевает
Пример. Найдите действительное число x такое, что и
Ответ.
 Для решения этой проблемы можно использовать множество способов. Воспользуемся приведенными выше формулами. У нас есть
Для решения этой проблемы можно использовать множество способов. Воспользуемся приведенными выше формулами. У нас естьСледовательно
Поскольку уравнение дает, а уравнение дает. Следовательно, решения уравнения
находятся
Пример. Подтвердите личность
Ответ. У нас есть
Используя приведенные выше формулы, получаем
Следовательно
что подразумевает
Поскольку мы получаем
[Тригонометрия] [Геометрия] [Алгебра] [Дифференциальные уравнения] [Исчисление] [Комплексные переменные] [Матричная алгебра] С.Домашняя страница O.S MATHematicsВам нужна дополнительная помощь? Пожалуйста, разместите свой вопрос на нашем S.O.S. Математика CyberBoard.
Мохамед А. Хамси
Вт 3 дек, 17:39:00 MST 1996 Авторские права 1999-2021 MathMedics, LLC. Все права защищены.
Все права защищены.
Свяжитесь с нами
Математическая медицина, ООО. - П.О. Box 12395 - El Paso TX 79913 - США
пользователей онлайн за последний часИскусство решения проблем
В тригонометрии Тригонометрические тождества - это уравнения, включающие тригонометрические функции, которые верны для всех входных значений.Тригонометрические функции имеют множество тождеств, из которых в эту статью включены только наиболее широко используемые.
Пифагорейские тождества
Пифагорейские тождества утверждают, что
Используя определение единичной окружности в тригонометрии, поскольку точка определена как находящаяся на единичной окружности, это расстояние, равное единице от начала координат. Тогда по формуле расстояния. Чтобы получить два других тождества Пифагора, разделите на или и подставьте соответствующую тригонометрию вместо соотношений, чтобы получить желаемый результат.
Идентификаторы сложения углов
Тригонометрические тождества сложения углов устанавливают следующие тождества:
Есть много доказательств этих личностей. Для краткости мы перечислим здесь только один.
Личность Эйлера утверждает, что. У нас есть это Рассматривая действительную и мнимую части, мы выводим формулы сложения синуса и косинуса угла.
Чтобы вывести формулу сложения касательных, мы сокращаем задачу до использования синуса и косинуса, делим числитель и знаменатель на и упрощаем.по желанию.
Идентификаторы двойные
Тригонометрические тождества с двумя углами легко выводятся из формул сложения углов, просто позволяя. Это дает:
Косинус двойной угловой идентичности
Вот две одинаково полезные формы тождества косинуса двойного угла. Оба получены через тождество Пифагора на тождестве с двойным углом косинуса, приведенном выше.
Кроме того, следующие тождества полезны при интегрировании и выводе тождеств половинного угла.Они представляют собой простую перестановку двух вышеупомянутых.
Идентификаторы полуугловые
Тригонометрические тождества полууглов устанавливают следующие равенства:
Плюс или минус не означает, что есть два ответа, но что синус угла зависит от квадранта, в котором находится угол.
Возьмите два выражения, перечисленные в разделе косинус двойного угла для и, и замените вместо. Затем извлечение квадратного корня дает желаемые тождества половинного угла для синуса и косинуса.
Идентификаторы суммы к продукту
Идентификаторы продукта к сумме
Скоро в продаже
Другие идентификационные данные
Вот несколько идентификаторов, которые менее важны, чем приведенные выше, но все же полезны.
Четно-нечетные тождества
Функции, и нечетные, а, и четные. Другими словами, шесть тригонометрических функций удовлетворяют следующим равенствам:
Они получены из определений единичной окружности в тригонометрии.Сделать любой угол отрицательным - это то же самое, что отразить его поперек оси x. При этом координата x остается неизменной, но координата y становится отрицательной. Таким образом, и.
Идентификаторы конверсии
Следующие тождества полезны при преобразовании тригонометрических функций.
Все это можно проверить с помощью идентификаторов с добавлением углов.
Тождество Эйлера
Идентичность Эйлера - это формула комплексного анализа, которая связывает комплексное возведение в степень с тригонометрией.В нем говорится, что для любого действительного числа, где - постоянная Эйлера, а - мнимая единица. Тождество Эйлера имеет фундаментальное значение для изучения комплексных чисел и широко считается одной из самых красивых формул в математике.
Разное
Это идентификаторы, которые не содержат достаточно материала, чтобы гарантировать наличие отдельного раздела.
ресурсов
. - Формулы для сложения и вычитания углов в тригонометрических выражениях позволяют нам найти синус, косинус или тангенс





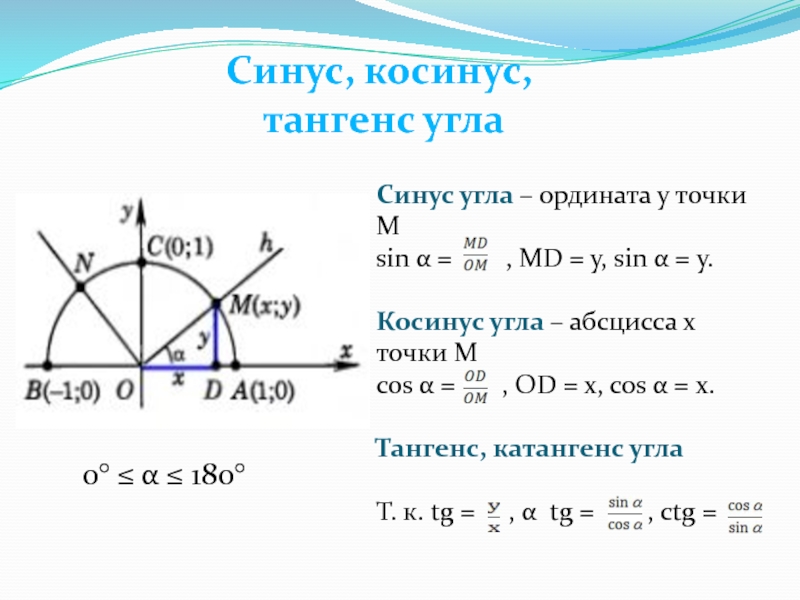 {\ circ} \ quad \ quad \ quad c \ приблизительно 6.5 [/ латекс]
{\ circ} \ quad \ quad \ quad c \ приблизительно 6.5 [/ латекс] Например, рассмотрим треугольник, у которого известны все три стороны, но неизвестны значения углов. В таких случаях недостаточно информации для использования закона синуса. Закон косинусов полезен для: 1) вычисления третьей стороны треугольника, когда известны две стороны и их внутренний угол, и 2) вычисления углов треугольника, если известны только три стороны.
Например, рассмотрим треугольник, у которого известны все три стороны, но неизвестны значения углов. В таких случаях недостаточно информации для использования закона синуса. Закон косинусов полезен для: 1) вычисления третьей стороны треугольника, когда известны две стороны и их внутренний угол, и 2) вычисления углов треугольника, если известны только три стороны. соответствующие стороны [латекс] a [/ латекс], [латекс] b [/ латекс] и [латекс] c [/ латекс].
соответствующие стороны [латекс] a [/ латекс], [латекс] b [/ латекс] и [латекс] c [/ латекс].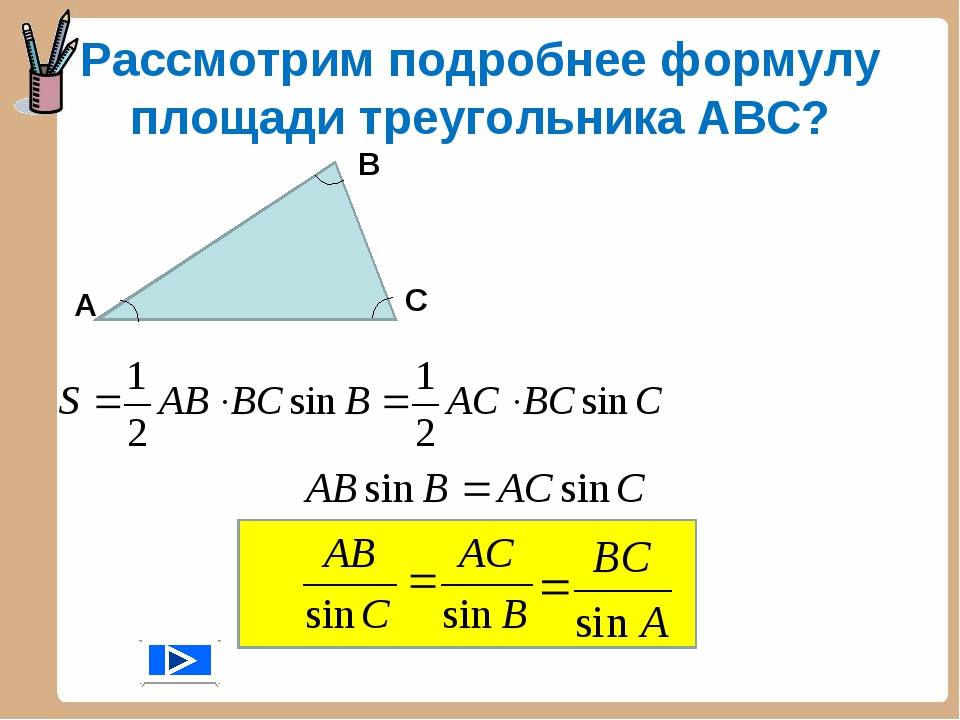 2 [/ латекс]
2 [/ латекс] 2 т [/ латекс] упрощается до [латекс] 5 [/ латекс].
2 т [/ латекс] упрощается до [латекс] 5 [/ латекс].
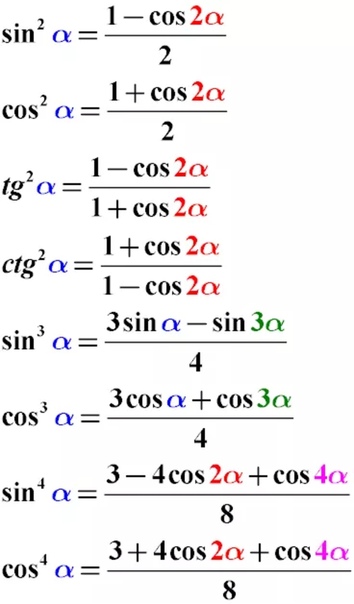
 2} [/ латекс]
2} [/ латекс] {\ circ} [/ латекс]. Можно найти тригонометрические функции любого такого угла.
{\ circ} [/ латекс]. Можно найти тригонометрические функции любого такого угла.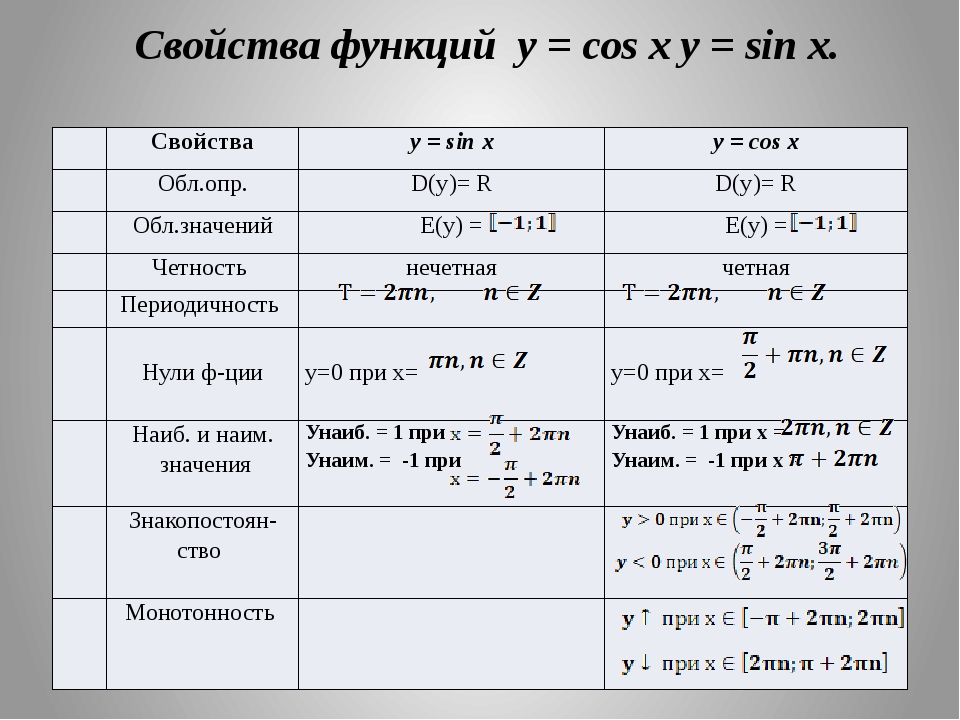 {\ circ} \ right)} = \ frac {\ sqrt {6} — \ sqrt {2}} {4}} [/ латекс]
{\ circ} \ right)} = \ frac {\ sqrt {6} — \ sqrt {2}} {4}} [/ латекс]
 {\ circ} \ right)} & = 2 \ left (\ frac {\ sqrt {3}} {4} \ right) \\ & = \ frac {\ sqrt {3}} {2} \ end {align} } [/ latex]
{\ circ} \ right)} & = 2 \ left (\ frac {\ sqrt {3}} {4} \ right) \\ & = \ frac {\ sqrt {3}} {2} \ end {align} } [/ latex] {\ circ}) [/ latex], следовательно, положительный.
{\ circ}) [/ latex], следовательно, положительный.
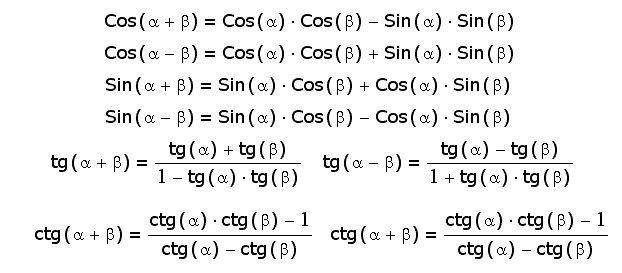 Эта симметрия используется для получения определенных идентичностей.
Эта симметрия используется для получения определенных идентичностей. Математически это выражается как [латекс] f (-x) = -f (x) [/ latex] для всех [latex] x [/ latex] в домене [latex] f [/ latex].
Математически это выражается как [латекс] f (-x) = -f (x) [/ latex] для всех [latex] x [/ latex] в домене [latex] f [/ latex].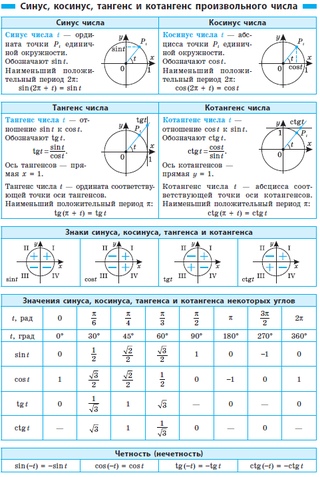


 Далее формулы тригонометрии составлены в соответствии с различными отношениями, используемыми в области, такими как синус, тангенс, косинус и т. Д. Таким образом, в основном есть номера формул, которые обычно используются в тригонометрии для измерения сторон треугольника. .
Далее формулы тригонометрии составлены в соответствии с различными отношениями, используемыми в области, такими как синус, тангенс, косинус и т. Д. Таким образом, в основном есть номера формул, которые обычно используются в тригонометрии для измерения сторон треугольника. . Значение Sin, Cos, Tan повторяется после 2𝛑
Значение Sin, Cos, Tan повторяется после 2𝛑 То же, что и обратная функция для всех функций Trignomentry, — это угол.
То же, что и обратная функция для всех функций Trignomentry, — это угол. Sin (A + B) не равно sin A + sin B .Это не похоже на удаление скобок в алгебре.
Sin (A + B) не равно sin A + sin B .Это не похоже на удаление скобок в алгебре. 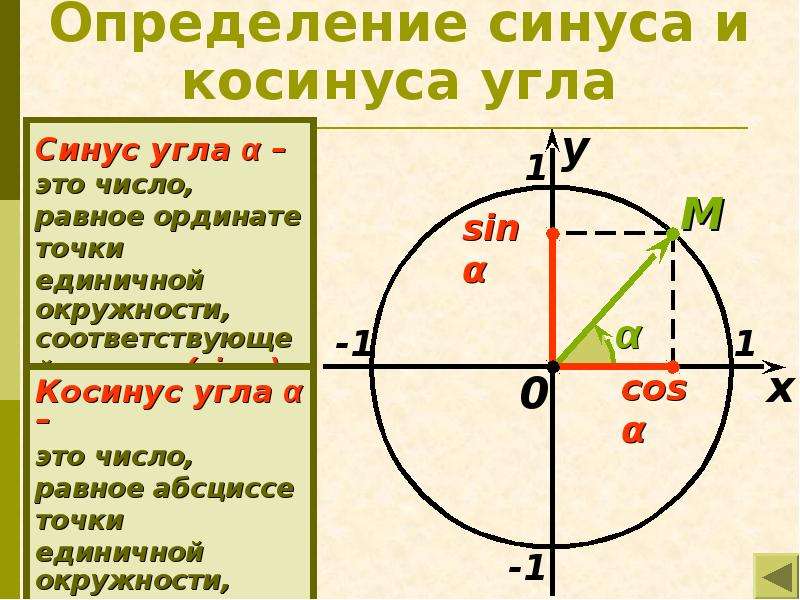 Нижняя часть, разделенная линией между углами (2), есть sin A. Линия между двумя углами, разделенная гипотенузой (3), есть cos B.Умножьте два вместе. Средняя линия находится как в числителе, так и в знаменателе, поэтому каждая из них отменяет и оставляет нижнюю часть противоположной точки над гипотенузой (4).
Нижняя часть, разделенная линией между углами (2), есть sin A. Линия между двумя углами, разделенная гипотенузой (3), есть cos B.Умножьте два вместе. Средняя линия находится как в числителе, так и в знаменателе, поэтому каждая из них отменяет и оставляет нижнюю часть противоположной точки над гипотенузой (4). 
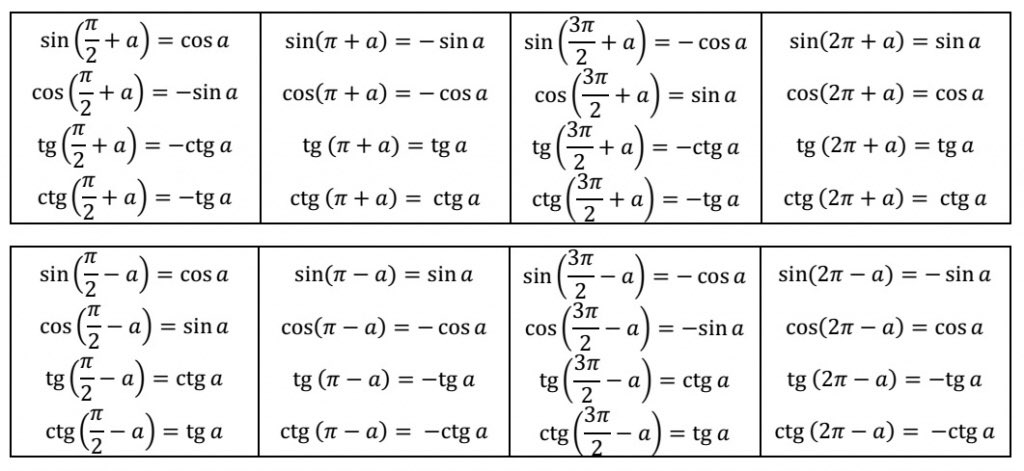 Вычитание дает cos (A + B) (8), поэтому нам нужна формула:
Вычитание дает cos (A + B) (8), поэтому нам нужна формула: После внесения основных замен в каждом случае черновая работа заключается в закрашивании — чтобы показать, как результат сводится к простейшей форме для оценки.
После внесения основных замен в каждом случае черновая работа заключается в закрашивании — чтобы показать, как результат сводится к простейшей форме для оценки.  Теперь воспользуйтесь этим методом для построения графиков.
Теперь воспользуйтесь этим методом для построения графиков. Вы начнете видеть закономерность в изменении этих тригонометрических соотношений углов.
Вы начнете видеть закономерность в изменении этих тригонометрических соотношений углов. Выполнение этой замены дает те же результаты, которые геометрически были получены в предыдущем разделе.
Выполнение этой замены дает те же результаты, которые геометрически были получены в предыдущем разделе.
 Это утверждение всегда верно, поскольку любое значение A.
Это утверждение всегда верно, поскольку любое значение A. Однако грех (А + А) на самом деле грех 2А. Итак, sin 2A — это sin A cos A + cos A sin A. Они оба являются одним и тем же произведением в противоположном порядке, поэтому это утверждение можно упростить до sin 2A = 2 sin A cos A.2 австралийских доллара
Однако грех (А + А) на самом деле грех 2А. Итак, sin 2A — это sin A cos A + cos A sin A. Они оба являются одним и тем же произведением в противоположном порядке, поэтому это утверждение можно упростить до sin 2A = 2 sin A cos A.2 австралийских доллара Равнобедренный треугольник используется несколько иначе. Но факт, на котором основано это использование, состоит в том, что равнобедренный треугольник имеет две равные стороны и два равных угла, противоположных этим двум сторонам. Перпендикуляр от третьего угла (не одного из равных) к третьей стороне (не одной из равных) делит эту третью сторону пополам.То есть он делит его на две равные части, превращая весь треугольник в зеркальные прямоугольные треугольники.
Равнобедренный треугольник используется несколько иначе. Но факт, на котором основано это использование, состоит в том, что равнобедренный треугольник имеет две равные стороны и два равных угла, противоположных этим двум сторонам. Перпендикуляр от третьего угла (не одного из равных) к третьей стороне (не одной из равных) делит эту третью сторону пополам.То есть он делит его на две равные части, превращая весь треугольник в зеркальные прямоугольные треугольники.
 + С.Сумма трех углов составляет 2A + 2B + 2C. Это, знаете ли, в сумме составляет 180 градусов.
+ С.Сумма трех углов составляет 2A + 2B + 2C. Это, знаете ли, в сумме составляет 180 градусов. Таким образом, все углы в окружности, основанной на одной и той же хорде, должны быть равны. Предположим, что хорда имеет угол 120 градусов. Углы на окружности будут ровно 60 градусов.
Таким образом, все углы в окружности, основанной на одной и той же хорде, должны быть равны. Предположим, что хорда имеет угол 120 градусов. Углы на окружности будут ровно 60 градусов.

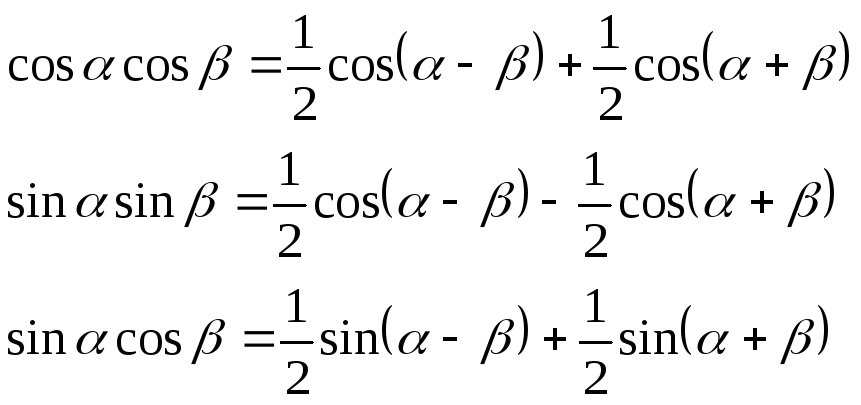
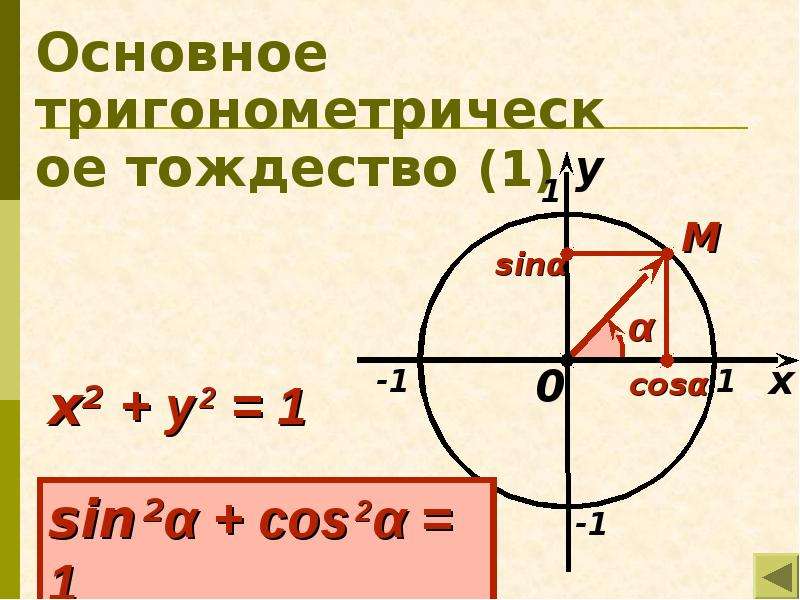
 .2 (x) = 1 $ можно доказать с помощью простой теоремы Пифагора в треугольнике с гипотенузой 1.
.2 (x) = 1 $ можно доказать с помощью простой теоремы Пифагора в треугольнике с гипотенузой 1.
 Поэтому я хочу дать ему очень четкое определение и уметь использовать все тригонометрические тождества.
Поэтому я хочу дать ему очень четкое определение и уметь использовать все тригонометрические тождества. Очевидно, что третья формула и четвертая эквивалентны (используйте свойство, чтобы увидеть это).
Очевидно, что третья формула и четвертая эквивалентны (используйте свойство, чтобы увидеть это). Для решения этой проблемы можно использовать множество способов. Воспользуемся приведенными выше формулами. У нас есть
Для решения этой проблемы можно использовать множество способов. Воспользуемся приведенными выше формулами. У нас есть Все права защищены.
Все права защищены.