Функции синуса и косинуса
Синус и косинус
| Синус и косинус: обзор Синус (сокращенно « sin «) и косинус (« cos «) являются двумя наиболее известными тригонометрические функции. Все остальные триггерные функции могут быть выражены через них. На самом деле синус и функции косинуса тесно связаны между собой и могут быть выражены через друг друга. Определение 1 — самое простое и интуитивно понятное определение функции синуса и косинуса. Определение синуса в основном говорит, что на прямоугольный треугольник, связаны следующие измерения:
С другой стороны, определение косинуса в основном говорит, что на прямоугольный треугольник, связаны следующие измерения:
Более того, определение I дает точное уравнения, описывающие каждое из этих отношений: sin(q) = противоположный / гипотенуза cos(q) = смежный / гипотенуза Это первое уравнение говорит, что если мы вычислим синус этого угла
q, мы получим точно такое же значение, как если бы мы разделили длину
стороны , противоположной , к этому углу на длину треугольника
гипотенуза. Основной результат таков: если мы знаем значения любых двух вышеуказанные величины, мы можем использовать приведенное выше соотношение для математически вывести третью величину. Например, синус Функция позволяет нам ответить на любой из следующих трех вопросов: «Данный прямоугольный треугольник, где измерение одного из неправильный углов (q) известна и длина сторона , противоположная , к этому углу q известна, найти длина гипотенузы треугольника ». «Данный прямоугольный треугольник, где измерение одного из непрямых углов (q) известны и длина известна гипотенуза треугольника , найти длина стороны , противоположной к этому углу q ». «Данный прямоугольный треугольник, где длина треугольник гипотенуза и длина одна из сторон треугольника известна, найти измерение угла (q) противоположного тому другая сторона ». Косинус аналогичен, за исключением того, что используется прилежащая сторона вместо противоположной стороны. Функции принимают вид y = sin(q) и х = cos(q) . Обычно q является измерением угла, а x и y обозначают длины. Функции синуса и косинуса, как и все триггерные функции, оценивают по-разному в зависимости от единиц на q, например градусов, радиан или градусов. Например, sin(90°) = 1, а sin(90)=0,89399…. объяснение Обе функции являются тригонометрическими кофункциями друг друга,
в той функции дополнительного угла, которая является «кофункцией»,
равна другой функции: sin(x) = cos(90°-x) и cos(x) = sin(90°-x). Более того, синус и косинус взаимно ортогональны . |
Это второе уравнение говорит, что если мы вычислим косинус этого угла
q, мы получим точно такое же значение, как если бы мы разделили длину
стороны рядом с к этому углу на длину треугольника
гипотенуза.
Эти соотношения справедливы для любого прямоугольного треугольника, независимо от
размера.
numpy.sin — Руководство NumPy v1.23
- Numpy.sin ( x , /, Out = None , * , где = true , Casting = ‘some_kind’ , Порядок = ‘K’ , Dtype = None 7070, , ‘K’ , DTYPE = None 70, , ‘K’ , DTYPE = None 70, . subok=True [ подпись , extobj ]) =
Тригонометрический синус, поэлементный.
- Параметры
- x array_like
Угол в радианах (\(2 \pi\) рад равен 360 градусам).
- out ndarray, None или кортеж из ndarray и None, необязательный
Местоположение, в котором сохраняется результат. Если он предусмотрен, он должен иметь форма, на которую транслируются входные данные.
- где array_like, необязательный
Это условие передается по входу. В местах, где условие равно True, массив из будет установлен в результат ufunc. В другом месте массив из сохранит исходное значение. Обратите внимание, что если неинициализированный массив из создан по умолчанию
out=None, места внутри него, где условие равно False, будут остаются неинициализированными.- **kwargs
Другие аргументы, содержащие только ключевые слова, см. документы ufunc.
- Возвращает
- y array_like
Синус каждого элемента x. Это скаляр, если x является скаляром.
См. также
-
arcsin,sinh,cos
Примечания
Синус — одна из фундаментальных функций тригонометрии (т.
математическое исследование треугольников). Рассмотрим круг радиуса 1
сосредоточены на происхождении. Луч входит от оси \(+x\), делает
угол в начале координат (измеряется против часовой стрелки от этой оси) и
уходит от истока. Координата \(y\) исходящего
пересечение луча с единичной окружностью есть синус этого угла. Это
варьируется от -1 для \(x=3\pi/2\) до +1 для \(\pi/2.\)
функция имеет нули там, где угол кратен \(\pi\).
Синусы углов между \(\pi\) и \(2\pi\) отрицательны.
Включены многочисленные свойства синуса и связанных с ним функций.
в любом стандартном тексте по тригонометрии.Примеры
Вывести синус одного угла:
>>> np.sin(np.pi/2.) 1,0
Вывести синусы массива углов, заданных в градусах:
>>> np.sin(np.array((0., 30., 45., 60., 90.)) * np.pi / 180. ) массив ([0., 0.5, 0.70710678, 0.8660254, 1.])
График функции синуса:
>>> импортировать matplotlib.pylab как plt >>> x = np.linspace(-np.pi, np.pi, 201) >>> plt.
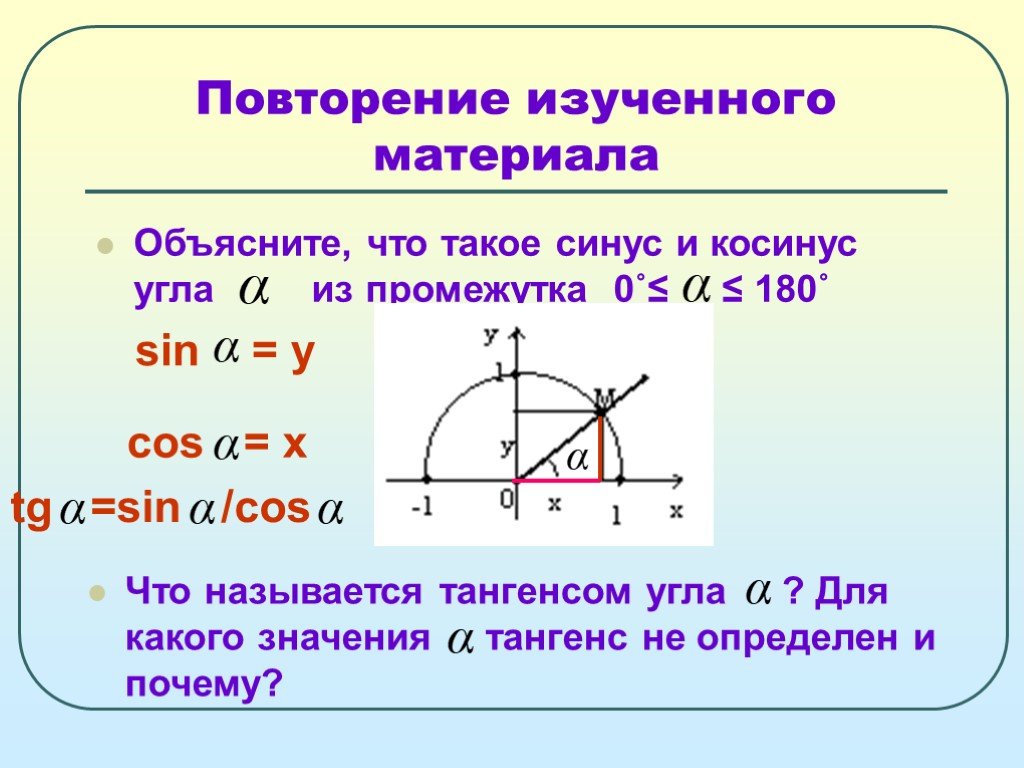
математическое исследование треугольников). Рассмотрим круг радиуса 1
сосредоточены на происхождении. Луч входит от оси \(+x\), делает
угол в начале координат (измеряется против часовой стрелки от этой оси) и
уходит от истока. Координата \(y\) исходящего
пересечение луча с единичной окружностью есть синус этого угла. Это
варьируется от -1 для \(x=3\pi/2\) до +1 для \(\pi/2.\)
функция имеет нули там, где угол кратен \(\pi\).
Синусы углов между \(\pi\) и \(2\pi\) отрицательны.
Включены многочисленные свойства синуса и связанных с ним функций.
в любом стандартном тексте по тригонометрии.