Косинус 15 чему равен – Чему равен косинус 15° градусов

Содержание

Чему равен косинус 15° градусов

Что такое косинус угла

Косинусом угла в прямоугольном треугольнике называется отношение длины противолежащего катета к длине гипотенузы.

На приведенном ниже рисунке для угла ‘х’ противолежащим катетом будет сторона ‘а’, а гипотенузой – сторона ‘с’. Таким образом, cos(х)=а/с.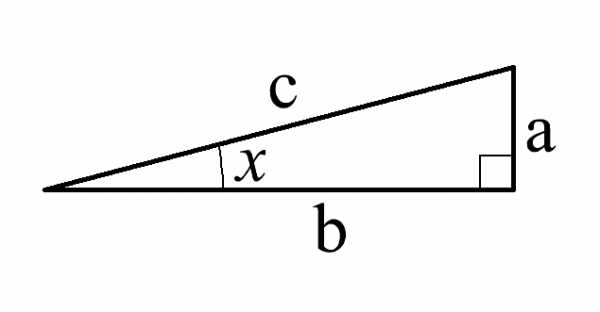

Как вычислить значение cos(15°)

Рассмотрим несколько способов вычисления этого значения.

Первый способ – по математическим таблицам

По таблицам Брадиса или с помощью калькулятора: cos(15°)=0,9659.

Второй способ – используя тригонометрические выражения

1) Так как угол 15° равен половине 30°, то его косинус можно рассчитать по формуле половинного угла:

Известно, что косинус угла 30° определяется простым выражением:

Подставляя значение cos(30°) в предыдущую формулу получим:

2) Угол 15° также можно представить как разность между 60° и 45°. Тогда косинус 15° можно рассчитать по тригонометрической формуле:

Значения косинусов и синусов углов 60° и 45° определяются простыми выражениями, подставляя которые в предыдущую формулу получим:

Третий способ – графически

Это наименее точный способ. Используя транспортир и линейку следует начертить прямоугольный треугольник произвольного размера, аналогичный показанному на рисунке. Затем с помощью линейки измерить длину сторон ‘а’ и ‘с’ треугольника и рассчитать их математическое отношение.

vovet.ru

cos 15 градусов

Если не использовать технические устройства, то косинус 15 градусов можно вычислить при помощи тригонометрических формул.
Один из вариантов — разложение аргумента функции 15 градусов на разницу 60 и 45 градусов. Почему именно на разность таких значений? Потому что они являются табличными, а, следовательно, можно применить формулу косинуса разности и вычислить косинус 15 градусов с помощью таблицы значений косинуса от основных углов, а также используя простые арифметические операции.

Выполним разложение косинуса 15 градусов на выше упомянутую разность:

Воспользуемся формулой косинуса разности:

Значения функций, которые присутствуют в выражении, можно получить из выше упомянутой таблицы значений синусов и косинусов:

Найдем приближенное значение:

Существует еще один возможный способ, не прибегая к применению формул, чтобы вычислить значение тригонометрической функции — это применение таблиц Брадиса.
По таблицам косинус 15 градусов равен 0,9659 — значение округлено до четырех знаков дробной части. При помощи тригонометрических формул было получено более точное значение.

ru.solverbook.com

Синус, ко синус, тангенс угла 15 градусов (sin 15 cos 15 tg 15)

Как найти значения тригонометрических функций для угла 15 градусов

Найдем значения синуса, косинуса и тангенса для угла 15 градусов аналитическим способом.
На первый взгляд, нахождение значений синуса, косинуса и тангенса для угла 15 градусов — задача сложная. Однако, это не совсем так.
Нам на помощь придут формулы преобразования двойного угла тригонометрических функций.

Дело в том, что мы можем представить угол в 30 градусов, как двойной угол 15 градусов ( 2 * 15 ).

Тогда, отталкиваясь от тождества:
cos 2α = 1 — 2sin²α

Принимаем двойной угол как 2 * 15 градусов, тогда
cos 30 = 1 — 2sin²15
sin²15 = ( 1 — cos 30 ) / 2

Значение косинуса для угла 30 градусов легко вычислить. Оно равно √3/2
sin²15 = ( 1 — √3/2 ) / 2
sin 15 = √ (( 1 — √3/2 ) / 2 )
верхнюю часть дроби под корнем приведем к общему знаменателю (2)

sin 15 = √ (( (2 — √3) /2 ) / 2 ) = √( (2 — √3) / 4 )
теперь у нас одна дробь под знаком корня. Умножим числитель и знаменатель на два
sin 15 = √( (2 — √3) / 4 ) = √( (4 — 2√3) / 8 )
самый интересный момент, мы можем представить 4 — 2√3 как (√3-1)²
тогда
sin 15 = √( (√3-1)² / 8 ) = (√3-1)/ √8 = (√3-1)/ (2√2)

путем несложных агебраических преобразований получаем:

Как видно из примера, значения тригонометрических функций углов синуса, косинуса и тангенса 15 градусов могут быть получены путем несложных тригонометрических преобразований с использованием тригонометрических тождеств преобразований двойных углов и половин заданных углов.

См. также полную таблицу значений тригонометрических функций (таблицу синусов, косинусов и тангенсов).

Ниже приведены также значения тригонометрических функций для угла 15 градусов в виде десятичной дроби с четырьмя знаками после запятой.

π/12	синус 15 sin 15	косинус 15 cos 15	тангенс 15 tg 15	котангенс 15 ctg 15
Значение	0.2588190451	0.96592582628	0.26794919243	3.73205080757

Таблица значений тригонометрических функций | Описание курса | Синус, косинус и тангенс угла 30 градусов (sin cos tg 30) — таблица значений

profmeter.com.ua

Чему равен sin 15 и cos 15 (и подробно опишите схему нахождения) Не надо говорить , чтоб я заглянул в таблицу Брадиса

Чертите с помощью циркуля окружность единичного радиуса (1 см, 1дм, 1 м и т. д.) . С помощью транспортира откладываете от оси Х угол равный 15 градусов и проводите под этим углом радиус. Замеряете с помощью линейки расстояние от точки пересечения радиуса с окружностью до оси Х, говоря научным языком, определяете ординату этой точки. Так вот эта длина и будет синусом угла 15 градусов. Удачи и успехов в вашем нелегком деле!!!

Загляни в калькулятор.

1. Берешь открываешь калькулятор Windows, набираешь «15» и нажимаешь «sin» или «cos» 2. Берёшь обычный инженерный калькулятор и проводишь те же манипуляции 3. Открываешь таблицу брадиса и ищешь : <a rel=»nofollow» href=»http://bradis-table.narod.ru/» target=»_blank»>http://bradis-table.narod.ru/</a>

Можно найти из формул синус 30 =2 (синус 15) (косинус 15) косинус 30 =(косинус 15)^2 — (синус 15)^2

sin15°=√[(1-cos30°)/2]=√[(1-√3/2)/2]=√[(2-√3)/4]≈0.259; cos15°=√[(1+cos30°)/2]=√[(1+√3/2)/2]=√[(2+√3)/4]≈0.966. Используйте формулы половинного угла.

touch.otvet.mail.ru

sin 15 градусов

Один из способов как найти синус 15 градусов, не применяя технические средства — это использование тригонометрических формул.
Например, аргумент 15 градусов можно разложить как разность 60 и 45 градусов, а эти величины являются табличными. Таким образом, можно воспользоваться формулой синуса разности и вычислить синус 15 градусов с помощью таблицы значений основных тригонометрических функций и простых арифметических действий.
Итак, разложим синус 15 градусов на разность двух аргументов:

Применим формулу синуса разности двух аргументов:

Поскольку получившиеся тригонометрические функции можно вычислить с помощью таблицы значений синуса и косинуса от 60 и 45 градусов, получим:

Можно вычислить приближенное значение получившейся дроби:

Еще одним способом, без применения формул, является использование для вычисления значений тригонометрических функций от любых углов таблиц Брадиса.
Согласно этим таблицам значение синуса 15 градусов равно 0,258819, что не на много отличается от полученного приближенного значения, которое было вычислено аналитическим путем.