Расчет вероятности объединения (логической суммы) событий
Объединением
(логической суммой)
N событий  называют событие
называют событие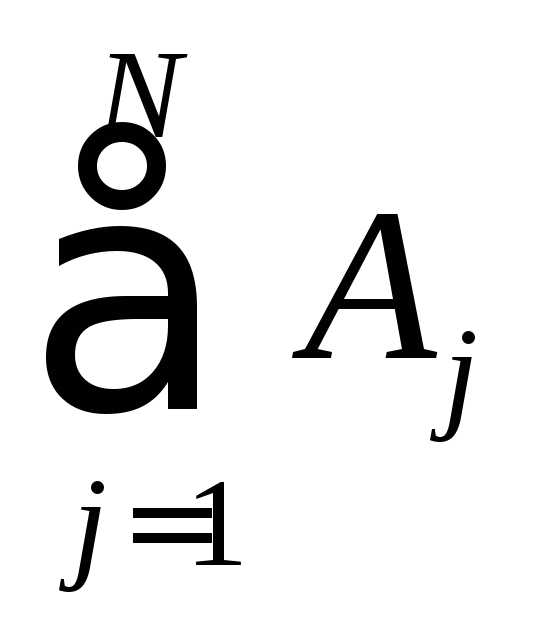 ,
которое наблюдается каждый раз, когда
наступаетхотя бы одно изсобытий
,
которое наблюдается каждый раз, когда
наступаетхотя бы одно изсобытий .
В частности, объединением
событий A и B
называют событие A+B (у некоторых авторов
.
В частности, объединением
событий A и B
называют событие A+B (у некоторых авторов 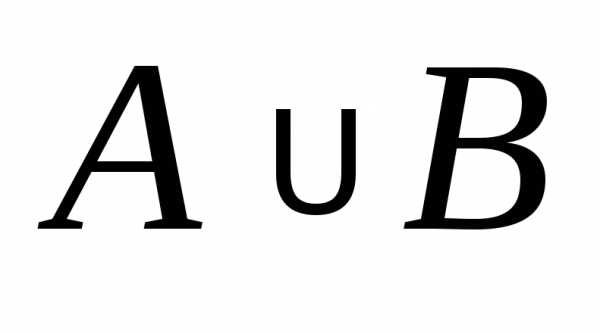 ),
которое наблюдается, когданаступает или A, или B или оба этих события одновременно(Рис. 7).
Признаком пересечения в текстовых
формулировках событий служит союз“или”.
),
которое наблюдается, когданаступает или A, или B или оба этих события одновременно(Рис. 7).
Признаком пересечения в текстовых
формулировках событий служит союз“или”.

Рис. 7. Объединение событий A+B
Необходимо
учитывать, что вероятности события
P{A} соответствует
как левая часть заштрихованной на Рис. 7
фигуры, так и её центральная часть,
помеченная как 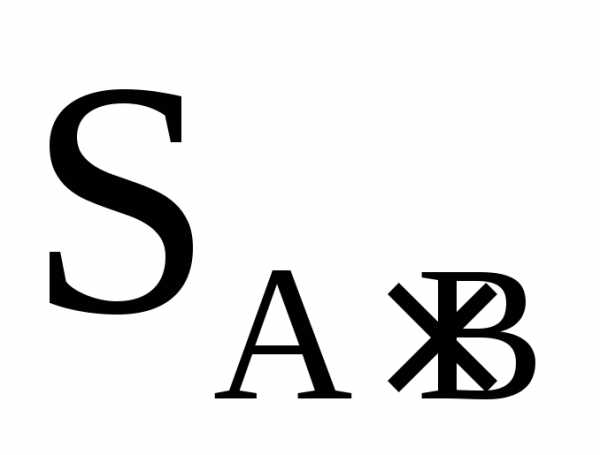 .
И исходы, соответствующие
событию B,
располагаются как в правой части
заштрихованной
фигуры, так и в помеченной
.
И исходы, соответствующие
событию B,
располагаются как в правой части
заштрихованной
фигуры, так и в помеченной 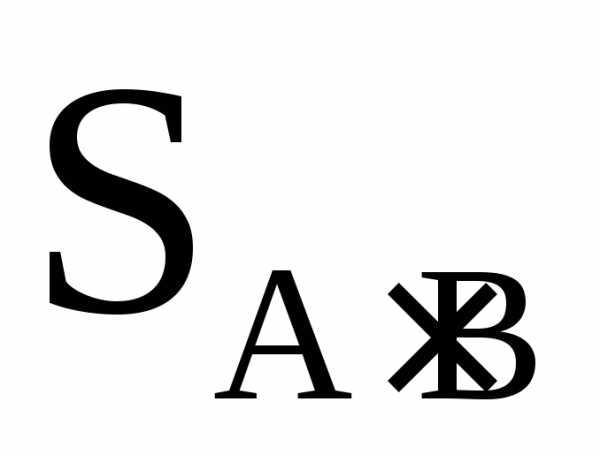 центральной части. Таким образом,
при сложении
центральной части. Таким образом,
при сложении и
и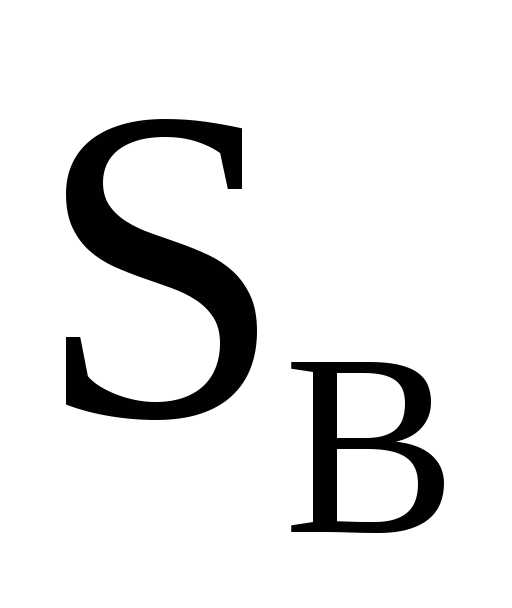 площадка
площадка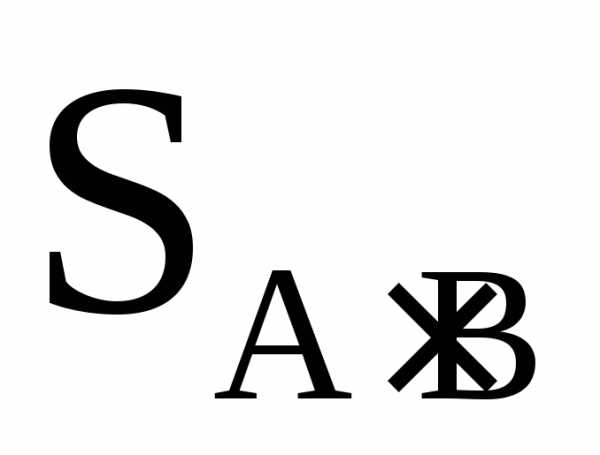 реально войдет в эту сумму дважды, а
точное выражение для площади заштрихованнойфигуры имеет
вид.
реально войдет в эту сумму дважды, а
точное выражение для площади заштрихованнойфигуры имеет
вид.
Итак, вероятность объединения двух событий A и B равна
, | (2.0) |
Аналогично из анализа характера взаимного наложения трёх геометрических областей для объединения трёх совместных событий можно получить расчетное выражение
(2.0) |
Для большего числа событий общее расчетное выражение становится крайне громоздким из-за необходимости учета многочисленных вариантов взаимного наложения областей. Однако, если объединяемые события являются несовместными (см. с. 33), то взаимное наложение областей оказывается невозможным, а благоприятная зона определяется непосредственно суммой областей, соответствующих отдельным событиям.
Вероятность объединения произвольного числанесовместныхсобытий определяется выражением
определяется выражением
(2.0) |
Следствие 1:
Полная группа
событий состоит из событий
несовместных, одно из которых в опыте
обязательно реализуется. В результате,если события  …
… ,образуют
полную группу,
то для них
,образуют
полную группу,
то для них
| (2.0) |
Следствие 2: Два противоположных события всегда образуют полную группу, поэтому
(2.0) |
Таким образом,
(2.0) |
Следствие
3 Учтем,
что противоположным
утверждению «произойдет хотя бы
одно из событий  …
…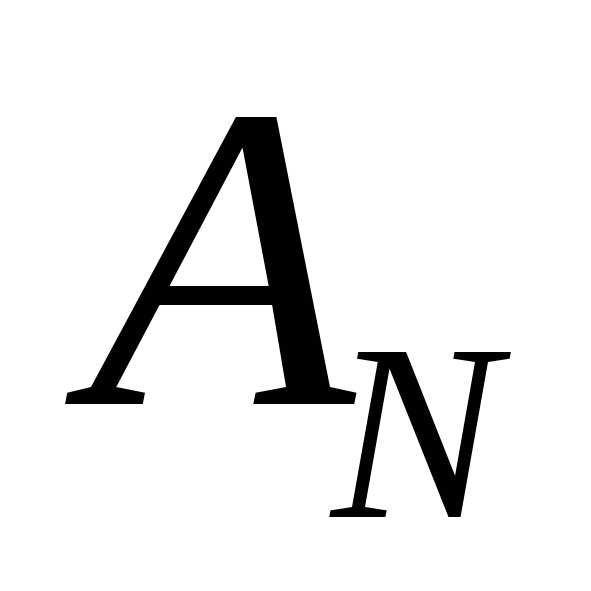 »
является утверждение «ни одно из событий
»
является утверждение «ни одно из событий …
… не реализуется». Т.е., иначе говоря, «в
опыте будут наблюдаться события
не реализуется». Т.е., иначе говоря, «в
опыте будут наблюдаться события ,
и
,
и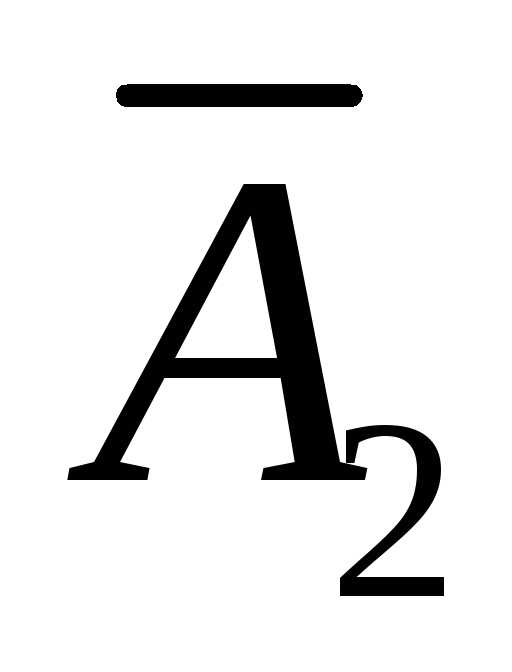 ,
и …, и
,
и …, и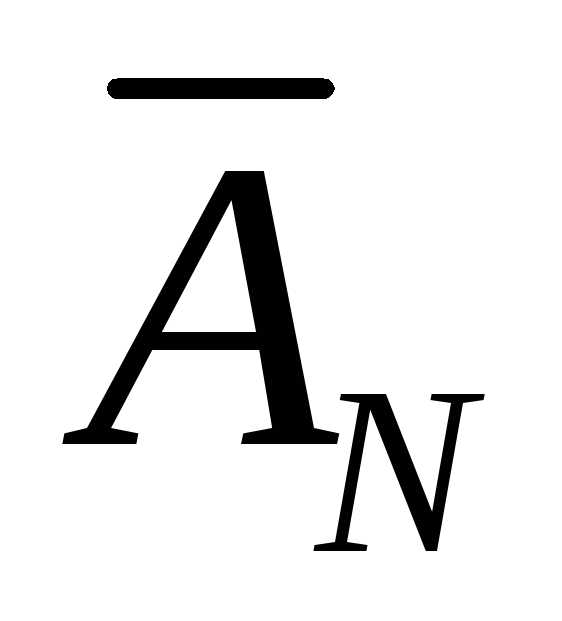 »,
что представляет собой уже пересечение
событий, противоположных исходному
набору. Отсюда, с учетом ( 2 .0), для
объединения произвольного числа событий
получаем
»,
что представляет собой уже пересечение
событий, противоположных исходному
набору. Отсюда, с учетом ( 2 .0), для
объединения произвольного числа событий
получаем
(2.0) |
Следствия
2, 3 показывают, что в тех случаях, когда
непосредственный расчет вероятности
какого-то события является проблематичным,
полезно оценить
трудоёмкость исследования события
ему противоположного. Ведь, зная значение 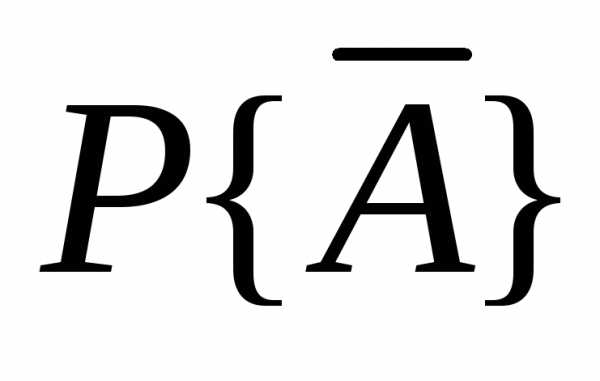 ,
получить из ( 2 .0) нужную величину
,
получить из ( 2 .0) нужную величину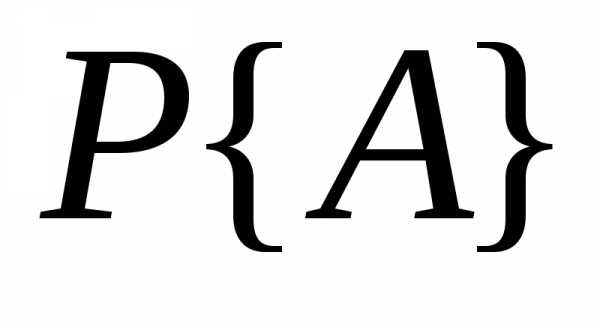 никакого труда уже не представляет.
никакого труда уже не представляет.
Примеры расчетов вероятностей сложных событий
Пример 1: Двое студентов (Иванов и Петров) вместе явились на защиту лабораторной работы, выучив первые 8 контрольных вопросов к этой работе из 10 имеющихся. Проверяя подготовленность, преподаватель задает каждому лишь один случайно выбираемый вопрос. Определить вероятность следующих событий:
A = “Иванов защитит лабораторную работу”;
B = “Петров защитит лабораторную работу”;C = “оба защитят лабораторную работу”;
D = “хотя бы один из студентов защитит работу”;
E = “только один из студентов защитит работу”;
F = “никто из них не защитит работу”.
Решение.Отметим, что способность защитить работу как Иванова, так и Петрова в отдельности определяется лишь числом освоенных вопросов, поэтому . (Примечание: в данном примере значения получаемых дробей сознательно не сокращались для упрощения сопоставления результатов расчетов.)
Событие C можно сформулировать иначе как «работу
защитит и Иванов, и Петров», т.е. произойдут и событие A, и событие B.
Таким образом, событие
,
где сомножитель “7/9” появляется из-за того, что наступление события A означает, что Иванову достался «удачный» вопрос, а значит на долю Петрова из оставшихся 9 вопросов приходится теперь лишь 7 «хороших» вопросов.
Событие D подразумевает, что «работу защитит или Иванов, или Петров, или они оба вместе», т.е. произойдёт хотя бы одно из событий A и B. Итак, событие D является объединением событий A и B, и в соответствии с ( 2 .0)
,
что соответствует ожиданиям, т.к. даже для каждого из студентов в отдельности шансы на успех довольно велики.
Событие Е означает, что «либо работу защитит Ивано
в, а Петров «провалится», или Иванову попадется неудачный вопрос, а Петров с защитой справится». Два альтернативных варианта являются взаимоисключающими (несовместными), поэтому,
Наконец, утверждение F окажется справедливым лишь если «и Иванов, и Петров с защитой не справятся». Итак,
.
На этом решение задачи завершено, однако полезно отметить следующие моменты:
1. Каждая из
полученных вероятностей удовлетворяет
условию ( 1 .0), но
если для 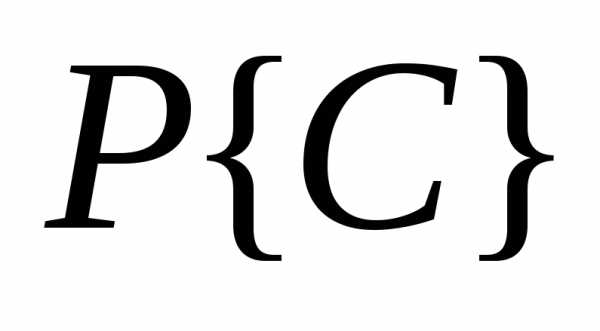 и
и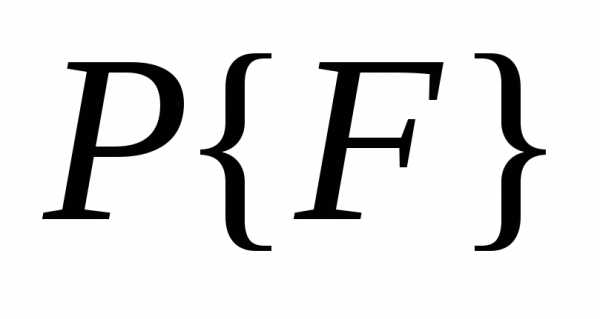 получить
конфликтующие с ( 1 .0) в
принципе невозможно, то для
получить
конфликтующие с ( 1 .0) в
принципе невозможно, то для  попытка использования
( 2 .0) вместо ( 2 .0) привела бы к явно
некорр
попытка использования
( 2 .0) вместо ( 2 .0) привела бы к явно
некорр
2. Найденные вероятности удовлетворяют соотношениям
,
.
Это вполне ожидаемо, т.к. события C, E и F образуют полную группу, а события D и F противоположны друг другу. Учет этих соотношений с одной стороны может быть использован для перепроверки расчетов, а в другой ситуации может послужить основой альтернативного способа решения задачи.
Примечание: Не пренебрегайте письменной фиксацией точной формулировки события, иначе по ходу решения задачи Вы можете непроизвольно перейти к иной трактовке смысла этого события, что повлечет ошибки в рассуждениях.
Пример 2: В крупной партии микросхем, не прошедших выходной контроль качества, 30% изделий являются бракованными. Если из этой партии наугад выбрать какие-либо две микросхемы, то какова вероятность, что среди них:
A = “обе годные”;
B = “ровно 1 годная микросхема”;
C = “обе бракованные”.
Проанализируем следующий вариант рассуждений (осторожно, содержит ошибку):
Так как речь идет о крупной партии изделий, то изъятие из неё нескольких микросхем практически не влияет на соотношение числа годных и бракованных изделий, а значит, выбирая несколько раз подряд какие-то микросхемы из этой партии, можно считать, что в каждом из случаев остаются неизменными вероятности

 = P{
выбрано годное изделие } = 0,7.
= P{
выбрано годное изделие } = 0,7.
Для наступления события A необходимо, чтобы и в первый, и во второй раз было выбрано годное изделии, а потому (учитывая независимость друг от друга успешности выбора первой и второй микросхемы) для пересечения событий имеем
.
Аналогично, для наступления события С нужно, чтобы оба изделия оказались бракованными , а для получения B нужно один раз выбрать годное, а один – бракованное изделие.
Признак ошибки.Хотя все полученные выше вероятности выглядят правдоподобными, при их совместном анализе легко заметить, что .Однако случаи A, B и C образуют полную группу событий, для которой должно выполняться .Это противоречие указывает на наличие какой-то ошибки в рассуждениях.
Суть ошибки. Введем в рассмотрение два вспомогательных события:
 = “первая
микросхема – годная, вторая — бракованная”;
= “первая
микросхема – годная, вторая — бракованная”;
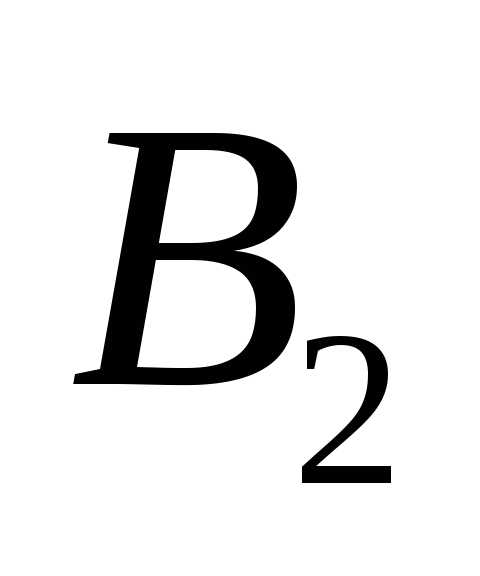 =
“первая микросхема – бракованная,
вторая – годная”.
=
“первая микросхема – бракованная,
вторая – годная”.
Очевидно, что
,
однако именно такой вариант расчета
был выше использован для получения
вероятности событияB,
хотя события B и  не являются эквивалентными.
На самом деле, ,
т.к. формулировкасобытия B требует, чтобы среди микросхем ровно одна, но совсем не
обязательно первая была годной
(а другая – бракованной). Поэтому, хотя событие
не являются эквивалентными.
На самом деле, ,
т.к. формулировкасобытия B требует, чтобы среди микросхем ровно одна, но совсем не
обязательно первая была годной
(а другая – бракованной). Поэтому, хотя событие 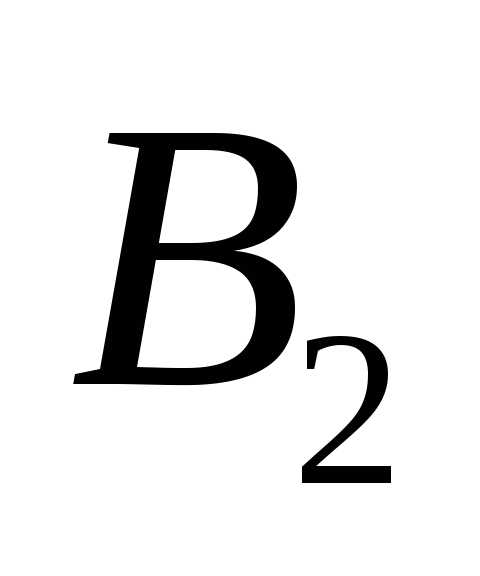 не является дублем события
не является дублем события ,
а должно учитываться независимо.
Учитывая несовместность событий
,
а должно учитываться независимо.
Учитывая несовместность событий  и
и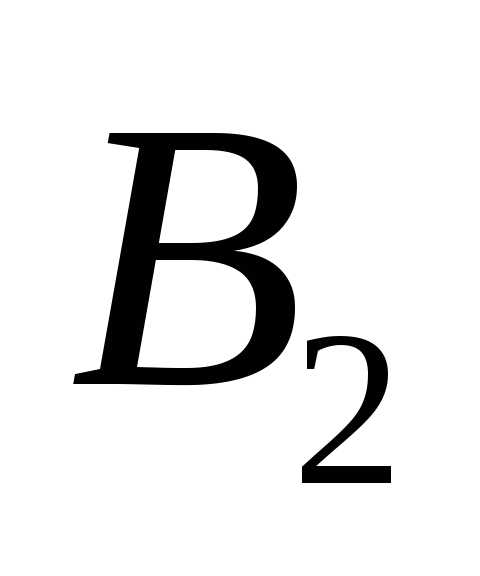 , вероятность их логической суммы будет
равна
, вероятность их логической суммы будет
равна
.
После указанного исправления расчетов имеем
что косвенно подтверждает корректность найденных вероятностей.
Примечание: Обращайте особое внимание на отличие в формулировках событий типа “только первый из перечисленных элементов должен…” и “только один из перечисленных элементов должен…”. Последнее событие явно шире и включает в свой состав первое как один из (возможно многочисленных) вариантов. Эти альтернативные варианты (даже при совпадении их вероятностей) следует учитывать независимо друг от друга.
Примечание: Слово “процент” произошло от “per cent”, т.е. “на сотню”. Представление частот и вероятностей в процентах позволяет оперировать более крупными значениями, что иногда упрощает восприятие значений “на слух”. Однако использовать в расчетах для правильной нормировки умножение или деление на “100 %” громоздко и неэффективно. В связи с этим, не забывайте при использовании значений, упомянутых в процентах, подставлять их в расчетные выражения уже в виде долей от единицы (например, 35% в расчете записывается как “0,35”), чтобы минимизировать риск ошибочной нормировки результатов.
Пример 3: Набор резисторов содержит один резистор номиналом 4 кОм, три резистора по 8 кОм и шесть резисторов с сопротивлением 15 кОм. Выбранные наугад три резистора соединяются друг с другом параллельно. Определить вероятность получения итогового сопротивления, не превышающего 4 кОм.
Решение. Сопротивление параллельного соединения резисторов может быть рассчитано по формуле
.
Это позволяет ввести в рассмотрение события, такие как
A = “выбраны три резистора по 15 кОм” = “”;
B = “взяты два резистора по 15 кОм и один с сопротивлением 8 кОм” =“”…
Полная группа событий, соответствующих условию задачи, включает ещё целый ряд вариантов, причем именно таких, которые соответствуют выдвинутому требованию о получении сопротивления не более чем 4 кОм. Однако, хотя “прямой” путь решения, предполагающий расчет (и последующее суммирование) вероятностей, характеризующих все эти события, и является правильным, действовать таким образом нецелесообразно.
Отметим, что для получения итогового сопротивления менее 4 кОм достаточно, чтобы в используемый набор вошел хотя бы один резистор с сопротивлением менее 15 кОм. Таким образом, лишь в случае A требование задачи не выполняется, т.е. событие A является противоположным исследуемому. Вместе с тем,
.
Таким образом, .
Примечание:
Рассчитывая вероятность некоторого
события A,
не забывайте проанализировать трудоемкость
определения вероятности
события ему противоположного. Если
рассчитать  легко, то
именно с этого и надо начинать решение
задачи, завершая его применением
соотношения ( 2 .0).
легко, то
именно с этого и надо начинать решение
задачи, завершая его применением
соотношения ( 2 .0).
Пример 4: В коробке имеются n белых, m черных и k красных шаров. Шары по одному наугад извлекаются из коробки и возвращаются обратно после каждого извлечения. Определить вероятность события A = “белый шар будет извлечен раньше, чем черный”.
Решение. Рассмотрим следующую совокупность событий
 = “белый шар
извлекли при первой же попытке”;
= “белый шар
извлекли при первой же попытке”;
 = “сначала вынули
красный шар, а затем — белый”;
= “сначала вынули
красный шар, а затем — белый”;
 =
“дважды вынули красный шар, а на третий
раз — белый”…
=
“дважды вынули красный шар, а на третий
раз — белый”…
Так как
шарики возвращаются, то последовательность
событий  может быть формально бесконечно
протяженной.
может быть формально бесконечно
протяженной.
Эти события являются несовместными и составляют в совокупности тот набор ситуаций, при которых происходит событие A. Таким образом,
Несложно заметить, что входящие в сумму слагаемые образуют геометрическую прогрессию с начальным элементом и знаменателем. Но сумма элементов бесконечной геометрической прогрессии равна
| (2.0) |
Таким образом, . Любопытно, что эта вероятность (как следует из полученного выражения) не зависит от числа красных шаров в коробке.
studfiles.net
Расчет вероятности сложных событий
Понятие сложного события
Если анализируемой задаче (ситуации) нельзя поставить в соответствие набор равновозможных исходов, то ни алгебраический, ни геометрический методы использовать для расчета вероятностей оказывается невозможно. В подобной ситуации имеет смысл попытаться представить анализируемые (сложные) события как логическую комбинацию каких-то более простых утверждений, для каждого из которых вероятность реализации известна или может быть рассчитана. Правила расчета вероятности итогового сложного события по вероятностям событий, его образующих, устанавливаются ниже.
Расчет вероятности пересечения (логического произведения) событий
Пересечением
(логическим произведением) N событий называют событие
называют событие  ,
заключающееся в наступлениивсех событий
,
заключающееся в наступлениивсех событий в одном опыте. В частности, пересечением
двух
в одном опыте. В частности, пересечением
двух
событий AиBназывают событиеA∙B, наблюдаемое, когда и A, и B наступают в одном и том же опыте. Признаком пересечения в текстовых формулировках событий служит союз“и”.
Примечание: Некоторые авторы для обозначения
пересечения и объединения событий
применяют символы 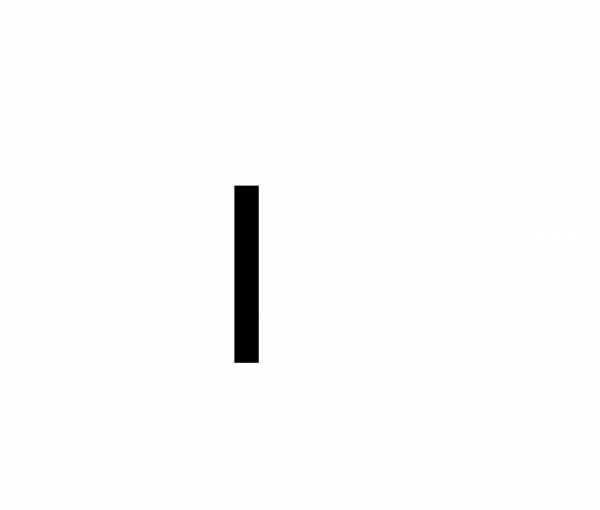 и
и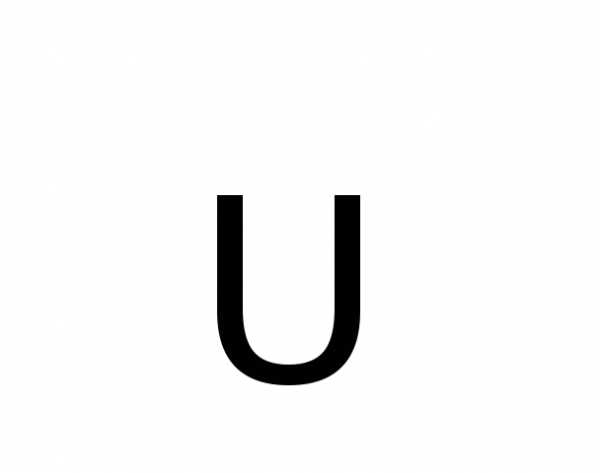 соответственно,
но в настоящем пособии эти символы не
используются.
Как правило, явной потребности в подобных
специфичных
символах не возникает,
а использование вместо символа
соответственно,
но в настоящем пособии эти символы не
используются.
Как правило, явной потребности в подобных
специфичных
символах не возникает,
а использование вместо символа 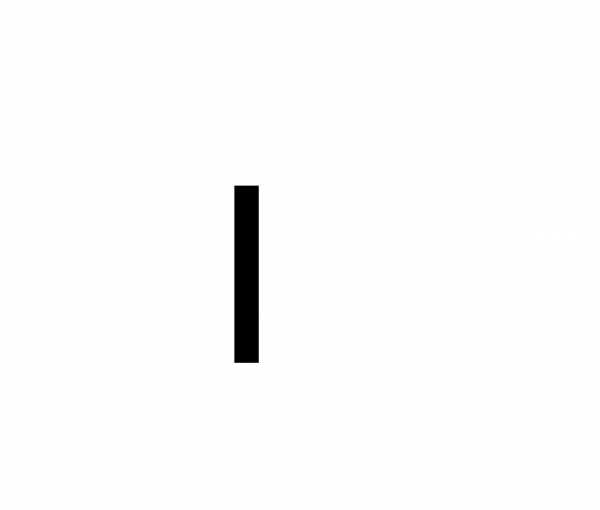 значка произведения и вместо
значка произведения и вместо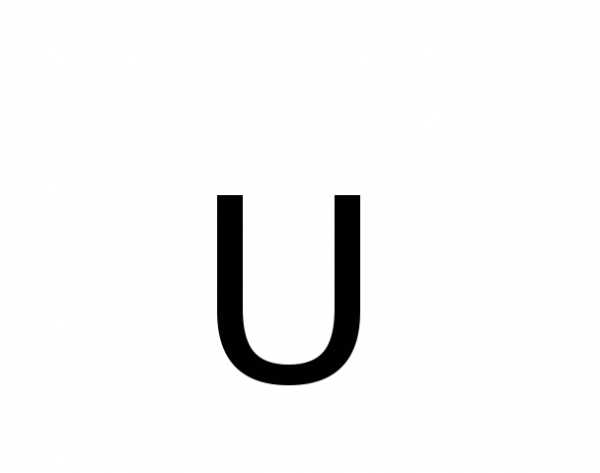 –
знака суммы к неясностям, как правило,
не приводит, но позволяет достичь большей
компактности записи.
–
знака суммы к неясностям, как правило,
не приводит, но позволяет достичь большей
компактности записи.
Для упрощения
рассуждений, определяющих правило
расчета вероятности
пересечения событий, будем полагать,
что возможным исходам анализируемого
опыта можно поставить в соответствие
какое-то геометрическое
место точек на плоскости. Вероятность
пересечения событийAиBбудет отличной от нуля
только если существует некая общая для
этих событий совокупность исходов.
Подобная ситуация представлена на Рис. 6,
гдесобытию A
соответствует группа точек, помеченная  ,
событиюB
– группа точек с пометкой
,
событиюB
– группа точек с пометкой 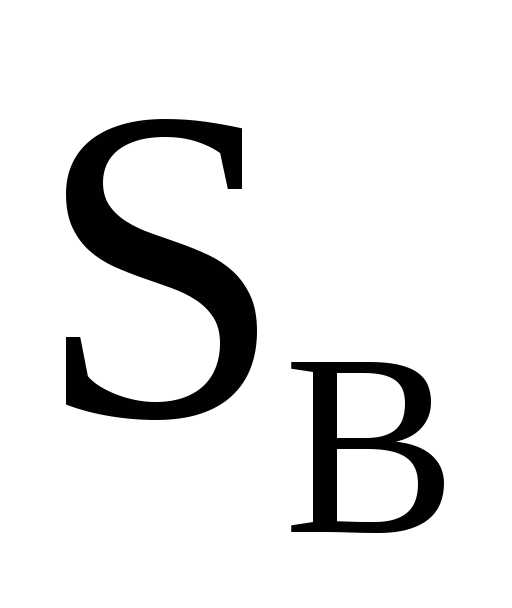 ,
а исходам общим для этих событий –
центральная область с площадью
,
а исходам общим для этих событий –
центральная область с площадью  .
.
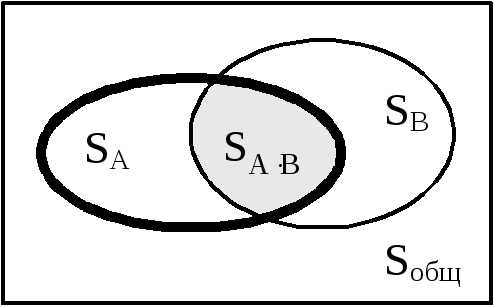
Рис. 6. Пересечение событий A∙B
Представим
временно, что вместо исходного эксперимента
мы проводим опыты, в которых событиеAгарантированно происходит. При подобном
изменении ситуации в качестве
геометрического места
точек, соответствующего всем исходам
опыта, выступала бы лишь площадка  ,
выделенная на Рис. 6жирной линией.
Соответственно, вероятность наблюдения
в этих условиях событияB(помимо обязательного событияA)
определялась бы соотношением площадей
,
выделенная на Рис. 6жирной линией.
Соответственно, вероятность наблюдения
в этих условиях событияB(помимо обязательного событияA)
определялась бы соотношением площадей 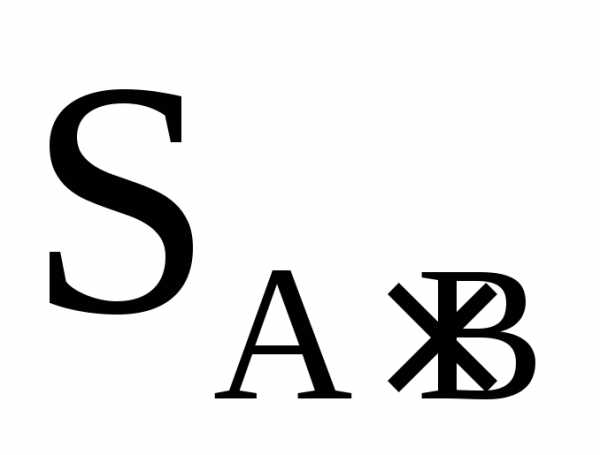 и
и .
Применительно же к условиям исходного
эксперимента указанное отношение есть
ни что иное, как условная вероятность
событияB
.
Применительно же к условиям исходного
эксперимента указанное отношение есть
ни что иное, как условная вероятность
событияB
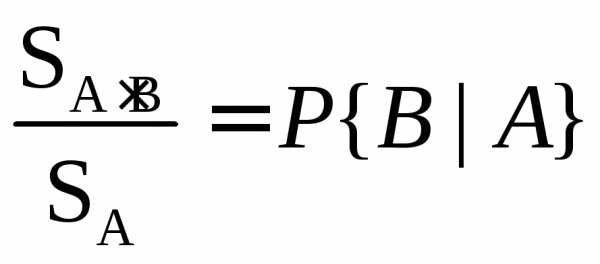 .
.
Возвращаясь к расчету вероятности пересечения событийAиB, в соответствии с геометрическим подходом получаем
.
Итак, вероятность пересечения двух событий A и B равна
, | (2.0) |
где P{B|A} – условная вероятность события B, т.е. вероятность, вычисленная при условии, что событие A уже произошло; P{A|B} – условная вероятность события А, определяющая возможность наступления этого события при уже свершившемся событии B.
Вероятность
пересечения произвольного числа N событий определяется выражением
определяется выражением
, | (2.0) |
где, в частности,
– это вероятность наступления события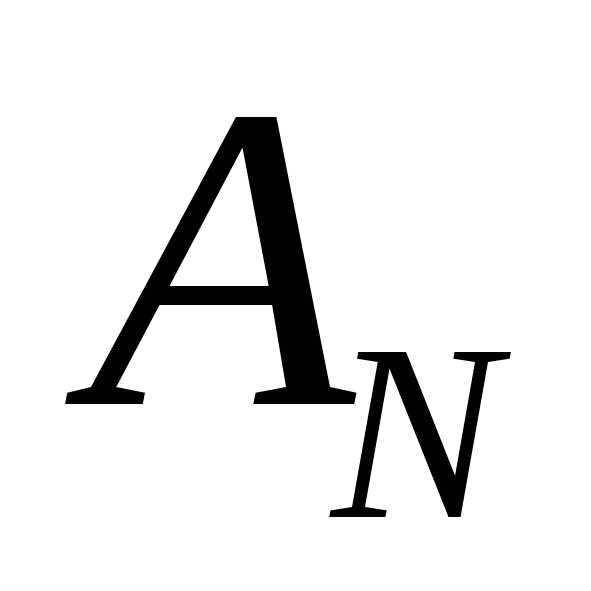 ,
вычисленная при условии,
что все события начиная с
,
вычисленная при условии,
что все события начиная с  и до
и до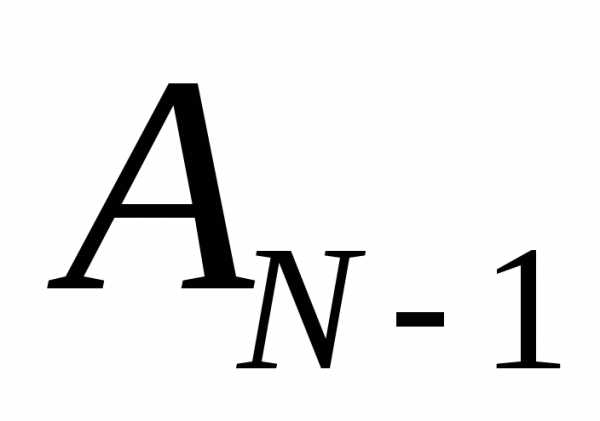 совершились.
совершились.
studfiles.net
Формулы для вычисления вероятности событий
1.3.1. Последовательность независимых испытаний (схема Бернулли)
Предположим, что некоторый эксперимент можно проводить неоднократно при одних и тех же условиях. Пусть этот опыт производится n раз, т. е. проводится последовательность из n испытаний.
Определение. Последовательность n испытаний называют взаимно независимой, если любое событие, связанное с данным испытанием, не зависит от любых событий, относящихся к остальным испытаниям.
Допустим, что некоторое событие A может произойти с вероятностью p в результате одного испытания или не произойти с вероятностью q=1—p.
Определение. Последовательность из n испытаний образует схему Бернулли, если выполняются следующие условия:
последовательность n испытаний взаимно независима;
2) вероятность события A не изменяется от испытания к испытанию и не зависит от результата в других испытаниях.
Событие A называют “ успехом” испытания, а
противоположное событие  — “неудачей”. Рассмотрим событие
— “неудачей”. Рассмотрим событие
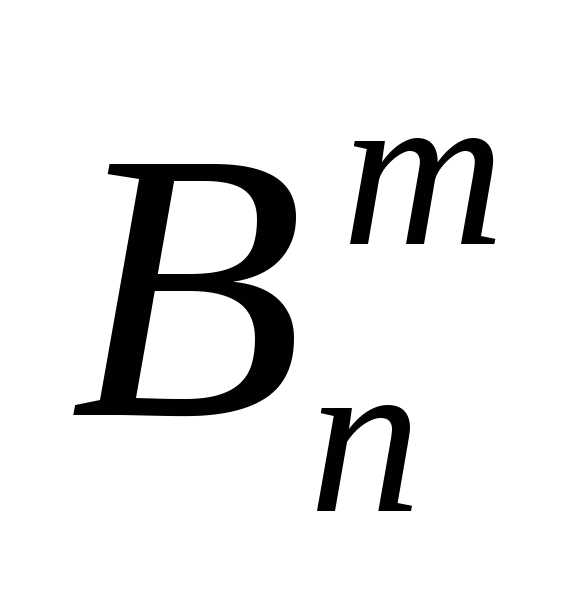 ={
в n испытаниях произошло ровно m “успехов”}.
={
в n испытаниях произошло ровно m “успехов”}.
Для вычисления вероятности этого события справедлива формула Бернулли
p(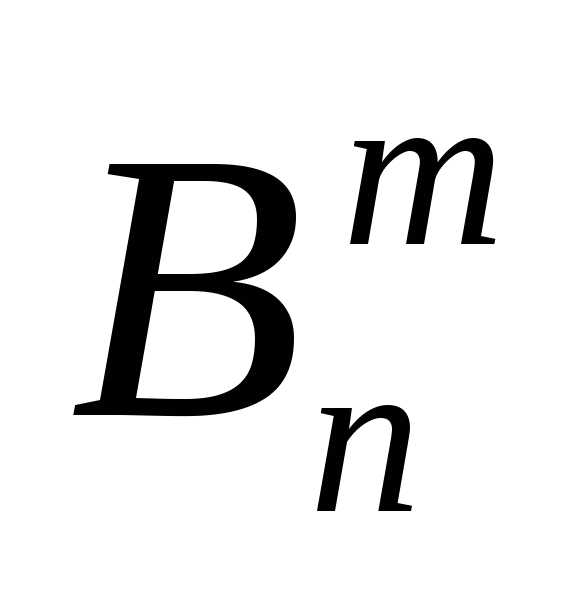 )
=
)
= 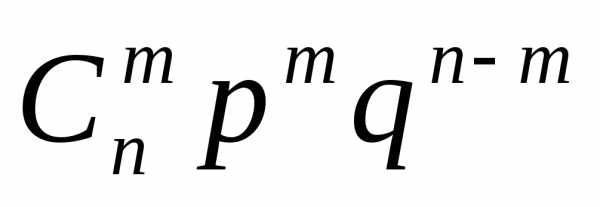 , m = 1, 2, …, n , (1.6)
, m = 1, 2, …, n , (1.6)
где 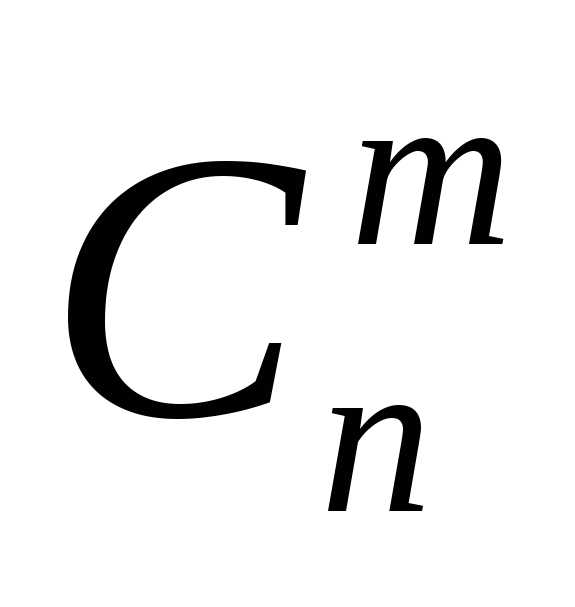 — число сочетаний из n элементов по m :
— число сочетаний из n элементов по m :
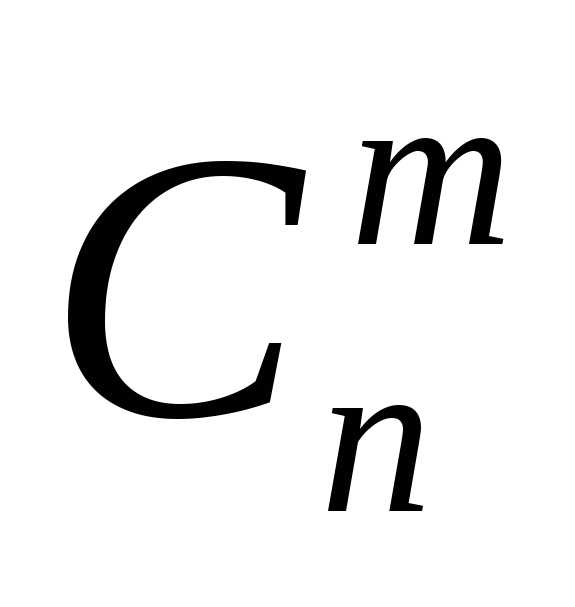 =
= 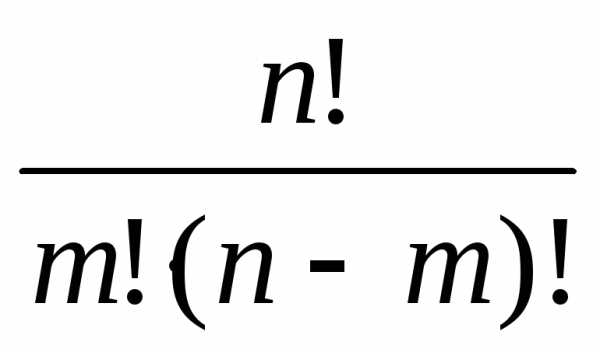 =.
=.
Пример 1.16. Три раза подбрасывают кубик. Найти:
а) вероятность того, что 6 очков выпадет два раза;
б) вероятность того, что число шестерок не появится более двух раз.
Решение. “Успехом” испытания будем считать выпадение на кубике грани с изображением 6 очков.
а)
Общее число испытаний – n =3,
число “успехов” – m =
2. Вероятность “успеха” — p=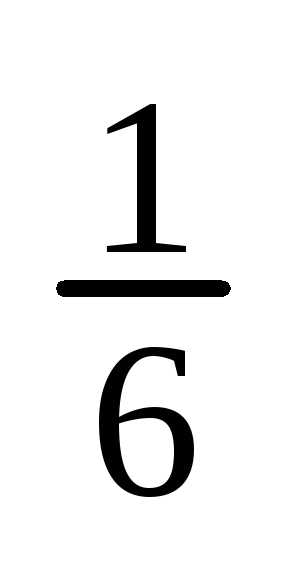 , а вероятность “неудачи” — q=
1 —
, а вероятность “неудачи” — q=
1 — 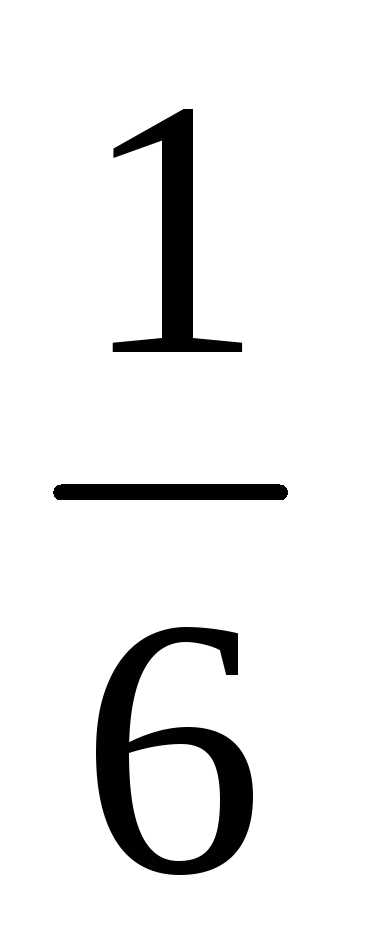 =
= .
Тогда по формуле Бернулли вероятность
того, что результате трехразового
бросания кубика два раза выпадет сторона
с шестью очками, будет равна
.
Тогда по формуле Бернулли вероятность
того, что результате трехразового
бросания кубика два раза выпадет сторона
с шестью очками, будет равна
.
б) Обозначим через А событие, которое заключается в том, что грань с числом очков 6 появится не более двух раз. Тогда событие можно представить в виде суммы трех несовместных событий А= ,
где В30 – событие, когда интересующая грань ни разу не появится,
В31 — событие, когда интересующая грань появится один раз,
В32 — событие, когда интересующая грань появится два раза.
По формуле Бернулли (1.6) найдем
p(А) =
р ()
= p()=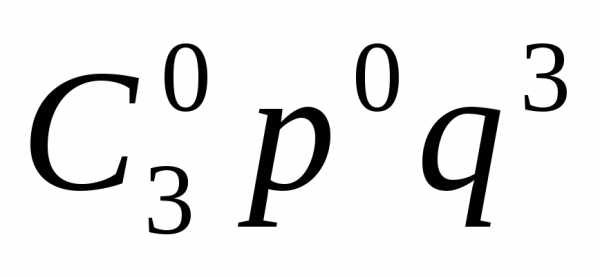 +
+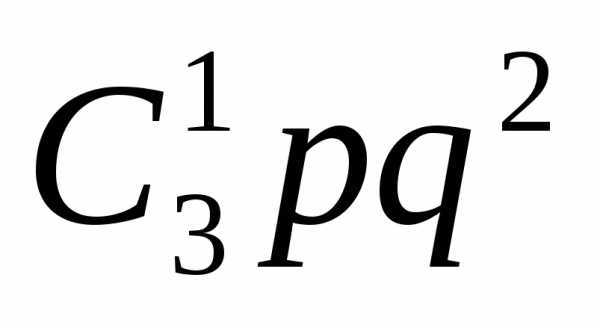 +
+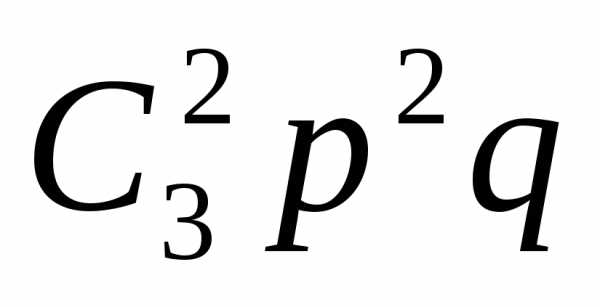 =
=
=.
1.3.2. Условная вероятность события
Условная вероятность отражает влияние одного события на вероятность другого. Изменение условий, в которых проводится эксперимент, также влияет
на вероятность появления интересующего события.
Определение. Пусть A и B – некоторые события, и вероятность p(B)>0.
Условной вероятностью события A при условии, что “событие B уже произошло” называется отношение вероятности произведения данных событий к вероятности события, которое произошло раньше, чем событие, вероятность которого требуется найти. Условная вероятность обозначается как p(AB). Тогда по определению
p (A B) =  .
(1.7)
.
(1.7)
Пример 1.17. Подбрасывают два кубика. Пространство элементарных событий состоит из упорядоченных пар чисел
(1,1) (1,2) (1,3) (1,4) (1,5) (1,6)
(2,1) (2,2) (2,3) (2,4) (2,5) (2,6)
(3,1) (3,2) (3,3) (3,4) (3,5) (3,6)
(4,1) (4,2) (4,3) (4,4) (4,5) (4,6)
(5,1) (5,2) (5,3) (5,4) (5,5) (5,6)
(6,1) (6,2) (6,3) (6,4) (6,5) (6,6).
В примере 1.16 было установлено, что событие A ={число очков на первом кубике > 4} и событие C ={сумма очков равна 8} зависимы. Составим отношение
 .
.
Это отношение можно интерпретировать следующим образом. Допустим, что о результате первого бросания известно, что число очков на первом кубике > 4. Отсюда следует, что бросание второго кубика может привести к одному из 12 исходов, составляющих событие A:
(5,1) (5,2) (5,3) (5,4) (5,5) (5,6)
(6,1) (6,2) (6,3) (6,4) (6,5) (6,6) .
При
этом событию C могут соответствовать только два из
них (5,3) (6,2). В этом случае вероятность
события C будет
равна 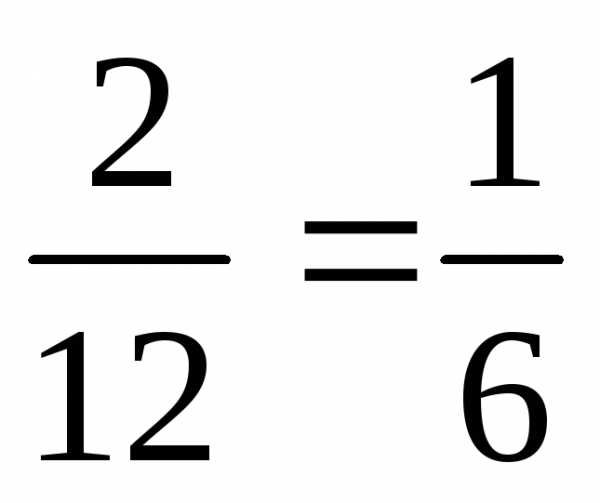 .
Таким образом, информация о наступлении
событияA оказала влияние на вероятность события C.
.
Таким образом, информация о наступлении
событияA оказала влияние на вероятность события C.
Вероятность произведения событий
Теорема умножения
Вероятность произведения событий A1 A2 An определяется формулой
p(A1 A2 An) = p(A1) p(A2 A1))p(An A1A2An-1). (1.8)
Для произведения двух событий отсюда следует, что
p(AB) = p(A B) p{B) = p(B A) p{A). (1.9)
Пример 1.18. В партии из 25 изделий 5 изделий бракованных. Последовательно наугад выбирают 3 изделия. Определить вероятность того, что все выбранные изделия бракованные.
Решение. Обозначим события:
A1 = {первое изделие бракованное},
A2 = {второе изделие бракованное},
A3 = {третье изделие бракованное},
A = {все изделия бракованные}.
Событие А есть произведение трех событий A = A1 A2 A3 .
Из теоремы умножения (1.6) получим
p(A) = р( A1 A2 A3 ) =p(A1) p(A2 A1))p(A3 A1A2).
Классическое определение вероятности позволяет найти p(A1) – это отношение числа бракованных изделий к общему количеству изделий:
p(A1)=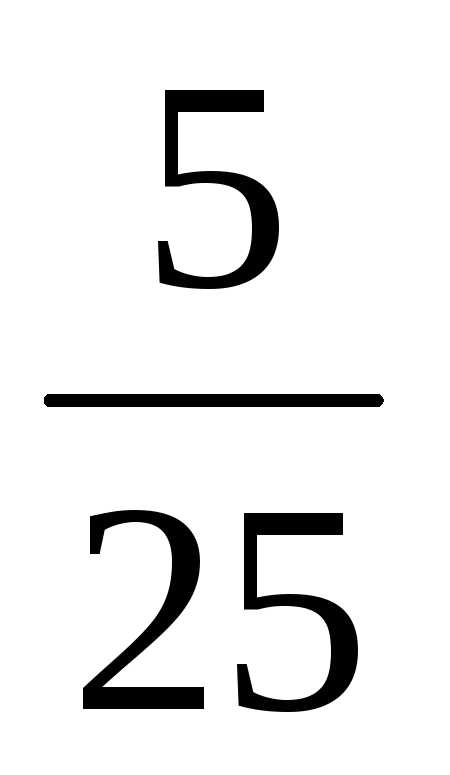 ;
;
p(A2) – это отношение числа бракованных изделий, оставшихся после изъятия одного, к общему числу оставшихся изделий:
p(A2 A1))=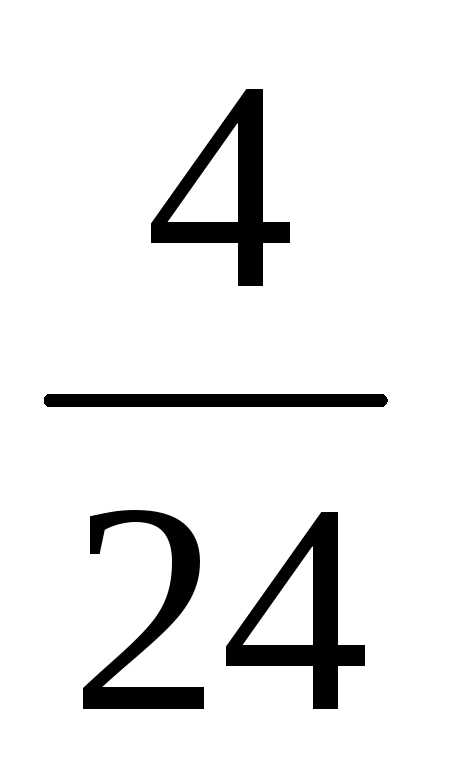 ;
;
p(A3 ) – это отношение числа бракованных изделий, оставшихся после изъятия двух бракованных, к общему числу оставшихся изделий:
p(A3 A1A2)=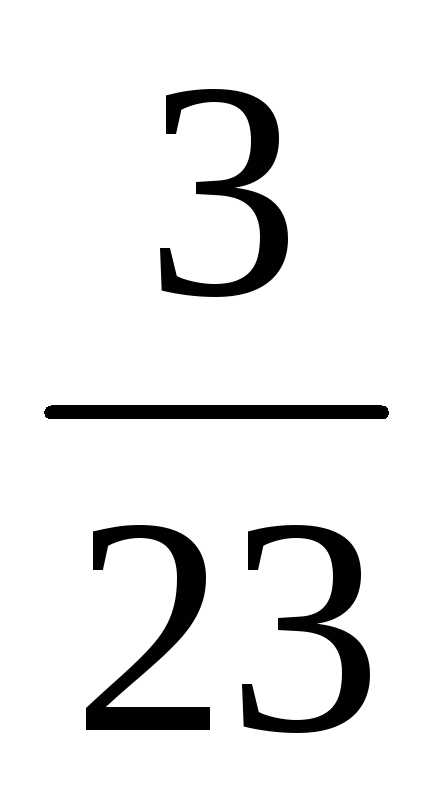 .
.
Тогда вероятность события A будет равна
p(A)
=
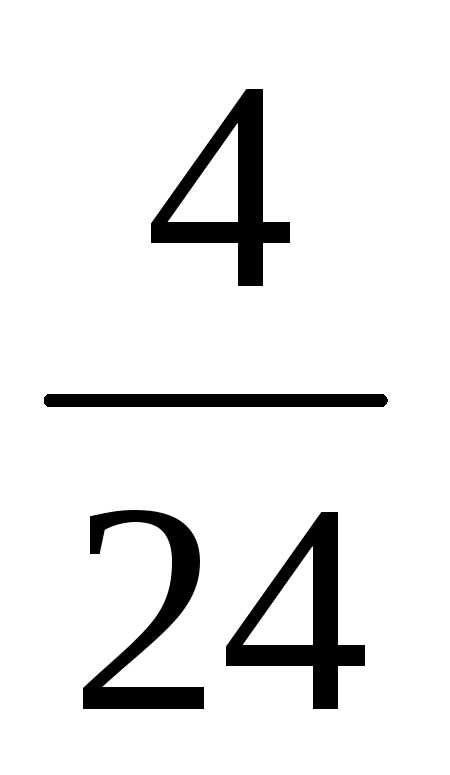
 =
=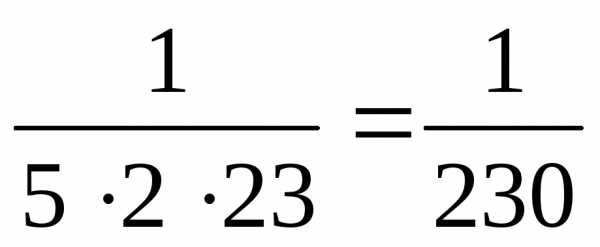 .
.
studfiles.net
Как рассчитать вероятность 🚩 вероятность события формула 🚩 Математика
Автор КакПросто!
Вероятность есть статистическая мера возможности. Почему статистическая? Потому что, с практической точки зрения, вам придется иметь дело с множеством (или множествами) событий, одно или несколько из которых в определенных условиях более возможны, чем остальные. Вот это «более» или «менее», выраженное математически – и есть вероятность.

Статьи по теме:
Инструкция
Классическая формула вероятности (формула Лапласа) такова:P(A) = M/N, где
P(A) – вероятность события А
M – число элементарных событий, благоприятствующих событию А
N – число всех элементарных событий.Два простейших примера. В ситуации бросания монеты, когда нужно рассчитать вероятность выпадения «решки» (события А), благоприятствует событию А оно само. Если же требуется вычислить вероятность выпадения четных граней при бросании кубика, благоприятствующих элементарных событий будет три (поскольку могут выпасть три четных числа). Соответственно, вероятности события А будут 0.5 и в первом, и во втором случаях. Еще пару слов про возможности. В теории вероятности событие, которое произойдет обязательно, называется «достоверным» (вероятность равна единице). Противоположное достоверному – «невозможное» событие (вероятность равна нулю). Событие, которое может случиться, а может и не произойти, называется «случайным» (вероятность случайного события 0
Существует еще одно определение вероятности (точнее говоря, геометрическая интерпретация вероятности):P(A) = Q/S, где
S – площадь фигуры, на которую случайным образом бросается точка
Q – часть площади фигуры S, на которую попадает точка.
P(A) – вероятность попадания случайно брошенной точки на площадь Q.
Классическая задача на геометрическую вероятность: пусть дан квадрат, в который вписана окружность. В квадрат бросают точку; вероятность того, что она попадет в круг, равна отношению площадей круга и квадрата (решение задачи см. на рисунке).
Источники:
- рассчитать вероятность события
Совет полезен?
Статьи по теме:
Не получили ответ на свой вопрос?
Спросите нашего эксперта:
www.kakprosto.ru
Расчет вероятности события Классическое определение вероятности
При классическом определении вероятность события определяется равенством
р(A)=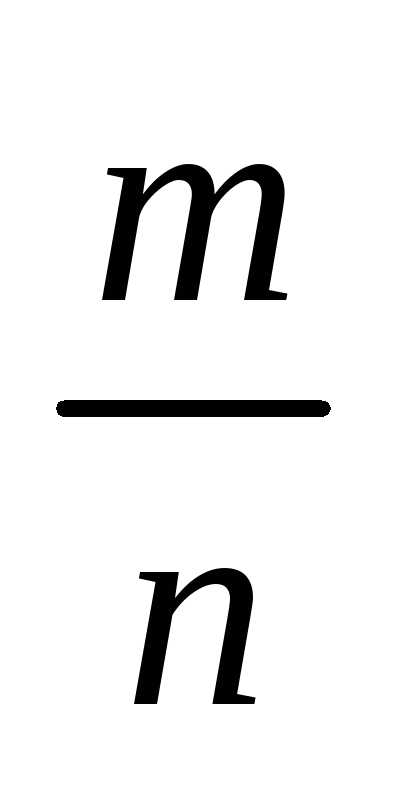 , (1)
, (1)
где m – число исходов проводимого опыта, благоприятствующих появлению события А; n – общее число возможных исходов.
Основные элементы комбинаторики
Пусть даны 2 множества:
{а,а ,…,а
,…,а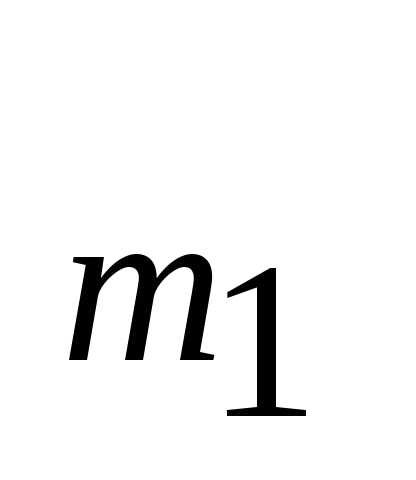 }
и {b, b
}
и {b, b ,…,b
,…,b }.
}.
Правило суммы: Если объект типа «а» может быть выбран m1 способами, а объект типа «b» – m2 способами, то выбор или «а», или «b» может быть осуществлен N = m1 + m2 способами.
Правило произведения: Если объект типа «а» может быть выбран m1 способами, и после любого такого выбора объект «b» может быть выбран m2 то выбор и «а», и «b» можно осуществить N = m1·m2 способами.
Основной принцип комбинаторики: Если имеется k множеств, причем из каждого можно составить комбинации соответственно n1, n2,…, nk способами, то комбинация, содержащая комбинации по одной из исходных множеств, может быть составлена N = n1·n2·…·nk способами.
Определение
1. Сочетаниями
из n различных элементов по m,
причем m n,
называются такие комбинации, каждая из
которых содержит ровно m элементов и отличается от любой другой
хотя бы одним элементом. Число сочетаний
из n элементов по m элементов обозначается С
n,
называются такие комбинации, каждая из
которых содержит ровно m элементов и отличается от любой другой
хотя бы одним элементом. Число сочетаний
из n элементов по m элементов обозначается С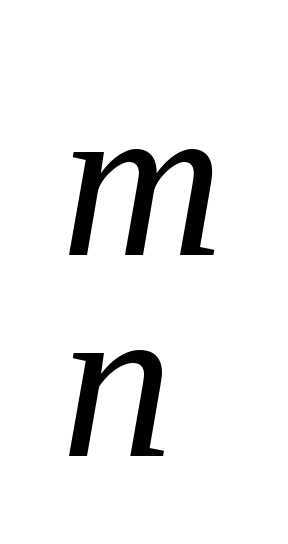 и находится по формуле
и находится по формуле
С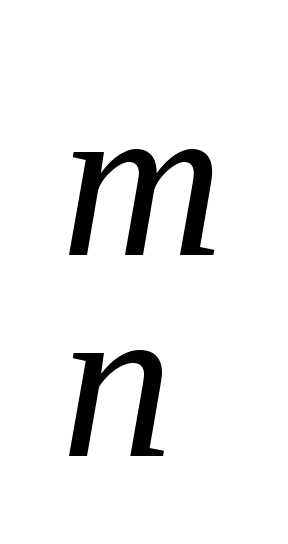 =
= ,
,
где n!, m!, (n – m)! – факториалы, то есть произведения соответственно n, m, n – m последовательных натуральных чисел, начиная с 1, например, 5! = 1·2·3·4·5 = 120. По определению 0! = 1.
Задача 1. В лотерее разыгрывается 100 билетов; из них 10 являются выигрышными, а остальные 90 – «пустые». Некто покупает 5 билетов. Какова вероятность, что среди них будет 2 выигрышных и 3 «пустых».
Решение. Событие А = {среди 5 отобранных билетов 2 выигрышных и 3 «пустых»}.
3
Для наглядности решения задачи составим схему взаимосвязанных множеств:
Всего Выигрышные Пустые
100 = 10 + 90
↓ ↓ ↓
5 = 2 + 3
Согласно (1)
вероятность события А определяется как p(А)
= 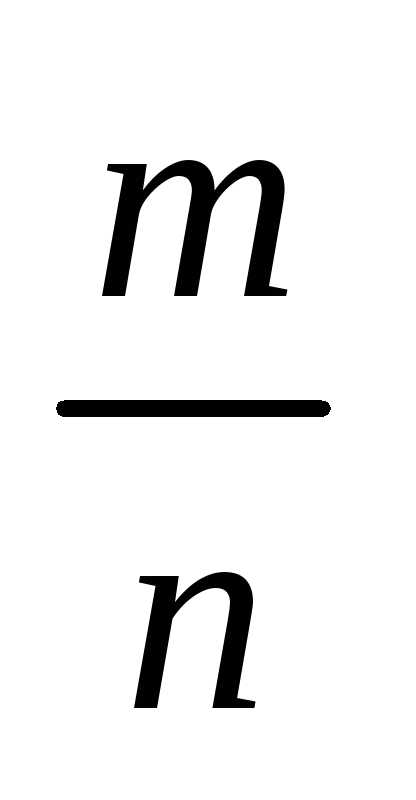 .
Общее числоn возможных различных способов отбора
равно числу способов, которыми можно
отобрать 5 билетов из 100: n = C
.
Общее числоn возможных различных способов отбора
равно числу способов, которыми можно
отобрать 5 билетов из 100: n = C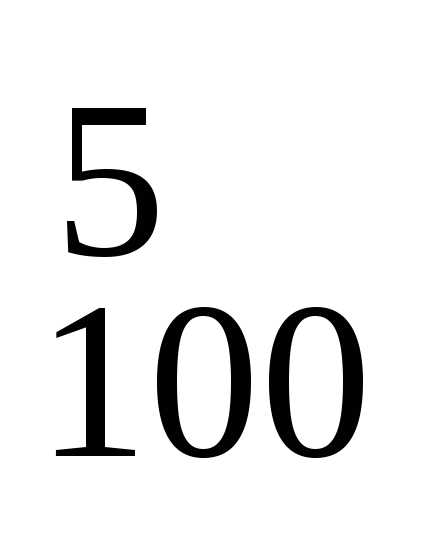 .
.
Число исходов m,
благоприятствующих событию А,
зависит от двух условий: среди отобранных
билетов должно оказаться 2 выигрышных
и 3 «пустых». Число различных способов
отбора двух выигрышных билетов из 10
возможных: m1 = C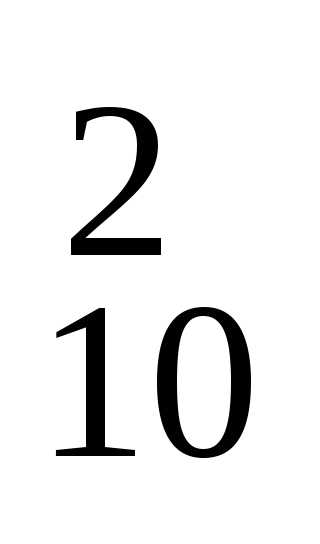 ;
а число различных способов отбора трех
«пустых» билетов из 90: m2 = C
;
а число различных способов отбора трех
«пустых» билетов из 90: m2 = C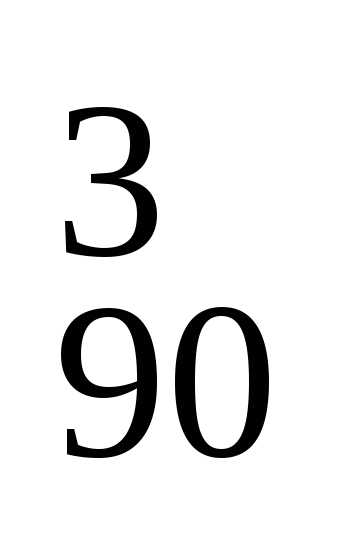 .
Используя правило произведения, получаем: m = m1·m2 – число способов, благоприятствующих
событию А.
Следовательно, искомая вероятность
.
Используя правило произведения, получаем: m = m1·m2 – число способов, благоприятствующих
событию А.
Следовательно, искомая вероятность
p(A)=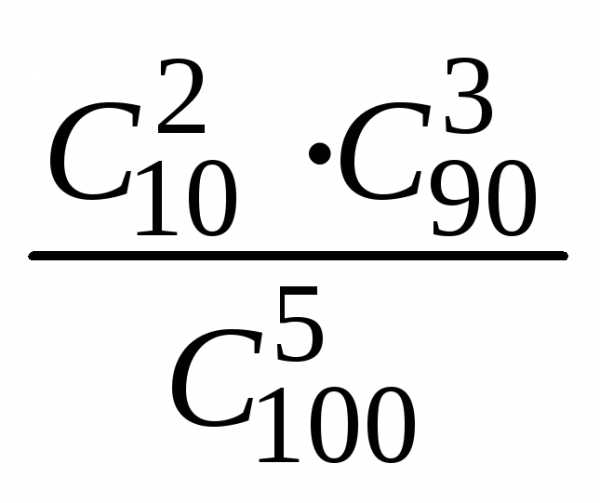 =
=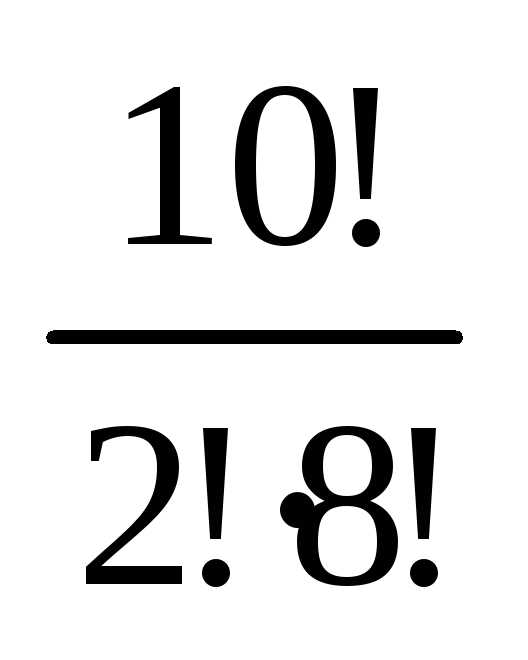 ·
· :
: ≈
0,07.
≈
0,07.
Ответ: p(A) ≈ 0.07.
Теоремы сложения и умножения вероятностей
Определение 2. Сумма двух событий А и В – это такое событие А+В, которое состоит в том, что произошло хотя бы одно из этих событий.
Определение 3. Произведение событий А и В – это такое событие А·В, состоящее в том, что эти события произошли совместно: и А и В.
Теорема 1. Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий:
р(А + В) = р(А) + р(В).
Следствие 1. Вероятность суммы попарно несовместных событий А1, А2,…, Аnравна сумме вероятностей этих событий:
p(А1 + А2 +…+ Аn) = p(А1) + p(А2)+…+ p(Аn).
Следствие 2. Сумма вероятностей событий, образующих полную группу (то есть, когда эти события попарно несовместны, но в результате испытания одно из них произойдет обязательно), равна 1.
Следствие 3. Сумма
вероятностей противоположных событий
равна 1: р(А)
+ р( )
= 1, где
)
= 1, где – событие противоположное событиюА.
– событие противоположное событиюА.
4
Таблица 3.
Значения
функции 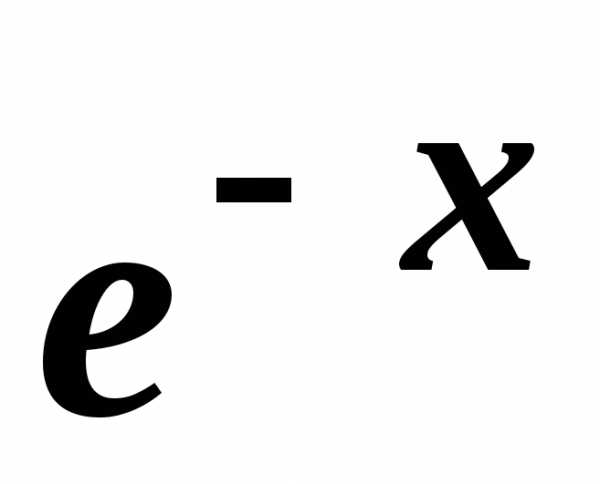 для
0 ≤ x< 1, e ≈ 2,7183
для
0 ≤ x< 1, e ≈ 2,7183
x | с о т ы е д о л и x | |||||||||
0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
0,0 | 1,0000 | 0,9900 | 0,9802 | 0,9704 | 0,9608 | 0,9512 | 0,9418 | 0,9324 | 0,9231 | 0,9139 |
0,1 | 0,9048 | 0,8958 | 0,8869 | 0,8781 | 0,8694 | 0,8607 | 0,8521 | 0,8437 | 0,8353 | 0,8270 |
0,2 | 0,8187 | 0,8106 | 0,8025 | 0,7945 | 0,7866 | 0,7788 | 0,7711 | 0,7634 | 0,7558 | 0,7483 |
0,3 | 0,7408 | 0,7334 | 0,7261 | 0,7189 | 0,7118 | 0,7047 | 0,6977 | 0,6907 | 0,6839 | 0,6771 |
0,4 | 0,6703 | 0,6637 | 0,6570 | 0,6505 | 0,6440 | 0,6376 | 0,6313 | 0,6250 | 0,6188 | 0,6126 |
0,5 | 0,6065 | 0,6005 | 0,5945 | 0,5886 | 0,5827 | 0,5769 | 0,5712 | 0,5655 | 0,5599 | 0,5543 |
0,6 | 0,5488 | 0,5434 | 0,5379 | 0,5326 | 0,5273 | 0,5220 | 0,5169 | 0,5117 | 0,5066 | 0,5016 |
0,7 | 0,4966 | 0,4916 | 0,4868 | 0,4819 | 0,4771 | 0,4724 | 0,4677 | 0,4630 | 0,4584 | 0,4538 |
0,8 | 0,4493 | 0,4449 | 0,4404 | 0,4360 | 0,4317 | 0,4274 | 0,4232 | 0,4190 | 0,4148 | 0,4107 |
0,9 | 0,4066 | 0,4025 | 0,3985 | 0,3946 | 0,3906 | 0,3867 | 0,3829 | 0,3791 | 0,3753 | 0,3716 |
studfiles.net
Расчет вероятностей событий
Задание № 1
Какова вероятность того, что наудачу взятое натуральное число не делится:
а) ни на два, ни на три;
б) на два или на три?
Решение:
Пусть А – событие, что натуральное число делится на 2→ p(A)=1/2 (каждое второе натуральное число кратно 2)
В-событие, что натуральное число делится на 3
p(В)=1/3 (каждое третье натуральное число кратно 3)
а) С – событие, что наудачу взятое натуральное число не делится ни на два, ни на три
Вероятность произведения двух независимых событий А и В равна произведению их вероятностей
Тогда вероятность события С:
Т.е. пять из шести натуральных чисел не делится ни на 2 ни на 3
б) D– событие, что наудачу взятое натуральное число не делится на 2 или на 3
.Вероятность суммы двух несовместных событий А и В равна сумме вероятностей этих событий
Тогда вероятность события D:
.Т.е. одно из трех натуральных чисел не делится на 2 или на 3
Задание №2
В ружейной пирамиде имеются винтовки двух систем: одна винтовка типа 1 и две винтовки типа 2. Вероятность попасть в мишень при выстреле из винтовки типа 1 равна р1, из винтовки типа 2 – р2.
Стрелок производит 7 выстрелов из наудачу взятой винтовки. Чему равна вероятность того, что мишень окажется поражённой не менее пяти раз?
Решение:
А – событие, что поражена мишень
Пусть событие Н1 – винтовка I типа; событие Н2 – винтовка II типа.
иА/Н1 – мишень поражена при выстреле из винтовки I типа
А/Н2 – мишень поражена при выстреле из винтовки II типа
Для нахождения вероятности
применяют формулу2. Р n (k ) – вероятность, что в n испытаниях событие наступит k раз находится по формуле Бернулли
.Вероятность события, что мишень окажется поражённой не менее пяти раз, если произведено 7 выстрелов из наудачу взятой винтовки.
Задание № 3
При измерении урожайности картофеля вес клубней в одном кусте распределился по интервалам следующим образом:
Построить гистограмму и найти средний вес одного куста.
Решение:
Гистограмма – служит для изображения интервальных рядов и представляет собой ступенчатую фигуру из прямоугольников с основаниями, равными интервалам значений признака
, и высотами, равными частотам интервалов.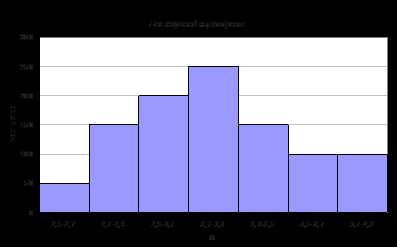
Для расчета среднего веса одного куста воспользуемся формулой средней арифметической.
Средней арифметической дискретного вариационного ряда
называется отношение суммы произведений вариантов на соответствующие частоты к объему совокупности:где
— варианты дискретного ряда или середины интервалов вариационного ряда, — соответствующие им частоты.Для каждого интервала найдем середины по формуле
.Ответ : средний вес одного куста составляет 3,22 кг.
Задание № 4
По следующим данным построить интервальный вариационный ряд и гистограмму: 24, 14, 15, 26, 16, 17, 14, 15, 1, 11, 14, 12, 16, 17, 13, 10, 11, 12, 13, 15, 14, 10, 11, 14, 7, 15, 14, 15, 15, 14, 15, 14, 2, 5, 18, 19, 16, 17, 9, 10, 18, 19, 20, 22, 28.
Найти среднее значение, дисперсию и стандартное отклонение.
Решение:
1. Проранжируем[1] исходный ряд, подсчитаем частоту вариантов. Получим вариационный ряд
2. Для определения числа групп воспользуемся формулой Стерджесса :
n = 1+3,322 * lgN
где n – число групп, N =45 – число единиц совокупности
Для данных задачи n = 1 + 3,322*lg 45 = 1 + 3,322 * 1,65 = 6б49 » 6 групп
Величина интервала представляет собой разность между максимальным и минимальным значением признака в каждой группе.
3. Выполним промежуточные вычисления во вспомогательной таблице и определим значения числовых характеристик:
Середины интервалов
Средняя арифметическая
где — варианты дискретного ряда или середины интервалов вариационного ряда, — соответствующие им частоты.Дисперсия .
Среднее квадратическое отклонение .
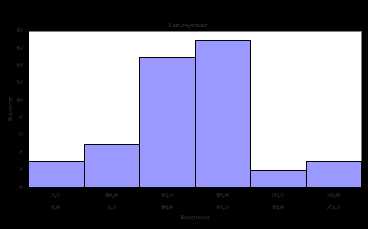
Среднее значение
Дисперсия
Среднее квадратическое отклонение
mirznanii.com
Расчет вероятности событий
Расчет вероятности событий
Задание 1
Предположим, что 5% всех мужчин и 0.25% всех женщин дальтоники. Наугад выбранное лицо оказалось дальтоником. Какова вероятность, что это мужчина? (Считать, что мужчин и женщин одинаковое число).
Решение
Будем считать гипотезами Н1 выбор мужчины, Н2 выбор женщины. Так как по условию задачи все гипотезы равновозможные, то Условная вероятность А при реализации каждой гипотезы по условию задачи:
Р (А/Н1) = 0,05; Р (А/Н2) = 0,25.
По формуле полной вероятности:
Р(А) = р(Н1)×р (А/Н1) + р(Н2)×р (А/Н2).
Р(А) = 0,5×0,05 + 0,5×0,25 = 0,15
Вероятность того, что дальтоник мужчина вычислим по формуле Байеса.
» 0,167
Ответ: 0,167
Задание 2
Бросается две уравновешенные игральные кости. Какова вероятность, что на них выпадут различные числа?
Решение
Воспользуемся классической формулой для вычисления вероятности:
где m — число благоприятных событию А случаев;
n — число всех случаев.
Обозначим событие А — на костях выпадут различные числа, рассмотрим противоположное событие — выпадут одинаковые числа.
n = 6×6 = 36
m = 6
Ответ:
Задание 3
Пусть в каждом цикле обзора радиолокатора цель может быть обнаружена с вероятностью 0.5. И пусть обнаружение в каждом цикле происходит независимо от других циклов. Определить с какой вероятностью цель будет обнаружена за 3 цикла.
Решение
Обозначим событие А — цель будет обнаружена за 3 цикла, рассмотрим противоположное событие — цель будет не будет обнаружена за 3 цикла.
= (1 — 0,5)3 = 0,125
= 1 — 0,125 = 0,875
Ответ: 0,875
Задание 4
Пусть вероятность того, что денежный автомат при опускании одной монеты сработает правильно, равна 0,95. Оценить вероятность того, что при 2 000 опусканиях монет количество случаев правильной работы автомата будет заключено в границах от 1 860 до 1 940 (включительно).
Решение
Воспользуемся интегральной теоремой Лапласа:
Справедлива формула: Pn(k1, k2) » Ф(х2) — Ф(х1).
где
n = 2000 р = 0,95 q = 0,05 k1 = 1860 k2 = 1940
=Ф (4,1) — Ф (-4,1) = Ф (4,1) + Ф (4,1) =2×Ф (4,1) » 2×0,5 = 1
Функция Лапласа является нечетной Ф(-х) = — Ф(х).
Ответ: 1
Задание 5
вероятность распределение функция гипотеза
Найти функцию распределения числа попаданий в цель, если стрелком произведено шесть выстрелов, а вероятность попадания при одном выстреле равна 0,2. Пользуясь этой функцией, вычислить вероятность того, что цель будет поражена не менее одного, но не меньше пяти раз.
Решение
Случайная величина Х — чи
сло попаданий в цель может принимать значения 0, 1, 2, 3, 4, 5, 6.
Формула Бернулли
n = 6 p=0,2 q= 0,8
×1×0,262144 = 0,262144
×0,2×0,32768 = 0,393216
×0,04×0,4096 = 0,24576
×0,008×0,512 = 0,08192
×0,0016×0,64 = 0,01536
×0,00032×0,8 = 0,01536
×0,000064×0,1 = 0,000064
Проверка: 0,262144 + 0,393216 + 0,24576 + 0,08192 + 0,01536 + 0,01536 + 0,000064 = 1
xi0123456pi0,2621440,3932160,245760,081920,015360,015360,000064
Найдем функцию распределения F(x) по формуле
Пользуясь этой функцией, вычислить вероятность того, что цель будет поражена не менее одного, но не меньше пяти раз.
Наверное, имелось ввиду:
Пользуясь этой функцией, вычислить вероятность того, что цель будет поражена не менее одного, но не больше пяти раз.
Р (a £ Х < b) = F(b) — F(a)
Р (1 £ Х < 5) = F(5) — F(1) = 0,9984 — 0,262144 = 0,736256
Задание 6
Деталь проходит три операции обработки. Вероятность того, что она окажется бракованной после первой операции, равна 0,02; после второй — 0,03; после третьей — 0,02. Найти вероятность того, что деталь будет бракованной после трех операций, предполагая, что появление брака на отдельных операциях независимые события.
Решение
Обозначим событие А — деталь будет бракованной после трех операций, рассмотрим противоположное событие — деталь окажется годной, т.е. не бракованной после трех операций.
= (1 — 0,02)×(1 — 0,03)×(1 — 0,02) = 0,98×0,97×0,98 » 0,932
= 1 — 0,932 = 0,068
Ответ: 0,875
Задание 7
Какова вероятность того, что наудачу поставленная точка в данном круге (радиус 2 см) окажется внутри вписанного в него квадрата.
Решение
Пусть радиус круга равен R, сторона квадрата а, тогда по теореме Пифагора^
а2 + а2 = (2R)2.
Площадь квадрата Sквадрата = а2 = 2R2.
Площадь круга Sкруга = pR2.
Ответ:
Задание 8
Найти вероятность того, что из 500 посеянных семян не взойдет 130, если всхожесть оценивается вероятностью 0,75.
Решение
Не взойдет 130 семян означает, что взойдет 500 — 130 = 370 семян.
Справедлива формула:
Pk,n» где
n = 500 р = 0,75 q = 0,25 k = 370
P370, 500 »
Функция j(х) — четная, т.е. j(-х) = j(х).
Ответ: 0,036
Задание 9
В классе имеется 12 компьютеров. Вероятность того, что компьютер будет занят студентами в течение дня, равна 0,8. Найти вероятность нормальной работы компьютерного класса в ближайший день, если для этого необходимо, чтобы были заняты хотя бы пять компьютеров.
Решение
Формула Бернулли
n = 12 k = от 5 до 12 p=0,8 q= 0,2
= 0,0033
= 0,0155
= 0,0532
= 0,1329
= 0,2362
= 0,2835
= 0,2062
= 0,0687
Р(А) = Р12(5) + Р12(6) + Р12(7) + Р12(8) + Р12(9) + Р12(10) + Р12(11) + Р12(12) = 0,0033 + 0,0155 + 0,0532 + 0,1329 + 0,2362 + 0,2835+ 0,2062+ 0,0687 = 0,9994
Ответ: 0,9994
Задание 10
Вероятность выигрыша по одному билету лотереи равна 1/7. Какова вероятность того, что лицо, имеющее шесть билетов, выиграет хотя бы по одному билету.
Решение
Обозначим событие А — выиграет хотя бы по одному билету, рассмотрим противоположное событие — не выиграет ни по одному билету
Ответ: 0,603
Литература
вероятность распределение функция гипотеза
1.Вентцель, Е.С. Теория случайных процессов и ее инженерные приложения / Е.С. Вентцель, Л.А. Овчаров. — М.: Высшая школа, 2001. — 382 с.
2.Ермаков, В.И. Общий курс высшей математики для экономистов: учебник / В.И. Ермаков. — М.: ИНФРА, 2007. — 656 с.
.Ермаков, В.И. Сборник задач по высшей математике для экономистов: учебник / В.И. Ермаков. — М.: ИНФРА, 2007. — 575 с.*
.Кремер, Н.Ш. Исследование операций в экономике: учебное пособие для вузов / Н.Ш. Кремер. — М.: ЮРАЙТ, 2010. — 432 с.
.Кремер, Н.Ш. Высшая математика для экономистов: учебное пособие для вузов / Н.Ш. Кремер. — М.:, ЮНИТИ-ДАНА 2007 — 479 с.
6.Миллер, Б.М. Теория случайных процессов в примерах и задачах / Б.М. Миллер, А.Р. Панков. — М.: ФИЗМАТЛИТ, 2002. — 320 с.
Теги: Расчет вероятности событий Контрольная работа Математика
Просмотров: 40386
Найти в Wikkipedia статьи с фразой: Расчет вероятности событий
diplomba.ru

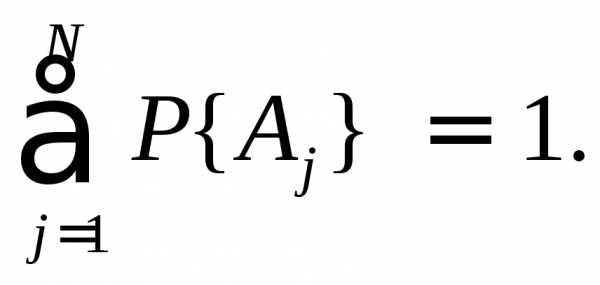
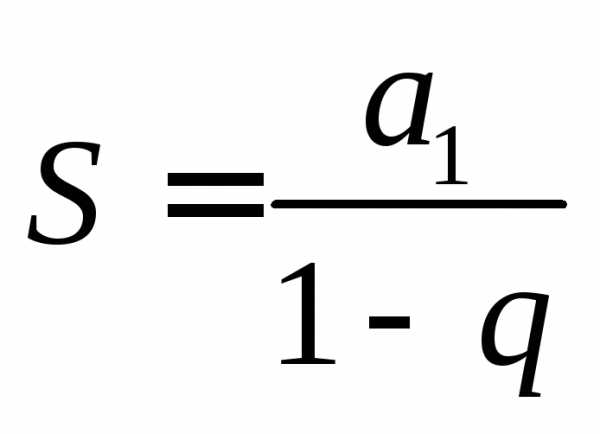 .
.