Таблица косинусов
Таблица косинусов 0° — 180°.
|
|
|
Таблица косинусов 180° — 360°.
|
|
|
Другие заметки по алгебре и геометрии
Таблица косинусов, полная таблица косинусов для студентов
Содержание:
Таблица косинусов — наровне с
таблицей синусов
изучается в самом начале тригонометрии (И вместе с таблицей синусов является основным материалом тригонометрии).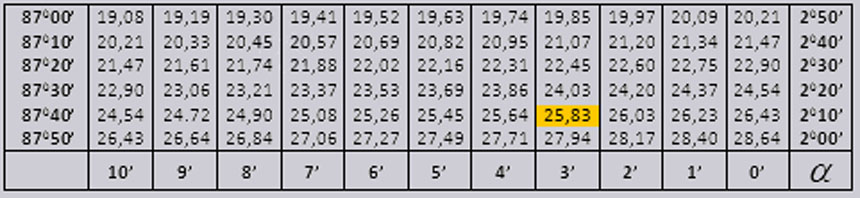 Без понимания данного материала и без знания хотя бы части таблицы косинусов будет очень сложно изучать тригонометрию и
применять тригонометричекие формулы.
Даже в университетском курсе часто используется тригонометрия, при решении интегралов и производных. Пользуйте таблицей косинусов на здоровье.
Без понимания данного материала и без знания хотя бы части таблицы косинусов будет очень сложно изучать тригонометрию и
применять тригонометричекие формулы.
Даже в университетском курсе часто используется тригонометрия, при решении интегралов и производных. Пользуйте таблицей косинусов на здоровье.
Таблица косинусов 0° — 180°
|
|
|
Таблица косинусов 180° — 360°
|
|
|
На нашем сайте в основном автоматические находятся программы для решения задач по математике, но также мы собрали много теоретического материала по математике и в частности по тригонометрии. Здесь Вы можете найти таблицы тригонометрических функций: таблицу косинусов, таблицу синусов, таблицу котангенсов и таблицу тангенсов. Также для улучшения понимания материала по тригонометрии мы добавили тригонометрические формулы, чтобы вызывало меньше затруднений решение тригонометрических задач по математике. Пользуйтесь нашим сайтом и таблицей косинусов на здоровье.
Слишком сложно?
Таблица косинусов, таблица значений косинусов не по зубам? Тебе ответит эксперт через 10 минут!
Таблица косинусов | Главный механик
Содержание статьи- Что такое косинус угла и как его применять в решении задач
- Как рассчитать косинус угла без формул
- Калькулятор расчета косинуса онлайн
- Примеры решения задач по геометрии по нахождению неизвестных величин с применением таблицы косинусов Брадиса
это удобное решение для проведения быстрых расчетов, когда нужно получить числовое значение косинуса того или иного угла.
 В статье мы узнаем, что такое косинус, чем похожи и как связаны таблица синусов и косинусов, как использовать таблицу синусов Брадиса для получения конкретных числовых значений косинуса того или иного угла.Что такое косинус угла и как его применять в решении задач
В статье мы узнаем, что такое косинус, чем похожи и как связаны таблица синусов и косинусов, как использовать таблицу синусов Брадиса для получения конкретных числовых значений косинуса того или иного угла.Что такое косинус угла и как его применять в решении задачНачнем с того, что каждый знает, что такое прямоугольный треугольник. Им называется такой треугольник, у которого один из углов (C) прямой (равен 90°), остальные два угла (? и ?) острые. Он имеет стандартное обозначение углов и сторон. Тогда, что такое косинус угла, можно рассмотреть дальше.
Прямоугольный треугольник: стороны a (BC) и b (AC) – катеты, сторона с (AB) – гипотенуза
Прямой угол всегда равен 90°, острый – всегда меньше, а тупой – больше 90°
Согласно теореме косинусов, что бы рассчитать угол α или β, нужно знать длину гипотенузы (АВ) и прилежащий к этому углу катет.
Косинус – это отношение прилежащей стороны к гипотенузе:- cos α = b деленное на с;
- cos β = а(BC)/с(AB) .

То есть, если вам нужно узнать, например, какой высоты делать крышу над домом, если известна ширина дома и угол наклона крыши, что бы снег не задерживался, то высоту конька рассчитать не составит труда, применяя теорему косинусов. Нужно помнить, что такие функции, как косинусы и синусы в формулах зависят от угла. Синус работает с противолежащей стороной, косинус с работает прилежащей.
Это тригонометрические формулы для вычисления углов в треугольнике через тригонометрические функции синус, косинус, тангенс, котангенс
Косинус – отношение прилежащего катета к гипотенузе
Если треугольник не прямоугольный, его параметры также можно рассчитать, используя теорему Евклида. Суть ее в том, что треугольник, лежащий на плоскости, и имеющий стороны а, b, с, а также углом α, который находится напротив стороны а, может быть рассчитан по следующей формуле:
а²= b²+с²-2²· b· cos α или:
Отсюда можем найти cos α, cos α =( b²+2²- а²) : 2bс.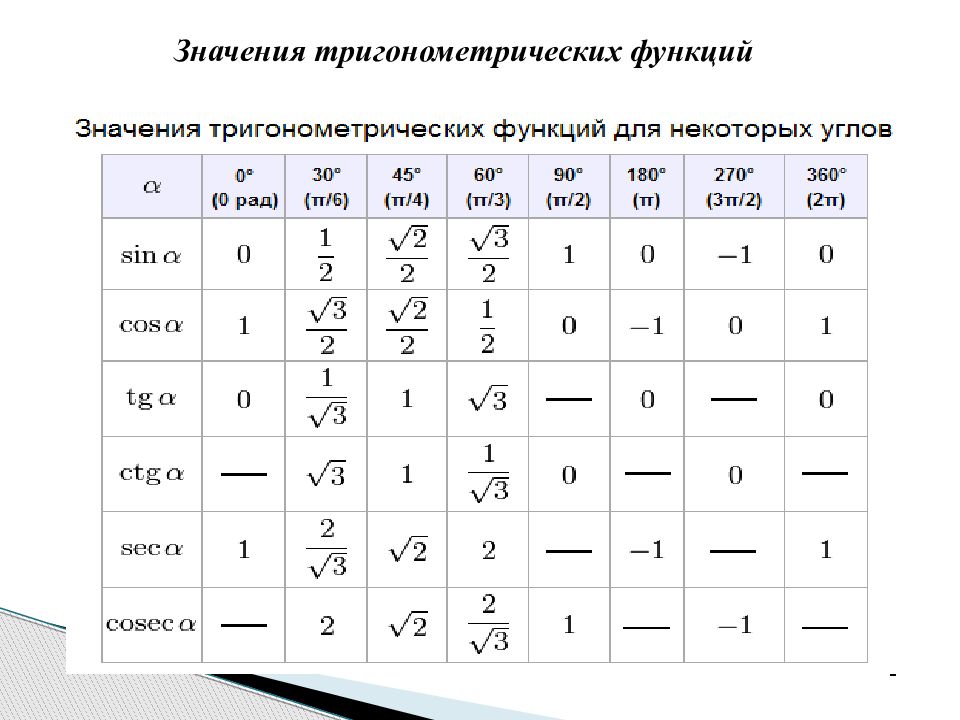
Небольшое уточнение: если угол α менее 90°, тогда b²+2²- а² > 0, если α =90°, то b²+2²- а²=0, если α >90°,то есть угол тупой, то и b²+2²- а²< 0.
То же самые расчеты делаем для других углов треугольника:
- с² = а² + b² – 2аb cosγ,
- b² = а² + с² – 2ас cosβ.
Есть некоторые углы, рассчитать косинус которых можно без формул, применяя
таблицу синусов и косинусов π. В ней расчет идет через число π, которое делится на целое число, в зависимости от размера угла, то есть sin 30° = π : 6 или 0,5, cos 30° = √3: 2. В такой таблице есть данные косинуса 30 градусов, косинуса 45 градусов, косинуса 60 градусов, косинуса 90 градусов, косинуса 120 градусов, косинус 180 градусов, косинус 270 градусов, косинус 360 градусов, косинус 0, а также аналогичные значения синусов.Ниже приведена таблица косинусов, дополнительно указаны синусы в их числовом выражении.
| Значение угла α (градусов) | Значение угла α в радианах | COS (косинус) |
|---|---|---|
| Косинус 0 градусов | 0 | 1 |
| Косинус 15 градусов | π/12 | 0.9659 |
| Косинус 30 градусов | π/6 | 0.866 |
| Косинус 45 градусов | π/4 | 0.7071 |
| Косинус 50 градусов | 5π/18 | 0.6428 |
| Косинус 60 градусов | π/3 | 0.5 |
| Косинус 65 градусов | 13π/36 | 0.4226 |
| Косинус 70 градусов | 7π/18 | 0.342 |
| Косинус 75 градусов | 5π/12 | 0.2588 |
| Косинус 90 градусов | π/2 | 0 |
| Косинус 105 градусов | 5π/12 | -0.2588 |
| Косинус 120 градусов | 2π/3 | -0.5 |
| Косинус 135 градусов | 3π/4 | -0.7071 |
| Косинус 140 градусов | 7π/9 | -0. 766 766 |
| Косинус 150 градусов | 5π/6 | -0.866 |
| Косинус 180 градусов | π | -1 |
| Косинус 270 градусов | 3π/2 | 0 |
| Косинус 360 градусов | 2π | 1 |
Пример 1: Для примера решим следующую задачу. Берем прямоугольный треугольник, у него нужно найти оба угла, но известны гипотенуза с = 12 см, сторона b = 9,2 см. По теореме косинусов
cos α = b : с, cos α = 9,2: 12 = 0, 7667. Далее открываем таблицу Брадиса и научимся, как ею пользоваться для нахождения косинуса угла. С левой стороны таблицы мы напротив косинусов находим ближайшее значение 0, 7672, которое соответствует 39°, поднимаем линию до значения минут и находим 54′.Но наше значение меньше табличного на 0,0006, что становит 3′.
Тогда мы вычитаем эту поправку 3′, 39°54′ – 3′ = 39°51′. Второй угол находим, исходя из того, что сумма всех углов в треугольнике не должна превышать 180°. Поэтому 180° – (90° + 39°51′) = 50° 09′. Угол β = 50° 09′. Решаем задачу дальше. Ищем сторону а. Для этого мы можем использовать два способа.
- по формуле а²= b²+с²-2²· b· cos α находим сторону а;
- по формуле cos β=sinα = а: с, а = с · cos β.
Второй вариант немного проще в вычислении. Обращаемся к таблице Брадиса снова. У нас ближайшее значение 50° 06′ = 0,6414. Поправка на 3′ составляет 0, 0007. Тогда 0, 6414 + 0,0007 = 0,6421.
По условию с = 12 см, тогда а = 12 · 0,6421 = 7,7 см. Задача решена. Если значения углов простые, таблица косинусов и синусов может упростить вычисление. Можно использовать следующие тождества: sin (90°+15°) = cos 15°= cos (90°-75°) = sin 75° Функции повторяются, только нужно учитывать знак. Если нужно найти косинус 145 градусов, находим угол до 90 градусов. 180 °– 145° = 35°.
Косинус 35 градусов будет 0,8192 по таблице, если это 145°, это будет значение с отрицательным значением -0,8192.
Пример 2: Рассмотрим треугольник с произвольными углами, ни один из которых не равен 90°. Мы имеем две стороны с =12 см, b = 8,2 см, а также угол α, который равен 31°12′. Найти третью сторону. Формула, которая применялась в предыдущей задаче, не подходит, так как у нас треугольник не прямоугольный (по крайней мере мы это ещё не рассчитали). Используем формулу из теоремы косинусов:
а² = b²+с²-2²· b· cos α. Косинус угла находим на пересечении угла 31° и 12′. Он равен числу 0,8554, которое мы и подставляем в формулу.
а² = 67, 24 + 144 -4 · 8,2 · 0,8554 = 211,24 – 28,07 = 183,17. Находим а = √183,17 = 13, 54 (см)
Если будет стоять задание найти ещё и углы треугольника, используем формулу:
с² = а² + b² – 2аb cos γ, отсюда cos γ = (b² + а² – с²): 2 bс. cos γ = (8,2² + 13,54² – 12²): 2· 8,2·12 = (64,24 + 183, 17 – 144): 196,8 = 0, 5255.
Открываем таблицу Брадиса. Это число соответствует 58° 18′. Согласно теореме о правилах трёх углов в треугольнике находим третий угол:
180° – 58° 18′-31°12′ =89° 30′. Задача решена!
Можно не рассчитывать самому, а использовать сервис и высчитать косинус онлайн, когда регистрируешься на сайте, и любое вычисление приходит автоматически. Минус такого сервиса, его нельзя применять на экзамене по математике. В качестве справочного материала таблицы предоставляются. Естественно, надо хорошо уметь ими пользоваться, так как на экзамен отводится ограниченное количество времени.
| COS | 0′ | 6′ | 12′ | 18′ | 24′ | 30′ | 36′ | 42′ | 48′ | 54′ | 60′ | 1′ | 2′ | 3′ | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| COS | 60′ | 54′ | 48′ | 42′ | 36′ | 30′ | 24′ | 18′ | 12′ | 6′ | 0′ | 1′ | 2′ | 3′ | |
| 90° | 0.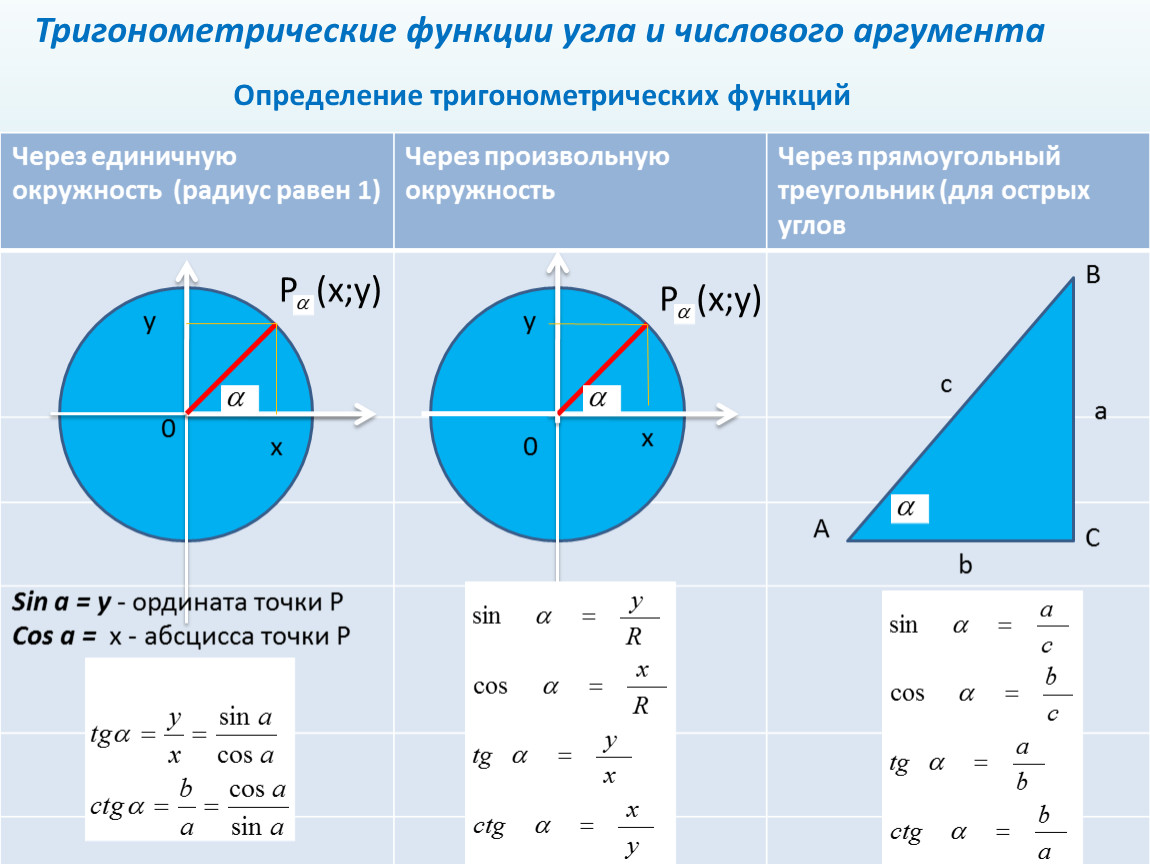 0000 0000 | ||||||||||||||
| 89° | 0.0000 | 17 | 35 | 52 | 70 | 87 | 105 | 122 | 140 | 157 | 175 | 3 | 6 | 9 | |
| 88° | 175 | 192 | 209 | 227 | 244 | 262 | 279 | 297 | 314 | 332 | 349 | 3 | 6 | 9 | |
| 87° | 349 | 366 | 384 | 401 | 419 | 436 | 454 | 471 | 488 | 506 | 523 | 3 | 6 | 9 | |
| 86° | 523 | 541 | 558 | 576 | 593 | 610 | 628 | 645 | 663 | 680 | 698 | 3 | 6 | 9 | |
| 85° | 698 | 715 | 732 | 750 | 767 | 785 | 802 | 819 | 837 | 854 | 0.0872 | 3 | 6 | 9 | |
| 84° | 0.0872 | 889 | 906 | 924 | 941 | 958 | 976 | 993 | 1011 | 1028 | 1045 | 3 | 6 | 9 | |
| 83° | 1045 | 1063 | 1080 | 1097 | 1115 | 1132 | 1149 | 1167 | 1184 | 1201 | 1219 | 3 | 6 | 9 | |
| 82° | 1219 | 1236 | 1253 | 1271 | 1288 | 1305 | 1323 | 1340 | 1357 | 1374 | 1392 | 3 | 6 | 9 | |
| 81° | 1392 | 1409 | 1426 | 1444 | 1461 | 1478 | 1495 | 1513 | 1530 | 1547 | 1564 | 3 | 6 | 9 | |
| 80° | 1564 | 1582 | 1599 | 1616 | 1633 | 1650 | 1668 | 1685 | 1702 | 1719 | 0. 1736 1736 | 3 | 6 | 9 | |
| 79° | 0.1736 | 1754 | 1771 | 1788 | 1805 | 1822 | 1840 | 1857 | 1874 | 1891 | 1908 | 3 | 6 | 9 | |
| 78° | 1908 | 1925 | 1942 | 1959 | 1977 | 1994 | 2011 | 2028 | 2045 | 2062 | 2079 | 3 | 6 | 9 | |
| 77° | 2079 | 2096 | 2113 | 2130 | 2147 | 2164 | 2181 | 2198 | 2215 | 2233 | 2250 | 3 | 6 | 9 | |
| 76° | 2250 | 2267 | 2284 | 2300 | 2317 | 2334 | 2351 | 2368 | 2385 | 2402 | 2419 | 3 | 6 | 8 | |
| 75° | 2419 | 2436 | 2453 | 2470 | 2487 | 2504 | 2521 | 2538 | 2554 | 2571 | 0.2588 | 3 | 6 | 8 | |
| 74° | 0. 2588 2588 | 2605 | 2622 | 2639 | 2656 | 2672 | 2689 | 2706 | 2723 | 2740 | 2756 | 3 | 6 | 8 | |
| 73° | 2756 | 2773 | 2790 | 2807 | 2823 | 2840 | 2857 | 2874 | 2890 | 2907 | 2924 | 3 | 6 | 8 | |
| 72° | 2942 | 2940 | 2957 | 2974 | 2990 | 3007 | 3024 | 3040 | 3057 | 3074 | 3090 | 3 | 6 | 8 | |
| 71° | 3090 | 3107 | 3123 | 3140 | 3156 | 3173 | 3190 | 3206 | 3223 | 3239 | 3256 | 3 | 6 | 8 | |
| 70° | 3256 | 3272 | 3289 | 3305 | 3322 | 3338 | 3355 | 3371 | 3387 | 3404 | 0.3420 | 3 | 5 | 8 | |
| 69° | 0.3420 | 3437 | 3453 | 3469 | 3486 | 3502 | 3518 | 3535 | 3551 | 3567 | 3584 | 3 | 5 | 8 | |
| 68° | 3584 | 3600 | 3616 | 3633 | 3649 | 3665 | 3681 | 3697 | 3714 | 3730 | 3746 | 3 | 5 | 8 | |
| 67° | 3746 | 3762 | 3778 | 3795 | 3811 | 3827 | 3843 | 3859 | 3875 | 3891 | 3907 | 3 | 5 | 8 | |
| 66° | 3097 | 3923 | 3939 | 3955 | 3971 | 3987 | 4003 | 4019 | 4035 | 4051 | 4067 | 3 | 5 | 8 | |
| 65° | 4067 | 4083 | 4099 | 4115 | 4131 | 4147 | 4163 | 4179 | 4195 | 4210 | 0. 4226 4226 | 3 | 5 | 8 | |
| 64° | 0.4226 | 4242 | 4258 | 4274 | 4289 | 4305 | 4321 | 4337 | 4352 | 4368 | 4384 | 3 | 5 | 8 | |
| 63° | 4384 | 4399 | 4415 | 4431 | 4446 | 4462 | 4478 | 4493 | 4509 | 4524 | 4540 | 3 | 5 | 8 | |
| 62° | 4540 | 4555 | 4571 | 4586 | 4602 | 4617 | 4633 | 4648 | 4664 | 4679 | 4695 | 3 | 5 | 8 | |
| 61° | 4695 | 4710 | 4726 | 4741 | 4756 | 4772 | 4787 | 4802 | 4818 | 4833 | 4848 | 3 | 5 | 8 | |
| 60° | 4848 | 4863 | 4879 | 4894 | 4909 | 4924 | 4939 | 4955 | 4970 | 4985 | 0.5000 | 3 | 5 | 8 | |
| 59° | 0. 5000 5000 | 5015 | 5030 | 5045 | 5060 | 5075 | 5090 | 5105 | 5120 | 5135 | 5150 | 3 | 5 | 8 | |
| 58° | 5150 | 5165 | 5180 | 5195 | 5210 | 5225 | 5240 | 5255 | 5270 | 5284 | 5299 | 2 | 5 | 7 | |
| 57° | 5299 | 5314 | 5329 | 5344 | 5358 | 5373 | 5388 | 5402 | 5417 | 5432 | 5446 | 2 | 5 | 7 | |
| 56° | 5446 | 5461 | 5476 | 5490 | 5505 | 5519 | 5534 | 5548 | 5563 | 5577 | 5592 | 2 | 5 | 7 | |
| 55° | 5592 | 5606 | 5621 | 5635 | 5650 | 5664 | 5678 | 5693 | 5707 | 5721 | 0.5736 | 2 | 5 | 7 | |
| 54° | 0.5736 | 5750 | 5764 | 5779 | 5793 | 5807 | 5821 | 5835 | 5850 | 5864 | 0. 5878 5878 | 2 | 5 | 7 | |
| 53° | 5878 | 5892 | 5906 | 5920 | 5934 | 5948 | 5962 | 5976 | 5990 | 6004 | 6018 | 2 | 5 | 7 | |
| 52° | 6018 | 6032 | 6046 | 6060 | 6074 | 6088 | 6101 | 6115 | 6129 | 6143 | 6157 | 2 | 5 | 7 | |
| 51° | 6157 | 6170 | 6184 | 6198 | 6211 | 6225 | 6239 | 6252 | 6266 | 6280 | 6293 | 2 | 5 | 7 | |
| 50° | 6293 | 6307 | 6320 | 6334 | 6347 | 6361 | 6374 | 6388 | 6401 | 6414 | 0.6428 | 2 | 4 | 7 | |
| 49° | 0.6428 | 6441 | 6455 | 6468 | 6481 | 6494 | 6508 | 6521 | 6534 | 6547 | 6561 | 2 | 4 | 7 | |
| 48° | 6561 | 6574 | 6587 | 6600 | 6613 | 6626 | 6639 | 6652 | 6665 | 6678 | 6691 | 2 | 4 | 7 | |
| 47° | 6691 | 6704 | 6717 | 6730 | 6743 | 6756 | 6769 | 6782 | 6794 | 6807 | 6820 | 2 | 4 | 6 | |
| 46° | 6820 | 6833 | 6845 | 6858 | 6871 | 6884 | 6896 | 8909 | 6921 | 6934 | 6947 | 2 | 4 | 6 | |
| 45° | 6947 | 6959 | 6972 | 6984 | 6997 | 7009 | 7022 | 7034 | 7046 | 7059 | 0. 7071 7071 | 2 | 4 | 6 | |
| 44° | 0.7071 | 7083 | 7096 | 7108 | 7120 | 7133 | 7145 | 7157 | 7169 | 7181 | 7193 | 2 | 4 | 6 | |
| 43° | 7193 | 7206 | 7218 | 7230 | 7242 | 7254 | 7266 | 7278 | 7290 | 7302 | 7314 | 2 | 4 | 6 | |
| 42° | 7314 | 7325 | 7337 | 7349 | 7361 | 7373 | 7385 | 7396 | 7408 | 7420 | 7431 | 2 | 4 | 6 | |
| 41° | 7431 | 7443 | 7455 | 7466 | 7478 | 7490 | 7501 | 7513 | 7524 | 7536 | 7547 | 2 | 4 | 6 | |
| 40° | 7547 | 7559 | 7570 | 7581 | 7593 | 7604 | 7615 | 7627 | 7638 | 7649 | 0.7660 | 2 | 4 | 6 | |
| 39° | 0. 7660 7660 | 7672 | 7683 | 7694 | 7705 | 7716 | 7727 | 7738 | 7749 | 7760 | 7771 | 2 | 4 | 6 | |
| 38° | 7771 | 7782 | 7793 | 7804 | 7815 | 7826 | 7837 | 7848 | 7859 | 7869 | 7880 | 2 | 4 | 5 | |
| 37° | 7880 | 7891 | 7902 | 7912 | 7923 | 7934 | 7944 | 7955 | 7965 | 7976 | 7986 | 2 | 4 | 5 | |
| 36° | 7986 | 7997 | 8007 | 8018 | 8028 | 8039 | 8049 | 8059 | 8070 | 8080 | 8090 | 2 | 3 | 5 | |
| 35° | 8090 | 8100 | 8111 | 8121 | 8131 | 8141 | 8151 | 8161 | 8171 | 8181 | 0.8192 | 2 | 3 | 5 | |
| 34° | 0.8192 | 8202 | 8211 | 8221 | 8231 | 8241 | 8251 | 8261 | 8271 | 8281 | 8290 | 2 | 3 | 5 | |
| 33° | 8290 | 8300 | 8310 | 8320 | 8329 | 8339 | 8348 | 8358 | 8368 | 8377 | 8387 | 2 | 3 | 5 | |
| 32° | 8387 | 8396 | 8406 | 8415 | 8425 | 8434 | 8443 | 8453 | 8462 | 8471 | 8480 | 2 | 3 | 5 | |
| 31° | 8480 | 8490 | 8499 | 8508 | 8517 | 8526 | 8536 | 8545 | 8554 | 8563 | 8572 | 2 | 3 | 5 | |
| 30° | 8572 | 8581 | 8590 | 8599 | 8607 | 8616 | 8625 | 8634 | 8643 | 8652 | 0. 8660 8660 | 1 | 3 | 4 | |
| 29° | 0.8660 | 8669 | 8678 | 8686 | 8695 | 8704 | 8712 | 8721 | 8729 | 8738 | 8746 | 1 | 3 | 4 | |
| 28° | 8746 | 8755 | 8763 | 8771 | 8780 | 8788 | 8796 | 8805 | 8813 | 8821 | 8829 | 1 | 3 | 4 | |
| 27° | 8829 | 8838 | 8846 | 8854 | 8862 | 8870 | 8878 | 8886 | 8894 | 8902 | 8910 | 1 | 3 | 4 | |
| 26° | 8910 | 8918 | 8926 | 8934 | 8942 | 8949 | 8957 | 8965 | 8973 | 8980 | 8988 | 1 | 3 | 4 | |
| 25° | 8988 | 8996 | 9003 | 9011 | 9018 | 9026 | 9033 | 9041 | 9048 | 9056 | 0.9063 | 1 | 3 | 4 | |
| 24° | 0.9063 | 9070 | 9078 | 9085 | 9092 | 9100 | 9107 | 9114 | 9121 | 9128 | 9135 | 1 | 2 | 4 | |
| 23° | 9135 | 9143 | 9150 | 9157 | 9164 | 9171 | 9178 | 9184 | 9191 | 9198 | 9205 | 1 | 2 | 3 | |
| 22° | 9205 | 9212 | 9219 | 9225 | 9232 | 9239 | 9245 | 9252 | 9259 | 9256 | 9272 | 1 | 2 | 3 | |
| 21° | 9272 | 9278 | 9285 | 9291 | 9298 | 9304 | 9311 | 9317 | 9323 | 9330 | 9336 | 1 | 2 | 3 | |
| 20° | 9336 | 9342 | 9348 | 9354 | 9361 | 9367 | 9373 | 9379 | 9383 | 9391 | 0.9397 | 1 | 2 | 3 | |
| 19° | 9397 | 9403 | 9409 | 9415 | 9421 | 9426 | 9432 | 9438 | 9444 | 9449 | 0.9455 | 1 | 2 | 3 | |
| 18° | 9455 | 9461 | 9466 | 9472 | 9478 | 9483 | 9489 | 9494 | 9500 | 9505 | 9511 | 1 | 2 | 3 | |
| 17° | 9511 | 9516 | 9521 | 9527 | 9532 | 9537 | 9542 | 9548 | 9553 | 9558 | 9563 | 1 | 2 | 3 | |
| 16° | 9563 | 9568 | 9573 | 9578 | 9583 | 9588 | 9593 | 9598 | 9603 | 9608 | 9613 | 1 | 2 | 2 | |
| 15° | 9613 | 9617 | 9622 | 9627 | 9632 | 9636 | 9641 | 9646 | 9650 | 9655 | 0.9659 | 1 | 2 | 2 | |
| 14° | 9659 | 9664 | 9668 | 9673 | 9677 | 9681 | 9686 | 9690 | 9694 | 9699 | 9703 | 1 | 1 | 2 | |
| 13° | 9703 | 9707 | 9711 | 9715 | 9720 | 9724 | 9728 | 9732 | 9736 | 9740 | 9744 | 1 | 1 | 2 | |
| 12° | 9744 | 9748 | 9751 | 9755 | 9759 | 9763 | 9767 | 9770 | 9774 | 9778 | 9781 | 1 | 1 | 2 | |
| 11° | 9781 | 9785 | 9789 | 9792 | 9796 | 9799 | 9803 | 9806 | 9810 | 9813 | 9816 | 1 | 1 | 2 | |
| 10° | 9816 | 9820 | 9823 | 9826 | 9829 | 9833 | 9836 | 9839 | 9842 | 9845 | 0.9848 | 1 | 1 | 2 | |
| 9° | 0.9848 | 9851 | 9854 | 9857 | 9860 | 9863 | 9866 | 9869 | 9871 | 9874 | 9877 | 0 | 1 | 1 | |
| 8° | 9877 | 9880 | 9882 | 9885 | 9888 | 9890 | 9893 | 9895 | 9898 | 9900 | 9903 | 0 | 1 | 1 | |
| 7° | 9903 | 9905 | 9907 | 9910 | 9912 | 9914 | 9917 | 9919 | 9921 | 9923 | 9925 | 0 | 1 | 1 | |
| 6° | 9925 | 9928 | 9930 | 9932 | 9934 | 9936 | 9938 | 9940 | 9942 | 9943 | 9945 | 0 | 1 | 1 | |
| 5° | 9945 | 9947 | 9949 | 9951 | 9952 | 9954 | 9956 | 9957 | 9959 | 9960 | 9962 | 0 | 1 | 1 | |
| 4° | 9962 | 9963 | 9965 | 9966 | 9968 | 9969 | 9971 | 9972 | 9973 | 9974 | 9976 | 0 | 0 | 1 | |
| 3° | 9976 | 9977 | 9978 | 9979 | 9980 | 9981 | 9982 | 9983 | 9984 | 9985 | 9986 | 0 | 0 | 0 | |
| 2° | 9986 | 9987 | 9988 | 9989 | 9990 | 9990 | 9991 | 9992 | 9993 | 9993 | 9994 | 0 | 0 | 0 | |
| 1° | 9994 | 9995 | 9995 | 9996 | 9996 | 9997 | 9997 | 9997 | 9998 | 9998 | 0.9998 | 0 | 0 | 0 | |
| 0° | 9998 | 9999 | 9999 | 9999 | 9999 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0 | 0 | 0 | |
| 1.0000 |
|
Вашему вниманию представлена тригонометрическая таблица синусов косинусов и тангенсов из таблицы Брадиса. Она дает данные с точностью до четвертого знака после запятой. Причем все численные величины углов идут с кратностью шесть минут. Промежуточные значения углов находятся методом поправок. Для того, чтобы узнать величину SIN мы выбираем значения угла слева, а чтобы узнать величину COS угол выбираем справой стороны, при этом значения минут для SIN будут сверху, а для COS снизу. Таблица Брадиса синусов и косинусов практически незаменима если вы проводите свои вычисления без инженерного калькулятора, поэтому постарайтесь овладеть всеми правилами использования предоставленных нами материалов. |
Как пользоватся таблицей Брадиса ⇒
| ||||||||||||||
Таблица косинусов — 2mb.ru
Таблица косинусов является одной из основных таблиц, которые используются в геометрии.
В ней представлены косинусы углов от 0 до 360 градусов. Таблица позволяет решать математические задачи, в которых необходимо использовать тригонометрические данные без применения расчетов и калькулятора.
Таблица косинусов 0° – 180°.
|
|
|
Таблица косинусов 180° – 360°.
|
|
|
Арксинус, арккосинус и арктангенс угла
К понятиям арксинус, арккосинус, арктангенс, арккотангенс учащийся народ относится с опаской. Не понимает он эти термины и, стало быть, не доверяет этой славной семейке.) А зря. Это очень простые понятия. Которые, между прочим, колоссально облегчают жизнь знающему человеку при решении тригонометрических уравнений!
Сомневаетесь насчёт простоты? Напрасно.) Прямо здесь и сейчас вы в этом убедитесь.
Разумеется, для понимания, неплохо бы знать, что такое синус, косинус, тангенс и котангенс. Да их табличные значения для некоторых углов… Хотя бы в самых общих чертах. Тогда и здесь проблем не будет.
Итак, удивляемся, но запоминаем: арксинус, арккосинус, арктангенс и арккотангенс — это просто какие-то углы. Ни больше ни меньше. Бывает угол, скажем 30°. А бывает угол arcsin0,4. Или arctg(-1,3). Всякие углы бывают.) Просто записать углы можно разными способами. Можно записать угол через градусы или радианы. А можно — через его синус, косинус, тангенс и котангенс…
Что означает выражение
arcsin 0,4 ?
Это угол, синус которого равен 0,4 ! Да-да. Это смысл арксинуса. Специально повторю: arcsin 0,4 — это угол, синус которого равен 0,4.
И всё.
Чтобы эта простая мысль сохранилась в голове надолго, я даже приведу разбивочку этого ужасного термина — арксинус:
arc sin 0,4
угол, синус которого равен 0,4
Как пишется, так и слышится.) Почти. Приставка arc означает дуга (слово арка знаете?), т.к. древние люди вместо углов использовали дуги, но это сути дела не меняет. Запомните эту элементарную расшифровку математического термина! Тем более, для арккосинуса, арктангенса и арккотангенса расшифровка отличается только названием функции.
Что такое arccos 0,8 ?
Это угол, косинус которого равен 0,8.
Что такое arctg(-1,3) ?
Это угол, тангенс которого равен -1,3.
Что такое arcctg 12 ?
Это угол, котангенс которого равен 12.
Такая элементарная расшифровка позволяет, кстати, избежать эпических ляпов.) Например, выражение arccos1,8 выглядит вполне солидно. Начинаем расшифровку: arccos1,8 — это угол, косинус которого равен 1,8… Скока-скока!? 1,8!? Косинус не бывает больше единицы!!!
Верно. Выражение arccos1,8 не имеет смысла. И запись такого выражения в какой-нибудь ответ изрядно повеселит проверяющего.)
Элементарно, как видите.) У каждого угла имеется свой персональный синус и косинус. И почти у каждого — свой тангенс и котангенс. Стало быть, зная тригонометрическую функцию, можно записать и сам угол. Для этого и предназначены арксинусы, арккосинусы, арктангенсы и арккотангенсы. Далее я всю эту семейку буду называть уменьшительно — арки. Чтобы печатать меньше.)
А можно переходить от арков к обычным градусам или радианам? — слышу осторожный вопрос.)
Почему — нет!? Легко. И туда можно, и обратно. Более того, это иногда нужно обязательно делать. Арки — штука простая, но без них как-то спокойнее, правда?)
Например: что такое arcsin 0,5?
Вспоминаем расшифровку: arcsin 0,5 — это угол, синус которого равен 0,5. Теперь включаем голову (или гугл)) и вспоминаем, у какого угла синус равен 0,5? Синус равен 0,5 у угла в 30 градусов. Вот и все дела: arcsin 0,5 — это угол 30°. Можно смело записать:
arcsin 0,5 = 30°
Или, более солидно, через радианы:
Всё, можно забыть про арксинус и работать дальше с привычными градусами или радианами.
Если вы осознали, что такое арксинус, арккосинус… Что такое арктангенс, арккотангенс… То легко разберётесь, например, с таким монстром.)
Несведущий человек отшатнётся в ужасе, да…) А сведущий вспомнит заклинание: арксинус — это угол, синус которого… Ну и так далее. Если сведущий человек знает ещё и таблицу синусов… Таблицу косинусов. Таблицу тангенсов и котангенсов, то проблем вообще нет!
Достаточно сообразить, что:
Переведу формулу в слова: угол, тангенс которого равен 1 (arctg1) — это угол 45°. Или, что едино, Пи/4. Аналогично:
и всё… Заменяем все арки на значения в радианах, всё посокращается, останется посчитать, сколько будет 1+1. Это будет 2.) Что и является правильным ответом.
Вот таким образом можно (и нужно) переходить от арксинусов, арккосинусов, арктангенсов и арккотангенсов к обычным градусам и радианам. Это здорово упрощает страшные примеры!
Частенько, в подобных примерах, внутри арков стоят отрицательные значения. Типа, arctg(-1,3), или, к примеру, arccos(-0,8)… Это не проблема. Вот вам простые формулы перехода от отрицательных значений к положительным:
Нужно вам, скажем, определить значение выражения:
Это можно и по тригонометрическому кругу решить, но вам не хочется его рисовать. Ну и ладно. Переходим от отрицательного значения внутри арккосинуса к положительному по второй формуле:
Внутри арккосинуса справа уже положительное значение. То, что
вы просто обязаны знать. Остаётся подставить радианы вместо арккосинуса и посчитать ответ:
Вот и всё.
Ограничения на арксинус, арккосинус, арктангенс, арккотангенс.
Те, кто освоил темы «Тригонометрический круг», и «Отсчёт углов на тригонометрическом круге» — люди грамотные. И, возможно, уже приготовили мне убойный вопрос.) По определению, скажем, arcsin 0,5 — это угол, синус которого равен 0,5. Т.е 30°. Но…
Грамотный человек знает, что синус равен 0,5 не только у угла 30°! Так как:
sin30° = 0,5
sin150° = 0,5
sin390° = 0,5
sin510° = 0,5
И так до бесконечности… Неоднозначно получается! Получается, что arcsin0,5 это и 30°, и 150°, и 390°, и 510°, и ….
Да. Именно так. Арксинус 0,5 — это действительно бесконечный набор углов. Но обозначается такой арксинус вот как: Arcsin0,5. С заглавной буквы. В школе такие арксинусы не изучают. В школе изучают арки с маленькой буквы: arcsin, arccos, arctg, arcctg. Такие арки называются главными значениями арксинуса, арккосинуса и т.д. и имеют жёсткие ограничения по величине. Для однозначности.
С этими ограничениями надо разобраться основательно. Тем более, что это дело простое.) Запоминаем:
arсsin (любой) — это угол, который располагается в интервале:
arсcos (любой) — это угол, который располагается в интервале:
arсtg (любой) — это угол, который располагается в интервале:
arсctg (любой) — это угол, который располагается в интервале:
Запомнить эти диапазоны очень легко по картинкам. Тригонометрический круг вам в помощь!) Для арксинуса:
Зелёным нарисованы углы, которые пробегают значения от — Пи/2 до + Пи/2. Это и есть разрешённая зона для арксинусов. И никаких дополнительных оборотов! Строго от -90° до +90°! Никакой arcsin не может быть равным, например 120°, 180° или 330°. А вот 50°, -65°, 90° или 25° — пожалуйста!
Теперь, я думаю, понятно, что arcsin 0,5 = 30°. И только 30°! Так как углы 150°, 390°, 510° и т.д., которые тоже дают синус, равный 0,5, арксинусами быть не могут. Они выпадают из разрешённого диапазона.
А теперь наведите курсор мышки на рисунок. Вы увидите диапазон арктангенсов. Найдите 2 отличия.) Да! Конечные точки на оси ОУ стали белыми! Это означает, что они не включаются в диапазон арктангенсов. Арктангенс не может быть равным ±90°. По той простой причине, что тангенс 90° (и -90°) не существует.
Уже проще, правда?) Ну и, аналогичная картинка для арккосинуса и арккотангенса (при наведённом курсоре):
Надеюсь, зрительная память вас спасёт, если что…)
А зачем все эти арки? — слышу ещё один осторожный вопрос.)
Вопрос резонный. В математике просто так, чисто для красоты, ничего не бывает. Только по острой необходимости!) А вы попробуйте ответить на такой вопрос:
У какого угла синус равен 0,4?
Для ответа в градусах или радианах вам придётся открывать таблицы Брадиса, или включать солидный калькулятор. Искать там значение синуса, равное (примерно!) 0,4 и смотреть, какой же угол имеет этот синус. После тяжких трудов вы определите, что это угол примерно 23 градуса и 36 минут. Про радианы я вообще молчу…)
А через арксинус мгновенно даётся абсолютно точный ответ: угол, у которого синус равен 0,4 — это arcsin 0,4 ! Просто по смыслу арксинуса: arcsin 0,4 — это и есть угол, синус которого равен 0,4. Разумеется, это не единственный угол, синус которого равен 0,4, но через арки и все остальные записываются в три секунды. Этим мы в тригонометрических уравнениях займёмся.
Нахождение значений синуса, косинуса, тангенса и котангенса
Для того, чтобы определить значение угла α, необходимо воспользоваться подходящей функции из тригонометрии. Во время решения задач постоянно возникает необходимость в том, чтобы узнать значение углов. Для некоторых углов можно найти точные значения, для других сложно определить точную цифру и можно вывести только приблизительное значение.
В этой статье мы подробно поговорим о функциях из тригонометрии. Мы не только расскажем о свойствах синуса, тангенса и других функций, но и узнаем, как правильно вычислять значения для каждого отдельного случая.
Рассмотрим подробно каждый случай.
Определение 1Приближенное число для каждой из известных функций можно найти по определению. Для одних можно указать точные значения, для других – только приблизительные.
Соотношения сторон и углов фигуры используются для того, чтобы определить значения для 30°, 45°, 60°. Если угол выходит за пределы 90°, то перед вычислением значения следует воспользоваться специальной формулой для того, чтобы привести угол к нужному виду.
Если известно значение синуса для α, можно быстро узнать значение косинуса для этого же угла. Это легко выполнить с помощью основных тождеств, которые представлены в геометрии.
В некоторых случаях для того, чтобы узнать sin или cos угла, можно использовать подходящую тригонометрическую формулу. Например, по известному значению синуса 45°, мы сможем определить значение синуса 30°, воспользовавшись правилом из тригонометрии.
Если для примера не подходит ни одно из приведенных выше решений, можно найти приближенное значение. В этом вам помогут таблицы основных тригонометрических функций, которые легко можно найти.
Если взять за основу определения, возможно определить значения для определенного угла α. Также можно вычислить значения тангенса и котангенса для определенного случая. Можно найти значений основных функций из тригонометрии для частных вариантов. Это углы 0°, 90°, 180°, 270°, 360°.
Разобьем эти углы на четыре группы: 360·z градусов (2π·z рад), 90+360·z градусов (π2+2π·z рад), 180+360·z градусов (π+2π·z рад) и 270+360·z градусов (3π2+2π·z рад), где z- любое целое число.
Изобразим данные формулы на рисунке:
Для каждой группы соответствуют свои значения.
Пример 1При повороте из точки A на 360·z°, она переходит в себя. А1(1, 0). Синус 0°, 360°, 720° равен 0, а косинус равен 1. Представим это в виде формулы: sin (360°·z)=0 и cos (360°·z)=1 .
Можно определить, что tg (360°·z)=01=0 , а котангенс не определен.
Пример 2Если А(1, 0) повернуть на 90+360·z°, то она перейдет в А1 (0, 1). По определению: sin (90°+360°·z) =1 и cos (90°+360°·z) =0 . Мы не сможем определить значение тангенса, но котангенс рассчитывается по данной формуле: ctg (90°+360°·z) =01=0 .
Пример 3Рассмотрим особенности для третьей группы углов. После поворота точки А(1, 0) на любой из углов 180+360·z°, она перейдет в A1(−1, 0). Мы находим значения функций кроме тангенса.
Пример 4Рассмотрим правила для четвертой группы углов. При повороте точки на 270+360·z° мы попадем в A1(0, −1). Мы находим значения всех функций кроме тангенса.
Для углов, которые не относятся к перечню от 0 °, 90 °, 180 °, 270 °, 360 °…, точных значений нет. Мы можем найти лишь приближенные значения. Рассмотрим пример. Условия – найти основные значения для угла −52 °. Выполним построения.
Согласно рисунку, абсцисса А1 ≈ 0,62, а ордината ≈ −0,78. Соответственно, sin(-52°)≈-0,78 и cos(-52°)≈0,62 . Осталось определиться с тангенсом и котангенсом.
Выполняем вычисления: tg(-52°)≈-0, 780, 62≈-1,26 и ctg(-52°)≈0,62-0,78≈-0,79.
Чем точнее выполняется чертеж, тем более точными будут значения для каждого индивидуального случая. Выполнять вычисления удобно только в теории, так как на практике довольно сложно и долго выполнять рисунки.
Линии тригонометрических функций
Определение 2Линии тригонометрических функций – это линии, которые изображаются вместе с единичной окружностью. Они имеют точку отсчета и единичный отрезок, которая равна единице в координатной системе. Они используются для наглядного изображения значений.
Рассмотрим их на подробном рисунке
Как найти sin α, cos α, tg α, ctg α
Для тридцати-, сорокопяти-, шестидесятиградусных углов мы имеем определенные значения. Чтобы найти их, можно воспользоваться правилами о прямоугольном треугольнике с острыми углами. Для этого используется теорема Пифагора.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать задание Пример 5Для того, чтобы узнать значения для углов тридцати- и шестидесятиградусных углов изображаем прямоугольный треугольник с углами данной величины. Длина гипотенузы должна быть равна 1. Согласно теореме Пифагора, катет, лежащий напротив тридцатиградусного угла, равен половине гипотенузы. Воспользуемся теоремой: 12-122=32 . Так как синус угла – это катет, деленный на гипотенузу, вычисляем, что sin 30°=121=12 и sin 60°=321=32 .
Косинус можно найти по формуле, которая предполагает деление прилежащего катета на гипотенузу. Вычисляем: cos 30°=321=32 и cos 60°=121=12 .
Тангенс можно найти по формуле, которая предполагает деление противолежащего катета на прилежащий. Котангенс находим по такой же схеме – делим прилежащий катет на противолежащий.
Вычисляем: tg 30°=1232=13=33 и tg 60°=3212=3 . Находим котангенс по подобной схеме: сtg 30°=3212=3 и сtg 60°=1232=13=33 . После этого приступаем к вычислению значений основных тригонометрических функций для сорока пятиградусного угла. Используем равнобедренный треугольник с углами 45° и гипотенузой, которая равна 1. Используем теорему Пифагора. Согласно формуле, длины катетов равны 22 . Т
Теперь мы сможем найти значения для основных тригонометрических функций. Используем формулу, которая предполагает деление длин соответствующих сторон рассматриваемого треугольника.
Выводим формулу: ctg 45°=2222=1 .
Полученные значения для тридцати-, сорокапяти-, шестидесятиградусных углов будут использоваться для решения различных задач. Запишите их – они часто будут использоваться. Для удобства можно использовать таблицу значений.
Проиллюстрируем значения для тридцати-, сорокапяти-, шестидесятиградусных углов с использованием окружности и линий.
Значения основных функций тригонометрии
Основные тождества из геометрии связывают с собой sin α, cos α, tg α, ctg α для определенного угла. С помощью одной функции вы легко сможете найти другую.
Определение 3Для того, чтобы найти синус по известному косинусу, sin2α+cos2α=1 .
Определение 4Тангенс по известному косинусу tg2α+1=1cos2α .
Определение 5Котангенс по известному синусу или наоборот 1+ctg2α= 1sin2α .
Определение 6Тангенс через котангенс или наоборот можно найти благодаря удобной формуле: tg α·ctg α=1 .
Для того, чтобы закрепить полученные знания, рассмотрим их на подробном примере
Пример 6Необходимо найти значение синуса угла π8, если tg π8=2-1 .
Сначала найдем котангенс угла: ctgπ8=1tgπ8=12-1=2+1(2-1)·(2+1)= 2+1(2)2-12=2+1 Воспользуемся формулой 1+ctg2α=1sin2α . Благодаря этому мы вычисляем значение синуса. Имеем
sin2π8=11+ctg2π8=11+(2+1)2=14+22=12·(2+2)=2-22·(2+2)·(2-2)==2-22·(22-(2)2)=2-24
Для завершения необходимо определить значение синуса. Угол π8 является углом первой четверти, то синус является положительным. Чтобы точно определить знак, вы можете воспользоваться таблицей, в которой определены знаки по четвертям координатной плоскости. Таким образом, sin π8=sin2π8=2-24=2-22 . sin π8=2-22.
Сведение к углу
Удобнее всего находить значения для угла от 0 до 90 °. Сведение к углу из интервала от 0 до 90 °. Если угол не соответствует заданному интервалу, можно использовать законы и тождества, которые мы учили на уроках геометрии. Тогда мы сможем найти значение, которое будет равно для угла указанных пределах.
Пример 7Задача заключается в том, чтобы найти синус 210°. Представим 210 как разность или сумму, разложив число на несколько. Воспользуемся соответствующей формулой для приведения. Используем формулу для нахождения значения синуса 30°: sin 210°=sin(180°+30°)=-sin 30°=-12 , или косинуса 60 ° sin 210°=sin(270°-60°)=-cos 60°=-12.
Для того, чтобы решать задачи было намного проще, при нахождении значений переходите к углам из интервала от 0 до 90° с помощью формул приведения, если угол не находится в этих пределах.
Использование формул
Раннее мы рассмотрели подробности, касающиеся нахождению значений основных функций с использованием формул тригонометрии. Для того, чтобы определить значение для определенного угла, используйте формулы и значения основных функций для известных углов.
Для примера вычислим значение тангенса π8, который был использован в предыдущем примере. Возьмем за основу основные формулы тригонометрии.
Пример 8Найдите значение tgπ8 .
Используя формулу тангенса, преобразуем уравнение до следующего равенства tg2π8=1-cosπ41+cosπ4 . Значения косинуса угла π4 известны из предыдущего примера. Благодаря этому мы быстро найдем значения тангенса.
tg2π8=1-cosπ41+cosπ4=1-221+22=2-22+2==(2-2)2(2+2)·(2-2)=(2-2)222-(2)2=(2-2)22
Угол π8 является углом первой четверти. Согласно таблице основных тригонометрических функций по четвертям координатной плоскости, тангенс этого угла положителен. Продолжаем вычисления для дальнейшего решения: tgπ8=tg2π8=(2-2)22=2-22=2-1
tgπ8=2-1.
Частные случаи
Тригонометрия – довольно сложная наука. Далеко не всегда можно найти формулы, используемые для вычисления. Существует множество уравнений, которые не поддаются стандартным формулам. Некоторые значения очень сложно обозначить точной цифрой. Это не так просто, как может показаться.
Однако точные значения не всегда нужны. Хватает и тех, что не претендуют на высокую точность. Благодаря существующим таблицам, которые можно найти в математических учебниках, можно найти любое приближенное значение основных функций. Благодаря справочным материалам вычислять формулы будет намного проще. В таблицах содержатся значения с высокой точностью.
Единичный круг: функции синуса и косинуса
Чтобы определить наши тригонометрические функции, мы начинаем с рисования единичного круга, круга с центром в начале координат и радиусом 1, как показано на рисунке 2. Угол (в радианах), который пересекает [latex] t [/ latex], образует дугу. длины [латекс] с [/ латекс]. Используя формулу [latex] s = rt [/ latex] и зная, что [latex] r = 1 [/ latex], мы видим, что для единичной окружности , [latex] s = t [/ latex].
Напомним, что оси x- и y- делят координатную плоскость на четыре четверти, называемых квадрантами.Мы помечаем эти квадранты, чтобы имитировать направление, в котором развернется положительный угол. Четыре квадранта обозначены I, II, III и IV.
Для любого угла [латекс] t [/ латекс] мы можем пометить пересечение конечной стороны и единичного круга его координатами, [латекс] \ left (x, y \ right) [/ latex]. Координаты [latex] x [/ latex] и [latex] y [/ latex] будут выходными данными тригонометрических функций [latex] f \ left (t \ right) = \ cos t [/ latex] и [latex] f \ left (t \ right) = \ sin t [/ latex] соответственно.Это означает [латекс] x = \ cos t [/ latex] и [латекс] y = \ sin t [/ latex].
Рис. 2. Единичная окружность с центральным углом [латекс] t [/ латекс] радиан
A Общее примечание: Unit Circle
Единичная окружность имеет центр [латекс] \ влево (0,0 \ вправо) [/ латекс] и радиус [латекс] 1 [/ латекс]. В единичном круге длина перехваченной дуги равна радианам центрального угла [латекс] 1 [/ латекс].
Пусть [latex] \ left (x, y \ right) [/ latex] будет конечной точкой единичной окружности дуги длиной [латекс] s [/ latex].Координаты [latex] \ left (x, y \ right) [/ latex] этой точки могут быть описаны как функции угла.
Определение функций синуса и косинуса
Теперь, когда у нас есть помеченная единичная окружность, мы можем узнать, как координаты [latex] \ left (x, y \ right) [/ latex] соотносятся с длиной дуги и углом . Функция синуса связывает действительное число [латекс] t [/ латекс] с координатой y точки, где соответствующий угол пересекает единичную окружность.Точнее, синус угла [латекс] t [/ латекс] равен y -значению конечной точки на единичной окружности дуги длиной [латекс] t [/ латекс]. На рисунке 2 синус равен [latex] y [/ latex]. Как и все функции, синусоидальная функция имеет вход и выход. Его вход — мера угла; его выход — координата y соответствующей точки на единичной окружности.
Функция косинуса угла [латекс] t [/ latex] равна значению x конечной точки на единичной окружности дуги длиной [латекс] t [/ латекс].{2} [/ латекс]. Имейте в виду, что многие калькуляторы и компьютеры не распознают сокращенную запись. В случае сомнений используйте дополнительные скобки при вводе вычислений в калькулятор или компьютер.
Общее примечание: функции синуса и косинуса
Если [латекс] t [/ latex] является действительным числом и точка [латекс] \ left (x, y \ right) [/ latex] на единичном круге соответствует углу [латекса] t [/ latex] , затем
[латекс] \ cos t = x [/ латекс]
[латекс] \ sin t = y [/ латекс]
Как сделать: по точке
P [латекс] \ left (x, y \ right) [/ latex] на единичной окружности, соответствующей углу [латекс] t [/ latex], найдите синус и косинус.- Синус [latex] t [/ latex] равен y -координате точки [latex] P: \ sin t = y [/ latex].
- Косинус [latex] t [/ latex] равен x -координате точки [latex] P: \ text {cos} t = x [/ latex].
Пример 1: Поиск значений функции для синуса и косинуса
Точка [латекс] P [/ латекс] — это точка на единичной окружности, соответствующая углу [латекс] t [/ латекс], как показано на рисунке 4. Найдите [латекс] \ cos \ left (t \ right) \\ [/ latex] и [latex] \ text {sin} \ left (t \ right) \\ [/ latex].
Рисунок 4
Решение
Мы знаем, что [latex] \ cos t [/ latex] — это координата x соответствующей точки на единичном круге, а [latex] \ sin t [/ latex] — это координата y соответствующей точка на единичной окружности. Итак:
[латекс] \ begin {массив} {l} \ begin {array} {l} \\ x = \ cos t = \ frac {1} {2} \ end {array} \ hfill \\ y = \ sin t = \ frac {\ sqrt {3}} {2} \ hfill \ end {array} \\ [/ latex]
Попробуй 1
Определенный угол [латекс] t [/ латекс] соответствует точке на единичной окружности в [латекс] \ left (- \ frac {\ sqrt {2}} {2}, \ frac {\ sqrt {2}} {2} \ right) \\ [/ latex], как показано на рисунке 5. {2} t = 1 [/ латекс]
Как сделать: учитывая синус некоторого угла [латекс] t [/ латекс] и его положение в квадранте, найдите косинус [латекс] t [/ латекс].
- Подставьте известное значение [latex] \ sin \ left (t \ right) [/ latex] в пифагорейскую идентичность.
- Решите относительно [латекс] \ cos \ left (t \ right) [/ latex].
- Выберите решение с соответствующим знаком для значений x в квадранте, где находится [латекс] t [/ латекс].
Пример 3: Нахождение косинуса из синуса или синуса из косинуса
Если [латекс] \ sin \ left (t \ right) = \ frac {3} {7} \\ [/ latex] и [latex] t [/ latex] находится во втором квадранте, найдите [latex] \ cos \ left (t \ right) \\ [/ латекс].{2} \ left (t \ right) = \ frac {40} {49} \ hfill \\ \ text {cos} \ left (t \ right) = \ pm \ sqrt {\ frac {40} {49}} = \ pm \ frac {\ sqrt {40}} {7} = \ pm \ frac {2 \ sqrt {10}} {7} \ hfill \ end {array} \\ [/ latex]
Поскольку угол находится во втором квадранте, мы знаем, что значение x- является отрицательным действительным числом, поэтому косинус также отрицателен. Итак,
[латекс] \ text {cos} \ left (t \ right) = — \ frac {2 \ sqrt {10}} {7} \\ [/ latex]
Попробовать 3
Если [латекс] \ cos \ left (t \ right) = \ frac {24} {25} \\ [/ latex] и [latex] t [/ latex] находится в четвертом квадранте, найдите [latex] \ text {грех} \ влево (т \ вправо) \\ [/ латекс].Треугольник \ circ [/ latex] — это равнобедренный треугольник, поэтому координаты x- и y соответствующей точки на окружности совпадают. Поскольку значения x- и y одинаковы, значения синуса и косинуса также будут равны.
Рисунок 9
При [latex] t = \ frac {\ pi} {4} [/ latex], что составляет 45 градусов, радиус единичной окружности делит пополам угол первого квадранта . Это означает, что радиус лежит вдоль линии [латекс] y = x [/ latex].{2} = \ frac {1} {2} \\ \ text {} x = \ pm \ frac {1} {\ sqrt {2}} \ end {array} \\ [/ latex]
В квадранте I [латекс] x = \ frac {1} {\ sqrt {2}} \\ [/ latex]. \ circ [/ latex] — это [латекс] \ left (\ frac {\ sqrt {2}} {2}, \ frac {\ sqrt {2}} {2} \ right) \\ [/ latex].\ circ [/ latex], как показано на рисунке 12.
Рисунок 11
Рисунок 12
Поскольку все углы равны, стороны также равны. Вертикальная линия имеет длину [латекс] 2y [/ latex], и, поскольку все стороны равны, мы также можем сделать вывод, что [latex] r = 2y [/ latex] или [latex] y = \ frac {1} {2 } г [/ латекс]. Поскольку [латекс] \ sin t = y [/ latex],
[латекс] \ sin \ left (\ frac {\ pi} {6} \ right) = \ frac {1} {2} r \\ [/ latex]
А поскольку [latex] r = 1 [/ latex] в нашем единичном круге ,
[латекс] \ begin {array} {l} \ sin \ left (\ frac {\ pi} {6} \ right) = \ frac {1} {2} \ left (1 \ right) \ hfill \\ \ текст {} = \ frac {1} {2} \ hfill \ end {array} \\ [/ latex]
Используя тождество Пифагора, мы можем найти значение косинуса.\ circ [/ латекс]. Теперь у нас есть равносторонний треугольник. Поскольку каждая сторона равностороннего треугольника [латекс] ABC [/ латекс] имеет одинаковую длину, и мы знаем, что одна сторона является радиусом единичного круга, все стороны должны иметь длину 1.
Рисунок 13
Угол наклона [латекс] ABD [/ латекс] составляет 30 °. Так, если двойной, угол [латекс] ABC [/ латекс] равен 60 °. [latex] BD [/ latex] — это серединный перпендикуляр к [latex] AC [/ latex], поэтому он разрезает [latex] AC [/ latex] пополам. Это означает, что [latex] AD [/ latex] — это [latex] \ frac {1} {2} [/ latex] радиус или [latex] \ frac {1} {2} [/ latex].\ circ [/ latex] — это [латекс] \ left (\ frac {1} {2}, \ frac {\ sqrt {3}} {2} \ right) \\ [/ latex], поэтому мы можем найти синус и косинус.
[латекс] \ begin {array} {l} \ left (x, y \ right) = \ left (\ frac {1} {2}, \ frac {\ sqrt {3}} {2} \ right) \ hfill \\ x = \ frac {1} {2}, y = \ frac {\ sqrt {3}} {2} \ hfill \\ \ cos t = \ frac {1} {2}, \ sin t = \ гидроразрыв {\ sqrt {3}} {2} \ hfill \ end {array} \\ [/ latex]
Теперь мы нашли значения косинуса и синуса для всех наиболее часто встречающихся углов в первом квадранте единичной окружности. В таблице ниже приведены эти значения.
| Угол | 0 | [латекс] \ frac {\ pi} {6} \\ [/ latex], или 30 | [латекс] \ frac {\ pi} {4} \\ [/ latex], или 45 ° | [латекс] \ frac {\ pi} {3} \\ [/ latex], или 60 ° | [латекс] \ frac {\ pi} {2} \\ [/ latex], или 90 ° |
| Косинус | 1 | [латекс] \ frac {\ sqrt {3}} {2} \\ [/ латекс] | [латекс] \ frac {\ sqrt {2}} {2} \\ [/ латекс] | [латекс] \ frac {1} {2} \\ [/ латекс] | 0 |
| Синус | 0 | [латекс] \ frac {1} {2} \\ [/ латекс] | [латекс] \ frac {\ sqrt {2}} {2} \\ [/ латекс] | [латекс] \ frac {\ sqrt {3}} {2} \\ [/ латекс] | 1 |
На рисунке 14 показаны общие углы в первом квадранте единичной окружности.
Рисунок 14
Использование калькулятора для поиска синуса и косинуса
Чтобы найти косинус и синус углов, отличных от специальных углов , мы обращаемся к компьютеру или калькулятору. Будьте внимательны. : Большинство калькуляторов можно установить в режим «градус» или «радиан», который сообщает калькулятору единицы измерения входного значения. Когда мы вычисляем [латекс] \ cos \ left (30 \ right) [/ latex] на нашем калькуляторе, он будет оценивать его как косинус 30 градусов, если калькулятор находится в режиме градусов, или косинус 30 радиан, если калькулятор находится в радианном режиме.
Как: заданный угол в радианах, используйте графический калькулятор, чтобы найти косинус.
- Если калькулятор имеет режим градусов и режим радиан, установите его в режим радиан.
- Нажмите кнопку COS.
- Введите значение угла в радианах и нажмите клавишу в скобках «)».
- Нажмите ENTER.
Пример 4: Использование графического калькулятора для поиска синуса и косинуса
Вычислить [латекс] \ cos \ left (\ frac {5 \ pi} {3} \ right) \\ [/ latex] с помощью графического калькулятора или компьютера.\ circ [/ latex], например, включив коэффициент преобразования в радианы как часть входных данных:
SIN (20 × π ÷ 180) ВВОД
Попробовать 4
Вычислить [латекс] \ sin \ left (\ frac {\ pi} {3} \ right) \\ [/ latex].
Решение
Определение области и диапазона функций синуса и косинуса
Теперь, когда мы можем найти синус и косинус угла, нам нужно обсудить их области и диапазоны. Каковы области определения функций синуса и косинуса? То есть, какие наименьшие и наибольшие числа могут входить в функции? Поскольку углы меньше 0 и углы больше [латекс] 2 \ pi [/ latex] все еще могут быть нанесены на единичный круг и имеют реальные значения [latex] x, y [/ latex] и [latex] r [/ latex], не существует нижнего или верхнего предела углов, которые могут входить в функции синуса и косинуса.Входными данными для функций синуса и косинуса является поворот от положительной оси x , и это может быть любое действительное число.
Каковы диапазоны функций синуса и косинуса? Каковы наименьшие и наибольшие возможные значения их производительности? Мы можем увидеть ответы, исследуя единичный круг , как показано на рисунке 15. Границы координаты x следующие: [latex] \ left [-1,1 \ right] [/ latex]. Границы координаты y также равны [latex] \ left [-1,1 \ right] [/ latex].Следовательно, диапазон функций синуса и косинуса равен [latex] \ left [-1,1 \ right] [/ latex].
Рисунок 15
Мы обсудили нахождение синуса и косинуса для углов в первом квадранте, но что, если наш угол находится в другом квадранте? Для любого заданного угла в первом квадранте существует угол во втором квадранте с тем же значением синуса. Поскольку значение синуса — это координата y на единичной окружности, другой угол с таким же синусом будет иметь такое же значение y , но будет иметь противоположное значение x .Следовательно, его значение косинуса будет противоположным значению косинуса первого угла.
Аналогично, в четвертом квадранте будет угол с таким же косинусом, что и исходный угол. Угол с таким же косинусом будет иметь одинаковое значение x , но будет иметь противоположное значение y . Следовательно, его значение синуса будет противоположным значению синуса исходного угла.
Как показано на рисунке 16, угол [латекс] \ альфа [/ латекс] имеет то же значение синуса, что и угол [латекс] t [/ латекс]; значения косинуса противоположны.Угол [латекс] \ бета [/ латекс] имеет то же значение косинуса, что и угол [латекс] t [/ латекс]; значения синуса противоположны.
[латекс] \ begin {array} {lll} \ sin \ left (t \ right) = \ sin \ left (\ alpha \ right) \ hfill & \ text {and} \ hfill & \ cos \ left (t \ right ) = — \ cos \ left (\ alpha \ right) \ hfill \\ \ sin \ left (t \ right) = — \ sin \ left (\ beta \ right) \ hfill & \ text {и} \ hfill & \ cos \ left (t \ right) = \ cos \ left (\ beta \ right) \ hfill \ end {array} [/ latex]Рисунок 16
Напомним, что опорный угол угла — это острый угол [латекс] t [/ латекс], образованный конечной стороной угла [латекс] t [/ латекс] и горизонтальной осью. \ circ \ mathrm {-t} | [/ latex].\ circ [/ латекс]
Попробовать 5
Найдите опорный угол [латекса] \ frac {5 \ pi} {3} [/ latex].
Решение
Использование опорных углов
А теперь давайте вернемся к колесу обозрения, представленному в начале этого раздела. Предположим, всадник делает снимок, остановившись на высоте двадцати футов над уровнем земли. Затем всадник совершает поворот на три четверти по кругу. Какая у всадника новая высота? Чтобы ответить на такие вопросы, как этот, нам нужно оценить функции синуса или косинуса при углах, превышающих 90 градусов, или при отрицательном угле .Базовые углы позволяют оценивать тригонометрические функции для углов вне первого квадранта. Их также можно использовать для поиска координат [latex] \ left (x, y \ right) [/ latex] для этих углов. Мы будем использовать опорный угол угла поворота в сочетании с квадрантом, в котором находится конечная сторона угла.
Использование опорных углов для оценки тригонометрических функций
Мы можем найти косинус и синус любого угла в любом квадранте, если мы знаем косинус или синус его опорного угла.Абсолютные значения косинуса и синуса угла такие же, как и у опорного угла. Знак зависит от квадранта исходного угла. Косинус будет положительным или отрицательным в зависимости от знака значений x в этом квадранте. Синус будет положительным или отрицательным в зависимости от знака значений и в этом квадранте.
Общее примечание: Использование опорных углов для определения косинуса и синуса
Углы имеют косинусы и синусы с тем же абсолютным значением, что и их опорные углы.Знак (положительный или отрицательный) можно определить по квадранту угла.
Как: для заданного угла в стандартном положении найдите опорный угол, а также косинус и синус исходного угла.
- Измерьте угол между конечной стороной заданного угла и горизонтальной осью. Это опорный угол.
- Определите значения косинуса и синуса опорного угла.
- Присвойте косинусу тот же знак, что и значениям x в квадранте исходного угла.\ circ \ right) = \ frac {1} {2} [/ latex]
- [латекс] \ frac {5 \ pi} {4} [/ latex] находится в третьем квадранте. Его опорный угол составляет [латекс] \ frac {5 \ pi} {4} — \ pi = \ frac {\ pi} {4} [/ latex]. Косинус и синус [latex] \ frac {\ pi} {4} [/ latex] оба равны [latex] \ frac {\ sqrt {2}} {2} [/ latex]. В третьем квадранте значения [latex] x [/ latex] и [latex] y [/ latex] отрицательны, поэтому:
[латекс] \ cos \ frac {5 \ pi} {4} = — \ frac {\ sqrt {2}} {2} \ text {и} \ sin \ frac {5 \ pi} {4} = — \ гидроразрыв {\ sqrt {2}} {2} [/ latex]
Попробуй 6
а.\ circ \ right) [/ латекс].
г. Используйте опорный угол [латекс] — \ frac {\ pi} {6} [/ latex], чтобы найти [латекс] \ cos \ left (- \ frac {\ pi} {6} \ right) [/ latex] и [латекс] \ sin \ left (- \ frac {\ pi} {6} \ right) [/ latex].
Использование опорных углов для поиска координат
Теперь, когда мы узнали, как находить значения косинуса и синуса для особых углов в первом квадранте, мы можем использовать симметрию и опорные углы, чтобы заполнить значения косинуса и синуса для остальных особых углов единичной окружности.Они показаны на рисунке 19. Найдите время, чтобы узнать координаты [latex] \ left (x, y \ right) [/ latex] всех основных углов в первом квадранте.
В дополнение к изучению значений специальных углов, мы можем использовать опорные углы, чтобы найти координаты [latex] \ left (x, y \ right) [/ latex] любой точки на единичной окружности, используя то, что мы знаем об опорных углах. вместе с удостоверениями личности
[латекс] \ begin {array} {l} x = \ cos t \ hfill \\ y = \ sin t \ hfill \ end {array} [/ latex]
Сначала мы находим опорный угол, соответствующий данному углу.Затем мы берем значения синуса и косинуса опорного угла и даем им знаки, соответствующие значениям квадранта y и x .
Как сделать: учитывая угол точки на окружности и радиус окружности, найдите координаты [latex] \ left (x, y \ right) [/ latex] точки.
- Найдите опорный угол, измерив наименьший угол к оси x .
- Найдите косинус и синус опорного угла.
- Определите соответствующие знаки для [латекс] x [/ латекс] и [латекс] y [/ латекс]
в данном квадранте.
Пример 6: Использование единичной окружности для поиска координат
Найдите координаты точки на единичной окружности под углом [latex] \ frac {7 \ pi} {6} [/ latex].
Решение
Мы знаем, что угол [латекс] \ frac {7 \ pi} {6} [/ латекс] находится в третьем квадранте.
Во-первых, давайте найдем опорный угол, измерив угол к оси x .Чтобы найти опорный угол угла, конечная сторона которого находится в квадранте III, мы находим разность угла и [латекс] \ pi [/ латекс].
[латекс] \ frac {7 \ pi} {6} — \ pi = \ frac {\ pi} {6} [/ latex]
Далее мы найдем косинус и синус опорного угла:
[латекс] \ cos \ left (\ frac {\ pi} {6} \ right) = \ frac {\ sqrt {3}} {2} \ sin \ left (\ frac {\ pi} {6} \ right ) = \ frac {1} {2} [/ латекс]
Мы должны определить соответствующие знаки для x и y в данном квадранте.Поскольку наш исходный угол находится в третьем квадранте, где оба [latex] x [/ latex] и [latex] y [/ latex] отрицательны, косинус и синус отрицательны.
[латекс] \ begin {array} {l} \ cos \ left (\ frac {7 \ pi} {6} \ right) = — \ frac {\ sqrt {3}} {2} \ hfill \\ \ sin \ left (\ frac {7 \ pi} {6} \ right) = — \ frac {1} {2} \ hfill \ end {array} [/ latex]
Теперь мы можем вычислить координаты [latex] \ left (x, y \ right) [/ latex], используя тождества [latex] x = \ cos \ theta [/ latex] и [latex] y = \ sin \ theta [ /латекс].
Координаты точки: [latex] \ left (- \ frac {\ sqrt {3}} {2}, — \ frac {1} {2} \ right) [/ latex] на единичной окружности.{2} t = 1 [/ латекс]
Ключевые понятия
- Нахождение значений функции для синуса и косинуса начинается с рисования единичной окружности с центром в начале координат и радиусом 1 единица.
- Используя единичную окружность, синус угла [латекс] t [/ latex] равен y -значению конечной точки на единичной окружности дуги длиной [латекс] t [/ латекс], тогда как косинус угол [latex] t [/ latex] равен x -значению конечной точки.
- Значения синуса и косинуса наиболее точно определяются, когда соответствующая точка единичной окружности попадает на ось.
- Когда синус или косинус известен, мы можем использовать пифагорову тождество, чтобы найти другое. Пифагорейская идентичность также полезна для определения синусов и косинусов особых углов.
- Калькуляторы и программное обеспечение для построения графиков полезны для поиска синусов и косинусов, если известна правильная процедура ввода информации.
- Все функции синуса и косинуса являются действительными числами.
- Диапазон функций синуса и косинуса: [latex] \ left [-1,1 \ right] [/ latex].
- Синус и косинус угла имеют то же абсолютное значение, что и синус и косинус его опорного угла.
- Знаки синуса и косинуса определяются из значений x и y в квадранте исходного угла.
- Опорный угол угла — это размерный угол, [латекс] t [/ латекс],
, образованный конечной стороной угла [латекс] t [/ латекс] и горизонтальной осью. - Опорные углы можно использовать для определения синуса и косинуса исходного угла.
- Опорные углы также можно использовать для определения координат точки на окружности.
Глоссарий
- функция косинуса
- значение x точки на единичной окружности, соответствующее заданному углу
- Пифагорейская идентичность
- следствие теоремы Пифагора, утверждающее, что квадрат косинуса заданного угла плюс квадрат синуса этого угла равняется 1
- синусоидальная функция
- значение y точки на единичной окружности, соответствующее заданному углу
- единичный круг
- круг с центром в [латекс] \ влево (0,0 \ вправо) [/ латекс]
и радиусом
Упражнения по разделам
- 1.Опишите единичный круг.
- 2. Что обозначают координаты x- и y- точек на единичной окружности?
3. Обсудите разницу между котерминальным углом и опорным углом.
4. Объясните, чем косинус угла во втором квадранте отличается от косинуса его опорного угла в единичной окружности.
5. Объясните, чем синус угла во втором квадранте отличается от синуса его опорного угла в единичной окружности.
В следующих упражнениях используйте заданный знак функций синуса и косинуса, чтобы найти квадрант, в котором лежит конечная точка, определяемая [latex] t [/ latex].
6. [латекс] \ text {sin} \ left (t \ right) <0 [/ latex] и [latex] \ text {cos} \ left (t \ right) <0 [/ latex]
7. [латекс] \ text {sin} \ left (t \ right)> 0 [/ latex] и [latex] \ cos \ left (t \ right)> 0 [/ latex]
8. [латекс] \ sin \ left (t \ right)> 0 [/ latex] и [латекс] \ cos \ left (t \ right) <0 [/ latex]
9.[латекс] \ sin \ left (t \ right) <0 [/ latex] и [латекс] \ cos \ left (t \ right)> 0 [/ latex]
Для следующих упражнений найдите точное значение каждой тригонометрической функции.
10. [латекс] \ sin \ frac {\ pi} {2} [/ латекс]
11. [латекс] \ sin \ frac {\ pi} {3} [/ латекс]
12. [латекс] \ cos \ frac {\ pi} {2} [/ латекс]
13. [латекс] \ cos \ frac {\ pi} {3} [/ латекс]
14. [латекс] \ sin \ frac {\ pi} {4} [/ латекс]
15. [латекс] \ cos \ frac {\ pi} {4} [/ латекс]
16.\ circ [/ латекс]
28. [латекс] \ frac {5 \ pi} {4} [/ латекс]
29. [латекс] \ frac {2 \ pi} {3} [/ латекс]
30. [латекс] \ frac {5 \ pi} {6} [/ латекс]
31. [латекс] \ frac {-11 \ pi} {3} [/ латекс]
32. [латекс] \ frac {-7 \ pi} {4} [/ латекс]
33. [латекс] \ frac {- \ pi} {8} [/ латекс]
Для следующих упражнений найдите опорный угол, квадрант конечной стороны, а также синус и косинус каждого угла. Если угол не является одним из углов единичной окружности, воспользуйтесь калькулятором и округлите до трех десятичных знаков.\ circ [/ латекс]
42. [латекс] \ frac {5 \ pi} {4} [/ латекс]
43. [латекс] \ frac {7 \ pi} {6} [/ латекс]
44. [латекс] \ frac {5 \ pi} {3} [/ латекс]
45. [латекс] \ frac {3 \ pi} {4} [/ латекс]
46. [латекс] \ frac {4 \ pi} {3} [/ латекс]
47. [латекс] \ frac {2 \ pi} {3} [/ латекс]
48. [латекс] \ frac {5 \ pi} {6} [/ латекс]
49. [латекс] \ frac {7 \ pi} {4} [/ латекс]
Найдите требуемое значение для следующих упражнений.
50. Если [латекс] \ text {cos} \ left (t \ right) = \ frac {1} {7} [/ latex] и [latex] t [/ latex] находится в квадранте 4 -го , найдите [латекс] \ text {sin} \ left (t \ right) [/ latex].
51. Если [латекс] \ text {cos} \ left (t \ right) = \ frac {2} {9} [/ latex] и [latex] t [/ latex] находится в квадранте 1 st , найдите [латекс] \ text {sin} \ left (t \ right) [/ latex].
52. Если [латекс] \ text {sin} \ left (t \ right) = \ frac {3} {8} [/ latex] и [latex] t [/ latex] находится в квадранте 2 nd , найдите [латекс] \ text {cos} \ left (t \ right) [/ latex].
53. Если [латекс] \ text {sin} \ left (t \ right) = — \ frac {1} {4} [/ latex] и [latex] t [/ latex] находится в квадранте 3 rd найдите [латекс] \ text {cos} \ left (t \ right) [/ latex].\ circ [/ латекс].
56. Найдите координаты точки на окружности с радиусом 8, соответствующей углу [latex] \ frac {7 \ pi} {4} [/ latex].
57. Найдите координаты точки на окружности с радиусом 16, соответствующей углу [латекс] \ frac {5 \ pi} {9} [/ latex].
58. Укажите область определения функций синуса и косинуса.
59. Укажите диапазон функций синуса и косинуса.
Для следующих упражнений используйте данную точку на единичном круге, чтобы найти значение синуса и косинуса [латекс] t [/ латекс].
60.
61.
62.
63.
64.
65.
66.
67.
68.
69.
70.
71.
72.
73.
74.
75.
76.
77.
78.
79.
Для следующих упражнений используйте графический калькулятор для оценки.\ circ [/ латекс]90. [латекс] \ sin \ left (\ frac {11 \ pi} {3} \ right) \ cos \ left (\ frac {-5 \ pi} {6} \ right) [/ latex]
91. [латекс] \ sin \ left (\ frac {3 \ pi} {4} \ right) \ cos \ left (\ frac {5 \ pi} {3} \ right) [/ latex]
92. [латекс] \ sin \ left (- \ frac {4 \ pi} {3} \ right) \ cos \ left (\ frac {\ pi} {2} \ right) [/ latex]
93. [латекс] \ sin \ left (\ frac {-9 \ pi} {4} \ right) \ cos \ left (\ frac {- \ pi} {6} \ right) [/ latex]
94. [латекс] \ sin \ left (\ frac {\ pi} {6} \ right) \ cos \ left (\ frac {- \ pi} {3} \ right) [/ latex]
95.[латекс] \ sin \ left (\ frac {7 \ pi} {4} \ right) \ cos \ left (\ frac {-2 \ pi} {3} \ right) [/ latex]
96. [латекс] \ cos \ left (\ frac {5 \ pi} {6} \ right) \ cos \ left (\ frac {2 \ pi} {3} \ right) [/ latex]
97. [латекс] \ cos \ left (\ frac {- \ pi} {3} \ right) \ cos \ left (\ frac {\ pi} {4} \ right) [/ latex]
98. [латекс] \ sin \ left (\ frac {-5 \ pi} {4} \ right) \ sin \ left (\ frac {11 \ pi} {6} \ right) [/ latex]
99. [латекс] \ sin \ left (\ pi \ right) \ sin \ left (\ frac {\ pi} {6} \ right) [/ latex]
Для следующих упражнений используйте этот сценарий. Ребенок входит в карусель, которая совершает один оборот за одну минуту.Ребенок входит в точку [latex] \ left (0,1 \ right) [/ latex], то есть в правильном положении на север. Предположим, карусель вращается против часовой стрелки.
100. Какие координаты ребенка через 45 секунд?
101. Какие координаты ребенка через 90 секунд?
102. Какие координаты ребенка через 125 секунд?
103. Когда у ребенка будут координаты [latex] \ left (0.707, -0.707 \ right) [/ latex], если поездка длится 6 минут? (Есть несколько ответов.)
104. Когда у ребенка будут координаты [latex] \ left (-0,866, -0,5 \ right) [/ latex], если поездка продлится 6 минут?
Вычисление тригонометрических функций
Вычисление тригонометрических функцийЭто совершенно необязательная страница. Необязательно знать, как вычислять триггерные функции и их обратные, чтобы использовать их. Тем не менее, многих интересует, как вычислялись значения этих функций до и после изобретения калькуляторов и компьютеров.Если вам интересно, читайте дальше. В противном случае переходите к следующему разделу, посвященному наклонным треугольникам.
Перед компьютерами: столы
Птолемей (100–178) создал одну из самых ранних таблиц для тригонометрии в своей работе, Альмагест, , и включил математику, необходимую для создания этой таблицы. Это была таблица хорд (обсуждаемая ранее) для каждой дуги от 1/2 ° до 180 ° с интервалами в 1/2 °. Также он объяснил, как выполнять интерполяцию между заданными углами.Вместо того, чтобы повторять то, что он сделал для аккордов, давайте посмотрим, как создавать таблицы для синусов и косинусов, используя его методы. Во-первых, на основе теоремы Пифагора и аналогичных треугольников синусы и косинусы определенных углов могут быть вычислены напрямую. В частности, вы можете напрямую найти синусы и косинусы для углов 30 °, 45 ° и 60 °, как описано в разделе, посвященном косинусам. Птолемей знал еще два угла, которые можно было построить, а именно 36 ° и 72 °. Эти углы были построены Евклидом в предложении IV.10 из его Элементов. Подобно Птолемею, мы можем использовать эту конструкцию для вычисления триггерных функций для этих углов. На этом этапе мы можем вычислить триггерные функции для углов 30 °, 36 °, 45 °, 60 ° и 72 °, и, конечно же, мы знаем значения для 0 ° и 90 °.
Имейте в виду, что если вы знаете синус угла θ , то вы знаете косинус дополнительного угла 90 ° — θ ; аналогично, если вы знаете косинус угла θ , тогда вы знаете синус дополнительного угла 90 ° — θ :
Таким образом, у вас есть триггерные функции для 18 ° и 54 °.
Затем вы можете использовать формулы половинного угла для синусов и косинусов, чтобы вычислить значения для половины угла, если вы знаете значения для угла. Если θ — это угол от 0 ° до 180 °, то
Используя их из значений для 18 °, 30 ° и 54 °, вы можете найти значения для 27 °, 15 ° и 9 ° и, следовательно, их дополнительные 63 °, 75 ° и 81 °.
С помощью формул суммы и разности
вы можете найти синус и косинус для 3 ° (от 30 ° до 27 °), а затем заполнить таблицы для синуса и косинуса для углов от 0 ° до 90 ° с шагом 3 °.
Опять же, используя формулы половинного угла, вы можете создать таблицу с шагом 1,5 ° (то есть 1 & deg; 30 ‘), затем 0,75 ° (что составляет 45′) или даже 0,375 ° (что составляет 22 ’30’). «). Но как получить таблицу с шагом в 1 °? Птолемей признал, что не существует евклидовой конструкции, чтобы разрезать угол 3 ° пополам, чтобы получить угол 1 °, но поскольку синусоидальная функция почти линейна для малых углов, вы можете приблизить sin 1 °, просто интерполируя на треть значения sin 0.75 & deg и sin 1.5 & deg. На этом шаге мы можем построить триггерные таблицы для триггерных функций с шагом 1 °.
Лучшие таблицы триггеров создавались веками. Например, Улугбек (15 век) построил таблицы синусов и тангенса для каждой угловой минуты с точностью примерно до девяти цифр!
| Улугбек (1394–1449) | |||
|---|---|---|---|
| Обсерватория Улугбека, Самарканд, Узбекистан | |||
Между прочим, если у вас есть таблица синусов, вы можете прочитать ее в обратном порядке, чтобы вычислить арксинус, поэтому для обоих требуется только одна таблица.
После компьютеров: серия power
Хотя компьютеры и калькуляторы могут просто хранить триггерные таблицы в своей памяти, они также могут напрямую вычислять триггерные функции, что они обычно и делают.В конце 17 века Ньютон и другие математики разработали степенные ряды. Степенный ряд подобен многочлену неограниченной степени. Для различных триггерных функций эти математики нашли степенные ряды. Вот степенной ряд для синуса и косинуса (где x — угол, измеренный в радианах):
Три точки… означает, что выражение должно продолжаться бесконечно, добавляя еще один термин, затем вычитая термин и т. д. Восклицательный знак! следует читать «факториал», и это означает, что вы умножаете целые числа от 1 до данного числа. Например, 5 !, «пять факториалов», равно 1 умножить на 2 умножить на 3 умножить на 4 умножить на 5, что составляет 120, и, таким образом, 6! = 720.
В этих степенных рядах бесконечно много членов, но они становятся маленькими настолько быстро, что только первые несколько членов вносят большой вклад.
Предположим, вы хотите вычислить синус 45 ° с поправкой на некоторое количество мест, используя этот степенной ряд. Сначала преобразуйте 45 ° в радианы, чтобы получить π /4, что составляет 0,78539816 в восьми знаках. Затем вычислите значение
- 0,78539816 — 0,78539816 3 /3! & Nbsp + 0,78539816 5 — 0,78539816 7 /7! + …
- 0,78539816 =
0.78539816
0,70465265 = 0,78539816 — 0,78539816 3 /3!
0,70714304 = 0,78539816 — 0,78539816 3 /3! & Nbsp + 0,78539816 5 /5!
0,70710647 = 0,78539816 — 0,78539816 3 /3! & Nbsp + 0,78539816 5 /5! — 0,78539816 7 /7!
0,70710678 = 0,78539816 — 0,78539816 3 /3! & Nbsp + 0,78539816 5 /5! — 0,78539816 7 /7! + 0.78539816 9 /9!
Требуется небольшой анализ, чтобы определить, сколько членов степенного ряда необходимо для достижения желаемой точности. Также можно использовать некоторые другие приемы для ускорения вычислений. В любом случае основная идея состоит в том, чтобы использовать первые несколько членов степенного ряда для вычисления триггерных функций.
Степенные ряды для остальных триггерных функций и степенные ряды для обратных триггерных функций можно найти в большинстве книг по исчислению, в которых обсуждаются степенные ряды.
7.5 Решение тригонометрических уравнений — предварительное вычисление
Цели обучения
В этом разделе вы:
- Решите линейные тригонометрические уравнения с синусом и косинусом.
- Решите уравнения, содержащие одну тригонометрическую функцию.
- Решите тригонометрические уравнения с помощью калькулятора.
- Решите тригонометрические уравнения квадратичной формы.
- Решайте тригонометрические уравнения, используя фундаментальные тождества.
- Решайте тригонометрические уравнения с несколькими углами.
- Решите проблемы с прямоугольным треугольником.
Рисунок 1 Египетские пирамиды, стоящие возле современного города. (кредит: Ойсин Малвихилл)
Фалес Милетский (около 625–547 гг. до н.э.) известен как основатель геометрии. Легенда гласит, что он рассчитал высоту Великой пирамиды в Гизе в Египте, используя теорию подобных треугольников , которую он разработал, измерив тень своего посоха.Эта теория, основанная на пропорциях, имеет приложения в ряде областей, включая фрактальную геометрию, инженерию и архитектуру. Часто угол возвышения и угол депрессии находят с помощью одинаковых треугольников.
В предыдущих разделах этой главы мы рассматривали тригонометрические тождества. Тождества верны для всех значений в домене переменной. В этом разделе мы начинаем изучение тригонометрических уравнений для изучения реальных сценариев, таких как определение размеров пирамид.
Решение линейных тригонометрических уравнений с синусом и косинусом
Тригонометрические уравнения, как следует из названия, включают в себя тригонометрические функции. Во многом похоже на решение полиномиальных или рациональных уравнений, только определенные значения переменной будут решениями, если решения вообще есть. Часто мы решаем тригонометрическое уравнение на заданном интервале. Однако так же часто нас просят найти все возможные решения, и, поскольку тригонометрические функции являются периодическими, решения повторяются в течение каждого периода.Другими словами, тригонометрические уравнения могут иметь бесконечное количество решений. Кроме того, как и в случае с рациональными уравнениями, область определения функции должна быть рассмотрена, прежде чем мы предполагаем, что какое-либо решение является действительным. Период синусоидальной функции и косинусной функции равен 2π.2π. Другими словами, каждые 2π2π единиц повторяются значения y-. Если нам нужно найти все возможные решения, мы должны добавить 2πk, 2πk, где kk — целое число, к начальному решению. Вспомните правило, которое дает формат для определения всех возможных решений для функции с периодом 2π: 2π:
sinθ = sin (θ ± 2kπ) sinθ = sin (θ ± 2kπ)Существуют аналогичные правила для указания всех возможных решений для других тригонометрических функций.Решение тригонометрических уравнений требует тех же методов, что и решение алгебраических уравнений. Мы читаем уравнение слева направо по горизонтали, как предложение. Мы ищем известные закономерности, множители, находим общие знаменатели и заменяем определенные выражения на переменные, чтобы упростить процесс решения. Однако с тригонометрическими уравнениями у нас также есть преимущество использования тождеств, которые мы разработали в предыдущих разделах.
Пример 1
Решение линейного тригонометрического уравнения с использованием функции косинуса
Найдите все возможные точные решения уравнения cosθ = 12.cosθ = 12.
Решение
Из единичного круга мы знаем, что
cosθ = 12 θ = π3,5π3cosθ = 12 θ = π3,5π3Это решения в интервале [0,2π]. [0,2π]. Все возможные решения дает
π3 ± 2kπ и 5π3 ± 2kππ3 ± 2kπ и 5π3 ± 2kπ, где kk — целое число.
Пример 2
Решение линейного уравнения с использованием функции синуса
Найдите все возможные точные решения уравнения sint = 12.sint = 12.
Решение
Решение для всех возможных значений t означает, что решения включают углы, превышающие период 2π.2π. Из рисунка 2 видно, что решениями являются π6π6 и 5π6,5π6. Но проблема в том, чтобы указать все возможные значения, которые решают уравнение. Следовательно, ответ
π6 ± 2πk и 5π6 ± 2πkπ6 ± 2πk и 5π6 ± 2πk, где kk — целое число.
Как это сделать
Для данного тригонометрического уравнения решите с помощью алгебры .
- Найдите шаблон, который предлагает алгебраическое свойство, такое как разность квадратов или возможность разложения на множители.
- Замените тригонометрическое выражение одной переменной, например xx или u.u.
- Решите уравнение так же, как и алгебраическое уравнение.
- Подставьте тригонометрическое выражение обратно вместо переменной в результирующих выражениях.
- Найдите угол.
Пример 3
Решите тригонометрическое уравнение в линейной форме
Точно решите уравнение: 2cosθ − 3 = −5,0≤θ <2π.2cosθ − 3 = −5,0≤θ <2π.
Решение
Используйте алгебраические методы для решения уравнения.
2cosθ − 3 = −5 2cosθ = −2 cosθ = −1 θ = π2cosθ − 3 = −5 2cosθ = −2 cosθ = −1 θ = πПопробуй # 1
Решите в точности следующее линейное уравнение на интервале [0,2π): 2sinx + 1 = 0. [0,2π): 2sinx + 1 = 0.
Решение уравнений, содержащих одну тригонометрическую функцию
Когда нам задают уравнения, которые включают только одну из шести тригонометрических функций, их решения требуют использования алгебраических методов и единичного круга (см. Рисунок 2).Когда уравнение включает тригонометрические функции, отличные от синуса и косинуса, необходимо учитывать несколько факторов. Проблемы, связанные с величинами, обратными первичным тригонометрическим функциям, необходимо рассматривать с алгебраической точки зрения. Другими словами, мы напишем обратную функцию и найдем углы, используя эту функцию. Кроме того, уравнение, включающее функцию тангенса, немного отличается от уравнения, содержащего функцию синуса или косинуса. Во-первых, как мы знаем, период касательной равен π, π, а не 2π.2π. Кроме того, область касательной — это все действительные числа, за исключением нечетных целых кратных π2, π2, если, конечно, проблема не накладывает свои собственные ограничения на область.
Пример 4
Решение задачи, связанной с одной тригонометрической функцией
Решите задачу точно: 2sin2θ − 1 = 0,0≤θ <2π. 2sin2θ − 1 = 0,0≤θ <2π.
Решение
Поскольку эту проблему нелегко разложить на множители, мы решим ее, используя свойство квадратного корня. Во-первых, мы используем алгебру, чтобы выделить sinθ.sinθ. Потом найдем углы.
2sin2θ − 1 = 0 2sin2θ = 1 sin2θ = 12 sin2θ = ± 12 sinθ = ± 12 = ± 22 θ = π4,3π4,5π4,7π42sin2θ − 1 = 0 2sin2θ = 1 sin2θ = 12 sin2θ = ± 12 sinθ = ± 12 = ± 22 θ = π4,3π4,5π4,7π4Пример 5
Решение тригонометрического уравнения с использованием косеканса
Точно решите следующее уравнение: cscθ = −2,0≤θ <4π.cscθ = −2,0≤θ <4π.
Решение
Нам нужны все значения θθ, для которых cscθ = −2cscθ = −2 в интервале 0≤θ <4π.0≤θ <4π.
cscθ = −21sinθ = −2sinθ = −12 θ = 7π6,11π6,19π6,23π6cscθ = −21sinθ = −2sinθ = −12 θ = 7π6,11π6,19π6,23π6Анализ
Поскольку sinθ = −12, sinθ = −12, обратите внимание, что все четыре решения находятся в третьем и четвертом квадрантах.
Пример 6
Решение уравнения с касательной
Точно решите уравнение: tan (θ − π2) = 1,0≤θ <2π.tan (θ − π2) = 1,0≤θ <2π.
Решение
Напомним, что касательная функция имеет период π.π. На интервале [0, π), [0, π) и под углом π4, π4 касательная имеет значение 1. Однако нам нужен угол (θ − π2). (Θ − π2) . Таким образом, если tan (π4) = 1, tan (π4) = 1, то
θ − π2 = π4θ = 3π4 ± kπθ − π2 = π4θ = 3π4 ± kπНа интервале [0,2π), [0,2π) имеем два решения:
3π4 и 3π4 + π = 7π43π4 и 3π4 + π = 7π4Попробуй # 2
Найдите все решения для tanx = 3.tanx = 3.
Пример 7
Определите все решения уравнения с касательной
Определите все точные решения уравнения 2 (tanx + 3) = 5 + tanx, 0≤x <2π.2 (tanx + 3) = 5 + tanx, 0≤x <2π.
Решение
Мы можем решить это уравнение, используя только алгебру. Выделите выражение tanxtanx слева от знака равенства.
2 (tanx) +2 (3) = 5 + tanx2tanx + 6 = 5 + tanx2tanx − tanx = 5−6tanx = −12 (tanx) +2 (3) = 5 + tanx2tanx + 6 = 5 + tanx2tanx − tanx = 5 −6tanx = −1На единичной окружности есть два угла, значение касательной которых равно −1: θ = 3π4−1: θ = 3π4 и θ = 7π4.θ = 7π4.
Решение тригонометрических уравнений с помощью калькулятора
Не все функции могут быть решены точно с использованием только единичной окружности.Когда мы должны решить уравнение с углом, отличным от одного из специальных углов, нам понадобится калькулятор. Убедитесь, что он установлен на правильный режим, градусы или радианы, в зависимости от критериев данной проблемы.
Пример 8
Использование калькулятора для решения тригонометрического уравнения с синусом
Воспользуйтесь калькулятором, чтобы решить уравнение sinθ = 0,8, sinθ = 0,8, где θθ выражается в радианах.
Решение
Убедитесь, что установлен режим радианы.Чтобы найти θ, θ, используйте функцию обратного синуса. На большинстве калькуляторов вам нужно будет нажать кнопку 2 ND , а затем кнопку SIN, чтобы вызвать функцию sin − 1sin − 1. На экране отображается sin − 1 (.sin − 1 (. Калькулятор готов к вводу в скобках. Для этой задачи мы вводим sin − 1 (0,8), sin − 1 (0,8)) и нажимаем ENTER. Таким образом, с точностью до четырех знаков после запятой,
sin − 1 (0,8) ≈0,9273 sin − 1 (0,8) ≈0,9273Решение
Угол в градусах
. θ≈53.1∘θ≈180∘ − 53,1∘ ≈126,9∘θ≈53,1∘θ≈180∘ − 53,1∘ ≈126,9∘Анализ
Обратите внимание, что калькулятор будет возвращать только угол в квадрантах I или IV для функции синуса, поскольку это диапазон обратного синуса. Другой угол получается с помощью π − θ.π − θ.
Пример 9
Использование калькулятора для решения тригонометрического уравнения, содержащего секанс
Воспользуйтесь калькулятором, чтобы решить уравнение secθ = −4, secθ = −4, получив ответ в радианах.
Решение
Мы можем начать с некоторой алгебры.
secθ = −41cosθ = −4cosθ = −14secθ = −41cosθ = −4cosθ = −14Убедитесь, что РЕЖИМ установлен в радианах. Теперь используйте функцию обратного косинуса.
cos − 1 (−14) ≈1,8235 θ≈1,8235 + 2πkcos − 1 (−14) ≈1,8235 θ≈1,8235 + 2πkПоскольку π2≈1,57π2≈1,57 и π≈3,14, π≈3,14, 1,8235 находится между этими двумя числами, поэтому θ≈1,8235θ≈1,8235 находится во втором квадранте. Косинус также отрицателен в квадранте III. Обратите внимание, что калькулятор возвращает только угол в квадрантах I или II для функции косинуса, поскольку это диапазон обратного косинуса.См. Рисунок 2.
Рисунок 2
Итак, нам также нужно найти меру угла в квадранте III. В квадранте III опорный угол равен θ’≈π − 1,8235≈1,3181. Θ’≈π − 1,8235≈1,3181. Другое решение в квадранте III: π + 1,3181≈4,4597.π + 1,3181≈4,4597.
Решения: 1.8235 ± 2πk1.8235 ± 2πk и 4.4597 ± 2πk.4.4597 ± 2πk.
Попробуй # 3
Решить cosθ = −0.2.cosθ = −0.2.
Решение тригонометрических уравнений в квадратичной форме
Решение квадратного уравнения может быть более сложным, но, опять же, мы можем использовать алгебру, как и любое квадратное уравнение.Посмотрите на схему уравнения. Есть ли в уравнении более одной тригонометрической функции или только одна? Какая тригонометрическая функция возводится в квадрат? Если представлена только одна функция и один из членов возведен в квадрат, подумайте о стандартной форме квадратичной функции. Замените тригонометрическую функцию переменной, например xx или u.u. Если после подстановки уравнение выглядит как квадратное уравнение, то мы можем использовать те же методы решения квадратичных уравнений для решения тригонометрических уравнений.
Пример 10
Решение тригонометрического уравнения в квадратичной форме
Точно решите уравнение: cos2θ + 3cosθ − 1 = 0,0≤θ <2π.cos2θ + 3cosθ − 1 = 0,0≤θ <2π.
Решение
Начнем с подстановки и замены cos θθ на x.x. Нет необходимости использовать замену, но это может облегчить визуальное решение проблемы. Пусть cosθ = x.cosθ = x. У нас
Уравнение нельзя разложить на множители, поэтому мы будем использовать квадратную формулу x = −b ± b2−4ac2a.х = −b ± b2−4ac2a.
x = −3 ± (3) 2−4 (1) (- 1) 2 = −3 ± 132x = −3 ± (3) 2−4 (1) (- 1) 2 = −3 ± 132Заменить xx с cosθ, cosθ и решить. Таким образом,
cosθ = −3 ± 132 θ = cos − 1 (−3 + 132) cosθ = −3 ± 132 θ = cos − 1 (−3 + 132)Обратите внимание, что используется только знак +. Это связано с тем, что мы получаем ошибку, когда решаем θ = cos − 1 (−3−132) θ = cos − 1 (−3−132) на калькуляторе, поскольку область определения функции обратного косинуса равна [−1,1 ]. [- 1,1]. Однако есть и второе решение:
. cos − 1 (−3 + 132) ≈1,26 cos − 1 (−3 + 132) ≈1,26Эта конечная сторона угла лежит в квадранте I.Поскольку косинус также положителен в квадранте IV, второе решение —
. 2π − cos − 1 (−3 + 132) ≈5.022π − cos − 1 (−3 + 132) ≈5.02Пример 11
Решение тригонометрического уравнения в квадратичной форме с помощью факторинга
Решите уравнение точно: 2sin2θ − 5sinθ + 3 = 0,0≤θ≤2π.2sin2θ − 5sinθ + 3 = 0,0≤θ≤2π.
Решение
Используя группировку, эту квадратичную величину можно разложить на множители. Либо сделайте настоящую замену, sinθ = u, sinθ = u, либо представьте ее, как мы множим:
2sin2θ − 5sinθ + 3 = 0 (2sinθ − 3) (sinθ − 1) = 0 2sin2θ − 5sinθ + 3 = 0 (2sinθ − 3) (sinθ − 1) = 0Теперь установите каждый множитель равным нулю.
2sinθ − 3 = 0 2sinθ = 3 sinθ = 32 sinθ − 1 = 0 sinθ = 12sinθ − 3 = 0 2sinθ = 3 sinθ = 32 sinθ − 1 = 0 sinθ = 1Затем решите относительно θ: sinθ ≠ 32, θ: sinθ ≠ 32, так как диапазон синусоидальной функции равен [−1,1]. [- 1,1]. Однако sinθ = 1, sinθ = 1, что дает решение π2.π2.
Анализ
Обязательно проверьте все решения в данном домене, так как некоторые факторы не имеют решения.
Попробуй # 4
Решить sin2θ = 2cosθ + 2,0≤θ≤2π.sin2θ = 2cosθ + 2,0≤θ≤2π.[Подсказка: сделайте замену, чтобы выразить уравнение только через косинус.]
Пример 12
Решение тригонометрического уравнения с помощью алгебры
Решите точно:
2sin2θ + sinθ = 0; 0≤θ <2π2sin2θ + sinθ = 0; 0≤θ <2πРешение
Эта задача должна показаться вам знакомой, поскольку она похожа на квадратичную. Пусть sinθ = x.sinθ = x. Уравнение принимает вид 2×2 + x = 0,2×2 + x = 0. Начнем с факторинга:
2×2 + x = 0x (2x + 1) = 0 2×2 + x = 0x (2x + 1) = 0Установите каждый коэффициент равным нулю.
x = 0 (2x + 1) = 0 x = −12 x = 0 (2x + 1) = 0 x = −12Затем подставьте обратно в уравнение исходное выражение sinθsinθ вместо x.x. Таким образом,
sinθ = 0 θ = 0, πsinθ = −12 θ = 7π6,11π6sinθ = 0 θ = 0, πsinθ = −12 θ = 7π6,11π6Решения в области 0≤θ <2π0≤θ <2π равны 0, π , 7π6,11π6. 0, π, 7π6,11π6.
Если мы предпочитаем не заменять, мы можем решить уравнение, следуя той же схеме факторизации и установив каждый коэффициент равным нулю.
2sin2θ + sinθ = 0sinθ (2sinθ + 1) = 0 sinθ = 0 θ = 0, π 2sinθ + 1 = 0 2sinθ = −1 sinθ = −12 θ = 7π6,11π6 2sin2θ + sinθ = 0sinθ (2sinθ + 1) = 0 sinθ = 0 θ = 0, π 2sinθ + 1 = 0 2sinθ = −1 sinθ = −12 θ = 7π6,11π6Анализ
Мы можем видеть решения на графике на рисунке 3. На интервале 0≤θ <2π, 0≤θ <2π график пересекает ось x- четыре раза в отмеченных решениях.Обратите внимание, что тригонометрические уравнения в квадратичной форме могут дать до четырех решений вместо ожидаемых двух, которые можно найти с помощью квадратных уравнений. В этом примере каждое решение (угол), соответствующее положительному значению синуса, даст два угла, которые приведут к этому значению.
Рисунок 3
Мы также можем проверить решения на единичном круге на Рисунке 2.
Пример 13
Решение тригонометрического уравнения, квадратичного по форме
Решите квадратное по форме уравнение: 2sin2θ − 3sinθ + 1 = 0,0≤θ <2π.2sin2θ − 3sinθ + 1 = 0,0≤θ <2π.
Решение
Мы можем факторизовать, используя группировку. Значения решения θθ можно найти на единичном круге:
(2sinθ − 1) (sinθ − 1) = 0 2sinθ − 1 = 0 sinθ = 12 θ = π6,5π6 sinθ = 1 θ = π2 (2sinθ − 1) (sinθ − 1) = 0 2sinθ − 1 = 0 sinθ = 12 θ = π6,5π6 sinθ = 1 θ = π2Попробуй # 5
Решите квадратное уравнение 2cos2θ + cosθ = 0.2cos2θ + cosθ = 0.
Решение тригонометрических уравнений с использованием фундаментальных тождеств
Хотя алгебру можно использовать для решения ряда тригонометрических уравнений, мы также можем использовать фундаментальные тождества, потому что они упрощают решение уравнений. Помните, что методы, которые мы используем для решения проблем, не совпадают с методами проверки личности. Здесь применяются основные правила алгебры, а не переписывание одной стороны идентичности для соответствия другой стороне. В следующем примере мы используем два тождества, чтобы упростить уравнение.
Пример 14
Использование идентичностей для решения уравнения
Используйте тождества, чтобы точно решить тригонометрическое уравнение в интервале 0≤x <2π.0≤x <2π.
cosxcos (2x) + sinxsin (2x) = 32cosxcos (2x) + sinxsin (2x) = 32Решение
Обратите внимание, что левая часть уравнения — это формула разности для косинуса.
cosxcos (2x) + sinxsin (2x) = 32 cos (x − 2x) = 32 Формула разности для косинуса cos (−x) = 32 Используйте тождество отрицательного угла.cosx = 32cosxcos (2x) + sinxsin (2x) = 32 cos (x − 2x) = 32 Формула разности для косинуса cos (−x) = 32 Используйте тождество отрицательного угла. cosx = 32Из единичного круга на рисунке 2 мы видим, что cosx = 32cosx = 32, когда x = π6,11π6.x = π6,11π6.
Пример 15
Решение уравнения с помощью формулы двойного угла
Точно решите уравнение, используя формулу двойного угла: cos (2θ) = cosθ.cos (2θ) = cosθ.
Решение
У нас есть три варианта выражения для замены двойного угла косинуса. Поскольку проще решать одну тригонометрическую функцию за раз, мы выберем тождество с двойным углом, включающее только косинус:
cos (2θ) = cosθ 2cos2θ − 1 = cosθ 2cos2θ − cosθ − 1 = 0 (2cosθ + 1) (cosθ − 1) = 0 2cosθ + 1 = 0 cosθ = −12 cosθ − 1 = 0 cosθ = 1 cos (2θ ) = cosθ 2cos2θ − 1 = cosθ 2cos2θ − cosθ − 1 = 0 (2cosθ + 1) (cosθ − 1) = 0 2cosθ + 1 = 0 cosθ = −12 cosθ − 1 = 0 cosθ = 1Итак, если cosθ = −12, cosθ = −12, тогда θ = 2π3 ± 2πkθ = 2π3 ± 2πk и θ = 4π3 ± 2πk; θ = 4π3 ± 2πk; если cosθ = 1, cosθ = 1, то θ = 0 ± 2πk.θ = 0 ± 2πk.
Пример 16
Решение уравнения с использованием идентификатора
Точно решите уравнение, используя тождество: 3cosθ + 3 = 2sin2θ, 0≤θ <2π. 3cosθ + 3 = 2sin2θ, 0≤θ <2π.
Решение
Если мы перепишем правую часть, мы можем записать уравнение через косинус:
3 cosθ + 3 = 2 sin2θ3 cosθ + 3 = 2 (1 − cos2θ) 3 cosθ + 3 = 2−2cos2θ2cos2θ + 3 cosθ + 1 = 0 (2 cosθ + 1) (cosθ + 1) = 02 cosθ + 1 = 0cosθ = −12θ = 2π3,4π3cosθ + 1 = 0cosθ = −1θ = π3 cosθ + 3 = 2 sin2θ3 cosθ + 3 = 2 (1 − cos2θ) 3 cosθ + 3 = 2−2cos2θ2cos2θ + 3 cosθ + 1 = 0 (2 cosθ +1) (cosθ + 1) = 02 cosθ + 1 = 0cosθ = −12θ = 2π3,4π3cosθ + 1 = 0cosθ = −1θ = πНаши решения: 2π3,4π3, π.2π3,4π3, π.
Решение тригонометрических уравнений с несколькими углами
Иногда невозможно решить тригонометрическое уравнение с тождествами, имеющими кратный угол, например sin (2x) sin (2x) или cos (3x) .cos (3x). Столкнувшись с этими уравнениями, вспомните, что y = sin (2x) y = sin (2x) — это горизонтальное сжатие с коэффициентом 2 функции y = sinx.y = sinx. На интервале 2π, 2π мы можем изобразить два периода y = sin (2x), y = sin (2x), в отличие от одного цикла y = sinx.y = sinx.Такое сжатие графика приводит нас к мысли, что может быть вдвое больше x -перехватов или решений sin (2x) = 0sin (2x) = 0 по сравнению с sinx = 0. sinx = 0. Эта информация поможет нам решить уравнение.
Пример 17
Решение многоугольного тригонометрического уравнения
Решите точно: cos (2x) = 12cos (2x) = 12 на [0,2π). [0,2π).
Решение
Мы видим, что это уравнение является стандартным уравнением с углом, кратным углу.Если cos (α) = 12, cos (α) = 12, мы знаем, что αα находится в квадрантах I и IV. Хотя θ = cos − 112θ = cos − 112 даст решения только в квадрантах I и II, мы понимаем, что решения уравнения cosθ = 12cosθ = 12 будут в квадрантах I и IV.
Следовательно, возможные углы равны θ = π3θ = π3 и θ = 5π3.θ = 5π3. Итак, 2x = π32x = π3 или 2x = 5π3,2x = 5π3, что означает, что x = π6x = π6 или x = 5π6.x = 5π6. Имеет ли это смысл? Да, потому что cos (2 (π6)) = cos (π3) = 12. cos (2 (π6)) = cos (π3) = 12.
Есть еще возможные ответы? Вернемся к нашему первому шагу.
В квадранте I 2x = π3,2x = π3, поэтому x = π6x = π6, как указано. Давайте снова обратимся по кругу:
2x = π3 + 2π = π3 + 6π3 = 7π32x = π3 + 2π = π3 + 6π3 = 7π3, поэтому x = 7π6.x = 7π6.
Еще один оборот дает
2x = π3 + 4π = π3 + 12π3 = 13π32x = π3 + 4π = π3 + 12π3 = 13π3x = 13π6> 2π, x = 13π6> 2π, поэтому это значение для xx больше 2π, 2π, поэтому оно не решение на [0,2π). [0,2π).
В квадранте IV 2x = 5π3,2x = 5π3, поэтому x = 5π6x = 5π6, как указано. Давайте снова обратимся по кругу:
2x = 5π3 + 2π = 5π3 + 6π3 = 11π32x = 5π3 + 2π = 5π3 + 6π3 = 11π3, поэтому x = 11π6.х = 11π6.
Еще один оборот дает
2x = 5π3 + 4π = 5π3 + 12π3 = 17π32x = 5π3 + 4π = 5π3 + 12π3 = 17π3x = 17π6> 2π, x = 17π6> 2π, поэтому это значение для xx больше 2π, 2π, поэтому оно не решение на [0,2π). [0,2π).
Наши решения: π6,5π6,7π6, 11π6.π6,5π6,7π6 и 11π6. Обратите внимание, что всякий раз, когда мы решаем задачу в форме sin (nx) = c, sin (nx) = c, мы должны обойти единичный круг nn раз.
Решение задач прямоугольного треугольника
Теперь мы можем использовать все изученные нами методы для решения задач, связанных с применением свойств прямоугольных треугольников и теоремы Пифагора.Мы начнем с известной теоремы Пифагора, a2 + b2 = c2, a2 + b2 = c2, и смоделируем уравнение в соответствии с ситуацией.
Пример 18
Использование теоремы Пифагора для моделирования уравнения
Используйте теорему Пифагора и свойства прямоугольных треугольников, чтобы смоделировать уравнение, которое соответствует задаче.
Один из тросов, которыми центр колеса обозрения London Eye крепится к земле, необходимо заменить. Центр колеса обозрения находится на высоте 69,5 метров над землей, а второй якорь на земле находится в 23 метрах от основания колеса обозрения.Примерно какой длины кабель и каков угол подъема (от земли до центра колеса обозрения)? См. Рисунок 4.
Рисунок 4
Решение
Используя предоставленную информацию, мы можем нарисовать прямоугольный треугольник. Мы можем найти длину кабеля с помощью теоремы Пифагора.
a2 + b2 = c2 (23) 2+ (69,5) 2≈5359 5359≈73,2 м a2 + b2 = c2 (23) 2+ (69,5) 2≈5359 5359≈73,2 мУгол возвышения θ, θ, образованный вторым якорем на земле и тросом, идущим к центру колеса.Мы можем использовать касательную функцию, чтобы найти ее меру. Округлить до двух десятичных знаков.
tanθ = 69,523tan − 1 (69,523) ≈1,2522 ≈71,69∘ tanθ = 69,523tan − 1 (69,523) ≈1,2522 ≈71,69∘Угол возвышения составляет примерно 71,7∘, 71,7∘, а длина кабеля составляет 73,2 метра. .
Пример 19
Использование теоремы Пифагора для моделирования абстрактной задачи
Правила безопасности OSHA требуют, чтобы основание лестницы располагалось на расстоянии 1 фута от стены на каждые 4 фута длины лестницы.Найдите угол, под которым лестница любой длины образует с землей, и высоту, на которой лестница касается стены.
Решение
Для лестницы любой длины основание должно находиться на расстоянии от стены, равном одной четвертой длины лестницы. Аналогично, если основание лестницы находится на расстоянии футов от стены, длина лестницы будет 4 на футов. См. Рисунок 5.
Рис. 5
Сторона, примыкающая к θθ, равна a , а гипотенуза — 4a.4а. Таким образом,
cosθ = a4a = 14cos − 1 (14) ≈75,5∘ cosθ = a4a = 14cos − 1 (14) ≈75,5∘Высота лестницы составляет 75,5∘75,5∘ с землей. Высота, на которой лестница касается стены, может быть найдена с помощью теоремы Пифагора:
a2 + b2 = (4a) 2 b2 = (4a) 2 − a2 b2 = 16a2 − a2 b2 = 15a2 b = 15aa2 + b2 = (4a) 2 b2 = (4a) 2 − a2 b2 = 16a2 − a2 b2 = 15a2 b = 15aТаким образом, лестница касается стены на высоте 15a15a футов от земли.
7.Упражнения из 5 частей
Устные
1.Всегда ли будут решения уравнений тригонометрических функций? Если нет, опишите уравнение, у которого не было бы решения. Объясните, почему да или почему нет.
2.При решении тригонометрического уравнения, включающего более одной тригонометрической функции, всегда ли мы хотим попытаться переписать уравнение так, чтобы оно выражалось в терминах одной тригонометрической функции? Почему или почему нет?
3.При решении линейных тригонометрических уравнений только с помощью синуса или косинуса, как мы узнаем, будут ли решения?
Алгебраический
Для следующих упражнений найдите все решения точно на интервале 0≤θ <2π.0≤θ <2π.
Для следующих упражнений решите точно на [0,2π). [0,2π).
19.2cos (3θ) = — 22cos (3θ) = — 2
20.cos (2θ) = — 32cos (2θ) = — 32
22.2cos (π5θ) = 32cos (π5θ) = 3
Для следующих упражнений найдите все точные решения на [0,2π). [0,2π).
23.сек (x) sin (x) −2sin (x) = 0sec (x) sin (x) −2sin (x) = 0
24.tan (x) −2sin (x) tan (x) = 0tan (x) −2sin (x) tan (x) = 0
25.2cos2t + cos (t) = 12cos2t + cos (t) = 1
26.2tan2 (t) = 3сек (t) 2tan2 (t) = 3сек (t)
27.2sin (x) cos (x) −sin (x) + 2cos (x) −1 = 02sin (x) cos (x) −sin (x) + 2cos (x) −1 = 0
30.tan2 (x) = — 1 + 2tan (−x) tan2 (x) = — 1 + 2tan (−x)
31.8sin2 (x) + 6sin (x) + 1 = 08sin2 (x) + 6sin (x) + 1 = 0
32.tan5 (x) = tan (x) tan5 (x) = tan (x)
Для следующих упражнений решайте методами, указанными в этом разделе, точно на интервале [0,2π). [0,2π).
33.sin (3x) cos (6x) −cos (3x) sin (6x) = — 0,9sin (3x) cos (6x) −cos (3x) sin (6x) = — 0.9
34.sin (6x) cos (11x) −cos (6x) sin (11x) = — 0,1 sin (6x) cos (11x) −cos (6x) sin (11x) = — 0,1
35.cos (2x) cosx + sin (2x) sinx = 1cos (2x) cosx + sin (2x) sinx = 1
36.6sin (2t) + 9sint = 06sin (2t) + 9sint = 0
37.9cos (2θ) = 9cos2θ − 49cos (2θ) = 9cos2θ − 4
40.cos (6x) −cos (3x) = 0cos (6x) −cos (3x) = 0
Для следующих упражнений решите точно на отрезке [0,2π). [0,2π). Если уравнения не учитываются, используйте формулу корней квадратного уравнения.
41.tan2x − 3tanx = 0tan2x − 3tanx = 0
42.sin2x + sinx − 2 = 0sin2x + sinx − 2 = 0
43.sin2x − 2sinx − 4 = 0sin2x − 2sinx − 4 = 0
44.5cos2x + 3cosx − 1 = 05cos2x + 3cosx − 1 = 0
45.3cos2x − 2cosx − 2 = 03cos2x − 2cosx − 2 = 0
46. 5sin2x + 2sinx − 1 = 05sin2x + 2sinx − 1 = 0
47.tan2x + 5tanx − 1 = 0tan2x + 5tanx − 1 = 0
48.cot2x = −cotxcot2x = −cotx
49.−tan2x − tanx − 2 = 0 − tan2x − tanx − 2 = 0
Для следующих упражнений найдите точные решения на интервале [0,2π). [0,2π). Ищите возможности использовать тригонометрические тождества.
50.sin2x − cos2x − sinx = 0sin2x − cos2x − sinx = 0
51.sin2x + cos2x = 0sin2x + cos2x = 0
52.sin (2x) −sinx = 0sin (2x) −sinx = 0
53.cos (2x) −cosx = 0cos (2x) −cosx = 0.
54.2tanx2 − sec2x − sin2x = cos2x2tanx2 − sec2x − sin2x = cos2x
55.1 − cos (2x) = 1 + cos (2x) 1 − cos (2x) = 1 + cos (2x).
57.10sinxcosx = 6cosx10sinxcosx = 6cosx
58.−3sint = 15costsint − 3sint = 15costsint
59.4cos2x − 4 = 15cosx4cos2x − 4 = 15cosx
60.8sin2x + 6sinx + 1 = 08sin2x + 6sinx + 1 = 0
61.8cos2θ = 3−2cosθ8cos2θ = 3−2cosθ
62.6cos2x + 7sinx − 8 = 06cos2x + 7sinx − 8 = 0.
63.12sin2t + cost − 6 = 012sin2t + cost − 6 = 0
Графический
Для следующих упражнений точно алгебраически определите все решения тригонометрического уравнения, затем проверьте результаты, построив уравнение на графике и найдя нули.
66.6sin2x − 5sinx + 1 = 06sin2x − 5sinx + 1 = 0
67.8cos2x − 2cosx − 1 = 08cos2x − 2cosx − 1 = 0.
68.100tan2x + 20tanx − 3 = 0100tan2x + 20tanx − 3 = 0
69.2cos2x − cosx + 15 = 02cos2x − cosx + 15 = 0.
70.20sin2x − 27sinx + 7 = 020sin2x − 27sinx + 7 = 0
71.2tan2x + 7tanx + 6 = 02tan2x + 7tanx + 6 = 0
72.130tan2x + 69tanx − 130 = 0130tan2x + 69tanx − 130 = 0
Технологии
Для следующих упражнений используйте калькулятор, чтобы найти все решения до четырех знаков после запятой.
Для следующих упражнений решите уравнения алгебраически, а затем с помощью калькулятора найдите значения на интервале [0,2π).[0,2π). Округлить до четырех знаков после запятой.
77.tan2x + 3tanx − 3 = 0tan2x + 3tanx − 3 = 0
78.6tan2x + 13tanx = −66tan2x + 13tanx = −6
79.tan2x − secx = 1tan2x − secx = 1
80.sin2x − 2cos2x = 0sin2x − 2cos2x = 0
81.2tan2x + 9tanx − 6 = 02tan2x + 9tanx − 6 = 0
82.4sin2x + sin (2x) secx − 3 = 04sin2x + sin (2x) secx − 3 = 0
Расширения
Для следующих упражнений найдите все решения уравнений в точности на интервале [0,2π). [0,2π).
83.csc2x − 3cscx − 4 = 0csc2x − 3cscx − 4 = 0
84.sin2x − cos2x − 1 = 0sin2x − cos2x − 1 = 0
85.sin2x (1 − sin2x) + cos2x (1 − sin2x) = 0sin2x (1 − sin2x) + cos2x (1 − sin2x) = 0
86.3sec2x + 2 + sin2x − tan2x + cos2x = 03sec2x + 2 + sin2x − tan2x + cos2x = 0
87.sin2x − 1 + 2cos (2x) −cos2x = 1sin2x − 1 + 2cos (2x) −cos2x = 1
88.tan2x − 1 − sec3xcosx = 0tan2x − 1 − sec3xcosx = 0
89.sin (2x) sec2x = 0sin (2x) sec2x = 0
90.sin (2x) 2csc2x = 0sin (2x) 2csc2x = 0
91.2cos2x − sin2x − cosx − 5 = 02cos2x − sin2x − cosx − 5 = 0
92.1sec2x + 2 + sin2x + 4cos2x = 41sec2x + 2 + sin2x + 4cos2x = 4
Реальные приложения
93.У самолета достаточно бензина, чтобы долететь до города в 200 милях к северо-востоку от его текущего местоположения. Если пилот знает, что город находится в 25 милях к северу, на сколько градусов к северу от востока должен лететь самолет?
94.Если погрузочная рампа размещена рядом с грузовиком на высоте 4 фута, а ее длина составляет 15 футов, какой угол образует аппарель с землей?
95.Если погрузочная рампа размещена рядом с грузовиком на высоте 2 фута, а ее длина составляет 20 футов, какой угол образует аппарель с землей?
96.Женщина наблюдает за запущенной ракетой на высоте 11 миль. Если она стоит в 4 милях от стартовой площадки, под каким углом она смотрит вверх из горизонтали?
97.Астронавт находится в запущенной ракете, которая сейчас находится на высоте 15 миль. Если мужчина стоит в 2 милях от стартовой площадки, под каким углом она смотрит на него сверху вниз из горизонтали? (Подсказка: это называется углом депрессии.)
98.Женщина стоит в 8 метрах от 10-метрового здания.Под каким углом она смотрит на вершину здания?
99.Мужчина стоит в 10 метрах от 6-метрового дома. Кто-то наверху здания смотрит на него сверху вниз. Под каким углом смотрит на него человек?
100.У здания высотой 20 футов есть тень длиной 55 футов. Какой угол подъема солнца?
101.У здания высотой 90 футов есть тень длиной 2 фута. Какой угол подъема солнца?
102.Прожектор на земле в 3 метрах от человека ростом 2 метра отбрасывает 6-метровую тень на стену в 6 метрах от человека.Под каким углом свет?
103.Прожектор на земле в 3 футах от женщины 5 футов высотой отбрасывает тень 15 футов высотой на стену в 6 футах от женщины. Под каким углом свет?
Для следующих упражнений найдите решение задачи со словами алгебраически. Затем воспользуйтесь калькулятором, чтобы проверить результат. Ответ округлите до десятых долей градуса.
104.Человек выполняет стойку на руках, когда его ноги касаются стены, а руки находятся на расстоянии 1,5 фута от стены.Если рост человека 6 футов, какой угол у его ступни со стеной?
105.Человек выполняет стойку на руках, при этом ноги касаются стены, а руки находятся на расстоянии 3 футов от стены. Если рост человека 5 футов, какой угол у его ступни со стеной?
106.23-футовая лестница стоит рядом с домом. Если лестница соскользнет на расстоянии 7 футов от дома при недостаточном сцеплении с грунтом, какой угол должна составлять лестница относительно земли, чтобы избежать скольжения?
Косинус
Косинус, записываемый как cos (θ), является одной из шести основных тригонометрических функций.
Определения косинусов
Существует два основных способа обсуждения тригонометрических функций: в терминах прямоугольных треугольников и в терминах единичной окружности. Чаще всего вводят определение тригонометрических функций в виде прямоугольного треугольника, за которым следуют их определения в терминах единичной окружности.
Определение прямоугольного треугольника
Для прямоугольного треугольника с острым углом θ значение синуса этого угла определяется как отношение длины соседней стороны к длине гипотенузы.
Стороны прямоугольного треугольника обозначаются следующим образом:
- Соседний: сторона рядом с θ, которая не является гипотенузой
- Справа: сторона, противоположная θ.
- Гипотенуза: самая длинная сторона треугольника напротив прямого угла.
Пример:
Найдите cos (θ) для прямоугольного треугольника ниже.
Мы также можем использовать функцию косинуса при решении реальных задач, связанных с прямоугольными треугольниками.
Пример:
Самолет пролетает над человеком. Человек регистрирует угол места 25 °, когда расстояние по прямой (гипотенуза треугольника) между человеком и самолетом составляет 14 миль. Какое расстояние по горизонтали между самолетом и человеком?
Учитывая информацию выше, мы можем сформировать прямоугольный треугольник, в котором x — это расстояние по горизонтали между человеком и плоскостью, расстояние по прямой между человеком и плоскостью — это гипотенуза, а расстояние по вертикали между конечными концами треугольника. x, а гипотенуза образует прямой угол треугольника.Затем мы можем найти горизонтальное расстояние x, используя функцию косинуса:
x = 14 × cos (25 °) ≈ 12,69
Горизонтальное расстояние между человеком и самолетом составляет около 12,69 миль.
Определение единичной окружности
Тригонометрические функции также могут быть определены как значения координат на единичной окружности. Единичный круг — это круг радиуса 1 с центром в начале координат. Определение тригонометрических функций в прямоугольном треугольнике допускает углы от 0 ° до 90 ° (0 и в радианах).Использование определений единичного круга позволяет нам расширить область определения тригонометрических функций на все действительные числа. См. Рисунок ниже.
Учитывая точку (x, y) на окружности единичной окружности, мы можем сформировать прямоугольный треугольник, как показано на рисунке. В таком треугольнике гипотенуза — это радиус единичного круга, или 1. θ — это угол, образованный между начальной стороной угла вдоль оси x и конечной стороной угла, образованной вращением луча по часовой стрелке или против часовой стрелки.Конечная сторона угла — это гипотенуза прямоугольного треугольника и радиус единичной окружности. Следовательно, он всегда имеет длину 1. Таким образом, мы можем использовать определение косинуса из прямоугольного треугольника, чтобы определить, что
означает, что значение x любой точки на окружности единичной окружности равно cos (θ).
В отличие от определений тригонометрических функций, основанных на прямоугольных треугольниках, это определение работает для любого угла, а не только для острых углов прямоугольных треугольников, если он находится в пределах области cos domain (θ).Область определения функции косинуса — (-∞, ∞), а диапазон функции косинуса — [-1, 1].
Значения функции косинуса
Существует множество методов, которые можно использовать для определения значения косинуса, например, обращение к таблице косинусов, использование калькулятора и аппроксимация с использованием ряда косинусов Тейлора. В большинстве практических случаев нет необходимости вычислять значение косинуса вручную, и вам будет предоставлена таблица, калькулятор или другие справочные материалы.
Калькулятор косинусов
Ниже приведен калькулятор, позволяющий определить значение косинуса угла или угол по значению косинуса.
Часто используемые уголки
Хотя мы можем найти cos (θ) для любого угла, есть некоторые углы, которые чаще используются в тригонометрии. Ниже приведены 16 часто используемых углов как в радианах, так и в градусах, а также координаты их соответствующих точек на единичной окружности.
Приведенный выше рисунок служит справочным материалом для быстрого определения косинусов (значение x) и синусов (значение y) углов, которые обычно используются в тригонометрии. Как видно из рисунка, косинус имеет значение 0 при 90 ° и значение 1 при 0 °.Синус следует противоположному шаблону; это потому, что синус и косинус являются совместными функциями (описанными позже). Другие часто используемые углы — 30 ° (), 45 ° (), 60 ° () и их соответствующие кратные. Значения косинуса и синуса этих углов стоит запомнить в контексте тригонометрии, поскольку они очень часто используются.
Один из методов, который может помочь запомнить эти значения, — это выразить все значения cos (θ) в виде дробей, содержащих квадратный корень. Начиная с 0 ° и до 90 °, cos (0 °) = 1 =.Последующие значения cos (30 °), cos (45 °), cos (60 °) и cos (90 °) следуют шаблону, так что, используя значение cos (0 °) в качестве эталона, найти значения косинуса для последующих углов, мы просто уменьшаем число под знаком корня в числителе на 1, как показано ниже:
С 90 ° до 180 ° вместо этого мы увеличиваем число под корнем на 1, но также должны учитывать квадрант, в котором находится угол. Косинус отрицателен в квадрантах II и III, поэтому значения будут равными, но отрицательными. .В квадрантах I и IV значения будут положительными. Этот шаблон периодически повторяется для соответствующих угловых измерений. Аналогичный метод запоминания можно использовать и для синуса. При необходимости обратитесь к странице синуса.
Знание значений косинуса и синуса для углов в первом квадранте позволяет нам определить их значения для соответствующих углов в остальных квадрантах в координатной плоскости с помощью опорных углов.
Базовые углы
Базовый угол — это острый угол (<90 °), который можно использовать для обозначения угла любой меры.Любой угол в координатной плоскости имеет опорный угол от 0 ° до 90 °. Это всегда наименьший угол (относительно оси x), который может быть получен с конечной стороны угла. На рисунке ниже показан угол θ и его опорный угол θ '.
Поскольку θ ‘является опорным углом θ, cos both (θ) и cos (θ’) имеют одинаковое значение. Например, 30 ° — это опорный угол 150 °, и если мы обратимся к единичному кругу, мы увидим, что косинусы обоих имеют величину, хотя и имеют разные знаки.Поскольку все углы имеют опорный угол, нам действительно нужно знать только значения cos (θ) (а также значения других тригонометрических функций) в квадранте I. Все другие соответствующие углы будут иметь значения той же величины, и мы просто нужно обратить внимание на их знаки, основанные на квадранте, в котором находится конечная сторона угла. Ниже приведена таблица, показывающая знаки косинуса, синуса и тангенса в каждом квадранте.
| Косинус | Синус | Тангенс | ||
| Квадрант I | + | + | + | |
| III | — | III —— | + | |
| Квадрант IV | + | — | — |
После определения опорного угла мы можем определить значение тригонометрических функций в любом из других квадрантов, применив соответствующий знак их значения для опорного угла.Следующие шаги можно использовать, чтобы найти опорный угол заданного угла, θ:
- Вычтите 360 ° или 2π из угла столько раз, сколько необходимо (угол должен быть от 0 ° до 360 ° или от 0 до 2π). Если полученный угол составляет от 0 ° до 90 °, это опорный угол.
- Определите, в каком квадранте лежит конечная сторона угла (начальная сторона угла расположена вдоль положительной оси x)
- В зависимости от того, в каком квадранте находится крайняя сторона угла, используйте уравнения в таблице ниже, чтобы найти опорный угол.В квадранте I θ ‘= θ.
| Квадрант II | Квадрант III | Квадрант IV |
|---|---|---|
| θ ‘= 180 ° — θ | θ ‘= θ — 180 ° | θ ‘= 360 ° — θ |
Пример:
Найдите cos (120 °).
- θ уже находится между 0 ° и 360 °
- 120 ° лежит во втором квадранте
- 180 ° — 120 ° = 60 °, поэтому исходный угол составляет 60 °
.120 ° находится в квадранте II, а косинус отрицателен во втором квадранте, поэтому:
Пример:
Найдите cos (1050 °).
- 1050 ° — 360 ° = 690 ° — 360 ° = 330 °
- 330 ° лежит в квадранте IV
- 360 ° — 330 ° = 30 °, поэтому исходный угол равен 30 °
. 330 ° находится в квадранте IV, а косинус положительный в квадранте IV, поэтому:
Свойства функции косинуса
Ниже приводится ряд свойств функции косинуса, которые может быть полезно знать при работе с тригонометрическими функциями.
Косинус является совместной функцией синуса
Кофункция — это функция, в которой f (A) = g (B) при условии, что A и B являются дополнительными углами. В контексте косинуса и синуса
cos (θ) = sin (90 ° — θ)
sin (θ) = cos (90 ° — θ)
Пример:
cos (30 °) = sin (90 ° — 30 °) = sin (60 °)
Ссылаясь на единичный круг, показанный выше, мы можем подставить значения для cos (30 °) и sin (60 °) и увидеть, что:
Косинус — четная функция
Четная функция — это функция, в которой f (x) = f (-x), что означает, что отражение графика по оси y даст тот же график.Таким образом,
cos (θ) = cos (-θ)
Пример:
cos (60 °) = cos (-60 °)
cos (60 °) = cos (300 °)
Обращаясь к единичной окружности, мы видим, что cos (60 °) = и cos (-60 °) эквивалентен cos (300 °), который также равен. Это только один пример, но это свойство верно для всех θ.
Косинус — периодическая функция
Периодическая функция — это функция f, в которой существует некоторое положительное значение p, такое что
е (х + р) = е (х)
для всех x в области f, p — наименьшее положительное число, для которого f является периодическим, и называется периодом f.
Тригонометрические функции обычно используются для моделирования периодических явлений из-за их периодичности; независимо от того, с какой точки мы начинаем на единичной окружности, если мы пройдем расстояние 2π (360 °) по единичной окружности от этой точки, мы вернемся к нашей начальной точке. Если мы посмотрим на функцию косинуса, мы обнаружим, что она повторяется каждые 2π, поэтому 2π — это период функции косинуса. Мы можем записать это как:
cos (θ + 2π) = cos (θ)
Для учета нескольких полных оборотов это также можно записать как
cos (θ + 2πn) = cos (θ)
, где n — целое число.
На рисунке ниже показан пример этой периодичности.
Синим цветом мы это видим. . Если мы прибавим 2π к, мы получим угол, показанный красным,. Как видно из рисунка, несмотря на разную степень поворота в обоих углах, их конечные стороны совершенно одинаковы, что означает, что. Мы могли бы добавить еще 2π и все равно увидеть, что оно имеет то же значение косинуса, что и. Такова природа периодических функций. называются концевыми углами; это углы с одинаковой начальной и конечной сторонами, но с разными поворотами.
Примеры:
1.
2.
График функции косинуса
График косинуса является периодическим, что означает, что он повторяется бесконечно и имеет область значений -∞ Если бесконечно повторять эту часть y = cos inde (x) слева и справа, то получится полный график косинуса.Ниже приведен график, показывающий четыре периода функции косинуса в интервале [-4π, 4π]. На этом графике мы можем видеть, что y = cos (x) демонстрирует симметрию оси y; отражение графика косинуса по оси y дает тот же график. Это подтверждает, что косинус является четной функцией, поскольку cos (x) = cos (-x). Общий вид функции косинуса y = A · cos (B (x — C)) + D где A, B, C и D — константы.Чтобы иметь возможность изобразить уравнение косинуса в общем виде, нам нужно сначала понять, как каждая из констант влияет на исходный график y = cos (x), как показано выше. Чтобы применить все, что написано ниже, уравнение должно иметь форму, указанную выше; будьте осторожны со знаками. A — амплитуда функции; высота от центра графика до максимума или минимума. В y = cos (x) центром является ось x, а амплитуда равна 1, или A = 1, поэтому самая высокая и самая низкая точки, которых достигает график, равны 1 и -1, диапазон cos (x) . По сравнению с y = cos (x), показанным ниже фиолетовым цветом, функция y = 2 cos (x) (красный) имеет амплитуду, которая в два раза больше, чем у исходного графика косинуса. B — используется для определения периода функции; период функции — это расстояние от пика до пика (или любой точки на графике до следующей точки совпадения), и его можно найти как. В y = cos (x) период равен 2π. Мы можем подтвердить это, посмотрев на пики на графике косинусов. При x = 0 y = cos (x) имеет пик.Первый раз на функции появляется еще один пик при x = & plusmn2π, подтверждая, что период косинуса равен 2π. По сравнению с y = cos (x), показанным ниже фиолетовым цветом, который имеет период 2π, y = cos (2x) (красный) имеет период
. Это означает, что график повторяется каждое π, а не каждые 2π. C — фазовый сдвиг функции; фазовый сдвиг определяет, как функция сдвигается по горизонтали. Если C отрицательно, функция сдвигается влево. Если C положительно, функция сдвигается вправо.Остерегайтесь знака; если у нас есть уравнение, то C нет, потому что это уравнение в стандартной форме. Таким образом, мы бы сместили единицы графика влево. На рисунке ниже показаны y = cos (x) (фиолетовый) и (красный). Используя один из пиков графика косинуса в качестве ориентира, мы можем увидеть, что пик в точке (0,1) был смещен влево от своего исходного положения и теперь находится в точке (, 1). D — сдвиг функции по вертикали; если D положительный, график сдвигается вверх на D единиц, а если он отрицательный, график сдвигается вниз. По сравнению с y = cos (x), показанным ниже фиолетовым цветом, с центром на оси x (y = 0), y = cos (x) +5 (красный) с центром на линии y = 5 (синий). Объединив все приведенные выше примеры, на рисунке ниже показан график (красный) по сравнению с графиком y = cos (x) (фиолетовый). См. Также синус, тангенс, единичную окружность, тригонометрические функции, тригонометрию. Рассмотрим прямоугольный треугольник \ (\ треугольник \, ABC \) с прямым углом в \ (C \) и длиной \ (a \), \ (b \) , и \ (c \), как на рисунке справа.Для острого угла \ (A \) назовите ножку \ (\ overline {BC} \) его противоположной стороной , а ножку \ (\ overline {AC} \) его смежной стороной . Напомним, что гипотенуза треугольника — это сторона \ (\ overline {AB} \). Соотношения сторон прямоугольного треугольника встречаются в практических приложениях достаточно часто, чтобы оправдать их собственные названия, поэтому мы определяем шесть тригонометрических функций из \ (A \) следующим образом: Таблица 1.2 Шесть тригонометрических функций \ (A \) Обычно мы будем использовать сокращенные названия функций.Обратите внимание на таблицу 1.2, что пары \ (\ sin A \) и \ (\ csc A \), \ (\ cos A \) и \ (\ sec A \), а также \ (\ tan A \) и \ ( \ cot A \) являются обратными величинами: Пример 1.5 Для прямоугольного треугольника \ (\ треугольник \, ABC \), показанного справа, найдите значения всех шести тригонометрических функций острых углов \ (A \) и \ (B \). Решение: Гипотенуза треугольника \ (\ треугольник \, ABC \) имеет длину \ (5 \). Для угла \ (A \) противоположная сторона \ (\ overline {BC} \) имеет длину \ (3 \), а соседняя сторона \ (\ overline {AC} \) имеет длину \ (4 \).Таким образом: \ [\ nonumber \ sin A ~ = ~ \ dfrac {\ text {напротив}} {\ text {hypotenuse}} ~ = ~ \ dfrac {3} {5} \ qquad \ qquad \ [\ nonumber \ csc A ~ = ~ \ dfrac {\ text {hypotenuse}} {\ text {напротив}} ~ = ~ \ dfrac {5} {3} \ qquad \ qquad Для угла \ (B \) противоположная сторона \ (\ overline {AC} \) имеет длину \ (4 \), а соседняя сторона \ (\ overline {BC} \) имеет длину \ (3 \).Таким образом: \ [\ sin B ~ = ~ \ dfrac {\ text {напротив}} {\ text {hypotenuse}} ~ = ~ \ dfrac {4} {5} \ qquad \ qquad \ [\ csc B ~ = ~ \ dfrac {\ text {hypotenuse}} {\ text {напротив}} ~ = ~ \ dfrac {5} {4} \ qquad \ qquad Уведомление в примере 1.5, что мы не указали единицы измерения длины. Это повышает вероятность того, что наши ответы зависели от треугольника определенного физического размера. Например, предположим, что этот учебник читают два разных студента: один в США, а другой — в Германии. Американский студент думает, что длины \ (3 \), \ (4 \) и \ (5 \) в примере 1.5 измеряются в дюймах, тогда как немецкий студент думает, что они измеряются в сантиметрах. Поскольку \ (1 \) в \ (\ приблизительно \) \ (2.54 \) см, учащиеся используют треугольники разных физических размеров (см. Рис. 1.2.1 ниже, не в масштабе). Если американский треугольник равен \ (\ треугольник \, ABC \), а немецкий треугольник — \ (\ треугольник \, A’B’C ‘\), то из рисунка 1.2.1 мы видим, что \ (\ треугольник \, ABC \) подобен \ (\ треугольник \, A’B’C ‘\), и, следовательно, соответствующие углы равны и отношения соответствующих сторон равны.Фактически, мы знаем это общее отношение: стороны \ (\ треугольник \, ABC \) примерно в \ (2.54 \) раз длиннее, чем соответствующие стороны \ (\ треугольник \, A’B’C ‘\). Итак, когда американский студент вычисляет \ (\ sin A \), а немецкий студент вычисляет \ (\ sin A ‘\), они получают тот же ответ: \ [\ треугольник \, ABC ~ \ sim ~ \ треугольник \, A’B’C ‘\ quad \ Rightarrow \ quad Аналогично, другие значения тригонометрических функций \ (A \) и \ (A ‘\) одинаковы.Фактически, наш аргумент был достаточно общим, чтобы работать с любыми подобными прямоугольными треугольниками. Это приводит нас к следующему выводу: При вычислении тригонометрических функций острого угла \ (A \) вы можете использовать любой прямоугольный треугольник , который имеет \ (A \) в качестве одного из углов. Поскольку мы определили тригонометрические функции в терминах отношений сторон, вы можете думать об единицах измерения для этих сторон как о сокращении этих отношений. Это означает, что значений тригонометрических функций представляют собой безразмерные числа .\ circ \; = \; \ dfrac {\ text {смежный}} {\ text {противоположный}} \; = \; Пример 1.8 \ (A \) — острый угол такой, что \ (\ sin A = \ frac {2} {3} \). Найдите значения других тригонометрических функций \ (A \). Решение: В общем, рисование прямоугольного треугольника помогает решать задачи этого типа. Причина в том, что тригонометрические функции были определены в терминах отношений сторон прямоугольного треугольника, и вам дана одна такая функция (в данном случае синус) уже в терминах отношения: \ (\ sin \; A = \ frac {2} {3} \).2 ~ = ~ 9 ~ — ~ 4 ~ = ~ 5 \ quad \ Rightarrow \ quad Теперь мы знаем длины всех сторон треугольника \ (\ треугольник \, ABC \), поэтому имеем: \ [\ cos \; A \; = \; \ dfrac {\ text {смежный}} {\ text {hypotenuse}} \; = \; \ dfrac {\ sqrt {5}} {3} \ qquad \ [\ csc \; A \; = \; \ dfrac {\ text {hypotenuse}} {\ text {напротив}} \; = \; \ dfrac {3} {2} \ qquad Возможно, вы заметили связь между синусом и косинусом, секансом и косекансом, а также тангенсом и котангенсом дополнительных углов в примерах 1.5 и 1.7. Обобщение этих примеров дает нам следующую теорему: Теорема 1.2 Теорема о функциях Если \ (A \) и \ (B \) — дополнительные острые углы в прямоугольном треугольнике \ (\ треугольник \, ABC \), то выполняются следующие соотношения: \ [\ sin \; A ~ = ~ \ cos \; B \ qquad \ qquad \ sec \; A ~ = ~ \ csc \; B \ qquad \ qquad \ tan \; A ~ = ~ \ cot \; B \] \ [\ sin \; B ~ = ~ \ cos \; A \ qquad \ qquad \ sec \; B ~ = ~ \ csc \; A \ qquad \ qquad \ tan \; B ~ = ~ \ cot \; A \] Мы говорим, что пары функций \ (\ lbrace \; \ sin, \ cos \; \ rbrace \), \ (\ lbrace \; \ sec, \ csc \; \ rbrace \) и \ (\ lbrace \ ; \ tan, \ cot \; \ rbrace \) являются \ (\ textbf {cofunctions} \).\ circ \), поместите \ (30-60-90 \) прямоугольный треугольник \ (\ треугольник \, ADB \) с катетами длины \ (\ sqrt {3} \) и \ (1 \) поверх гипотенуза прямоугольного треугольника \ (45-45-90 \) \ (\ треугольник \, ABC \), длина гипотенузы которого равна \ (\ sqrt {3} \), как на рисунке справа. Из рисунка 1.2.2 (а) мы знаем, что длина каждого катета \ (\ треугольника \, ABC \) равна длине гипотенузы, деленной на \ (\ sqrt {2} \). Итак, \ (AC = BC = \ frac {\ sqrt {3}} {\ sqrt {2}} = \ sqrt {\ frac {3} {2}} \). Нарисуйте \ (\ overline {DE} \) перпендикулярно \ (\ overline {AC} \) так, чтобы \ (\ треугольник \, ADE \) был прямоугольным треугольником.\ circ \), поскольку это дополнение к \ (\ angle \, BDF \). Гипотенуза \ (\ overline {BD} \) треугольника \ (\ треугольник \, DFB \) имеет длину \ (1 \), а \ (\ треугольник \, DFB \) является \ (45-45-90 \) правой треугольник, поэтому мы знаем, что \ (DF = FB = \ frac {1} {\ sqrt {2}} \). Теперь мы знаем, что \ (\ overline {DE} \ perp \ overline {AC} \) и \ (\ overline {BC} \ perp \ overline {AC} \), поэтому \ (\ overline {FE} \) и \ (\ overline {BC} \) параллельны. Аналогично, \ (\ overline {FB} \) и \ (\ overline {EC} \) оба перпендикулярны \ (\ overline {DE} \) и, следовательно, \ (\ overline {FB} \) параллельны \ ( \ overline {EC} \).\ circ = \ frac {\ sqrt {6} — \ sqrt {2}} {\ sqrt {6} + \ sqrt {2}} \). Мы уже узнали некоторые свойства специальных углов, такие как преобразование радианов в градусы. Мы также можем вычислить синусы и косинусы особых углов, используя Пифагорова идентичность и наши знания о треугольниках. Сначала мы рассмотрим углы \ (45 ° \) или \ (\ dfrac {π} {4} \), как показано на рисунке \ (\ PageIndex {9} \).Треугольник \ (45 ° –45 ° –90 ° \) является равнобедренным треугольником, поэтому координаты \ (x \) и \ (y \) соответствующей точки на окружности совпадают. Поскольку значения x- и \ (y \) одинаковы, значения синуса и косинуса также будут равны. В \ (t = \ frac {π} {4} \), что составляет 45 градусов, радиус единичной окружности делит пополам первый квадратный угол . Это означает, что радиус лежит вдоль прямой \ (y = x \). Единичный круг имеет радиус, равный 1.2 & = \ dfrac {1} {2} \\ x & = ± \ dfrac {1} {\ sqrt {2}} \ end {align *} \] В квадранте I, \ (x = \ dfrac {1} {\ sqrt {2}} \). При \ (t = \ dfrac {π} {4} \) или 45 градусах, \ [\ begin {align *} (x, y) & = (x, x) = (\ dfrac {1} {\ sqrt {2}}, \ dfrac {1} {\ sqrt {2}}) \ » \ x & = \ dfrac {1} {\ sqrt {2}}, \; y = \ dfrac {1} {\ sqrt {2}} \\ \ cos t & = \ dfrac {1} {\ sqrt {2}}, \; \ sin t = \ dfrac {1} {\ sqrt {2}} \ end {align *} \] Если мы затем рационализируем знаменатели, мы получим \ [\ begin {align *} \ cos t & = \ dfrac {1} {\ sqrt {2}} \ dfrac {\ sqrt {2}} {\ sqrt {2}} \\ & = \ dfrac {\ sqrt {2}} {2} \\ \ sin t & = \ dfrac {1} {\ sqrt {2}} \ dfrac {\ sqrt {2}} {\ sqrt {2}} \\ & = \ dfrac { \ sqrt {2}} {2} \ end {align *} \] Следовательно, координаты \ ((x, y) \) точки на окружности радиуса \ (1 \) под углом \ (45 ° \) равны \ (\ left (\ dfrac {\ sqrt {2 }} {2}, \ dfrac {\ sqrt {2}} {2} \ right) \). Затем мы найдем косинус и синус под углом \ (30 °, \) или \ (\ tfrac {π} {6} \). Сначала мы нарисуем треугольник внутри круга, одна сторона которого расположена под углом \ (30 °, \), а другая — под углом \ (- 30 °, \), как показано на рисунке \ (\ PageIndex {11} \ ). Если полученные два прямоугольных треугольника объединить в один большой треугольник, обратите внимание, что все три угла этого большего треугольника будут равны \ (60 °, \), как показано на рисунке \ (\ PageIndex {12} \). Поскольку все углы равны, стороны также равны. Вертикальная линия имеет длину \ (2y \), и поскольку все стороны равны, мы также можем заключить, что \ (r = 2y \) или \ (y = \ frac {1} {2} r \). Поскольку \ (\ sin t = y \), \ [\ sin \ left (\ frac {π} {6} \ right) = \ dfrac {1} {2} \ nonumber \] А поскольку \ (r = 1 \) в нашем единичном круге , \ [\ begin {align *} \ sin \ left (\ frac {π} {6} \ right) & = \ dfrac {1} {2} (1) \\ & = \ dfrac {1} {2} \ end {align *} \] Используя тождество Пифагора, мы можем найти значение косинуса.2 \ left (\ frac {π} {6} \ right) & = \ dfrac {3} {4} && \ text {Используйте свойство квадратного корня.} \\ Координаты \ ((x, y) \) точки на окружности радиуса \ (1 \) под углом \ (30 ° \): \ (\ left (\ dfrac {\ sqrt {3}} {2}, \ dfrac {1} {2} \ right) \). В точке \ (t = \ dfrac {π} {3} \) (60 °) радиус единичной окружности, 1, служит гипотенузой прямоугольного треугольника 30-60-90 градусов, \ (BAD, \) как показано на рисунке \ (\ PageIndex {13} \).Угол \ (A \) имеет меру 60 °. 60 °. В точке \ (B, \) проведем угол \ (ABC \) с мерой \ (60 ° \). Мы знаем, что сумма углов в треугольнике равна \ (180 ° \), поэтому мера угла \ (C \) также равна \ (60 ° \). Теперь у нас есть равносторонний треугольник. Поскольку каждая сторона равностороннего треугольника \ (ABC \) имеет одинаковую длину, и мы знаем, что одна сторона является радиусом единичного круга, все стороны должны иметь длину 1. Угол \ (ABD \) равен 30 °. Итак, если двойной, угол \ (ABC \) равен 60 °.2 & = \ dfrac {3} {4} \\ y & = ± \ dfrac {\ sqrt {3}} {2} \ end {align *} \] Поскольку \ (t = \ dfrac {π} {3} \) имеет конечную сторону в квадранте I, где \ (y \) — координата положительна, мы выбираем \ (y = \ dfrac {\ sqrt {3}} {2} \), положительное значение. В \ (t = \ dfrac {π} {3} \) (60 °) координаты \ ((x, y) \) точки на окружности радиуса \ (1 \) под углом \ (60 ° \) равны \ (\ left (\ dfrac {1} {2}, \ dfrac {\ sqrt {3}} {2} \ right) \), поэтому мы можем найти синус и косинус. \ ((x, y) = \ left (\ dfrac {1} {2}, \ dfrac {\ sqrt {3}} {2} \ right) \) \ (x = \ dfrac {1} {2}, \; y = \ dfrac {\ sqrt {3}} {2} \) \ (\ cos t = \ dfrac {1} {2}, \; \ sin t = \ dfrac {\ sqrt {3}} {2} \) Теперь мы нашли значения косинуса и синуса для всех наиболее часто встречающихся углов в первом квадранте единичной окружности.Таблица \ (\ PageIndex {1} \) суммирует эти значения. На рисунке \ (\ PageIndex {14} \) показаны общие углы в первом квадранте единичной окружности. Чтобы найти косинус и синус углов, отличных от специальных углов , мы обращаемся к компьютеру или калькулятору. Будьте внимательны. : Большинство калькуляторов можно установить в режим «градус» или «радиан», который сообщает калькулятору единицы измерения входного значения. Когда мы вычисляем \ (\ cos (30) \) на нашем калькуляторе, он будет оценивать его как косинус 30 градусов, если калькулятор находится в режиме градусов, или косинус 30 радиан, если калькулятор находится в режиме радиан. Как сделать: если задан угол в радианах, с помощью графического калькулятора найдите косинус Пример \ (\ PageIndex {4} \): использование графического калькулятора для поиска синуса и косинуса Оцените \ (\ cos \ left (\ dfrac {5π} {3} \ right) \) с помощью графического калькулятора или компьютера. Решение Введите следующие нажатия клавиш: \ (\ mathrm {COS (5 × π ÷ 3) \; ENTER} \) \ [\ cos \ left (\ dfrac {5π} {3} \ right) = 0,5 \ nonumber \] Анализ Мы можем найти косинус или синус угла в градусах прямо на калькуляторе в градусном режиме. Для калькуляторов или программного обеспечения, которые используют только режим радиан, мы можем найти знак \ (20 ° \), например, включив коэффициент преобразования в радианы как часть входных данных: \ [\ mathrm {SIN (20 × π ÷ 180) \; ENTER} \ nonumber \] Попробовать \ (\ PageIndex {4} \) Вычислить \ (\ sin \ left (\ dfrac {π} {3} \ right) \). приблизительно 0,866025403 Правило косинуса говорит нам, что когда у нас есть прямоугольный треугольник, косинус = ahcosine = \ frac {a} {h} cosine = ha. « a » в данном случае означает смежный. « h » обозначает гипотенузу, которую можно найти с помощью теоремы Пифагора.Все, что вам нужно, чтобы найти косинус, — это прилегающая сторона и гипотенуза. Когда вы сталкиваетесь с синусом, вы можете найти ответ в прямоугольном треугольнике, взяв противоположную сторону над гипотенузой в виде sine = ohsine = \ frac {o} {h} sine = ho. Для правила касательной, когда у вас есть прямоугольный треугольник, вы можете использовать противоположное значение для смежных сторон треугольника, чтобы найти свое отношение. Это означает, что tan = oatan = \ frac {o} {a} tan = ao. Когда вы слышите SohCahToa, не сразу понятно, что это значит. Но на самом деле это более простой способ запомнить, как использовать синус, косинус и тангенс, который мы только что выучили. Это три основные функции, с которыми вы будете иметь дело в задачах тригонометрии. Soh Cah Toa означает: Это может помочь вам найти длину стороны прямоугольного треугольника, если у вас есть угол θ \ thetaθ и некоторая информация о других сторонах треугольника. В этой главе мы сосредоточимся на правиле косинуса. Это означает, что мы будем работать только с частью SohCahToaSohCahToaSohCahToa «CahCahCah». Попробуйте вместе с нами следующие триггерные задачи, чтобы узнать, как решать вопросы с помощью правила косинуса. Вопрос 1 Определите каждое косинусное отношение с помощью калькулятора а) cos \ coscos 50 ° Просто введите число в свой калькулятор, и вы получите 0.640.640.64. б) cos \ coscos -50 ° Просто введите число в свой калькулятор, и вы получите 0,640,640,64. cos \ coscos 50 ° и cos \ coscos -50 ° оба = 0,640,640,64. Почему? Приведенная выше диаграмма ASTC помогает определить, какой коэффициент срабатывания положительный в каком квадранте. cos \ coscos 50 ° лежит в квадранте I, где все триггерные отношения положительны. cos \ coscos -50 ° лежит в квадранте 4, где косинус положительный. Вот почему мы получаем 0,640,640,64 как для cos \ coscos 50 °, так и для cos \ coscos -50 °. Вопрос 2 Определить угол с точностью до градуса Решение а) cosθ = 0,24 \ cos \ theta = 0,24 cosθ = 0,24 Используйте в калькуляторе обратный косинус, у которого рядом с coscoscos стоит немного −1-1−1: arccos (0,24) = 76 \ arccos (0,24) = 76arccos (0,24) = 76 ° б) cosθ = −0,45 \ cos \ theta = -0,45 cosθ = −0,45 Используйте обратный косинус в калькуляторе, чтобы найти: arccos (−0.45) = 117 \ arccos (-0,45) = 117arccos (-0,45) = 117 ° Вопрос 3 Определите углы и стороны с помощью косинуса Решение: a) Найдите угол AAA и BBB: cosθ = смежная гипотенуза \ cos \ theta = \ frac {смежная} {гипотенуза} cosθ = смежная гипотенуза Уголок AAA cosA = 817 \ cos A = \ frac {8} {17} cosA = 178 Решить на вашем калькуляторе arccos817 = 62 \ arccos \ frac {8} {17} = 62arccos178 = 62 ° Уголок BBB cosB = 1517 \ cos B = \ frac {15} {17} cosB = 1715 Решить на вашем калькуляторе arccos1517 = 28 \ arccos \ frac {15} {17} = 28arccos1715 = 28 ° б) Найдите значение «ххх», используя косинус Уравнение общего косинуса
1.2: Тригонометрические функции острого угла
\ cos A ~ = ~ \ dfrac {\ text {смежный}} {\ text {hypotenuse}} ~ = ~ \ dfrac {4} {5} \ qquad \ qquad
\ tan A ~ = ~ \ dfrac {\ text {напротив}} {\ text { смежный}} ~ = ~ \ dfrac {3} {4} \]
\ sec A ~ = ~ \ dfrac {\ text {hypotenuse}} {\ text {смежный}} ~ = ~ \ dfrac {5} {4} \ qquad \ qquad
\ cot A ~ = ~ \ dfrac {\ text {смежный}} {\ text { напротив}} ~ = ~ \ dfrac {4} {3} \]
\ cos B ~ = ~ \ dfrac { \ text {смежный}} {\ text {hypotenuse}} ~ = ~ \ dfrac {3} {5} \ qquad \ qquad
\ tan B ~ = ~ \ dfrac {\ text {противоположный}} {\ text {смежный} } ~ = ~ \ dfrac {4} {3} \]
\ sec B ~ = ~ \ dfrac { \ text {hypotenuse}} {\ text {смежный}} ~ = ~ \ dfrac {5} {3} \ qquad \ qquad
\ cot B ~ = ~ \ dfrac {\ text {смежный}} {\ text {напротив} } ~ = ~ \ dfrac {3} {4} \]
Рисунок 1.2.1: \ (△ ABC ∼ △ A ′ B ′ C ′ \)
\ dfrac {BC} {B’C’} ~ = ~ \ dfrac {AB} {A ‘B’} \ quad \ Rightarrow \ quad
\ dfrac {BC} {AB} ~ = ~ \ dfrac {B’C ‘} {A’B’} \ quad \ Rightarrow \ quad \ sin A ~ = ~ \ sin А ‘\]
\ dfrac {\ sqrt {3}} {1} \; = \; \ sqrt {3} \]
b ~ = ~ \ sqrt {5} \]
\ tan \; A \; = \; \ dfrac {\ text {напротив}} {\ text {смежный}} \; = \;
\ dfrac {2} {\ sqrt {5}} \ quad \ quad \]
\ sec \; A \; = \; \ dfrac {\ text {hypotenuse}} {\ text {смежный}} \; = \; \ dfrac {3} {\ sqrt {5}} \ qquad
\ cot \; A \; = \; \ dfrac {\ text {смежный}} {\ text {противоположный}} \; = \; \ dfrac {\ sqrt {5}} {2} \] Авторы и авторство
5.2: Единичная окружность — функции синуса и косинуса
Нахождение синусов и косинусов углов 45 °
Нахождение синусов и косинусов углов 30 ° и 60 °
\ cos \ left (\ frac {π} { 6} \ right) & = \ pm \ sqrt {\ dfrac {3} {4}} = \ dfrac {\ sqrt {3}} {2} && \ text {Поскольку \ (y \) положительное значение, выберите положительный корень. } \\
\ конец {выровнено} \) Угол 0 \ (\ dfrac {π} {6} \) или 30 \ (\ dfrac {π} {4} \) или 45 ° \ (\ dfrac {π} {3} \) или 60 ° \ (\ dfrac {π} {2} \) или 90 ° Косинус 1 \ (\ dfrac {\ sqrt {3}} {2} \) \ (\ dfrac {\ sqrt {2}} {2} \) \ (\ dfrac {1} {2} \) 0 Синус 0 \ (\ dfrac {1} {2} \) \ (\ dfrac {\ sqrt {2}} {2} \) \ (\ dfrac {\ sqrt {3}} {2} \) 1 Использование калькулятора для поиска синуса и косинуса
Что такое косинусный коэффициент в тригонометрии?
Тригонометрические отношения
правило косинуса
правило синуса
линейка касательной
SohCahToa
Примеры задач

 7193
7193 4067
4067 0175
0175 4067
4067 7071
7071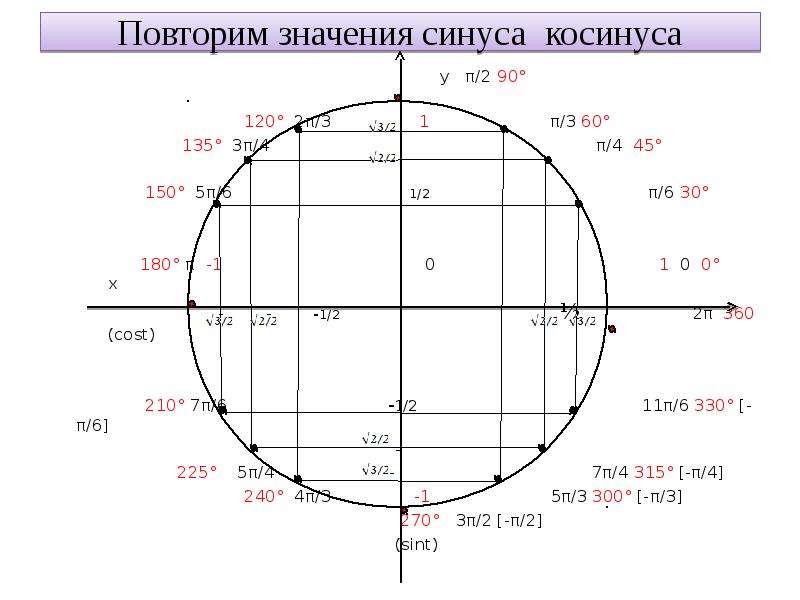 9272
9272 9336
9336 7193
7193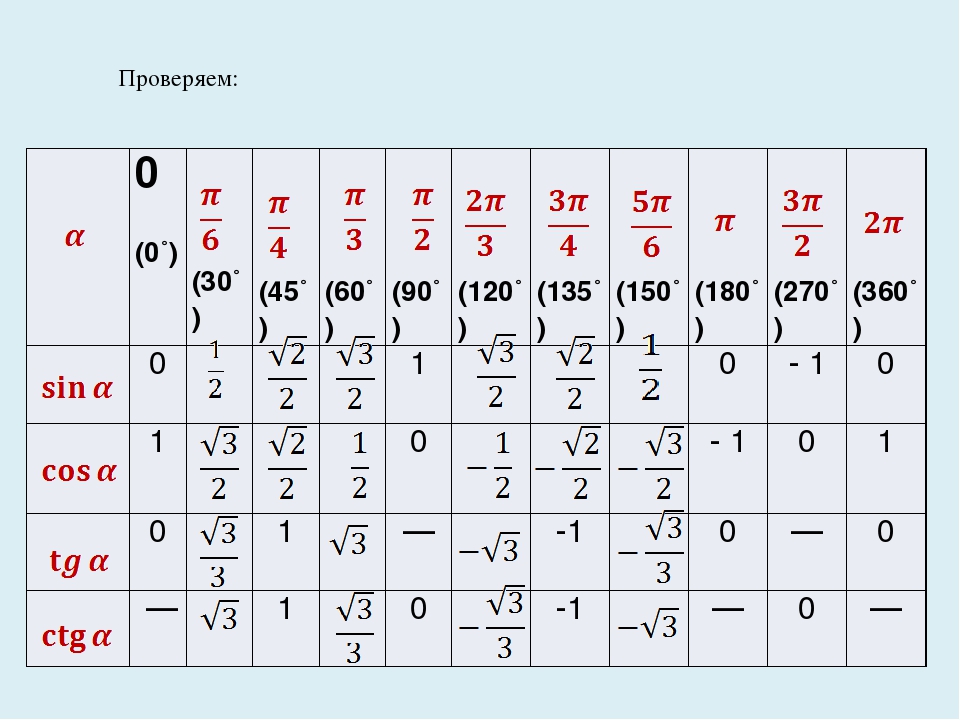 4226
4226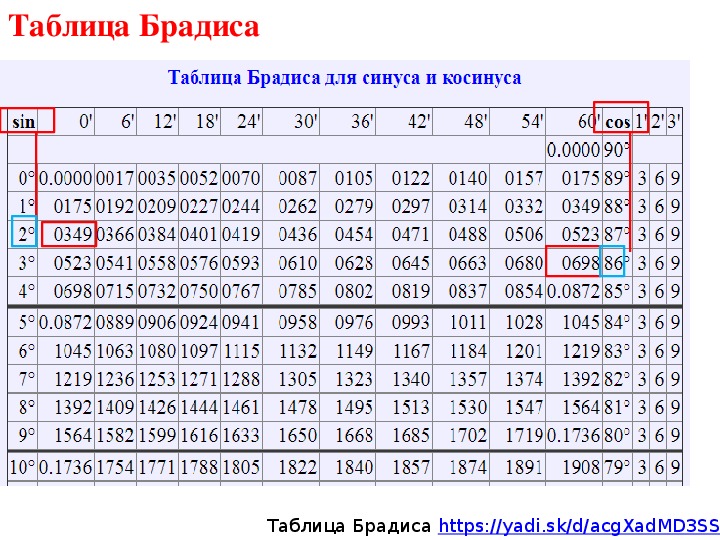 0349
0349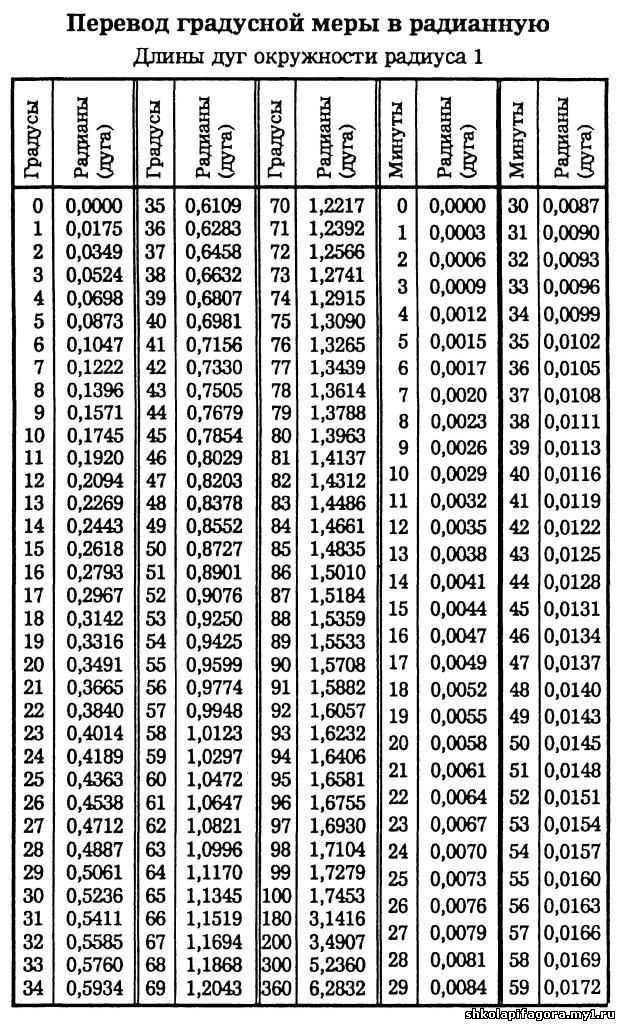 3746
3746 682
682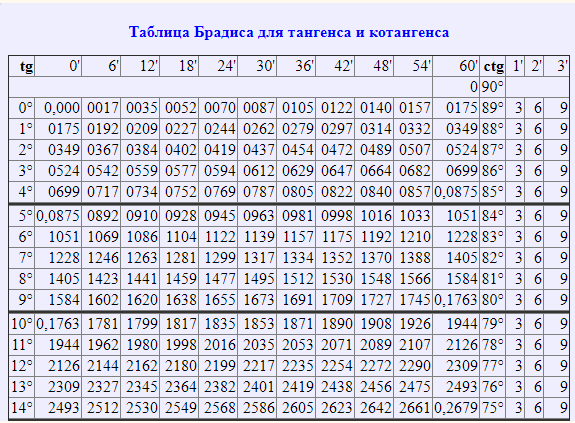 9205
9205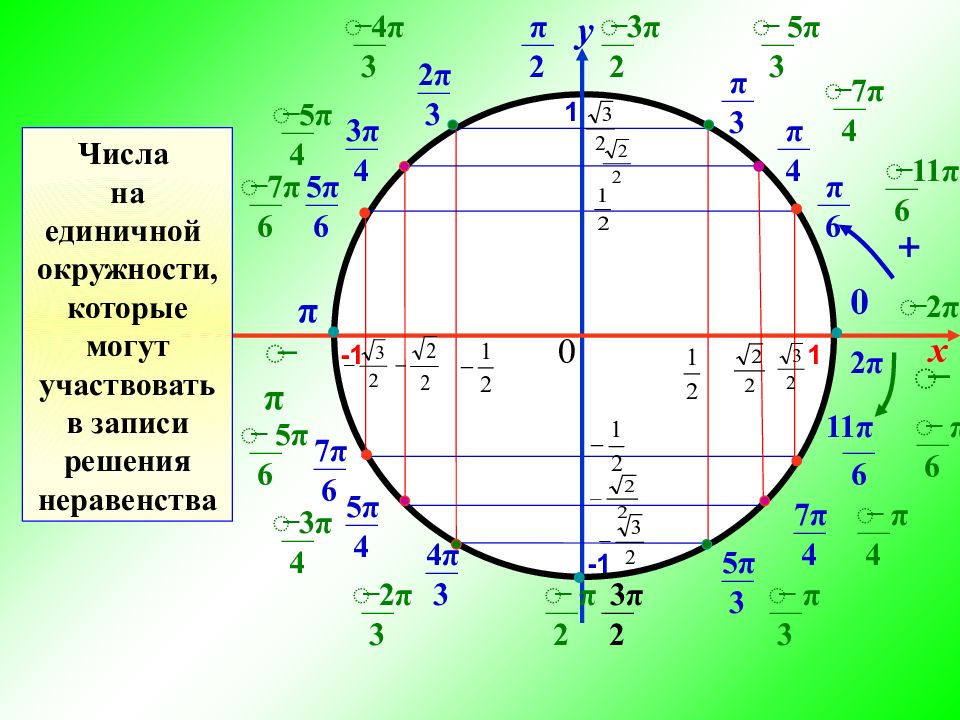 9659
9659 7771
7771 4695
4695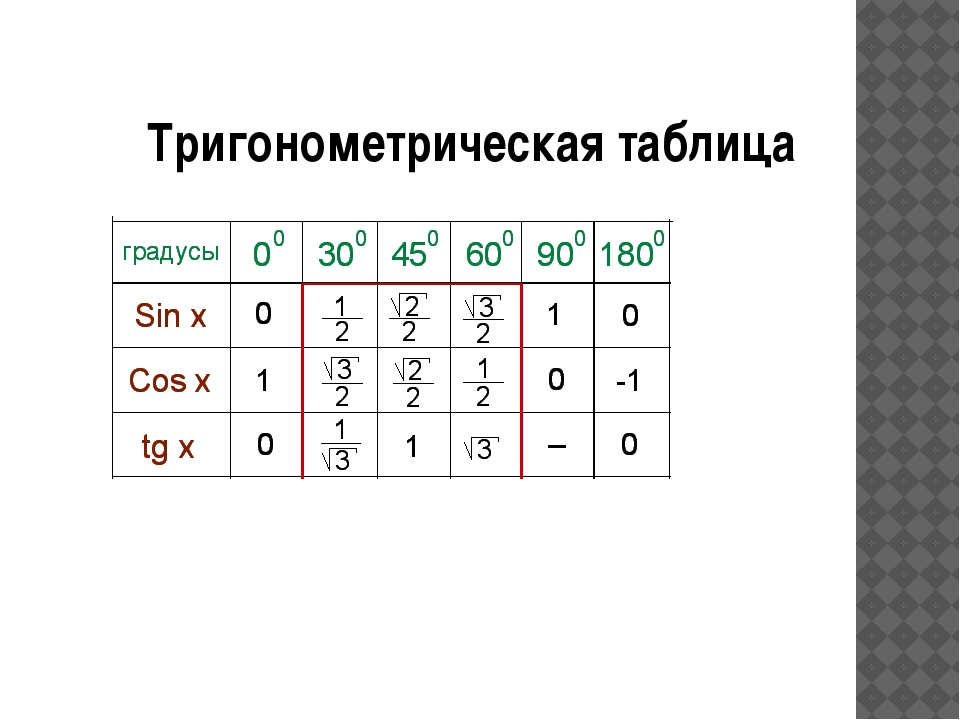 0698
0698 3256
3256 6561
6561 8988
8988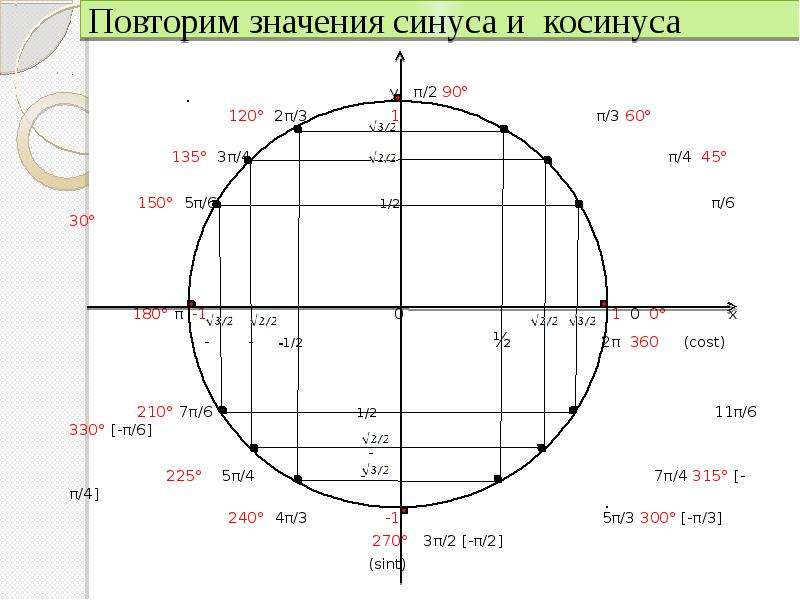 9986
9986 9563
9563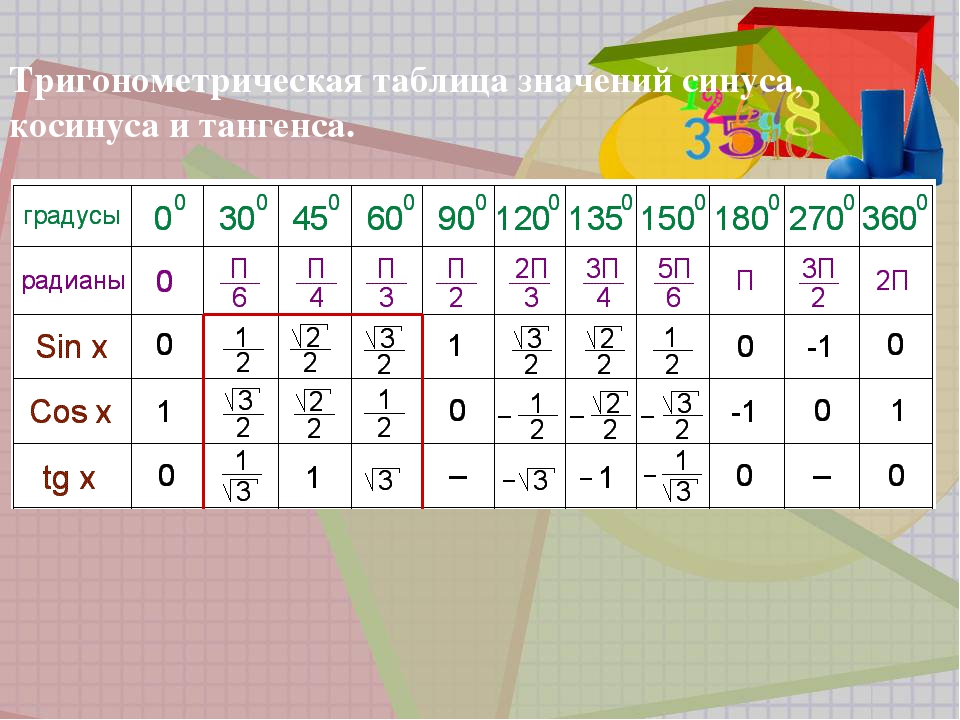 766
766 4695
4695 0872
0872 309
309 6561
6561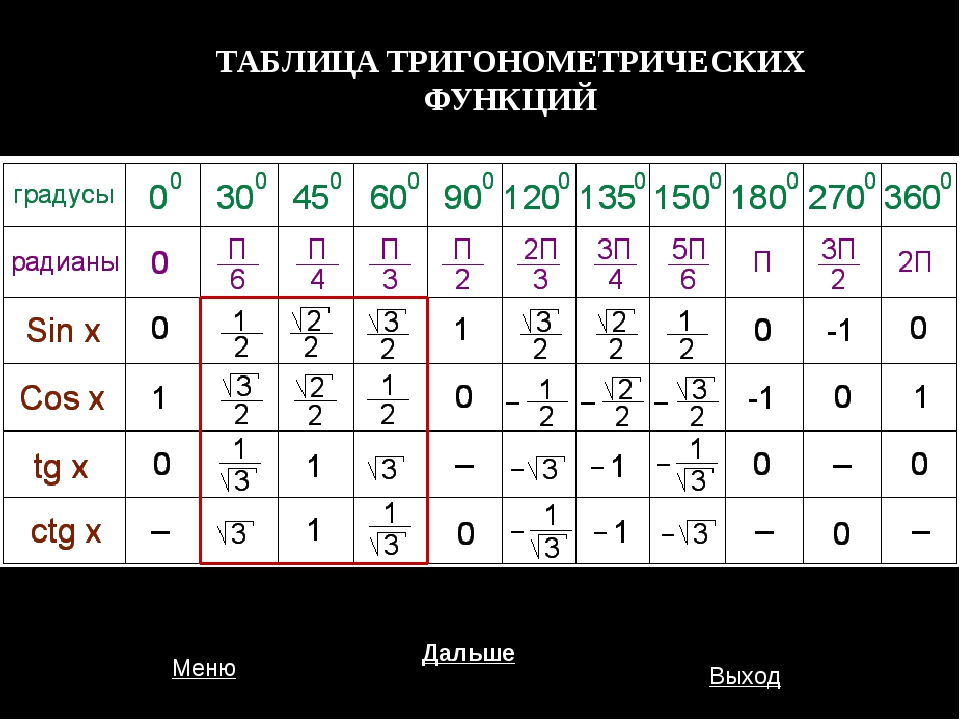 8988
8988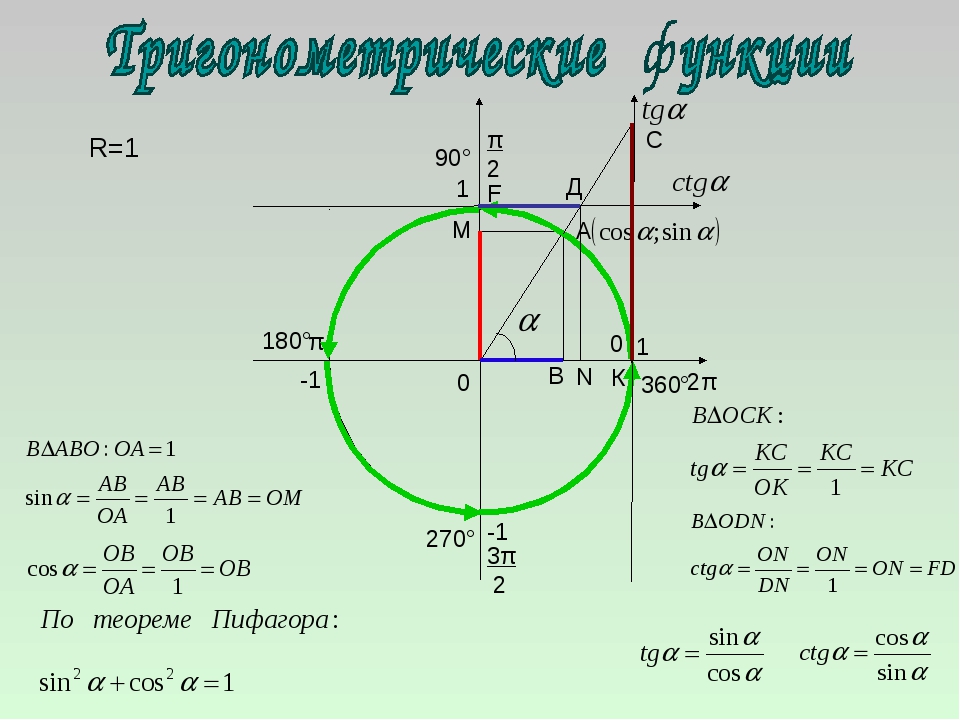 9986
9986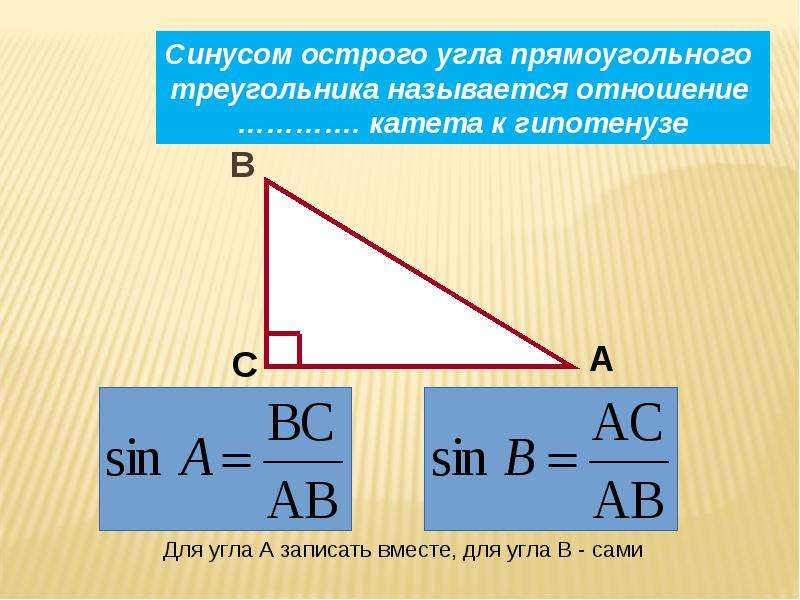
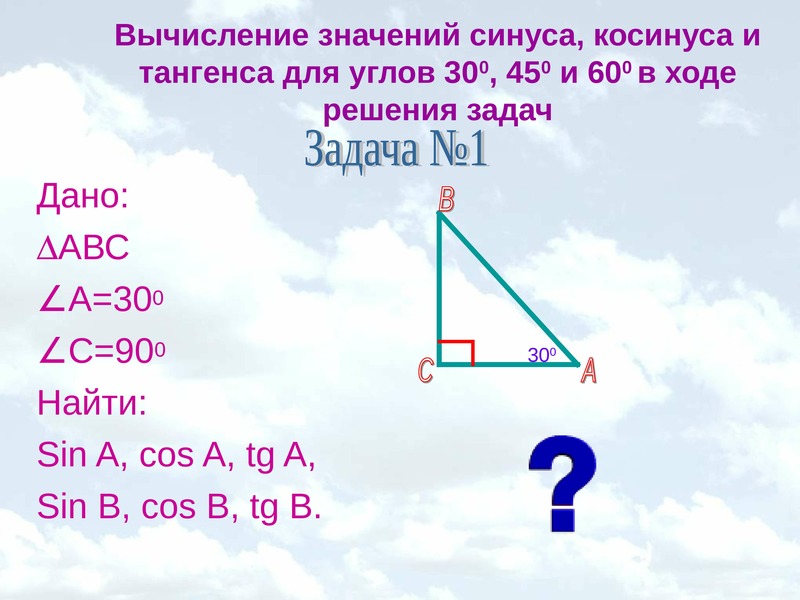 Тогда мы вычитаем эту поправку 3′, 39°54′ – 3′ = 39°51′. Второй угол находим, исходя из того, что сумма всех углов в треугольнике не должна превышать 180°. Поэтому 180° – (90° + 39°51′) = 50° 09′. Угол β = 50° 09′. Решаем задачу дальше. Ищем сторону а. Для этого мы можем использовать два способа.
Тогда мы вычитаем эту поправку 3′, 39°54′ – 3′ = 39°51′. Второй угол находим, исходя из того, что сумма всех углов в треугольнике не должна превышать 180°. Поэтому 180° – (90° + 39°51′) = 50° 09′. Угол β = 50° 09′. Решаем задачу дальше. Ищем сторону а. Для этого мы можем использовать два способа. Косинус 35 градусов будет 0,8192 по таблице, если это 145°, это будет значение с отрицательным значением -0,8192.
Косинус 35 градусов будет 0,8192 по таблице, если это 145°, это будет значение с отрицательным значением -0,8192. Открываем таблицу Брадиса. Это число соответствует 58° 18′. Согласно теореме о правилах трёх углов в треугольнике находим третий угол:
Открываем таблицу Брадиса. Это число соответствует 58° 18′. Согласно теореме о правилах трёх углов в треугольнике находим третий угол: