Косинус квадрат плюс косинус квадрат равно 1: Доказательство основного тригонометрического тождества (видео)

Содержание

Использование тригонометрических тождеств — Задача 3

Я хочу поговорить еще об одном пифагорейском тождестве, и оно исходит из исходного пифагорейского тождества косинус в квадрате плюс синус в квадрате равно 1. Чтобы получить его, я просто делю обе части этого уравнения на синус в квадрате тета , и я получаю квадрат котангенса тета плюс 1 равно квадрату косеканса тета, и у нас будет возможность использовать это в следующем доказательстве.

Задача требует подтвердить личность; котангенс в квадрате минус тангенс в квадрате над котангенсом плюс тангенс величина в квадрате равна 1 минус 2 синус в квадрате тета, и значение этого выражения появится позже, когда мы будем изучать тождество двойного угла, так что это тождество двойного угла для косинуса.

В любом случае, когда вы доказываете тригонометрическую идентичность, хорошо начать с одной стороны, выполнить алгебраические манипуляции и использовать все тригонометрические идентичности, чтобы добраться до другой стороны, вот что я собираюсь сделать, я начну с наименьшей стороны.

Теперь этот числитель представляет собой разность квадратов, так что я просто возьму его на множители, и я получу котангенс тета минус тангенс тета, умноженный на котангенс тета плюс тангенс тета, и это то, что у меня есть в знаменателе котангенс тета плюс тангенс тета в квадрате, поэтому я получу хорошую отмену и позвольте мне сделать это. Позвольте мне отменить один из них с этим, и у меня есть котангенс тета минус тангенс тета над котангенс тета плюс тангенс тета.

Куда нам двигаться дальше? Уловка очевидна, но если я умножу на котангенс тета на котангенс тета, помните, что котангенс есть величина, обратная тангенсу, поэтому, когда я умножаю эти два числа, я получаю единицу, и, конечно же, когда я умножаю котангенс и котангенс, я получаю котангенс в квадрате, поэтому я смогу использовать свою новую личность. Котангенс в квадрате тета минус 1 и котангенс в квадрате тета плюс 1.

Теперь котангенс в квадрате тета плюс 1 есть косеканс в квадрате тета, поэтому позвольте мне сделать эту замену. Котангенс в квадрате тета минус 1 над косекансом в квадрате тета, и в этот момент я хочу использовать трюк переключения на синусы и косинусы.

Это равно косинусу в квадрате тета и синусу в квадрате тета минус 1 больше, и это равно 1 больше квадрату тета. Теперь у меня есть сложная дробь, которая на самом деле не выглядит такой простой, но я мог бы легко упростить ее, используя прием разрыва дроби, который умножается на наименьший общий знаменатель меньших дробей, эти маленькие дроби здесь и здесь, и это синус в квадрате, поэтому я умножаю верх на синус в квадрате, а низ на синус в квадрате и просто не забываю распределить этот синус в квадрате на оба члена.

Теперь сверху я получу отмену, так что сверху я получу косинус в квадрате. Косинус в квадрате тета минус У меня здесь знак минус, так что минус синус в квадрате тета, синус в квадрате и внизу у меня просто 1, что ж, это хорошо. Еще одна вещь, которую мне нужно получить, чтобы получить 1 минус 2 синуса в квадрате тета пифагорейского тождества, я хочу использовать пифагорейское тождество на этом, и это форма исходного пифагорейского тождества, которое мы имели здесь; косинус в квадрате тета равен 1 минус синус в квадрате тета, поэтому позвольте мне сделать эту замену.

Косинус в квадрате становится 1 минус синус в квадрате, и у меня есть еще минус синус в квадрате, и тогда мы получаем его, окончательный ответ 1 минус 2 синуса в квадрате тета. Вот и все, поэтому мы доказали, что это уродливое месиво на самом деле равно 1 минус 2 синус в квадрате тэта, и мы поставили маленькую рамку в конце нашего доказательства.

Пифагорейские тождества — формулы, вывод, примеры

Пифагорейские тождества, как следует из названия, получены из теоремы Пифагора. Согласно этой теореме, в любом прямоугольном треугольнике квадрат гипотенузы (наибольшая сторона) равен сумме квадратов двух других сторон (катетов). Эта теорема может быть применена к тригонометрическим отношениям (как они определены для прямоугольного треугольника), что приводит к тождествам Пифагора.

Давайте узнаем больше о пифагорейских тождествах вместе с их доказательством, примерами и другими практическими задачами.

1.	Что такое пифагорейские тождества?
2.	Вывод пифагорейских тождеств
3.	Применение пифагорейских тождеств
4.	Часто задаваемые вопросы о пифагорейских тождествах

Что такое пифагорейские тождества?

Тождества Пифагора — важные тождества в тригонометрии, полученные из теоремы Пифагора. Эти тождества используются при решении многих тригонометрических задач, где задано одно тригонометрическое соотношение, а необходимо найти другие соотношения. Фундаментальное пифагорейское тождество дает отношение между sin и cos, и это наиболее часто используемое пифагорейское тождество, которое гласит:

sin ² θ + cos ² θ = 1 (что дает соотношение между sin и cos)

Есть еще два пифагорейских тождества:

sec ² θ — tan ² θ = 1 (которое дает отношение между sec и tan)
csc ² θ — кроватка ² θ = 1 (что дает связь между csc и кроваткой)

Пифагорейские триггеры

Все пифагорейские тригонометрические тождества упомянуты ниже вместе.

Каждое из них может быть записано в различных формах с помощью алгебраических операций. т. е. каждое тождество Пифагора можно записать в 3 формах следующим образом:

sin ² θ + cos ² θ = 1 ⇒ 1 — sin ² θ = cos ^{2 0 ⇒ 6 cos θ} θ = sin ² θ
с ² θ — тангенс ² θ = 1 ⇒ с ² θ = 1 + тангенс ² θ ⇒ сек ² θ — 1 = тангенс ² θ
csc ² θ — кроватка ² θ = 1 ⇒ csc ² θ = 1 + кроватка ² θ ⇒ csc ² θ 9090 — 1 = 5 θ 9090

Вывод пифагорейских тождеств

Мы собираемся доказать тождества Пифагора, используя теорему Пифагора. Рассмотрим прямоугольный треугольник ABC с прямым углом в точке C. Тогда AB — гипотенуза. Предположим, что AB = c, BC = a и CA = b для нашего удобства. Предположим, что угол при B равен θ.

На рисунке выше:

Противоположная сторона (от θ) = b
Прилегающая сторона (θ) = a
Гипотенуза = c

Давайте сначала определим все тригонометрические соотношения, которые в дальнейшем будут полезны при выводе тождеств Пифагора в тригонометрии.

sin θ = (противоположное)/(гипотенуза) = b / c ⇒ csc θ = c / b
потому что θ = (прилегающий)/(гипотенуза) = а/с ⇒ сек θ = с/а
загар θ = (напротив) / (прилегающий) = b / a ⇒ кроватка θ = a / b

Докажем каждое тождество пифагорейских триггеров одно за другим.

Доказательство пифагорской идентификации sin²θ + cos²θ = 1

Применение теоремы Pythagoras к треугольнику, мы получаем

A ² + B ² = C ²

Divident Dividend Dividending на оба Sides на C ^{. 2} ,

а ² / с ² + б ² / с ² = с ² / с ² 90

6 + (б/в) ² = 1

(cos θ) ² + (sin θ) ² = 1 (или)

sin ² θ0

Отсюда доказано.

ПРЕДУПРЕЖДЕНИЕ ПИТАГОРЕСОВАЯ ИДЕНТИКА SEC²θ — TAN²θ = 1

Опять же, по теореме Pythagoras

A ² + B ² = C ²

Разделив каждый термин на обеих местах на ²,

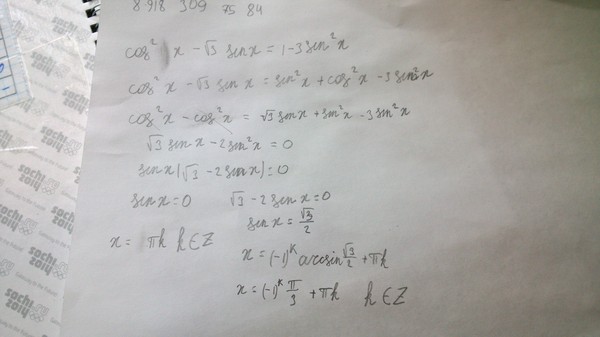а ² / а ² + б ² / а ² = в ² / а ²

1 + (б / а) ² = (в / а) ²

1 + (90 θ 0 6 ) 6 (20 θ 0 6 ) сек θ) ² (или)

сек ² θ — тангенс ² θ = 1

Отсюда доказано.

Доказательство тождества Пифагора csc²θ — cot²θ = 1

По теореме Пифагора,

a ² + b ² = c ²

065 2

A ² / B ² + B ² / B ² = C ² / B ²

(A / B) ² + 1 = (C / B) ² + 1 = (C / B) ^{2 ^{+ 1. / b) ²}}

(COT θ)

2 + 1 = (CSC θ) ² (OR)

CSC ² θ — COT ² θ = 1

arced.

Применение пифагорейских тождеств

Тождества Пифагора используются для доказательства других тригонометрических тождеств.
Пример: Докажите идентичность sin ⁴ x — cos ⁴ x = sin ² x — cos ² x.
Решение:
Мы можем написать
LHS = sin ⁴ x — cos ⁴ x = (sin ² x) ² — (cos ² x) ²
Используя формулу a² — b²,
= (sin ² x — cos ² x) (sin ² x + cos ² x)
Используя пифагорейские тождества, sin ² х + cos ² х = 1.
= (sin ² x — cos ² x) (1)
= sin ² x — cos ² x
= RHS
Значит доказано.
Тождества Пифагора полезны при решении задач, связанных с высотами и расстояниями.
Тождества Пифагора используются для нахождения любого тригонометрического соотношения, когда задано другое тригонометрическое соотношение.
Пример: Найти cos x, если sin x = 3/5 и x находится в диапазоне 1 ^ст квадрант.
Решение:
Из пифагорейских тождеств,
cos ² x = 1 — sin ² x
cos x = ±√1 — sin²x
= ±√1 — (3/5)²
= ±√1 — (9/25)
= ±√16/25
= ± 4/5
Поскольку x находится в первом квадранте, cos x положителен. Итак, cos x = 4 / 5.

Связанные темы:

Формулы полууглов
Формулы касательной
Формулы двойного угла
Тригонометрические формулы

Формулы косинуса
Тригонометрические функции

Часто задаваемые вопросы о пифагорейских тождествах

Список всех Пифагорейских Тождеств.

Вот три пифагорейских тождества. Каждая идентичность может быть записана альтернативными способами, как показано.

Пифагорейская идентичность	Альтернативные способы
sin ² θ + cos ² θ = 1	1 — sin ² θ = cos ² θ (или) 1 — cos ² θ = sin ² θ
сек ² θ — рыжевато-коричневый ² θ = 1	1 + тангенс ² θ = сек ² θ (или) сек ² θ — 1 = тангенс ² θ
csc ² θ — детская кроватка ² θ = 1	1 + детская кроватка ² θ = csc ² θ (или) csc ² θ — 1 = детская кроватка ² θ

Как доказать пифагорейские тождества в тригонометрии?

Для доказательства пифагорейских тождеств воспользуемся теоремой Пифагора.

Например, если ABC — прямоугольный треугольник с прямым углом в точке B, а x — угол в точке A, то:

AB ² + BC ² = AC ² … (1)
Разделив обе стороны на AC ² ,
(АВ/АС) ² + (ВС/АС) ² = 1
sin ² x + cos ² x = 1

Точно так же, разделив обе части (1) на AB ² и BC ² , мы можем получить два других пифагорейских тождества.

Что такое Пифагорейский список тождеств?

Вот список пифагорейских тождеств:

sin ² x + cos ² x = 1
1 + тангенс ² x = сек ² х
1 + детская кроватка ² x = csc ² x

Сколько у нас пифагорейских идентичностей?

У нас есть 3 тождества Пифагора в тригонометрии. Они следующие:

sin ² θ + cos ² θ = 1
сек ² θ — загар ² θ = 1
csc ² θ — детская кроватка ² θ = 1

Как вы используете пифагорейские тождества?

Тождества Пифагора используются для доказательства других тригонометрических тождеств, нахождения значения тригонометрического отношения с использованием любого другого тригонометрического отношения и для решения задач, связанных с высотами и расстояниями.