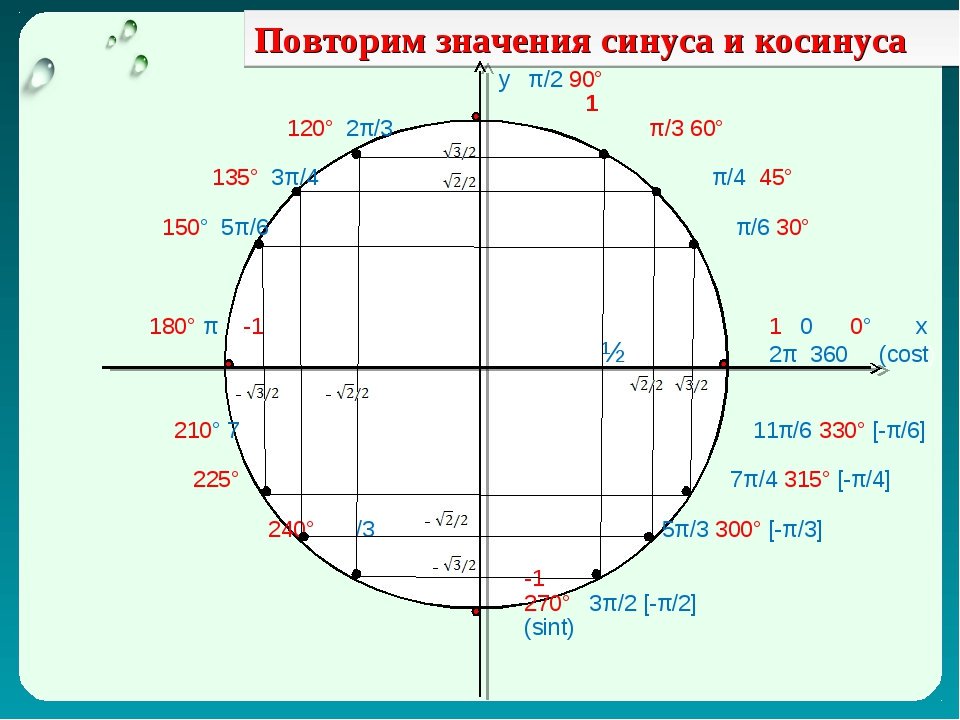
| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | cos(pi/4) | ||
| 9 | Найти точное значение | sin(45 град. ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) | |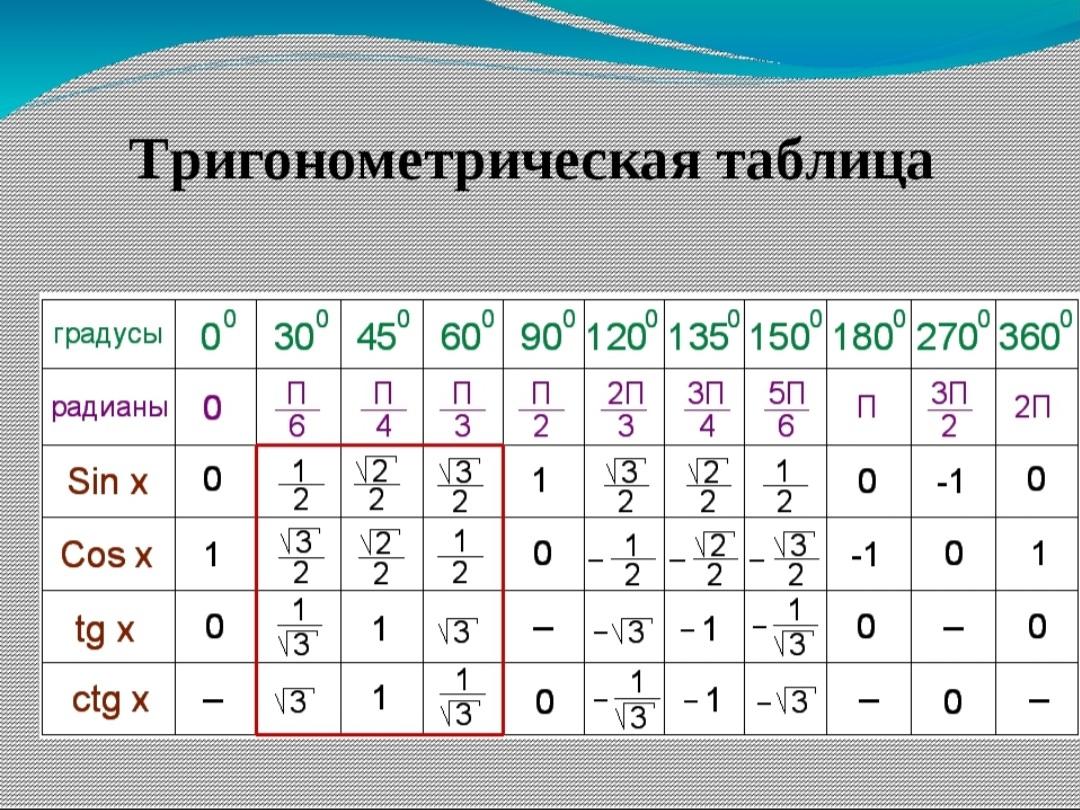
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) | |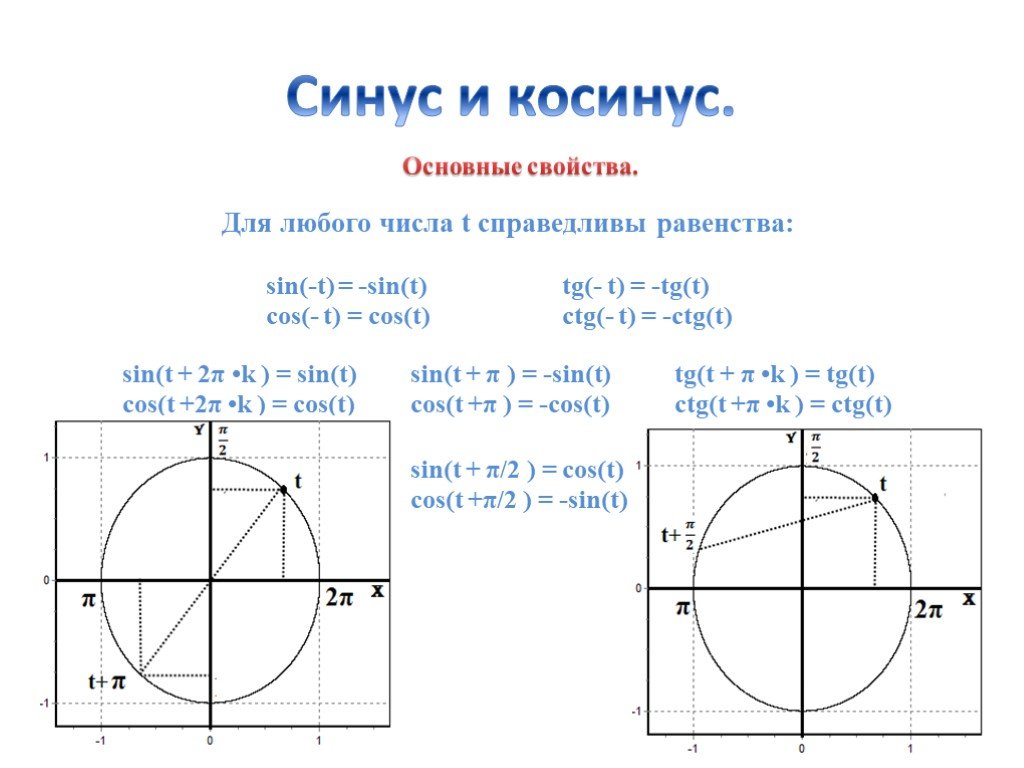
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) | |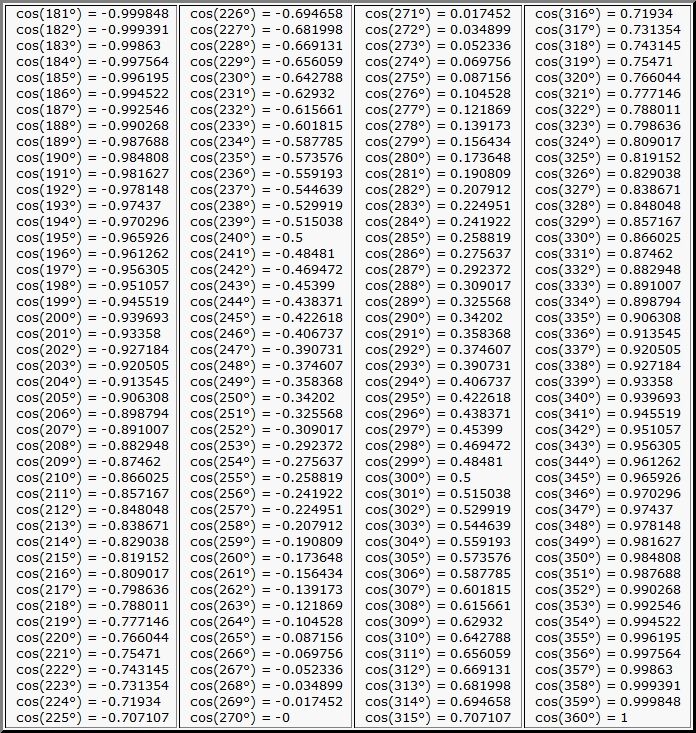
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град. ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
Как найти синус от арксинуса, косинус от арккосинуса, синус от арккосинуса, косинус от арксинуса
12+7 месяцев назад
Проголосовать за видео
Математика от Баканчиковой323 подписчика
Тригонометрия 8-11 класс.
Как решать нестандартные задачи по обратным тригонометрическим функциям? Как найти синус от арксинуса, косинус от арккосинуса, синус от арккосинуса, косинус от арксинуса? Сегодня мы ответим на эти вопросы. Если Вы не видели наши предыдущие уроки по теме «Функция y=arcsin x, y=arccos x, y=arctg x, y=arcctg x, их графики и свойства», то обязательно посмотрите их, тогда этот урок будет Вам очень понятен. Мы покажем Вам, чему равны синус от арксинуса и косинус от арккосинуса. Научим Вас находить синус от арккосинуса, косинус от арксинуса. Для закрепления материала мы предложим Вам небольшое домашнее задание. Подробный план урока и ссылки на предыдущие уроки Вы можете найти в описании под видео.
00:00 Начало видео.
00:54 Как вычислить sin (arcsin 1/2) и cos (arccos 1/2)?
03:06 Как вычислить sin (arccos 2/7)?
07:09 Как вычислить cos (arcsin (-3/4))?
09:21 Домашнее задание.
Если Вы впервые на нашем канале или не смотрели наши предыдущие уроки, то рекомендуем Вам посмотреть следующие видео:
Чётность и нечётность обратных тригонометрических функций.
ru/plst/57182
#обратныетригонометрическиефункции #чётностьобратныхтригонометрическихфункций #нечётностьобратныхтригонометрическихфункций #синусотарксинуса #косинусотарккосинуса #тангенсотарктангенса #котангенсотарккотангенса #sinarcsin #cosarccos #tgarctg #ctgarcctg #cosarcsin #sinarccos #тригонометрическиефункцииалгебра10 #МатематикаОтБаканчиковой
тригонометрия, алгебра тригонометрические функции, тригонометрические функции алгебра 10, обратные тригонометрические функции, синус от арксинуса, косинус от арккосинуса, тангенс от арктангенса, котангенс от арккотангенса, sin arcsin, cos arccos, tg arctg, ctg arcctg, cos arcsin, sin arcosКак найти косинус угла
Все математические ресурсы ACT
14 Диагностические тесты 767 практических тестов Вопрос дня Карточки Learn by Concept
ACT Math Help » Тригонометрия » косинус » Как найти косинус угла
Если , где и ,
то что такое ?
Возможные ответы: Правильный ответ: Объяснение: В приведенном ниже треугольнике тангенс или противоположная сторона угла, деленная на прилежащую сторону угла.
Согласно теореме Пифагора
,
Таким образом, гипотенуза равна .
Косинус угла — это прилежащая сторона угла, деленная на гипотенузу треугольника, что дает нам .
Однако, поскольку равно , и когда находится между , является положительным, а – отрицательным. Таким образом отрицательно, что дает нам окончательный ответ .
Сообщить об ошибке
Что такое cos θ?
Возможные ответы: Правильный ответ: Объяснение:cos = смежный/гипотенуза =
Чтобы получить радикал из знаменателя, умножьте:
Сообщить об ошибке линия проходящий с уклоном ? Округлить до сотых.
Возможные ответы: Правильный ответ: Объяснение: Вам даже не нужно вычислять строку для этого вопроса. Все, что вам нужно сделать, это отметить, что вы можете сделать маленький прямоугольный треугольник с высотой и основанием , который вы получите из наклона линии.
Итак, чтобы вычислить косинус, вам нужно будет найти гипотенузу по теореме Пифагора:
Итак, наш маленький треугольник выглядит так:
Косинусом будет смежная сторона, деленная на гипотенузу, :
, или приблизительно .
Сообщить об ошибке
Чему равен угол с ?
Возможные ответы: Правильный ответ: Объяснение:Поскольку синус угла равен , это означает, что противоположная сторона треугольника равна , а гипотенуза равна . Автоматически вы знаете, что это особый прямоугольный треугольник 3-4-5 и что недостающая сторона равна 3. Если нет, вы также можете найти 3-ю сторону, применив теорему Пифагора. Это дает вам ответ
Сообщить об ошибке
Прямоугольный треугольник со сторонами , и . Что такое косинус ?
Возможные ответы: Правильный ответ: Объяснение: SOHCATOA говорит нам об этом, а мы знаем, что гипотенуза — самая длинная сторона треугольника, .
Наша смежная сторона будет другой стороной, имеющей в качестве вершины .
Таким образом, .
Сообщить об ошибке
Прямоугольный треугольник со сторонами , и . Что такое косинус ?
Возможные ответы: Правильный ответ: Объяснение:SOHCATOA говорит нам об этом, а мы знаем, что гипотенуза — самая длинная сторона треугольника, . Наша смежная сторона будет другой стороной, имеющей в качестве вершины .
Таким образом, .
Сообщить об ошибке
Уведомление об авторских правах
Все математические ресурсы ACT
14 Диагностические тесты 767 практических тестов Вопрос дня Карточки Учитесь по концепции
Как вычислить косинус угла
Авторы: Ян Куанг и Эллейн Кейс и
Обновлено: 13 апреля 2017 г.
Предварительное вычисление для чайников 9 0169 Исследуйте книгу Купить на Amazon
Потому что вы тратите массу времени на предварительное исчисление, работая с тригонометрическими функциями, вам нужно понимать отношения. Одним из важных соотношений прямоугольных треугольников является косинус. косинус угла, или
определяется как отношение прилежащего катета к гипотенузе, или
Рассмотрим следующий пример: Лестница прислонена к зданию, образуя с землей угол 75 градусов. Основание лестницы находится в 3 футах от здания. Какой длины лестница? Ваше сердце просто упало, когда вы поняли, что имеете дело с . . . проблема со словом? Нет проблем! Просто выполните следующие действия, чтобы решить; здесь вы ищете длину лестницы:
Нарисуйте картинку, чтобы увидеть знакомую форму.
Одна лестница плюс одно здание равняется одной косинусной задаче.
На предыдущем рисунке изображена лестница, прислоненная к зданию.
Между зданием и землёй проходит прямой угол, потому что в противном случае здание будет искривлено и упадёт. Поскольку вы знаете, где находится прямой угол, вы знаете, что гипотенуза — это сама лестница. Данный угол направлен вниз на землю, что означает, что противоположная нога — это расстояние на здании от того места, где вершина лестницы касается ее до земли. Третья сторона, смежная ножка, представляет собой расстояние, на котором низ лестницы опирается на здание.
Составьте уравнение тригонометрии, используя информацию с картинки.
Вы знаете, что прилежащая сторона равна 3 футам, и вы ищете длину лестницы или гипотенузы. Следовательно, вы должны использовать отношение косинуса, потому что это отношение прилежащего катета к гипотенузе. У вас есть
Здание не имеет сейчас никакого отношения к этой проблеме, кроме того, что держит лестницу.
Почему вы используете 75 градусов в функции косинуса? Потому что вам сказали, что угол лестницы с землей составляет 75 градусов.
