Функції Acos, Acot, Asin, Atan, Atan2, Cos, Cot, Degrees, Pi, Radians, Sin і Tan у Power Apps — Power Platform
- Стаття
Обчислює тригонометричні значення.
Опис
Основні функції
Функція Cos повертає косинус свого аргументу, кута в радіанах.
Функція Cot повертає котангенс свого аргументу, кута в радіанах.
Функція Sin повертає синус свого аргументу, кута в радіанах.
Функція Tan повертає тангенс свого аргументу, кута в радіанах.
Обернені функції
Функція Acos повертає арккосинус, або обернений косинус, свого аргументу. Арккосинус – це кут, косинусом якого є аргумент. Кут повертається в радіанах у діапазоні від 0 (нуль) до π.
Арккосинус – це кут, косинусом якого є аргумент. Кут повертається в радіанах у діапазоні від 0 (нуль) до π.
Функція Acot повертає арифметичне значення арккотангенса, або оберненого котангенса, свого аргументу. Кут повертається в радіанах у діапазоні від 0 (нуль) до π.
Функція Asin повертає арксинус, або обернений синус, свого аргументу. Арксинус – це кут, синусом якого є аргумент. Кут повертається в радіанах у діапазоні від -π/2 to π/2.
Функція Atan повертає арктангенс, або обернений тангенс, свого аргументу. Арктангенс – це кут, тангенсом якого є аргумент. Кут повертається в радіанах у діапазоні від -π/2 to π/2.
Функція Atan2 повертає арктангенс, або обернений тангенс, заданих як аргументів координат x і y. Арктангенс – це кут від осі x до лінії, що містить вихідну точку (0, 0) і точку з координатами (x; y). Кут указується в радіанах від -π до π, виключаючи -π. Додатний результат являє собою кут проти годинникової стрілки від осі x; від’ємний результат являє собою кут за годинниковою стрілкою. Atan2(a,b) дорівнює Atan(b/a), за винятком того, що у функції Atan2a може дорівнювати 0 (нулю).
Додатний результат являє собою кут проти годинникової стрілки від осі x; від’ємний результат являє собою кут за годинниковою стрілкою. Atan2(a,b) дорівнює Atan(b/a), за винятком того, що у функції Atan2a може дорівнювати 0 (нулю).
Допоміжні функції
Функція Degrees перетворює радіани на градуси. π радіанів — це 180 градусів.
Функція Pi повертає трансцендентне число π, яке починається 3,141592…
Функція Radians перетворює градуси на радіани.
Примітки
Якщо ви надаєте цим функціям одне число, то повертається один результат. Якщо передати таблицю з одним стовпцем, яка містить числа, повернуте значення – це таблиця результатів з одним стовпцем зі стовпцемЗначення , по одному результату для кожного запису в таблиці аргументу. Якщо ваша таблиця має кілька стовпців, ви можете переробити її на таблицю з одним стовпцем, як описано в розділі Робота з таблицями.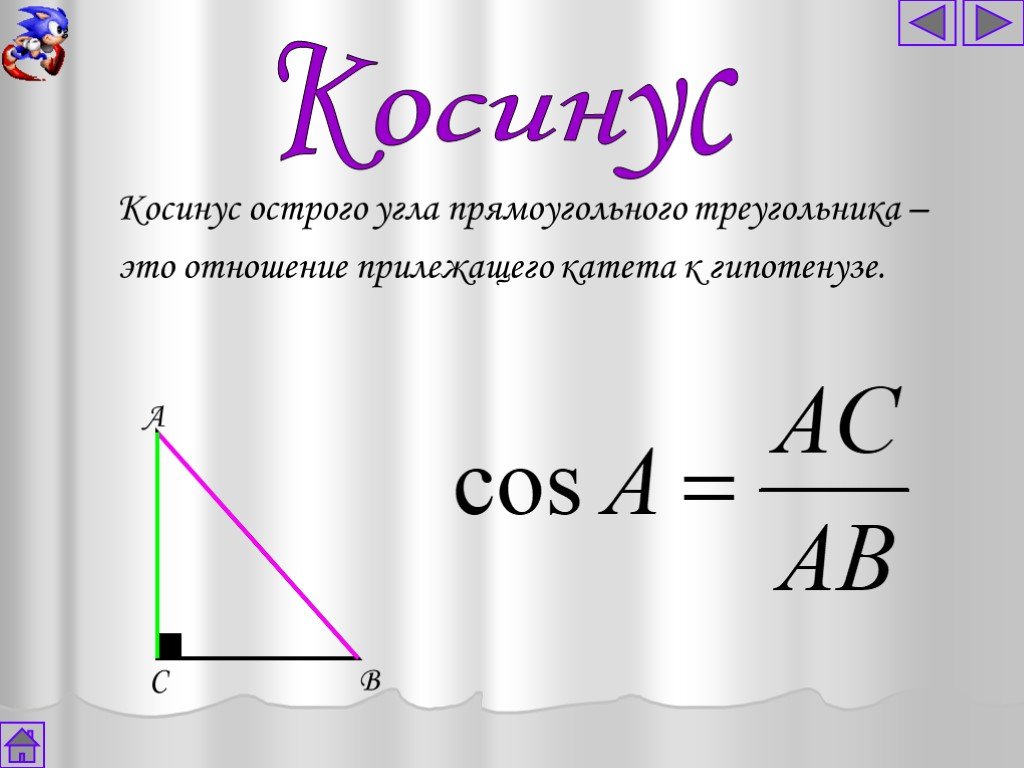
Якщо аргумент призведе до невизначеного значення, то результат буде пустим. Це може статися, наприклад, під час використання обернених функцій з аргументами поза межами діапазону.
Синтаксис
Основні функції
Cos( Radians )
Cot( Radians )
Sin( Radians )
Tan( Radians )
- Radians — обов’язковий аргумент. Це кут, для якого потрібно виконати операцію.
Cos( SingleColumnTable )
Cot( SingleColumnTable )
Sin( SingleColumnTable )
Tan( SingleColumnTable )
- SingleColumnTable — обов’язковий аргумент. Таблиця з одним стовпцем, що містить кути, для яких потрібно виконати операцію.
Обернені функції
Acos( Number )
Acot( Number )
Asin( Number )
Atan( Number )
- Number — обов’язковий аргумент.
 Це число, для якого потрібно виконати операцію.
Це число, для якого потрібно виконати операцію.
Acos( SingleColumnTable )
Acot( SingleColumnTable )
Asin( SingleColumnTable )
Atan( SingleColumnTable )
- SingleColumnTable — обов’язковий аргумент. Таблиця з одним стовпцем, що містить числа, для яких потрібно виконати операцію.
Atan2( X; Y )
- X — обов’язковий аргумент. Координата по осі X.
- Y — обов’язковий аргумент. Координата по осі Y.
Допоміжні функції
Degrees( Radians )
- Radians — обов’язковий аргумент. Кут у радіанах, який потрібно перевести в градуси.
Pi()
Radians( Degrees )
- Degrees — обов’язковий аргумент. Кут у градусах, який потрібно перевести в радіани.

Приклади
Одне число
| Формула | Опис | Результат |
|---|---|---|
| Cos( 1.047197 ) | Повертає косинус 1,047197 радіана або 60 градусів. | 0.5 |
| Cot( Pi()/4 ) | Повертає котангенс 0,785398… радіана або 45 градусів. | 1 |
| Sin( Pi()/2 ) | Повертає синус 1,570796… радіана або 90 градусів. | 1 |
| Tan( Radians(60) ) | Повертає тангенс 1,047197… радіана або 60 градусів. | 1,732050… |
| Acos( 0.5 ) | Повертає арккосинус 0,5, у радіанах. | 1,047197… |
| Acot( 1 ) | Повертає арккотангенс 1, у радіанах. | 0,785398… |
| Asin( 1 ) | Повертає арксинус 1, у радіанах. | 1,570796… |
| Atan( 1.732050 ) | Повертає арктангенс 1,732050, у радіанах. | 1,047197… |
| Atan2( 5, 3 ) | Повертає арктангенс кута від осі x до лінії, яка містить вихідну точку (0; 0) і координату (5; 3), що становить приблизно 31 градус. | 0,540419… |
| Atan2( 4, 4 ) | Повертає арктангенс кута від осі x до лінії, яка містить вихідну точку (0; 0) і координату (4; 4), що становить точно π/4 радіана або 45 градусів. | 0,785398… |
| Degrees( 1.047197 ) | Повертає еквівалентну кількість градусів для 1,047197 радіана. | 60 |
| Pi() | Повертає трансцендентне число π. | 3,141592… |
| Radians( 15 ) | Повертає еквівалентну кількість радіанів для 15 градусів. | 0,261799… |
Таблиця з одним стовпцем
Для прикладів у цьому розділі використовується джерело даних під назвою ValueTable, яке містить зазначені нижче дані. Останній запис у таблиці становить π/2 радіана або 90 градусів.
Останній запис у таблиці становить π/2 радіана або 90 градусів.
| Значення |
|---|
| 0.5 |
| -2 |
| 1,570796… |
| Формула | Опис | Результат |
|---|---|---|
| Cos( ValueTable ) | Повертає косинус кожного числа в таблиці. | Таблиця з одним стовпцем зі Value стовпцем, що містить такі значення: 0.877582…, -0.416146…, 0 |
| Cot( ValueTable ) | Повертає котангенс кожного числа в таблиці. | Таблиця з одним стовпцем зі Value стовпцем, що містить такі значення: 1.830487…, 0.457657…, 0 |
| Sin( ValueTable ) | Повертає синус кожного числа в таблиці. | Таблиця з одним стовпцем зі Value стовпцем, що містить такі значення: 0.479425, -0.909297…, 1 |
| Tan( ValueTable ) | Повертає тангенс кожного числа в таблиці. | Таблиця з одним стовпцем зі Value стовпцем, що містить такі значення: 0.546302…, 2.185039…, 3060023.306952… |
| Acos( ValueTable ) | Повертає арккосинус кожного числа в таблиці. | Таблиця з одним стовпцем зі Value стовпцем, що містить такі значення: 1.047197…, Blank(), Blank() |
| Acot( ValueTable ) | Повертає арккотангенс кожного числа в таблиці. | Таблиця з одним стовпцем зі Value стовпцем, що містить такі значення: 1.107138…, 2.677945…, 0.566911… |
| Asin( ValueTable ) | Повертає арксинус кожного числа в таблиці. | Таблиця з одним стовпцем зі Value стовпцем, що містить такі значення: 0.523598…, пусто(), пусто() |
| Atan( ValueTable ) | Повертає арктангенс кожного числа в таблиці. | Таблиця з одним стовпцем зі Value стовпцем, що містить такі значення: 0. 463647…, -1.107148…, 1.00388… 463647…, -1.107148…, 1.00388… |
| Degrees( ValueTable ) | Повертає еквівалентну кількість градусів для кожного числа в таблиці; припускається, що кути вказано в радіанах. | Таблиця з одним стовпцем зі Value стовпцем, що містить такі значення: 28.647889…, -114.591559…, 90 |
| Radians( ValueTable ) | Повертає еквівалентну кількість радіанів для кожного числа в таблиці; припускається, що кути вказано в градусах. | Таблиця з одним стовпцем зі Value стовпцем, що містить такі значення: 0.008726…, -0.034906…, 0.027415… |
2.1.5: Синус і косинус комплементарних кутів — LibreTexts
- Last updated
- Save as PDF
- Page ID
- 54668
Синус кута дорівнює косинусу його доповнення. {\circ}\) і\(\sin A=k\). Що таке\(\cos B\)?
{\circ}\) і\(\sin A=k\). Що таке\(\cos B\)?
Синус і
косинус комплементарних кутівНагадаємо, що синус і косинус кутів — це співвідношення пар сторін в прямих трикутниках.
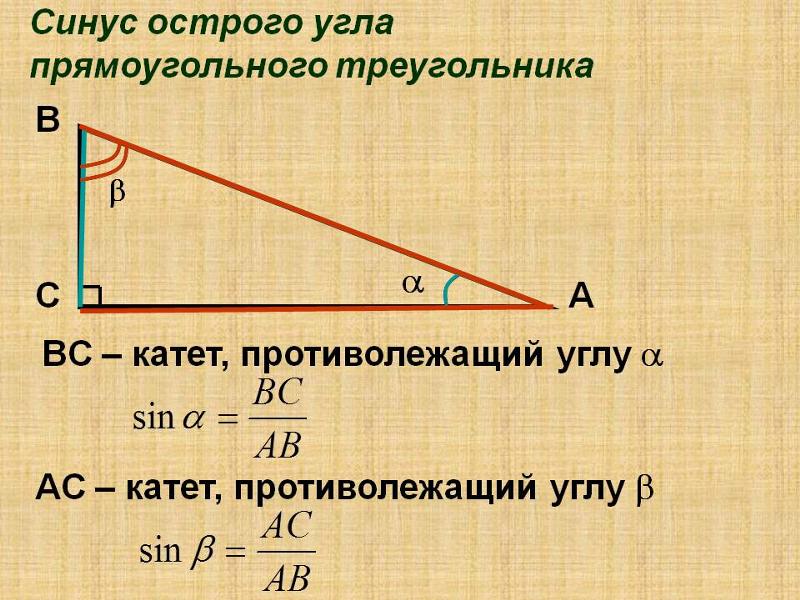
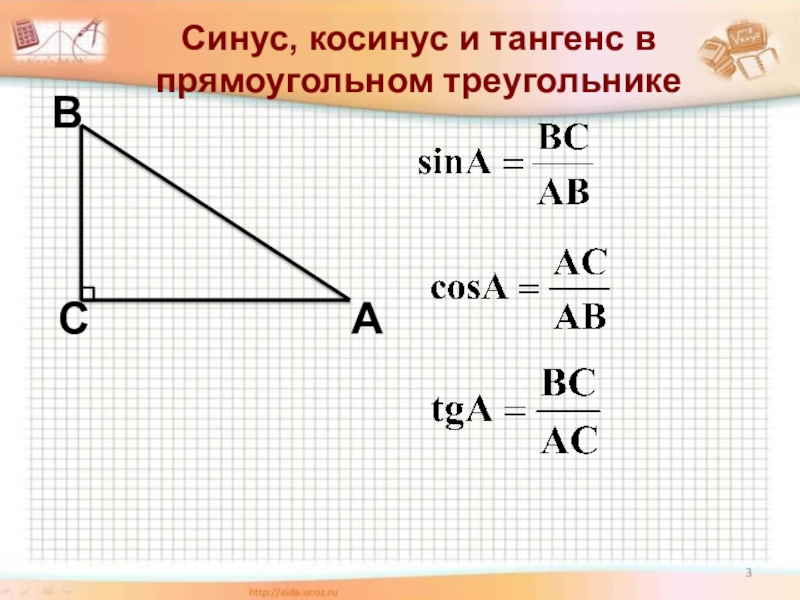
- Синус кута в прямокутному трикутнику — це відношення сторони, протилежної куту, до гіпотенузи.
- Косинус кута в прямокутному трикутнику — це відношення сторони, прилеглої до кута, до гіпотенузи.
У наведених нижче задачах ви вивчите, як пов’язані синус і косинус кутів у прямокутному трикутнику.
Давайте розглянемо кілька прикладів проблем.
1. Розглянемо прямокутний трикутник нижче. Знайти синус і косинус кутів A і B через a, b і c Що ви помітили?
Малюнок\(\PageIndex{1}\)\(\sin A=\dfrac{a}{c}\),\(\sin B=\dfrac{b}{c}\)\(\cos A=\dfrac{b}{c}\),\(\cos B=\dfrac{a}{c}\) Зверніть увагу, що\(\sin A=\cos B\) і\(\sin B=\cos A\). {\circ}=\dfrac{1}{2}\).
{\circ}=\dfrac{1}{2}\).
Приклад\(\PageIndex{3}\)
Розглянемо прямокутний трикутник нижче. Знайти\(\tan A\) і\(\tan B\).
Малюнок\(\PageIndex{3}\)Рішення
\(\tan A=\dfrac{a}{b}\)і\(\tan B=\dfrac{b}{a}\).
Приклад\(\PageIndex{4}\)
Загалом, яка залежність між дотичними доповнюють кутів?
Рішення
Взагалі, тангенси взаємодоповнюючих кутів є взаємними.
Рецензія
1. Як пов’язані два непрямі кути в прямокутному трикутнику? Поясніть.
2. Як пов’язані синус і косинус взаємодоповнюючих кутів? Поясніть.
3. Як пов’язані тангенси взаємодоповнюючих кутів? Поясніть.
Нехай A і B бути два непрямі кути в прямокутний трикутник.
4. Якщо\(\tan A=\dfrac{1}{2}\), що таке\(\tan B\)?
5. Якщо\(\sin A=\dfrac{7}{10}\), що таке\(\cos B\)?
6. Якщо\(\cos A=\dfrac{1}{4}\) що таке\(\sin B\)?
7. Якщо\(\sin A=\dfrac{3}{5}\),\(\cos \stackrel?{=} \dfrac{3}{5}\)?
8. Спростити\(\dfrac{\sin A+\cos B}{2}\). {\circ}\).
{\circ}\).
Додаткові ресурси
Інтерактивний елемент
Практика: Синус і косинус комплементарних кутів
- Back to top
- Was this article helpful?
- Article type
- Section or Page
- License
- CK-12
- Show Page TOC
- No on Page
- Tags
- authorname:ck12
- program:ck12
- source@https://www.
 ck12.org/c/trigonometry
ck12.org/c/trigonometry - source[translate]-k12-4216
Cos (a — b) — Формула, Доказательство, Примеры | Что такое Cos(a
) В тригонометрии cos(a — b) является одним из важных тригонометрических тождеств, которое находит применение при нахождении значения тригонометрической функции косинуса для разности углов. Разложение cos(a — b) ) помогает в представлении cos составного угла в терминах тригонометрических функций синуса и косинуса.Давайте разберемся в тождестве cos(a-b) и его доказательстве подробно в следующих разделах.
| 1. | Что такое тождество Cos(a — b) в тригонометрии? |
| 2. | Cos(a — b) Формула составного угла |
| 3. | Доказательство формулы Cos(a — b) |
| 4. | Как применить Cos(a — b)? |
5. | Часто задаваемые вопросы по Cos(a — b) |
Что такое тождество Cos(a — b) в тригонометрии?
Cos (a — b) является тригонометрическим тождеством для составных углов. Применим формулу тождества косинуса (a-b), когда угол, для которого нужно вычислить значение функции косинуса, задан в виде разности углов. Угол (a-b) представляет собой составной угол.
cos(a — b) Формула составного угла
Мы называем формулу cos(a — b) формулой вычитания в тригонометрии. Формула cos(a — b) для составного угла (a-b) может быть представлена как
cos (a — b) = cos a cos b + sin a sin b
Доказательство формулы Cos(a — b)
Доказательство разложения формулы cos(a-b) может быть дано методом геометрического построения. Рассмотрим пошаговый вывод формулы косинуса тригонометрической функции разности двух углов. В геометрическом доказательстве формулы cos (a-b) мы изначально предполагаем, что «a» и «b» — положительные острые углы, так что угол a > угла b. Эта формула, вообще говоря, верна для любых положительных или отрицательных значений a и b.
Эта формула, вообще говоря, верна для любых положительных или отрицательных значений a и b.
Чтобы доказать: cos (a — b) = cos a cos b + sin a sin b
Построение: Нарисуйте линию OX на плоскости и поверните ее вокруг O против часовой стрелки, чтобы точка Z, образующая острую ∠XOZ = a, от начального положения до его конечного положения. Снова поверните линию, на этот раз в обратном направлении, начиная с положения OZ, пока она не достигнет точки Y, образуя таким образом острый угол, заданный как ∠ZOY = b. Следовательно, ∠XOY = a — b.
Затем возьмите точку P на OY и проведите перпендикуляры PQ и PR к OX и OZ соответственно. Проведите перпендикуляры RS и RT из точки R на OX и PQ соответственно.
Теперь из прямоугольного треугольника PQO получаем
cos (a — b) = OQ/OP
= (ОС+КВ)/OP
= ОС/ОП + КВ/ОП
= ОС/ОП + ТР/ОП
= ОС/ИЛИ ∙ ИЛИ/ОП + ТР/ПР ∙ ПР/ОП
= cos a cos b + sin ∠TPR sin b
= cos a cos b + sin a sin b, (так как мы знаем, ∠TPR = a)
Следовательно, cos ( a — b) = cos a cos b + sin a sin б.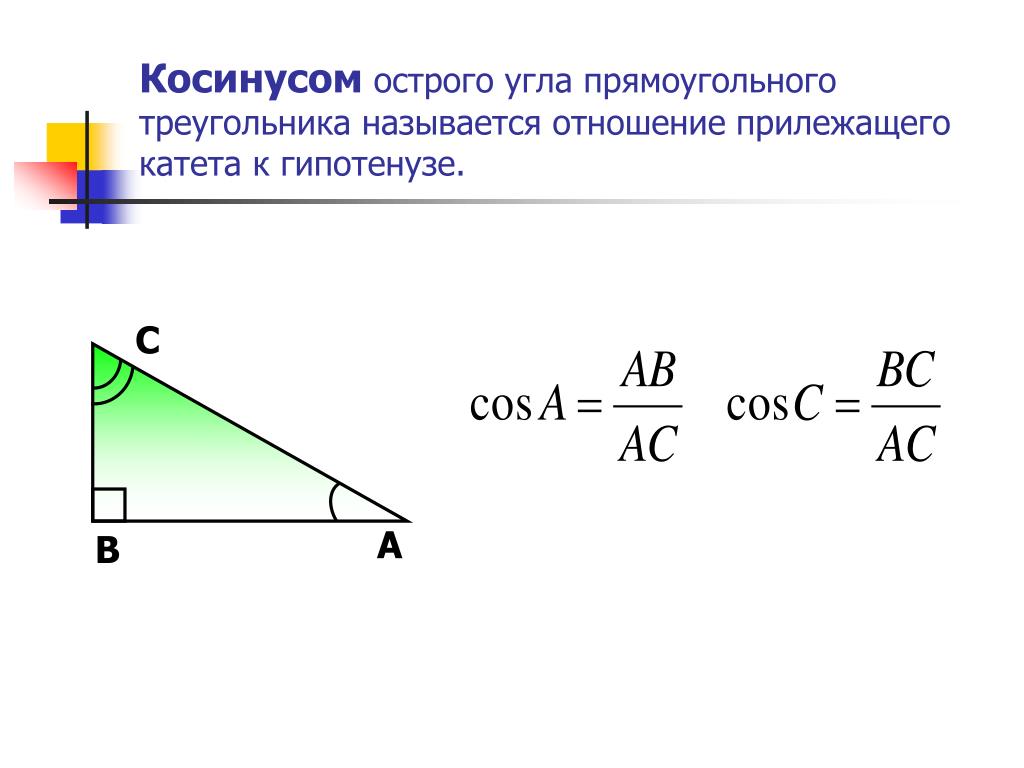
Как применить Cos(a — b)?
Разложение cos(a — b) можно использовать для нахождения значения тригонометрической функции косинуса для углов, которые можно представить как разность стандартных углов в тригонометрии. Мы можем выполнить шаги, указанные ниже, чтобы научиться применять идентичность cos (a — b). Давайте оценим cos(90º — 30º), чтобы лучше понять это.
- Шаг 1: Сравните выражение cos(a — b) с данным выражением, чтобы определить углы ‘a’ и ‘b’. Здесь а = 90º и b = 30º.
- Шаг 2: Мы знаем, cos (a — b) = cos a cos b + sin a sin b.
⇒ cos(90º — 30º) = cos 90ºcos 30º + sin 90ºsin 30º
поскольку sin 90º = 1, sin 30º = 1/2, cos 90º = 0, cos 30º = √3/2
⇒ cos(90º — 30º) = (0)(√3/2) + (1)(1/2) = 0 + 1/2 = 1/2
Также мы знаем, что cos 60º = 1/2. Поэтому результат проверен.
Давайте рассмотрим несколько решенных примеров, чтобы лучше понять формулу cos(a-b).
Часто задаваемые вопросы по Cos(a — b)
Что такое Cos(a-b)?
Cos(a — b) — одно из важных тригонометрических тождеств, также называемое формулой вычитания косинуса в тригонометрии. Cos(a-b) можно представить как cos(a — b) = cos a cos b + sin a sin b, где «a» и «b» — углы.
Что такое формула Cos(a-b)?
Формула cos(a-b) используется для выражения формулы косинуса составного угла через синус и косинус отдельных углов. Формула тригонометрии cos (a-b) может быть представлена как cos (a — b) = cos a cos b + sin a sin b.
Что такое расширение cos(a-b)
Расширение cos(a-b) задается как cos (a — b) = cos a cos b + sin a sin b. Здесь a и b — меры углов.
Как доказать формулу Cos(a-b)?
Доказательство формулы cos(a-b) может быть дано методом геометрического построения. Сначала мы предполагаем, что a и b — положительные острые углы, так что a > b. Нажмите здесь, чтобы понять пошаговый метод получения формулы cos(a-b).
Каковы применения формулы Cos(a-b)?
cos(a-b) можно использовать для нахождения значения функции косинуса для углов, которые можно представить как разность стандартных или более простых углов. Таким образом, это упрощает вычет. Его также можно использовать для нахождения расширения других формул двойного и кратного угла.
Как найти значение Cos 30º, используя тождество Cos (a — b).
Значение cos 30º с использованием тождества cos(a — b) можно вычислить, сначала записав его как cos[(90º — 60º)], а затем применив тождество cos(a — b).
⇒cos[(90º — 60º)] = cos 90ºcos 60º + sin 90ºsin 60º = (0)(1/2) + (1)(√3/2) = 0 + (√3/2) = √3/2 .
Как найти Cos(a + b — c), используя Cos(a — b)?
Мы можем выразить cos(a+b-c) как cos((a+b)-c) и расширить с помощью формул cos(a-b), cos(a+b) и sin(a+b) как, cos(a+ b-c) = cos(a+b).cos c + sin(a+b).sin c = cos c.(cos a cos b — sin a sin b) + sin c.(sin a cos b + cos sin б) = cos a cos b cos c — sin a sin b cos c + sin a cos b sin c + cos a sin b sin c.
Правило косинусов (закон косинусов)
Патрик Энгельманн, Алекс Г, Мэй Ли, и способствовалСодержимое
- Формулировка и доказательство теоремы
- Нахождение недостающих длин сторон и углов
- Приложения к задачам пеленга и курса
- Векторная форма правила косинуса
- Вывод других законов с помощью правила косинусов
- Решение проблем
- Смотрите также
92 — 3 \sqrt{2} \lvert \overline{AC} \rvert + 4 &=0 \\
\left(\lvert \overline{AC} \rvert-\sqrt{2}\right)\left(\lvert \overline{AC} \rvert-2\sqrt{2}\right)&=0.
 \конец{выравнивание}\]
\конец{выравнивание}\]Следовательно, \( \lvert \overline{AC} \rvert=\sqrt{2} \text{ или } 2\sqrt{2}\). \( _\квадрат \)
Примечание. Это похоже на «неоднозначный случай» правила синусов, поскольку мы имеем \( 3 \sin \frac {\pi}{4} < \sqrt{5} < 3\), что является условием \( с \sin \alpha < a < c \).
\[\sqrt{7}\] \[5\] \[2\sqrt{7}\] \[5\sqrt{5}\] 92 — 2\cdot 2\sqrt3 \cdot \big(\sqrt{6} — \sqrt{2}\big) \cdot \cos {\angle ABC}\\\\ 8 &= 6 — 4\sqrt{3} + 2 + 12 — \big(12\sqrt{2} — 4\sqrt{6}\big)\cos{\angle ABC}\\\\ -12 +4\sqrt{3} &= (-12\sqrt{2}+4\sqrt{6})\cos{\угол ABC}\\\\ \cos{\угол ABC} &=\dfrac{-12 +4\sqrt{3}}{-12\sqrt{2}+4\sqrt{6}} \\\\ &=\dfrac{1}{\sqrt2} \cdot \dfrac {-12 +4\sqrt{3}}{-12+4\sqrt{3}} =\dfrac{\sqrt2}{2}\\\\ \стрелка вправо \угол ABC &= \dfrac{\pi}{4}.\ _\квадрат \конец{выравнивание}\]
Попробуйте решить следующую задачу: 92\big).


 Це число, для якого потрібно виконати операцію.
Це число, для якого потрібно виконати операцію.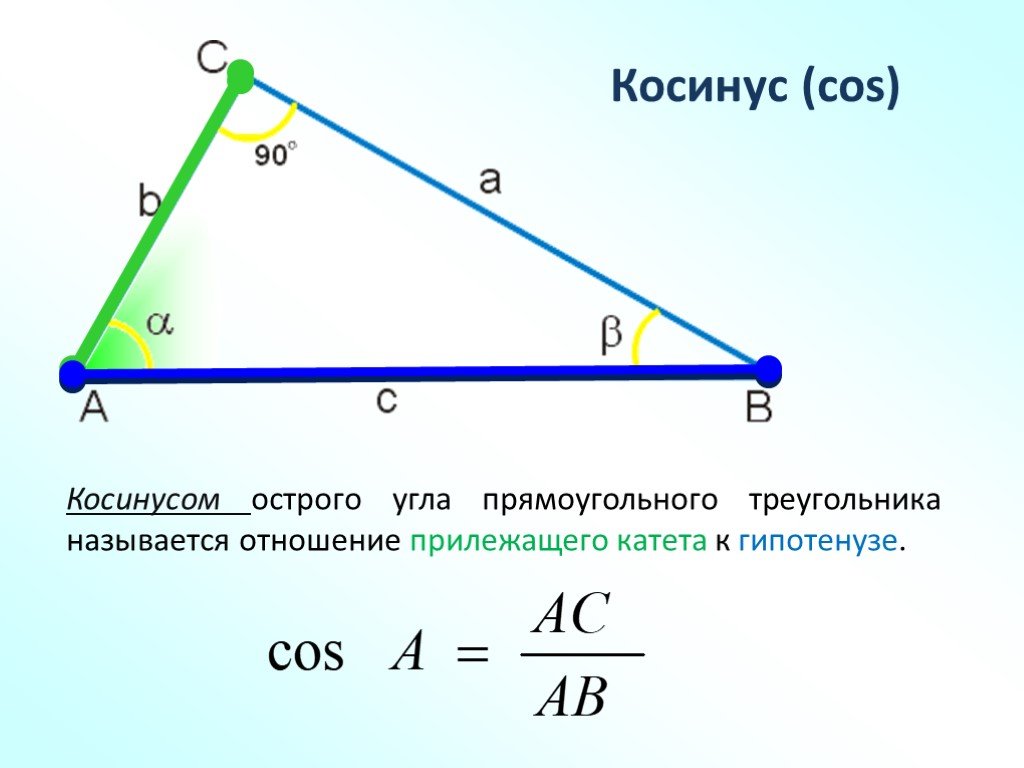
 ck12.org/c/trigonometry
ck12.org/c/trigonometry \конец{выравнивание}\]
\конец{выравнивание}\]