| \begin{align} \text{угол} \end{align} | \begin{align} 0 \end{align} | \begin{align} \frac{\pi}{6} \end{align} | \begin{align} \frac{\pi}{4} \end{align} | \begin{align} \frac{\pi}{3} \end{align} | \begin{align} \frac{\pi}{2} \end{align} | \begin{align} \frac{2\pi}{3} \end{align} | \begin{align} \frac{3\pi}{4} \end{align} | \begin{align} \frac{5\pi}{6} \end{align} | \begin{align} \pi \end{align} |
|---|---|---|---|---|---|---|---|---|---|
| \begin{align} \sin{x} \end{align} | \begin{align} \frac{\sqrt{0}}{2} \end{align} | \begin{align} \frac{\sqrt{1}}{2} \end{align} | \begin{align} \frac{\sqrt{2}}{2} \end{align} | \begin{align} \frac{\sqrt{4}}{2} \end{align} | \begin{align} \frac{\sqrt{3}}{2} \end{align} | \begin{align} \frac{\sqrt{2}}{2} \end{align} | \begin{align} \frac{\sqrt{1}}{2} \end{align} | \begin{align} \frac{\sqrt{0}}{2} \end{align} | |
| \begin{align} \cos{x} \end{align} | \begin{align} \frac{\sqrt{4}}{2} \end{align} | \begin{align} \frac{\sqrt{3}}{2} \end{align} | \begin{align} \frac{\sqrt{2}}{2} \end{align} | \begin{align} \frac{\sqrt{1}}{2} \end{align} | \begin{align} \frac{\sqrt{0}}{2} \end{align} | \begin{align} -\frac{\sqrt{1}}{2} \end{align} | \begin{align} -\frac{\sqrt{2}}{2} \end{align} | \begin{align} -\frac{\sqrt{3}}{2} \end{align} | \begin{align} -\frac{\sqrt{4}}{2} \end{align} |
| \begin{align} \text{tg x} \end{align} | \begin{align} \sqrt{\frac{0}{4}} \end{align} | \begin{align} \sqrt{\frac{1}{3}} \end{align} | \begin{align} \sqrt{\frac{2}{2}} \end{align} | \begin{align} \sqrt{\frac{3}{1}} \end{align} | \begin{align} \varnothing \end{align} | \begin{align} -\sqrt{\frac{3}{1}} \end{align} | \begin{align} -\sqrt{\frac{2}{2}} \end{align} | \begin{align} -\sqrt{\frac{1}{3}} \end{align} | \begin{align} -\sqrt{\frac{0}{4}} \end{align} |
| \begin{align} \text{ctg x} \end{align} | \begin{align} \varnothing \end{align} | \begin{align} \sqrt{\frac{3}{1}} \end{align} | \begin{align} \sqrt{\frac{2}{2}} \end{align} | \begin{align} \sqrt{\frac{1}{3}} \end{align} | \begin{align} 0 \end{align} | \begin{align} -\sqrt{\frac{1}{3}} \end{align} | \begin{align} -\sqrt{\frac{2}{2}} \end{align} | \begin{align} -\sqrt{\frac{3}{1}} \end{align} | \begin{align} \varnothing \end{align} |
| \begin{align} \text{cosec x} \end{align} | \begin{align} \varnothing \end{align} | \begin{align} \frac{2}{\sqrt{1}} \end{align} | \begin{align} \frac{2}{\sqrt{2}} \end{align} | \begin{align} \frac{2}{\sqrt{3}} \end{align} | \begin{align} \frac{2}{\sqrt{4}} \end{align} | \begin{align} \frac{2}{\sqrt{3}} \end{align} | \begin{align} \frac{2}{\sqrt{2}} \end{align} | \begin{align} \frac{2}{\sqrt{1}} \end{align} | \begin{align} \varnothing \end{align} |
| \begin{align} \sec{x} \end{align} | \begin{align} \frac{2}{\sqrt{4}} \end{align} | \begin{align} \frac{2}{\sqrt{3}} \end{align} | \begin{align} \frac{2}{\sqrt{2}} \end{align} | \begin{align} \frac{2}{\sqrt{1}} \end{align} | \begin{align} \varnothing \end{align} | \begin{align} -\frac{2}{\sqrt{1}} \end{align} | \begin{align} -\frac{2}{\sqrt{2}} \end{align} | \begin{align} -\frac{2}{\sqrt{3}} \end{align} | \begin{align} -\frac{2}{\sqrt{4}} \end{align} |
Тангенс и котангенс 10 класс онлайн-подготовка на Ростелеком Лицей
Тема: Тригонометрические функции
Урок: Тангенс и котангенс
1.
 Тема урока, введение
Тема урока, введение
На предыдущем уроке мы вспомнили определение синуса и косинуса. Дадим определение тангенса и котангенса.
2. Определение тангенса и котангенса
Рассмотрим числовую окружность в координатной плоскости. Дано произвольное число Ему соответствует единственная точка на окружности. У точки есть две координаты (рис. 1).
Координату назвали косинусом числа координату синусом числа
Тангенсом числа называется отношение синуса к косинусу Котангенсом называется отношение косинуса к синусу .
Определим связь между тангенсом и котангенсом.
Линии синусов и косинусов – это координатные оси. Линией тангенсов является касательная к окружности в точке A, параллельная оси y, линией котангенсов – касательная в точке B, параллельная оси x (рис. 2).
3. Значения тангенса и котангенса основных точек, геометрическая интерпретация
Вычислим тангенсы и котангенсы основных углов.
|
|
|||||
| 1 | |||||
|
1 |
0 |
Значения тангенса и котангенса угла найдем из прямоугольного равнобедренного треугольника (рис.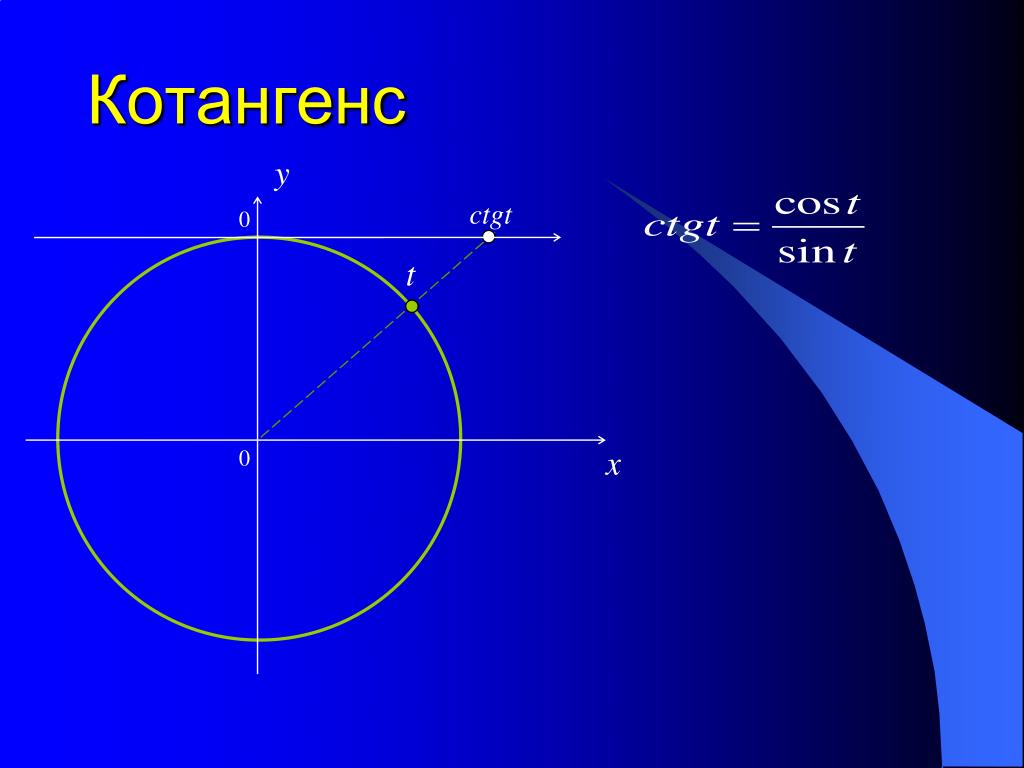 3):
3):
Изобразим полученные значения тангенсов на числовой окружности (рис. 4).
4. Решение задач
Пример 1. Найти
Решение (рис. 5).
Пример 2. Решить уравнение
Решение:
Найдем на линии тангенсов точку проведём прямую через эту точку и начало координат и получим две точки пересечения с окружностью – (рис. 6).
Ответ:
Пример 3. Решить уравнение
Решение (рис. 7).
Ответ:
5. Вывод, заключение
Мы рассмотрели функции тангенса и котангенса, стандартные задачи, составили таблицу значений тангенса и котангенса, решили простейшие тригонометрические уравнения. Решение тригонометрических уравнений продолжится и на следующем уроке.
Список литературы
1. Алгебра и начала анализа, 10 класс (в двух частях). Учебник для общеобразовательных учреждений (профильный уровень) под ред.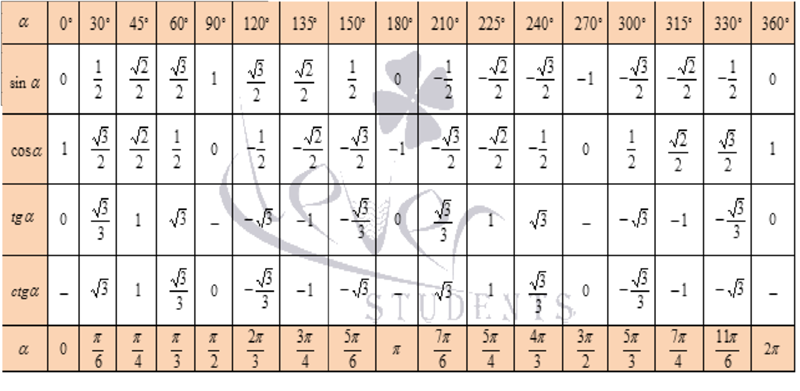 А. Г. Мордковича. –М.: Мнемозина, 2009.
А. Г. Мордковича. –М.: Мнемозина, 2009.
2. Алгебра и начала анализа, 10 класс (в двух частях). Задачник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2007.
3. Виленкин Н.Я., Ивашев-Мусатов О.С., Шварцбурд С.И. Алгебра и математический анализ для 10 класса (учебное пособие для учащихся школ и классов с углубленным изучением математики).-М.: Просвещение, 1996.
4. Галицкий М.Л., Мошкович М.М., Шварцбурд С.И. Углубленное изучение алгебры и математического анализа.-М.: Просвещение, 1997.
5. Сборник задач по математике для поступающих во ВТУЗы (под ред. М.И.Сканави).-М.:Высшая школа, 1992.
6. Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебраический тренажер.-К.: А.С.К., 1997.
7. Саакян С.М., Гольдман А.М., Денисов Д.В. Задачи по алгебре и началам анализа (пособие для учащихся 10-11 классов общеобразов. учреждений).-М.: Просвещение, 2003.
8. Карп А.П. Сборник задач по алгебре и началам анализа : учеб. пособие для 10-11 кл. с углубл. изуч. математики.-М.: Просвещение, 2006.
пособие для 10-11 кл. с углубл. изуч. математики.-М.: Просвещение, 2006.
Домашнее задание
Алгебра и начала анализа, 10 класс (в двух частях). Задачник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2007.
№№ 13.7 – 13.10.
Дополнительные веб-ресурсы
1. Математика (Источник).
2. Интернет-портал Problems.ru (Источник).
3. Образовательный портал для подготовки к экзаменам (Источник).
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктан(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | 92|||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктан(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт.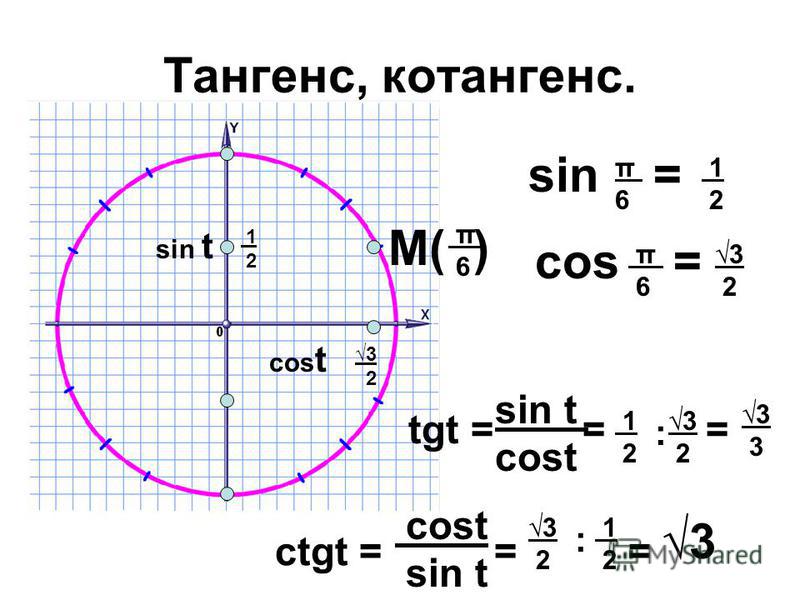 )/3 )/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | тан(пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | соз(30) | |
| 47 | Найти точное значение | соз(60) | |
| 48 | Найти точное значение | соз(0) | |
| 49 | Найти точное значение | соз(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | сек(60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найти точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | загар((5pi)/3) | |
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 пи)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | угловой синус(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | КСК(45) | |
| 83 | Упростить | арктан(квадратный корень из 3) | |
| 84 | Найти точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найти точное значение | грех(150 градусов) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | загар((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найти точное значение | грех(пи/2) | |
| 91 | Найти точное значение | сек(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | угловой синус(0) | |
| 95 | Найти точное значение | грех(120 градусов) | |
| 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найти точное значение | соз(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
| 6 | Решить для ? | cos(x)=1/2 | ||
| 7 | Найти x | sin(x)=-1/2 | ||
| 8 | Преобразование градусов в радианы | 225 | ||
| 9 | Решить для ? | cos(x)=(квадратный корень из 2)/2 | ||
| 10 | Найти x | cos(x)=(квадратный корень из 3)/2 | ||
| 11 | Найти x | sin(x)=(квадратный корень из 3)/2 | 92=9 | |
| 14 | Преобразование градусов в радианы | 120 градусов | ||
| 15 | Преобразование градусов в радианы | 180 | ||
| 16 | Найти точное значение | желтовато-коричневый(195) | 92-4||
| 38 | Найти точное значение | грех(255) | ||
| 39 | Оценить | лог база 27 из 36 | ||
| 40 | Преобразовать из радианов в градусы | 2 шт. |
