Котангенс х график: Функция y = ctgx и её свойства — урок. Алгебра, 10 класс.

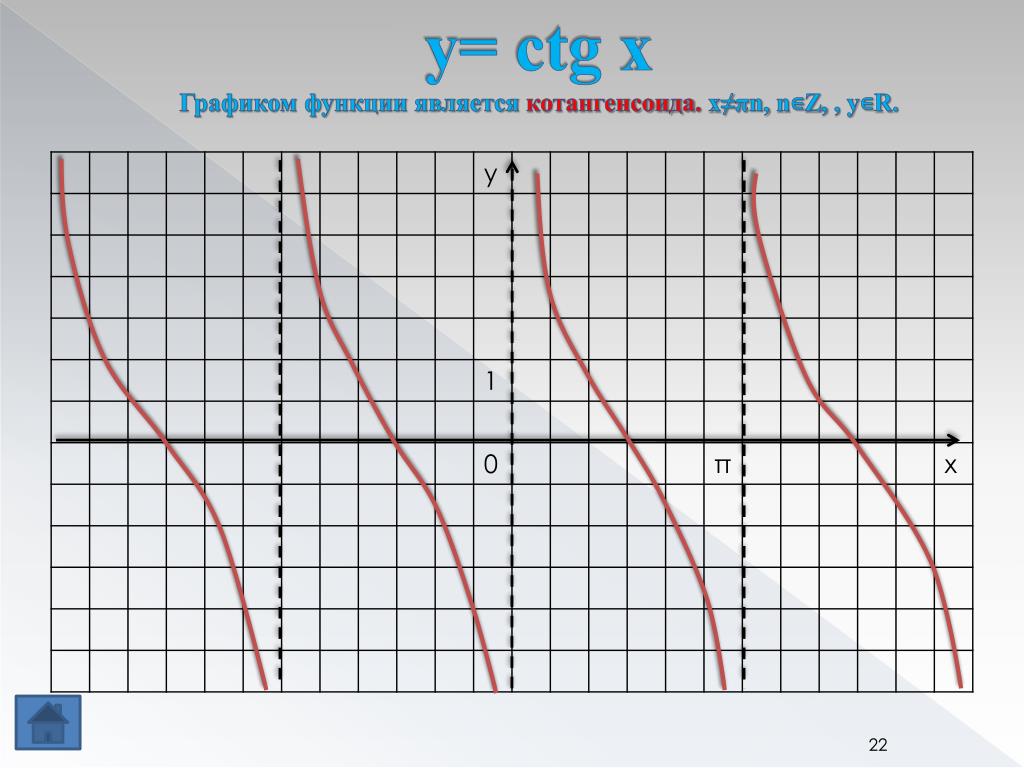
10 класс. Алгебра. Тригонометрические функции. Модификация графиков. Функции y=tg x, y=ctg x. — Функция y=сtgx, ее свойства и график.

Комментарии преподавателя

Функ­ция y=ctgt, её свой­ства и гра­фик

За­да­дим един­ствен­ное число  Каж­до­му дей­стви­тель­но­му числу  со­от­вет­ству­ет един­ствен­ная точка  на чис­ло­вой окруж­но­сти (рис. 1). Точка  имеет абс­цис­су и ор­ди­на­ту, абс­цис­су на­зы­ва­ют ко­си­ну­сом числа  ор­ди­на­ту – си­ну­сом числа  От­но­ше­ние ко­си­ну­са к си­ну­су на­зы­ва­ет­ся ко­тан­ген­сом числа 

Каж­до­му до­пу­сти­мо­му зна­че­нию  со­от­вет­ству­ет един­ствен­ная точка на окруж­но­сти, един­ствен­ная пара её ко­ор­ди­нат, а зна­чит и един­ствен­ное зна­че­ние дроби  т.е. един­ствен­ное зна­че­ние ко­тан­ген­са Таким об­ра­зом, за­да­ёт­ся функ­ция  или 

Ар­гу­мен­том функ­ции ко­тан­генс может быть число  или угол . Вспом­ним связь между чис­ло­вым и уг­ло­вым ар­гу­мен­та­ми.

Ра­ди­а­ном на­зы­ва­ет­ся такой цен­траль­ный угол, длина дуги ко­то­ро­го равна  (рис. 2).

В окруж­но­сти  штук ра­ди­ан.

Если  то 

Если есть угол  и окруж­ность ра­ди­у­са 1, то длина этой дуги или ар­гу­мент  свя­за­ны с  сле­ду­ю­щим об­ра­зом:

Как опре­де­лить зна­че­ния ко­тан­ген­са для кон­крет­ных зна­че­ний чис­ло­во­го или уг­ло­во­го ар­гу­мен­та? Они рас­по­ло­же­ны на линии ко­тан­ген­сов – ка­са­тель­ной к окруж­но­сти в точке B (рис. 3).

Возь­мем ар­гу­мент  или угол  Ар­гу­мен­ту  или углу в ра­ди­а­нах со­от­вет­ству­ют синус и ко­си­нус. Рас­смот­рим 

Изоб­ра­зим гра­фик функ­ции  в ко­ор­ди­нат­ной плос­ко­сти. По фор­му­лам при­ве­де­ния  По­это­му для по­стро­е­ния гра­фи­ка функ­ции до­ста­точ­но гра­фик функ­ции  сим­мет­рич­но отоб­ра­зить от­но­си­тель­но оси х и сдви­нуть вдоль оси х на  влево (рис. 4).

Ис­сле­ду­ем гра­фик функ­ции 

1) Об­ласть опре­де­ле­ния: 

2) Об­ласть зна­че­ний:

a) Каж­до­му до­пу­сти­мо­му  со­от­вет­ству­ет един­ствен­ное зна­че­ние 

b) Любой  до­сти­га­ет­ся при одном либо несколь­ких зна­че­ни­ях 

3) Функ­ция нечет­на:

Гра­фик сим­мет­ри­чен от­но­си­тель­но на­ча­ла ко­ор­ди­нат.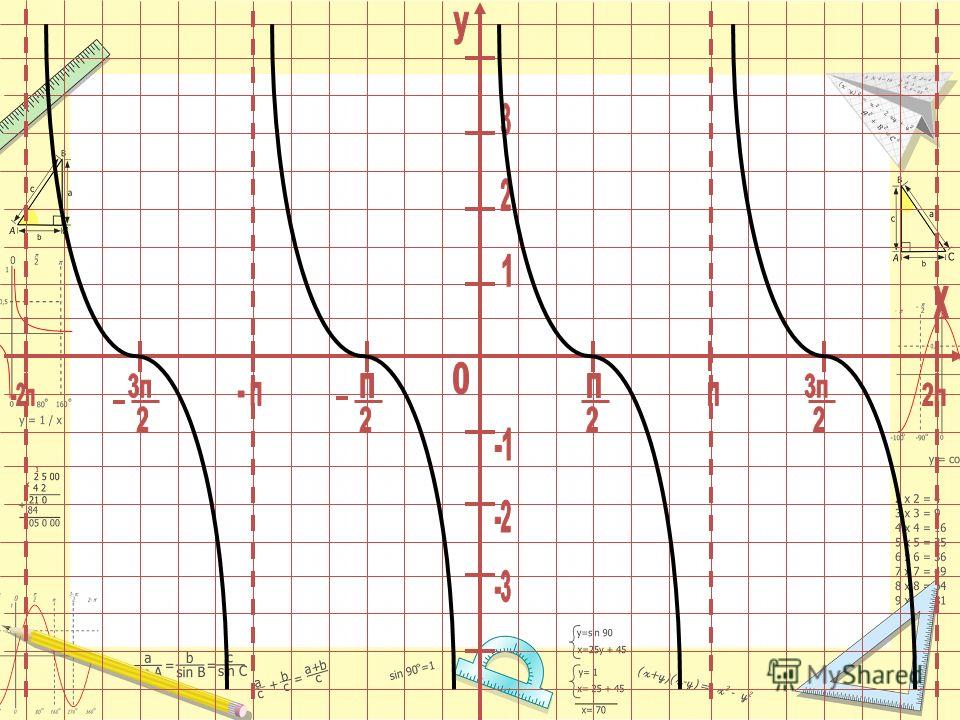

4) Наи­мень­ший по­ло­жи­тель­ный пе­ри­од 

Зна­че­ние пе­ри­о­да ко­тан­ген­са  также сле­ду­ет из фор­му­лы

  при том, что нам из­ве­стен пе­ри­од тан­ген­са.

5) Точки пе­ре­се­че­ния с осью x: 

Точки пе­ре­се­че­ния с осью y от­сут­ству­ют (рис. 4).

6) Опре­де­лим ин­тер­ва­лы зна­ко­по­сто­ян­ства (рис. 5):

7) Функ­ция мо­но­тон­но убы­ва­ет на каж­дом из ин­тер­ва­лов 

По­ка­жем это:

Рас­смот­рим про­ме­жу­ток  дли­ной в пе­ри­од. Функ­ция мо­но­тон­но убы­ва­ет от  до  

Дей­стви­тель­но, если мы возь­мем две точки из этого про­ме­жут­ка, такие, что то  боль­ше­му зна­че­нию ар­гу­мен­та со­от­вет­ству­ет мень­шее зна­че­ние функ­ции (рис. 6).

На каж­дом из от­дель­но взя­тых участ­ков дли­ной в пе­ри­од функ­ция также мо­но­тон­но убы­ва­ет.

8) Функ­ция не имеет ни наи­боль­ше­го, ни наи­мень­ше­го зна­че­ния.

Мы изу­чи­ли функ­цию  её гра­фик и свой­ства. 

ИСТОЧНИК

http://interneturok.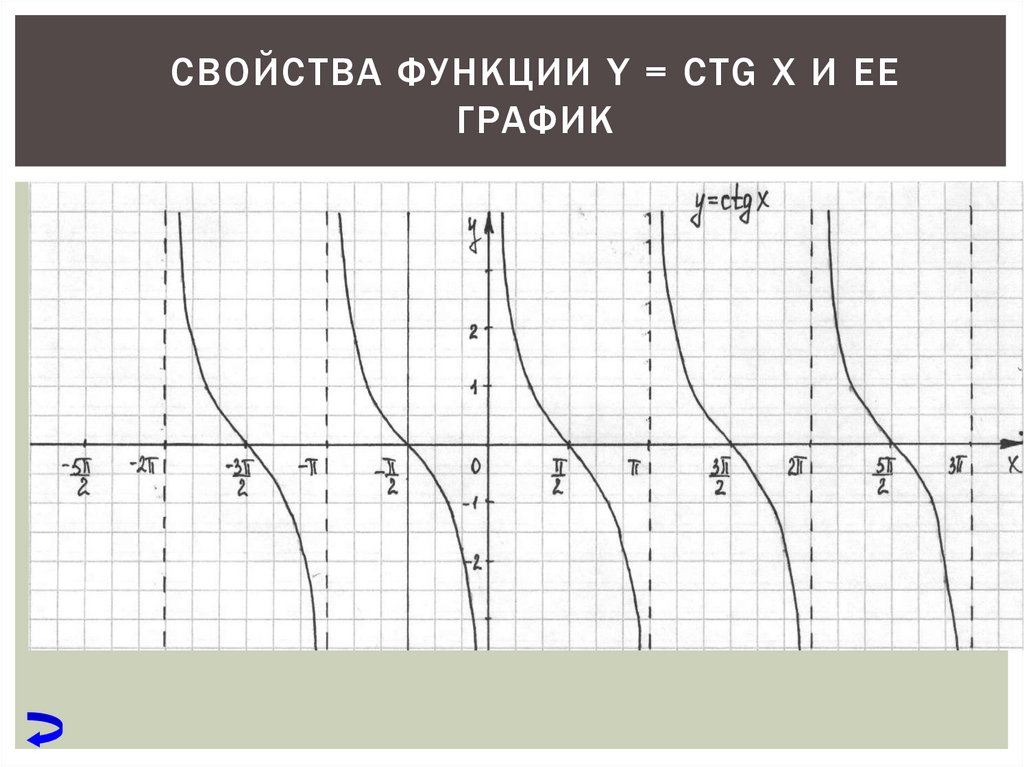 ru/ru/school/algebra/10-klass/trigonometricheskie-funkcii/funktsiya-y-stgx-ee-svoystva-i-grafik

http://www.youtube.com/watch?v=-i3CbcZC6kI

http://5klass.net/datas/algebra/Osnovnye-trigonometricheskie-funktsii/0022-022-Svojstva-funktsii-y-tg-x.jpg

http://11book.ru/images/shcoolbook_ru/10/10_a_mord_baz.pdf

http://v.5klass.net/zip/2418f24263056cb69cc9115af959108a.zip

http://chaulitasjo.science/pic-zadacha.uanet.biz/uploads/61/76/6176c60983745d17f71a3337ee5c8100/%D0%9C%D0%B5%D1%80%D0%B7%D0%BB%D1%8F%D0%BA-%D0%90.%D0%93.-%D0%9F%D0%BE%D0%BB%D0%BE%D0%BD%D1%81%D0%BA%D0%B8%D0%B9-%D0%92.%D0%91.-%D0%A0%D0%B0%D0%B1%D0%B8%D0%BD%D0%BE%D0%B2%D0%B8%D1%87-%D0%95.%D0%9C.-%D0%AF%D0%BA%D0%B8%D1%80-%D0%9C.%D0%A1.-%D0%A2%D1%80%D0%B8%D0%B3%D0%BE%D0%BD%D0%BE%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D1%8F.-%D0%97%D0%B0%D0%B4%D0%B0%D1%87%D0%BD%D0%B8%D0%BA-%D0%BA-%D1%88%D0%BA%D0%BE%D0%BB%D1%8C%D0%BD%D0%BE%D0%BC%D1%83-%D0%BA%D1%83%D1%80%D1%81%D1%83.-8-11-%D0%BA%D0%BB%D0%B0%D1%81%D1%81-1998.jpg

http://cdndl. zaycev.net/117190/12852/didyulya_-_put_domoy_(zaycev.net).mp3

 

 

Как построить график \\[y = \\cot x\\]?

Подсказка: Нам нужно построить график данной функции. Мы будем использовать домен и некоторые значения \[x\], лежащие между \[ — 2\pi \] и \[2\pi \], чтобы найти некоторые значения \[y\]. Затем мы будем наблюдать за поведением значения \[y\] и использовать его и полученные координаты для построения графика функции.

Полное пошаговое решение:
Область определения функции \[y = \cot x\] определяется выражением \[\left\{ {x:x \in R{\rm{and}} x \ne n\pi ,n \in Z} \right\}\]. Это означает, что котангенс любого кратного \[\pi \] не существует.
График функции котангенса достигает сколь угодно больших положительных или отрицательных значений при этих кратных \[\pi \].
Теперь мы найдем некоторые значения \[y\] для некоторых значений \[x\], лежащих между \[ — 2\pi \] и \[2\pi \].
Подставляя \[x = — \dfrac{{3\pi }}{2}\] в функцию \[y = \cot x\], получаем
\[\begin{array}{l}y = \ кроватка \left( { — \dfrac{{3\pi}}{2}} \right)\\ \Rightarrow y = 0\end{array}\]
Подстановка \[x = — \dfrac{\pi} }{ 2}\] в функции \[y = \cot x\] получаем
\[\begin{array}{l}y = \cot \left( { — \dfrac{\pi }{2}} \right)\\ \Стрелка вправо y = 0\end{array}\]
Замена \ [x = \dfrac{\pi }{2}\] в функции \[y = \cot x\], мы получаем
\[\begin{array}{l}y = \cot \left( {\dfrac {\pi }{2}} \right)\\ \Rightarrow y = 0\end{array}\]
Подстановка \[x = \dfrac{{3\pi }}{2}\] в функции \[ y = \cot x\], мы получаем
\[\begin{array}{l}y = \cot \left( {\dfrac{{3\pi}}{2}} \right)\\ \Rightarrow y = 0\end{array}\]
Значение \[y\] в точке \[x = 2\pi ,\pi ,0,\pi ,2\pi \] бесконечно.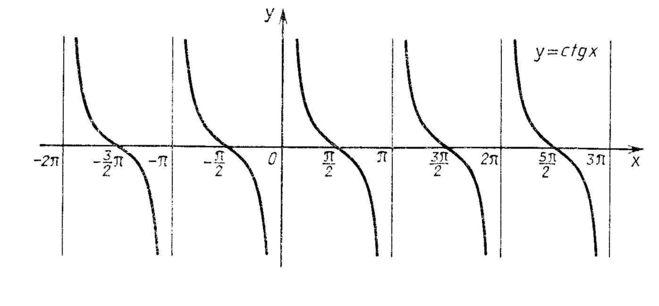
Расставив значения \[x\] и \[y\] в таблице и записав координаты, получим

\[x\]	\[y\]
\[ — 2\pi \]	\[\infty \]
\[ — \dfrac{{3\pi }}{2}\]	\[0\]
\[ — \ pi \]	\[\infty \]
\[ — \dfrac{\pi }{2}\]	\[0\]
\[0\]	\[\ инфты \]
\[\dfrac{\pi }{2}\]	\[0\]
\[\pi \]	\[\infty \]
\[\dfrac{{ 3\pi }}{2}\]	\[0\]
\[2\pi \]	\[\infty \]

Значение \[y = \ cot x\] убывает от \[\infty \] до 0 в точке \[x = — \dfrac{{3\pi }}{2}\], а затем до \[ — \infty \] в интервале \[ \left( { — 2\pi , — \pi } \right)\].
Аналогично, значение \[y = \cot x\] уменьшается от \[\infty \] до 0 при \[x = — \dfrac{\pi }{2},\dfrac{\pi }{2} ,\dfrac{{3\pi }}{2}\], а затем в \[ — \infty \] в промежутках \[\left( { — \pi ,0} \right)\], \[\ влево ({0,\pi} \right)\] и \[\left({\pi,2\pi} \right)\].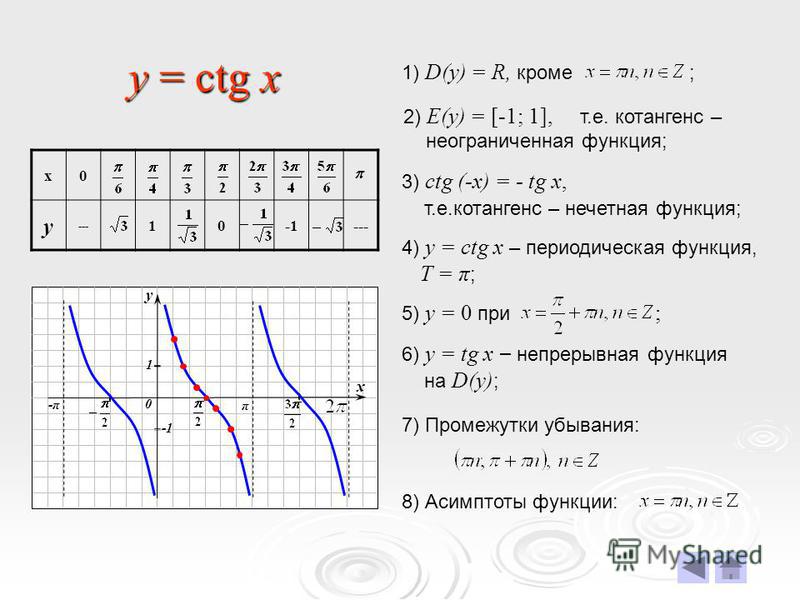
Теперь мы будем использовать точки \[\left( { — \dfrac{{3\pi }}{2},0} \right)\], \[\left( { — \dfrac{\pi }{ 2},0} \right)\], \[\left( {\dfrac{\pi} {2},0} \right)\], \[\left({\dfrac{{3\pi}} {2},0} \right)\] и поведение значения \[y = \cot x\] для построения графика функции.
Таким образом, мы получаем график

Это и есть искомый график функции \[y = \cot x\].

Примечание:
Период функции \[y = \cot x\] равен \[\pi \]. Это означает, что график \[y = \cot x\] будет повторяться для каждого расстояния \[\pi \] по оси \[x\]. Можно заметить, что структура и форма графика \[y = \cot x\] одинаковы от \[ — 2\pi \] до \[ — \pi \], от \[ — \pi \ ] до 0, от 0 до \[\pi \] и от \[\pi \] до \[2\pi \]. Диапазон функций котангенса от \[ — \infty \] до \[\infty \]. Так как функция тангенса является функцией обратной функции котангенса, то их графики обращены друг к другу противоположно.

Урок 5. Построение графиков других тригонометрических функций

w3.org/1999/xhtml» cellspacing=»0″>

Теперь, когда вы научились строить графики функций синуса и косинуса, вы научитесь строить графики других четырех тригонометрических функций: тангенса, котангенса, секанса и косеканса. . Тангенс и котангенс Вот как выглядит график для y =tan( x ): Как видите, график тангенса сильно отличается от синуса и косинуса. Домен: В x  направление, домен равен x≠((2π-1)/2)*π. Диапазон: В направлении y график бесконечно продолжается в обоих направлениях (-∞,∞) Период: Период касательного графика равен π. График пересекает ось x каждые π единиц, начиная с (0,0), что также является точкой пересечения y . Диаграммы тангенса отличаются от графиков синуса и косинуса тем, что они имеют вертикальные асимптоты, которые представляют собой тип границы, которой график никогда не касается. Для y =tan( x ) вертикальная асимптота встречается каждые π единиц, начиная с π/2. График для y =cot( x ) немного похож на тангенс. Домен: в направлении x домен равен x≠nπ. Диапазон: В направлении y график продолжается бесконечно в обоих направлениях (-∞,∞) Период: период для котангенса графика также равен π, но начинается с π/2. График пересекает ось x каждые ((2π-1)/2)*π единиц, начиная с (0,0), и никогда не пересекает ось y , потому что для y =cot ( x ), вертикальная асимптота встречается каждые π единиц, начиная с (0,0). Чтобы построить график функции тангенса или котангенса, сначала найдите период и обозначьте вертикальные асимптоты. Затем посчитайте наполовину между двумя вертикальными асимптотами вдоль средней линии, чтобы найти первую точку. Затем снова сосчитайте наполовину от точки до обеих вертикальных асимптот, затем увеличьте число единиц, эквивалентное вашей амплитуде, чтобы найти вторую и третью точки. Не волнуйтесь, тригги. После того, как вы освоитесь, графическое отображение этих функций станет очень простым и быстрым. Секанс и косеканс Функции секанса (сек) и косеканса (csc) являются обратными функциями косинуса и синуса соответственно. Однако они имеют свойства, более похожие на функции тангенса-котангенса, чем на соответствующие основные триггерные функции. Вот график для Y = CSC ( x ) и Y = Sec ( x ) y = CSC ( x ) Y = Sec )) Просто взглянув на эти графики, вы можете сказать, что они имеют свойства, аналогичные графам тангенса и котангенса, в основном их домены: x≠((2π-1)*π)/2 для секанса и x≠nπ для косеканса. Они также имеют общую вертикальную асимптоту x=nπ. Однако они имеют тот же период, что и график синуса или косинуса: 2π. Уникальность секанса и косеканса заключается в их диапазонах. Поскольку секанс и косеканс являются величинами, обратными косинусу и синусу, их диапазон равен (-∞, (-1)) и (1,∞). No related posts. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт