Критерий гурвица пример решения: Критерий Вальда, Сэвиджа, Гурвица, Лапласа, максимакса

Критерий Вальда, Сэвиджа, Гурвица, Лапласа, максимакса

Основные критерии применяемые в процессе принятия решений в условиях неопределённости и риска, а также в игре с природой 

Формула критерия среднего выигрыша

Формула оптимального решения

Пример

Пусть даны вероятности, p₁=0.2 p₂=0.1 p₃=0.3 p₄=0.2, тогда получаем

K(a₁)=0.2*0.4+0.1*0.5+0.3*0.2+0.2*0.4=0.3
K(a₂)=0.2*0.3+0.1*0.2+0.3*0.3+0.2*0.5=0.27
K(a₃)=0.2*0.6+0.1*0.3+0.3*0.3+0.2*0.2=0.28
K(a₄)=0.2*0.4+0.1*0.5+0.3*0.2+0.2*0.3=0.25
K_опт=max{0.27; 0.48; 0.43; 0.51}=0. 51

В итоги оптимальным вариантом выбора программы по критерию среднего выигрыша является вариант первой программы.

Формула критерия Вальда или максимина

Формула оптимального решения по критерию Лапласа

Пример

K(a₁)=min(0.4;0.5;0.3;0.4)=0.3
K(a₂)=min(0.3;0.2;0.3;0.5)=0.2
K(a₃)=min(0.6;0.3;0.3;0.2)=0.2
K(a₄)=min(0.4;0.5;0.2;0.3)=0.2
K_опт=max{0.3; 0.2; 0.2; 0.2}=0.3

По критерию Вальда оптимальным решением является выбор первой программы.

Формула критерия максимакса

Формула оптимального решения по критерию максимакса

Пример

K(a₁)=max(0.4;0.5;0. 3;0.4)=0.5
K(a₂)= max (0.3;0.2;0.3;0.5)=0.5
K(a₃)= max (0.6;0.3;0.3;0.2)=0.6
K(a₄)= max (0.4;0.5;0.2;0.3)=0.5
K_опт=max{0.5; 0.5; 0.6; 0.5}=0.6

По критерию максимакса оптимальным решением является выбор третьей программы.

Формула критерия Лапласа

Формула оптимального решения по критерию Лапласа

Пример

Решение
K(a₁)=0.25*(0.4+0.5+0.3+0.4)=0.4
K(a₂)=0.25*(0.3+0.2+0.3+0.5)=0.325
K(a₃)=0.25*(0.6+0.3+0.3+0.2)=0.35
K(a₄)=0.25*(0.4+0.5+0.2+0.3)=0.35
K_опт=max{0.4; 0.325; 0.35; 0.35}=0.4

По критерию Лапласа оптимальным решением является выбор первой программы.

Пример

Формула критерия Гурвица

Формула оптимального решения по Гурвица критерию

Коэффициент α принимает значения от 0 до 1. Если α стремится к 1, то критерий Гурвица приближается к критерию Вальда, а при α стремящемуся к 0, то критерий Гурвица приближается к критерию максимакса.

Пусть α=0.7

K(a₁)= 0.7* 0.5+(1-0.7)*0.3=0.44
K(a₂)= 0.7* 0.5+(1-0.7)*0.2=0.41
K(a₃)= 0.7* 0.6+(1-0.7)*0.2=0.48
K(a₄)= 0.7* 0.5+(1-0.7)*0.2=0.41
K_опт=max{0.44; 0.41; 0.48; 0.41}=0.48

По критерию Гурвица оптимальным решением является выбор третьей программы.

Формула критерия Сэвиджа для построения матрицы потерь

Формула для выбора максимального значения из матрицы потерь

Формула оптимального решения по критерию Сэвиджа

Для примера

Строим матрицу потерь по столбцам выбираем максимальное значение и поочередно вычитаем значения каждой ячейки соответствующего столбца согласно формуле, в итоге получим матрицу вида

K(a₁)= max{0. 2; 0; 0; 0.1}=0.2
K(a₂)= max{0.3; 0.3; 0; 0}=0.3
K(a₃)= max{0; 0.2; 0; 0.3}=0.3
K(a₄)= max{0.2; 0; 0.1; 0.2}=0.2
K_опт=min{0.2; 0.3; 0.3; 0.2}=0.2

По критерию Сэвиджа оптимальным решением является выбор первой или четвёртой программы.

Таким образом, в соответствии со всеми приведёнными критериями большинство решений указывает на выбор первой программы.

Примеры решения задач — Математическое программирование — Исследование операций — ЭММ

Условие задачи

Фермер может посеять на данном участке одну из трех культур . Урожайность каждой из культур во многом зависит от погоды, которая может быть засушливой, нормальной или дождливой (влияние других факторов не учитывается). Известна цена  одного центнера культуры , а также урожайности (ц/га) каждой культуры    – урожайность при засушливой погоде,  –урожайность при нормальной погоде,  – урожайность при дождливой погоде. Многолетние наблюдения за погодой данного района показывают, что вероятности засушливой, нормальной и дождливой погоды составляют соответственно .

Требуется:

• придать описанной ситуации игровую схему и составить платежную матрицу;
• пользуясь критериями Бейеса, Вальда, Сэвиджа и Гурвица (величина параметра  для критерия Гурвица задается) выяснить, какую культура следует сеять, чтобы обеспечить наибольший доход.

Решение задачи

Игровая схема

Игра парная,  статистическая. В игре участвуют два игрока. Первый игрок — фермер. Его возможные стратегии:

  — посадить 1-ю культуру

  — посадить 2-ю культуру

  — посадить 3-ю культуру

Второй игрок — природа.  Под природой  мы  понимаем  совокупность внешних условий, определяющих урожайность. Стратегии природы будут следующими:

 – погода будет засушливая

 – погода будет нормальная

 – погода будет дождливая

 

Платежная матрица

Составляем платежную матрицу. Элементы этой матрицы – цена реализации выращенного урожая.

 

Или

	6	9	3
	5	10	30
	8	12	4

 

Критерий Байеса

При известных вероятностях воспользуемся критерием Байеса.

Определяем средние выигрыши:

Оптимальной  является стратегия 

 

Критерий Вальда

Оптимальной является стратегия .

 

Критерий Сэвиджа

Составляем матрицу рисков:

	2	3	27	27
	3	2	0	3
	0	0	26	26

Оптимальной является стратегия

 

Критерий Гурвица

Согласно критерию Гурвица, наи­лучшим решением является чистая стратегия, соответствующая условию:

Оптимальной является стратегия

В соответствии со всеми критериями фермеру необходимо выращивать 2-ю культуру.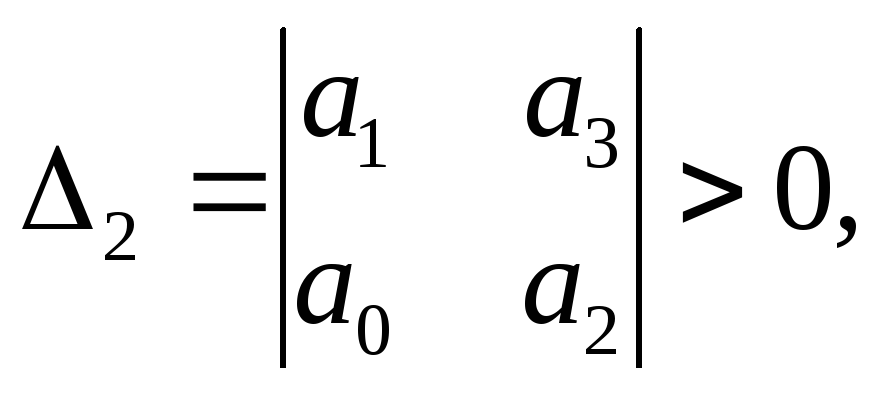

Необходимо решить задачи, сделать контрольную в короткий срок, онлайн-помощь на экзамене? Оставляйте заявку:

ВКонтакте
WhatsApp
Telegram

Все будет сделано в срок!

Критерий Рауса-Гурвица Часть 2 — 3.3 — Электроника…

Опубликовано 2 июня 2021 г.

В предыдущем уроке мы начали с критерия Рауса-Гурвица для проверки стабильности систем управления. Мы закончили предыдущий урок двумя характеристическими уравнениями. Как уже упоминалось, есть уравнения, на которых мы застрянем, формируя массив маршрута, и мы использовали два уравнения в качестве примеров. Это частные случаи критерия Рауса-Гурвица. В этом уроке мы начнем с понимания особых случаев, затем мы увидим, как использовать критерий RH для проектирования систем управления, и, наконец, мы узнаем, как можно избежать всех этих вычислений с помощью Scilab с помощью нескольких строк кода.

Возьмем первое характеристическое уравнение, упомянутое в конце прошлого урока.

Особый случай 1

Теперь мы сформируем массив routh для приведенного выше характеристического уравнения, используя шаги, которые мы изучили в предыдущем уроке.

Как видно, первый элемент третьей строки становится равным 0, поэтому первый элемент следующей строки не определен. Так что же нам делать?

Вот решение: если первый элемент любой строки в массиве Рауса становится нулем, то ноль заменяется небольшим положительным числом, которое обычно представляется как ϵ (произносится как эпсилон).

Теперь, чтобы оценить устойчивость, находим знак первого элемента соответствующих строк, приближая ϵ к нулю. Затем, как обычно, ищут изменения знака для анализа устойчивости. Пример ниже прояснит это.

Как видите, при ϵ → 0 первый элемент четвертой строки положителен, а пятой — отрицателен. Так как один из элементов первого столбца отрицательный, то система неустойчива, а так как перемены знака две, то в правой половине s-плоскости два полюса.

Особый случай 2

Давайте теперь возьмем второе характеристическое уравнение, которое упоминалось в конце последнего урока.

Формирование его массива Рауса,

Вся третья строка становится нулевой и из-за этого мы не можем пройти дальше и сформировать четвертую строку. Итак, что нам теперь делать?

В этом случае мы берем многочлен, образованный строкой над строкой нулей (этот многочлен известен как вспомогательный многочлен), и затем дифференцируем по s. Затем ряд нулей заменяется коэффициентами многочлена, полученного после дифференцирования. На примере будет понятно.

Вторая строка берется для формирования вспомогательного многочлена.

Теперь замените нули третьей строки на 10 и 0 и действуйте как обычно.

Поскольку все элементы в первом столбце положительны, система устойчива. Чтобы быть более точным, система маргинально устойчива из-за появления ряда нулей. Вот почему.

Вспомогательный многочлен — это многочлен, корни которого симметричны относительно начала координат в s-плоскости.

Это происходит при трех условиях.

Решив вспомогательный многочлен, полученный в предыдущем примере,

А так как на мнимой оси есть корни, мы заключаем, что система маргинально устойчива.

Попробуйте это сами,

Проверьте устойчивость системы, характеристическое уравнение которой задается выражением,

Решение:

Массив Рауса

Поскольку вся 3 ^rd строка равна нулю, вспомогательный полином равен

Заменив нули в третьей строке на 4, 4 и 0 и продолжая как обычно, массив Рауса становится равным

Теперь снова вся 5 ^-я -я строка равна нулю, поэтому снова составим вспомогательное уравнение.

Заменив нули в пятой строке на 2 и 0 и действуя как обычно, получим массив Рауса следующим образом.

Вы можете подумать, что, поскольку все элементы в первом столбце массива Рауса положительны, система стабильна. Но это неправильно. Вот почему.

Решив первое вспомогательное уравнение, получим

А теперь решив второе вспомогательное уравнение, получим

На воображаемой оси повторяются полюса. Если вы помните из урока 3.1, система становится нестабильной, если на воображаемой оси есть повторяющиеся полюса. Следовательно, система, описанная в приведенном выше примере, неустойчива.

Практический пример создания стабильных систем

Рассмотрев эти особые случаи, мы можем двигаться дальше и узнать, как мы можем проектировать стабильные системы. Для этого возьмем пример.

Рассмотрим систему с передаточной функцией без обратной связи

, где K положительный.

Найдем его передаточную функцию с обратной связью.

Характеристическое уравнение

Массив Рауса для вышеуказанной системы становится

Чтобы система была стабильной, элементы первого столбца массива Рауса должны быть положительными. Следовательно,

и

, то есть

. Чтобы система была стабильной, дизайн должен быть таким, что

Если

, то первый элемент третьей строки становится отрицательным, а первый элемент четвертой строки остается положительным. Следовательно, система становится неустойчивой с двумя полюсами справа от s-плоскости, что следует из двух изменений знака.

Если

, то третья строка становится нулевой, и система маргинально устойчива.

С Scilab жизнь намного проще.

Рассмотрим большое характеристическое уравнение:

Давайте воспользуемся Scilab для получения массива routh.

И на выходе

Как видите, две смены знака, поэтому система нестабильна. Но это гораздо проще, чем делать расчеты вручную.

Резюме

Подводя итог, в этом руководстве мы обсудили два особых случая критерия Рауса-Гурвица. Затем мы узнали, как критерий RH можно применять при проектировании систем управления, и, наконец, мы использовали Scilab для вычисления массива Рауса большого характеристического уравнения. Хотя критерий Рауса-Гурвица дает хорошее представление об устойчивости системы, он не говорит нам точное расположение полюсов. Следовательно, в следующем уроке мы начнем понимать график корневого локуса, который дает нам хорошее визуальное представление о стабильности системы.

• Системы управления (18)
• Теория управления (17)

Автор:

Кушал Гауда

Инженер-электрик и электронщик. Любит играть в настольный теннис, крикет и бадминтон. Всегда готов учиться и учить. В сферу его интересов входят силовая электроника, электронные приводы, теория управления и аккумуляторные системы.

Получите новейшие инструменты и учебные пособия, только что из тостера.

Критерий Рауса-Гурвица — Страница 2

92} + 3\лямбда + 2 = 0.\]

Коэффициенты \({a_i}\) равны

\[ {а_0} = 1,\;\; {а_1} = 6,\;\; {а_2} = 3,\;\; {а_3} = 2.\]

Сформировать матрицу Гурвица

\[\ влево [ {\ begin {массив} {* {20} {c}} {{a_1}}&{{a_0}}&0\\ {{a_3}}&{{a_2}}&{{a_1}}\\ 0&{{a_4}}&{{a_3}} \end{массив}} \right] = \left[ {\begin{массив}}{*{20}{c}} 6&1&0\\ 2&3&6\\ 0&0&2 \конец{массив}} \справа]\]

и найти все его главные миноры: 92} + 7\лямбда + 3 = 0.\]

Коэффициенты \({a_i}\) в этом уравнении равны

\[ {а_0} = 1,\;\; {а_1} = 2,\;\; {а_2} = 4,\;\; {а_3} = 7,\;\; {а_4} = 3.\]

Запишем матрицу Гурвица и найдем ее главные диагональные миноры:

\[\ влево [ {\ begin {массив} {* {20} {c}} {{a_1}}&{{a_0}}&0&0\\ {{a_3}}&{{a_2}}&{{a_1}}&{{a_0}}\\ 0&{{a_4}}&{{a_3}}&{{a_2}}\\ 0&0&0&{{a_4}} \end{массив}} \right] = \left[ {\begin{массив}}{*{20}{c}} 2&1&0&0\\ 7&7&2&1\\ 0&3&7&4\\ 0&0&0&3 \end{массив}} \right];\]

\[ {\Delta _1} = 2 \gt 0,\;\; {\Дельта _2} = \влево| {\начать{массив}{*{20}{с}} 2&1\\ 7 и 4 \end{массив}} \right| = 8 — 7 = 1 \gt 0,\;\; {\Дельта _3} = \влево| {\начать{массив}{*{20}{с}} 2&1&0\\ 7&4&2\\ 0&3&7 \end{массив}} \right| = — 2 \cdot \влево| {\начать{массив}{*{20}{с}} 2&1\\ 0 и 3 \end{массив}} \right| + 7 \cdot \влево| {\начать{массив}{*{20}{с}} 2&1\\ 7 и 4 \end{массив}} \right| = — 12 + 7 = — 5 \lt 0.

\]

В ходе вычислений мы получили отрицательный минор \({\Delta _3} \lt 0.\) Это означает, что нулевое решение неустойчиво. 92} + \бета \лямбда + 1 = 0.\]

Коэффициенты имеют следующие значения:

\[ {а_0} = 1,\;\; {а_1} = 1,\;\; {a_2} = \альфа,\;\; {a_3} = \бета,\;\; {а_4} = 1.\]

Сформировать матрицу Гурвица

\[\ влево [ {\ begin {массив} {* {20} {c}} {{a_1}}&{{a_0}}&0&0\\ {{a_3}}&{{a_2}}&{{a_1}}&{{a_0}}\\ 0&{{a_4}}&{{a_3}}&{{a_2}}\\ 0&0&0&{{a_4}} \end{массив}} \right] = \left[ {\begin{массив}}{*{20}{c}} 1&1&0&0\\ \бета&\альфа&1&1\\ 0&1&\бета&\альфа\\ 0&0&0&1 \end{массив}} \right]\]

и запишите условие устойчивости Рауса-Гурвица:

\[{\Delta _1} = 1 \gt 0,\]

\[{\Delta _2} = \left| {\начать{массив}{*{20}{с}} 1&1\\ \бета &\альфа \end{массив}} \right| = \альфа — \бета\gt 0,\]

\[ {\Дельта _3} = \влево| {\начать{массив}{*{20}{с}} 1&1&0\\ \бета &\альфа &1\\ 0&1&\бета \end{массив}} \right| = \ влево | {\начать{массив}{*{20}{с}} \альфа &1\\ 1&\бета \end{массив}} \right| — \бета\левый| {\начать{массив}{*{20}{с}} 1&0\\ 0&\бета \end{массив}} \right| = \ альфа \ бета — 1 — {\ бета ^ 2} = \ бета \ влево ( {\ альфа — \ бета } \ вправо) — 1 \ gt 0, \]

\[{\Delta _4} = {a_4}{\Delta _3} \gt 0,\;\; \стрелка вправо {a_4} = 1 \gt 0. \]

Таким образом, система неравенств, описывающая область устойчивости, имеет следующий вид:

\[\left\{ \begin{массив}{l} {\Дельта _2} \gt 0\\ {\Дельта _3}\gt 0 \end{массив} \right.,\;\; \Стрелка вправо \влево\{ {\ begin {массив} {* {20} {l}} {\ альфа — \ бета \ gt 0} \\ {\ бета \ влево ( {\ альфа — \ бета} \ вправо) \ gt 1} \конец{массив}} \право..\]

Рассмотрим сначала второе неравенство. Решаем относительно \(\alpha.\) Здесь возможны два случая:

1. Если \(\beta \gt 0,\), то разделив обе части неравенства на \(\beta,\), получим:

   \[\alpha — \beta \gt \frac{1}{\beta },\;\; \Rightarrow \alpha \gt \beta + \frac{1}{\beta};\]

2. Если \(\beta \lt 0,\), то имеем:

   \[\alpha — \beta \lt \frac{1}{\beta },\;\; \Rightarrow \alpha \lt\beta + \frac{1}{\beta }.\]

Очевидно, что случай \(\beta = 0\) не удовлетворяет этому неравенству.

Итак, решением неравенства являются две бесконечные области, симметричные относительно начала координат и ограниченные кривой \(\alpha = \beta + {\frac{1}{\beta }}\) (рис. \(1 \)).

Рис. 1.

Первому неравенству \(\alpha \gt \beta\) удовлетворяет множество точек над прямой \(\alpha = \beta.\) В результате решение всей системы есть единственное область \(\ alpha \gt \beta + {\frac{1}{\beta}}\) в правом верхнем квадранте (с \(\beta \gt 0,\) \(\alpha \gt 0\)) . На рисунке \(1,\) эта область показана зеленым цветом. Эта область плоскости \(\left( {\beta ,\alpha} \right)\) является областью асимптотической устойчивости исходного уравнения.

Пример 4.

Исследуйте, при каких значениях параметров \(\alpha\) и \(\beta\) нулевое решение системы асимптотически устойчиво:

\[ \frac{{dx}}{{dt}} = \alpha x + \beta y,\;\; \frac{{dy}}{{dt}} = x — z,\;\; \frac{{dz}}{{dt}} = — x + y.\]

Раствор.

Вспомогательное уравнение задается как

\[ \влево| {\начать{массив}{*{20}{с}} {\ альфа — \ лямбда} & \ бета & 0 \\ 1&{-\лямбда}&{-1}\\ {-1}&1&{-\лямбда} \end{массив}} \right| = 0,\;\; \Правая стрелка \ влево ( {\ альфа — \ лямбда} \ вправо) \ влево | {\начать{массив}{*{20}{г}} {-\лямбда}&{-1}\\ 1&{-\лямбда} \end{массив}} \right| — \бета\левый| {\начать{массив}{*{20}{г}} 1&{ — 1}\\ {-1}&{-\лямбда} \end{массив}} \right| = 0,\;\; \Правая стрелка \left( {\alpha — \lambda } \right)\left( {{\lambda ^2} + 1} \right) — \beta \left( { — \lambda — 1} \right) = 0,\; \; \Правая стрелка \alpha {\lambda ^2} — {\lambda ^3} + \alpha — \lambda + \beta \lambda + \beta = 0,\;\; \Правая стрелка {\lambda ^3} — \alpha {\lambda ^2} + \left( {1 — \beta } \right)\lambda — \alpha — \beta = 0. \]

Здесь коэффициенты \({a_i}\) имеют следующие значения:

\[ {а_0} = 1,\;\; {a_1} = — \альфа,\;\; {a_2} = 1 — \бета,\;\; {a_3} = — \alpha — \beta .\]

Сначала определим, при каких значениях \(\alpha\) и \(\beta\) выполняется необходимое условие устойчивости:

\[{a_i} \gt 0,\;\;i = 0,1,2,3.\]

Получаем следующую систему неравенств:

\[\left\{ \begin{массив}{l} — \альфа\gt 0\\ 1 — \бета\gt 0\\ — \альфа -\бета\gt 0 \end{массив} \right.,\;\; \стрелка вправо \влево\{ \begin{массив}{l} \альфа\lt 0\\ \бета\lt 1\\ \бета\lt — \альфа \end{массив} \right..\]

Решение этой системы удобно рисовать на плоскости ) \(\beta = 1,\) \(\beta = -\alpha\) и области, соответствующие решению каждого неравенства. Пересечение этих областей отмечено желтым цветом.

\[\left\{ \begin{массив}{l} — \альфа\gt 0\\ 1 — \бета\gt 0\\ — \альфа -\бета\gt 0 \end{массив} \right.,\;\; \стрелка вправо \влево\{ \begin{массив}{l} \альфа\lt 0\\ \бета\lt 1\\ \бета\lt — \альфа \end{массив} \right. .\]

Рис. 2.

Теперь рассмотрим достаточные условия устойчивости. Напишите матрицу Гурвица:

\[\ влево [ {\ begin {массив} {* {20} {c}} {{a_1}}&{{a_0}}&0\\ {{a_3}}&{{a_2}}&{{a_1}}\\ 0&0&{{a_3}} \end{массив}} \right] = \left[ {\begin{массив}}{*{20}{c}} {-\альфа}&1&0\\ {-\альфа-\бета}&{1-\бета}&{-\альфа}\\ 0&0&{-\альфа-\бета} \end{массив}} \right].\]

Главные диагональные миноры \({\Delta _i}\) равны

\[{\Delta _1} = — \альфа,\]

\[{\Delta _2} = \left| {\начать{массив}{*{20}{с}} {-\альфа}&1\\ {-\альфа-\бета}&{1-\бета} \end{массив}} \right| = \ альфа \ влево ( {\ бета — 1} \ вправо) + \ альфа + \ бета = \alpha \beta — \cancel{\alpha} + \cancel{\alpha} + \beta = \ влево ( {\ альфа + 1} \ вправо) \ бета , \]

\[{\Delta _3} = {a_3}{\Delta _2} = \left( { — \alpha — \beta} \right)\left({\alpha + 1} \right)\beta .\]

Согласно критерию устойчивости Рауса-Гурвица должны выполняться следующие неравенства:

\[{\Delta _1} = — \alpha \gt 0,\;\;\; {\Delta _2} = \left( {\alpha + 1} \right)\beta \gt 0,\;\;\; {a_3} \gt 0. \]

Из этих неравенств дополнительным (по сравнению с необходимыми условиями) является единственное неравенство

\[{\Delta _2} \gt 0\;\;\;\text{or}\;\;\; \left( {\alpha + 1} \right)\beta \gt 0.\]

Его решение включает два случая:

1. \(\beta \gt 0,\;\; \) \(\Стрелка вправо \alpha + 1 \gt 0\;\;\) \(\text{or}\;\;\alpha \gt — 1 ;\)
2. \(\beta \lt 0,\;\; \) \(\Стрелка вправо \alpha + 1 \lt 0\;\;\) \(\text{or}\;\;\alpha \lt — 1. \)

Эти два случая представлены двумя квадрантами, ограниченными линиями \(\alpha = -1,\) \(\beta = 0\) (они изображены фиолетовым цветом на рисунке \(2\)).

Область устойчивости системы ограничена значениями параметров \(\alpha, \beta,\), при которых выполняются как необходимые, так и достаточные условия асимптотической устойчивости. Эта область состоит из левого нижнего квадранта, ограниченного линиями \(\alpha = -1,\) \(\beta = 0,\) и правого треугольника с вершинами \(\left( {0,0} \right) ,\) \(\left( {-1,0} \right),\) \(\left( {-1,1} \right).