Значение критерия Фишера | Геологический портал GeoKniga
Значение критерия Фишера пр уровне значимости Р=0,05 для числа степеней свободы к1 и к2
(по Математическое моделирование в геологии и разведке полезных ископаемых, Каждан А.Б. и др., 1979)
| κ1 | ||||||||||||
| κ2 | 1 | 2 | 3 | 4 | 5 | 6 | 8 | 12 | 16 | 24 | 50 | >50 |
| 1 | 161,40 | 199,50 | 215,70 | 224,60 | 230,20 | 234,00 | 238,90 | 243,90 | 246,50 | 249,00 | 251,80 | 254,30 |
| 2 | 18,51 | 19,00 | 19,16 | 19,25 | 19,30 | 19,33 | 19,37 | 19,41 | 19,43 | 19,45 | 19,47 | 19,50 |
| 3 | 10,13 | 9,55 | 9,28 | 9,12 | 9,01 | 8,94 | 8,84 | 8,74 | 8,69 | 8,64 | 8,58 | 8,53 |
| 4 | 7,71 | 6,94 | 6,59 | 6,39 | 6,26 | 6,16 | 6,04 | 5,91 | 5,84 | 5,77 | 5,70 | 5,63 |
| 5 | 6,61 | 5,79 | 5,41 | 5,19 | 5,05 | 4,95 | 4,82 | 4,68 | 4,60 | 4,53 | 4,44 | 4,36 |
| 6 | 5,99 | 5,14 | 4,76 | 4,53 | 4,39 | 4,28 | 4,15 | 4,00 | 3,92 | 3,84 | 3,75 | 3,67 |
| 7 | 5,59 | 4,74 | 4,35 | 4,12 | 3,97 | 3,87 | 3,73 | 3,57 | 3,49 | 3,41 | 3,32 | 3,23 |
| 8 | 5,32 | 4,48 | 4,07 | 3. 84 84 | 3,69 | 3,58 | 3,44 | 3,28 | 3,20 | 3 12 | 3,02 | 2 93 |
| 9 | 5,12 | 4,26 | 3,86 | 3,63 | 3,48 | 3,37 | 3,23 | 3,07 | 2,98 | 2,90 | 2,80 | 2.71 |
| 10 | 4,96 | 4,10 | 3,71 | 3,48 | 3,33 | 3,22 | 3,07 | 2,91 | 2,82 | 2,74 | 2,64 | 2,54 |
| 11 | 4,84 | 3,98 | 3,59 | 3,36 | 3,20 | 3,09 | 2,95 | 2,79 | 2,70 | 2,61 | 2,50 | 2,40 |
| 12 | 4,75 | 3,88 | 3,49 | 3,26 | 3,11 | 3,00 | 2,85 | 2,69 | 2,60 | 2,50 | 2,40 | 2,30 |
| 13 | 4,67 | 3,80 | 3,41 | 3,18 | 3,02 | 2,92 | 2,77 | 2,60 | 2,51 | 2,42 | 2,32 | 2,21 |
| 14 | 4,60 | 3,74 | 3,34 | 3,11 | 2,96 | 2,85 | 2,70 | 2,53 | 2,44 | 2,35 | 2,24 | 2,13 |
| 15 | 4,54 | 3,68 | 3,29 | 3,06 | 2,90 | 2,79 | 2,64 | 2,48 | 2,39 | 2,29 | 2,18 | 2,07 |
| 16 | 4,49 | 3,63 | 3,24 | 3,01 | 2,85 | 2,74 | 2,59 | 2,42 | 2,33 | 2,24 | 2,13 | 2,01 |
| 17 | 4,45 | 3,59 | 3,20 | 2,96 | 2,81 | 2,70 | 2,55 | 2,38 | 2,29 | 2,19 | 2,08 | 1,96 |
| 18 | 4,41 | 3,55 | 3,16 | 2,93 | 2,77 | 2,66 | 2,51 | 2,34 | 2,25 | 2,15 | 2,04 | 1,92 |
| 19 | 4,38 | 3,52 | 3,13 | 2,90 | 2,74 | 2,63 | 2,48 | 2,31 | 2,21 | 2,11 | 2,00 | 1,88 |
| 20 | 4,35 | 3,49 | 3,10 | 2,87 | 3,71 | 2,60 | 2,45 | 2,28 | 2,18 | 2,08 | 1,96 | 1,84 |
| 21 | 4,32 | 3,47 | 3,07 | 2,84 | 2,68 | 2,57 | 2,42 | 2,25 | 2,15 | 2,05 | 1,93 | 1,81 |
| 22 | 4,30 | 3,44 | 3,05 | 2,82 | 2,66 | 2,55 | 2,40 | 2,23 | 2,13 | 2,03 | 1,91 | 1,78 |
| 23 | 4,28 | 3,42 | 3,03 | 2,80 | 2,64 | 2,53 | 2,38 | 2,20 | 2,11 | 2,00 | 1,88 | 1,76 |
| 24 | 4,26 | 3,40 | 3,01 | 2,78 | 2,62 | 2,51 | 2,36 | 2,18 | 2,09 | 1,98 | 1,86 | 1,73 |
| 25 | 4,24 | 3,38 | 2,99 | 2,76 | 2,60 | 2,49 | 2,34 | 2,16 | 2,07 | 1,96 | 1,84 | 1,71 |
| 26 | 4,22 | 3,37 | 2,98 | 2,74 | 2,59 | 2,47 | 2,32 | 2,15 | 2,05 | 1,95 | 1,82 | 1,69 |
| 27 | 4,21 | 3,35 | 2,96 | 2,73 | 2,57 | 2,46 | 2,30 | 2,13 | 2,03 | 1,93 | 1,80 | 1,67 |
| 28 | 4,20 | 3,34 | 2,95 | 2,71 | 2,56 | 2,44 | 2,29 | 2,12 | 2,02 | 1,91 | 1,78 | 1,65 |
| 29 | 4,18 | 3,33 | 2,93 | 2,70 | 2,54 | 2,43 | 2,28 | 2,10 | 2,00 | 1,90 | 1,77 | 1,64 |
| 30 | 4,17 | 3,32 | 2,92 | 2,69 | 2,53 | 2,42 | 2,27 | 2,09 | 1,99 | 1,89 | 1,76 | 1,62 |
| 35 | 4,12 | 3,26 | 2,87 | 2,64 | 2,48 | 2,37 | 2,22 | 2,04 | 1,94 | 1,83 | 1,70 | 1,57 |
| 40 | 4,08 | 5,23 | 2,84 | 2,61 | 2,45 | 2,34 | 2,18 | 2,00 | 1,90 | 1,79 | 1,66 | 1,51 |
| 45 | 4,06 | 3,21 | 2,81 | 2,58 | 2,42 | 2,31 | 2,15 | 1,97 | 1,87 | 1,76 | 1,63 | 1,48 |
| 50 | 4,03 | 3,18 | 2,79 | 2,56 | 2,40 | 2,29 | 2,13 | 1,95 | 1,85 | 1,74 | 1,60 | 1,44 |
| 60 | 4,00 | 3,15 | 2,76 | 2,52 | 2,37 | 2,25 | 2,10 | 1,92 | 1,81 | 1,70 | 1,56 | 1,39 |
| 70 | 3,98 | 3,13 | 2,74 | 2,50 | 2,35 | 2,23 | 2,07 | 1,89 | 1,79 | 1,67 | 1,53 | 1,35 |
| 80 | 3,96 | 3,11 | 2,72 | 2,49 | 2,33 | 2,21 | 2,06 | 1,88 | 1,77 | 1,65 | 1,,51 | 1,32 |
| 90 | 3,95 | 3,10 | 2,71 | 2,47 | 2,32 | 2,20 | 2,04 | 1,86 | 1,76 | 1,64 | 1,49 | 1,30 |
| 100 | 3,94 | 3,09 | 2,70 | 2,46 | 2,30 | 2,19 | 2,03 | 1,85 | 1,75 | 1,63 | 1,48 | 1,28 |
| 125 | 3,92 | 3,07 | 2,68 | 2,44 | 2,29 | 2,17 | 2,01 | 1,83 | 1,72 | 1,60 | 1,45 | 1,25 |
| 150 | 3,90 | 3,06 | 2,66 | 2,43 | 2,27 | 2,16 | 2,00 | 1,82 | 1,71 | 1,59 | 1,44 | 1,22 |
| 200 | 3,89 | 3,04 | 2,65 | 2,42 | 2,26 | 2,14 | 1,98 | 1,80 | 1,69 | 1,57 | 1,42 | 1,19 |
| 300 | 3,87 | 3,03 | 2,64 | 2,41 | 2,25 | 2,13 | 1,97 | 1,79 | 1,68 | 1,55 | 1,39 | 1,15 |
| 400 | 3,86 | 3,02 | 2,63 | 2,40 | 2,24 | 2,12 | 1,96 | 1,78 | 1,67 | 1,54 | 1,38 | 1,13 |
| 500 | 3,86 | 3,01 | 2,62 | 2,39 | 2,23 | 2,11 | 1,96 | 1,77 | 1,66 | 1,54 | 1,38 | 1,11 |
| 1000 | 3,85 | 3,00 | 2,61 | 2,38 | 2,22 | 2,10 | 1,95 | 1,76 | 1,65 | 1,53 | 1,36 | 1,08 |
| >1000 | 3,84 | 2,99 | 2,60 | 2,37 | 2,21 | 2,09 | 1,94 | 1,75 | 1,64 | 1,52 | 1,35 | 1,00 |
Значение критерия Фишера пр уровне значимости Р=0,01 для числа степеней свободы к1 и к2
(по Математическое моделирование в геологии и разведке полезных ископаемых, Каждан А.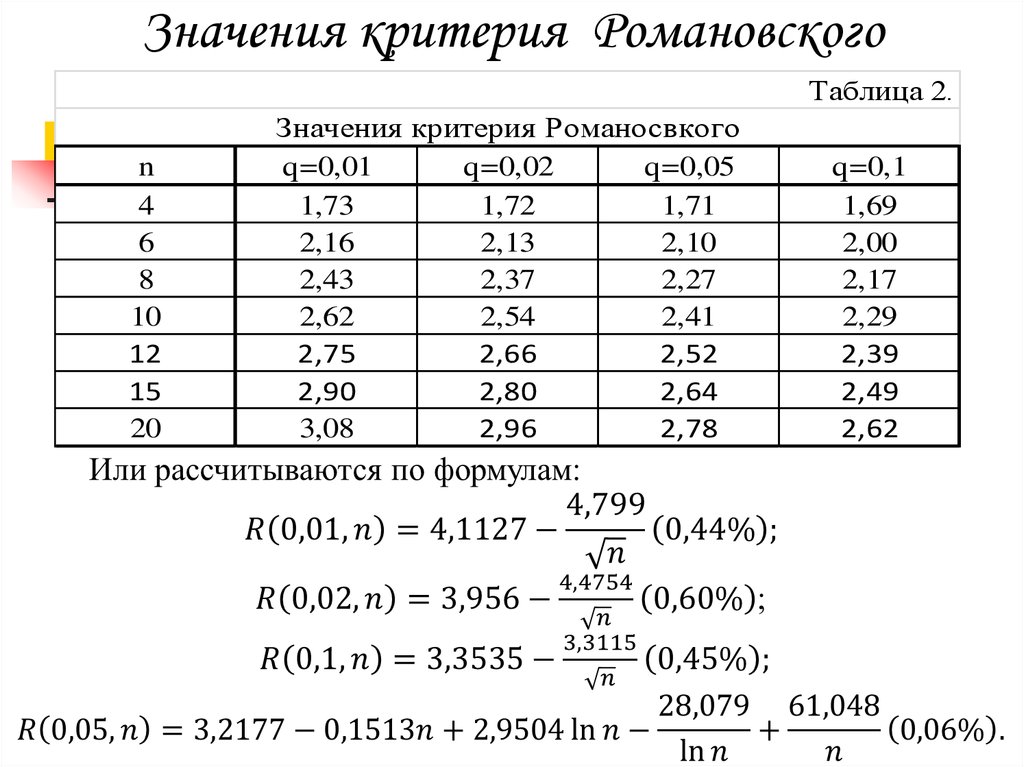 Б. и др., 1979)
Б. и др., 1979)
| κ1 | ||||||||||||
| κ2 | 1 | 2 | 3 | 4 | 5 | 6 | 8 | 12 | 16 | 24 | 50 | >50 |
| 1 | 1 4052 | 4999 | 5403 | 5625 | 5764 | 5859 | 5981 | 6106 | 6169 | 6234 | 6302 | 6366 |
| 2 | 98,49 | 99,00 | 99,17 | 99,25 | 99,30 | 99,33 | 99,36 | 99,42 | 99,44 | 99,46 | 99,48 | 99,50 |
| 3 | 34,12 | 30,81 | 29,46 | 28,71 | 28,24 | 27,91 | 27,49 | 27,05 | 26,83 | 26,60 | 26,35 | 26,12 |
| 4 | 21,20 | 18,00 | 16,69 | 15,98 | 15,52 | 15,21 | 14,80 | 14,37 | 14,15 | 13,93 | 13,69 | 13,46 |
| 5 | 16,26 | 13,27 | 12,06 | 11,39 | 10,97 | 10,67 | 10,29 | 9,89 | 9,68 | 9,47 | 9,24 | 9,02 |
| 6 | 13,74 | 10,92 | 9,78 | 9,15 | 8,75 | 8,47 | 8,10 | 7,72 | 7,52 | 7,31 | 7,09 | 6,88 |
| 7 | 12,25 | 9,55 | 8,45 | 7,85 | 7,46 | 7,19 | 6,84 | 6,47 | 6,27 | 6,07 | 5,85 | 5,65 |
| 8 | 11,26 | 8,65 | 7,59 | 7,01 | 6,63 | 6,37 | 6,03 | 5,67 | 5,48 | 5,28 | 5,06 | 4,86 |
| 9 | 10,56 | 8,02 | 6,99 | 6,42 | 6,06 | 5,80 | 5,47 | 5,11 | 4,92 | 4,73 | 4,51 | 4,31 |
| 10 | 10,04 | 7,56 | 6,55 | 5,99 | 5,64 | 5,39 | 5,06 | 4,71 | 4,52 | 4,33 | 4,12 | 3,91 |
| 11 | 9,65 | 7,20 | 9,22 | 5,67 | 5,32 | 5,07 | 4,74 | 4,40 | 4,21 | 4,02 | 3,80 | 3,60 |
| 12 | 9,33 | 6,93 | 5,95 | 5,41 | 5,06 | 4,82 | 4,50 | 4,16 | 3,98 | 3,78 | 3,56 | 3,36 |
| 13 | 9,07 | 6,70 | 5,74 | 5,20 | 4,86 | 4,62 | 4,30 | 3,96 | 3,78 | 3,59 | 3,37 | 3,16 |
| 14 | 8,86 | 6,51 | 5,56 | 5,03 | 4,69 | 4,46 | 4,14 | 3,80 | 3,62 | 3,43 | 3,21 | 3,00 |
| 15 | 8,68 | 6,36 | 5,42 | 4,89 | 4,56 | 4,32 | 4,00 | 3,67 | 3,48 | 3,29 | 3,07 | 2,87 |
| 16 | 8,53 | 6,23 | 5,29 | 4,77 | 4,44 | 4,20 | 3,89 | 3,55 | 3,37 | 3,18 | 2,96 | 2,75 |
| 17 | 8,40 | 6,11 | 5,18 | 4,67 | 4,34 | 4,10 | 3,79 | 3,45 | 3,27 | 3,08 | 2,86 | 2,65 |
| 18 | 8,28 | 6,01 | 5,09 | 4,58 | 4,25 | 4,01 | 3,71 | 3,37 | 3,20 | 3,00 | 2,79 | 2,57 |
| 19 | 8,18 | 5,93 | 5,01 | 4,50 | 4,17 | 3,94 | 3,63 | 3,30 | 3,12 | 2,92 | 2,70 | 2,49 |
| 20 | 8,10 | 5,85 | 4,94 | 4,43 | 4,10 | 3,87 | 3,56 | 3,23 | 3,05 | 2,86 | 2,63 | 2,42 |
| 21 | 8,02 | 5,78 | 4,87 | 4,37 | 4,04 | 3,81 | 3,51 | 3,17 | 2,99 | 2,80 | 2,58 | 2,36 |
| 22 | 7,94 | 5,72 | 4,82 | 4,31 | 3,99 | 3,76 | 3,45 | 3,12 | 2,94 | 2,75 | 2,53 | 2,31 |
| 23 | 7,88 | 5,66 | 4,76 | 4,26 | 3,94 | 3,71 | 3,41 | 3,07 | 2,89 | 2,70 | 2,48 | 2,26 |
| 24 | 7,82 | 5,61 | 4,72 | 4,22 | 3,90 | 3,67 | 3,36 | 3,03 | 2,85 | 2,66 | 2,44 | 2,21 |
| 25 | 7,77 | 5,57 | 4,68 | 4,18 | 3,86 | 3,63 | 3,32 | 2,09 | 2,81 | 2,62 | 2,40 | 2,17 |
| 26 | 7,72 | 5,53 | 4,64 | 4,14 | 3,82 | 3,59 | 3,29 | 2,96 | 2,78 | 2,58 | 2,36 | 2,13 |
| 27 | 7,68 | 5,49 | 4,60 | 4,11 | 3,78 | 3,56 | 3,26 | 2,93 | 2,74 | 2,55 | 2,33 | 2,10 |
| 28 | 7,64 | 5,45 | 4,57 | 4,07 | 3,75 | 3,53 | 3,23 | 2,90 | 2,71 | 2,52 | 2,30 | 2,06 |
| 29 | 7,60 | 5,42 | 4,54 | 4,04 | 3,73 | 3,50 | 3,20 | 2,87 | 2,68 | 2,49 | 2,27 | 2,03 |
| 30 | 7,56 | 5,39 | 4,51 | 4,02 | 3,70 | 3,47 | 3,17 | 2,84 | 2,66 | 2,47 | 2,24 | 2,01 |
| 35 | 7,42 | 5,27 | 4,40 | 3,91 | 3,59 | 3,37 | 3,07 | 2,74 | 2,56 | 2,37 | 2,13 | 1,90 |
| 40 | 7,31 | 5,18 | 4,31 | 3,83 | 3,51 | 3,29 | 2,99 | 2,66 | 2,48 | 2,29 | 2,05 | 1,80 |
| 45 | 7,23 | 5,11 | 4,25 | 3,77 | 3,45 | 3,23 | 2,94 | 2,61 | 2,43 | 2,23 | 1,99 | 1,75 |
| 50 | 7,17 | 5,06 | 4,20 | 3,72 | 3,41 | 3,19 | 2,89 | 2,56 | 2,38 | 2,18 | 1,94 | 1,68 |
| 60 | 7,08 | 4,98 | 4,13 | 3,65 | 3,34 | 3,12 | 2,82 | 2,50 | 2,32 | 2,12 | 1,87 | 1,60 |
| 70 | 7,01 | 4,92 | 4,07 | 3,60 | 3,29 | 3,07 | 2,78 | 2,45 | 2,28 | 2,07 | 1,82 | 1,53 |
| 80 | 6,96 | 4,88 | 4,04 | 3,56 | 3,26 | 3,04 | 2,74 | 2,42 | 2,24 | 2,03 | 1,78 | 1,49 |
| 90 | 6,92 | 4,85 | 4,01 | 3,53 | 3,23 | 3,01 | 2,72 | 2,39 | 2,21 | 2,00 | 1,75 | 1,45 |
| 100 | 6,90 | 4,82 | 3,98 | 3,51 | 3,21 | 2,99 | 2,69 | 2,37 | 2,19 | 1,98 | 1,73 | 1,43 |
| 125 | 6,84 | 4,78 | 3,94 | 3,47 | 3,17 | 2,95 | 2,66 | 2,33 | 2,15 | 1,94 | 1,69 | 1,37 |
| 150 | 6,81 | 4,75 | 3,91 | 3,45 | 3,14 | 2,92 | 2,63 | 2,31 | 2,13 | 1,92 | 1,66 | 1,33 |
| 200 | 6,76 | 4,71 | 3,88 | 3,41 | 3,11 | 2,89 | 2,60 | 2,28 | 2,09 | 1,88 | 1,62 | 1,28 |
| 300 | 6,72 | 4,68 | 3,85 | 3,38 | 3,08 | 2,86 | 2,57 | 2,24 | 2,06 | 1,85 | 1,59 | 1,22 |
| 400 | 6,70 | 4,66 | 3,83 | 3,37 | 3,06 | 2,85 | 2,56 | 2,23 | 2,04 | 1,84 | 1,57 | 1,15 |
| 500 | 6,69 | 4,65 | 3,82 | 3,36 | 3,05 | 2,84 | 2,55 | 2,22 | 2,03 | 1,83 | 1,56 | 1,16 |
| 1000 | 6,66 | 4,63 | 3,80 | 3,34 | 3,04 | 2,82 | 2,53 | 2,20 | 2,01 | 1,81 | 1,54 | 1,11 |
| >1000 | 6,64 | 4,60 | 3,78 | 3,32 | 3,02 | 2,80 | 2,51 | 2,18 | 1,99 | 1,79 | 1,52 | 1,00 |
Таблица.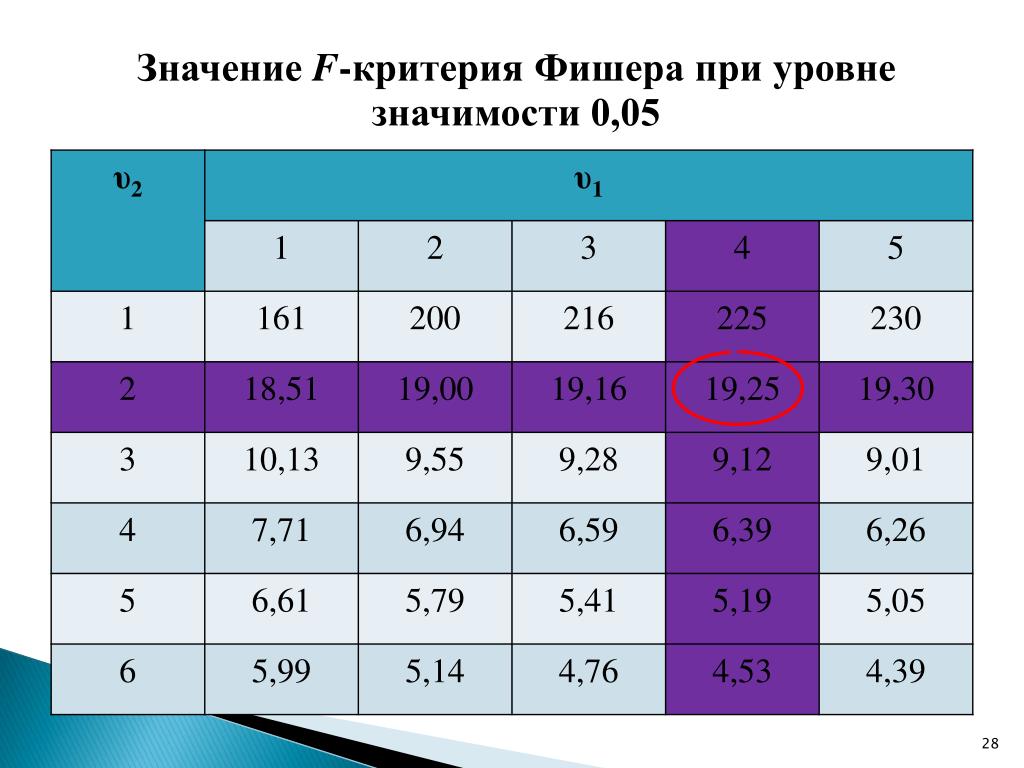 Часть 1
Часть 1
Таблица. Часть 2
Распределение Фишера (F-распределение)
Примеры решенийКоэффициент СпирменаКоэффициент Фехнера Множественная регрессияНелинейная регрессия Уравнение регрессии Автокорреляция Расчет параметров трендаОшибка аппроксимации
| a=0.10 | число степеней свободы v1 | |||||||||||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 15 | 20 | 24 | 30 | 40 | 60 | 120 | ||
| число степеней свободы v2 | 1 | 39,86 | 49,50 | 53,59 | 55,83 | 57,24 | 58,20 | 58,91 | 59,44 | 59,86 | 60,19 | 60,50 | 60,71 | 61,22 | 61,74 | 62,00 | 62,26 | 62,53 | 62,79 | 63,06 |
| 2 | 8,53 | 9,00 | 9,16 | 9,24 | 9,29 | 9,33 | 9,35 | 9,37 | 9,38 | 9,39 | 9,40 | 9,41 | 9,42 | 9,44 | 9,45 | 9,46 | 9,47 | 9,47 | 9,48 | |
| 3 | 5,54 | 5,46 | 5,39 | 5,34 | 5,31 | 5,28 | 5,27 | 5,25 | 5,24 | 5,23 | 5,22 | 5,22 | 5,20 | 5,18 | 5,18 | 5,17 | 5,16 | 5,15 | 5,14 | |
| 4 | 4,54 | 4,32 | 4,19 | 4,11 | 4,05 | 4,01 | 3,98 | 3,95 | 3,94 | 3,92 | 3,91 | 3,90 | 3,87 | 3,84 | 3,83 | 3,82 | 3,80 | 3,79 | 3,78 | |
| 5 | 4,06 | 3,78 | 3,62 | 3,52 | 3,45 | 3,40 | 3,37 | 3,34 | 3,32 | 3,30 | 3,28 | 3,27 | 3,24 | 3,21 | 3,19 | 3,17 | 3,16 | 3,14 | 3,12 | |
| 6 | 3,78 | 3,46 | 3,29 | 3,11 | 3,05 | 3,01 | 2,98 | 2,96 | 2,94 | 2,92 | 2,90 | 2,87 | 2,84 | 2,82 | 2,80 | 2,78 | 2,76 | 2,74 | ||
| 7 | 3,59 | 3,26 | 3,07 | 2,96 | 2,88 | 2,83 | 2,78 | 2,75 | 2,72 | 2,70 | 2,68 | 2,67 | 2,63 | 2,59 | 2,58 | 2,56 | 2,54 | 2,51 | 2,49 | |
| 8 | 3,46 | 3,11 | 2,92 | 2,81 | 2,73 | 2,67 | 2,62 | 2,59 | 2,56 | 2,54 | 2,52 | 2,50 | 2,46 | 2,42 | 2,40 | 2,38 | 2,36 | 2,34 | 2,32 | |
| 9 | 3,36 | 3,01 | 2,81 | 2,69 | 2,61 | 2,55 | 2,51 | 2,47 | 2,44 | 2,42 | 2,40 | 2,38 | 2,34 | 2,30 | 2,28 | 2,25 | 2,23 | 2,21 | 2,18 | |
| 10 | 3,29 | 2,92 | 2,73 | 2,61 | 2,52 | 2,46 | 2,41 | 2,38 | 2,35 | 2,32 | 2,30 | 2,28 | 2,24 | 2,20 | 2,18 | 2,16 | 2,13 | 2,11 | 2,08 | |
| 11 | 3,23 | 2,86 | 2,66 | 2,54 | 2,45 | 2,39 | 2,34 | 2,30 | 2,27 | 2,25 | 2,23 | 2,21 | 2,17 | 2,12 | 2,10 | 2,08 | 2,05 | 2,03 | 2,00 | |
| 12 | 3,18 | 2,81 | 2,61 | 2,48 | 2,39 | 2,33 | 2,28 | 2,24 | 2,21 | 2,19 | 2,17 | 2,15 | 2,10 | 2,06 | 2,04 | 2,01 | 1,99 | 1,96 | 1,93 | |
| 13 | 3,14 | 2,76 | 2,56 | 2,43 | 2,35 | 2,28 | 2,23 | 2,20 | 2,16 | 2,14 | 2,12 | 2,10 | 2,05 | 2,01 | 1,98 | 1,96 | 1,93 | 1,90 | 1,88 | |
| 14 | 3,10 | 2,73 | 2,52 | 2,39 | 2,31 | 2,24 | 2,19 | 2,15 | 2,12 | 2,10 | 2,08 | 2,05 | 2,01 | 1,96 | 1,94 | 1,91 | 1,89 | 1,86 | 1,83 | |
| 15 | 3,07 | 2,70 | 2,49 | 2,36 | 2,27 | 2,21 | 2,16 | 2,12 | 2,09 | 2,06 | 2,04 | 2,02 | 1,97 | 1,92 | 1,90 | 1,87 | 1,85 | 1,82 | 1,79 | |
| 16 | 3,05 | 2,67 | 2,46 | 2,33 | 2,24 | 2,18 | 2,13 | 2,09 | 2,06 | 2,03 | 1,99 | 1,94 | 1,89 | 1,87 | 1,84 | 1,81 | 1,78 | 1,75 | ||
| 17 | 3,03 | 2,64 | 2,44 | 2,31 | 2,22 | 2,15 | 2,10 | 2,06 | 2,03 | 2,00 | 1,98 | 1,96 | 1,91 | 1,86 | 1,84 | 1,81 | 1,78 | 1,75 | 1,72 | |
| 18 | 3,01 | 2,62 | 2,42 | 2,29 | 2,20 | 2,13 | 2,08 | 2,04 | 2,00 | 1,98 | 1,96 | 1,93 | 1,89 | 1,84 | 1,81 | 1,78 | 1,75 | 1,72 | 1,69 | |
| 19 | 2,99 | 2,61 | 2,40 | 2,27 | 2,18 | 2,11 | 2,06 | 2,02 | 1,98 | 1,96 | 1,94 | 1,91 | 1,86 | 1,81 | 1,79 | 1,76 | 1,73 | 1,70 | 1,67 | |
| 20 | 2,97 | 2,59 | 2,38 | 2,25 | 2,16 | 2,09 | 2,04 | 2,00 | 1,96 | 1,94 | 1,92 | 1,89 | 1,84 | 1,79 | 1,77 | 1,74 | 1,71 | 1,68 | 1,64 | |
| 22 | 2,95 | 2,56 | 2,35 | 2,22 | 2,13 | 2,06 | 2,01 | 1,97 | 1,93 | 1,90 | 1,88 | 1,86 | 1,81 | 1,76 | 1,73 | 1,70 | 1,67 | 1,64 | 1,60 | |
| 24 | 2,93 | 2,54 | 2,33 | 2,19 | 2,10 | 2,04 | 1,98 | 1,94 | 1,91 | 1,88 | 1,85 | 1,83 | 1,78 | 1,73 | 1,70 | 1,67 | 1,64 | 1,61 | 1,57 | |
| 26 | 2,91 | 2,52 | 2,31 | 2,17 | 2,08 | 2,01 | 1,96 | 1,92 | 1,88 | 1,86 | 1,84 | 1,81 | 1,76 | 1,71 | 1,68 | 1,65 | 1,61 | 1,58 | 1,54 | |
| 28 | 2,89 | 2,50 | 2,29 | 2,16 | 2,06 | 2,00 | 1,94 | 1,90 | 1,87 | 1,84 | 1,81 | 1,79 | 1,74 | 1,69 | 1,66 | 1,63 | 1,59 | 1,56 | 1,52 | |
| 30 | 2,88 | 2,49 | 2,28 | 2,14 | 2,05 | 1,98 | 1,93 | 1,88 | 1,85 | 1,82 | 1,79 | 1,77 | 1,72 | 1,67 | 1,64 | 1,61 | 1,57 | 1,54 | 1,50 | |
| 40 | 2,84 | 2,44 | 2,23 | 2,09 | 2,00 | 1,93 | 1,87 | 1,83 | 1,79 | 1,76 | 1,73 | 1,71 | 1,66 | 1,61 | 1,57 | 1,54 | 1,51 | 1,47 | 1,42 | |
| 60 | 2,79 | 2,39 | 2,18 | 2,04 | 1,95 | 1,87 | 1,82 | 1,77 | 1,74 | 1,71 | 1,68 | 1,66 | 1,60 | 1,54 | 1,51 | 1,48 | 1,44 | 1,40 | 1,35 | |
| 120 | 2,75 | 2,35 | 2,13 | 1,99 | 1,90 | 1,82 | 1,77 | 1,72 | 1,68 | 1,65 | 1,62 | 1,60 | 1,55 | 1,48 | 1,45 | 1,41 | 1,37 | 1,32 | 1,26 | |
α=0. 05 05
| число степеней свободы v1 | |||||||||||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 15 | 20 | 24 | 30 | 40 | 60 | 120 | ||
| число степеней свободы v2 | 1 | 161 | 200 | 216 | 225 | 230 | 234 | 237 | 239 | 271 | 242 | 243 | 244 | 246 | 248 | 249 | 250 | 251 | 252 | 253 |
| 2 | 18,5 | 19,0 | 19,2 | 19,2 | 19,3 | 19,3 | 19,4 | 19,4 | 19,4 | 19,4 | 19,4 | 19,4 | 19,4 | 19,4 | 19,5 | 19,5 | 19,5 | 19,5 | 19,5 | |
| 3 | 10,1 | 9,55 | 9,28 | 9,12 | 9,01 | 8,94 | 8,89 | 8,85 | 8,81 | 8,79 | 8,76 | 8,74 | 8,70 | 8,66 | 8,64 | 8,62 | 8,59 | 8,57 | 8,55 | |
| 4 | 7,71 | 6,94 | 6,59 | 6,39 | 6,26 | 6,16 | 6,09 | 6,04 | 6,00 | 5,96 | 5,94 | 5,91 | 5,86 | 5,80 | 5,77 | 5,75 | 5,72 | 5,69 | 5,66 | |
| 5 | 6,61 | 5,79 | 5,41 | 5,19 | 5,05 | 4,95 | 4,88 | 4,82 | 4,77 | 4,74 | 4,71 | 4,68 | 4,62 | 4,56 | 4,53 | 4,50 | 4,46 | 4,43 | 4,40 | |
| 6 | 5,99 | 5,14 | 4,76 | 4,53 | 4,39 | 4,28 | 4,21 | 4,15 | 4,10 | 4,06 | 4,03 | 4,00 | 3,94 | 3,87 | 3,84 | 3,81 | 3,77 | 3,74 | 3,70 | |
| 7 | 5,59 | 4,74 | 4,35 | 4,12 | 3,97 | 3,87 | 3,79 | 3,73 | 3,68 | 3,64 | 3,60 | 3,57 | 3,51 | 3,44 | 3,41 | 3,38 | 3,34 | 3,30 | 3,27 | |
| 8 | 5,32 | 4,46 | 4,07 | 3,84 | 3,69 | 3,58 | 3,50 | 3,44 | 3,39 | 3,35 | 3,31 | 3,28 | 3,22 | 3,15 | 3,12 | 3,08 | 3,04 | 3,01 | 2,97 | |
| 9 | 5,12 | 4,26 | 3,86 | 3,63 | 3,48 | 3,37 | 3,29 | 3,23 | 3,18 | 3,14 | 3,10 | 3,07 | 3,01 | 2,94 | 2,90 | 2,86 | 2,83 | 2,79 | 2,75 | |
| 10 | 4,96 | 4,10 | 3,71 | 3,48 | 3,33 | 3,22 | 3,14 | 3,07 | 3,02 | 2,98 | 2,94 | 2,91 | 2,85 | 2,77 | 2,74 | 2,70 | 2,66 | 2,62 | 2,58 | |
| 11 | 4,84 | 3,98 | 3,59 | 3,36 | 3,20 | 3,09 | 3,01 | 2,95 | 2,90 | 2,85 | 2,82 | 2,79 | 2,72 | 2,65 | 2,61 | 2,57 | 2,53 | 2,49 | 2,45 | |
| 12 | 4,75 | 3,89 | 3,49 | 3,26 | 3,11 | 3,00 | 2,91 | 2,85 | 2,80 | 2,75 | 2,72 | 2,69 | 2,62 | 2,54 | 2,51 | 2,47 | 2,43 | 2,38 | 2,34 | |
| 13 | 4,67 | 3,81 | 3,41 | 3,18 | 3,03 | 2,92 | 2,83 | 2,77 | 2,71 | 2,67 | 2,63 | 2,60 | 2,53 | 2,46 | 2,42 | 2,38 | 2,34 | 2,30 | 2,25 | |
| 14 | 4,60 | 3,74 | 3,34 | 3,11 | 2,96 | 2,85 | 2,76 | 2,70 | 2,65 | 2,60 | 2,57 | 2,53 | 2,46 | 2,39 | 2,35 | 2,31 | 2,27 | 2,22 | 2,18 | |
| 15 | 4,54 | 3,68 | 3,29 | 3,06 | 2,90 | 2,79 | 2,71 | 2,64 | 2,59 | 2,54 | 2,51 | 2,48 | 3,52 | 3,37 | 3,29 | 3,21 | 3,13 | 3,05 | 2,96 | |
| 16 | 4,49 | 3,63 | 3,24 | 3,01 | 2,85 | 2,74 | 2,66 | 2,59 | 2,54 | 2,49 | 2,46 | 2,42 | 2,35 | 2,28 | 2,24 | 2,19 | 2,15 | 2,11 | 2,06 | |
| 17 | 4,45 | 3,59 | 3,20 | 2,96 | 2,81 | 2,70 | 2,61 | 2,55 | 2,49 | 2,45 | 2,41 | 2,38 | 2,31 | 2,23 | 2,19 | 2,15 | 2,10 | 2,06 | 2,01 | |
| 18 | 4,41 | 3,55 | 3,16 | 2,93 | 2,77 | 2,66 | 2,58 | 2,51 | 2,46 | 2,41 | 2,37 | 2,34 | 2,27 | 2,19 | 2,15 | 2,11 | 2,06 | 2,02 | 1,97 | |
| 19 | 4,38 | 3,52 | 3,13 | 2,90 | 2,74 | 2,63 | 2,54 | 2,48 | 2,42 | 2,38 | 2,34 | 2,31 | 2,23 | 2,16 | 2,11 | 2,07 | 2,03 | 1,98 | 1,93 | |
| 20 | 4,35 | 3,49 | 3,10 | 2,87 | 2,71 | 2,60 | 2,51 | 2,45 | 2,39 | 2,35 | 2,31 | 2,28 | 2,20 | 2,12 | 2,08 | 2,04 | 1,99 | 1,95 | 1,90 | |
| 22 | 4,30 | 3,44 | 3,05 | 2,82 | 2,66 | 2,55 | 2,46 | 2,40 | 2,34 | 2,30 | 2,26 | 2,23 | 2,15 | 2,07 | 2,03 | 1,98 | 1,94 | 1,89 | 1,84 | |
| 24 | 4,26 | 3,40 | 3,01 | 2,78 | 2,62 | 2,51 | 2,42 | 2,36 | 2,30 | 2,25 | 2,21 | 2,18 | 2,11 | 2,03 | 1,98 | 1,94 | 1,89 | 1,84 | 1,79 | |
| 26 | 4,23 | 3,37 | 2,98 | 2,74 | 2,59 | 2,47 | 2,39 | 2,32 | 2,27 | 2,22 | 2,18 | 2,15 | 2,07 | 1,99 | 1,95 | 1,90 | 1,85 | 1,80 | 1,75 | |
| 28 | 4,20 | 3,34 | 2,95 | 2,71 | 2,56 | 2,45 | 2,36 | 2,29 | 2,24 | 2,19 | 2,15 | 2,12 | 2,04 | 1,96 | 1,91 | 1,87 | 1,82 | 1,77 | 1,71 | |
| 30 | 4,17 | 3,32 | 2,92 | 2,69 | 2,53 | 2,42 | 2,33 | 2,27 | 2,21 | 2,16 | 2,13 | 2,09 | 2,01 | 1,93 | 1,89 | 1,84 | 1,79 | 1,74 | 1,68 | |
| 40 | 4,08 | 3,23 | 2,84 | 2,61 | 2,45 | 2,34 | 2,25 | 2,18 | 2,12 | 2,08 | 2,04 | 2,00 | 1,92 | 1,84 | 1,79 | 1,74 | 1,69 | 1,64 | 1,58 | |
| 60 | 4,00 | 3,15 | 2,76 | 2,53 | 2,37 | 2,25 | 2,17 | 2,10 | 2,04 | 1,99 | 1,95 | 1,92 | 1,84 | 1,75 | 1,70 | 1,65 | 1,59 | 1,53 | 1,47 | |
| 120 | 3,92 | 3,07 | 2,68 | 2,45 | 2,29 | 2,17 | 2,09 | 2,02 | 1,96 | 1,91 | 1,87 | 1,83 | 1,75 | 1,66 | 1,61 | 1,55 | 1,50 | 1,43 | 1,35 | |
k2—число степеней свободы меньшей дисперсии)
Уровень значимости a =0.
 01
01
| k1k2 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 1 | 4052 | 4999 | 5403 | 5625 | 5764 | 5889 | 5928 | 5981 | 6022 | 6056 | 6082 | 6106 |
| 2 | 98.49 | 99.01 | 90.17 | 99.25
| 99.33
| 99.30
| 99.34
| 99.36
| 99.36
| 99.40
| 99.41
| 99.42 |
| 3 | 34.12 | 30.81 | 29.46 | 28.71
| 28.24
| 27.91
| 27.67
| 27.49
| 27. 34 34
| 27.23
| 27.13
| 27.05 |
| 4 | 21.20 | 18.00 | 16.69 | 15.98
| 15.52
| 15.21
| 14.98
| 14.80
| 14.66
| 14.54
| 14.45
| 14.37 |
| 5 | 16.26 | 13.27 | 12.06 | 11.39
| 10.97
| 10.67
| 10.45
| 10.27
| 10.15
| 10.05
| 9.96
| 9.89 |
| 6 | 13.74 | 10.92 | 9.78 | 9.15
| 8.75
| 8.47
| 8.26
| 8.10
| 7.98
| 7.87
| 7.79
| 7.72 |
| 7 | 12.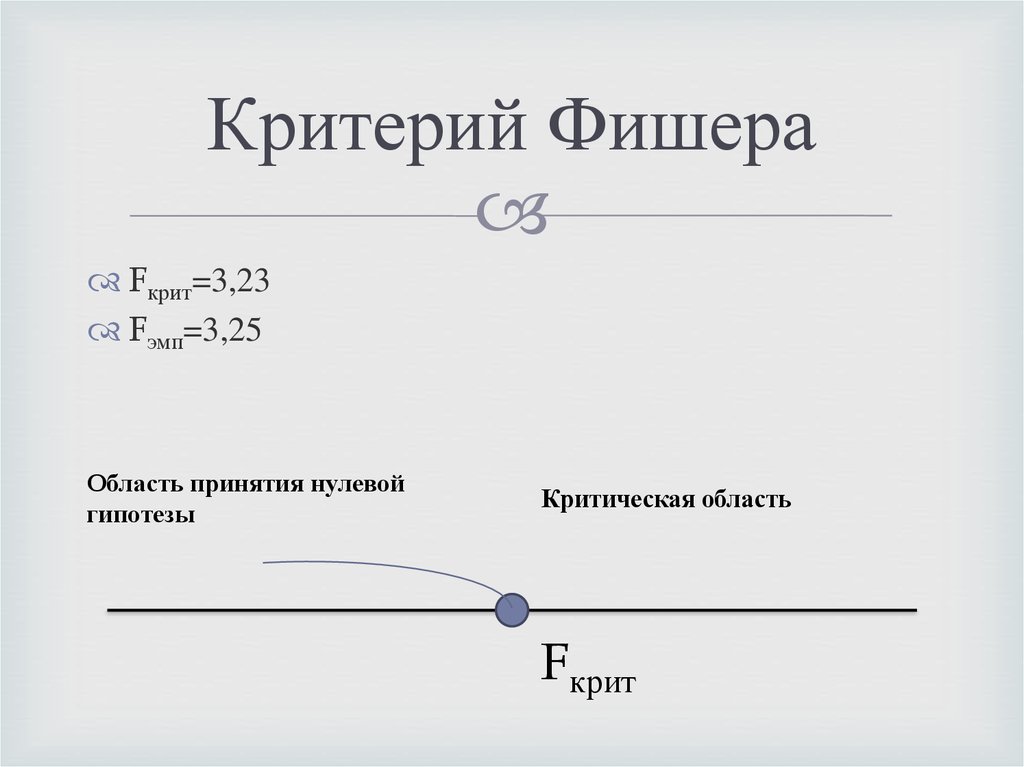 25 25
| 9.55 | 8.45 | 7.85
| 7.46
| 7.19
| 7.00
| 6.84
| 6.71
| 6.62
| 6.54
| 6.47 |
| 8 | 11.26 | 8.65 | 7.59 | 7.01
| 6.63
| 6.37
| 6.19
| 6.03
| 5.91
| 5.82
| 5.74
| 5.67 |
| 9 | 10.56 | 8.02 | 6.99 | 6.42 | 6.06 | 5.80 | 5.62 | 5.47 | 5.35 | 5.26 | 5.18 | 5.11 |
| 10 | 10.04 | 7.56 | 6.55 | 5.99 | 5.64 | 5.39 | 5.21 | 5.06 | 4.95 | 4.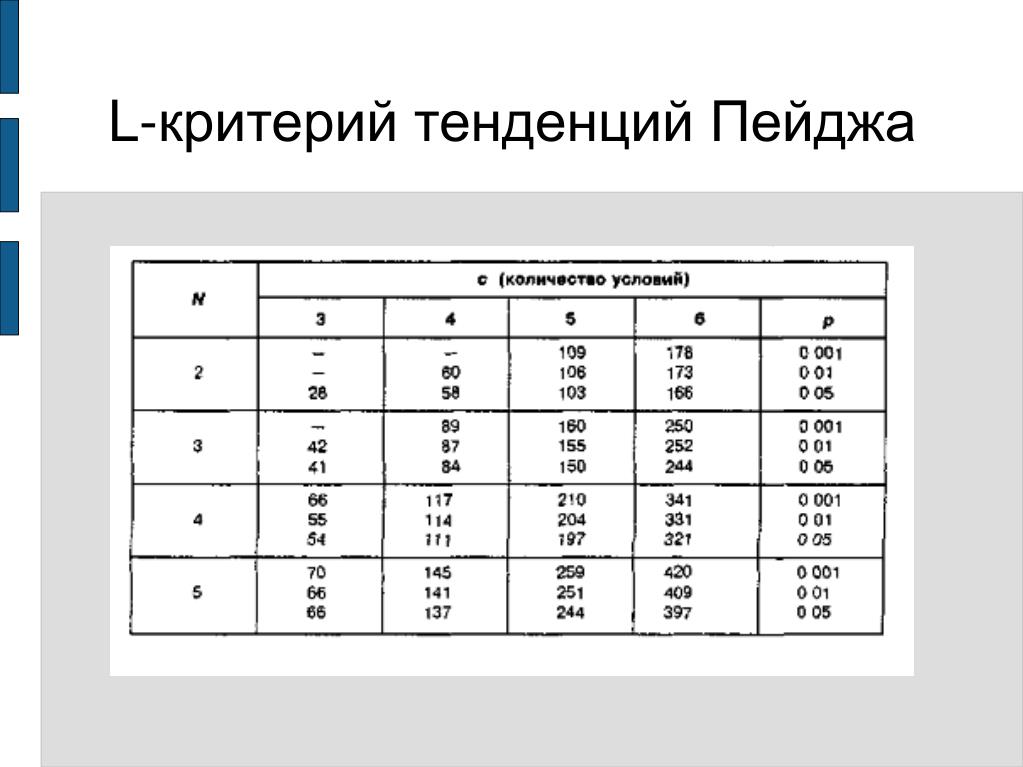 85 85
| 4.78 | 4.71 |
| 11 | 9.86 | 7.20 | 6.22 | 5.67 | 5.32 | 5.07 | 4.88 | 4.74 | 4.63 | 4.54 | 4.46 | 4.40 |
| 12 | 9.33 | 6.93 | 5.95 | 5.41 | 5.06 | 4.82 | 4.65 | 4.50 | 4.39 | 4.30 | 4.22 | 4.16 |
| 13 | 9.07 | 6.70 | 5.74 | 5.20 | 4.86 | 4.62 | 4.44 | 4.30 | 4.19 | 4.10 | 4.02 | 3.96 |
| 14 | 8.86 | 6.51 | 5.56 | 5.03 | 4.69 | 4.46 | 4.28 | 4.14 | 4.03 | 3. 94 94
| 3.86 | 3.80 |
| 15 | 8.68 | 6.36 | 5.42 | 4.89 | 4.56 | 4.32 | 4.14 | 4.00 | 3.89 | 3.80 | 3.73 | 3.67 |
| 16 | 8.53 | 6.23 | 5.29 | 4.77 | 4.44 | 4.20 | 4.03 | 3.89 | 3.78 | 3.69 | 3.61 | 3.55 |
| 17 | 8.40 | 6.11 | 5.18 | 4.67 | 4.34 | 4.10 | 3.93 | 3.79 | 3.68 | 3.59 | 3.52 | 3.45 |
Уровень значимости a=0.05
| k1k2 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 1 | 161 | 200 | 216 | 225 | 230 | 234 | 237 | 239 | 241 | 242 | 243 | 244 |
| 2 | 18. 5 5
| 19.00 | 19.16 | 19.25 | 19:30 | 19.33 | 19.36 | 19.37 | 19.38 | 19.39 | 19.40 | 19.41 |
| 3 | 10.13 | 9.55 | 9.28 | 9.12 | 9.01 | 8.94 | 8.88 | 8.84 | 8.81 | 8.78 | 8.76 | 8.74 |
| 4 | 7.71 | 6.94 | 6.59 | 6.39 | 6.26 | 6.16 | 6.09 | 6.04 | 6.00 | 5.96 | 5.93 | 5.91 |
| 5 | 6.61 | 5.79 | 5.41 | 5.19 | 5.05 | 4.95 | 4.88 | 4.82 | 4.78 | 4.74 | 4.70 | 4.68 |
| 6 | 5.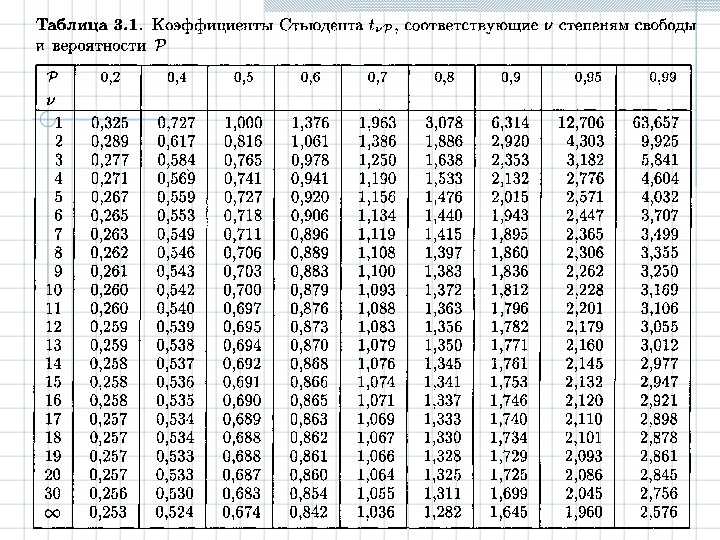 99 99
| 5.14 | 4.76 | 4.53 | 4.39 | 4.28 | 4.21 | 4.15 | 4.10 | 4.06 | 4.03 | 4.00 |
| 7 | 5.59 | 4.74 | 4.35 | 4.12 | 3.97 | 3.87 | 3.79 | 3.73 | 3.68 | 3.63 | 3.60 | 3.57 |
| 8 | 5.32 | 4.46 | 4.07 | 3.84 | 3.69 | 3.58 | 3.50 | 3.44 | 3.39 | 3.34 | 3.31 | 3.28 |
| 9 | 5.12 | 4.26 | 3.86 | 3.63 | 3.48 | 3.37 | 3.29 | 3.23 | 3.18 | 3.13 | 3.10 | 3.07 |
| 10 | 4. 96 96
| 4.10 | 3.71 | 3.48 | 3.33 | 3.22 | 3.14 | 3.07 | 3.02 | 2.97 | 2.94 | 2.91 |
| 11 | 4.84 | 3.98 | 3.59 | 3.36 | 3.20 | 3.09 | 3.01 | 2.95 | 2.90 | 2.86 | 2.82 | 2.79 |
| 12 | 4.75 | 3.88 | 3.49 | 3.26 | 3.11 | 3.00 | 2.92 | 2.85 | 2.80 | 2.76 | 2.72 | 2.69 |
| 13 | 4.67 | 3.80 | 3.41 | 3.18 | 3.02 | 2.92 | 2.84 | 2.77 | 2.72 | 2.67 | 2.63 | 2.60 |
| 14 | 4. 60 60
| 3.74 | 3.34 | 3.11 | 2.96 | 2.85 | 2.77 | 2.70 | 2.65 | 2.60 | 2.56 | 2.53 |
| 15 | 4.54 | 3.68 | 3.29 | 3.06 | 2.90 | 2.79 | 2.70 | 2.64 | 2.59 | 2.55 | 2.51 | 2.48 |
| 16 | 4.49 | 3.63 | 3.24 | 3.01 | 2.85 | 2.74 | 2.66 | 2.59 | 2.54 | 2.49 | 2.45 | 2.42 |
| 17 | 4.45 | 3.59 | 3.20 | 2.96 | 2.81 | 2.70 | 2.62 | 2.55 | 2.50 | 2.45 | 2.41 | 2.38 |
Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).
Таблица значений критерия Фишера (F-критерия)
Artman Таблицы
При α=0.05
f1 — число степеней свободы большей дисперсии
f2 — число степеней свободы меньшей дисперсии:
| f2 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 15 |
| 1 | 161. 45 45 | 199.50 | 215.71 | 224.58 | 230.16 | 233.99 | 236.77 | 238.88 | 240.54 | 241.88 | 245.95 |
| 2 | 18.51 | 19.00 | 19.16 | 19.25 | 19.30 | 19.33 | 19.35 | 19.37 | 19.38 | 19.40 | 19.43 |
| 3 | 10.13 | 9.55 | 9.28 | 9.12 | 9.01 | 8.94 | 8.89 | 8. 85 85 | 8.81 | 8.79 | 8.70 |
| 4 | 7.71 | 6.94 | 6.59 | 6.39 | 6.26 | 6.16 | 6.09 | 6.04 | 6.00 | 5.96 | 5.86 |
| 5 | 6.61 | 5.79 | 5.41 | 5.19 | 5.05 | 4.95 | 4.88 | 4.82 | 4.77 | 4.74 | 4.62 |
| 6 | 5.99 | 5.14 | 4. 76 76 | 4.53 | 4.39 | 4.28 | 4.21 | 4.15 | 4.10 | 4.06 | 3.94 |
| 7 | 5.59 | 4.74 | 4.35 | 4.12 | 3.97 | 3.87 | 3.79 | 3.73 | 3.68 | 3.64 | 3.51 |
| 8 | 5.32 | 4.46 | 4.07 | 3.84 | 3.69 | 3.58 | 3.50 | 3.44 | 3.39 | 3.35 | 3. 22 22 |
| 9 | 5.12 | 4.26 | 3.86 | 3.63 | 3.48 | 3.37 | 3.29 | 3.23 | 3.18 | 3.14 | 3.01 |
| 10 | 4.96 | 4.10 | 3.71 | 3.48 | 3.33 | 3.22 | 3.14 | 3.07 | 3.02 | 2.98 | 2.85 |
| 11 | 4.84 | 3.98 | 3.59 | 3.36 | 3.20 | 3. 09 09 | 3.01 | 2.95 | 2.90 | 2.85 | 2.72 |
| 12 | 4.75 | 3.89 | 3.49 | 3.26 | 3.11 | 3.00 | 2.91 | 2.85 | 2.80 | 2.75 | 2.62 |
| 13 | 4.67 | 3.81 | 3.41 | 3.18 | 3.03 | 2.92 | 2.83 | 2.77 | 2.71 | 2.67 | 2.53 |
| 14 | 4.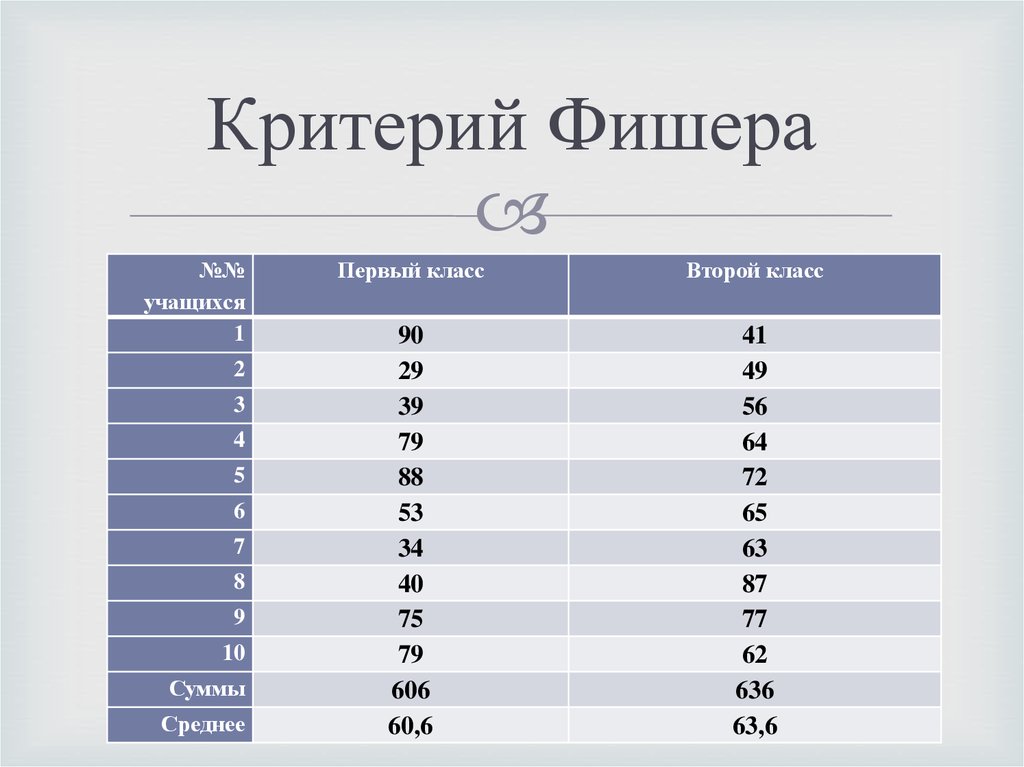 60 60 | 3.74 | 3.34 | 3.11 | 2.96 | 2.85 | 2.76 | 2.70 | 2.65 | 2.60 | 2.46 |
| 15 | 4.54 | 3.68 | 3.29 | 3.06 | 2.90 | 2.79 | 2.71 | 2.64 | 2.59 | 2.54 | 2.40 |
| 16 | 4.49 | 3.63 | 3.24 | 3.01 | 2.85 | 2.74 | 2.66 | 2.59 | 2. 54 54 | 2.49 | 2.35 |
| 17 | 4.45 | 3.59 | 3.20 | 2.96 | 2.81 | 2.70 | 2.61 | 2.55 | 2.49 | 2.45 | 2.31 |
| 18 | 4.41 | 3.55 | 3.16 | 2.93 | 2.77 | 2.66 | 2.58 | 2.51 | 2.46 | 2.41 | 2.27 |
| 19 | 4.38 | 3.52 | 3.13 | 2. 90 90 | 2.74 | 2.63 | 2.54 | 2.48 | 2.42 | 2.38 | 2.23 |
| 20 | 4.35 | 3.49 | 3.10 | 2.87 | 2.71 | 2.60 | 2.51 | 2.45 | 2.39 | 2.35 | 2.20 |
9755
35. Таблица значений F-критерия Фишера при уровне значимости
1 | 2 | 3 | 4 | 5 | 6 | 8 | 12 | 24 | ||
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
1 | 161,5 | 199,5 | 215,7 | 224,6 | 230,2 | 233,9 | 238,9 | 243,9 | 249,0 | 254,3 |
2 | 18,51 | 19,00 | 19,16 | 19,25 | 19,30 | 19,33 | 19,37 | 19,41 | 19,45 | 19,50 |
3 | 10,13 | 9,55 | 9,28 | 9,12 | 9,01 | 8,94 | 8,84 | 8,74 | 8,64 | 8,53 |
4 | 7,71 | 6,94 | 6,59 | 6,39 | 6,26 | 6,16 | 6,04 | 5,91 | 5,77 | 5,63 |
5 | 6,61 | 5,79 | 5,41 | 5,19 | 5,05 | 4,95 | 4,82 | 4,68 | 4,53 | 4,36 |
6 | 5,99 | 5,14 | 4,76 | 4,53 | 4,39 | 4,28 | 4,15 | 4,00 | 3,84 | 3,67 |
7 | 5,59 | 4,74 | 4,35 | 4,12 | 3,97 | 3,87 | 3,73 | 3,57 | 3,41 | 3,23 |
8 | 5,32 | 4,46 | 4,07 | 3,84 | 3,69 | 3,58 | 3,44 | 3,28 | 3,12 | 2,93 |
9 | 5,12 | 4,26 | 3,86 | 3,63 | 3,48 | 3,37 | 3,23 | 3,07 | 2,90 | 2,71 |
10 | 4,96 | 4,10 | 3,71 | 3,48 | 3,33 | 3,22 | 3,07 | 2,91 | 2,74 | 2,54 |
11 | 4,84 | 3,98 | 3,59 | 3,36 | 3,20 | 3,09 | 2,95 | 2,79 | 2,61 | 2,40 |
12 | 4,75 | 3,88 | 3,49 | 3,26 | 3,11 | 3,00 | 2,85 | 2,69 | 2,50 | 2,30 |
13 | 4,67 | 3,80 | 3,41 | 3,18 | 3,02 | 2,92 | 2,77 | 2,60 | 2,42 | 2,21 |
14 | 4,60 | 3,74 | 3,34 | 3,11 | 2,96 | 2,85 | 2,70 | 2,53 | 2,35 | 2,13 |
15 | 4,54 | 3,68 | 3,29 | 3,06 | 2,90 | 2,79 | 2,64 | 2,48 | 2,29 | 2,07 |
16 | 4,49 | 3,63 | 3,24 | 3,01 | 2,85 | 2,74 | 2,59 | 2,42 | 2,24 | 2,01 |
17 | 4,45 | 3,59 | 3,20 | 2,96 | 2,81 | 2,70 | 2,55 | 2,38 | 2,19 | 1,96 |
18 | 4,41 | 3,55 | 3,16 | 2,93 | 2,77 | 2,66 | 2,51 | 2,34 | 2,15 | 1,92 |
19 | 4,38 | 3,52 | 3,13 | 2,90 | 2,74 | 2,63 | 2,48 | 2,31 | 2,11 | 1,88 |
20 | 4,35 | 3,49 | 3,10 | 2,87 | 2,71 | 2,60 | 2,45 | 2,28 | 2,08 | 1,84 |
21 | 4,32 | 3,47 | 3,07 | 2,84 | 2,68 | 2,57 | 2,42 | 2,25 | 2,05 | 1,81 |
22 | 4,30 | 3,44 | 3,05 | 2,82 | 2,66 | 2,55 | 2,40 | 2,23 | 2,03 | 1,78 |
23 | 4,28 | 3,42 | 3,03 | 2,80 | 2,64 | 2,53 | 2,38 | 2,20 | 2,00 | 1,76 |
24 | 4,26 | 3,40 | 3,01 | 2,78 | 2,62 | 2,51 | 2,36 | 2,18 | 1,98 | 1,73 |
25 | 4,24 | 3,38 | 2,99 | 2,76 | 2,60 | 2,49 | 2,34 | 2,16 | 1,96 | 1,71 |
26 | 4,22 | 3,37 | 2,98 | 2,74 | 2,59 | 2,47 | 2,32 | 2,15 | 1,95 | 1,69 |
27 | 4,21 | 3,35 | 2,96 | 2,73 | 2,57 | 2,46 | 2,30 | 2,13 | 1,93 | 1,67 |
28 | 4,20 | 3,34 | 2,95 | 2,71 | 2,56 | 2,44 | 2,29 | 2,12 | 1,91 | 1,65 |
29 | 4,18 | 3,33 | 2,93 | 2,70 | 2,54 | 2,43 | 2,28 | 2,10 | 1,90 | 1,64 |
30 | 4,17 | 3,32 | 2,92 | 2,69 | 2,53 | 2,42 | 2,27 | 2,09 | 1,89 | 1,62 |
35 | 4,12 | 3,26 | 2,87 | 2,64 | 2,48 | 2,37 | 2,22 | 2,04 | 1,83 | 1,57 |
40 | 4,08 | 3,23 | 2,84 | 2,61 | 2,45 | 2,34 | 2,18 | 2,00 | 1,79 | 1,51 |
45 | 4,06 | 3,21 | 2,81 | 2,58 | 2,42 | 2,31 | 2,15 | 1,97 | 1,76 | 1,48 |
50 | 4,03 | 3,18 | 2,79 | 2,56 | 2,40 | 2,29 | 2,13 | 1,95 | 1,74 | 1,44 |
60 | 4,00 | 3,15 | 2,76 | 2,52 | 2,37 | 2,25 | 2,10 | 1,92 | 1,70 | 1,39 |
70 | 3,98 | 3,13 | 2,74 | 2,50 | 2,35 | 2,23 | 2,07 | 1,89 | 1,67 | 1,35 |
80 | 3,96 | 3,11 | 2,72 | 2,49 | 2,33 | 2,21 | 2,06 | 1,88 | 1,65 | 1,31 |
90 | 3,95 | 3,10 | 2,71 | 2,47 | 2,32 | 2,20 | 2,04 | 1,86 | 1,64 | 1,28 |
100 | 3,94 | 3,09 | 2,70 | 2,46 | 2,30 | 2,19 | 2,03 | 1,85 | 1,63 | 1,26 |
125 | 3,92 | 3,07 | 2,68 | 2,44 | 2,29 | 2,17 | 2,01 | 1,83 | 1,60 | 1,21 |
150 | 3,90 | 3,06 | 2,66 | 2,43 | 2,27 | 2,16 | 2,00 | 1,82 | 1,59 | 1,18 |
200 | 3,89 | 3,04 | 2,65 | 2,42 | 2,26 | 2,14 | 1,98 | 1,80 | 1,57 | 1,14 |
300 | 3,87 | 3,03 | 2,64 | 2,41 | 2,25 | 2,13 | 1,97 | 1,79 | 1,55 | 1,10 |
400 | 3,86 | 3,02 | 2,63 | 2,40 | 2,24 | 2,12 | 1,96 | 1,78 | 1,54 | 1,07 |
500 | 3,86 | 3,01 | 2,62 | 2,39 | 2,23 | 2,11 | 1,96 | 1,77 | 1,54 | 1,06 |
1000 | 3,85 | 3,00 | 2,61 | 2,38 | 2,22 | 2,10 | 1,95 | 1,76 | 1,53 | 1,03 |
3,84 | 2,99 | 2,60 | 2,37 | 2,21 | 2,09 | 1,94 | 1,75 | 1,52 | 1 |
| < Предыдущая | Следующая > |
|---|
35.
 Таблица значений F-критерия Фишера при уровне значимости a=0,05
Таблица значений F-критерия Фишера при уровне значимости a=0,05K1 K2 | 1 | 2 | 3 | 4 | 5 | 6 | 8 | 12 | 24 | ¥ |
1 | 161,45 | 199,50 | 215,72 | 224,57 | 230,17 | 233,97 | 238,89 | 243,91 | 249,04 | 254,32 |
2 | 18,51 | 19,00 | 19,16 | 19,25 | 19,30 | 19,33 | 19,37 | 19,41 | 19,45 | 19,50 |
3 | 10,13 | 9,55 | 9,28 | 9,12 | 9,01 | 8,94 | 8,84 | 8,74 | 8,64 | 8,53 |
4 | 7,71 | 6,94 | 6,59 | 6,39 | 6,26 | 6,16 | 6,04 | 5,91 | 5,77 | 5,63 |
5 | 6,61 | 5,79 | 5,41 | 5,19 | 5,05 | 4,95 | 4,82 | 4,68 | 4,53 | 4,36 |
6 | 5,99 | 5,14 | 4,76 | 4,53 | 4,39 | 4,28 | 4,15 | 4,00 | 3,84 | 3,67 |
7 | 5,59 | 4,74 | 4,35 | 4,12 | 3,97 | 3,87 | 3,73 | 3,57 | 3,41 | 3,23 |
8 | 5,32 | 4,46 | 4,07 | 3,84 | 3,69 | 3,58 | 3,44 | 3,28 | 3,12 | 2,93 |
9 | 5,12 | 4,26 | 3,86 | 3,63 | 3,48 | 3,37 | 3,23 | 3,07 | 2,90 | 2,71 |
10 | 4,96 | 4,10 | 3,71 | 3,48 | 3,33 | 3,22 | 3,07 | 2,91 | 2,74 | 2,54 |
11 | 4,84 | 3,98 | 3,59 | 3,36 | 3,20 | 3,09 | 2,95 | 2,79 | 2,61 | 2,40 |
12 | 4,75 | 3,88 | 3,49 | 3,26 | 3,11 | 3,00 | 2,85 | 2,69 | 2,50 | 2,30 |
13 | 4,67 | 3,80 | 3,41 | 3,18 | 3,02 | 2,92 | 2,77 | 2,60 | 2,42 | 2,21 |
14 | 4,60 | 3,74 | 3,34 | 3,11 | 2,96 | 2,85 | 2,70 | 2,53 | 2,35 | 2,13 |
15 | 4,54 | 3,68 | 3,29 | 3,06 | 2,90 | 2,79 | 2,64 | 2,48 | 2,29 | 2,07 |
16 | 4,49 | 3,63 | 3,24 | 3,01 | 2,85 | 2,74 | 2,59 | 2,42 | 2,24 | 2,01 |
17 | 4,45 | 3,59 | 3,20 | 2,96 | 2,81 | 2,70 | 2,55 | 2,38 | 2,19 | 1,96 |
18 | 4,41 | 3,55 | 3,16 | 2,93 | 2,77 | 2,66 | 2,51 | 2,34 | 2,15 | 1,92 |
19 | 4,38 | 3,52 | 3,13 | 2,90 | 2,74 | 2,63 | 2,48 | 2,31 | 2,11 | 1,88 |
20 | 4,35 | 3,49 | 3,10 | 2,87 | 2,71 | 2,60 | 2,45 | 2,28 | 2,08 | 1,84 |
21 | 4,32 | 3,47 | 3,07 | 2,84 | 2,68 | 2,57 | 2,42 | 2,25 | 2,05 | 1,81 |
22 | 4,30 | 3,44 | 3,05 | 2,82 | 2,66 | 2,55 | 2,40 | 2,23 | 2,03 | 1,78 |
23 | 4,28 | 3,42 | 3,03 | 2,80 | 2,64 | 2,53 | 2,38 | 2,20 | 2,00 | 1,76 |
24 | 4,26 | 3,40 | 3,01 | 2,78 | 2,62 | 2,51 | 2,36 | 2,18 | 1,98 | 1,73 |
25 | 4,24 | 3,38 | 2,99 | 2,76 | 2,60 | 2,49 | 2,34 | 2,16 | 1,96 | 1,71 |
26 | 4,22 | 3,37 | 2,98 | 2,74 | 2,59 | 2,47 | 2,32 | 2,15 | 1,95 | 1,69 |
27 | 4,21 | 3,35 | 2,96 | 2,73 | 2,57 | 2,46 | 2,30 | 2,13 | 1,93 | 1,67 |
28 | 4,20 | 3,34 | 2,95 | 2,71 | 2,56 | 2,44 | 2,29 | 2,12 | 1,91 | 1,65 |
29 | 4,18 | 3,33 | 2,93 | 2,70 | 2,54 | 2,43 | 2,28 | 2,10 | 1,90 | 1,64 |
30 | 4,17 | 3,32 | 2,92 | 2,69 | 2,53 | 2,42 | 2,27 | 2,09 | 1,89 | 1,62 |
35 | 4,12 | 3,26 | 2,87 | 2,64 | 2,48 | 2,37 | 2,22 | 2,04 | 1,83 | 1,57 |
40 | 4,08 | 3,23 | 2,84 | 2,61 | 2,45 | 2,34 | 2,18 | 2,00 | 1,79 | 1,51 |
45 | 4,06 | 3,21 | 2,81 | 2,58 | 2,42 | 2,31 | 2,15 | 1,97 | 1,76 | 1,48 |
50 | 4,03 | 3,18 | 2,79 | 2,56 | 2,40 | 2,29 | 2,13 | 1,95 | 1,74 | 1,44 |
60 | 4,00 | 3,15 | 2,76 | 2,52 | 2,37 | 2,25 | 2,10 | 1,92 | 1,70 | 1,39 |
70 | 3,98 | 3,13 | 2,74 | 2,50 | 2,35 | 2,23 | 2,07 | 1,89 | 1,67 | 1,35 |
80 | 3,96 | 3,11 | 2,72 | 2,49 | 2,33 | 2,21 | 2,06 | 1,88 | 1,65 | 1,31 |
90 | 3,95 | 3,10 | 2,71 | 2,47 | 2,32 | 2,20 | 2,04 | 1,86 | 1,64 | 1,28 |
100 | 3,94 | 3,09 | 2,70 | 2,46 | 2,30 | 2,19 | 2,03 | 1,85 | 1,63 | 1,26 |
125 | 3,92 | 3,07 | 2,68 | 2,44 | 2,29 | 2,17 | 2,01 | 1,83 | 1,60 | 1,21 |
150 | 3,90 | 3,06 | 2,66 | 2,43 | 2,27 | 2,16 | 2,00 | 1,82 | 1,59 | 1,18 |
200 | 3,89 | 3,04 | 2,65 | 2,42 | 2,26 | 2,14 | 1,98 | 1,80 | 1,57 | 1,14 |
300 | 3,87 | 3,03 | 2,64 | 2,41 | 2,25 | 2,13 | 1,97 | 1,79 | 1,55 | 1,10 |
400 | 3,86 | 3,02 | 2,63 | 2,40 | 2,24 | 2,12 | 1,96 | 1,78 | 1,54 | 1,07 |
500 | 3,86 | 3,01 | 2,62 | 2,39 | 2,23 | 2,11 | 1,96 | 1,77 | 1,54 | 1,06 |
1000 | 3,85 | 3,00 | 2,61 | 2,38 | 2,22 | 2,10 | 1,95 | 1,76 | 1,53 | 1,03 |
¥ | 3,84 | 2,99 | 2,60 | 2,37 | 2,21 | 2,09 | 1,94 | 1,75 | 1,52 | 1,00 |
| < Предыдущая | Следующая > |
|---|
Статистико-математические таблицы.
 Таблица значений F-критерия Фишера при уровне значимости α =0,05 k1 k2 — Студопедия
Таблица значений F-критерия Фишера при уровне значимости α =0,05 k1 k2 — СтудопедияПоделись
Таблица значений F-критерия Фишера
при уровне значимости α =0,05
| k1 k2 | ∞ | |||||||||
| 161,45 | 199,50 | 215,72 | 224,57 | 230,17 | 233,97 | 238,89 | 243,91 | 249,04 | 254,32 | |
| 18,51 | 19,00 | 19,16 | 19,25 | 19,30 | 19,33 | 19,37 | 19,41 | 19,45 | 19,50 | |
| 10,13 | 9,55 | 9,28 | 9,12 | 9,01 | 8,94 | 8,84 | 8,74 | 8,64 | 8,53 | |
| 7,71 | 6,94 | 6,59 | 6,39 | 6,26 | 6,16 | 6,04 | 5,91 | 5,77 | 5,63 | |
| 6,61 | 5,79 | 5,41 | 5,19 | 5,05 | 4,95 | 4,82 | 4,68 | 4,53 | 4,36 | |
| 5,99 | 5,14 | 4,76 | 4,53 | 4,39 | 4,28 | 4,15 | 4,00 | 3,84 | 3,67 | |
| 5,59 | 4,74 | 4,35 | 4,12 | 3,97 | 3,87 | 3,73 | 3,57 | 3,41 | 3,23 | |
| 5,32 | 4,46 | 4,07 | 3,84 | 3,69 | 3,58 | 3,44 | 3,28 | 3,12 | 2,93 | |
| 5,12 | 4,26 | 3,86 | 3,63 | 3,48 | 3,37 | 3,23 | 3,07 | 2,90 | 2,71 | |
| 4,96 | 4,10 | 3,71 | 3,48 | 3,33 | 3,22 | 3,07 | 2,91 | 2,74 | 2,54 | |
| 4,84 | 3,98 | 3,59 | 3,36 | 3,20 | 3,09 | 2,95 | 2,79 | 2,61 | 2,40 | |
| 4,75 | 3,88 | 3,49 | 3,26 | 3,11 | 3,00 | 2,85 | 2,69 | 2,50 | 2,30 | |
| 4,67 | 3,80 | 3,41 | 3,18 | 3,02 | 2,92 | 2,77 | 2,60 | 2,42 | 2,21 | |
| 4,60 | 3,74 | 3,34 | 3,11 | 2,96 | 2,85 | 2,70 | 2,53 | 2,35 | 2,13 | |
| 4,54 | 3,68 | 3,29 | 3,06 | 2,90 | 2,79 | 2,64 | 2,48 | 2,29 | 2,07 | |
| 4,49 | 3,63 | 3,24 | 3,01 | 2,85 | 2,74 | 2,59 | 2,42 | 2,24 | 2,01 | |
| 4,45 | 3,59 | 3,20 | 2,96 | 2,81 | 2,70 | 2,55 | 2,38 | 2,19 | 1,96 | |
| 4,41 | 3,55 | 3,16 | 2,93 | 2,77 | 2,66 | 2,51 | 2,34 | 2,15 | 1,92 | |
| 4,38 | 3,52 | 3,13 | 2,90 | 2,74 | 2,63 | 2,48 | 2,31 | 2,11 | 1,88 | |
| 4,35 | 3,49 | 3,10 | 2,87 | 2,71 | 2,60 | 2,45 | 2,28 | 2,08 | 1,84 | |
| 4,32 | 3,47 | 3,07 | 2,84 | 2,68 | 2,57 | 2,42 | 2,25 | 2,05 | 1,81 | |
| 4,30 | 3,44 | 3,05 | 2,82 | 2,66 | 2,55 | 2,40 | 2,23 | 2,03 | 1,78 | |
| 4,28 | 3,42 | 3,03 | 2,80 | 2,64 | 2,53 | 2,38 | 2,20 | 2,00 | 1,76 | |
| 4,26 | 3,40 | 3,01 | 2,78 | 2,62 | 2,51 | 2,36 | 2,18 | 1,98 | 1,73 | |
| 4,24 | 3,38 | 2,99 | 2,76 | 2,60 | 2,49 | 2,34 | 2,16 | 1,96 | 1,71 | |
| 4,22 | 3,37 | 2,98 | 2,74 | 2,59 | 2,47 | 2,32 | 2,15 | 1,95 | 1,69 | |
| 4,21 | 3,35 | 2,96 | 2,73 | 2,57 | 2,46 | 2,30 | 2,13 | 1,93 | 1,67 | |
| 4,20 | 3,34 | 2,95 | 2,71 | 2,56 | 2,44 | 2,29 | 2,12 | 1,91 | 1,65 | |
| 4,18 | 3,33 | 2,93 | 2,70 | 2,54 | 2,43 | 2,28 | 2,10 | 1,90 | 1,64 | |
| 4,17 | 3,32 | 2,92 | 2,69 | 2,53 | 2,42 | 2,27 | 2,09 | 1,89 | 1,62 | |
| 4,12 | 3,26 | 2,87 | 2,64 | 2,48 | 2,37 | 2,22 | 2,04 | 1,83 | 1,57 | |
| 4,08 | 3,23 | 2,84 | 2,61 | 2,45 | 2,34 | 2,18 | 2,00 | 1,79 | 1,51 | |
| 4,06 | 3,21 | 2,81 | 2,58 | 2,42 | 2,31 | 2,15 | 1,97 | 1,76 | 1,48 | |
| 4,03 | 3,18 | 2,79 | 2,56 | 2,40 | 2,29 | 2,13 | 1,95 | 1,74 | 1,44 | |
| 4,00 | 3,15 | 2,76 | 2,52 | 2,37 | 2,25 | 2,10 | 1,92 | 1,70 | 1,39 | |
| 3,98 | 3,13 | 2,74 | 2,50 | 2,35 | 2,23 | 2,07 | 1,89 | 1,67 | 1,35 | |
| 3,96 | 3,11 | 2,72 | 2,49 | 2,33 | 2,21 | 2,06 | 1,88 | 1,65 | 1,31 | |
| 3,95 | 3,10 | 2,71 | 2,47 | 2,32 | 2,20 | 2,04 | 1,86 | 1,64 | 1,28 | |
| 3,94 | 3,09 | 2,70 | 2,46 | 2,30 | 2,19 | 2,03 | 1,85 | 1,63 | 1,26 | |
| 3,92 | 3,07 | 2,68 | 2,44 | 2,29 | 2,17 | 2,01 | 1,83 | 1,60 | 1,21 | |
| 3,90 | 3,06 | 2,66 | 2,43 | 2,27 | 2,16 | 2,00 | 1,82 | 1,59 | 1,18 | |
| 3,89 | 3,04 | 2,65 | 2,42 | 2,26 | 2,14 | 1,98 | 1,80 | 1,57 | 1,14 | |
| 3,87 | 3,03 | 2,64 | 2,41 | 2,25 | 2,13 | 1,97 | 1,79 | 1,55 | 1,10 | |
| 3,86 | 3,02 | 2,63 | 2,40 | 2,24 | 2,12 | 1,96 | 1,78 | 1,54 | 1,07 | |
| 3,86 | 3,01 | 2,62 | 2,39 | 2,23 | 2,11 | 1,96 | 1,77 | 1,54 | 1,06 | |
| 3,85 | 3,00 | 2,61 | 2,38 | 2,22 | 2,10 | 1,95 | 1,76 | 1,53 | 1,03 | |
| ¥ | 3,84 | 2,99 | 2,60 | 2,37 | 2,21 | 2,09 | 1,94 | 1,75 | 1,52 | 1,00 |
Критические значения t-критерия Стьюдента
при уровне значимости 0,10; 0,05; 0,01 (двухсторонний)
Число степеней свободы d.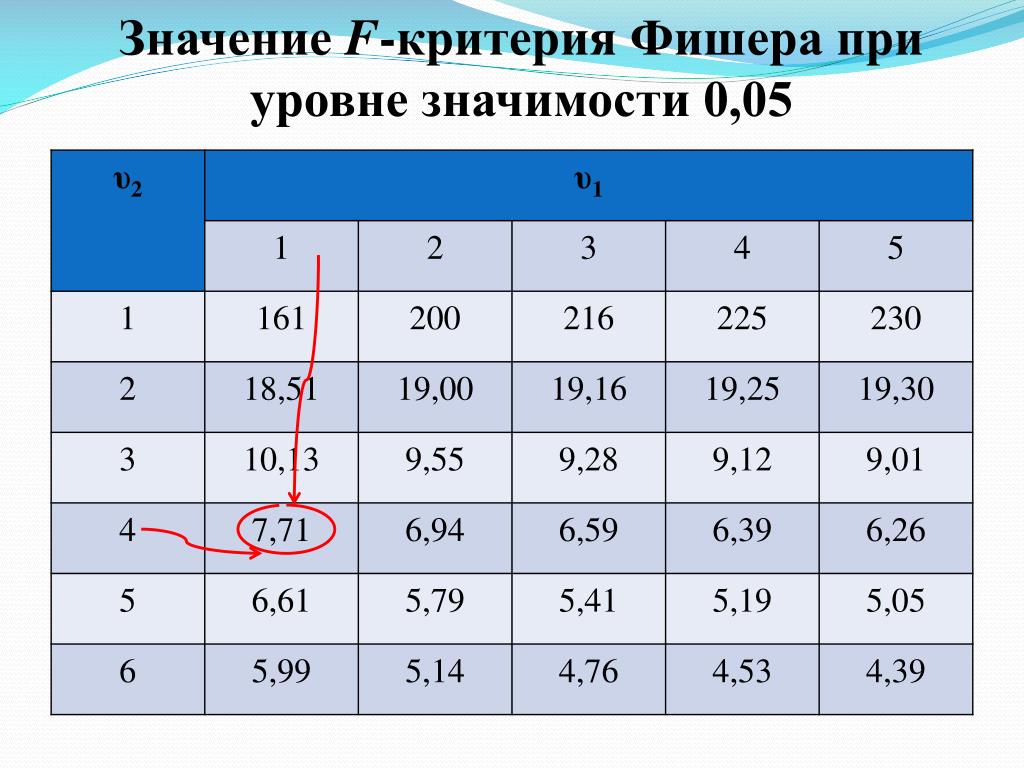 f. f.
| a | Число степеней свободы d.f. | a | ||||
| 0,10 | 0,05 | 0,01 | 0,10 | 0,05 | 0,01 | ||
| 6,3138 | 12,706 | 63,657 | 1,7341 | 2,1009 | 2,8784 | ||
| 2.9200 | 4,3027 | 9,9248 | 1,7291 | 2,0930 | 2,8609 | ||
| 2,3534 | 3,1825 | 5,8409 | 1,7247 | 2,0860 | 2,8453 | ||
| 2,1318 | 2,7764 | 4,6041 | 1,7207 | 2,0796 | 2,8314 | ||
| 2,0150 | 2,5706 | 4,0321 | 1,7171 | 2,0739 | 2,8188 | ||
| 1,9432 | 2,4469 | 3,7074 | 1,7139 | 2,0687 | 2,8073 | ||
| 1,8946 | 2,3646 | 3,4995 | 1,7109 | 2,0639 | 2,7969 | ||
| 1,8595 | 2,3060 | 3,3554 | 1,7081 | 2,0595 | 2,7874 | ||
| 1,8331 | 2,2622 | 3,2498 | 1,7056 | 2,0555 | 2,7787 | ||
| 1,8125 | 2,2281 | 3,1693 | 1,7033 | 2,0518 | 2,7707 | ||
| 1,7959 | 2,2010 | 3,1058 | 1,7011 | 2,0484 | 2,7633 | ||
| 1,7823 | 2,1788 | 3,0545 | 1,6991 | 2,0452 | 2,7564 | ||
| 1,7709 | 2,1604 | 3,0123 | 1,6973 | 2,0423 | 2,7500 | ||
| 1,7613 | 2,1448 | 2,9768 | 1,6839 | 2,0211 | 2,7045 | ||
| 1,7530 | 2,1315 | 2,9467 | 1,6707 | 2,0003 | 2,6603 | ||
| 1,7459 | 2,1199 | 2,9208 | 1,6577 | 1,9799 | 2,6174 | ||
| 1,7396 | 2,1098 | 2,8982 | ¥ | 1,6449 | 1,9600 | 2,5758 |
Критические значения корреляции
для уровневой значимости 0,05 и 0,01
d. f. f.
| a= 0,05 | a = 0,01 | d.f. | a = 0,05 | a = 0,01 |
| 0.996917 | 0,9998766 | 0,4555 | 0,5751 | ||
| 0,95000 | 0,99000 | 0,4438 | 0,5614 | ||
| 0,8783 | 0,95873 | 0,4329 | 0,5487 | ||
| 0,8114 | 0,91720 | 0,4227 | 0,5368 | ||
| 0,7545 | 0,8745 | 0,3809 | 0,4869 | ||
| 0,7067 | 0,8343 | 0,3494 | 0,4487 | ||
| 0,6664 | 0,7977 | 0,3246 | 0,4182 | ||
| 0,6319 | 0,7646 | 0,3044 | 0,3932 | ||
| 0,6021 | 0,7348 | 0,2875 | 0,3721 | ||
| 0,5760 | 0,7079 | 0,2732 | 0,3541 | ||
| 0,5529 | 0,6835 | 0,2500 | 0,3248 | ||
| 0,5324 | 0,6614 | 0,2319 | 0,3017 | ||
| 0,5139 | 0,6411 | 0,2172 | 0,2830 | ||
| 0,4973 | 0,6226 | 0,2050 | 0,2673 | ||
| 0,4821 | 0,6055 | 0,1946 | 0,2540 | ||
| 0,4683 | 0,5897 |
Для простой корреляции d. f. на 2 меньше, чем число пар вариантов; в случае частной корреляции необходимо также вычесть число исключаемых переменных.
f. на 2 меньше, чем число пар вариантов; в случае частной корреляции необходимо также вычесть число исключаемых переменных.
Значения статистик Дарбина-Уотсона
для 5%-го уровня значимости
| n | K=1 | K=2 | K=3 | K=4 | K=5 | |||||
| dL | dU | dL | dU | dL | dU | dL | dU | dL | dU | |
| 0,61 | 1,40 | - | - | - | - | |||||
| 0,7 | 1,36 | 0,47 | 1,9 | - | - | |||||
| 0,76 | 1,33 | 0,56 | 1,78 | 0,37 | 2,29 | |||||
| 0,82 | 1,32 | 0,63 | 1,7 | 0,46 | 2,13 | |||||
| 0,88 | 1,32 | 0,7 | 1,64 | 0,53 | 2,02 | |||||
| 0,93 | 1,32 | 0,66 | 1,6 | 0,6 | 1,93 | |||||
| 0,97 | 1,33 | 0,81 | 1,58 | 0,66 | 1,86 | |||||
| 1,01 | 1,34 | 0,86 | 1,56 | 0,72 | 1,82 | |||||
| 1,05 | 1,35 | 0,91 | 1,55 | 0,77 | 1,78 | |||||
| 0,8 | 1,36 | 0,95 | 1,54 | 0,82 | 0,75 | 0,69 | 1,97 | 0,56 | 2,21 | |
| 1,10 | 1,37 | 0,98 | 1,54 | 0,86 | 1,73 | 0,74 | 1,93 | 0,62 | 2,15 | |
| 1,13 | 1,38 | 1,02 | 1,54 | 0,90 | 1,71 | 0,78 | 1,90 | 0,67 | 2,10 | |
| 1,16 | 1,39 | 1,05 | 1,53 | 0,93 | 1,69 | 0,82 | 1,87 | 0,71 | 2,06 | |
| 1,18 | 1,40 | 1,08 | 1,53 | 0,97 | 1,68 | 0,86 | 1,85 | 0,75 | 2,02 | |
| 1,20 | 1,41 | 1,10 | 1,54 | 1,00 | 1,68 | 0,90 | 1,83 | 0,79 | 1,99 | |
| 1,22 | 1,42 | 1,13 | 1,54 | 1,03 | 1,67 | 0,93 | 1,81 | 0,83 | 1,96 | |
| 1,24 | 1,43 | 1,15 | 1,54 | 1,05 | 1,66 | 0,96 | 1,80 | 0,86 | 1,94 | |
| 1,26 | 1,44 | 1,17 | 1,54 | 1,08 | 1,66 | 0,99 | 1,79 | 0,90 | 1,92 | |
| 1,27 | 1,45 | 1,19 | 1,55 | 1,10 | 1,66 | 1,01 | 1,78 | 0,93 | 1,90 | |
| 1,29 | 1,45 | 1,21 | 1,55 | 1,12 | 1,66 | 1,04 | 1,77 | 0,95 | 1,89 | |
| 1,30 | 1,46 | 1,22 | 1,55 | 1,14 | 1,65 | 1,06 | 1,76 | 0,98 | 1,88 | |
| 1,32 | 1,47 | 1,24 | 1,56 | 1,16 | 1,65 | 1,08 | 1,76 | 1,01 | 1,86 | |
| 1,33 | 1,48 | 1,26 | 1,56 | 1,18 | 1,65 | 1,10 | 1,75 | 1,03 | 1,85 | |
| 1,34 | 1,48 | 1,27 | 1,56 | 1,20 | 1,65 | 1,12 | 1,74 | 1,05 | 1,84 | |
| 1,35 | 1,49 | 1,28 | 1,57 | 1,21 | 1,65 | 1,14 | 1,74 | 0,07 | 1,83 |
Критические границы отношения RS на 5% уровне значимости
| Объем выборки | RSнижн | RSверх | Объем выборки | RSнижн | RSверх |
| 1,758 | 1,999 | 3,58 | 5,04 | ||
| 1,980 | 2,429 | 3,67 | 5,16 | ||
| 2,150 | 2,753 | 3,75 | 5,26 | ||
| 2,280 | 3,012 | 3,63 | 5,35 | ||
| 2,400 | 3,222 | 3,90 | 5,43 | ||
| 2,500 | 3,399 | 3,96 | 5,51 | ||
| 2,590 | 3,552 | 4,01 | 5,57 | ||
| 2,670 | 3,685 | 4,06 | 5,63 | ||
| 2,74 | 3,80 | 4,11 | 5,68 | ||
| 2,80 | 3,91 | 4,16 | 5,73 | ||
| 2,86 | 4,00 | 4,20 | 5,78 | ||
| 2,92 | 4,09 | 4,24 | 5,82 | ||
| 2,97 | 4,17 | 4,27 | 5,86 | ||
| 3,01 | 4,24 | 4,31 | 5,90 | ||
| 3,06 | 4,31 | 4,59 | 6,18 | ||
| 3,10 | 4,37 | 4,78 | 6,39 | ||
| 3,14 | 4,43 | 5,37 | 6,94 | ||
| 3,18 | 4,49 | 5,79 | 7,33 | ||
| 3,34 | 4,71 | ||||
| 3,47 | 4,89 |
Содержание
1. Парная регрессия и корреляция. 1
Парная регрессия и корреляция. 1
1.1. Оценка параметров, оценка адекватности модели. 1
1.2. Виды нелинейной регрессии. Оценка параметров модели. 6
1.3. Коэффициент эластичности как характеристика силы связи фактора с результатом 9
1.4. Анализ гетероскедастичности. 11
2. Множественная регрессия и корреляция. 14
2.1. Нормальная линейная модель множественной регрессии. 14
2.2. Традиционный метод наименьших квадратов для многомерной регрессии (OLS) 15
2.3. Парный, частный и множественный коэффициент корреляции. 17
3. Моделирование одномерных временных рядов. 18
3.1. Основные понятия и определения. 18
3.2. Требования к исходной информации. 20
3.3. Этапы построения прогноза по временным рядам.. 21
4. Типичные примеры анализа моделей. 22
5. Задания для выполнения контрольных работ. 46
Вариант 1. 46
Вариант 2. 49
Вариант 3. 52
Вариант 4. 55
Вариант 5. 59
Вариант 6. 62
Вариант 7. 65
65
Вариант 8. 69
Вариант 9. 72
Вариант 10. 75
Приложение 1. 79
[1] Данные взяты из книги Сборник задач по эконометрике: Учебное пособие для стедентов экономических вузов / Сост. Е.Ю. Дорохина, Л.Ф. Преснякова, Н.П. Тихомиров. – М.: Издательство «Экзамен», 2003 – с 4.
N} \newcommand{\by}{\mathbf{y}} \newcommand{\bX}{\mathbf{X}} \ новая команда {\ bx} {\ mathbf {x}} \newcommand{\bbeta}{\boldsymbol{\beta}} \newcommand{\btheta}{\boldsymbol{\theta}} \newcommand{\bbetahat}{\boldsymbol{\шляпа{\beta}}} \newcommand{\bthetahat}{\boldsymbol{\шляпа{\theta}}} \newcommand{\bmu}{\boldsymbol{\mu}} \newcommand{\bSigma}{\boldsymbol{\Sigma}} \newcommand{\bT}{\mathbf{T}} \newcommand{\dadb}[2]{\frac{\partial #1}{\partial #2}} \newcommand{\iid}{\overset{\small{\text{i.i.d.}}}}{\sim}} \] Интуитивно, хороший классификатор — это тот, который объединяет наблюдения в одном классе и разделяет наблюдения между классами. Линейный дискриминант Фишера пытается сделать это за счет уменьшения размерности. В частности, он проецирует точки данных на одно измерение и классифицирует их в соответствии с их расположением в этом измерении. Как мы увидим, его цель состоит в том, чтобы найти проекцию, которая максимизирует отношение межклассовой вариации к внутриклассовой вариации. Линейный дискриминант Фишера можно применять к многоклассовым задачам, но здесь мы рассмотрим только двоичный случай. 9\top \bx_n \geq 2\), мы видим, что большинство случаев классифицируются правильно, хотя некоторые классифицируются неправильно. Мы можем улучшить модель двумя способами: либо изменив \(\bbeta\), либо изменив отсечку.
В частности, он проецирует точки данных на одно измерение и классифицирует их в соответствии с их расположением в этом измерении. Как мы увидим, его цель состоит в том, чтобы найти проекцию, которая максимизирует отношение межклассовой вариации к внутриклассовой вариации. Линейный дискриминант Фишера можно применять к многоклассовым задачам, но здесь мы рассмотрим только двоичный случай. 9\top \bx_n \geq 2\), мы видим, что большинство случаев классифицируются правильно, хотя некоторые классифицируются неправильно. Мы можем улучшить модель двумя способами: либо изменив \(\bbeta\), либо изменив отсечку.
На практике линейный дискриминант сообщит нам \(\bбета\), но не сообщит нам пороговое значение. Вместо этого дискриминант ранжирует \(f(\bx_n)\) так, чтобы классы были максимально разделены. Это зависит от нас, чтобы выбрать значение отсечки.
Критерий Фишера
9{-1}(\bmu_2 — \bmu_1). \] На изображении ниже слева показано \(\bбетахат\) (выделено красным), найденное линейным дискриминантом Фишера.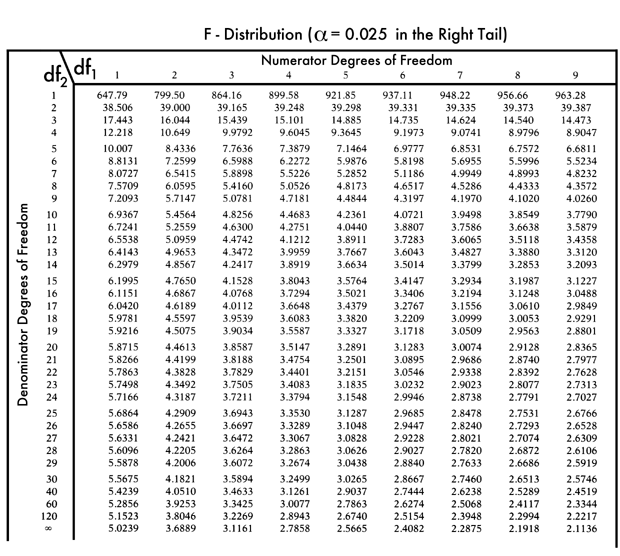 Справа мы снова видим проекции этих точек данных из \(\bbetahat\). Отсечка выбрана равной примерно 0,05. Обратите внимание, что этот дискриминатор, в отличие от приведенного выше, успешно разделяет два класса!
Справа мы снова видим проекции этих точек данных из \(\bbetahat\). Отсечка выбрана равной примерно 0,05. Обратите внимание, что этот дискриминатор, в отличие от приведенного выше, успешно разделяет два класса!
Табличное значение критерия Фишера зависит. Описание функции Фишера в excel
Точный критерий Фишера — критерий, который используется для сравнения двух относительных показателей, характеризующих частоту встречаемости того или иного признака, имеющего два значения. Исходные данные для расчета точного критерия Фишера обычно группируются в виде таблицы из четырех полей.
1. История развития критерия
Критерий был впервые предложен Рональдом Фишером в его книге «Планирование экспериментов». Это произошло в 1935 году. Сам Фишер утверждал, что на эту идею натолкнула Мюриэль Бристоль. В начале 1920-х годов Рональд, Мюриэль и Уильям Роуч находились в Англии на экспериментальной сельскохозяйственной станции. Мюриэль утверждала, что может определить последовательность, в которой в ее чашку наливали чай и молоко. На тот момент не было возможности проверить правильность ее заявления.
На тот момент не было возможности проверить правильность ее заявления.
Это породило у Фишера идею «нулевой гипотезы». Цель состояла не в том, чтобы попытаться доказать, что Мюриэль может определить разницу между чашками чая, приготовленными по-разному. Было решено опровергнуть гипотезу о том, что женщина делает выбор наугад. Было установлено, что нулевая гипотеза не может быть ни доказана, ни обоснована. Но это можно опровергнуть в ходе экспериментов.
Изготовлено 8 чашек. В первые четыре сначала наливают молоко, в остальные четыре — чай. Чашки испортились. Бристоль пригласили попробовать чай и разделить чашки по способу заваривания чая. В итоге должно было получиться две группы. История говорит, что эксперимент удался.
Благодаря тесту Фишера вероятность того, что Бристоль действует интуитивно, снижена до 0,01428. То есть правильно определить кубок удавалось в одном случае из 70. Но все равно никак не свести к нулю шансы, которые Мадам определяет случайно. Даже если увеличить количество чашек.
Эта история дала толчок развитию «нулевой гипотезы». При этом был предложен точный критерий Фишера, суть которого состоит в переборе всех возможных комбинаций зависимых и независимых переменных.
2. Для чего используется точный критерий Фишера?
Точный критерий Фишера в основном используется для сравнения небольших образцов . На это есть две существенные причины. Во-первых, вычисление критерия довольно громоздко и может занять много времени или потребовать мощных вычислительных ресурсов. Во-вторых, критерий достаточно точен (что отражено даже в его названии), что позволяет использовать его в исследованиях с небольшим количеством наблюдений.
Особое место в медицине отводится точному критерию Фишера. Это важный метод обработки медицинских данных, который нашел свое применение во многих научных исследованиях. Благодаря ему можно исследовать взаимосвязь тех или иных факторов и исходов, сравнивать частоту патологических состояний между двумя группами испытуемых и т.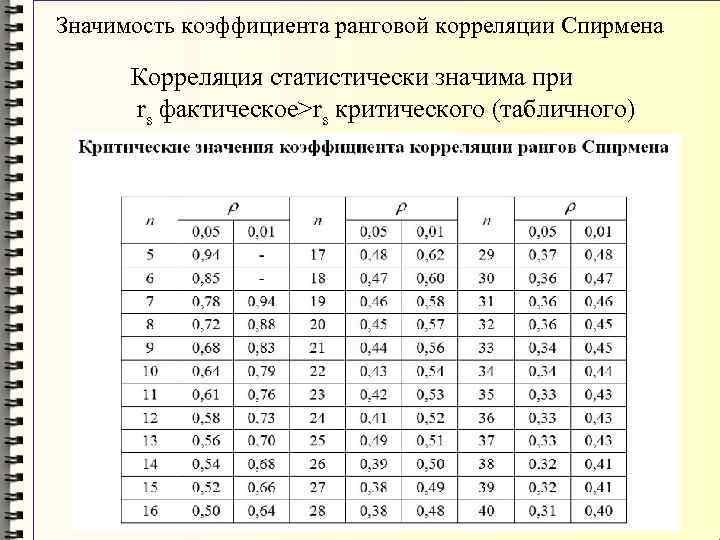 д.
д.
3. В каких случаях можно использовать точный критерий Фишера?
- Сравниваемые переменные должны измеряться в номинальной шкале и иметь только два значения , например, артериальное давление нормальное или повышенное, исход благоприятный или неблагоприятный, есть послеоперационные осложнения или нет.
- Точный критерий Фишера предназначен для сравнения двух независимых групп , разделенных факторным критерием. Соответственно, фактор также должен иметь только два возможных значения.
- Тест подходит для сравнения очень малых выборок: точный критерий Фишера можно использовать для анализа четырех полных таблиц в случае значений ожидаемых явлений менее 5, что является ограничением для применения критерия хи-квадрат Пирсона, даже с поправкой Йейтса.
- Точный критерий Фишера односторонний и двусторонний . При одностороннем варианте точно известно, куда отклонится один из показателей. Например, в исследовании сравнивается количество выздоровевших пациентов по сравнению с контрольной группой.
 Предполагается, что терапия не может ухудшить состояние больных, а только либо излечить, либо нет.
Предполагается, что терапия не может ухудшить состояние больных, а только либо излечить, либо нет.
Двусторонний тест оценивает частотные различия двумя способами. То есть оценивается вероятность как большей, так и меньшей частоты явления в экспериментальной группе по сравнению с контрольной группой.
Аналогом точного критерия Фишера является критерий хи-квадрат Пирсона, при этом точный критерий Фишера имеет более высокую мощность, особенно при сравнении небольших выборок, и поэтому имеет преимущество в данном случае.
4. Как рассчитать точный критерий Фишера?
Например, мы изучаем зависимость частоты рождения детей с врожденными пороками развития (ВПР) от курения матери во время беременности. Для этого были отобраны две группы беременных, одна из которых экспериментальная, состоящая из 80 женщин, куривших в I триместре беременности, и вторая группа сравнения, включающая 90 женщин, ведущих здоровый образ жизни на протяжении всей беременности. Количество случаев пороков развития плода, установленных при УЗИ, в опытной группе составило 10, в группе сравнения — 2,9. 0003
0003
Сначала составим четырехпольную таблицу сопряженности :
Точный критерий Фишера вычисляется по следующей формуле:
где N — общее количество обучаемых в двух группах; ! — факториал, представляющий собой произведение числа и последовательности чисел, каждое из которых меньше предыдущего на 1 (например, 4! = 4 3 2 1)
В результате вычислений находим, что Р = 0,0137.
5. Как интерпретировать значение точного критерия Фишера?
Достоинством метода является соответствие полученного критерия точному значению уровня значимости p . То есть значение 0,0137, полученное в нашем примере, является уровнем значимости различий между сравниваемыми группами по частоте встречаемости ВМ плода. Нужно только сопоставить данное число с критическим уровнем значимости, обычно принимаемым в медицинских исследованиях за 0,05.
- Если значение точного критерия Фишера больше критического значения, то нулевая гипотеза и делается вывод об отсутствии статистически значимых различий частоты исхода в зависимости от наличия фактора риска.

- Если значение точного критерия Фишера меньше критического значения, то альтернативная гипотеза и делается вывод о наличии статистически значимых различий частоты исхода в зависимости от воздействия фактора риска.
В нашем примере P статистически значимо выше, чем у некурящих.
Функция ФИШЕР возвращает преобразование Фишера аргументов X . Это преобразование строит функцию, которая имеет нормальное, а не асимметричное распределение. Функция ФИШЕРа используется для проверки гипотезы с использованием коэффициента корреляции.
Описание функции ФИШЕР в Excel
При работе с этой функцией необходимо установить значение переменной. Сразу стоит отметить, что бывают ситуации, когда данная функция не вернет результат. Это возможно, если переменная:
- — это не число. В такой ситуации функция ФИШЕР вернет ошибку #ЗНАЧ! значение ошибки;
- имеет значение меньше -1 или больше 1. В этом случае функция ФИШЕР вернет #ЧИСЛО! значение ошибки.

Уравнение, используемое для математического описания функции ФИШЕРА, имеет вид:
Z»=1/2*ln(1+x)/(1-x)
Рассмотрим применение этой функции на 3-х конкретных примерах
Оценка связи между прибылью и затратами с помощью функции ФИШЕРА
Пример 1. Используя данные о деятельности коммерческих организаций, требуется произвести оценку зависимости между прибылью Y (млн руб.) и затратами Х (млн руб.), направленными на разработку продукции (приведены в таблице 1).
Таблица 1 — Исходные данные:
| № | Х | Д |
| 1 | 210 000 000,00 руб. | 95 000 000,00 долл. США |
| 2 | 1 068 000 000,00 руб. | 76 000 000,00 руб. |
| 3 | 1 005 000 000,00 руб. | 78 000 000,00 руб. |
| 4 | 610 000 000,00 руб. | 89 000 000,00 руб. |
| 5 | 768 000 000,00 руб. | 77 000 000,00 руб. |
| 6 | 799 000 000,00 руб. | 85 000 000,00 руб. |
Схема решения таких задач следующая:
- Расчетные линейные коэффициенты корреляции r xy ;
- Значимость коэффициента линейной корреляции проверяется на основе критерия Стьюдента. При этом выдвигается и проверяется гипотеза о равенстве коэффициента корреляции нулю. При проверке этой гипотезы используется t-статистика. Если гипотеза подтверждается, t-статистика имеет распределение Стьюдента. Если расчетное значение t p > t кр, то гипотеза отвергается, что свидетельствует о значимости коэффициента линейной корреляции, а, следовательно, о статистической значимости связи между X и Y;
- Определена интервальная оценка для статистически значимого коэффициента линейной корреляции.
- Интервальная оценка коэффициента линейной корреляции определяется на основе обратного z-преобразования Фишера;
- Вычислена стандартная ошибка коэффициента линейной корреляции.

Результаты решения данной задачи с применением прикладных функций в пакете Excel представлены на рисунке 1.
Рисунок 1 – Пример расчетов.
| № п/п | Наименование показателя | Формула расчета |
| 1 | Коэффициент корреляции | =КОРРЕЛ(B2:B7,C2:C7) |
| 2 | Расчетное значение t-критерия tp | =ABS(C8)/ROOT(1-POWER(C8,2))*ROOT(6-2) |
| 3 | Табличное значение t-критерия trh | =STUDISP(0.05,4) |
| 4 | Табличное значение стандартного нормального распределения zy | =НОРМИНОБ((0,95+1)/2) |
| 5 | Значение преобразования Фишера z’ | =FISHER(C8) |
| 6 | Оценка левого интервала для z | =C12-C11*ROOT(1/(6-3)) |
| 7 | Оценка правого интервала для z | =C12+C11*ROOT(1/(6-3)) |
| 8 | Оценка левого интервала для rxy | =FISCHEROBR(C13) |
| 9 | Оценка правого интервала для rxy 92)/4) |
Таким образом, с вероятностью 0,95 коэффициент линейной корреляции лежит в диапазоне от (–0,386) до (–0,990) со стандартной ошибкой 0,205.
Проверка статистической значимости регрессии по функции FDISP
Пример 2: Проверка статистической значимости уравнений множественной регрессии с помощью F-критерия Фишера, сделать выводы.
Для проверки значимости уравнения в целом выдвигаем гипотезу Н 0 о статистической незначимости коэффициента детерминации и противоположную гипотезу Н 1 о статистической значимости коэффициента детерминации:
H 1: R 2 ≠ 0.
Проверим гипотезы с помощью F-критерия Фишера. Показатели приведены в таблице 2.
Таблица 2 — Исходные данные
Для этого воспользуемся следующей функцией в пакете Excel:
FDISP(α;p;n-p-1)
- α — вероятность связанные с данным дистрибутивом;
- p и n — числитель и знаменатель степеней свободы соответственно.
Зная, что α = 0,05, p = 2 и n = 53, получаем следующее значение F крит (см. рис. 2).
Рисунок 2 – Пример расчетов.
Таким образом, можно сказать, что F расч > F крит. В результате принимается гипотеза H 1 о статистической значимости коэффициента детерминации.
В результате принимается гипотеза H 1 о статистической значимости коэффициента детерминации.
Расчет значения показателя корреляции в Excel
Пример 3. Использование данных 23 предприятий о: X — цена товара А, тыс. руб.; Y — прибыль торгового предприятия, млн руб., изучается их зависимость. Модель регрессии оценок дала следующее: ∑(yi-yx) 2 = 50000; ∑(yi-yср) 2 = 130000. Какой показатель корреляции можно определить по этим данным? Рассчитайте значение индекса корреляции и с помощью критерия Фишера сделайте вывод о качестве регрессионной модели.
Определим F крит из выражения:
F расч = R 2 / 23 * (1-R 2)
где R — коэффициент детерминации, равный 0,67.
Таким образом, расчетное значение F рассч = 46.
Для определения F крит воспользуемся распределением Фишера (см. рис. 3).
Рисунок 3 – Пример расчетов.
Таким образом, полученная оценка уравнения регрессии достоверна.
Возвращает обратное значение (правостороннего) распределения F-вероятности. Если p = FDISP(x;…), то FDISP(p;…) = x.
Если p = FDISP(x;…), то FDISP(p;…) = x.
F-распределение можно использовать в F-тесте, который сравнивает степень дисперсии двух наборов данных. Например, вы можете проанализировать распределение доходов в США и Канаде, чтобы определить, похожи ли эти две страны с точки зрения плотности доходов.
Важно: Эта функция была заменена одной или несколькими новыми функциями, которые обеспечивают большую точность и имеют имена, которые лучше отражают их назначение. Хотя эта функция по-прежнему используется для обеспечения обратной совместимости, она может стать недоступной в будущих версиях Excel, поэтому мы рекомендуем использовать новые функции.
Дополнительные сведения о новых функциях см. в разделах Функция F.ОБР и Функция F.ОБР.ПХ.
Синтаксис
FINV(вероятность, степени_свободы1, степени_свободы2)
Синтаксис функции FDISP имеет следующие аргументы:
Вероятность — обязательный аргумент. Вероятность, связанная с кумулятивным F-распределением.
степеней_свободы1 — обязательный аргумент. Числитель степеней свободы.
Degrees_of_freedom2 — обязательный аргумент. Знаменатель степеней свободы.
Примечания
Если какой-либо из аргументов не является числом, функция FОБР возвращает ошибку #ЗНАЧ! значение ошибки.
Если «вероятность» 1, функция FОБР возвращает значение #ЧИСЛО! значение ошибки.
Если значение аргумента «степени_свободы1» или «степени_свободы2» не является целым числом, оно усекается.
Если «степени_свободы1»
Если «степень_свободы2»
Функцию FDISP можно использовать для определения критических значений F-распределения. Например, результаты дисперсионного анализа обычно включают данные для F-статистики, F-вероятности и F-распределения критического значения с уровнем значимости 0,05. Чтобы определить критическое значение F, вам нужно использовать уровень значимости в качестве аргумента «вероятность» функции FINV.
Учитывая значение вероятности, FDISP ищет значение x, для которого FDISP(x, Степени_свободы1, Степени_свободы2) = вероятность. Таким образом, точность функции FРАСП зависит от точности функции FРАСП. Функция FDISP использует метод итерации для поиска. Если поиск не завершился после 100 итераций, возвращается значение ошибки #Н/Д.
Пример
Скопируйте образцы данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формулы, выберите их и нажмите F2, а затем ENTER. При необходимости измените ширину столбцов, чтобы увидеть все данные.
1. Таблица значений F-критерия Фишера для уровня значимости α = 0,05
| 1 | 2 | 3 | 4 | 5 | 6 | 8 | 12 | 24 | ∞ | |
| 1 | 161,45 | 199,50 | 215,72 | 224,57 | 230,17 | 233,97 | 238,89 | 243,91 | 249,04 | 254,32 |
| 2 | 18,51 | 19,00 | 19,16 | 19,25 | 19,30 | 19,33 | 19,37 | 19,41 | 19,45 | 19,50 |
| 3 | 10,13 | 9,55 | 9,28 | 9,12 | 9,01 | 8,94 | 8,84 | 8,74 | 8,64 | 8,53 |
| 4 | 7,71 | 6,94 | 6,59 | 6,39 | 6,26 | 6,16 | 6,04 | 5,91 | 5,77 | 5,63 |
| 5 | 6,61 | 5,79 | 5,41 | 5, 19 | 5,05 | 4,95 | 4,82 | 4,68 | 4,53 | 4,36 |
| 6 | 5,99 | 5,14 | 4,76 | 4,53 | 4,39 | 4,28 | 4,15 | 4,00 | 3,84 | 3,67 |
| 7 | 5,59 | 4,74 | 4,35 | 4,12 | 3,97 | 3,87 | 3,73 | 3,57 | 3,41 | 3,23 |
| 8 | 5,32 | 4,46 | 4,07 | 3,84 | 3,69 | 3,58 | 3,44 | 3,28 | 3,12 | 2,93 |
| 9 | 5,12 | 4,26 | 3,86 | 3,63 | 3,48 | 3,37 | 3,23 | 3,07 | 2,90 | 2,71 |
| 10 | 4,96 | 4,10 | 3,71 | 3,48 | 3,33 | 3,22 | 3,07 | 2,91 | 2,74 | 2,54 |
| 11 | 4,84 | 3,98 | 3,59 | 3,36 | 3, 20 | 2,95 | 2,79 | 2,61 | 2,40 |
Когда m=1, выберите 1 столбец.
k 2 = n-m = 7-1 = 6 — т.е. 6-я строка — берем значение таблицы Фишера
F таблица = 5,99, ср. = total: 7
Влияние x на y умеренное и отрицательное
ŷ — модельное значение.
| F расч. = | 28 648: 1 | = 0,92 |
| 200,50:5 |
А = 1/7 * 398,15 * 100% = 8,1%
допустимое значение
Модель достаточно точная.
F расч. = 1/0,92 = 1,6
F расч. = 1,6
Должно быть F расч. > Таблица F
нарушила эту модель, поэтому это уравнение не является статистически значимым.
Поскольку расчетное значение меньше табличного значения, модель не имеет значения.
| 1 | Σ | (y-ŷ) | *100% | |
| Н | У |
Ошибка приближения.
A= 1/7*0,563494* 100% = 8,04991% 8,0%
Модель считается точной, если средняя ошибка аппроксимации меньше 10%.
Параметрическая парилка Идентификация нелинейной регрессии
Модель y = a * x b — степенная функция
Чтобы применить известную формулу, необходимо взять логарифм нелинейной модели.
log y = log a + b log x
Y=C+b*X — линейная модель.
C \ U003D 1,7605 — ( — 0,298) *1,7370 \ U003D 2,278
Возврат в исходную модель
ŷ = 10 S *X B = 10 2,278 *X -0,298
| № P / P | 211111111111111111111111111111111111111111111111111111111111111н. | Х | Д | Х | Д*Х | At | I (y-ŷ) /yI | |
| 1 | 68,80 | 45,10 | 1,8376 | 1,6542 | 3,039758 | 2,736378 | 60,9614643 | 0,113932 |
| 2 | 61, 20 | 59,00 | 1 7868 | 1,7709 | 3,164244 | 3,136087 | 56,2711901 | 0,080536 |
| 3 | 59,90 | 57, 20 | 1 7774 | 1,7574 | 3,123603 | 3,088455 | 56,7931534 | 0,051867 |
| 4 | 56,70 | 61,80 | 1,7536 | 1,7910 | 3,140698 | 3, 207681 | 55,49 | 0,021181 |
| 5 | 55,00 | 58,80 | 1,7404 | 1,7694 | 3,079464 | 3,130776 | 56,3281590 | 0,024148 |
| 6 | 54,30 | 47, 20 | 1,7348 | 1,6739 | 2, 2 | 2,801941 | 60,1402577 | 0,107555 |
| 7 | 49,30 | 55, 20 | 1 6928 | 1,7419 | 2,948688 | 3,034216 | 57,3987130 | 0,164274 |
| Итого | 405, 20 | 384,30 | 12 3234 | 12 1587 | 21,40034 | 21,13553 | 403,3 | 0,563493 |
| Средний | 57,88571 | 54,90 | 1,760486 | 1,736957 | 3,057191 | 3,019362 | 57,62742 | 0,080499 |
Входим в EXCEL через «Пуск»-программы. Вносим данные в таблицу. В «Сервис» — «Анализ данных» — «Регрессия» — ОК
Вносим данные в таблицу. В «Сервис» — «Анализ данных» — «Регрессия» — ОК
Если в меню «Сервис» отсутствует строка «Анализ данных», то ее необходимо установить через «Сервис» — «Настройки» — «Пакет анализа данных»
Прогнозирование спроса на продукцию компании. Использование в MS Excel Функции «Тренд»
А — спрос на товар. Б — время, дни
| № п/п | А | |
| 1 | 11 | 1 |
| 2 | 14 | 2 |
| 3 | 13 | 3 |
| 4 | 15 | 4 |
| 5 | 17 | 5 |
| 6 | 17,9 | |
| 7 | 18,4 | 7 |
Шаг 1. Подготовка исходных данных
Шаг 2. Продлеваем ось времени, переводим ее на 6,7 вперед; мы имеем право предсказывать 1/3 данных.
Шаг 3. Выберите диапазон A6: A7 для будущего прогноза.
Выберите диапазон A6: A7 для будущего прогноза.
Шаг 4. Функция вставки
Вставка пользовательских сглаженных диаграмм
Диапазон u готов.
Если каждое последующее значение нашей временной оси отличается не на несколько процентов, а в несколько раз, то нужно использовать не функцию «Тренд», а функцию «Рост».
Библиография
1. Елисеева «Эконометрика»
2. Елисеева «Практикум по эконометрике»
3. Carlsberg «Excel для целей анализа»
Приложение
| РЕЗУЛЬТАТЫ | ||||||||
Статистика регистрации | ||||||||
| Несколько R | 0,947541801 | |||||||
| R-квадрат | 0,897835464 | |||||||
| Нормализованный R-квадрат | 0,829725774 | |||||||
| стандартная ошибка | 0,226013867 | |||||||
| Наблюдения | 6 | |||||||
| Дисперсионный анализ | ||||||||
Значение F | ||||||||
| Регрессия | 2 | 1,346753196 | 0,673376598 | 13,18219855 | 0,032655042 | |||
| Остаток | 3 | 0,153246804 | 0,051082268 | |||||
| Итого | 5 | 1,5 | ||||||
Коэффициенты | стандартная ошибка | t-статистика | р-значение | дно 95% | Топ 95% | дно 95% | Топ 95% | |
| Y-пересечение | 4,736816539 | 0,651468195 | 7,27098664 | 0,005368842 | 2,66355399 | 6,810079088 | 2,66355399 | 6,810079088 |
| Переменная X1 | 0,333424008 | 0,220082134 | 1,51499807 | 0,227014505 | -0,366975566 | 1,033823582 | -0,366975566 | |
Точный критерий Фишера | Реальная статистика с использованием Excel
ВведениеКогда условия критерия хи-квадрат Пирсона не выполняются, особенно когда одна или несколько ячеек имеют exp i < 5 или с таблицами сопряженности 2 × 2, альтернативным подходом является используйте точный тест Фишера . Поскольку этот метод требует больших вычислительных ресурсов, его лучше всего использовать для выборок меньшего размера.
Пример таблицы непредвиденных обстоятельств 2 × 2Пример 1 : Повторите пример 2 из независимого тестирования, используя данные в диапазоне A5:D8 на рисунке 1; то есть определить, не зависит ли показатель излечения от используемой терапии.
Рисунок 1. Данные и критерий хи-квадрат для примера 1
Как видно из рисунка 1, математическое ожидание для двух ячеек (G6 и H6) меньше 5. таблицу непредвиденных обстоятельств 2 × 2 при относительно небольшом размере выборки лучше использовать точный критерий Фишера.
Точный критерий Фишера вычисляет, сколькими различными способами могут быть достигнуты вышеуказанные предельные частоты, а затем определяет вероятность того, что наблюдаемая выше конфигурация ячейки может быть получена просто случайно.
Мы можем ограничить наше внимание любой из ячеек, поскольку, как только частота для одной ячейки определена, частоты для других ячеек могут быть определены из предельных сумм. Мы выбираем ячейку B6, так как она имеет наименьшую предельную сумму (а именно 9 в ячейке D6) и ее значение меньше, чем другой элемент, который составляет эту предельную сумму (а именно 7 в ячейке C6).
Теперь ячейка B6 может принимать любое значение от 0 до 9; как только это значение установлено, значения трех других ячеек могут быть скорректированы для сохранения предельных сумм.
Расчет вероятностей Вероятность того, что ячейка B6 примет конкретное значение x , эквивалентна вероятности получения x успешных результатов в выборке размером 9 (ячейка D6), взятой без замены из совокупности размер 21 (ячейка D8), который содержит 11 (ячейка B8) успешных вариантов.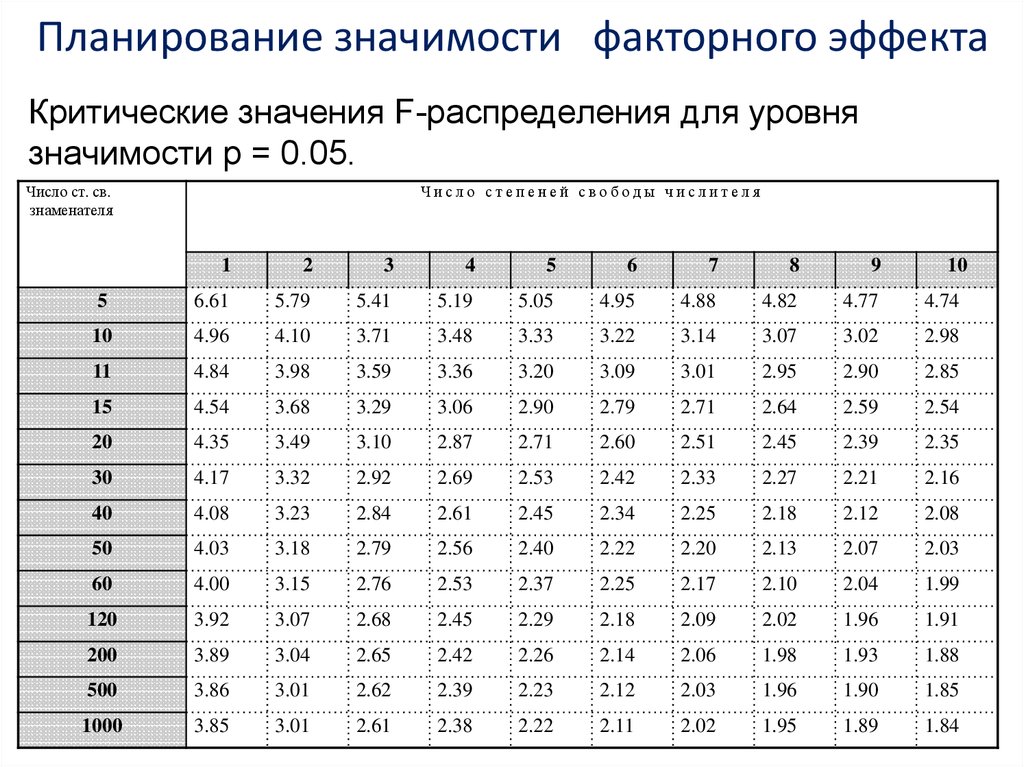 Это можно рассчитать с помощью гипергеометрического распределения. Здесь ячейки D6 и B8 — это ячейки с предельными суммами, соответствующими ячейке B6, а ячейка D8 содержит общую сумму.
Это можно рассчитать с помощью гипергеометрического распределения. Здесь ячейки D6 и B8 — это ячейки с предельными суммами, соответствующими ячейке B6, а ячейка D8 содержит общую сумму.
Рисунок 2 содержит таблицу вероятностей для каждого возможного значения x . Рисунок 2. Точный критерий Фишера для примера 1 DIST(K11,$B$8,$D$6,$D$8,FALSE)
Как видно из гипергеометрического распределения, роли предельных сумм B8 и D6 можно поменять местами в приведенной выше формуле.
Пользователи Excel, предшествующие Excel 2010, могут вместо этого использовать следующую формулу: формула
=HYPGEOM.DIST(K11,$B$8,$D$6,$D$8,ИСТИНА)
Поскольку формула для cdf недоступна в Excel до Excel 2010, пользователи этих версий Excel могут вставьте формулу = L6 в ячейку M6, формулу = L7+M6 в ячейку M7, затем выделите диапазон M7:M15 и нажмите Ctrl-D . Ячейка M11 теперь будет содержать значение cdf для значения в ячейке K11 по формуле =M10+L11.
Анализ Точный критерий Фишера заключается в определении того, меньше ли вероятность, чем 0,05, что не более 2 из тех, кто принимает терапию 1, излечатся (наблюдаемое число в ячейке B6). Из ячейки L17 на рисунке 2 мы видим, что cdf в точке 2 составляет 0,024172 < 0,05 = α , поэтому мы отвергаем нулевую гипотезу и делаем вывод, что существует значительная разница между показателями излечения для двух методов лечения.
Из ячейки L17 на рисунке 2 мы видим, что cdf в точке 2 составляет 0,024172 < 0,05 = α , поэтому мы отвергаем нулевую гипотезу и делаем вывод, что существует значительная разница между показателями излечения для двух методов лечения.
Существуют односторонний и двусторонний варианты теста. Значение p для одностороннего теста (ячейка L17) задается формулой =СУММ(L6:L8) или эквивалентной (для версий Excel, начиная с Excel 2010)
= ГИПГЕОМ.РАСП(K8,B8,D6 ,D8,TRUE)
Значение p для двустороннего теста (ячейка L18) определяется по формуле
=СУММ(L6:L8)+СУММ(L14:L15)
, где K14 — крайняя левая ячейка в правом хвосте, который имеет значение PDF ≤ L8 (поскольку 0,005614 ≤ 0,022454, но 0,050522> 0,022454). Аналогично, мы можем использовать формулу (для версий Excel, начиная с Excel 2010)
= ГИПГЕОМ.РАСП(K8,B8,D6,D8,ИСТИНА)+1− ГИПГЕОМ.РАСП(K13,B8,D6,D8,ИСТИНА)
Функция рабочего листа Реальная статистика Функция Excel : Real Statistics Resource Pack предоставляет следующую функцию рабочего листа.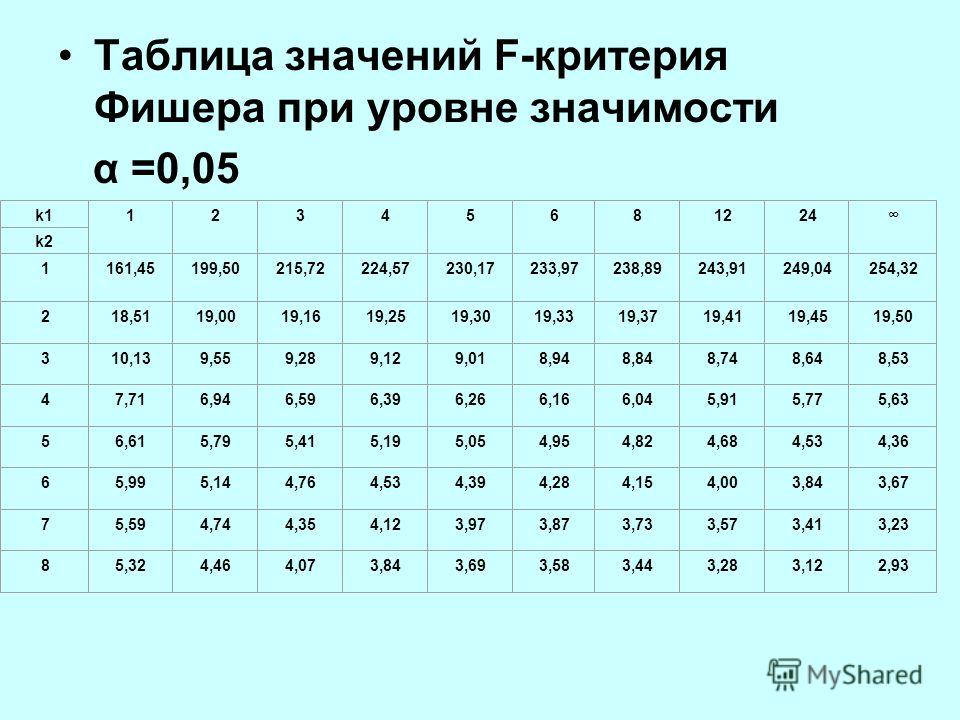
FISHERTEST (R1, хвостов ) = значение p, рассчитанное с помощью точного критерия Фишера для 2 × 2, 2 × 3, 2 × 4, 2 × 5, 2 × 6, 2 × 7, 2 × 8, 2 × 9, 3 × 3, 3 × 4 или 3 × 5 таблица непредвиденных обстоятельств, содержащаяся в R1.
R1 должен содержать только числовые значения. Когда R1 содержит таблицу непредвиденных обстоятельств 2 × 2, имеется необязательный второй аргумент, решек = 1 (односторонний тест) или 2 (двухсторонний тест, по умолчанию). Для таблиц сопряженности других размеров может быть возвращено только p-значение двустороннего теста.
Для примера 1 FISHERTEST(B6:C7,1) = 0,024172 и FISHERTEST(B6:C7, 2) = 0,029973.
Ограничения Поскольку точный критерий Фишера может быть ресурсоемким, были установлены ограничения на сумму всех ячеек в поддерживаемых таблицах непредвиденных обстоятельств. Эти ограничения в настоящее время установлены на уровне 2000 для стола 2 × 3, 1250 для стола 2 × 4, 360 для стола 2 × 5, 175 для стола 2 × 6, 110 для стола 2 × 7, 75 для стола 2.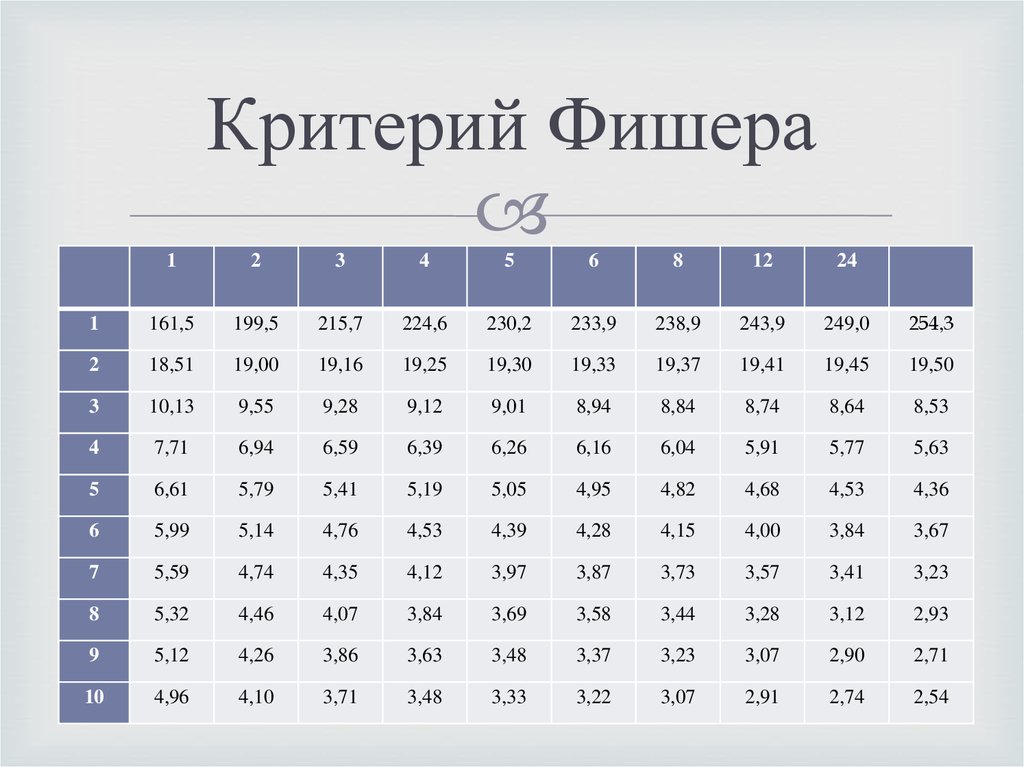 × 8 стол, 40 для 2 × 9стол, 320 для стола 3 × 3, 95 для стола 3 × 4 и 30 для стола 3 × 5. Для таблиц 2 × 2 ограничений нет.
× 8 стол, 40 для 2 × 9стол, 320 для стола 3 × 3, 95 для стола 3 × 4 и 30 для стола 3 × 5. Для таблиц 2 × 2 ограничений нет.
Если вы хотите превысить эти пределы, вы можете добавить третий аргумент в функцию FISHERTEST, который указывает, насколько вы хотите увеличить предел. Например. если вы хотите использовать точный критерий Фишера для таблицы непредвиденных обстоятельств 3 × 3 в диапазоне A1: C3, сумма ячеек которого равна 350, вы можете использовать формулу массива = FISHERTEST (A1: C3, 1.1). В 1.1 указано, что вы увеличили предел для таблицы непредвиденных обстоятельств 3 × 3 с 320 до 320 × 1,1 = 352.
Так как 350 < 352, функция будет работать, хотя это займет немного больше времени. Точно так же вы можете использовать =FISHERTEST(A1:C3,1.5) для любой таблицы непредвиденных обстоятельств 3 × 3, сумма записей которой составляет не более 320 × 1,5 = 480. Если сумма равна 480, ожидайте, что обработка займет некоторое время.
Таблица непредвиденных обстоятельств 3 × 2 Пример Пример 2 : Определить, не зависит ли движение за выбор или за жизнь от политической партии гражданина США, на основе выборки, показанной в диапазоне A3:D7 на рисунке 3.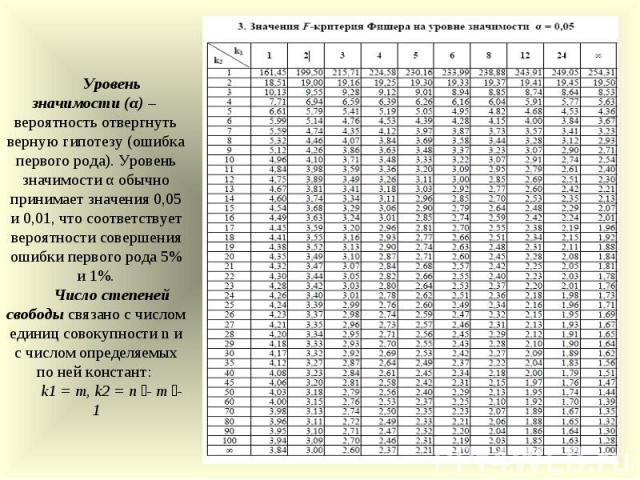
Вы можете выполнить точный тест Фишера, используя формулу рабочего листа =FISHERTEST(B4:C6). Результат, как показано в ячейке h23 на рис. 3, заключается в том, что сторонники выбора или защиты жизни не зависят от партийной принадлежности, поскольку значение p = 4,574E-06 < 0,05 = α (двусторонний критерий). . Рис. 3. Точный критерий Фишера для примера 21546, чтобы получить тот же результат, отметив параметр Fisher Exact Test в появившемся диалоговом окне (как показано на рис. 3 критерия хи-квадрат для независимости).
Коррекция среднего значения pТочный критерий Фишера для таблиц непредвиденных обстоятельств 2 × 2 можно рассматривать как слишком консервативный. Чтобы решить эту проблему, вы можете использовать так называемую коррекцию среднего p-значения .
Чтобы применить эту поправку к примеру 1, вам нужно вычесть половину значения в ячейке L8 на рисунке 2 из рассчитанного p-значения.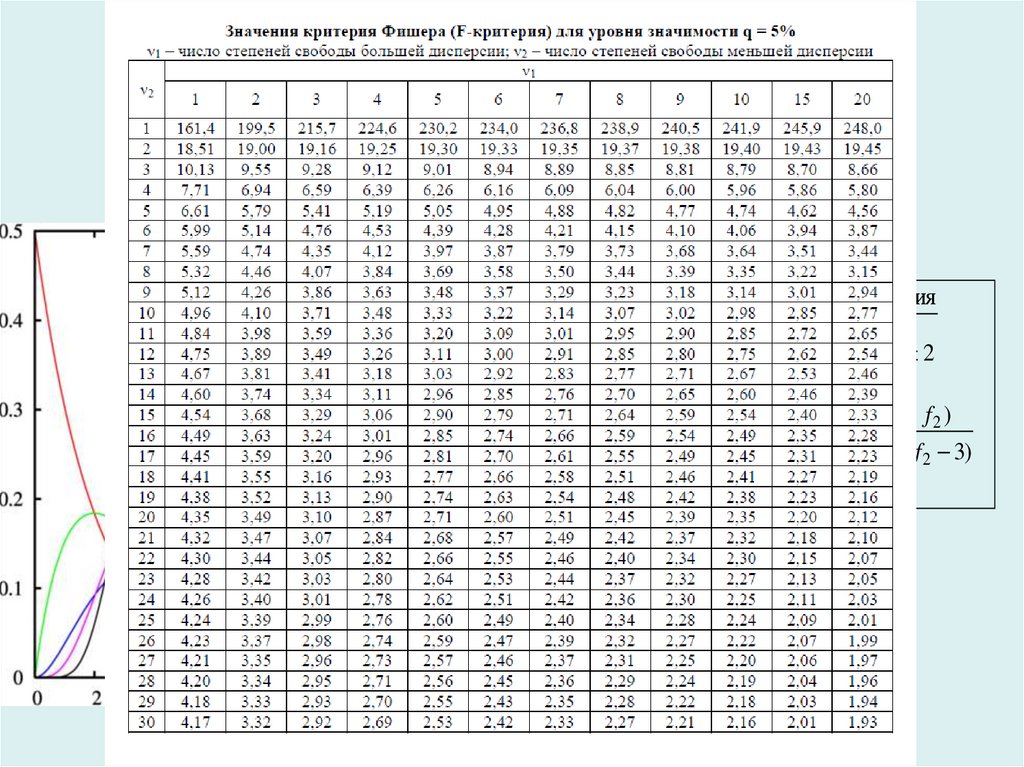 Это приводит к p-значению для одностороннего теста 0,0129.45 (т.е. .024172 – .022454/2) и .018746 (т.е. .029973 – .022454/2) для двухстороннего теста.
Это приводит к p-значению для одностороннего теста 0,0129.45 (т.е. .024172 – .022454/2) и .018746 (т.е. .029973 – .022454/2) для двухстороннего теста.
Функция реальной статистики : Ресурсный пакет реальной статистики предоставляет следующую функцию:
FISHER_MIDP (R1, ) = среднее p-значение для таблицы непредвиденных обстоятельств 2 × 2, содержащейся в R1. хвосты = 1 или 2 (по умолчанию)
Книга примеровНажмите здесь , чтобы загрузить книгу Excel с примерами, описанными на этой веб-странице.
Ссылки Википедия (2012) Точное определение Фишера st
https://en.wikipedia.org/wiki/Fisher%27s_exact_test
Ghent, A.W. 2, 2×3, 3×3 и другие таблицы сопряженности с использованием биномиальных коэффициентов
https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.135.4796&rep=rep1&type=pdf
Фриман, Г. Х. и Халтон, Дж. Х. (1951). Замечание о точной обработке непредвиденных обстоятельств, согласия и других важных проблем . Биометрика, 38, 141-149.
Х. (1951). Замечание о точной обработке непредвиденных обстоятельств, согласия и других важных проблем . Биометрика, 38, 141-149.
https://academic.oup.com/biomet/article-abstract/38/1-2/141/245705?redirectedFrom=fulltext
Агрести, А. (2007) Введение в категориальный анализ данных. 2-е изд. Wiley
https://mregresion.files.wordpress.com/2012/08/agresti-introduction-to-categorical-data.pdf
spss — точный критерий Фишера в таблицах непредвиденных обстоятельств размером более 2×2
Вопрос задан
Изменено 7 месяцев назад
Просмотрено 72k раз
$\begingroup$
Меня учили применять точный критерий Фишера только к таблицам непредвиденных обстоятельств размером 2×2.
Вопросы:
Фишер когда-нибудь предполагал, что этот тест можно использовать в таблицах размером более 2×2 (мне известна история о том, как он изобрел тест, пытаясь угадать, может ли пожилая женщина определить, было ли добавлено молоко в чай или чай добавляли в молоко)
Stata позволяет мне использовать точный критерий Фишера для любой таблицы непредвиденных обстоятельств.
 Это действительно?
Это действительно?Предпочтительно ли использовать полевой транзистор, если ожидаемое количество ячеек в таблице непредвиденных обстоятельств < 5?
- spss
- stata
- таблицы непредвиденных обстоятельств
- точный тест рыбака
$\endgroup$
6
$\begingroup$
Единственная проблема с применением точного критерия Фишера к таблицам размером более 2×2 заключается в том, что вычисления становятся намного сложнее. Версия 2×2 является единственной, которую можно выполнить вручную, и поэтому я сомневаюсь, что Фишер когда-либо представлял тест в больших таблицах, потому что вычисления были бы за пределами всего, что он мог себе представить.
Тем не менее, тест можно применить к любой таблице mxn, и некоторые программы, включая Stata и SPSS, предоставляют такую возможность. Тем не менее, расчет часто аппроксимируется с использованием метода Монте-Карло.
Тем не менее, расчет часто аппроксимируется с использованием метода Монте-Карло.
Да, если ожидаемое число клеток невелико, лучше использовать точный тест, поскольку в таких случаях критерий хи-квадрат больше не является хорошим приближением.
$\endgroup$
5
$\begingroup$
Эта страница в MathWorld объясняет, как работают расчеты. Он указывает, что тест может быть определен различными способами:
Чтобы вычислить P-значение теста, столы должны быть заказаны некоторыми критерий, который измеряет зависимость, и те таблицы, которые представляют равные или большее отклонение от независимости чем наблюдаемая таблица вероятности которых складываются вместе. Есть множество критерии, по которым можно измерить зависимость.
Мне не удалось найти других статей или текстов, объясняющих, как это делается с таблицами размером более 2×2.
Этот калькулятор вычисляет точный критерий Фишера для таблиц с 2 столбцами и до 5 строк. Используемый критерий — гипергеометрическая вероятность каждой таблицы. Общее значение P представляет собой сумму гипергеометрической вероятности всех таблиц с одинаковыми предельными суммами, вероятности которых меньше или равны вероятности, вычисленной на основе фактических данных.
$\endgroup$
0
$\begingroup$
Если вы ищете другие способы вычисления точного критерия Фишера с большими таблицами непредвиденных обстоятельств, вот онлайн-калькулятор для точного критерия Фишера для таблиц непредвиденных обстоятельств 2×3. Кроме того, вот одна для таблиц непредвиденных обстоятельств 3×3 и одна для таблиц непредвиденных обстоятельств 2×4.
Да, если ожидаемое число клеток невелико, по возможности лучше использовать точный критерий Фишера вместо критерия хи-квадрат.
$\endgroup$
$\begingroup$
Чтобы получить точный критерий Фишера в SPSS, используйте опцию Statistics = Exact в Crosstabs. Методы вычисления точного Tedt для больших таблиц существуют по крайней мере с 1960-х годов. Скорость современных микропроцессоров делает время вычислений несущественным в наши дни. Действительно, выполнить точный тест настолько просто, что важно не использовать его слишком широко.
$\endgroup$
$\begingroup$
Здесь важно помнить, что точный критерий Фишера обычно применяется для таблиц непредвиденных обстоятельств с фиксированными полями, т. е. эффективные алгоритмы, используемые в Stata и R, включают либо создание всех таблиц с фиксированными полями, либо выборку всех таблиц с фиксированными полями.
Однако допущение о фиксированной марже подходит не во всех случаях. На самом деле, я думаю, Агрести утверждает, что это редко уместно, хотя это мнение обсуждается. В любом случае, прежде чем использовать точный критерий Фишера в том виде, в котором он обычно реализуется, вам нужно подумать о том, подходит ли для вашего приложения обработка сумм строк и столбцов как фиксированных.
На самом деле, я думаю, Агрести утверждает, что это редко уместно, хотя это мнение обсуждается. В любом случае, прежде чем использовать точный критерий Фишера в том виде, в котором он обычно реализуется, вам нужно подумать о том, подходит ли для вашего приложения обработка сумм строк и столбцов как фиксированных.
$\endgroup$
1
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя адрес электронной почты и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
функция ФИШЕР в Excel с примерами ее работы
Функция ФИШЕР выполняет преобразование Фишера для возврата аргументов X. Это преобразование строит функцию, имеющую нормальное, а не асимметричное распределение. Функция ФИШЕРа используется для проверки гипотезы с использованием коэффициента корреляции.
Описание функции ФИШЕР в Excel
При работе с данной функцией необходимо установить значение переменной. Сразу следует отметить, что есть некоторые ситуации, в которых эта функция не даст результатов. Это возможно, если переменная:
- — это не число. В такой ситуации функция ФИШЕР вернет значение ошибки #ЗНАЧ!;
- либо меньше -1, либо больше 1. В этом случае функция ФИШЕР вернет #ЧИСЛО! значение ошибки.
Уравнение, которое используется для математического описания функции ФИШЕРА, имеет вид:
Z ‘= 1/2 * ln (1 + x) / (1-x)
Рассмотрим использование этой функции в 3 -x конкретные примеры.
Оценка взаимосвязи функции прибыли и затрат по ФИШЕРУ
Пример 1. Используя данные о деятельности коммерческих организаций, требуется произвести оценку зависимости между прибылью Y (млн) и затратами X (млн), использованными на разработку продукта (приведены в табл. 1).
Table 1 — Baseline:
| No | X | Y |
| 1 | 210 000 000 | 95 000 000 |
| 2 | 1 068 000 000 | 76 000 000 |
| 3 | 1 005 000 000 | 78 000 000 |
| 4 | 610 000 000 | 89 000 000 |
| 5 | 768 000 000 | 77 000 000 |
| 6 | 799 000 000 | 85 000 000 |
Схема решения таких задач следующая:
- Рассчитать коэффициент линейной корреляции r xy .

- Значимость коэффициента линейной корреляции проверяется на основе t-критерия Стьюдента. В этом случае выдвигается и проверяется гипотеза о равенстве коэффициента корреляции нулю. При проверке этой гипотезы используется t-статистика. Если гипотеза подтверждается, t-статистика имеет распределение Стьюдента. Если расчетное значение t p > t cr , то гипотеза отвергается, что свидетельствует о значимости коэффициента линейной корреляции, а значит, и о статистической значимости связи между X и Y.
- Определена интервальная оценка для статистически значимого коэффициента линейной корреляции.
- Интервальная оценка коэффициента линейной корреляции определяется на основе обратного z-преобразования Фишера.
- Вычислена стандартная ошибка коэффициента линейной корреляции.
Результаты решения этой задачи с использованием функций, используемых в пакете Excel, представлены на рисунке 1.
Рисунок 1 – Пример расчетов.
| . | =ABS(C8)/КОРРЕКЦИЯ(1-ПИТАНИЕ(C8,2))*КОРРЕКЦИЯ(6-2) | |||
| 3 | Табличное значение t-критерия trh | =TINV(0.05,4) | ||
| 4 | Табличное значение стандарт. нормальный Дистр. ZY | = normsInv ((0,95+1)/2) | ||
| 5 | Трансформационное значение Fisher Z ‘ | = Fisher (C8) | ||
| 6 | 1111112 | |||
| 6 | 1111112 | |||
| 6 | 11111111 2 | |||
| 6 | 11111111111 2 | 110 | 6 | 11111111111 2 |
| . C11*SQRT(1/(6-3)) | ||||
| 7 | Оценка правого интервала для z | =C12+C11*SQRT(1/(6-3)) 92)/4) |
Таким образом, с вероятностью 0,95 коэффициент линейной корреляции лежит в интервале от (–0,386) до (–0,990) со стандартной ошибкой 0,205.
Проверка статистической значимости регрессии функцией FINV
Пример 2. Проверить статистическую значимость уравнения множественной регрессии с помощью F-критерия Фишера, сделать выводы.
Чтобы проверить значимость уравнения в целом, мы выдвигаем гипотезу H 0 о статистической значимости коэффициента детерминации и противоположной ей гипотезе H 1 о статистической значимости коэффициента детерминации:
H 0 : R 2 = 0;
H 1 : R 2 ≠ 0.
Проверяем гипотезы с помощью F-критерия Фишера. Показатели приведены в таблице 2.
Таблица 2 — Исходный уровень
| Индикатор | SS | MS | F calc |
| Regression | 454,814 | 227,407 | 7,075 |
| Remainder | 1607,014 | 32,14 | |
| Total | 2061,828 | — |
Для этого используем функцию в Excel:
=FОБР(α,p,np-1)
Где:
- α вероятность, связанная с данным распределением;
- p и n — числитель и знаменатель степеней свободы соответственно.

Зная, что α = 0,05, p = 2 и n = 53, мы получаем следующее значение для F crit (см. рис. 2).
Рисунок 2 – Пример расчетов.
Таким образом, мы можем сказать, что F вычисл > F крит . В результате принимается гипотеза H 1 о статистической значимости коэффициента детерминации.
Расчет индекса корреляции в Excel
Пример 3. Использование данных 23 компаний по: Х — цена товара А, тыс.; Y — прибыль коммерческого предприятия, проведено исследование их зависимости. Оценка регрессионной модели дала следующее: ∑(yi-yx) 2 = 50 000; ∑(yi-yср) 2 = 130000. Какой показатель корреляции можно определить по этим данным? Рассчитайте значение показателя корреляции и, используя критерий Фишера, сделайте вывод о качестве регрессионной модели.
Определим F крит из выражения:
F вычисл =R 2 /23*(1-R 2 )
где R — коэффициент детерминации, равный 0,67.
Таким образом, расчетное значение F вычисл = 46.
Чтобы определить F крит , используйте распределение Фишера (см. рис. 3).
Рисунок 3 – Пример расчетов.
Скачать примеры функций FISHER в Excel
Таким образом, полученная оценка уравнения регрессии достоверна.
scipy.stats.fisher_exact — Руководство по SciPy v1.9.1
- scipy.stats.fisher_exact( таблица , альтернатива=’двусторонний’ )[источник]
Выполните точный критерий Фишера для таблицы непредвиденных обстоятельств 2×2.
Нулевая гипотеза состоит в том, что истинное отношение шансов популяций лежащий в основе наблюдений один, и наблюдения были отобраны из этих популяций при условии: маргиналы результирующая таблица должна совпадать с наблюдаемой таблицей. Статистика возвращается безусловная оценка максимального правдоподобия шансов отношение, а p-значение — это вероятность при нулевой гипотезе получение таблицы, по крайней мере, столь же экстремальной, как та, которая была на самом деле наблюдаемый.
 Существуют и другие возможные варианты статистического и двустороннего анализа.
определение p-значения, связанное с точным критерием Фишера; пожалуйста, смотрите
Примечания для получения дополнительной информации.
Существуют и другие возможные варианты статистического и двустороннего анализа.
определение p-значения, связанное с точным критерием Фишера; пожалуйста, смотрите
Примечания для получения дополнительной информации.- Параметры
- table array_like of ints
Таблица непредвиденных обстоятельств 2×2. Элементы должны быть неотрицательными целыми числами.
- альтернатива {‘двусторонний’, ‘меньше’, ‘больше’}, необязательно
Определяет альтернативную гипотезу. Доступны следующие параметры (по умолчанию «двусторонний»):
«двусторонний»: отношение шансов основной популяции не равно единице
«меньше»: отношение шансов основной популяции меньше единицы
«больше»: отношение шансов основной популяции больше более одного
Подробнее см. в примечаниях.
- Возвращает
- отношение шансов число с плавающей запятой
Это априорное отношение шансов, а не апостериорная оценка.

- p_value float
P-значение, вероятность при нулевой гипотезе получения таблице, по крайней мере, столь же экстремальной, как та, которая действительно наблюдалась.
См. также
-
chi2_contingency Критерий хи-квадрат независимости переменных в таблице непредвиденных обстоятельств. Это можно использовать в качестве альтернативы
fisher_exact, когда числа в таблице большие.-
barnard_exact Точный критерий Барнарда, который является более мощной альтернативой точному критерию Фишера для таблиц непредвиденных обстоятельств 2×2.
boschloo_exactТочный критерий Бошлоо, который является более мощной альтернативой точному критерию Фишера для таблиц непредвиденных обстоятельств 2×2.
Примечания
Нулевая гипотеза и p-значения
Нулевая гипотеза состоит в том, что истинное отношение шансов популяций лежащий в основе наблюдений один, и наблюдения были отобраны в случайно из этих популяций при условии: маргиналы результирующая таблица должна совпадать с наблюдаемой таблицей.
 Эквивалентно,
нулевая гипотеза состоит в том, что входная таблица взята из гипергеометрической
распределение с параметрами (как используется в
Эквивалентно,
нулевая гипотеза состоит в том, что входная таблица взята из гипергеометрической
распределение с параметрами (как используется в гипергеом)M = a + b + c + d,n = a + bиN = a + c, где входная таблица:[[a, b], [c, d]]. Этот дистрибутив поддерживаетmax(0, N + n - M) <= x <= min(N, n), или, с точки зрения значений во входной таблицеmin(0, a - d) <= x <= a + min(b, c).хможно интерпретировать как верхний левый элемент таблицы 2x2, поэтому таблицы в раздаче имеют вид:[ х п - х ] [Н - х М - (п + Н) + х]
Например, если:
Таблица= [6 2] [1 4]то поддержка
2 <= x <= 7, а таблицы в раздаче являются:[2 6] [3 5] [4 4] [5 3] [6 2] [7 1] [5 0] [4 1] [3 2] [2 3] [1 4] [0 5]
Вероятность каждой таблицы определяется гипергеометрическим распределением
гипергеом.. Для этого примера это (округлено до три значащие цифры): pmf(x, M, n, N)
pmf(x, M, n, N) х 2 3 4 5 6 7 р 0,0163 0,163 0,408 0,326 0,0816 0,00466
Можно вычислить с помощью:
>>> из scipy.stats импортировать гипергеом >>> таблица = np.array([[6, 2], [1, 4]]) >>> М = таблица.сумма() >>> n = таблица[0].sum() >>> N = таблица[:, 0].sum() >>> начало, конец = hypergeom.support(M, n, N) >>> hypergeom.pmf(np.arange(начало, конец+1), M, n, N) массив([0,01631702, 0,16317016, 0,40792541, 0,32634033, 0,08158508, 0,004662 ])Двустороннее p-значение — это вероятность того, что при нулевой гипотезе случайная таблица будет иметь вероятность, равную или меньшую, чем вероятность входной таблицы. Для нашего примера вероятность входная таблица (где
х = 6) равно 0,0816. Значения x, где вероятность не превышает это 2, 6 и 7, поэтому двустороннее значение p0,0163 + 0,0816 + 0,00466 ~= 0,10256:>>> из scipy.stats импортировать fisher_exact >>> odsr, p = fisher_exact(таблица, альтернатива='двусторонняя') >>> р 0,10256410256410257
Одностороннее значение p для
альтернатива='больше'- это вероятность что случайная таблица имеетx >= a, что в нашем примере равнох >= 6, или0,0816 + 0,00466 ~= 0,08626:>>> шансы, p = fisher_exact (таблица, альтернатива = 'больше') >>> р 0,08624708624708627
Это эквивалентно вычислению функции выживания распределение на
х = 5(на единицу меньше, чемхиз входной таблицы, потому что мы хотим включить вероятностьx = 6в сумму):>>> hypergeom.
 sf(5, M, n, N)
0,08624708624708627
sf(5, M, n, N)
0,08624708624708627
Для
альтернатива = 'меньше'одностороннее значение p является вероятностью что случайная таблица имеетx <= a(т.е.x <= 6в нашем примере), или0,0163 + 0,163 + 0,408 + 0,326 + 0,0816 ~= 0,9949:>>> шансы, p = fisher_exact (таблица, альтернатива = 'меньше') >>> р 0,9953379953379957
Это эквивалентно вычислению кумулятивной функции распределения распределения при
x = 6:>>> hypergeom.cdf(6, M, n, N) 0,9953379953379957
Отношение шансов
Расчетное отношение шансов отличается от того, которое использует R. Этот SciPy реализация возвращает (более распространенный) «безусловный максимальный Оценка правдоподобия», в то время как R использует «условную оценку максимального правдоподобия». Оценивать".
Примеры
Скажем, мы проводим несколько дней, считая китов и акул в Атлантике и Индийские океаны.


 Предполагается, что терапия не может ухудшить состояние больных, а только либо излечить, либо нет.
Предполагается, что терапия не может ухудшить состояние больных, а только либо излечить, либо нет. 

 Задача оценки параметров такой разветвленной модели решается с помощью сложных и причудливых методов. Однако все они имеют одну и ту же теоретическую основу. Поэтому, чтобы получить первоначальное представление о содержании эконометрических методов, ограничимся в следующих параграфах рассмотрением простой линейной регрессии. …
Задача оценки параметров такой разветвленной модели решается с помощью сложных и причудливых методов. Однако все они имеют одну и ту же теоретическую основу. Поэтому, чтобы получить первоначальное представление о содержании эконометрических методов, ограничимся в следующих параграфах рассмотрением простой линейной регрессии. …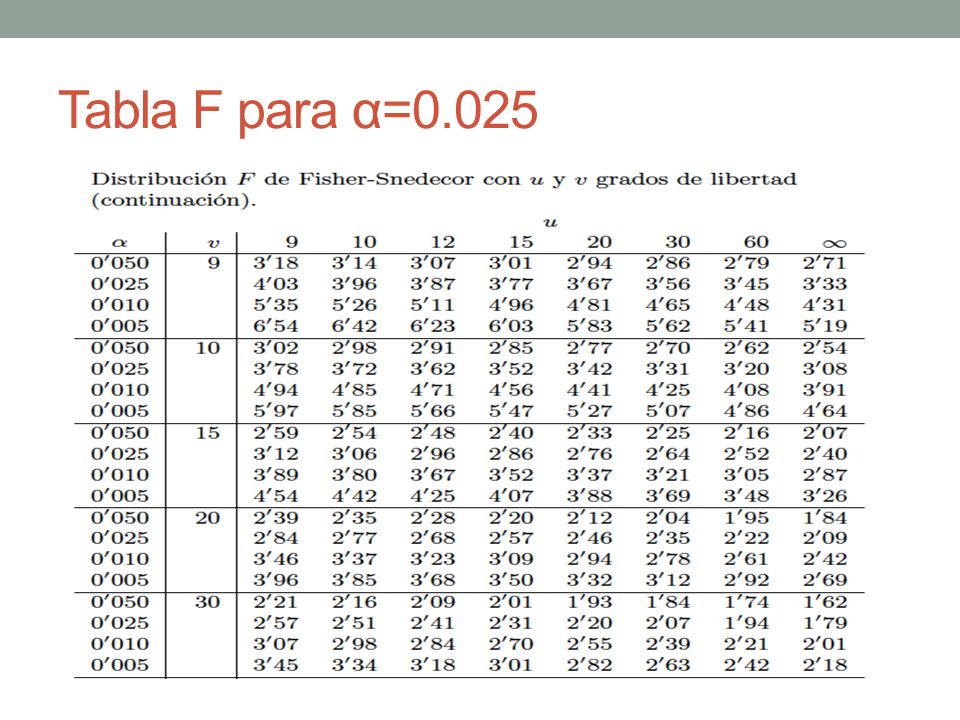 ..
.. Это действительно?
Это действительно?