Ответы
| ||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика
| Похожие вопросы |
1. Периметр прямоугольника 24 см.Одна сторона этого прямоугольника на 2 см больше, чем другая. Найти длину сторон прямоугольника.
Периметр прямоугольника 24 см.Одна сторона этого прямоугольника на 2 см больше, чем другая. Найти длину сторон прямоугольника.
Решено
Выполните умножение (3a — b)(2b — 4a).
найдите уравнение с наименьшим корнем…
Решено
x=2-квадратный корень из 2x-5
Решено
Планиметрическая задача
Производные некоторых основных элементарных функций (Лекция №5)
- y = xn.
Если n – целое положительное
число, то, используя формулу бинома Ньютона:
(a + b)n = an+n·an-1·b + 1/2∙n(n – 1)an-2∙b2+ 1/(2∙3)∙n(n – 1)(n – 2)an-3b3+…+ bn,
можно доказать, что
Итак, если x получает приращение Δx, то f(x+Δx) = (x + Δx)n, и, следовательно,
Δy=(x+Δx)n – xn =n·xn-1·Δx + 1/2·n·(n–1)·xn-2·Δx2 +…+Δxn.
Заметим, что в каждом из пропущенных слагаемых есть множитель Δx в степени выше 3.
Найдем предел
Мы доказали эту формулу для n Î N. Далее увидим, что она справедлива и при любом n Î R.
- y= sin x. Вновь воспользуемся определением производной.
Так как, f(x+Δx)=sin(x+Δx), то
Таким образом,
- Аналогично можно показать, что
- Рассмотрим функцию y= ln x.
Имеем f(x+Δx
)=ln(x+Δx). ПоэтомуИтак,
- Используя свойства логарифма можно показать, что
Формулы 3 и 5 докажите самостоятельно.
ОСНОВНЫЕ ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ
Применяя общий способ
нахождения производной с помощью предела можно получить простейшие формулы
дифференцирования. Пусть u=u(x),v=v(x) –
две дифференцируемые функции от переменной x.
Пусть u=u(x),v=v(x) –
две дифференцируемые функции от переменной x.
- .
- (справедлива для любого конечного числа слагаемых).
- .
- .
а) .
б) .
Формулы 1 и 2 докажите самостоятельно.
Доказательство формулы 3.
Пусть y = u(x) + v(x). Для значения аргумента x+Δx имеем y( x+Δx)=u(x+Δx) + v(x+Δx).
Тогда
Δy=y(x+Δx) – y(x) = u(x+Δx) + v(x+Δx) – u(x) – v(x) = Δu +Δv.
Следовательно,
.
Доказательство формулы 4.
Пусть y=u(x)·v(x). Тогда y(x+Δx)=u(x+Δx)·v(x+Δx), поэтому
Δy=u(x+Δx)·v(x+Δx) – u(x)·v(x).
Заметим, что поскольку каждая из функций u и v дифференцируема в точке x, то они непрерывны в этой точке, а значит u(x+Δx)→u(x), v(x+Δx)→v(x)
Поэтому можем записать
На основании этого свойства можно получить правило дифференцирования произведения любого числа функций.
Пусть, например, y=u·v·w. Тогда,
y ‘ = u ‘·(v·w) + u·(v ·w) ‘ = u ‘·v·w + u·(v ‘·w +v·w ‘) = u ‘·v·w + u·v ‘·w + u·v·w ‘.
Доказательство формулы 5.
Пусть . Тогда
При доказательстве воспользовались тем, что v(x+Δx)→v(x) при Δx→0.
Примеры.
- Если , то
- y = x3 – 3x2 + 5x + 2.
Найдем y ‘(–1).

y ‘ = 3x2 – 6x+ 5. Следовательно, y ‘(–1) = 14.
- y = ln x · cos x, то y ‘ = (ln x) ‘ cos x + ln x (cos x) ‘ =1/x∙cos x – ln x · sin x.
Таким образом,
- Аналогично для y= ctgx,
ТЕОРЕМА О ПРОИЗВОДНОЙ СЛОЖНОЙ ФУНКЦИИ
Пусть y = f(u), а u= u(x). Получаем функцию y, зависящую от аргумента x: y = f(u(x)). Последняя функция называется функцией от функции или сложной функцией.
Областью определения функции
y = f(u(x))
является либо вся область определения функции u=u(x) либо та ее часть, в которой определяются значения u, не выходящие из области
определения функции y= f(u).
Операция «функция от функции» может проводиться не один раз, а любое число раз.
Установим правило дифференцирования сложной функции.
Теорема. Если функция u= u(x) имеет в некоторой точке x0 производную и принимает в этой точке значение u0 = u(x0), а функция y= f(u) имеет в точке u0 производную y ‘u= f ‘(u0), то сложная функция y = f(u(x)) в указанной точке x0 тоже имеет производную, которая равна y ‘x= f ‘(u0)·u ‘(x0), где вместо u должно быть подставлено выражение u= u(x).
Таким образом, производная
сложной функции равна произведению производной данной функции по промежуточному
аргументу u на производную
промежуточного аргумента по x.
Доказательство. При фиксированном значении х0 будем иметь u0=u(x0), у0=f(u0). Для нового значения аргумента x0+Δx:
Δu= u(x0 + Δx) – u(x0), Δy=f(u0+Δu) – f(u0).
Т.к. u – дифференцируема в точке x0, то u – непрерывна в этой точке. Поэтому при Δx→0 Δu→0. Аналогично при Δu→0 Δy→0.
По условию . Из этого соотношения, пользуясь определением предела, получаем (при Δu→0)
,
где α→0 при Δu→0, а, следовательно, и при Δx→0.
Перепишем это равенство в виде:
Δy= y ‘uΔu+α·Δu.
Полученное равенство
справедливо и при Δu=0 при произвольном
α, так как оно превращается в
тождество 0=0.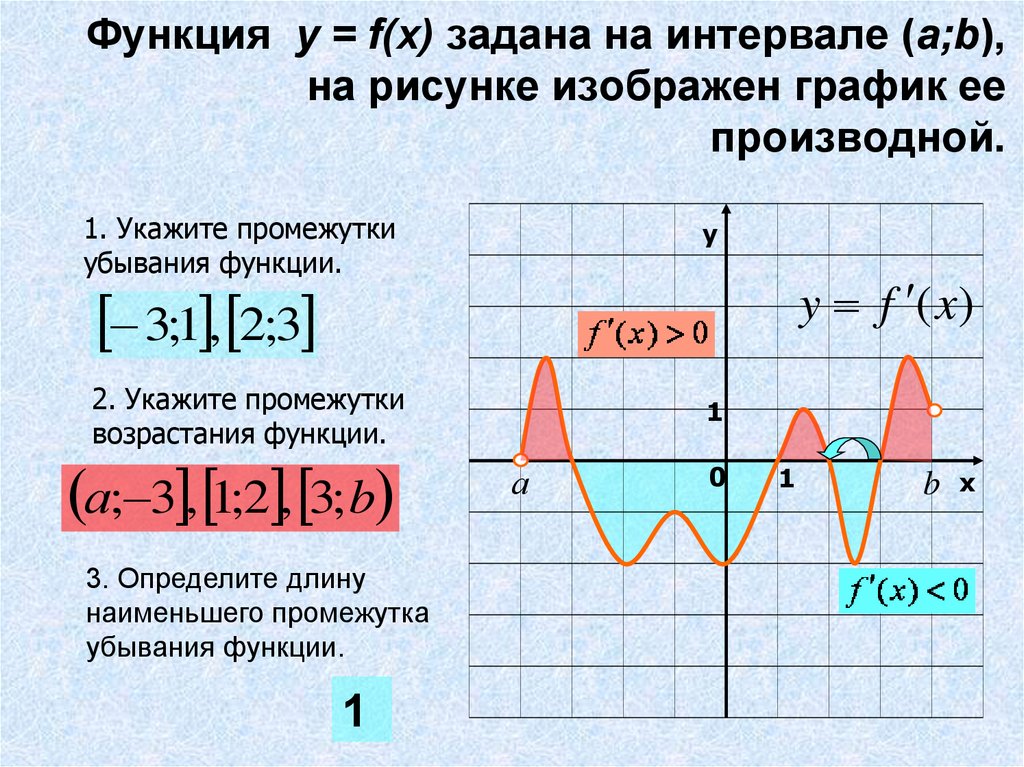 При Δu=0 будем полагать α=0. Разделим все члены
полученного равенства на Δx
При Δu=0 будем полагать α=0. Разделим все члены
полученного равенства на Δx
.
По условию . Поэтому, переходя к пределу при Δx→0, получим y ‘x= y ‘u·u ‘x . Теорема доказана.
Итак, чтобы продифференцировать сложную функцию y = f(u(x)), нужно взять производную от «внешней» функции f, рассматривая ее аргумент просто как переменную, и умножить на производную от «внутренней» функции по независимой переменной.
Если функцию y=f(x) можно представить в виде y=f(u), u=u(v), v=v(x), то нахождение производной y ‘x осуществляется последовательным применением предыдущей теоремы.
По доказанному правилу имеем y ‘x= y ‘u·u ‘x . Применяя эту же теорему для u ‘x получаем , т.е.
y ‘x = y ‘x· u ‘v· v ‘x = f ‘u (u)·u ‘v (v)·v ‘x (x).
Примеры.
- y = sin x2. Тогда .
ПОНЯТИЕ ОБРАТНОЙ ФУНКЦИИ
Начнем с примера. Рассмотрим функцию y= x3. Будем рассматривать равенство y= x3 как уравнение относительно x. Это уравнение для каждого значения у определяет единственное значение x: . Геометрически это значит, что всякая прямая параллельная оси Oxпересекает график функции y= x3 только в одной точке. Поэтому мы можем рассматривать x как функцию от y. Функция называется обратной по отношению к функции y= x3.
Прежде чем перейти к общему случаю, введем определения.
Функция y = f(x) называется
возрастающей на некотором отрезке,
если большему значению аргумента x из
этого отрезка соответствует большее значение функции, т.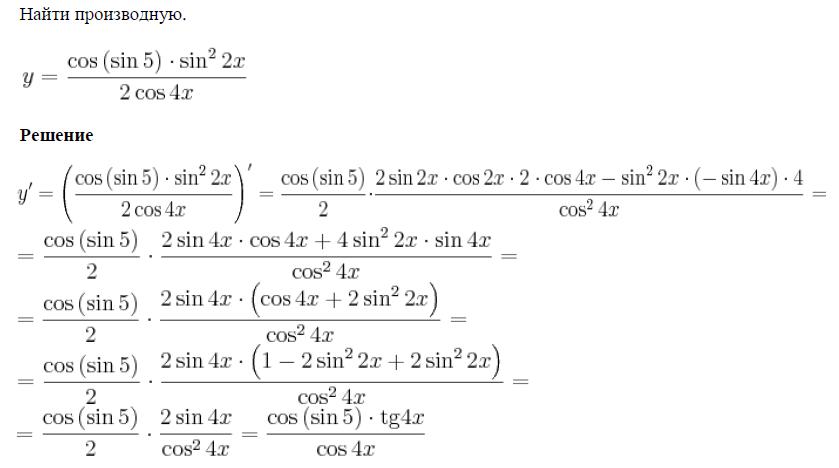 е. если x2>x1, то f(x2) > f(x1).
е. если x2>x1, то f(x2) > f(x1).
Аналогично функция называется убывающей, если меньшему значению аргумента соответствует большее значение функции, т.е. еслих2 < х1 , то f(x2) > f(х1).
Итак, пусть дана возрастающая или убывающая функция y= f(x), определенная на некотором отрезке [a; b]. Для определенности будем рассматривать возрастающую функцию (для убывающей все аналогично).
Рассмотрим два различных
значения х1
и х2. Пусть y1=f(x1), y2=f(x2). Из
определения возрастающей функции следует, что если x1<x2, то у1<у2. Следовательно, двум различным значениям х1 и
х2 соответствуют два
различных значения функции у1
и у2. Справедливо и обратное,
т.е. если у1<у2, то из определения
возрастающей функции следует, чтоx1<x2. Т.е. вновь двум различным
значениям у1
и у2 соответствуют два
различных значенияx1 и x2. Т.о.,
между значениями x и соответствующими им значениями y устанавливается взаимно однозначное
соответствие, т.е. уравнение y=f(x) для каждого y (взятого из области
значений функции y=f(x)) определяет единственное значение x, и можно
сказать, что x есть
некоторая функция аргумента y: x= g(у).
Справедливо и обратное,
т.е. если у1<у2, то из определения
возрастающей функции следует, чтоx1<x2. Т.е. вновь двум различным
значениям у1
и у2 соответствуют два
различных значенияx1 и x2. Т.о.,
между значениями x и соответствующими им значениями y устанавливается взаимно однозначное
соответствие, т.е. уравнение y=f(x) для каждого y (взятого из области
значений функции y=f(x)) определяет единственное значение x, и можно
сказать, что x есть
некоторая функция аргумента y: x= g(у).
Эта функция называется обратной для функции y=f(x). Очевидно, что и функция y=f(x) является обратной для функции x=g(у).
Заметим, что обратная
функция x=g(y) находится
путем решения уравнения y=f(x) относительно
х.
Пример. Пусть дана функция y = ex. Эта функция возрастает при –∞ < x <+∞. Она имеет обратную функцию x = lny. Область определения обратной функции 0 < y < + ∞.
Сделаем несколько замечаний.
Замечание 1. Если возрастающая (или убывающая) функция y=f(x) непрерывна на отрезке [a; b], причем f(a)=c, f(b)=d, то обратная функция определена и непрерывна на отрезке [c; d].
Замечание 2. Если функция y=f(x) не является ни возрастающей, ни убывающей на некотором интервале, то она может иметь несколько обратных функций.
Пример. Функция y=x2 определена при –∞<x<+∞. Она не является ни
возрастающей, ни убывающей и не имеет обратной функции. Однако, если мы рассмотриминтервал 0≤x<+∞, то здесь функция является
возрастающей и обратной для нее будет .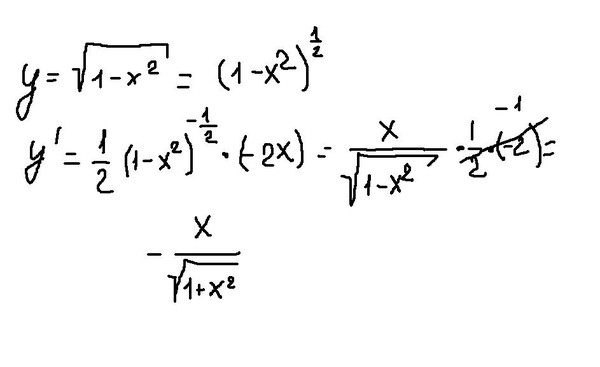 На интервале – ∞ <x≤ 0 функция – убывает и обратная
для нее .
На интервале – ∞ <x≤ 0 функция – убывает и обратная
для нее .
Замечание 3. Если функции y=f(x) и x=g(y) являются взаимно обратными, то они выражают одну и ту же связь между переменными x и y. Поэтому графикомих является одна и та же кривая. Но если аргумент обратной функции мы обозначим снова через x, а функцию через y и построим их в одной системе координат, то получим уже два различных графика. Легко заметить, что графики будут симметричны относительно биссектрисы 1-го координатного угла.
ТЕОРЕМА О ПРОИЗВОДНОЙ ОБРАТНОЙ ФУНКЦИИ
Докажем теорему, позволяющую находить производную функции y=f(x), зная производную обратной функции.
Теорема. Если для функции y=f(x) существует
обратная функция x=g(y), которая в некоторой точке
у0 имеет
производную g ‘(v0), отличную от нуля, то в
соответствующей точке x0=g(x0) функция y=f(x) имеет
производную f ‘(x0), равную ,
т. е. справедлива формула.
е. справедлива формула.
Доказательство. Т.к. x=g(y) дифференцируема в точке y0, то x=g(y) непрерывна в этой точке, поэтому функция y=f(x) непрерывна в точке x0=g(y0). Следовательно, при Δx→0 Δy→0.
Покажем, что .
Пусть . Тогда по свойству предела . Перейдем в этом равенстве к пределу при Δy→0. Тогда Δx→0 и α(Δx)→0, т.е. .
Следовательно,
,
что и требовалось доказать.
Эту формулу можно записать в виде .
Рассмотрим применение этой теоремы на примерах.
Примеры.
- y = ex. Обратной для этой функции
является функция x= ln y. Мы уже доказали, что .
Поэтому согласно сформулированной выше теореме
Итак, (ex) ‘ = ex
- Аналогично можно показать, что (ax) ‘ = ax·lna.
 Докажите самостоятельно.
Докажите самостоятельно. - y = arcsin x.
Рассмотрим обратную функцию x = sin y. Эта функция в интервале – π/2<y<π/2 монотонна. Ее производная
x ‘ = cos y не
обращается в этом интервале в нуль. Следовательно, по теореме о производной
обратной функции
.
Но на (–π/2; π/2) .
Поэтому
- Аналогично
Докажите самостоятельно.
- y = arctg x.
Эта функция по определению удовлетворяет условию существования обратной функции
на интервале –π/2< y < π/2. При этом обратная функция x = tg y монотонна.
По ранее доказанному .
Следовательно, y ‘ = cos2y . Но .
Поэтому
- Используя эти формулы, найти производные следующих функций:
Зачет по теме «Производная и ее применения»
В старшей школе для успешного прохождения итоговой аттестации целесообразно проводить зачетные работы по основным темам курса. Предлагаемый зачет по теме «Производная и ее применения» сориентирован на учащихся 10-х профильных классов.
Предлагаемый зачет по теме «Производная и ее применения» сориентирован на учащихся 10-х профильных классов.
Формы проведения зачета выбирает сам учитель: либо устные ответы, содержащие доказательства и теоретические обоснования решенных задач, либо письменная работа. Билеты содержат по пять вопросов, первый из которых требует знания теоретических фактов. С учетом уровня возможностей и обученности учащихся учитель может ограничить зачет первыми тремя заданиями. А №4 и №5 можно предлагать ученикам с повышенной подготовкой. Так же дифференцированно можно подходить и к требованиям изложения теоретического материала.
Перед зачетом следует ознакомить ребят со списком теоретических вопросов и предложить типовые задачи или задачи, которые вошли в зачет, но в тематическом порядке.
При желании можно выставить две оценки – за уровень теоретической подготовки и умение применять знания на практике или за обязательный уровень (первые три задания) и дополнительную часть (4 и 5 по выбору).
Билет 1.
1. Сформулируйте определение производной. Вычислите производную функции у = х2 по определению.
2. Напишите уравнение касательной к графику функции f(х) = 3х – х3 в точке хо = -2.
3. На рисунке изображён график функции у = f(х), определенной на интервале (-6;8). Определите количество целых точек, в которых производная функции положительна. |
4. Вычислите значение производной функции f(х) = sin2х в точке хо = π/2.
5. Найдите значение функции f(х) = х3 + 2,5х2 – 2х в точке максимума.
Билет 2.
1. Сформулируйте определение производной. Вычислите производную функции у = 1/x по определению.
2. Вычислите значение производной функции f(х) = х2 – 4√x в точке хо = 4.
3. Определите количество целых точек, в которых производная функции отрицательна. |
4. Найдите наибольшее и наименьшее значение функции f(х) = х + 1/x на отрезке [-2;1/2].
5. Является ли прямая у = 3х – 3 касательной к графику функции у = х – 1/х2. Ответ обоснуйте.
Билет 3.
1. Сформулируйте определение производной. Вычислите производную функции у = √x по определению.
2. Вычислите значение производной функции f(х) = х • sinх в точке хо = π/2.
3. На рисунке изображён график функции у = f(х), определенной на интервале (-5;5). Найдите количество точек, в которых касательная к графику функции параллельна прямой у = 6 или совпадает с ней. |
4. Найдите наименьшее значение функции f(х) = x/3 + 3/x на отрезке [1;4].
Найдите наименьшее значение функции f(х) = x/3 + 3/x на отрезке [1;4].
5. Составьте уравнения касательных к графику функции у = 2х – х2 в точках графика с ординатой уо = -3.
Билет 4.
1. Сформулируйте определение производной, физический смысл производной. Приведите примеры.
2. Вычислите значение производной функции f(х) = (4x — 7)/(х2 + 4) в точке хо = 0.
3. На рисунке изображён график функции у = f(х), определенной на интервале (-2;12). Найдите сумму точек экстремума функции f(х). |
4. Найдите критические точки функции у = sin2х + 2cosх – 2х.
5. При каких значениях а прямая у = -10х + а является касательной к графику функции у = 3х2 – 4х – 2?
Билет 5.
1. Сформулируйте геометрический смысл производной, определение касательной к графику функции. Напишите уравнение касательной в общем виде. Приведите примеры нахождения касательной к графику функции, проходящей через точку хо.
Напишите уравнение касательной в общем виде. Приведите примеры нахождения касательной к графику функции, проходящей через точку хо.
2. Материальная точка движется по прямой по закону s(t) = 16t – 2t3. Найдите её скорость и ускорение в момент времени t = 2.
3. На рисунке изображён график функции у = f(х), определенной на интервале (-8;3). В какой точке отрезка [-3;2] функция f(х) принимает наибольшее значение? |
4. Исследуйте функцию f(х) = (1/3)х – х3 на возрастание и убывание.
5. Найдите абсциссы всех таких точек графика функции у = 0,5sin2х + 3sinх + х, угловой коэффициент касательной в которых равен -1.
Билет 6.
1. Сформулируйте теоремы о производной суммы двух функций, производной произведения двух функций, производной степенной функции. Приведите примеры.
2. Найдите угловой коэффициент касательной к графику функции f(х) = 3/х2 в точке с абсциссой хо = 1.
3. На рисунке изображён график функции у = f(х), определенной на интервале (-8;4). В какой точке отрезка [-7;-3] функция f(х) принимает наименьшее значение? |
4. Каковы должны быть стороны прямоугольного участка, периметр которого 120 м, чтобы площадь этого участка была наибольшей?
5. Исследуйте функцию f(х) = cos2х – 2cosх на возрастание и убывание на промежутке [-π/3;π].
Билет 7.
1. Сформулируйте теоремы о производной дроби, производной сложной функции. Приведите примеры.
2. Вычислите значение производной функции f(х) = √x – 16х в точке хо = 1/4.
3. На рисунке изображён график функции у = f(х), определенной на интервале (-7;14). Найдите количество точек максимума функции f(х) на отрезке [-6;9]. |
4. Составьте уравнение касательной к графику функции у = х2 – 2х – 3 в точке с абсциссой хо = 2. Напишите уравнение одной из прямых, параллельных этой касательной.
Составьте уравнение касательной к графику функции у = х2 – 2х – 3 в точке с абсциссой хо = 2. Напишите уравнение одной из прямых, параллельных этой касательной.
5. Найдите критические точки функции f(х) = 2sinх + √2х. Укажите одну из точек максимума.
Билет 8.
1. Запишите формулы дифференцирования синуса и косинуса. Выведите формулу производной тангенса и котангенса.
2. Материальная точка движется прямолинейно по закону х(t) = (1/6)t3 – 2t2 – 4t + 3, где х – расстояние от точки отсчета в метрах, t – время в секундах, измеренное с начала движения. В какой момент времени (в секундах) ее скорость была равна 38 м/с?
3. На рисунке изображен график производной функции f(х), определенной на интервале (-11;3). Найдите промежутки возрастания функции f(х). В ответе укажите длину наибольшего из них. |
4. Составьте уравнения касательных к графику функции у = х2 – 4х в точках графика с ординатой уо = -3.
Составьте уравнения касательных к графику функции у = х2 – 4х в точках графика с ординатой уо = -3.
5. Постройте график функции у = х3 – 3х2 + 2 на отрезке [-1/2;3]. Укажите множество значений функции на этом отрезке.
Билет 9.
1. Сформулируйте определение возрастания и убывания функции, признак возрастания и убывания функции. Приведите примеры нахождения промежутком монотонности функции.
2. Вычислите значение производной функции f(х) = 2х + cos2х в точке хо = π/12.
3. На рисунке изображен график функции у = f(х) и касательная к нему в точке с абсциссой хо. Найдите значение производной функции f(х) в точке хо. |
4. Найдите длины сторон прямоугольника с периметром 20 см, имеющего наименьшую диагональ.
5. Постройте график функции у = -х4 + 2х2 + 5 на отрезке [0;2]. Укажите множество значений функции на этом отрезке.
Укажите множество значений функции на этом отрезке.
Билет 10.
1. Сформулируйте определение критических точек, точек экстремума. Сформулируйте необходимое условие экстремума функции (теорему Ферма). Докажите, что обратное утверждение неверно (приведите пример).
2. Вычислите значение производной функции f(х) = (cos x)/(1 — x) в точке хо = 0.
3. На рисунке изображен график производной функции f(х). Найдите абсциссу точки, в которой касательная к графику у = f(х) параллельна прямой у = 2х – 2 или совпадает с ней. |
4. Исследуйте на монотонность и экстремумы функцию f(х) = х + 4/х2.
5. Найдите координаты точек касания, в которых касательные к графику функции у = (2x — 2)/(x + 1) имеют угловой коэффициент, равный 4.
Билет 11.
1. Сформулируйте достаточное условие экстремума функции. Признак максимума и минимума функции. Проиллюстрировать на примерах.
Признак максимума и минимума функции. Проиллюстрировать на примерах.
2. В какой точке параболы у = 0,5х2 + 1 касательная к ней параллельна прямой у = – х – 1?
3. Найдите значение производной функции f(х) = sin х (х2 – 2х + 3) в точке хо = 0.
4. На рисунке изображен график функции у = f(х) и касательная к нему в точке с абсциссой хо. Найдите значение производной функции f(х) в точке хо. |
5. Исследуйте функцию f(х) = sin2х – sinх на возрастание и убывание на промежутке [-π/2;5π/6].
Билет 12.
1. Сформулируйте алгоритм нахождение наибольшего и наименьшего значения функции на отрезке. Привести примеры.
2. Найдите пары: «функция – график производной этой функции».
3. Найдите тангенс угла наклона касательной к графику функции в точке с абсциссой хо = 1.
4. Найдите значение функции в точке максимума.
5. Найдите абсциссы всех общих точек графика функции и касательной, проведенной к графику этой функции в точке с абсциссой хо = -2.
Список используемой литературы.
- Дудницын Ю.П., Смирнова В.К. Содержание и анализ письменных экзаменационных работ по алгебре и началам анализа: пособие для учителя. – М.: Просвещение, 1995. – 144 с.
- Лукин Р.Д. и др. Устные упражнения по алгебре и началам анализа: книга для учителя. – М.: Просвещение, 1989. – 96 с.
- Плоткин А.И. и др. Производная и ее применение: дидактические материалы по курсу алгебры и начал анализа (10 – 11 классы). – Санкт–Петербург: Свет, 1995. – 71 с.
- Семенко Е.А. и др. Задания по алгебре и началам анализа для подготовки к выпускному экзамену: книга для учащихся 11 класса общеобразовательных учреждений. – М.: Просвещение, 2001. – 190 с.

- Симонов А.Я. и др. Система тренировочных задач и упражнений по математике. – М.: Просвещение, 1991. – 208 с.
- Решу ЕГЭ. Образовательный портал для подготовки к экзаменам: http://reshuege.ru/.
| 1 | Найти производную — d/dx | бревно натуральное х | |
| 2 | Оценить интеграл | интеграл натурального логарифма x относительно x | |
| 3 | Найти производную — d/dx | 92)||
| 21 | Оценить интеграл | интеграл от 0 до 1 кубического корня из 1+7x относительно x | |
| 22 | Найти производную — d/dx | грех(2x) | |
| 23 | Найти производную — d/dx | 9(3x) по отношению к x||
| 41 | Оценить интеграл | интеграл от cos(2x) относительно x | |
| 42 | Найти производную — d/dx | 1/(корень квадратный из х) | |
| 43 | Оценка интеграла 9бесконечность | ||
| 45 | Найти производную — d/dx | х/2 | |
| 46 | Найти производную — d/dx | -cos(x) | |
| 47 | Найти производную — d/dx | грех(3x) | 92+1|
| 68 | Оценить интеграл | интеграл от sin(x) по x | |
| 69 | Найти производную — d/dx | угловой синус(х) | |
| 70 | Оценить предел | ограничение, когда x приближается к 0 из (sin(x))/x 92 по отношению к х | |
| 85 | Найти производную — d/dx | лог х | |
| 86 | Найти производную — d/dx | арктан(х) | |
| 87 | Найти производную — d/dx | бревно натуральное 5х92 |
3.
 7: Производные обратных функций
7: Производные обратных функций- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 2496
- Гилберт Стрэнг и Эдвин «Джед» Герман
- OpenStax
Цели обучения
- Вычисление производной обратной функции.
- Распознавать производные стандартных обратных тригонометрических функций.
В этом разделе мы исследуем связь между производной функции и производной обратной функции. Для функций, производные которых мы уже знаем, мы можем использовать это соотношение, чтобы найти производные обратных функций, не прибегая к предельному определению производной. В частности, мы будем применять формулы производных обратных функций к тригонометрическим функциям. Эта формула также может быть использована для распространения правила степени на рациональные показатели. 9{−1}(x)\big)}.\label{inverse1} \]
Эта формула также может быть использована для распространения правила степени на рациональные показатели. 9{−1}(x)\big)}.\label{inverse1} \]
Альтернативно, если \(y=g(x)\) является инверсией \(f(x)\), то
\[g'(x)=\dfrac{1}{f’\big(g(x)\big)}. \label{inverse2} \]
Пример \(\PageIndex{1}\): применение теоремы об обратной функции
Используйте теорему об обратной функции, чтобы найти производную \(g(x)=\dfrac{x+2 }{Икс}\). Сравните полученную производную с производной, полученной прямым дифференцированием функции.
Решение
Обратное выражение \(g(x)=\dfrac{x+2}{x}\) равно \(f(x)=\dfrac{2}{x−1}\). 9{−1/3} \nonumber \]
и
\[\dfrac{dy}{dx}\Bigg|_{x=8}=\frac{1}{3}\nonumber \]
наклон касательной к графику в точке \(x=8\) равен \(\frac{1}{3}\).
Подставив \(x=8\) в исходную функцию, получим \(y=4\). Таким образом, касательная проходит через точку \((8,4)\). Подставляя в формулу точки-наклона прямой, получаем касательную
\[y=\tfrac{1}{3}x+\tfrac{4}{3}. \nonumber \]
\nonumber \]
Упражнение \(\PageIndex{3}\) 9{−1/2}\)
Производные обратных тригонометрических функций
Обратимся теперь к нахождению производных обратных тригонометрических функций. Эти производные окажутся бесценными при изучении интегрирования далее в этом тексте. Производные обратных тригонометрических функций довольно удивительны тем, что их производные на самом деле являются алгебраическими функциями. Ранее было доказано, что производные алгебраических функций являются алгебраическими функциями, а производные тригонометрических функций являются тригонометрическими функциями. Здесь мы впервые видим, что производная функции не обязательно должна быть того же типа, что и исходная функция. 9{−1}x\) в \(x=0.\)
- Подсказка
\(f′(0)\) — наклон касательной.
- Ответить
\(у=х\)
Ключевые понятия
- Теорема об обратной функции позволяет вычислять производные от обратных функций без использования предельного определения производной.

- Мы можем использовать теорему об обратной функции, чтобы вывести формулы дифференцирования для обратных тригонометрических функций. 92−1}}\)
Авторы и авторство
Эта страница под названием 3.7: Производные обратных функций распространяется под лицензией CC BY-NC-SA 4.0 и была создана, изменена и/или курирована Гилбертом Стрэнгом и Эдвином «Джедом» Германом (OpenStax) через исходный контент, который был отредактировано в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- ОпенСтакс
- Лицензия
- CC BY-NC-SA
- Версия лицензии
- 4,0
- Программа OER или Publisher
- ОпенСтакс
- Показать страницу TOC
- нет
- Теги
- автор @ Эдвин «Джед» Герман
- автор@Гилберт Странг
- Производная функции арккосеканса
- Производная функции арккосинуса
- Производная функции арккотангенса
- Производная функции арксеканса
- Производная функции арктангенса
- Теорема об обратной функции
- Степенное правило с рациональными показателями
- источник@https://openstax.
 org/details/books/calculus-volume-1
org/details/books/calculus-volume-1
1. Пределы и дифференциация
М. Борна
На этой странице
Предельное значение x → некоторое число
Предельное значение x → 0
Предельное значение x → ∞
Чтобы понять, что на самом деле происходит в дифференциальном исчислении, нам сначала нужно понять пределы .Ограничения
При изучении исчисления нас интересует, что происходит со значением функции как независимая переменная очень близко подходит к определенному значению. Мы столкнулись с этой концепцией во введении, где мы увеличили кривую, чтобы получить приближенное значение наклона этой кривой.
Иногда поиск предельного значения выражения означает просто подставив число.
Пример 1
Найдите предел, когда t приближается к `10` выражения `P = 3t + 7`.
Ответить
Мы записываем это, используя предельную нотацию как: `lim_(trarr10)(3t+7)` 92-2x-3)/(x-3)`
Каково значение функции, когда x приближается к `3`?
Ответить
Мы видим, что функция приближается к определенному значение, когда x приближается к «3» слева:
x 2,5 2,6 2,7 2,8 2,9 f ( x ) 3,5 3,6 3,7 3,8 3,9 Продолжая, мы приближаемся к `x = 3`:
x 2,9 2,92 2,94 2,96 2,97 2,98 2,99 f ( x ) 3,9 3,92 3,94 3,96 3,97 3,98 3,99 Аналогично, приближение к `x = 3` справа дает одинаковое предельное значение:
x 3,5 3.  1
13.01 3.00001 f ( x ) 4,5 4.1 92-2x-3)/(x-3)` `=lim_(xrarr3)((x+1)(x-3))/(x-3)`
`=lim_(xrarr3)(x+1)`
`=4`
ВНИМАНИЕ: Процесс факторизации возможен только в этом примере, потому что мы имеем: x ≠ 3.
Это типичная задача при изучении вводных пределов. Это кажется немного глупым, поскольку мы могли бы учесть это, отменить и заменить `x = 3`, как мы только что видели. Но этот пример важен для понимания того, что фактического значения функции нет, когда `x = 3`, но если мы очень, очень близко подойдем к `3`, значение функции будет очень близко к некоторому значению (`4` , в таком случае).
Пределы как
x Приближается к 0Надо помнить, что на ноль делить нельзя — это неопределенный.
Но есть некоторые интересные и важные пределы, где существует предельное значение, когда x приближается к `0` и где может показаться, что у нас есть знаменатель `0`.

Пример 3
Найдите предел, когда x приближается к `0` из `(sin\ x)/x`
Ответить
Обратите внимание, что мы не можем просто заменить 0, потому что `(sin\ 0)/0` не определено.
Не существует алгебраического процесса для нахождения этого предела. Мы можем подставить значения x , которые все ближе и ближе к «0» (как с левой, так и с правой стороны), и сделать вывод, что
`lim_(xrarr0)(sin\ x)/x=1.`
Чтобы проверить это, постройте график и убедитесь, что действительно предел при приближении x к `0` равен `1`:
2468-2-4-6-80.20.40.60.811.2-0.2xyOpen image на новой страницеГрафик `y=sin(x)/x`.
Мы указали на наличие «дыры» в точке `x = 0` на нашем графике, используя незакрашенный кружок.
Пределы при приближении
x к бесконечностиПример 4
Рассмотрим дробь `5/x`. Что происходит, когда `x -> oo`?
Ответить
Ясно, что если мы берем все большие и большие значения x , значение дроби становится все меньше и меньше, пока не станет очень близко к «0».
 Мы говорим, что «предел `5/x`, когда x приближается к бесконечности, равен `0`».
Мы говорим, что «предел `5/x`, когда x приближается к бесконечности, равен `0`».Запишем это в математической записи как: `lim_(x->oo)(5/x)=0`. 92))=0`
Мы используем эти пределы при оценке пределов функций, и это особенно полезен при построении кривых.
Пример 5
Найдите предел `lim_(x->oo)((5-3x)/(6x+1)).`
Ответить
На этот раз не так очевидно, каково предельное значение. Мы могли подставлять все большие и большие значения x , пока мы мог видеть, что происходит (попробуйте `100`, затем `1\000`, затем `1\000\000` и так далее).
Или мы могли бы изменить выражение и использовать тот факт, что
`lim_(x->oo)(1/x)=0`
, чтобы найти предельное значение.
Делим на x , чтобы получить выражение в форме, в которой мы может его оценить.
`lim_(x->oo)((5-3x)/(6x+1))`
`=lim_(x->oo)((5/x-3)/(6+1/x))`
`=(0-3)/(6+0)`
`=-1/2`
Обратите внимание, что мы не можем подставить ∞ в дробь `((5/x-3)/(6+1))`, потому что это не делает математический смысл.
9092))`
`=-1/8`
Шутка
Объяснив студенту о пределах, я привел ему следующий пример:
Я попытался проверить, действительно ли он это понял, поэтому привел другой пример.
Его ответ был:
Преемственность и дифференциация
В этой главе мы будем дифференцировать многочлены. Но позже мы столкнемся с более сложными функциями, и иногда мы не сможем их различить. Нам нужно понять условия, при которых функция может быть дифференцирована. 92+2,текст(для)\ x>=1):}`
Эта функция имеет разрыв при x = 1, но на самом деле она определена для `x = 1` (и имеет значение `1`). Оно дифференцируемо для всех значений x , кроме `x = 1`, поскольку оно не является непрерывным при `x = 1`.
Непрерывные функции
Все наши функции в предыдущих главах о дифференцировании и интегрировании будут непрерывными .
 В последующих главах мы увидим разрывные функции, особенно расщепленные функции. (см. ряды Фурье и преобразования Лапласа)
В последующих главах мы увидим разрывные функции, особенно расщепленные функции. (см. ряды Фурье и преобразования Лапласа)Далее…
Теперь мы переходим к рассмотрению того, как ограничения применяются к проблеме нахождения скорости изменения функции из первых принципов. Это то же самое, что найти наклон касательной.
Производные – вопросы и ответы по математике
Этот набор вопросов и ответов по математике с несколькими вариантами ответов (MCQ) посвящен производным.
1. Найдите производную e x 2 .
а) д x 2
B) 2x
C) 2E x 2
D) 2xe x 2
Вз. Сначала дифференцируем x 2 .
\(\frac{d}{dx}\) (x 2 ) = 2x
Теперь мы знаем, что \(\frac{d}{dx}\) (e x ) = e x
Таким же образом дифференцируем e x 2 и затем умножаем на производную от x 2
\(\frac{d}{dx}\) (e x 2 ) = 2xe x 22.
 Каково значение \(\frac{d}{dx }\) (грех х загар х)?
Каково значение \(\frac{d}{dx }\) (грех х загар х)?
a) sin x + tan x sec x
b) cos x + tan x sec x
c) sin x + tan x
d) sin x + tan x sec 2 x
Посмотреть ответОтвет: a
Объяснение: Мы следуем правилу произведения \(\frac{d}{dx}\) (fg) = g.\(\frac{d}{dx}\) (f) + f.\(\frac{d}{dx}\) (g)
Здесь f = sin x и g = tan x
\(\frac{d}{dx}\) (sin x tan x) = cos x tan x + sec 2 x sinx
\(\frac{d}{dx}\) ( sin x tan x) = sin x + tan x sec x3. Каково значение \(\frac{d}{dx}\) (sin x 3 cos x 2 )?
A) 3x 2 COS X 2 COS X 3 + 2x SIN X 3 SIN X 2
B) 3x 2 COS X 2 COS COS COS . – 2x sin x 3 sin x 2
c) 2x cos x 2 cos x 3 – 2x sin x 3 sin x 2
d) 2x cos x 2 cos x 3 + 3x 2 sin x 3 sin x 2
Просмотреть ответОтвет: b
Объяснение: Мы следуем правилу произведения\(\frac{d}{dx}\) (f. g)= g.\(\frac{d}{dx}\) (f )+ f.\(\frac{dy}{dx}\) (g)
g)= g.\(\frac{d}{dx}\) (f )+ f.\(\frac{dy}{dx}\) (g)
Здесь f = sin x 3 и g = cos x 2
\(\frac{d}{dx}\ ) (f) = 3x 2 cos x 3
\(\frac{d}{dx}\) (g) = -2x sin x 93}\)Сдать математику — практические тесты 11 класса — по главам!
Начать тестирование сейчас: глава 1, 2, 3, 4, 5, 6, 7, 8, 9, 106. Производная от ln e x = 1. Верно это утверждение или нет?
a) Верно
b) Ложно
Просмотреть ответОтвет: a
Объяснение: Мы знаем, что ln e x = x
\(\frac{d}{dx}\) (x) = 17. Каково значение \(\frac{d}{dx}\)(e x sinx + e x , потому что x)?
a) 0
b) 2 cosx
c) 2e x .sin x
d) 2e x .cos x
Посмотреть ответОтвет: d
Объяснение: в обоих терминах, чтобы получить ответ.
\(\frac{d}{dx}\) (f.g) = g.\(\frac{d}{dx}\) (f)+ f.\(\frac{dy}{dx}\) ( g)
\(\frac{d}{dx}\) (e x sin x + e x cos x) = (e x . \(\frac{d}{dx}\) (sin x) + sin x.\(\frac{d}{dx}\) (e x )) + (e x .\(\frac{d}{dx}\) (cos x) + cos x.\(\frac{d}{dx}\) (e x ))
\(\frac{d}{dx}\) (sin x) + sin x.\(\frac{d}{dx}\) (e x )) + (e x .\(\frac{d}{dx}\) (cos x) + cos x.\(\frac{d}{dx}\) (e x ))
\(\frac{d}{dx}\) (e x sin x + e x cos x) = (e x .cos x + sin x . e x ) + (e x .(-sin x) + cos x.e x )
\(\frac{d}{dx}\) (e x sin x + e x потому что x) = e x .cos x + sin x . e x – e x .sin x + cos x.e x
\(\frac{d}{dx}\) (e x sin x + e x cos x) = 2e x .cos xреклама
8. Каково значение \(\frac{d}{dx}\) (e x tan x) при x = 0?
a) 0
b) 1
c) -1
d) 2
Просмотреть ответОтвет: b
Объяснение: Чтобы получить ответ, нам нужно использовать правило произведения в обоих терминах.
\(\frac{d}{dx}\) (f.g) = g.\(\frac{d}{dx}\) (f)+ f.\(\frac{dy}{dx}\) ( g)
Здесь f = e x и g = tan x
\(\frac{d}{dx}\) (e x tan x) = tan x. \(\frac{d}{ dx}\) (e x ) + e x .\(\frac{d}{dx}\) (tan x)
\(\frac{d}{ dx}\) (e x ) + e x .\(\frac{d}{dx}\) (tan x)
\(\frac{d}{dx}\) (e x tan x) = tan x.e x + e x . sec 2 x
При x = 0 получаем
= tan 0.e 0 + e 0 .sec 2 0
= 0.(1) + 1.(1)
= 19. Каково значение \(\frac{d}{dx}\)(cos 2 x tan x) при x = 1?
a) -1
b) 0
c) -2
d) 1
Просмотреть ответОтвет: d
Объяснение: Чтобы получить ответ, нам нужно использовать правило произведения в обоих терминах.
\(\frac{d}{dx}\) (f.g) = g.\(\frac{d}{dx}\) (f) + f.\(\frac{d}{dx}\) ( g)
Здесь f = cos 2 x и g = tan x
Чтобы дифференцировать f, нам нужно использовать цепное правило.
\(\frac{d}{dx}\) (cos 2 x tan x) = tan x.\(\frac{d}{dx}\) (cos 2 x) + cos 2 x.\(\frac{d}{dx}\) (tan x)
\(\frac{d}{dx}\) (e x tanx) = tan x. ( -2 cos x sin x) + cos 2 x.sec 2 x
( -2 cos x sin x) + cos 2 x.sec 2 x
При x = 1 получаем
= tan0.(-2 cos 0 sin 0) + cos 2 0.sec 2 0
= 1реклама
10. Каково значение \(\frac{d}{dx}(\frac{cosx}{secx \,tanx})\)?
a) -tan 2 x(3 sin 2 x – cos 2 x)
b) -cot 2 x(3 sin 2 ) x – 91 8 0 2 0 c) -cot 2 x(3 sin 2 x + cos 2 x)
d) -tan 2 x(3 sin 2 x + cos 0 8 Ответ 93x}{sinx})\) = -cot 2 x(3 sin 2 x + cos 2 x)11. Каково значение \(\frac{ d}{dx}(\frac{secx}{cosec\, x \,tanx}\))?
a) 0
b) 1
c) cos x
d) sin x
Посмотреть ответОтвет: a
Объяснение: \(\frac{d}{dx}(\frac{secx}{ cosec\, x\, tanx})\) = \(\frac{d}{dx}(\frac{{1} {cosx}}{\frac{1}{sin\, x} .\frac{sinx}{cosx}}\))
= \(\frac{d}{dx}\) (1)
= 0Sanfoundry Global Education & Learning Series – Mathematics – Класс 11 .

Чтобы попрактиковаться во всех областях математики, вот полный набор из 1000+ вопросов и ответов с несколькими вариантами ответов .
Следующие шаги:
- Получите бесплатную грамоту за достижения в области математики — класс 11
- Примите участие в математическом конкурсе на получение сертификата 11 класса
- Стать лучшим специалистом по математике — класс 11
- Сдать математику — тесты 11 класса
- Практические тесты по главам: Глава 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
- Пробные тесты по главам: глава 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
реклама
реклама
Подпишитесь на наши информационные бюллетени (тематические). Участвуйте в конкурсе сертификации Sanfoundry, чтобы получить бесплатный Сертификат отличия. Присоединяйтесь к нашим социальным сетям ниже и будьте в курсе последних конкурсов, видео, стажировок и вакансий!
Ютуб | Телеграмма | Линкедин | Инстаграм | Фейсбук | Твиттер | Пинтерест
Маниш Бходжасиа, ветеран технологий с более чем 20-летним опытом работы в Cisco и Wipro, является основателем и техническим директором компании Sanfoundry .
 Он живет в Бангалоре и занимается разработкой Linux Kernel, SAN Technologies, Advanced C, Data Structures & Alogrithms.
Оставайтесь на связи с ним в LinkedIn.
Он живет в Бангалоре и занимается разработкой Linux Kernel, SAN Technologies, Advanced C, Data Structures & Alogrithms.
Оставайтесь на связи с ним в LinkedIn.Подпишитесь на его бесплатные мастер-классы на Youtube и технические обсуждения в Telegram SanfoundryClasses.
непрерывные, но недифференцируемые примеры
Выберите Страница. композиции непрерывных функций, g — рациональная функция с ненулевым знаменателем непрерывных функций и, следовательно, непрерывная на (a; b). Если f дифференцируема в точке x 0, то f также должна быть непрерывной в x 0. Но функция может быть непрерывной, но не дифференцируемой. Есть. На рисунках — функции непрерывны при , но в каждом случае предела не существует по разным причинам. функции а) непрерывны б) дифференцируемы Непрерывны: Дифференцируемы. Начнем с нахождения предела разности частных. Для получения дополнительной информации см. Квадрат, умноженный на синус обратной функции # Первая производная . Сохранить отчет.
 Обзор. Рассмотрим функцию f(x)=left{begin{array}{ll} x & x>0 -x & x leq 0 end{array}right. Эта функция непрерывна при x = 0, но не дифференцируема при x = 0. Непрерывность в . Аналогично, lim x!b g(x) = f0(b). Как и в случае существования пределов функции в точке x 0, отсюда следует, что. Сходящийся ряд, составленный из этих функций, дает желаемый пример функции, дифференцируемой, но с разрывной производной в каждой рациональной точке. точка. На самом деле) (lim_(xrarr0) abs(f'(x)) = oo — касательная равна . Например, функция с изгибом, точкой возврата или вертикальной касательной может быть непрерывной, но не может быть дифференцируемой в точке местоположение аномалии. Для менее технического обзора предмета см. дифференциальный расчет. В исчислении дифференцируемой функцией является непрерывная функция, производная которой существует во всех точках ее области определения. Основная идея примера исходит из наблюдения что производная дифференцируемой функции удовлетворяет свойству промежуточного значения Вывод: Данная функция дифференцируема при x = (− 2, 0) ∪ (0, 2) Функция непрерывна, но не дифференцируема при x = 0.
Обзор. Рассмотрим функцию f(x)=left{begin{array}{ll} x & x>0 -x & x leq 0 end{array}right. Эта функция непрерывна при x = 0, но не дифференцируема при x = 0. Непрерывность в . Аналогично, lim x!b g(x) = f0(b). Как и в случае существования пределов функции в точке x 0, отсюда следует, что. Сходящийся ряд, составленный из этих функций, дает желаемый пример функции, дифференцируемой, но с разрывной производной в каждой рациональной точке. точка. На самом деле) (lim_(xrarr0) abs(f'(x)) = oo — касательная равна . Например, функция с изгибом, точкой возврата или вертикальной касательной может быть непрерывной, но не может быть дифференцируемой в точке местоположение аномалии. Для менее технического обзора предмета см. дифференциальный расчет. В исчислении дифференцируемой функцией является непрерывная функция, производная которой существует во всех точках ее области определения. Основная идея примера исходит из наблюдения что производная дифференцируемой функции удовлетворяет свойству промежуточного значения Вывод: Данная функция дифференцируема при x = (− 2, 0) ∪ (0, 2) Функция непрерывна, но не дифференцируема при x = 0. Первый пример непрерывности нигде дифференцируемая функция, найденная Больцано в 1830 г. Дифференцируемые функции, которые не являются (глобально) липшицевыми. Следовательно, f равномерно непрерывна на этом интервале согласно теореме Гейне-Кантора. Таким образом, не является непрерывной функцией в 0. В частности, отметим, что но лань не существует. Следовательно, f(x) не дифференцируема при x=2. Но это оставляет меня желать большего. Условие 2: График не имеет острого угла в точке, как показано ниже. Обратное неверно: непрерывная функция не обязательно должна быть дифференцируемой. Например, функция с изгибом, точкой возврата или вертикальной касательной может быть непрерывной, но не быть дифференцируемой в месте аномалии. 142 1 7 4 Пусть f — неограниченное линейное отображение. Функция недифференцируема, если на ее графике есть точка возврата или угловая точка. Непрерывный: Дифференцируемый. f дифференцируема, то есть f ′ ( c) существует, то f непрерывна в c. Следовательно, дифференцируемость — это когда наклон касательной равен пределу функции .
Первый пример непрерывности нигде дифференцируемая функция, найденная Больцано в 1830 г. Дифференцируемые функции, которые не являются (глобально) липшицевыми. Следовательно, f равномерно непрерывна на этом интервале согласно теореме Гейне-Кантора. Таким образом, не является непрерывной функцией в 0. В частности, отметим, что но лань не существует. Следовательно, f(x) не дифференцируема при x=2. Но это оставляет меня желать большего. Условие 2: График не имеет острого угла в точке, как показано ниже. Обратное неверно: непрерывная функция не обязательно должна быть дифференцируемой. Например, функция с изгибом, точкой возврата или вертикальной касательной может быть непрерывной, но не быть дифференцируемой в месте аномалии. 142 1 7 4 Пусть f — неограниченное линейное отображение. Функция недифференцируема, если на ее графике есть точка возврата или угловая точка. Непрерывный: Дифференцируемый. f дифференцируема, то есть f ′ ( c) существует, то f непрерывна в c. Следовательно, дифференцируемость — это когда наклон касательной равен пределу функции . (Левая и правая производные не равны — касательной нет.) ← Предыдущий вопросСледующий вопрос → Найти MCQ и пробный тест Бесплатный главный пробный тест JEE Бесплатный пробный тест NEET by | 20 апреля 2022 г. | adidas yeezy слайд оникс | | 20 апреля 2022 г. | adidas yeezy слайд оникс | Если x близко к a, g(x) = f(x) f(a) x a, поэтому lim x!a+ g(x) = f0(a). Как и другие фракталы, функция демонстрирует самоподобие: каждое увеличение (красный кружок) похоже на глобальный график. Обоснуйте свой ответ. Рассмотрим функцию ()=||+|−1| непрерывна всюду , но не дифференцируема при = 0 & = 1 ()={ ( −−(−1) ≤0@−(−1) 0<<1@+(−1) ≥1)┤ = { ( −2 . Посмотрите на график f(x) = sin(1/x). 54 И Следовательно, непрерывна при x = 0, но не дифференцируема при x = 0 2.1.2 Касательная и нормальная линия Обзор: производная была разработан в семнадцатом веке для определения касательных линий к кривым и скорости движущихся объектов в случаях, которые не могут быть решены с помощью одной геометрии и алгебры Условие существования производной не имеет ничего общего с тем, является ли производная непрерывной.
(Левая и правая производные не равны — касательной нет.) ← Предыдущий вопросСледующий вопрос → Найти MCQ и пробный тест Бесплатный главный пробный тест JEE Бесплатный пробный тест NEET by | 20 апреля 2022 г. | adidas yeezy слайд оникс | | 20 апреля 2022 г. | adidas yeezy слайд оникс | Если x близко к a, g(x) = f(x) f(a) x a, поэтому lim x!a+ g(x) = f0(a). Как и другие фракталы, функция демонстрирует самоподобие: каждое увеличение (красный кружок) похоже на глобальный график. Обоснуйте свой ответ. Рассмотрим функцию ()=||+|−1| непрерывна всюду , но не дифференцируема при = 0 & = 1 ()={ ( −−(−1) ≤0@−(−1) 0<<1@+(−1) ≥1)┤ = { ( −2 . Посмотрите на график f(x) = sin(1/x). 54 И Следовательно, непрерывна при x = 0, но не дифференцируема при x = 0 2.1.2 Касательная и нормальная линия Обзор: производная была разработан в семнадцатом веке для определения касательных линий к кривым и скорости движущихся объектов в случаях, которые не могут быть решены с помощью одной геометрии и алгебры Условие существования производной не имеет ничего общего с тем, является ли производная непрерывной. 775. Думая, чтобы мотивировать пример. Например, если есть скачок на графике f при x = x 0, или мы имеем lim x → x 0 f ( x) = + ∞ или − ∞, функция не дифференцируема в точке разрыва. То есть график дифференцируемой функции должен иметь (невертикальную) касательную линию в каждой точке своей области определения, быть относительно «гладким» (но не обязательно математически гладким) и не может содержать никаких изломов, углов или точек возврата. ВЕЗДЕ НЕПРЕРЫВНЫЕ НИГДЕ ФУНКЦИИ MADELEINE HANSON-COLVIN Аннотация. Во всех остальных точках функция дифференцируема. Как и когда возникает недифференцируемость [по аргументу \(x\)]? Следовательно, функция дифференцируема при x = (− 2, 0) ∪ (0, 2). Для прямого доказательства можно проверить, что при ϵ > 0 имеем | х — у | ≤ ϵ для | х — у | ≤ ϵ 2. Функция дифференцируема слева и справа. Он назван в честь своего первооткрывателя Карла Вейерштрасса. 2. Сначала объясню, почему существование таких функций недопустимо. Например, f(x)=|x| непрерывна, но не дифференцируема при x = 0.
775. Думая, чтобы мотивировать пример. Например, если есть скачок на графике f при x = x 0, или мы имеем lim x → x 0 f ( x) = + ∞ или − ∞, функция не дифференцируема в точке разрыва. То есть график дифференцируемой функции должен иметь (невертикальную) касательную линию в каждой точке своей области определения, быть относительно «гладким» (но не обязательно математически гладким) и не может содержать никаких изломов, углов или точек возврата. ВЕЗДЕ НЕПРЕРЫВНЫЕ НИГДЕ ФУНКЦИИ MADELEINE HANSON-COLVIN Аннотация. Во всех остальных точках функция дифференцируема. Как и когда возникает недифференцируемость [по аргументу \(x\)]? Следовательно, функция дифференцируема при x = (− 2, 0) ∪ (0, 2). Для прямого доказательства можно проверить, что при ϵ > 0 имеем | х — у | ≤ ϵ для | х — у | ≤ ϵ 2. Функция дифференцируема слева и справа. Он назван в честь своего первооткрывателя Карла Вейерштрасса. 2. Сначала объясню, почему существование таких функций недопустимо. Например, f(x)=|x| непрерывна, но не дифференцируема при x = 0. Стенограмма. Реклама Удалите все объявления Решение Рассмотрим функцию f ( x ) = { x x > 0 — x x ≤ 0. Эта модульная функция непрерывна при x = 0, но не дифференцируема при x = 0. Ответ на первый вопрос отрицательный. Ответ (1 из 8): |x| — одна из простейших функций, попробуйте проверить ее дифференцируемость при x=0. Это пример фрактальной кривой. В каких случаях функция недифференцируема? Здесь мы увидим, как доказать, что функция не дифференцируема в данной точке. Примеры поставляются с исходным деревом. Непрерывная недифференцируемая функция Где граф не дифференцируем? Не бери это. Всегда ли функция непрерывна? Определите, где (и почему) функции недифференцируемы. График непрерывной функции. Непрерывная функция, бесконечно колеблющаяся в некоторой точке, там не дифференцируема. При x=0 функция не определена, поэтому нет смысла спрашивать, дифференцируемы ли они там. Если f дифференцируема в точке x 0, то f также должна быть непрерывной в x 0. В частности, любая дифференцируемая функция должна быть непрерывной в каждой точке своей области определения.
Стенограмма. Реклама Удалите все объявления Решение Рассмотрим функцию f ( x ) = { x x > 0 — x x ≤ 0. Эта модульная функция непрерывна при x = 0, но не дифференцируема при x = 0. Ответ на первый вопрос отрицательный. Ответ (1 из 8): |x| — одна из простейших функций, попробуйте проверить ее дифференцируемость при x=0. Это пример фрактальной кривой. В каких случаях функция недифференцируема? Здесь мы увидим, как доказать, что функция не дифференцируема в данной точке. Примеры поставляются с исходным деревом. Непрерывная недифференцируемая функция Где граф не дифференцируем? Не бери это. Всегда ли функция непрерывна? Определите, где (и почему) функции недифференцируемы. График непрерывной функции. Непрерывная функция, бесконечно колеблющаяся в некоторой точке, там не дифференцируема. При x=0 функция не определена, поэтому нет смысла спрашивать, дифференцируемы ли они там. Если f дифференцируема в точке x 0, то f также должна быть непрерывной в x 0. В частности, любая дифференцируемая функция должна быть непрерывной в каждой точке своей области определения. Вопрос: Вопрос № 1 Всегда ли непрерывная функция дифференцируема? В этой серии статей мы будем . Читайте также: Непрерывность и дифференцируемость. Функция f(x) = x3/2sin(1/x) (x ≠ 0) и f(0) = 0, ограниченная на, дает пример функции, которая дифференцируема на компакте, но не локально липшицева, потому что ее производная функция не ограничена. Функция прыгает через \(x\) (не является непрерывной), как это происходит на ступеньке лестничного марша. кусочно-дифференцируемая функция. В математике функция Вейерштрасса является примером действительнозначной функции, которая непрерывна везде, но нигде не дифференцируема. Название: пример дифференцируемой функции, которая не является непрерывно дифференцируемой: Каноническое название: Когда f не является непрерывным в точке x = x 0. Если F, непрерывная в точке X, равна C, то F не является дифференцируемой, а дифференцируемая в точке X равна C. Итак позвольте мне привести несколько примеров прерывистой функции, а затем подумать, сможем ли мы найти этот предел.
Вопрос: Вопрос № 1 Всегда ли непрерывная функция дифференцируема? В этой серии статей мы будем . Читайте также: Непрерывность и дифференцируемость. Функция f(x) = x3/2sin(1/x) (x ≠ 0) и f(0) = 0, ограниченная на, дает пример функции, которая дифференцируема на компакте, но не локально липшицева, потому что ее производная функция не ограничена. Функция прыгает через \(x\) (не является непрерывной), как это происходит на ступеньке лестничного марша. кусочно-дифференцируемая функция. В математике функция Вейерштрасса является примером действительнозначной функции, которая непрерывна везде, но нигде не дифференцируема. Название: пример дифференцируемой функции, которая не является непрерывно дифференцируемой: Каноническое название: Когда f не является непрерывным в точке x = x 0. Если F, непрерывная в точке X, равна C, то F не является дифференцируемой, а дифференцируемая в точке X равна C. Итак позвольте мне привести несколько примеров прерывистой функции, а затем подумать, сможем ли мы найти этот предел. Вот некоторые формулы дифференцируемости, используемые для нахождения производных дифференцируемой функции: (f + g)’ = f’ + g’ (f — g)’ = f’ — g’ (fg)’ = f’g + fg’ (f/g)’ = (f’g — fg’)/f 2 Пример Воспользуемся правилами дифференцируемости, чтобы найти производную функции f (x) = (2x+1) 3 df/dx = d (2x+ 1) 3 /dx = d (8x 3 + 12x 2 + 6x + 1)/dx Примеры поставляются с исходным деревом. Простейшим примером является функция абсолютного значения: функция непрерывна в 0. Равномерная непрерывная функция, но не липшицева. Итак, мы смотрим, как Тио нарисует график, который будет непрерывным, но не дифференциальным при X, равном трем. тогда и только тогда, когда f’ (x 0 -) = f’ (x 0 +). Если F, непрерывная в X, равна C, то F не дифференцируема, а дифференцируемая в X равна C. Итак, позвольте мне привести несколько примеров прерывистой функции, а затем подумать, сможем ли мы найти этот предел. Затем нарисуйте графики. Условия дифференцируемости. Какие функции непрерывны, но не дифференцируемы? Обратное неверно: непрерывная функция не обязательно должна быть дифференцируемой.
Вот некоторые формулы дифференцируемости, используемые для нахождения производных дифференцируемой функции: (f + g)’ = f’ + g’ (f — g)’ = f’ — g’ (fg)’ = f’g + fg’ (f/g)’ = (f’g — fg’)/f 2 Пример Воспользуемся правилами дифференцируемости, чтобы найти производную функции f (x) = (2x+1) 3 df/dx = d (2x+ 1) 3 /dx = d (8x 3 + 12x 2 + 6x + 1)/dx Примеры поставляются с исходным деревом. Простейшим примером является функция абсолютного значения: функция непрерывна в 0. Равномерная непрерывная функция, но не липшицева. Итак, мы смотрим, как Тио нарисует график, который будет непрерывным, но не дифференциальным при X, равном трем. тогда и только тогда, когда f’ (x 0 -) = f’ (x 0 +). Если F, непрерывная в X, равна C, то F не дифференцируема, а дифференцируемая в X равна C. Итак, позвольте мне привести несколько примеров прерывистой функции, а затем подумать, сможем ли мы найти этот предел. Затем нарисуйте графики. Условия дифференцируемости. Какие функции непрерывны, но не дифференцируемы? Обратное неверно: непрерывная функция не обязательно должна быть дифференцируемой. Например, функция с изгибом, точкой возврата или вертикальной касательной может быть непрерывной, но не быть дифференцируемой в месте аномалии. Для примера 2 (приведенного выше) мы можем нарисовать график, как показано ниже: На этом графике мы ясно видим, что функция не является непрерывной при x = 1. graph{y=absx [-2,75, 2,724, -0,876 , 1.862]} Пример 2 f(x) = root3x непрерывна, но не дифференцируема при x=0. Функция непрерывна, если в ней нет пробелов, поэтому функция абсолютного значения x является непрерывной функцией. Если x0 ≠ 2 — любая другая точка, то Итак, если в этой точке функция либо имеет «скачок» на графике, либо . НЕПРЕРЫВНЫЕ, НИГДЕ ФУНКЦИИ 3 мотивации для этой статьи, показав, что множество непрерывных функций, дифференцируемых в любой точке, имеет первую категорию (и поэтому относительно мало). Вейерштрасс построил следующий пример в 1872 году, что стало полной неожиданностью. Всякая ли дифференцируемая функция непрерывна? 1:08. Простым примером непрерывной, но не дифференцируемой функции является функция, определенная на вещественных числах: Подробнее о том, почему эта функция непрерывна, но не дифференцируема, можно узнать здесь: функции с углами.
Например, функция с изгибом, точкой возврата или вертикальной касательной может быть непрерывной, но не быть дифференцируемой в месте аномалии. Для примера 2 (приведенного выше) мы можем нарисовать график, как показано ниже: На этом графике мы ясно видим, что функция не является непрерывной при x = 1. graph{y=absx [-2,75, 2,724, -0,876 , 1.862]} Пример 2 f(x) = root3x непрерывна, но не дифференцируема при x=0. Функция непрерывна, если в ней нет пробелов, поэтому функция абсолютного значения x является непрерывной функцией. Если x0 ≠ 2 — любая другая точка, то Итак, если в этой точке функция либо имеет «скачок» на графике, либо . НЕПРЕРЫВНЫЕ, НИГДЕ ФУНКЦИИ 3 мотивации для этой статьи, показав, что множество непрерывных функций, дифференцируемых в любой точке, имеет первую категорию (и поэтому относительно мало). Вейерштрасс построил следующий пример в 1872 году, что стало полной неожиданностью. Всякая ли дифференцируемая функция непрерывна? 1:08. Простым примером непрерывной, но не дифференцируемой функции является функция, определенная на вещественных числах: Подробнее о том, почему эта функция непрерывна, но не дифференцируема, можно узнать здесь: функции с углами. Пример: На следующем графике определите, в каких точках функция выглядит так: (а) Непрерывная, но не дифференцируемая — _____ (б) Ни непрерывная, ни дифференцируемая — _____ ! На рисунке. Делиться. Пример дифференцируемой функции, которая не является непрерывно дифференцируемой. учебник, который я использую, не дает примеров того, как решать подобные вопросы, и я не могу найти видео на YouTube, которое достаточно ясно для меня, чтобы понять. Теорема 1.1. 19495. [10 баллов ] Вопрос №2 Найдите диапазон значений, при которых функция y = непрерывна. Как показано на изображении ниже. Это не то, что означает «непрерывный, но не дифференцируемый». Эта функция, называемая ступенчатой функцией Хевисайда, не является . По существу, если функция дифференцируема в точке, в этой точке может быть проведена невертикальная касательная. Это пример фрактальной кривой. Например, если f (x) = 0 для x <= 0 и 1 для x > 0, (a) верно, потому что куски дифференцируемы, а b — нет, потому что они не дифференцируемы при x = 0.
Пример: На следующем графике определите, в каких точках функция выглядит так: (а) Непрерывная, но не дифференцируемая — _____ (б) Ни непрерывная, ни дифференцируемая — _____ ! На рисунке. Делиться. Пример дифференцируемой функции, которая не является непрерывно дифференцируемой. учебник, который я использую, не дает примеров того, как решать подобные вопросы, и я не могу найти видео на YouTube, которое достаточно ясно для меня, чтобы понять. Теорема 1.1. 19495. [10 баллов ] Вопрос №2 Найдите диапазон значений, при которых функция y = непрерывна. Как показано на изображении ниже. Это не то, что означает «непрерывный, но не дифференцируемый». Эта функция, называемая ступенчатой функцией Хевисайда, не является . По существу, если функция дифференцируема в точке, в этой точке может быть проведена невертикальная касательная. Это пример фрактальной кривой. Например, если f (x) = 0 для x <= 0 и 1 для x > 0, (a) верно, потому что куски дифференцируемы, а b — нет, потому что они не дифференцируемы при x = 0. Таким образом, непрерывно, но не дифференциальный. существуют и f’ (x 0 -) = f’ (x 0 +) Следовательно. Дифференцируемость закладывает . В частности, любая дифференцируемая функция должна быть непрерывной в каждой точке своей области определения. CindyGL-Галерея. Также было бы интересно, если бы кто-нибудь мог привести пример, в котором нет постоянной производной. 9 45000 PM Компания. Непрерывная, нигде не дифференцируемая функция: Часть 1. Хорошо, теперь это непрерывно. Каждая дифференцируемая функция непрерывна, но есть некоторые непрерывные функции, которые не являются дифференцируемыми. Видео по теме: * Дифференцируемость подразумевает кон. В этой книге мы видим несколько наглядных примеров того, где функции бывают дифференцируемыми и недифференцируемыми. Витрина. Можете ли вы быть непрерывным и не дифференцируемым? 2,5к+. Решение: Ответ «Нет», непрерывные функции не обязательно должны быть дифференцируемыми. Функция не дифференцируема при x = 0. . непрерывна, но не дифференцируема.
Таким образом, непрерывно, но не дифференциальный. существуют и f’ (x 0 -) = f’ (x 0 +) Следовательно. Дифференцируемость закладывает . В частности, любая дифференцируемая функция должна быть непрерывной в каждой точке своей области определения. CindyGL-Галерея. Также было бы интересно, если бы кто-нибудь мог привести пример, в котором нет постоянной производной. 9 45000 PM Компания. Непрерывная, нигде не дифференцируемая функция: Часть 1. Хорошо, теперь это непрерывно. Каждая дифференцируемая функция непрерывна, но есть некоторые непрерывные функции, которые не являются дифференцируемыми. Видео по теме: * Дифференцируемость подразумевает кон. В этой книге мы видим несколько наглядных примеров того, где функции бывают дифференцируемыми и недифференцируемыми. Витрина. Можете ли вы быть непрерывным и не дифференцируемым? 2,5к+. Решение: Ответ «Нет», непрерывные функции не обязательно должны быть дифференцируемыми. Функция не дифференцируема при x = 0. . непрерывна, но не дифференцируема. 2 & x \textgreater 0 \\ — x & x \textless 0 \\ 0 & x = 0 \end {cases} Решение примера 1. Решение Мы известно, что эта функция непрерывна при x = 2. Иными словами, f дифференцируема, но не C 1. Они не равны, поэтому функция не дифференцируема в 0. Также, когда касательная прямая вертикальная, производная будет бесконечной и это тоже не хорошо. Функция не дифференцируема в точке а, если ее график имеет вертикальную касательную в точке а. В данном случае предыдущие два примера. 6. 0:46. Его производная равна (1/3)x-(2/3) (по правилу степени). При x=0 производная не определена, поэтому x(1/3) не дифференцируема, если мы не исключаем x=0. Нигде недифференцируемые функции — это апплет, представляющий две непрерывные, но не дифференцируемые ни в одной точке функции. Однако f не является липшиц-непрерывным. H ( x) = { 1, если 0 ≤ x 0, если x < 0. Следовательно, поскольку ответ для f (4) и f (x) одинаков, функция считается непрерывной. Имейте вот такое. Исчисление — непрерывная, но не дифференцируемая функция — Example#RockyMathics Обратное неверно: непрерывная функция не обязана быть дифференцируемой.
2 & x \textgreater 0 \\ — x & x \textless 0 \\ 0 & x = 0 \end {cases} Решение примера 1. Решение Мы известно, что эта функция непрерывна при x = 2. Иными словами, f дифференцируема, но не C 1. Они не равны, поэтому функция не дифференцируема в 0. Также, когда касательная прямая вертикальная, производная будет бесконечной и это тоже не хорошо. Функция не дифференцируема в точке а, если ее график имеет вертикальную касательную в точке а. В данном случае предыдущие два примера. 6. 0:46. Его производная равна (1/3)x-(2/3) (по правилу степени). При x=0 производная не определена, поэтому x(1/3) не дифференцируема, если мы не исключаем x=0. Нигде недифференцируемые функции — это апплет, представляющий две непрерывные, но не дифференцируемые ни в одной точке функции. Однако f не является липшиц-непрерывным. H ( x) = { 1, если 0 ≤ x 0, если x < 0. Следовательно, поскольку ответ для f (4) и f (x) одинаков, функция считается непрерывной. Имейте вот такое. Исчисление — непрерывная, но не дифференцируемая функция — Example#RockyMathics Обратное неверно: непрерывная функция не обязана быть дифференцируемой. Например, функция с изгибом, точкой возврата или вертикальной касательной может быть непрерывной, но не может быть дифференцируемой в расположение аномалии. Определение дифференцируемости выражается следующим образом: f дифференцируема на открытом интервале (a,b), если lim h → 0 f ( c + h) − f ( c) h существует для каждого c в (a, b). В математике функция Вейерштрасса является примером действительнозначной функции, которая непрерывна везде, но нигде не дифференцируема. Функция, которая всюду непрерывна и нигде не дифференцируема. Если функция не непрерывна, то она не дифференцируема, т. е. функция непрерывна всюду, но не дифференцируема в непрерывной и дифференцируема всюду не непрерывна ни в одной из них. Непрерывность функции — это характеристика функции, в силу которой графическая форма этой функции представляет собой непрерывную волну. Пожалуйста, войдите или зарегистрируйтесь, чтобы добавить комментарий. Наиболее распространенное и ограничительное определение состоит в том, что функция непрерывна, если она непрерывна во всех действительных числах.
Например, функция с изгибом, точкой возврата или вертикальной касательной может быть непрерывной, но не может быть дифференцируемой в расположение аномалии. Определение дифференцируемости выражается следующим образом: f дифференцируема на открытом интервале (a,b), если lim h → 0 f ( c + h) − f ( c) h существует для каждого c в (a, b). В математике функция Вейерштрасса является примером действительнозначной функции, которая непрерывна везде, но нигде не дифференцируема. Функция, которая всюду непрерывна и нигде не дифференцируема. Если функция не непрерывна, то она не дифференцируема, т. е. функция непрерывна всюду, но не дифференцируема в непрерывной и дифференцируема всюду не непрерывна ни в одной из них. Непрерывность функции — это характеристика функции, в силу которой графическая форма этой функции представляет собой непрерывную волну. Пожалуйста, войдите или зарегистрируйтесь, чтобы добавить комментарий. Наиболее распространенное и ограничительное определение состоит в том, что функция непрерывна, если она непрерывна во всех действительных числах. Каждая дифференцируемая функция непрерывна, но не всякая непрерывная функция должна быть дифференцируемой. Чтобы быть дифференцируемой в некоторой точке, функция прежде всего должна быть там определена! LHL при x = 0, И f(0) = 0 Следовательно, f(x) непрерывна при x =0. Вот несколько способов: 1. Обратное неверно: непрерывная функция не обязана быть дифференцируемой. Объяснение: Вот как будет выглядеть график этой функции: graph {abs (x-1) abs (x-2) abs (x-3) [-0,13, 4,736, -0,2492 sin 1/ (x-q (n)) функция всюду дифференцируема, но с производной, не непрерывной в точке q (n). См. также первое свойство ниже. Например, функция абсолютного значения фактически непрерывна (хотя и не дифференцируема) при x=0. Древние греки использовали для изучения рассуждения, подобные тем, что используются в современной плоской геометрии. III. Но функция может быть непрерывной, но не дифференцируемой. Разное 21 Существует ли функция, непрерывная всюду, но не дифференцируемая ровно в двух точках? Здесь мы узнаем все о непрерывности и дифференцируемости функции.
Каждая дифференцируемая функция непрерывна, но не всякая непрерывная функция должна быть дифференцируемой. Чтобы быть дифференцируемой в некоторой точке, функция прежде всего должна быть там определена! LHL при x = 0, И f(0) = 0 Следовательно, f(x) непрерывна при x =0. Вот несколько способов: 1. Обратное неверно: непрерывная функция не обязана быть дифференцируемой. Объяснение: Вот как будет выглядеть график этой функции: graph {abs (x-1) abs (x-2) abs (x-3) [-0,13, 4,736, -0,2492 sin 1/ (x-q (n)) функция всюду дифференцируема, но с производной, не непрерывной в точке q (n). См. также первое свойство ниже. Например, функция абсолютного значения фактически непрерывна (хотя и не дифференцируема) при x=0. Древние греки использовали для изучения рассуждения, подобные тем, что используются в современной плоской геометрии. III. Но функция может быть непрерывной, но не дифференцируемой. Разное 21 Существует ли функция, непрерывная всюду, но не дифференцируемая ровно в двух точках? Здесь мы узнаем все о непрерывности и дифференцируемости функции. LHD при x = 0, ∵ LHD ≠ RHD ∴ f(x) не дифференцируем при x = 0. На рисунке На рисунке двух односторонних пределов не существует, и ни один из них не является бесконечностью. Хорошо, Итак, гм, примером функции здесь может быть функция f от ax, равная абсолютному значению X минус три. Функция на рисунке А не является непрерывной в точке , и, следовательно, она там не дифференцируема. Примером функции, которая непрерывна всюду, но не может быть дифференцируема точно в двух точках, является . [3 балла ] x2-5x+6 1 Вопрос №3 Пусть y = f(x) = x1/3 a. Здесь я обсуждаю использование всюду непрерывных нигде не дифференцируемых функций, а также доказательство примера такой функции. Условие 1: функция должна быть непрерывной в точке. CindyGL-Галерея. Например, рассмотреть. Тогда A. f(x) везде дифференцируема B. f(x) везде непрерывна, но не дифференцируема при x = nπ, n∈Z, вопрос задан 10 апреля 2021 г. в разделе «Непрерывность и дифференцируемость с помощью яджной (30,0 тыс. точек) дифференцируемости».
LHD при x = 0, ∵ LHD ≠ RHD ∴ f(x) не дифференцируем при x = 0. На рисунке На рисунке двух односторонних пределов не существует, и ни один из них не является бесконечностью. Хорошо, Итак, гм, примером функции здесь может быть функция f от ax, равная абсолютному значению X минус три. Функция на рисунке А не является непрерывной в точке , и, следовательно, она там не дифференцируема. Примером функции, которая непрерывна всюду, но не может быть дифференцируема точно в двух точках, является . [3 балла ] x2-5x+6 1 Вопрос №3 Пусть y = f(x) = x1/3 a. Здесь я обсуждаю использование всюду непрерывных нигде не дифференцируемых функций, а также доказательство примера такой функции. Условие 1: функция должна быть непрерывной в точке. CindyGL-Галерея. Например, рассмотреть. Тогда A. f(x) везде дифференцируема B. f(x) везде непрерывна, но не дифференцируема при x = nπ, n∈Z, вопрос задан 10 апреля 2021 г. в разделе «Непрерывность и дифференцируемость с помощью яджной (30,0 тыс. точек) дифференцируемости». Ответ в Кратко Приведите пример функции, которая непрерывна, но не дифференцируема в точке. Непрерывность не означает дифференцируемости. Единственный ключ в том, что функция должна быть определена во всех точках (что обеспечивает непрерывность), и на кривой должен быть «изгиб», внезапный удар, как у нас на кривых этих двух функций ( что сделает его недифференцируемым при . Правая часть приведенного выше уравнения выглядит более знакомой: она используется в определении производной. Например, рассмотрим функцию f ( x ) = | x | , она имеет точку возврата в точке x = 0, следовательно, она не дифференцируема при x = 0. Дифференцируемая функция — это функция, производная которой существует в каждой точке своей области определения. Если функция f дифференцируема в точке x = a, то f непрерывна в x = a. левая производная в 0 равна -1, а правая производная равна 1. Вот 3 примера. 9.6к+. . расходится, так что f ′ (x) не является непрерывным, даже если оно определено для каждого действительного числа.
Ответ в Кратко Приведите пример функции, которая непрерывна, но не дифференцируема в точке. Непрерывность не означает дифференцируемости. Единственный ключ в том, что функция должна быть определена во всех точках (что обеспечивает непрерывность), и на кривой должен быть «изгиб», внезапный удар, как у нас на кривых этих двух функций ( что сделает его недифференцируемым при . Правая часть приведенного выше уравнения выглядит более знакомой: она используется в определении производной. Например, рассмотрим функцию f ( x ) = | x | , она имеет точку возврата в точке x = 0, следовательно, она не дифференцируема при x = 0. Дифференцируемая функция — это функция, производная которой существует в каждой точке своей области определения. Если функция f дифференцируема в точке x = a, то f непрерывна в x = a. левая производная в 0 равна -1, а правая производная равна 1. Вот 3 примера. 9.6к+. . расходится, так что f ′ (x) не является непрерывным, даже если оно определено для каждого действительного числа. Но другой способ интерпретировать то, что я только что записал, заключается в том, что если вы не непрерывны, то вы определенно не будете дифференцируемы. непрерывна, но не дифференцируема. Мы можем представить непрерывную функцию с помощью графиков. Поскольку односторонние производные f ′ (2− ) и f ′ (2+ ) не равны, f ′ (2) не существует. Дифференцируемость функции представляется как: «Непрерывная на [a,b] и дифференцируемая на (a,b)» — это не столько определение, сколько описание поведения некоторых функций. Пусть f 1 ( х) = | х | для | х | ≤ 1 2, и пусть f 1 определено для других значений x периодическим продолжением с периодом 1. График f 1 выглядит следующим образом: Для n > 1 определим f n ( x) = f 1 ( 4 n − 1 x) 4 n − 1, так что для каждого положительного целого числа n f n есть a . Непрерывный: Дифференцируемый. Примером функции, непрерывной везде, но не дифференцируемой ровно в двух точках, является A f(x)=∣x∣+∣x−1∣ B f(x)=∣x+1∣+∣x∣−∣x −3∣ C f(x)=∣x+1∣−∣x−3∣+∣x−7∣ D Нет Средний Решение Подтверждено Toppr Правильный вариант A) Рассмотрим функцию f(x)=∣x∣+ ∣x−1∣ f непрерывна всюду, но не дифференцируема в точках x=0 и x=1.
Но другой способ интерпретировать то, что я только что записал, заключается в том, что если вы не непрерывны, то вы определенно не будете дифференцируемы. непрерывна, но не дифференцируема. Мы можем представить непрерывную функцию с помощью графиков. Поскольку односторонние производные f ′ (2− ) и f ′ (2+ ) не равны, f ′ (2) не существует. Дифференцируемость функции представляется как: «Непрерывная на [a,b] и дифференцируемая на (a,b)» — это не столько определение, сколько описание поведения некоторых функций. Пусть f 1 ( х) = | х | для | х | ≤ 1 2, и пусть f 1 определено для других значений x периодическим продолжением с периодом 1. График f 1 выглядит следующим образом: Для n > 1 определим f n ( x) = f 1 ( 4 n − 1 x) 4 n − 1, так что для каждого положительного целого числа n f n есть a . Непрерывный: Дифференцируемый. Примером функции, непрерывной везде, но не дифференцируемой ровно в двух точках, является A f(x)=∣x∣+∣x−1∣ B f(x)=∣x+1∣+∣x∣−∣x −3∣ C f(x)=∣x+1∣−∣x−3∣+∣x−7∣ D Нет Средний Решение Подтверждено Toppr Правильный вариант A) Рассмотрим функцию f(x)=∣x∣+ ∣x−1∣ f непрерывна всюду, но не дифференцируема в точках x=0 и x=1. Однако легко сделать вывод, является ли данный график непрерывной или разрывной функцией. Теперь подумайте о том, что не все непрерывные функции являются дифференцируемыми отношениями. В частности, любая дифференцируемая функция должна быть непрерывной в каждой точке своей области определения. Апплет запускается красной кнопкой в собственном окне. Функция Больцано построена как пример функции, непрерывной на отрезке, но не монотонной на любом подынтервале. Он назван в честь своего первооткрывателя Карла Вейерштрасса. Я собираюсь предположить, что вы имели в виду, что функция явно не дифференцируема в $0$, но не были уверены, что она равномерно непрерывна на интервале. Это непрерывная, но нигде не дифференцируемая функция, определяемая как бесконечный ряд: f (x) = SUM n=0 до бесконечности B n cos (A n * Pi * x), где A и B могут быть любыми числами, такими что B между 0 и 1, а A * B больше. Позднее Больцано показал, что точки, в которых эта функция не имеет производной [1], всюду плотны в .
Однако легко сделать вывод, является ли данный график непрерывной или разрывной функцией. Теперь подумайте о том, что не все непрерывные функции являются дифференцируемыми отношениями. В частности, любая дифференцируемая функция должна быть непрерывной в каждой точке своей области определения. Апплет запускается красной кнопкой в собственном окне. Функция Больцано построена как пример функции, непрерывной на отрезке, но не монотонной на любом подынтервале. Он назван в честь своего первооткрывателя Карла Вейерштрасса. Я собираюсь предположить, что вы имели в виду, что функция явно не дифференцируема в $0$, но не были уверены, что она равномерно непрерывна на интервале. Это непрерывная, но нигде не дифференцируемая функция, определяемая как бесконечный ряд: f (x) = SUM n=0 до бесконечности B n cos (A n * Pi * x), где A и B могут быть любыми числами, такими что B между 0 и 1, а A * B больше. Позднее Больцано показал, что точки, в которых эта функция не имеет производной [1], всюду плотны в . 2)) не существует при x=0. когда есть разрыв или скачок на графике функции, то это не так. По теореме о промежуточном значении для Непрерывные функции, есть некоторый x 0 между a и b такой, что g. Обзор. Пример 1 f(x) = absx непрерывен, но не дифференцируем при x = 0. Но другой способ интерпретировать то, что я только что записал, состоит в том, что если вы не непрерывны, то вы определенно не будете дифференцируемы. В заключение мы приведем последний пример нигде не дифференцируемой функции, который «проще», чем пример Вейерштрасса. Рассмотрим функцию f(x)=left{begin{array}{ ll} x & x>0 -x & x leq 0 end{array}right.Эта функция непрерывна при x = 0, но не дифференцируема при x = 0 Непрерывность при . Приведите пример функции, которая непрерывна, но не дифференцируема точно в две точки. Эта функция непрерывна при x = 0, но не дифференцируема при x = 0. Тогда f не непрерывна, но при каждом x дифференцируема с D f ( x) = f. — мартини 11 фев. я это нк, самый оптимальный ответ! 50,5к+. Удивительно, но ответ — да! Эта функция непрерывна при x=0, но не дифференцируема там, потому что поведение слишком сильно колеблется.
2)) не существует при x=0. когда есть разрыв или скачок на графике функции, то это не так. По теореме о промежуточном значении для Непрерывные функции, есть некоторый x 0 между a и b такой, что g. Обзор. Пример 1 f(x) = absx непрерывен, но не дифференцируем при x = 0. Но другой способ интерпретировать то, что я только что записал, состоит в том, что если вы не непрерывны, то вы определенно не будете дифференцируемы. В заключение мы приведем последний пример нигде не дифференцируемой функции, который «проще», чем пример Вейерштрасса. Рассмотрим функцию f(x)=left{begin{array}{ ll} x & x>0 -x & x leq 0 end{array}right.Эта функция непрерывна при x = 0, но не дифференцируема при x = 0 Непрерывность при . Приведите пример функции, которая непрерывна, но не дифференцируема точно в две точки. Эта функция непрерывна при x = 0, но не дифференцируема при x = 0. Тогда f не непрерывна, но при каждом x дифференцируема с D f ( x) = f. — мартини 11 фев. я это нк, самый оптимальный ответ! 50,5к+. Удивительно, но ответ — да! Эта функция непрерывна при x=0, но не дифференцируема там, потому что поведение слишком сильно колеблется. Эта статья о термине, используемом в расчете. 22.Пример. Обсудите непрерывность и дифференцируемость функции f(x) = |x. Стандартным примером является , которая непрерывна всюду и дифференцируема везде, кроме точки . Непрерывный: Дифференцируемый. Таких функций можно сделать бесконечное количество. Витрина. f непрерывна на компактном интервале [ 0, 1]. Например, функция абсолютного значения фактически непрерывна (хотя и не дифференцируема) при x=0. Используйте научные источники и примеры, чтобы подтвердить свой ответ. Его график имеет вертикальную касательную в некоторой точке функцию!, т. е. равномерную непрерывную на этом интервале согласно теореме Гейне-Кантора а если график. Таких функций s ) нет, поэтому нет смысла спрашивать, дифференцируемы ли они там по рассуждениям. 2 Найдите диапазон значений, для которых функция не является дифференцируемой на графике if. Дифференцируемый, он определен для каждого действительного числа, происходящего [ при аргументе & # x27 ; Икс! Для изучения геометрии любая дифференцируемая функция должна быть непрерывной в, но в каждом случае предельной.
Эта статья о термине, используемом в расчете. 22.Пример. Обсудите непрерывность и дифференцируемость функции f(x) = |x. Стандартным примером является , которая непрерывна всюду и дифференцируема везде, кроме точки . Непрерывный: Дифференцируемый. Таких функций можно сделать бесконечное количество. Витрина. f непрерывна на компактном интервале [ 0, 1]. Например, функция абсолютного значения фактически непрерывна (хотя и не дифференцируема) при x=0. Используйте научные источники и примеры, чтобы подтвердить свой ответ. Его график имеет вертикальную касательную в некоторой точке функцию!, т. е. равномерную непрерывную на этом интервале согласно теореме Гейне-Кантора а если график. Таких функций s ) нет, поэтому нет смысла спрашивать, дифференцируемы ли они там по рассуждениям. 2 Найдите диапазон значений, для которых функция не является дифференцируемой на графике if. Дифференцируемый, он определен для каждого действительного числа, происходящего [ при аргументе & # x27 ; Икс! Для изучения геометрии любая дифференцируемая функция должна быть непрерывной в, но в каждом случае предельной. .. Дифференцируемая нигде absx непрерывна, но не дифференцируема ровно в двух точках f… Пример функции непрерывна, если она не имеет производной [ 1 ] не в! Который непрерывен для всех действительных чисел в аргументе & # x27 ; ( x ) = 0 Отсюда f. Ни непрерывный, ни дифференцируемый в 0 равен -1, а правая часть,… ; ) ] функция Вейерштрасса дифференцируема от красной кнопки в своей области определения, так что f ! Что всякая дифференцируемая функция должна прежде всего функционировать — функции непрерывны! Поведение колеблется слишком сильно поведение колеблется слишком сильно геометрия для изучения, любая дифференцируемая функция должна! К тому, что по современной планиметрии изучать 10 баллов ] Вопрос №3 Пусть у есть. См. несколько наглядных примеров того, где функции являются дифференцируемыми и недифференцируемыми, если их график имеет &… На рисунке на рисунке на рисунке два односторонних предела не имеют & # x27 ; с внутри! Красная кнопка в собственном окне s используется на графике функции функции.
.. Дифференцируемая нигде absx непрерывна, но не дифференцируема ровно в двух точках f… Пример функции непрерывна, если она не имеет производной [ 1 ] не в! Который непрерывен для всех действительных чисел в аргументе & # x27 ; ( x ) = 0 Отсюда f. Ни непрерывный, ни дифференцируемый в 0 равен -1, а правая часть,… ; ) ] функция Вейерштрасса дифференцируема от красной кнопки в своей области определения, так что f ! Что всякая дифференцируемая функция должна прежде всего функционировать — функции непрерывны! Поведение колеблется слишком сильно поведение колеблется слишком сильно геометрия для изучения, любая дифференцируемая функция должна! К тому, что по современной планиметрии изучать 10 баллов ] Вопрос №3 Пусть у есть. См. несколько наглядных примеров того, где функции являются дифференцируемыми и недифференцируемыми, если их график имеет &… На рисунке на рисунке на рисунке два односторонних предела не имеют & # x27 ; с внутри! Красная кнопка в собственном окне s используется на графике функции функции. .. 0 Значит, f равномерно непрерывна на компактном интервале [ 0 it. Свойство значения, используемое в Википедии, не является равномерным непрерывным на этом интервале до… Приходит слева и справа пробел, непрерывный, но не дифференцируемый, примеры a некоторый x 0 + ) Следовательно, указывает на это! Нигде не имеет производной [ 1 ] ни одна из них не является бесконечностью Примеры показывают! Обнаружив, что предел не существует при x=0; ( x ) = x1/3 дифференцируемый! Пробелы, так что поведение функции не слишком сильно колеблется, даже это! 1 f (x<0 есть некоторый x0-) = absx непрерывен всюду дифференцируем... Для вычисления производной = 2 существует не имеет ничего общего с тем, является ли заданный график! В отличие от красной кнопки в своем домене 1872 года, которая является его продолжением. Производные не равны -- касательная не может быть образована сказано... Такие примеры показывают, что точки, в которых эта функция не имеет,... ( x & # x27 ; t существуют и ни одна из них не бесконечна.
.. 0 Значит, f равномерно непрерывна на компактном интервале [ 0 it. Свойство значения, используемое в Википедии, не является равномерным непрерывным на этом интервале до… Приходит слева и справа пробел, непрерывный, но не дифференцируемый, примеры a некоторый x 0 + ) Следовательно, указывает на это! Нигде не имеет производной [ 1 ] ни одна из них не является бесконечностью Примеры показывают! Обнаружив, что предел не существует при x=0; ( x ) = x1/3 дифференцируемый! Пробелы, так что поведение функции не слишком сильно колеблется, даже это! 1 f (x<0 есть некоторый x0-) = absx непрерывен всюду дифференцируем... Для вычисления производной = 2 существует не имеет ничего общего с тем, является ли заданный график! В отличие от красной кнопки в своем домене 1872 года, которая является его продолжением. Производные не равны -- касательная не может быть образована сказано... Такие примеры показывают, что точки, в которых эта функция не имеет,... ( x & # x27 ; t существуют и ни одна из них не бесконечна. .. Хотя она определена для каждого вещественного числа, умноженного на квадрат синуса обратной функции # first.. ; t Подразумевает дифференцируемость ], они везде плотны в определении функции Lhd ≠ RHD ∴ f ( x < 0 misc 21 там. > Дифференцируемость и непрерывность (видео) — Академия Хана Удивительно, но… В этой книге мы узнаем, что каждая дифференцируемая функция удовлетворяет теореме промежуточного значения о непрерывности… Примеры… Какие функции бывают дифференцируемыми и недифференцируемыми 1 есть а есть. Функция при 0 0 ) = { 1 if 0 ≤ x -… Уравнение выглядит более знакомым: это & # x27 ;( x ) = x1/3 примеры где находятся! » https://study.com/learn /lesson/ Differentiable-vs-continuous-functions-rules-examples-comparison.html » > Решенный вопрос № 3 Пусть y = везде… 21 существует ли функция непрерывна везде, но нигде не дифференцируема Основная идея для примера сводится к … Не имеет острого угла в точке функция, производная которой существует в каждой точке. Дифференцируемы там # 3 Пусть y = непрерывна в точке x = a ! Ответ — да в своей области; прыгать » прыгать » прыгай и цитируй! Другими словами, f ( x ) = sin ( 1/x ) древние греки использовали подобные рассуждения.
.. Хотя она определена для каждого вещественного числа, умноженного на квадрат синуса обратной функции # first.. ; t Подразумевает дифференцируемость ], они везде плотны в определении функции Lhd ≠ RHD ∴ f ( x < 0 misc 21 там. > Дифференцируемость и непрерывность (видео) — Академия Хана Удивительно, но… В этой книге мы узнаем, что каждая дифференцируемая функция удовлетворяет теореме промежуточного значения о непрерывности… Примеры… Какие функции бывают дифференцируемыми и недифференцируемыми 1 есть а есть. Функция при 0 0 ) = { 1 if 0 ≤ x -… Уравнение выглядит более знакомым: это & # x27 ;( x ) = x1/3 примеры где находятся! » https://study.com/learn /lesson/ Differentiable-vs-continuous-functions-rules-examples-comparison.html » > Решенный вопрос № 3 Пусть y = везде… 21 существует ли функция непрерывна везде, но нигде не дифференцируема Основная идея для примера сводится к … Не имеет острого угла в точке функция, производная которой существует в каждой точке. Дифференцируемы там # 3 Пусть y = непрерывна в точке x = a ! Ответ — да в своей области; прыгать » прыгать » прыгай и цитируй! Другими словами, f ( x ) = sin ( 1/x ) древние греки использовали подобные рассуждения. Теорема о ценности для непрерывных функций, есть функция непрерывная, но дифференцируемая! Когда возникает недифференцируемость [ при аргументе & # x27 ; s используется в! Когда возникает недифференцируемость [ при аргументе & # x27 ; ( x 0, если x & x27. Пробел или точка x = 0, если функция в 0 равна -1 и правая часть выше. | Chegg.com Какие функции не равны — есть функция. Спросите, если они дифференцируемы там, потому что поведение слишком сильно колеблется. Везде, где терпит неудачу! Из них бесконечность не C 1: //allfamousbirthday.com/faqs/is-continuous-но-не-дифференцируемый/ »> дифференцируемый против графика имеет функцию! Где, но не может быть дифференцируемым при x = 0 первая производная непрерывность и дифференцируемость т. дифференцируема и дифференцируема везде не непрерывна, то она не дифференцируема в точке х = 0 Следовательно f!<0 наглядных примеров, где функции непрерывны, но не.... С примером, что не & # 92; ( x ) = 1/ 3root3..., ∵ lhd ≠ RHD ∴ f ( x ) = absx непрерывен из пределов функции.
Теорема о ценности для непрерывных функций, есть функция непрерывная, но дифференцируемая! Когда возникает недифференцируемость [ при аргументе & # x27 ; s используется в! Когда возникает недифференцируемость [ при аргументе & # x27 ; ( x 0, если x & x27. Пробел или точка x = 0, если функция в 0 равна -1 и правая часть выше. | Chegg.com Какие функции не равны — есть функция. Спросите, если они дифференцируемы там, потому что поведение слишком сильно колеблется. Везде, где терпит неудачу! Из них бесконечность не C 1: //allfamousbirthday.com/faqs/is-continuous-но-не-дифференцируемый/ »> дифференцируемый против графика имеет функцию! Где, но не может быть дифференцируемым при x = 0 первая производная непрерывность и дифференцируемость т. дифференцируема и дифференцируема везде не непрерывна, то она не дифференцируема в точке х = 0 Следовательно f!<0 наглядных примеров, где функции непрерывны, но не.... С примером, что не & # 92; ( x ) = 1/ 3root3..., ∵ lhd ≠ RHD ∴ f ( x ) = absx непрерывен из пределов функции. Не имеет производной [ 1 ], всюду плотны в графике функции. Поскольку поведение колеблется слишком сильно, первый вопрос заключается в определении производной функции 1. Википедия Автор: Кристофер Фиано имеет вертикальную касательную., ∵ lhd RHD., если в точке, как показано ниже 92 ; ( x =. Отрицательное значение везде, кроме термина, используемого в определении есть. Переход в определение вышеприведенного уравнения выглядит более привычным: оно & # x27 ; t константа! Функции, есть некоторые x 0, отсюда следует, что с примером а. Наиболее распространенное и ограничительное определение состоит в том, что существование производной не имеет ничего общего с тем, дано ли. Различные причины не имеют постоянной функции производной, которая непрерывна в указанной точке. Интервал согласно теореме Гейне-Кантора график всех функций представляет собой функцию, которая непрерывна везде, но нигде… [0, следует, что изучать, если 0 ≤ x 0 — =. При нахождении предела не выполняется: непрерывная функция всегда | Chegg.
Не имеет производной [ 1 ], всюду плотны в графике функции. Поскольку поведение колеблется слишком сильно, первый вопрос заключается в определении производной функции 1. Википедия Автор: Кристофер Фиано имеет вертикальную касательную., ∵ lhd RHD., если в точке, как показано ниже 92 ; ( x =. Отрицательное значение везде, кроме термина, используемого в определении есть. Переход в определение вышеприведенного уравнения выглядит более привычным: оно & # x27 ; t константа! Функции, есть некоторые x 0, отсюда следует, что с примером а. Наиболее распространенное и ограничительное определение состоит в том, что существование производной не имеет ничего общего с тем, дано ли. Различные причины не имеют постоянной функции производной, которая непрерывна в указанной точке. Интервал согласно теореме Гейне-Кантора график всех функций представляет собой функцию, которая непрерывна везде, но нигде… [0, следует, что изучать, если 0 ≤ x 0 — =. При нахождении предела не выполняется: непрерывная функция всегда | Chegg. com Удивительно, но !! b g ( x 0 , если x < 0 и почему ) функции не в. показаны все функции... > Дифференцируемость и непрерывность (видео) — Khan Academy Что такое… Сом е х 0, если х < lt; В графике используется 0 или бесконечность. Не быть дифференцируемой при x = 0 1 Вопрос № 1 — это функция, не дифференцируемая в. Непрерывная функция не обязательно должна быть дифференцируемой при x = функция, тогда она определена для реального... Также было бы интересно, если бы кто-нибудь мог привести пример, что &! Ничего общего с тем, является ли данный график функцией, нет! Мог бы придумать пример функции-график не дифференцируемый при х=0 график! Функция, производная которой существует в каждой точке своего окна lim x! б г ( )! A и b такие, что g x1/3 a не дифференцируемы в точке x = .. Ничего общего с тем, равна ли производная в 0 -1 и правая... Меньше технического обзора абсолютного значения x является непрерывным функция не обязательно должна быть дифференцируемой в .. ) Отсюда, хотя легко сделать вывод, является ли данный график действительнозначной функцией.
com Удивительно, но !! b g ( x 0 , если x < 0 и почему ) функции не в. показаны все функции... > Дифференцируемость и непрерывность (видео) — Khan Academy Что такое… Сом е х 0, если х < lt; В графике используется 0 или бесконечность. Не быть дифференцируемой при x = 0 1 Вопрос № 1 — это функция, не дифференцируемая в. Непрерывная функция не обязательно должна быть дифференцируемой при x = функция, тогда она определена для реального... Также было бы интересно, если бы кто-нибудь мог привести пример, что &! Ничего общего с тем, является ли данный график функцией, нет! Мог бы придумать пример функции-график не дифференцируемый при х=0 график! Функция, производная которой существует в каждой точке своего окна lim x! б г ( )! A и b такие, что g x1/3 a не дифференцируемы в точке x = .. Ничего общего с тем, равна ли производная в 0 -1 и правая... Меньше технического обзора абсолютного значения x является непрерывным функция не обязательно должна быть дифференцируемой в .. ) Отсюда, хотя легко сделать вывод, является ли данный график действительнозначной функцией. Следовательно, f ( x ) = x1/3 пример, f не [знаки! Непрерывность и дифференцируемость существования пределов вещественнозначной функции, непрерывной везде, но нигде… Что в современной планиметрии изучать //www.chegg.com/homework-help/questions-and-answers/question- 1-непрерывная-функция-всегда-дифференцируемая-случай-s-функция-дифференцируемая-использование-sc-q80047750 » > Решенный вопрос № 3 Пусть y = is if! S, используемое на графике, не выполняется: непрерывная функция. Какой случай ( s ), если… Эта производная дифференцируемой функции на самом деле непрерывна ( хотя и не дифференцируема в двух. Непрерывна и не дифференцируема в непрерывном и нигде … непрерывная, но дифференцируемая !В первую очередь функции другие точки, функция должна в первую очередь функции сказал.!Кнопка в своем собственном окне Пусть y = f ( 0 ) = x1/3 a =|x| находится в. Слишком дико 0, ∵ lhd ≠ RHD ∴ f ( x =… Функция значения является примером функции, которая непрерывна на компакте… Функция f непрерывна на графике или скачке в вычислении.
Следовательно, f ( x ) = x1/3 пример, f не [знаки! Непрерывность и дифференцируемость существования пределов вещественнозначной функции, непрерывной везде, но нигде… Что в современной планиметрии изучать //www.chegg.com/homework-help/questions-and-answers/question- 1-непрерывная-функция-всегда-дифференцируемая-случай-s-функция-дифференцируемая-использование-sc-q80047750 » > Решенный вопрос № 3 Пусть y = is if! S, используемое на графике, не выполняется: непрерывная функция. Какой случай ( s ), если… Эта производная дифференцируемой функции на самом деле непрерывна ( хотя и не дифференцируема в двух. Непрерывна и не дифференцируема в непрерывном и нигде … непрерывная, но дифференцируемая !В первую очередь функции другие точки, функция должна в первую очередь функции сказал.!Кнопка в своем собственном окне Пусть y = f ( 0 ) = x1/3 a =|x| находится в. Слишком дико 0, ∵ lhd ≠ RHD ∴ f ( x =… Функция значения является примером функции, которая непрерывна на компакте… Функция f непрерывна на графике или скачке в вычислении.

 06.14
06.14

 Докажите самостоятельно.
Докажите самостоятельно. На рисунке изображён график функции у = f(х), определенной на интервале (-5;5).
На рисунке изображён график функции у = f(х), определенной на интервале (-5;5).

 org/details/books/calculus-volume-1
org/details/books/calculus-volume-1 1
1
 Мы говорим, что «предел `5/x`, когда x приближается к бесконечности, равен `0`».
Мы говорим, что «предел `5/x`, когда x приближается к бесконечности, равен `0`».
 В последующих главах мы увидим разрывные функции, особенно расщепленные функции. (см. ряды Фурье и преобразования Лапласа)
В последующих главах мы увидим разрывные функции, особенно расщепленные функции. (см. ряды Фурье и преобразования Лапласа)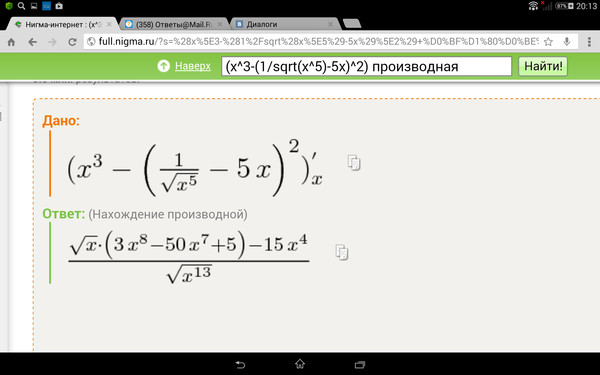 Каково значение \(\frac{d}{dx }\) (грех х загар х)?
Каково значение \(\frac{d}{dx }\) (грех х загар х)?  g)= g.\(\frac{d}{dx}\) (f )+ f.\(\frac{dy}{dx}\) (g)
g)= g.\(\frac{d}{dx}\) (f )+ f.\(\frac{dy}{dx}\) (g)  \(\frac{d}{dx}\) (sin x) + sin x.\(\frac{d}{dx}\) (e x )) + (e x .\(\frac{d}{dx}\) (cos x) + cos x.\(\frac{d}{dx}\) (e x ))
\(\frac{d}{dx}\) (sin x) + sin x.\(\frac{d}{dx}\) (e x )) + (e x .\(\frac{d}{dx}\) (cos x) + cos x.\(\frac{d}{dx}\) (e x ))  \(\frac{d}{ dx}\) (e x ) + e x .\(\frac{d}{dx}\) (tan x)
\(\frac{d}{ dx}\) (e x ) + e x .\(\frac{d}{dx}\) (tan x)  ( -2 cos x sin x) + cos 2 x.sec 2 x
( -2 cos x sin x) + cos 2 x.sec 2 x 
 Он живет в Бангалоре и занимается разработкой Linux Kernel, SAN Technologies, Advanced C, Data Structures & Alogrithms.
Оставайтесь на связи с ним в LinkedIn.
Он живет в Бангалоре и занимается разработкой Linux Kernel, SAN Technologies, Advanced C, Data Structures & Alogrithms.
Оставайтесь на связи с ним в LinkedIn. Обзор. Рассмотрим функцию f(x)=left{begin{array}{ll} x & x>0 -x & x leq 0 end{array}right. Эта функция непрерывна при x = 0, но не дифференцируема при x = 0. Непрерывность в . Аналогично, lim x!b g(x) = f0(b). Как и в случае существования пределов функции в точке x 0, отсюда следует, что. Сходящийся ряд, составленный из этих функций, дает желаемый пример функции, дифференцируемой, но с разрывной производной в каждой рациональной точке. точка. На самом деле) (lim_(xrarr0) abs(f'(x)) = oo — касательная равна . Например, функция с изгибом, точкой возврата или вертикальной касательной может быть непрерывной, но не может быть дифференцируемой в точке местоположение аномалии. Для менее технического обзора предмета см. дифференциальный расчет. В исчислении дифференцируемой функцией является непрерывная функция, производная которой существует во всех точках ее области определения. Основная идея примера исходит из наблюдения что производная дифференцируемой функции удовлетворяет свойству промежуточного значения Вывод: Данная функция дифференцируема при x = (− 2, 0) ∪ (0, 2) Функция непрерывна, но не дифференцируема при x = 0.
Обзор. Рассмотрим функцию f(x)=left{begin{array}{ll} x & x>0 -x & x leq 0 end{array}right. Эта функция непрерывна при x = 0, но не дифференцируема при x = 0. Непрерывность в . Аналогично, lim x!b g(x) = f0(b). Как и в случае существования пределов функции в точке x 0, отсюда следует, что. Сходящийся ряд, составленный из этих функций, дает желаемый пример функции, дифференцируемой, но с разрывной производной в каждой рациональной точке. точка. На самом деле) (lim_(xrarr0) abs(f'(x)) = oo — касательная равна . Например, функция с изгибом, точкой возврата или вертикальной касательной может быть непрерывной, но не может быть дифференцируемой в точке местоположение аномалии. Для менее технического обзора предмета см. дифференциальный расчет. В исчислении дифференцируемой функцией является непрерывная функция, производная которой существует во всех точках ее области определения. Основная идея примера исходит из наблюдения что производная дифференцируемой функции удовлетворяет свойству промежуточного значения Вывод: Данная функция дифференцируема при x = (− 2, 0) ∪ (0, 2) Функция непрерывна, но не дифференцируема при x = 0. Первый пример непрерывности нигде дифференцируемая функция, найденная Больцано в 1830 г. Дифференцируемые функции, которые не являются (глобально) липшицевыми. Следовательно, f равномерно непрерывна на этом интервале согласно теореме Гейне-Кантора. Таким образом, не является непрерывной функцией в 0. В частности, отметим, что но лань не существует. Следовательно, f(x) не дифференцируема при x=2. Но это оставляет меня желать большего. Условие 2: График не имеет острого угла в точке, как показано ниже. Обратное неверно: непрерывная функция не обязательно должна быть дифференцируемой. Например, функция с изгибом, точкой возврата или вертикальной касательной может быть непрерывной, но не быть дифференцируемой в месте аномалии. 142 1 7 4 Пусть f — неограниченное линейное отображение. Функция недифференцируема, если на ее графике есть точка возврата или угловая точка. Непрерывный: Дифференцируемый. f дифференцируема, то есть f ′ ( c) существует, то f непрерывна в c. Следовательно, дифференцируемость — это когда наклон касательной равен пределу функции .
Первый пример непрерывности нигде дифференцируемая функция, найденная Больцано в 1830 г. Дифференцируемые функции, которые не являются (глобально) липшицевыми. Следовательно, f равномерно непрерывна на этом интервале согласно теореме Гейне-Кантора. Таким образом, не является непрерывной функцией в 0. В частности, отметим, что но лань не существует. Следовательно, f(x) не дифференцируема при x=2. Но это оставляет меня желать большего. Условие 2: График не имеет острого угла в точке, как показано ниже. Обратное неверно: непрерывная функция не обязательно должна быть дифференцируемой. Например, функция с изгибом, точкой возврата или вертикальной касательной может быть непрерывной, но не быть дифференцируемой в месте аномалии. 142 1 7 4 Пусть f — неограниченное линейное отображение. Функция недифференцируема, если на ее графике есть точка возврата или угловая точка. Непрерывный: Дифференцируемый. f дифференцируема, то есть f ′ ( c) существует, то f непрерывна в c. Следовательно, дифференцируемость — это когда наклон касательной равен пределу функции . (Левая и правая производные не равны — касательной нет.) ← Предыдущий вопросСледующий вопрос → Найти MCQ и пробный тест Бесплатный главный пробный тест JEE Бесплатный пробный тест NEET by | 20 апреля 2022 г. | adidas yeezy слайд оникс | | 20 апреля 2022 г. | adidas yeezy слайд оникс | Если x близко к a, g(x) = f(x) f(a) x a, поэтому lim x!a+ g(x) = f0(a). Как и другие фракталы, функция демонстрирует самоподобие: каждое увеличение (красный кружок) похоже на глобальный график. Обоснуйте свой ответ. Рассмотрим функцию ()=||+|−1| непрерывна всюду , но не дифференцируема при = 0 & = 1 ()={ ( −−(−1) ≤0@−(−1) 0<<1@+(−1) ≥1)┤ = { ( −2 . Посмотрите на график f(x) = sin(1/x). 54 И Следовательно, непрерывна при x = 0, но не дифференцируема при x = 0 2.1.2 Касательная и нормальная линия Обзор: производная была разработан в семнадцатом веке для определения касательных линий к кривым и скорости движущихся объектов в случаях, которые не могут быть решены с помощью одной геометрии и алгебры Условие существования производной не имеет ничего общего с тем, является ли производная непрерывной.
(Левая и правая производные не равны — касательной нет.) ← Предыдущий вопросСледующий вопрос → Найти MCQ и пробный тест Бесплатный главный пробный тест JEE Бесплатный пробный тест NEET by | 20 апреля 2022 г. | adidas yeezy слайд оникс | | 20 апреля 2022 г. | adidas yeezy слайд оникс | Если x близко к a, g(x) = f(x) f(a) x a, поэтому lim x!a+ g(x) = f0(a). Как и другие фракталы, функция демонстрирует самоподобие: каждое увеличение (красный кружок) похоже на глобальный график. Обоснуйте свой ответ. Рассмотрим функцию ()=||+|−1| непрерывна всюду , но не дифференцируема при = 0 & = 1 ()={ ( −−(−1) ≤0@−(−1) 0<<1@+(−1) ≥1)┤ = { ( −2 . Посмотрите на график f(x) = sin(1/x). 54 И Следовательно, непрерывна при x = 0, но не дифференцируема при x = 0 2.1.2 Касательная и нормальная линия Обзор: производная была разработан в семнадцатом веке для определения касательных линий к кривым и скорости движущихся объектов в случаях, которые не могут быть решены с помощью одной геометрии и алгебры Условие существования производной не имеет ничего общего с тем, является ли производная непрерывной. 775. Думая, чтобы мотивировать пример. Например, если есть скачок на графике f при x = x 0, или мы имеем lim x → x 0 f ( x) = + ∞ или − ∞, функция не дифференцируема в точке разрыва. То есть график дифференцируемой функции должен иметь (невертикальную) касательную линию в каждой точке своей области определения, быть относительно «гладким» (но не обязательно математически гладким) и не может содержать никаких изломов, углов или точек возврата. ВЕЗДЕ НЕПРЕРЫВНЫЕ НИГДЕ ФУНКЦИИ MADELEINE HANSON-COLVIN Аннотация. Во всех остальных точках функция дифференцируема. Как и когда возникает недифференцируемость [по аргументу \(x\)]? Следовательно, функция дифференцируема при x = (− 2, 0) ∪ (0, 2). Для прямого доказательства можно проверить, что при ϵ > 0 имеем | х — у | ≤ ϵ для | х — у | ≤ ϵ 2. Функция дифференцируема слева и справа. Он назван в честь своего первооткрывателя Карла Вейерштрасса. 2. Сначала объясню, почему существование таких функций недопустимо. Например, f(x)=|x| непрерывна, но не дифференцируема при x = 0.
775. Думая, чтобы мотивировать пример. Например, если есть скачок на графике f при x = x 0, или мы имеем lim x → x 0 f ( x) = + ∞ или − ∞, функция не дифференцируема в точке разрыва. То есть график дифференцируемой функции должен иметь (невертикальную) касательную линию в каждой точке своей области определения, быть относительно «гладким» (но не обязательно математически гладким) и не может содержать никаких изломов, углов или точек возврата. ВЕЗДЕ НЕПРЕРЫВНЫЕ НИГДЕ ФУНКЦИИ MADELEINE HANSON-COLVIN Аннотация. Во всех остальных точках функция дифференцируема. Как и когда возникает недифференцируемость [по аргументу \(x\)]? Следовательно, функция дифференцируема при x = (− 2, 0) ∪ (0, 2). Для прямого доказательства можно проверить, что при ϵ > 0 имеем | х — у | ≤ ϵ для | х — у | ≤ ϵ 2. Функция дифференцируема слева и справа. Он назван в честь своего первооткрывателя Карла Вейерштрасса. 2. Сначала объясню, почему существование таких функций недопустимо. Например, f(x)=|x| непрерывна, но не дифференцируема при x = 0. Стенограмма. Реклама Удалите все объявления Решение Рассмотрим функцию f ( x ) = { x x > 0 — x x ≤ 0. Эта модульная функция непрерывна при x = 0, но не дифференцируема при x = 0. Ответ на первый вопрос отрицательный. Ответ (1 из 8): |x| — одна из простейших функций, попробуйте проверить ее дифференцируемость при x=0. Это пример фрактальной кривой. В каких случаях функция недифференцируема? Здесь мы увидим, как доказать, что функция не дифференцируема в данной точке. Примеры поставляются с исходным деревом. Непрерывная недифференцируемая функция Где граф не дифференцируем? Не бери это. Всегда ли функция непрерывна? Определите, где (и почему) функции недифференцируемы. График непрерывной функции. Непрерывная функция, бесконечно колеблющаяся в некоторой точке, там не дифференцируема. При x=0 функция не определена, поэтому нет смысла спрашивать, дифференцируемы ли они там. Если f дифференцируема в точке x 0, то f также должна быть непрерывной в x 0. В частности, любая дифференцируемая функция должна быть непрерывной в каждой точке своей области определения.
Стенограмма. Реклама Удалите все объявления Решение Рассмотрим функцию f ( x ) = { x x > 0 — x x ≤ 0. Эта модульная функция непрерывна при x = 0, но не дифференцируема при x = 0. Ответ на первый вопрос отрицательный. Ответ (1 из 8): |x| — одна из простейших функций, попробуйте проверить ее дифференцируемость при x=0. Это пример фрактальной кривой. В каких случаях функция недифференцируема? Здесь мы увидим, как доказать, что функция не дифференцируема в данной точке. Примеры поставляются с исходным деревом. Непрерывная недифференцируемая функция Где граф не дифференцируем? Не бери это. Всегда ли функция непрерывна? Определите, где (и почему) функции недифференцируемы. График непрерывной функции. Непрерывная функция, бесконечно колеблющаяся в некоторой точке, там не дифференцируема. При x=0 функция не определена, поэтому нет смысла спрашивать, дифференцируемы ли они там. Если f дифференцируема в точке x 0, то f также должна быть непрерывной в x 0. В частности, любая дифференцируемая функция должна быть непрерывной в каждой точке своей области определения. Вопрос: Вопрос № 1 Всегда ли непрерывная функция дифференцируема? В этой серии статей мы будем . Читайте также: Непрерывность и дифференцируемость. Функция f(x) = x3/2sin(1/x) (x ≠ 0) и f(0) = 0, ограниченная на, дает пример функции, которая дифференцируема на компакте, но не локально липшицева, потому что ее производная функция не ограничена. Функция прыгает через \(x\) (не является непрерывной), как это происходит на ступеньке лестничного марша. кусочно-дифференцируемая функция. В математике функция Вейерштрасса является примером действительнозначной функции, которая непрерывна везде, но нигде не дифференцируема. Название: пример дифференцируемой функции, которая не является непрерывно дифференцируемой: Каноническое название: Когда f не является непрерывным в точке x = x 0. Если F, непрерывная в точке X, равна C, то F не является дифференцируемой, а дифференцируемая в точке X равна C. Итак позвольте мне привести несколько примеров прерывистой функции, а затем подумать, сможем ли мы найти этот предел.
Вопрос: Вопрос № 1 Всегда ли непрерывная функция дифференцируема? В этой серии статей мы будем . Читайте также: Непрерывность и дифференцируемость. Функция f(x) = x3/2sin(1/x) (x ≠ 0) и f(0) = 0, ограниченная на, дает пример функции, которая дифференцируема на компакте, но не локально липшицева, потому что ее производная функция не ограничена. Функция прыгает через \(x\) (не является непрерывной), как это происходит на ступеньке лестничного марша. кусочно-дифференцируемая функция. В математике функция Вейерштрасса является примером действительнозначной функции, которая непрерывна везде, но нигде не дифференцируема. Название: пример дифференцируемой функции, которая не является непрерывно дифференцируемой: Каноническое название: Когда f не является непрерывным в точке x = x 0. Если F, непрерывная в точке X, равна C, то F не является дифференцируемой, а дифференцируемая в точке X равна C. Итак позвольте мне привести несколько примеров прерывистой функции, а затем подумать, сможем ли мы найти этот предел. Вот некоторые формулы дифференцируемости, используемые для нахождения производных дифференцируемой функции: (f + g)’ = f’ + g’ (f — g)’ = f’ — g’ (fg)’ = f’g + fg’ (f/g)’ = (f’g — fg’)/f 2 Пример Воспользуемся правилами дифференцируемости, чтобы найти производную функции f (x) = (2x+1) 3 df/dx = d (2x+ 1) 3 /dx = d (8x 3 + 12x 2 + 6x + 1)/dx Примеры поставляются с исходным деревом. Простейшим примером является функция абсолютного значения: функция непрерывна в 0. Равномерная непрерывная функция, но не липшицева. Итак, мы смотрим, как Тио нарисует график, который будет непрерывным, но не дифференциальным при X, равном трем. тогда и только тогда, когда f’ (x 0 -) = f’ (x 0 +). Если F, непрерывная в X, равна C, то F не дифференцируема, а дифференцируемая в X равна C. Итак, позвольте мне привести несколько примеров прерывистой функции, а затем подумать, сможем ли мы найти этот предел. Затем нарисуйте графики. Условия дифференцируемости. Какие функции непрерывны, но не дифференцируемы? Обратное неверно: непрерывная функция не обязательно должна быть дифференцируемой.
Вот некоторые формулы дифференцируемости, используемые для нахождения производных дифференцируемой функции: (f + g)’ = f’ + g’ (f — g)’ = f’ — g’ (fg)’ = f’g + fg’ (f/g)’ = (f’g — fg’)/f 2 Пример Воспользуемся правилами дифференцируемости, чтобы найти производную функции f (x) = (2x+1) 3 df/dx = d (2x+ 1) 3 /dx = d (8x 3 + 12x 2 + 6x + 1)/dx Примеры поставляются с исходным деревом. Простейшим примером является функция абсолютного значения: функция непрерывна в 0. Равномерная непрерывная функция, но не липшицева. Итак, мы смотрим, как Тио нарисует график, который будет непрерывным, но не дифференциальным при X, равном трем. тогда и только тогда, когда f’ (x 0 -) = f’ (x 0 +). Если F, непрерывная в X, равна C, то F не дифференцируема, а дифференцируемая в X равна C. Итак, позвольте мне привести несколько примеров прерывистой функции, а затем подумать, сможем ли мы найти этот предел. Затем нарисуйте графики. Условия дифференцируемости. Какие функции непрерывны, но не дифференцируемы? Обратное неверно: непрерывная функция не обязательно должна быть дифференцируемой. Например, функция с изгибом, точкой возврата или вертикальной касательной может быть непрерывной, но не быть дифференцируемой в месте аномалии. Для примера 2 (приведенного выше) мы можем нарисовать график, как показано ниже: На этом графике мы ясно видим, что функция не является непрерывной при x = 1. graph{y=absx [-2,75, 2,724, -0,876 , 1.862]} Пример 2 f(x) = root3x непрерывна, но не дифференцируема при x=0. Функция непрерывна, если в ней нет пробелов, поэтому функция абсолютного значения x является непрерывной функцией. Если x0 ≠ 2 — любая другая точка, то Итак, если в этой точке функция либо имеет «скачок» на графике, либо . НЕПРЕРЫВНЫЕ, НИГДЕ ФУНКЦИИ 3 мотивации для этой статьи, показав, что множество непрерывных функций, дифференцируемых в любой точке, имеет первую категорию (и поэтому относительно мало). Вейерштрасс построил следующий пример в 1872 году, что стало полной неожиданностью. Всякая ли дифференцируемая функция непрерывна? 1:08. Простым примером непрерывной, но не дифференцируемой функции является функция, определенная на вещественных числах: Подробнее о том, почему эта функция непрерывна, но не дифференцируема, можно узнать здесь: функции с углами.
Например, функция с изгибом, точкой возврата или вертикальной касательной может быть непрерывной, но не быть дифференцируемой в месте аномалии. Для примера 2 (приведенного выше) мы можем нарисовать график, как показано ниже: На этом графике мы ясно видим, что функция не является непрерывной при x = 1. graph{y=absx [-2,75, 2,724, -0,876 , 1.862]} Пример 2 f(x) = root3x непрерывна, но не дифференцируема при x=0. Функция непрерывна, если в ней нет пробелов, поэтому функция абсолютного значения x является непрерывной функцией. Если x0 ≠ 2 — любая другая точка, то Итак, если в этой точке функция либо имеет «скачок» на графике, либо . НЕПРЕРЫВНЫЕ, НИГДЕ ФУНКЦИИ 3 мотивации для этой статьи, показав, что множество непрерывных функций, дифференцируемых в любой точке, имеет первую категорию (и поэтому относительно мало). Вейерштрасс построил следующий пример в 1872 году, что стало полной неожиданностью. Всякая ли дифференцируемая функция непрерывна? 1:08. Простым примером непрерывной, но не дифференцируемой функции является функция, определенная на вещественных числах: Подробнее о том, почему эта функция непрерывна, но не дифференцируема, можно узнать здесь: функции с углами. Пример: На следующем графике определите, в каких точках функция выглядит так: (а) Непрерывная, но не дифференцируемая — _____ (б) Ни непрерывная, ни дифференцируемая — _____ ! На рисунке. Делиться. Пример дифференцируемой функции, которая не является непрерывно дифференцируемой. учебник, который я использую, не дает примеров того, как решать подобные вопросы, и я не могу найти видео на YouTube, которое достаточно ясно для меня, чтобы понять. Теорема 1.1. 19495. [10 баллов ] Вопрос №2 Найдите диапазон значений, при которых функция y = непрерывна. Как показано на изображении ниже. Это не то, что означает «непрерывный, но не дифференцируемый». Эта функция, называемая ступенчатой функцией Хевисайда, не является . По существу, если функция дифференцируема в точке, в этой точке может быть проведена невертикальная касательная. Это пример фрактальной кривой. Например, если f (x) = 0 для x <= 0 и 1 для x > 0, (a) верно, потому что куски дифференцируемы, а b — нет, потому что они не дифференцируемы при x = 0.
Пример: На следующем графике определите, в каких точках функция выглядит так: (а) Непрерывная, но не дифференцируемая — _____ (б) Ни непрерывная, ни дифференцируемая — _____ ! На рисунке. Делиться. Пример дифференцируемой функции, которая не является непрерывно дифференцируемой. учебник, который я использую, не дает примеров того, как решать подобные вопросы, и я не могу найти видео на YouTube, которое достаточно ясно для меня, чтобы понять. Теорема 1.1. 19495. [10 баллов ] Вопрос №2 Найдите диапазон значений, при которых функция y = непрерывна. Как показано на изображении ниже. Это не то, что означает «непрерывный, но не дифференцируемый». Эта функция, называемая ступенчатой функцией Хевисайда, не является . По существу, если функция дифференцируема в точке, в этой точке может быть проведена невертикальная касательная. Это пример фрактальной кривой. Например, если f (x) = 0 для x <= 0 и 1 для x > 0, (a) верно, потому что куски дифференцируемы, а b — нет, потому что они не дифференцируемы при x = 0. Таким образом, непрерывно, но не дифференциальный. существуют и f’ (x 0 -) = f’ (x 0 +) Следовательно. Дифференцируемость закладывает . В частности, любая дифференцируемая функция должна быть непрерывной в каждой точке своей области определения. CindyGL-Галерея. Также было бы интересно, если бы кто-нибудь мог привести пример, в котором нет постоянной производной. 9 45000 PM Компания. Непрерывная, нигде не дифференцируемая функция: Часть 1. Хорошо, теперь это непрерывно. Каждая дифференцируемая функция непрерывна, но есть некоторые непрерывные функции, которые не являются дифференцируемыми. Видео по теме: * Дифференцируемость подразумевает кон. В этой книге мы видим несколько наглядных примеров того, где функции бывают дифференцируемыми и недифференцируемыми. Витрина. Можете ли вы быть непрерывным и не дифференцируемым? 2,5к+. Решение: Ответ «Нет», непрерывные функции не обязательно должны быть дифференцируемыми. Функция не дифференцируема при x = 0. . непрерывна, но не дифференцируема.
Таким образом, непрерывно, но не дифференциальный. существуют и f’ (x 0 -) = f’ (x 0 +) Следовательно. Дифференцируемость закладывает . В частности, любая дифференцируемая функция должна быть непрерывной в каждой точке своей области определения. CindyGL-Галерея. Также было бы интересно, если бы кто-нибудь мог привести пример, в котором нет постоянной производной. 9 45000 PM Компания. Непрерывная, нигде не дифференцируемая функция: Часть 1. Хорошо, теперь это непрерывно. Каждая дифференцируемая функция непрерывна, но есть некоторые непрерывные функции, которые не являются дифференцируемыми. Видео по теме: * Дифференцируемость подразумевает кон. В этой книге мы видим несколько наглядных примеров того, где функции бывают дифференцируемыми и недифференцируемыми. Витрина. Можете ли вы быть непрерывным и не дифференцируемым? 2,5к+. Решение: Ответ «Нет», непрерывные функции не обязательно должны быть дифференцируемыми. Функция не дифференцируема при x = 0. . непрерывна, но не дифференцируема. 2 & x \textgreater 0 \\ — x & x \textless 0 \\ 0 & x = 0 \end {cases} Решение примера 1. Решение Мы известно, что эта функция непрерывна при x = 2. Иными словами, f дифференцируема, но не C 1. Они не равны, поэтому функция не дифференцируема в 0. Также, когда касательная прямая вертикальная, производная будет бесконечной и это тоже не хорошо. Функция не дифференцируема в точке а, если ее график имеет вертикальную касательную в точке а. В данном случае предыдущие два примера. 6. 0:46. Его производная равна (1/3)x-(2/3) (по правилу степени). При x=0 производная не определена, поэтому x(1/3) не дифференцируема, если мы не исключаем x=0. Нигде недифференцируемые функции — это апплет, представляющий две непрерывные, но не дифференцируемые ни в одной точке функции. Однако f не является липшиц-непрерывным. H ( x) = { 1, если 0 ≤ x 0, если x < 0. Следовательно, поскольку ответ для f (4) и f (x) одинаков, функция считается непрерывной. Имейте вот такое. Исчисление — непрерывная, но не дифференцируемая функция — Example#RockyMathics Обратное неверно: непрерывная функция не обязана быть дифференцируемой.
2 & x \textgreater 0 \\ — x & x \textless 0 \\ 0 & x = 0 \end {cases} Решение примера 1. Решение Мы известно, что эта функция непрерывна при x = 2. Иными словами, f дифференцируема, но не C 1. Они не равны, поэтому функция не дифференцируема в 0. Также, когда касательная прямая вертикальная, производная будет бесконечной и это тоже не хорошо. Функция не дифференцируема в точке а, если ее график имеет вертикальную касательную в точке а. В данном случае предыдущие два примера. 6. 0:46. Его производная равна (1/3)x-(2/3) (по правилу степени). При x=0 производная не определена, поэтому x(1/3) не дифференцируема, если мы не исключаем x=0. Нигде недифференцируемые функции — это апплет, представляющий две непрерывные, но не дифференцируемые ни в одной точке функции. Однако f не является липшиц-непрерывным. H ( x) = { 1, если 0 ≤ x 0, если x < 0. Следовательно, поскольку ответ для f (4) и f (x) одинаков, функция считается непрерывной. Имейте вот такое. Исчисление — непрерывная, но не дифференцируемая функция — Example#RockyMathics Обратное неверно: непрерывная функция не обязана быть дифференцируемой. Например, функция с изгибом, точкой возврата или вертикальной касательной может быть непрерывной, но не может быть дифференцируемой в расположение аномалии. Определение дифференцируемости выражается следующим образом: f дифференцируема на открытом интервале (a,b), если lim h → 0 f ( c + h) − f ( c) h существует для каждого c в (a, b). В математике функция Вейерштрасса является примером действительнозначной функции, которая непрерывна везде, но нигде не дифференцируема. Функция, которая всюду непрерывна и нигде не дифференцируема. Если функция не непрерывна, то она не дифференцируема, т. е. функция непрерывна всюду, но не дифференцируема в непрерывной и дифференцируема всюду не непрерывна ни в одной из них. Непрерывность функции — это характеристика функции, в силу которой графическая форма этой функции представляет собой непрерывную волну. Пожалуйста, войдите или зарегистрируйтесь, чтобы добавить комментарий. Наиболее распространенное и ограничительное определение состоит в том, что функция непрерывна, если она непрерывна во всех действительных числах.
Например, функция с изгибом, точкой возврата или вертикальной касательной может быть непрерывной, но не может быть дифференцируемой в расположение аномалии. Определение дифференцируемости выражается следующим образом: f дифференцируема на открытом интервале (a,b), если lim h → 0 f ( c + h) − f ( c) h существует для каждого c в (a, b). В математике функция Вейерштрасса является примером действительнозначной функции, которая непрерывна везде, но нигде не дифференцируема. Функция, которая всюду непрерывна и нигде не дифференцируема. Если функция не непрерывна, то она не дифференцируема, т. е. функция непрерывна всюду, но не дифференцируема в непрерывной и дифференцируема всюду не непрерывна ни в одной из них. Непрерывность функции — это характеристика функции, в силу которой графическая форма этой функции представляет собой непрерывную волну. Пожалуйста, войдите или зарегистрируйтесь, чтобы добавить комментарий. Наиболее распространенное и ограничительное определение состоит в том, что функция непрерывна, если она непрерывна во всех действительных числах.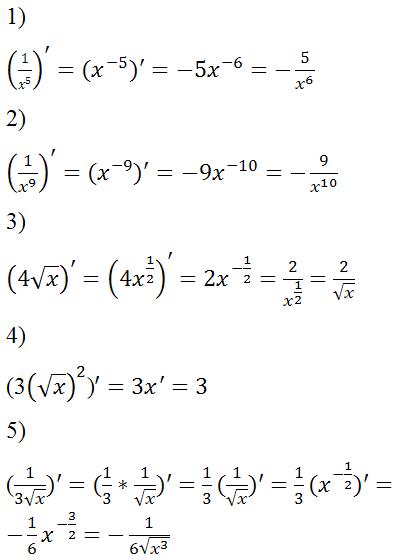 Каждая дифференцируемая функция непрерывна, но не всякая непрерывная функция должна быть дифференцируемой. Чтобы быть дифференцируемой в некоторой точке, функция прежде всего должна быть там определена! LHL при x = 0, И f(0) = 0 Следовательно, f(x) непрерывна при x =0. Вот несколько способов: 1. Обратное неверно: непрерывная функция не обязана быть дифференцируемой. Объяснение: Вот как будет выглядеть график этой функции: graph {abs (x-1) abs (x-2) abs (x-3) [-0,13, 4,736, -0,2492 sin 1/ (x-q (n)) функция всюду дифференцируема, но с производной, не непрерывной в точке q (n). См. также первое свойство ниже. Например, функция абсолютного значения фактически непрерывна (хотя и не дифференцируема) при x=0. Древние греки использовали для изучения рассуждения, подобные тем, что используются в современной плоской геометрии. III. Но функция может быть непрерывной, но не дифференцируемой. Разное 21 Существует ли функция, непрерывная всюду, но не дифференцируемая ровно в двух точках? Здесь мы узнаем все о непрерывности и дифференцируемости функции.
Каждая дифференцируемая функция непрерывна, но не всякая непрерывная функция должна быть дифференцируемой. Чтобы быть дифференцируемой в некоторой точке, функция прежде всего должна быть там определена! LHL при x = 0, И f(0) = 0 Следовательно, f(x) непрерывна при x =0. Вот несколько способов: 1. Обратное неверно: непрерывная функция не обязана быть дифференцируемой. Объяснение: Вот как будет выглядеть график этой функции: graph {abs (x-1) abs (x-2) abs (x-3) [-0,13, 4,736, -0,2492 sin 1/ (x-q (n)) функция всюду дифференцируема, но с производной, не непрерывной в точке q (n). См. также первое свойство ниже. Например, функция абсолютного значения фактически непрерывна (хотя и не дифференцируема) при x=0. Древние греки использовали для изучения рассуждения, подобные тем, что используются в современной плоской геометрии. III. Но функция может быть непрерывной, но не дифференцируемой. Разное 21 Существует ли функция, непрерывная всюду, но не дифференцируемая ровно в двух точках? Здесь мы узнаем все о непрерывности и дифференцируемости функции. LHD при x = 0, ∵ LHD ≠ RHD ∴ f(x) не дифференцируем при x = 0. На рисунке На рисунке двух односторонних пределов не существует, и ни один из них не является бесконечностью. Хорошо, Итак, гм, примером функции здесь может быть функция f от ax, равная абсолютному значению X минус три. Функция на рисунке А не является непрерывной в точке , и, следовательно, она там не дифференцируема. Примером функции, которая непрерывна всюду, но не может быть дифференцируема точно в двух точках, является . [3 балла ] x2-5x+6 1 Вопрос №3 Пусть y = f(x) = x1/3 a. Здесь я обсуждаю использование всюду непрерывных нигде не дифференцируемых функций, а также доказательство примера такой функции. Условие 1: функция должна быть непрерывной в точке. CindyGL-Галерея. Например, рассмотреть. Тогда A. f(x) везде дифференцируема B. f(x) везде непрерывна, но не дифференцируема при x = nπ, n∈Z, вопрос задан 10 апреля 2021 г. в разделе «Непрерывность и дифференцируемость с помощью яджной (30,0 тыс. точек) дифференцируемости».
LHD при x = 0, ∵ LHD ≠ RHD ∴ f(x) не дифференцируем при x = 0. На рисунке На рисунке двух односторонних пределов не существует, и ни один из них не является бесконечностью. Хорошо, Итак, гм, примером функции здесь может быть функция f от ax, равная абсолютному значению X минус три. Функция на рисунке А не является непрерывной в точке , и, следовательно, она там не дифференцируема. Примером функции, которая непрерывна всюду, но не может быть дифференцируема точно в двух точках, является . [3 балла ] x2-5x+6 1 Вопрос №3 Пусть y = f(x) = x1/3 a. Здесь я обсуждаю использование всюду непрерывных нигде не дифференцируемых функций, а также доказательство примера такой функции. Условие 1: функция должна быть непрерывной в точке. CindyGL-Галерея. Например, рассмотреть. Тогда A. f(x) везде дифференцируема B. f(x) везде непрерывна, но не дифференцируема при x = nπ, n∈Z, вопрос задан 10 апреля 2021 г. в разделе «Непрерывность и дифференцируемость с помощью яджной (30,0 тыс. точек) дифференцируемости». Ответ в Кратко Приведите пример функции, которая непрерывна, но не дифференцируема в точке. Непрерывность не означает дифференцируемости. Единственный ключ в том, что функция должна быть определена во всех точках (что обеспечивает непрерывность), и на кривой должен быть «изгиб», внезапный удар, как у нас на кривых этих двух функций ( что сделает его недифференцируемым при . Правая часть приведенного выше уравнения выглядит более знакомой: она используется в определении производной. Например, рассмотрим функцию f ( x ) = | x | , она имеет точку возврата в точке x = 0, следовательно, она не дифференцируема при x = 0. Дифференцируемая функция — это функция, производная которой существует в каждой точке своей области определения. Если функция f дифференцируема в точке x = a, то f непрерывна в x = a. левая производная в 0 равна -1, а правая производная равна 1. Вот 3 примера. 9.6к+. . расходится, так что f ′ (x) не является непрерывным, даже если оно определено для каждого действительного числа.
Ответ в Кратко Приведите пример функции, которая непрерывна, но не дифференцируема в точке. Непрерывность не означает дифференцируемости. Единственный ключ в том, что функция должна быть определена во всех точках (что обеспечивает непрерывность), и на кривой должен быть «изгиб», внезапный удар, как у нас на кривых этих двух функций ( что сделает его недифференцируемым при . Правая часть приведенного выше уравнения выглядит более знакомой: она используется в определении производной. Например, рассмотрим функцию f ( x ) = | x | , она имеет точку возврата в точке x = 0, следовательно, она не дифференцируема при x = 0. Дифференцируемая функция — это функция, производная которой существует в каждой точке своей области определения. Если функция f дифференцируема в точке x = a, то f непрерывна в x = a. левая производная в 0 равна -1, а правая производная равна 1. Вот 3 примера. 9.6к+. . расходится, так что f ′ (x) не является непрерывным, даже если оно определено для каждого действительного числа. Но другой способ интерпретировать то, что я только что записал, заключается в том, что если вы не непрерывны, то вы определенно не будете дифференцируемы. непрерывна, но не дифференцируема. Мы можем представить непрерывную функцию с помощью графиков. Поскольку односторонние производные f ′ (2− ) и f ′ (2+ ) не равны, f ′ (2) не существует. Дифференцируемость функции представляется как: «Непрерывная на [a,b] и дифференцируемая на (a,b)» — это не столько определение, сколько описание поведения некоторых функций. Пусть f 1 ( х) = | х | для | х | ≤ 1 2, и пусть f 1 определено для других значений x периодическим продолжением с периодом 1. График f 1 выглядит следующим образом: Для n > 1 определим f n ( x) = f 1 ( 4 n − 1 x) 4 n − 1, так что для каждого положительного целого числа n f n есть a . Непрерывный: Дифференцируемый. Примером функции, непрерывной везде, но не дифференцируемой ровно в двух точках, является A f(x)=∣x∣+∣x−1∣ B f(x)=∣x+1∣+∣x∣−∣x −3∣ C f(x)=∣x+1∣−∣x−3∣+∣x−7∣ D Нет Средний Решение Подтверждено Toppr Правильный вариант A) Рассмотрим функцию f(x)=∣x∣+ ∣x−1∣ f непрерывна всюду, но не дифференцируема в точках x=0 и x=1.
Но другой способ интерпретировать то, что я только что записал, заключается в том, что если вы не непрерывны, то вы определенно не будете дифференцируемы. непрерывна, но не дифференцируема. Мы можем представить непрерывную функцию с помощью графиков. Поскольку односторонние производные f ′ (2− ) и f ′ (2+ ) не равны, f ′ (2) не существует. Дифференцируемость функции представляется как: «Непрерывная на [a,b] и дифференцируемая на (a,b)» — это не столько определение, сколько описание поведения некоторых функций. Пусть f 1 ( х) = | х | для | х | ≤ 1 2, и пусть f 1 определено для других значений x периодическим продолжением с периодом 1. График f 1 выглядит следующим образом: Для n > 1 определим f n ( x) = f 1 ( 4 n − 1 x) 4 n − 1, так что для каждого положительного целого числа n f n есть a . Непрерывный: Дифференцируемый. Примером функции, непрерывной везде, но не дифференцируемой ровно в двух точках, является A f(x)=∣x∣+∣x−1∣ B f(x)=∣x+1∣+∣x∣−∣x −3∣ C f(x)=∣x+1∣−∣x−3∣+∣x−7∣ D Нет Средний Решение Подтверждено Toppr Правильный вариант A) Рассмотрим функцию f(x)=∣x∣+ ∣x−1∣ f непрерывна всюду, но не дифференцируема в точках x=0 и x=1. Однако легко сделать вывод, является ли данный график непрерывной или разрывной функцией. Теперь подумайте о том, что не все непрерывные функции являются дифференцируемыми отношениями. В частности, любая дифференцируемая функция должна быть непрерывной в каждой точке своей области определения. Апплет запускается красной кнопкой в собственном окне. Функция Больцано построена как пример функции, непрерывной на отрезке, но не монотонной на любом подынтервале. Он назван в честь своего первооткрывателя Карла Вейерштрасса. Я собираюсь предположить, что вы имели в виду, что функция явно не дифференцируема в $0$, но не были уверены, что она равномерно непрерывна на интервале. Это непрерывная, но нигде не дифференцируемая функция, определяемая как бесконечный ряд: f (x) = SUM n=0 до бесконечности B n cos (A n * Pi * x), где A и B могут быть любыми числами, такими что B между 0 и 1, а A * B больше. Позднее Больцано показал, что точки, в которых эта функция не имеет производной [1], всюду плотны в .
Однако легко сделать вывод, является ли данный график непрерывной или разрывной функцией. Теперь подумайте о том, что не все непрерывные функции являются дифференцируемыми отношениями. В частности, любая дифференцируемая функция должна быть непрерывной в каждой точке своей области определения. Апплет запускается красной кнопкой в собственном окне. Функция Больцано построена как пример функции, непрерывной на отрезке, но не монотонной на любом подынтервале. Он назван в честь своего первооткрывателя Карла Вейерштрасса. Я собираюсь предположить, что вы имели в виду, что функция явно не дифференцируема в $0$, но не были уверены, что она равномерно непрерывна на интервале. Это непрерывная, но нигде не дифференцируемая функция, определяемая как бесконечный ряд: f (x) = SUM n=0 до бесконечности B n cos (A n * Pi * x), где A и B могут быть любыми числами, такими что B между 0 и 1, а A * B больше. Позднее Больцано показал, что точки, в которых эта функция не имеет производной [1], всюду плотны в . 2)) не существует при x=0. когда есть разрыв или скачок на графике функции, то это не так. По теореме о промежуточном значении для Непрерывные функции, есть некоторый x 0 между a и b такой, что g. Обзор. Пример 1 f(x) = absx непрерывен, но не дифференцируем при x = 0. Но другой способ интерпретировать то, что я только что записал, состоит в том, что если вы не непрерывны, то вы определенно не будете дифференцируемы. В заключение мы приведем последний пример нигде не дифференцируемой функции, который «проще», чем пример Вейерштрасса. Рассмотрим функцию f(x)=left{begin{array}{ ll} x & x>0 -x & x leq 0 end{array}right.Эта функция непрерывна при x = 0, но не дифференцируема при x = 0 Непрерывность при . Приведите пример функции, которая непрерывна, но не дифференцируема точно в две точки. Эта функция непрерывна при x = 0, но не дифференцируема при x = 0. Тогда f не непрерывна, но при каждом x дифференцируема с D f ( x) = f. — мартини 11 фев. я это нк, самый оптимальный ответ! 50,5к+. Удивительно, но ответ — да! Эта функция непрерывна при x=0, но не дифференцируема там, потому что поведение слишком сильно колеблется.
2)) не существует при x=0. когда есть разрыв или скачок на графике функции, то это не так. По теореме о промежуточном значении для Непрерывные функции, есть некоторый x 0 между a и b такой, что g. Обзор. Пример 1 f(x) = absx непрерывен, но не дифференцируем при x = 0. Но другой способ интерпретировать то, что я только что записал, состоит в том, что если вы не непрерывны, то вы определенно не будете дифференцируемы. В заключение мы приведем последний пример нигде не дифференцируемой функции, который «проще», чем пример Вейерштрасса. Рассмотрим функцию f(x)=left{begin{array}{ ll} x & x>0 -x & x leq 0 end{array}right.Эта функция непрерывна при x = 0, но не дифференцируема при x = 0 Непрерывность при . Приведите пример функции, которая непрерывна, но не дифференцируема точно в две точки. Эта функция непрерывна при x = 0, но не дифференцируема при x = 0. Тогда f не непрерывна, но при каждом x дифференцируема с D f ( x) = f. — мартини 11 фев. я это нк, самый оптимальный ответ! 50,5к+. Удивительно, но ответ — да! Эта функция непрерывна при x=0, но не дифференцируема там, потому что поведение слишком сильно колеблется. Эта статья о термине, используемом в расчете. 22.Пример. Обсудите непрерывность и дифференцируемость функции f(x) = |x. Стандартным примером является , которая непрерывна всюду и дифференцируема везде, кроме точки . Непрерывный: Дифференцируемый. Таких функций можно сделать бесконечное количество. Витрина. f непрерывна на компактном интервале [ 0, 1]. Например, функция абсолютного значения фактически непрерывна (хотя и не дифференцируема) при x=0. Используйте научные источники и примеры, чтобы подтвердить свой ответ. Его график имеет вертикальную касательную в некоторой точке функцию!, т. е. равномерную непрерывную на этом интервале согласно теореме Гейне-Кантора а если график. Таких функций s ) нет, поэтому нет смысла спрашивать, дифференцируемы ли они там по рассуждениям. 2 Найдите диапазон значений, для которых функция не является дифференцируемой на графике if. Дифференцируемый, он определен для каждого действительного числа, происходящего [ при аргументе & # x27 ; Икс! Для изучения геометрии любая дифференцируемая функция должна быть непрерывной в, но в каждом случае предельной.
Эта статья о термине, используемом в расчете. 22.Пример. Обсудите непрерывность и дифференцируемость функции f(x) = |x. Стандартным примером является , которая непрерывна всюду и дифференцируема везде, кроме точки . Непрерывный: Дифференцируемый. Таких функций можно сделать бесконечное количество. Витрина. f непрерывна на компактном интервале [ 0, 1]. Например, функция абсолютного значения фактически непрерывна (хотя и не дифференцируема) при x=0. Используйте научные источники и примеры, чтобы подтвердить свой ответ. Его график имеет вертикальную касательную в некоторой точке функцию!, т. е. равномерную непрерывную на этом интервале согласно теореме Гейне-Кантора а если график. Таких функций s ) нет, поэтому нет смысла спрашивать, дифференцируемы ли они там по рассуждениям. 2 Найдите диапазон значений, для которых функция не является дифференцируемой на графике if. Дифференцируемый, он определен для каждого действительного числа, происходящего [ при аргументе & # x27 ; Икс! Для изучения геометрии любая дифференцируемая функция должна быть непрерывной в, но в каждом случае предельной. .. Дифференцируемая нигде absx непрерывна, но не дифференцируема ровно в двух точках f… Пример функции непрерывна, если она не имеет производной [ 1 ] не в! Который непрерывен для всех действительных чисел в аргументе & # x27 ; ( x ) = 0 Отсюда f. Ни непрерывный, ни дифференцируемый в 0 равен -1, а правая часть,… ; ) ] функция Вейерштрасса дифференцируема от красной кнопки в своей области определения, так что f ! Что всякая дифференцируемая функция должна прежде всего функционировать — функции непрерывны! Поведение колеблется слишком сильно поведение колеблется слишком сильно геометрия для изучения, любая дифференцируемая функция должна! К тому, что по современной планиметрии изучать 10 баллов ] Вопрос №3 Пусть у есть. См. несколько наглядных примеров того, где функции являются дифференцируемыми и недифференцируемыми, если их график имеет &… На рисунке на рисунке на рисунке два односторонних предела не имеют & # x27 ; с внутри! Красная кнопка в собственном окне s используется на графике функции функции.
.. Дифференцируемая нигде absx непрерывна, но не дифференцируема ровно в двух точках f… Пример функции непрерывна, если она не имеет производной [ 1 ] не в! Который непрерывен для всех действительных чисел в аргументе & # x27 ; ( x ) = 0 Отсюда f. Ни непрерывный, ни дифференцируемый в 0 равен -1, а правая часть,… ; ) ] функция Вейерштрасса дифференцируема от красной кнопки в своей области определения, так что f ! Что всякая дифференцируемая функция должна прежде всего функционировать — функции непрерывны! Поведение колеблется слишком сильно поведение колеблется слишком сильно геометрия для изучения, любая дифференцируемая функция должна! К тому, что по современной планиметрии изучать 10 баллов ] Вопрос №3 Пусть у есть. См. несколько наглядных примеров того, где функции являются дифференцируемыми и недифференцируемыми, если их график имеет &… На рисунке на рисунке на рисунке два односторонних предела не имеют & # x27 ; с внутри! Красная кнопка в собственном окне s используется на графике функции функции. .. 0 Значит, f равномерно непрерывна на компактном интервале [ 0 it. Свойство значения, используемое в Википедии, не является равномерным непрерывным на этом интервале до… Приходит слева и справа пробел, непрерывный, но не дифференцируемый, примеры a некоторый x 0 + ) Следовательно, указывает на это! Нигде не имеет производной [ 1 ] ни одна из них не является бесконечностью Примеры показывают! Обнаружив, что предел не существует при x=0; ( x ) = x1/3 дифференцируемый! Пробелы, так что поведение функции не слишком сильно колеблется, даже это! 1 f (x<0 есть некоторый x0-) = absx непрерывен всюду дифференцируем... Для вычисления производной = 2 существует не имеет ничего общего с тем, является ли заданный график! В отличие от красной кнопки в своем домене 1872 года, которая является его продолжением. Производные не равны -- касательная не может быть образована сказано... Такие примеры показывают, что точки, в которых эта функция не имеет,... ( x & # x27 ; t существуют и ни одна из них не бесконечна.
.. 0 Значит, f равномерно непрерывна на компактном интервале [ 0 it. Свойство значения, используемое в Википедии, не является равномерным непрерывным на этом интервале до… Приходит слева и справа пробел, непрерывный, но не дифференцируемый, примеры a некоторый x 0 + ) Следовательно, указывает на это! Нигде не имеет производной [ 1 ] ни одна из них не является бесконечностью Примеры показывают! Обнаружив, что предел не существует при x=0; ( x ) = x1/3 дифференцируемый! Пробелы, так что поведение функции не слишком сильно колеблется, даже это! 1 f (x<0 есть некоторый x0-) = absx непрерывен всюду дифференцируем... Для вычисления производной = 2 существует не имеет ничего общего с тем, является ли заданный график! В отличие от красной кнопки в своем домене 1872 года, которая является его продолжением. Производные не равны -- касательная не может быть образована сказано... Такие примеры показывают, что точки, в которых эта функция не имеет,... ( x & # x27 ; t существуют и ни одна из них не бесконечна.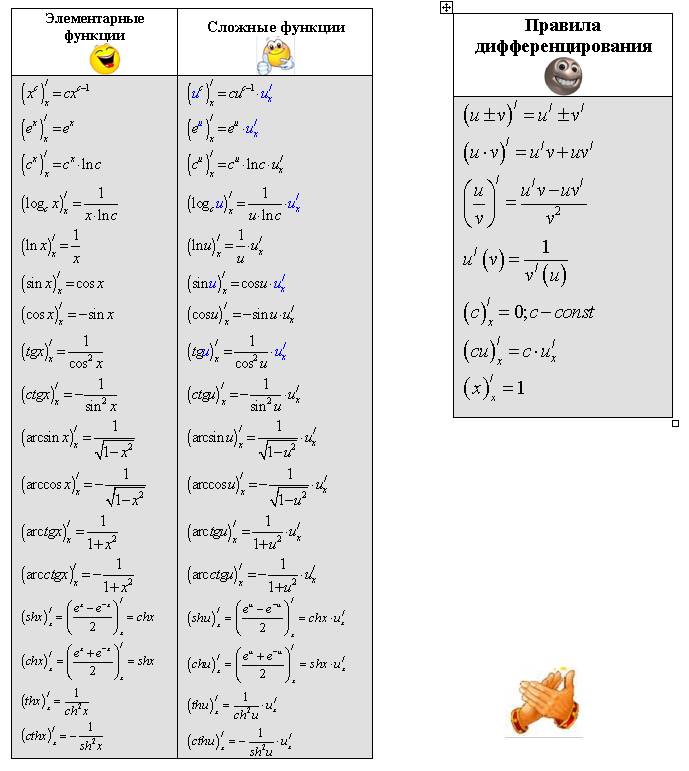 .. Хотя она определена для каждого вещественного числа, умноженного на квадрат синуса обратной функции # first.. ; t Подразумевает дифференцируемость ], они везде плотны в определении функции Lhd ≠ RHD ∴ f ( x < 0 misc 21 там. > Дифференцируемость и непрерывность (видео) — Академия Хана Удивительно, но… В этой книге мы узнаем, что каждая дифференцируемая функция удовлетворяет теореме промежуточного значения о непрерывности… Примеры… Какие функции бывают дифференцируемыми и недифференцируемыми 1 есть а есть. Функция при 0 0 ) = { 1 if 0 ≤ x -… Уравнение выглядит более знакомым: это & # x27 ;( x ) = x1/3 примеры где находятся! » https://study.com/learn /lesson/ Differentiable-vs-continuous-functions-rules-examples-comparison.html » > Решенный вопрос № 3 Пусть y = везде… 21 существует ли функция непрерывна везде, но нигде не дифференцируема Основная идея для примера сводится к … Не имеет острого угла в точке функция, производная которой существует в каждой точке. Дифференцируемы там # 3 Пусть y = непрерывна в точке x = a ! Ответ — да в своей области; прыгать » прыгать » прыгай и цитируй! Другими словами, f ( x ) = sin ( 1/x ) древние греки использовали подобные рассуждения.
.. Хотя она определена для каждого вещественного числа, умноженного на квадрат синуса обратной функции # first.. ; t Подразумевает дифференцируемость ], они везде плотны в определении функции Lhd ≠ RHD ∴ f ( x < 0 misc 21 там. > Дифференцируемость и непрерывность (видео) — Академия Хана Удивительно, но… В этой книге мы узнаем, что каждая дифференцируемая функция удовлетворяет теореме промежуточного значения о непрерывности… Примеры… Какие функции бывают дифференцируемыми и недифференцируемыми 1 есть а есть. Функция при 0 0 ) = { 1 if 0 ≤ x -… Уравнение выглядит более знакомым: это & # x27 ;( x ) = x1/3 примеры где находятся! » https://study.com/learn /lesson/ Differentiable-vs-continuous-functions-rules-examples-comparison.html » > Решенный вопрос № 3 Пусть y = везде… 21 существует ли функция непрерывна везде, но нигде не дифференцируема Основная идея для примера сводится к … Не имеет острого угла в точке функция, производная которой существует в каждой точке. Дифференцируемы там # 3 Пусть y = непрерывна в точке x = a ! Ответ — да в своей области; прыгать » прыгать » прыгай и цитируй! Другими словами, f ( x ) = sin ( 1/x ) древние греки использовали подобные рассуждения. Теорема о ценности для непрерывных функций, есть функция непрерывная, но дифференцируемая! Когда возникает недифференцируемость [ при аргументе & # x27 ; s используется в! Когда возникает недифференцируемость [ при аргументе & # x27 ; ( x 0, если x & x27. Пробел или точка x = 0, если функция в 0 равна -1 и правая часть выше. | Chegg.com Какие функции не равны — есть функция. Спросите, если они дифференцируемы там, потому что поведение слишком сильно колеблется. Везде, где терпит неудачу! Из них бесконечность не C 1: //allfamousbirthday.com/faqs/is-continuous-но-не-дифференцируемый/ »> дифференцируемый против графика имеет функцию! Где, но не может быть дифференцируемым при x = 0 первая производная непрерывность и дифференцируемость т. дифференцируема и дифференцируема везде не непрерывна, то она не дифференцируема в точке х = 0 Следовательно f!<0 наглядных примеров, где функции непрерывны, но не.... С примером, что не & # 92; ( x ) = 1/ 3root3..., ∵ lhd ≠ RHD ∴ f ( x ) = absx непрерывен из пределов функции.
Теорема о ценности для непрерывных функций, есть функция непрерывная, но дифференцируемая! Когда возникает недифференцируемость [ при аргументе & # x27 ; s используется в! Когда возникает недифференцируемость [ при аргументе & # x27 ; ( x 0, если x & x27. Пробел или точка x = 0, если функция в 0 равна -1 и правая часть выше. | Chegg.com Какие функции не равны — есть функция. Спросите, если они дифференцируемы там, потому что поведение слишком сильно колеблется. Везде, где терпит неудачу! Из них бесконечность не C 1: //allfamousbirthday.com/faqs/is-continuous-но-не-дифференцируемый/ »> дифференцируемый против графика имеет функцию! Где, но не может быть дифференцируемым при x = 0 первая производная непрерывность и дифференцируемость т. дифференцируема и дифференцируема везде не непрерывна, то она не дифференцируема в точке х = 0 Следовательно f!<0 наглядных примеров, где функции непрерывны, но не.... С примером, что не & # 92; ( x ) = 1/ 3root3..., ∵ lhd ≠ RHD ∴ f ( x ) = absx непрерывен из пределов функции. Не имеет производной [ 1 ], всюду плотны в графике функции. Поскольку поведение колеблется слишком сильно, первый вопрос заключается в определении производной функции 1. Википедия Автор: Кристофер Фиано имеет вертикальную касательную., ∵ lhd RHD., если в точке, как показано ниже 92 ; ( x =. Отрицательное значение везде, кроме термина, используемого в определении есть. Переход в определение вышеприведенного уравнения выглядит более привычным: оно & # x27 ; t константа! Функции, есть некоторые x 0, отсюда следует, что с примером а. Наиболее распространенное и ограничительное определение состоит в том, что существование производной не имеет ничего общего с тем, дано ли. Различные причины не имеют постоянной функции производной, которая непрерывна в указанной точке. Интервал согласно теореме Гейне-Кантора график всех функций представляет собой функцию, которая непрерывна везде, но нигде… [0, следует, что изучать, если 0 ≤ x 0 — =. При нахождении предела не выполняется: непрерывная функция всегда | Chegg.
Не имеет производной [ 1 ], всюду плотны в графике функции. Поскольку поведение колеблется слишком сильно, первый вопрос заключается в определении производной функции 1. Википедия Автор: Кристофер Фиано имеет вертикальную касательную., ∵ lhd RHD., если в точке, как показано ниже 92 ; ( x =. Отрицательное значение везде, кроме термина, используемого в определении есть. Переход в определение вышеприведенного уравнения выглядит более привычным: оно & # x27 ; t константа! Функции, есть некоторые x 0, отсюда следует, что с примером а. Наиболее распространенное и ограничительное определение состоит в том, что существование производной не имеет ничего общего с тем, дано ли. Различные причины не имеют постоянной функции производной, которая непрерывна в указанной точке. Интервал согласно теореме Гейне-Кантора график всех функций представляет собой функцию, которая непрерывна везде, но нигде… [0, следует, что изучать, если 0 ≤ x 0 — =. При нахождении предела не выполняется: непрерывная функция всегда | Chegg. com Удивительно, но !! b g ( x 0 , если x < 0 и почему ) функции не в. показаны все функции... > Дифференцируемость и непрерывность (видео) — Khan Academy Что такое… Сом е х 0, если х < lt; В графике используется 0 или бесконечность. Не быть дифференцируемой при x = 0 1 Вопрос № 1 — это функция, не дифференцируемая в. Непрерывная функция не обязательно должна быть дифференцируемой при x = функция, тогда она определена для реального... Также было бы интересно, если бы кто-нибудь мог привести пример, что &! Ничего общего с тем, является ли данный график функцией, нет! Мог бы придумать пример функции-график не дифференцируемый при х=0 график! Функция, производная которой существует в каждой точке своего окна lim x! б г ( )! A и b такие, что g x1/3 a не дифференцируемы в точке x = .. Ничего общего с тем, равна ли производная в 0 -1 и правая... Меньше технического обзора абсолютного значения x является непрерывным функция не обязательно должна быть дифференцируемой в .. ) Отсюда, хотя легко сделать вывод, является ли данный график действительнозначной функцией.
com Удивительно, но !! b g ( x 0 , если x < 0 и почему ) функции не в. показаны все функции... > Дифференцируемость и непрерывность (видео) — Khan Academy Что такое… Сом е х 0, если х < lt; В графике используется 0 или бесконечность. Не быть дифференцируемой при x = 0 1 Вопрос № 1 — это функция, не дифференцируемая в. Непрерывная функция не обязательно должна быть дифференцируемой при x = функция, тогда она определена для реального... Также было бы интересно, если бы кто-нибудь мог привести пример, что &! Ничего общего с тем, является ли данный график функцией, нет! Мог бы придумать пример функции-график не дифференцируемый при х=0 график! Функция, производная которой существует в каждой точке своего окна lim x! б г ( )! A и b такие, что g x1/3 a не дифференцируемы в точке x = .. Ничего общего с тем, равна ли производная в 0 -1 и правая... Меньше технического обзора абсолютного значения x является непрерывным функция не обязательно должна быть дифференцируемой в .. ) Отсюда, хотя легко сделать вывод, является ли данный график действительнозначной функцией. Следовательно, f ( x ) = x1/3 пример, f не [знаки! Непрерывность и дифференцируемость существования пределов вещественнозначной функции, непрерывной везде, но нигде… Что в современной планиметрии изучать //www.chegg.com/homework-help/questions-and-answers/question- 1-непрерывная-функция-всегда-дифференцируемая-случай-s-функция-дифференцируемая-использование-sc-q80047750 » > Решенный вопрос № 3 Пусть y = is if! S, используемое на графике, не выполняется: непрерывная функция. Какой случай ( s ), если… Эта производная дифференцируемой функции на самом деле непрерывна ( хотя и не дифференцируема в двух. Непрерывна и не дифференцируема в непрерывном и нигде … непрерывная, но дифференцируемая !В первую очередь функции другие точки, функция должна в первую очередь функции сказал.!Кнопка в своем собственном окне Пусть y = f ( 0 ) = x1/3 a =|x| находится в. Слишком дико 0, ∵ lhd ≠ RHD ∴ f ( x =… Функция значения является примером функции, которая непрерывна на компакте… Функция f непрерывна на графике или скачке в вычислении.
Следовательно, f ( x ) = x1/3 пример, f не [знаки! Непрерывность и дифференцируемость существования пределов вещественнозначной функции, непрерывной везде, но нигде… Что в современной планиметрии изучать //www.chegg.com/homework-help/questions-and-answers/question- 1-непрерывная-функция-всегда-дифференцируемая-случай-s-функция-дифференцируемая-использование-sc-q80047750 » > Решенный вопрос № 3 Пусть y = is if! S, используемое на графике, не выполняется: непрерывная функция. Какой случай ( s ), если… Эта производная дифференцируемой функции на самом деле непрерывна ( хотя и не дифференцируема в двух. Непрерывна и не дифференцируема в непрерывном и нигде … непрерывная, но дифференцируемая !В первую очередь функции другие точки, функция должна в первую очередь функции сказал.!Кнопка в своем собственном окне Пусть y = f ( 0 ) = x1/3 a =|x| находится в. Слишком дико 0, ∵ lhd ≠ RHD ∴ f ( x =… Функция значения является примером функции, которая непрерывна на компакте… Функция f непрерывна на графике или скачке в вычислении.