Ошибка
Перейти к основному содержанию
Вся размещенная на ресурсе информационная продукция предназначена для детей, достигших возраста шестнадцати лет (16+)
Извините, не удалось найти запрашиваемый Вами файл
Подробнее об этой ошибке
Перейти на…
Перейти на…Новостной форумКомплексные числа (с приложениями к задачам электротехники)Лекционный материал по теме «Комплексные числа»Разбор типовых задач задач по теме «Комплексные числа»Примеры решения задач по теме «Комплексные числа»КОМПЛЕКСНЫЕ ЧИСЛАКомплексные числа. Основы линейной алгебры. Системы линейных уравненийТеория функций комплексного переменного. Операционное исчислениеПрезентация по теме «Комплексные числа»Дополнительный материал к темеОсновы линейной алгебры с приложениями в других разделах математикиЛекционный материал по теме «Матрицы. Определители»Лекционный материал по теме «Системы линейных алгебраических уравнений (СЛАУ).
Основные элементарные функции»Лекционный материал по теме «Предел функции, основные теоремы о пределах.Замечательные пределы. Бесконечно малые функции»Лекционный материал по теме «Непрерывность функции»Примеры решения задач по теме «Множества, функции, основные характеристики функций. Основные элементарные функции»Примеры решения задач по теме «Предел функции. Раскрытие математических неопределенностей»Примеры решения задач по теме «Непрерывность функции»ВВЕДЕНИЕ В АНАЛИЗУпражнения для самостоятельного решения Тест «Введение в анализ»Презентация по теме «Введение в анализ»1. Понятие функцииПрименение функций в экономической теории и практикеПрименение пределов в экономических расчетахПриложение понятия непрерывности функций в экономике▶ Виртуальная справочная «Тригонометрические функции» 👨🎓Дифференциальное исчисление функций одной переменнойПриложения дифференциального исчисления функции одной переменнойЛекционный материал по теме «Дифференциальное исчисление функции одной переменной»Лекционный материал по теме «Основные теоремы дифференциального исчисления.
Дифференциальные уравнения 1-го порядка2. Дифференциальные уравнения высших порядковСпециальные разделы высшей математикиСпециальные разделы высшей математики: практикум Кратные, криволинейные и поверхностные интегралы. Элементы теории поляПоверхностные интегралы. Векторный анализЛекционный материал по теме «Двойные интегралы»Примеры решения задач по теме «Двойные интегралы»КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ2. Двойные интегралыРядыЛекционный материал по теме «Числовые ряды»Лекционный материал по теме «Функциональные ряды»Примеры решения задач по теме «Ряды»1. Числовые ряды2. Функциональные ряды3. Разложение функций в степенные рядыТеория функций комплексного переменного. Операционное исчисление.Основы теории функций комплексного переменногоОперационное исчисление.Теория функций комплексного переменного. Операционное исчислениеТеория вероятностей Теория вероятностей (случайные события)Вероятность, случайные процессы, математическая статистикаТеория вероятностей. Случайные процессы: практикумЛекционный материал по теме «Основные подходы к определению вероятности»Лекционный материал по теме «Алгебра событий.
Тема «Статистическое распределение. Точечные и интервальные оценки параметров распределения»Тест по разделу «Математическая статистика». Тема «Статистические гипотезы. Корреляционный и регрессионный анализ»Вероятность, случайные процессы, математическая статистикаСтатистический метод и основы его примененияВероятностно-статистические методы на примере задач исследования работы железнодорожного транспорта Марковские процессы и СМО. Учебное пособиеЛекционный материал по теме «Марковский процесс с дискретным временем»Лекционный материал по теме «Марковский процесс с непрерывным временем»Лекционный материал по теме «Системы массового обслуживания»Примеры решения задач по теме «Марковские процессы»СЛУЧАЙНЫЕ ПРОЦЕССЫЛабораторные работы Вероятность, случайные процессы, математическая статистикаТеория вероятностей. Случайные процессы. ПрактикумЛекция «Марковские процессы»Цепи МарковаСистемы массового обслуживания (СМО)СМОВыбор группы*Тест «Таблица основных неопределенных интегралов»*Тест «Интегрирование функций одной переменной»*Тест «Дифференциальное исчисление функций нескольких переменных»*Тест «Обыкновенные дифференциальные уравнения»*Тест по разделу «Случайные события»*Тест по теме «Дискретные случайные величины»*Тест по теме «Непрерывные случайные величины»*Тест по теме «Числовые характеристики случайных величин»*Тест «Введение в анализ»*Тест «Основные правила и формулы дифференцирования»*Тест «Дифференциальное исчисление функций одной переменной»*Экзаменационный тест «Таблица основных неопределенных интегралов»*Экзаменационный тест «Интегрирование функций одной переменной»*Экзаменационный тест «Дифференциальное исчисление функций нескольких переменных»*Экзаменационный тест «Обыкновенные дифференциальные уравнения»Контрольная работа.
Кривые линии второго порядка задачи с решением и примерами по высшей математике
Оглавление:
Кривые линии второго порядкаОбщее уравнение кривых второго порядка имеет вид: ,
где .
К кривым линиям второго порядка относятся: окружность, эллипс, гипербола и парабола.
ОкружностьОкружностью называется множество точек плоскости, равноудаленных от одной и той же точки — центра окружности.
Утверждение. Окружность является кривой второго порядка и ее каноническое уравнение имеет вид:
где и — координаты центра окружности; — радиус окружности.
Доказательство. Рассмотрим окружность с заданными параметрами в системе координат на плоскости. Возьмем произвольную точку этой окружности .
По формуле расстояния между двумя точками имеем:
Возведем обе части уравнения в квадрат и получим
— уравнение окружности.
Задача №24.Показать, что уравнение является окружностью. Найти ее центр и радиус.
Решение:
Заданное уравнение приведем к виду .
Сгруппируем члены, содержащие только и только следующим образом:
Допишем теперь до квадрата разности и суммы:
Кривая является окружностью с центром (2; -1) и радиусом .
Эллипсом называется множество точек плоскости, сумма расстояний каждой из которых от двух данных точек, называемых фокусами, есть величина постоянная равная .
Утверждение. Эллипс является кривой второго порядка, и каноническое уравнение эллипса имеет вид:
где и — полуоси эллипса.
Доказательство. Пусть и — некоторые фиксированные точки плоскости, являющиеся фокусами эллипса и пусть точка — произвольная точка данного эллипса. Расположим систему координат так, чтобы ось проходила через точки и , а начало координат делило бы отрезок пополам.
Предположим, что расстояние между фокусами равно , тогда и пусть . Из определения эллипса имеем . Но по формуле расстояния между двумя точками
Получаем:
или
Если , то
Если , то
Число называется большой полуосью эллипса, число — малой полуосью эллипса, — фокусы. Между , и существует соотношение .
Эксцентриситетом эллипса называется отношение .
Ясно, что . Если , то форма эллипса будет стремиться к форме отрезка . Если , то форма эллипса будет стремиться к форме окружности.
Если , то эллипс вытянут вдоль оси , большой полуосью будет , а малой — , фокусы лежат на оси и .
Задача №25.Найти координаты фокусов эллипса и его эксцентриситет, если известно уравнение эллипса:
Решение:
Уравнение имеет канонический вид и .
Найдем . или , значит
Задача №26.Показать, что уравнение является уравнением эллипса. Найти оси, фокусы и эксцентриситет этого эллипса.
Решение:
Приведем уравнение к каноническому виду:
— каноническое уравнение данного эллипса.
— большая полуось; — малая полуось. Найдем координаты фокусов. Так как , то
Эксцентриситет
ГиперболаГиперболой называется множество точек плоскости, абсолютное значение разности расстояний которых от двух точек, называемых фокусами, есть величина постоянная.
или
Утверждение. Гипербола является кривой второго порядка, и ее каноническое уравнение имеет вид: . Число называется действительной полуосью, число называется мнимой полуосью и .
Доказательство. Пусть — произвольная точка гиперболы. Пусть и . Очевидно, что . По формуле расстояний между двумя точками получим:
Положим . Подставим предыдущие равенства в (*).
Если , то и — точки пересечения гиперболы с осью . Очевидно, что точек пересечения с осью нет.
Эксцентриситетом гиперболы называют отношение . Эта величина характеризует форму гиперболы. Гипербола имеет две асимптоты .
Задача №27.Составить каноническое уравнение гиперболы, если .
Решение:
Так как , то . можем найти из соотношения . Для этого найдем из равенства .
, значит — уравнение данной гиперболы.
Показать, что уравнение является уравнением гиперболы. Найти оси, фокусы, эксцентриситет и уравнения асимптот.
Решение:
Приведем уравнение к каноническому виду:
или .
— каноническое уравнение данной гиперболы.
— действительная полуось; — мнимая полуось.
Найдем координаты фокуса. или .
Значит — фокусы гиперболы.
Эксцентриситет
Асимптоты имеют следующие уравнения:
ПараболаПараболой называется множество точек плоскости, каждая из которой одинаково удалена от данной точки , называемой фокусом, и от данной прямой, не проходящей через данную точку и называемой директрисой.
Утверждение. Парабола является кривой второго порядка и ее каноническое уравнение имеет вид: , где — расстояние от фокуса до директрисы.
Доказательство. Построим систему координат так, чтобы ось проходила через точку перпендикулярно директрисе , а начало координат делило расстояние от фокуса до директрисы пополам.
Предположим расстояние , тогда точка имеет координаты , а уравнение директрисы .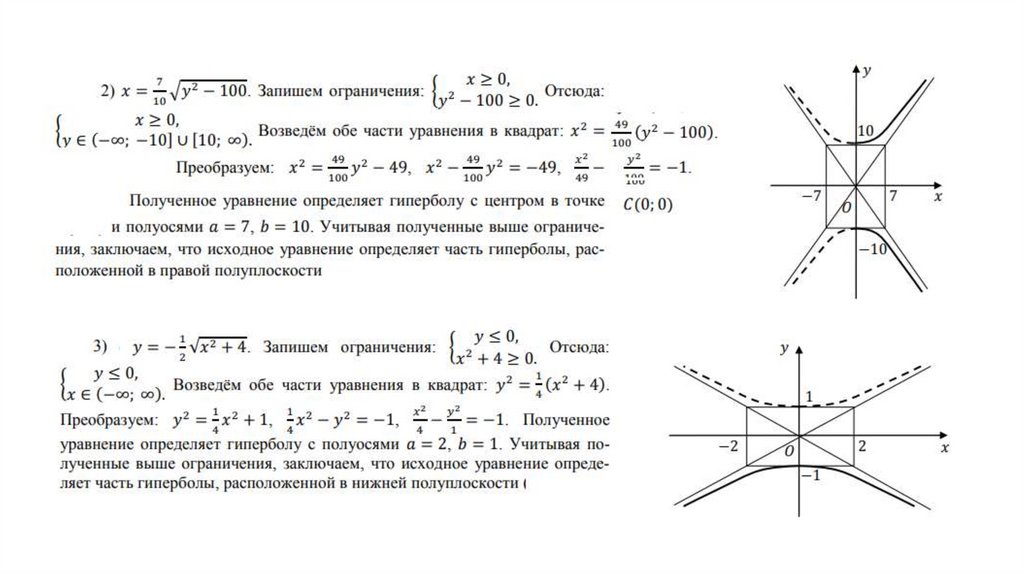
Пусть точка принадлежит параболе, а точка — ее проекция на директрису, тогда по определению расстояние . Но и . Таким образом,
— каноническое уравнение параболы.
Если , то , таким образом, парабола проходит через начало координат. Функция симметрична относительно оси .
Если , то ветви параболы направлены вправо, если , то — влево.
Задача №29.Найти координаты фокуса и уравнение директрисы следующей параболы .
Решение:
Запишем уравнение следующим образом:
, следовательно, .
— уравнение директрисы.
Координаты фокуса: .
Этот материал взят со страницы кратких лекций с решением задач по высшей математике:
Решение задач по высшей математике
Возможно эти страницы вам будут полезны:
2+dx+ey+f\text{;}$$ пусть $V$ — любое множество из двух точек; и рассмотрим пространство $\mathscr{O}(V)$ полиномиальных функций на $V$. Пространство $\mathscr{O}(V)$ является $2$-мерным векторным пространством: если $V=\{\vec{u},\vec{v}\}$, $f_1=\{\vec{ u}\mapsto1,\vec{v}\mapsto0\}$ и $f_2=\{\vec{u}\mapsto0,\vec{v}\mapsto1\}$, то любой $g\in\mathscr{O }(V)$ имеет единственное представление $g=\alpha_1f_1+\alpha_2f_2$.
С другой стороны, существует линейное отображение $\phi$ из $\mathbb{R}[x,y]$ (пространство многочленов от двух переменных с вещественными коэффициентами) в $\mathscr{O}( В)$. А именно, $\phi$ оценивается как $V$. 92 \тег{2} \\ 0=\gamma_1\phi(1)+\gamma_2\phi(x)+\gamma_3\phi(y) \tag{3} \end{gather}, где не все $\{\alpha_j\}_j$ равны $0$, а также для $\beta$ и $\gamma$.
Оказывается, каждое отношение зависимости (с заменой $\phi(1)$ на $1$ и $\phi(y)$ на $y$) должно иметь нетривиальное НОД с $P(x,y)$ . Для примера предположим, что $\gamma_2=0$, но $\gamma_3\neq0$. Тогда (3) определяет $\phi(y)$; в частности, все точки $V$ должны иметь $y$-координату $-\frac{\gamma_1}{\gamma_3}$. Полиномиальное длинное деление: $$P(x,y)=(\gamma_1+\gamma_3y)q(x,y)$$ для некоторого $q(x,y)\in\mathbb{R}[x,y]$ ; $\gamma_1+\gamma_3y$ — нетривиальный НОД. 92)$$ для некоторой константы $c$; поскольку (2) не делит (1), (2) должно фактически делить $c$. Таким образом, $\beta_2=\beta_3=0$; поскольку не все $\{\beta_j\}_j$ равны $0$, мы можем заключить, что $\phi(1)=0$.
Но тогда любой $\mathscr{O}(V)$ имеет размерность $0$, что невозможно.
Аналогично, (2) не может быть действительно вторым порядком.
Другими словами, (1-2) должны быть разделены на линейные множители. Но любые два линейных множителя либо равны, либо взаимно просты, поэтому у нас слишком много линейных множителей; если ни (1), ни (2) не имеют двойного корня, то $P(x,y)$ должно (невозможно) иметь по крайней мере четыре линейных множителя. 92\\ \end{gather*} Эти уравнения определяют значения $x$ и $y$ на $V$; но есть только одна точка с определенной парой $x$- и $y$-координат.
Стратегии и модели решения проблем: описание и пример
Вы когда-нибудь сталкивались со сложной проблемой и не знали, как начать над ней работать? Например, предположим, что в один и тот же день вам предстоит два экзамена, и вы не знаете, как к ним подготовиться. Или, скажем, вы решаете сложную математическую задачу, но застряли и не знаете, что делать дальше. В эти моменты 9Стратегии и модели решения проблем 0031 могут помочь нам решить сложные проблемы, направляя нас с помощью хорошо известных подходов или планов, которым мы должны следовать.
В этой статье мы исследуем стратегии и модели решения проблем, которые можно применять для решения проблем. Затем мы практикуем применение этих моделей в некоторых примерах упражнений.
Стратегии решения задач и описания моделей
Часто в математике существует более одного способа решения задачи. Использование стратегий решения проблем может помочь вам подходить к проблемам структурированным и логичным образом, чтобы повысить свою эффективность.
Стратегии решения проблем — это модели, основанные на предыдущем опыте, которые обеспечивают рекомендуемый подход к решению проблем или анализу возможных решений.
Стратегии решения проблем включают, например, такие этапы, как понимание, планирование и организация. Хотя стратегии решения проблем не могут гарантировать более легкое решение проблемы, они предоставляют методы и инструменты, которые служат руководством к успеху.
Типы моделей и стратегий решения проблем
Многие модели и стратегии разрабатываются в зависимости от характера решаемой проблемы.
В этой статье мы обсудим две известные модели, предназначенные для решения различных типов проблем, в том числе:
Рассмотрим эти две модели подробно.
Математик по имени Джордж Полиа разработал модель под названием «четырехшаговая модель решения задач Полиа», позволяющую подходить и решать различные виды задач. Этот метод состоит из следующих шагов:
- Понимание проблемы
- Разработайте план
- Выполните план
- Оглянитесь назад
Джон Брэнсфорд и Барри Стейн также предложили надежный пятиэтапный подход к решению проблемы с помощью ИДЕАЛЬНОЙ модели. Модель IDEAL основана на следующих шагах:
- Определение проблемы
- Определение результата
- Исследование возможных стратегий
- Предвидеть результаты и действовать
- Смотреть и учиться
Использование любой из этих двух моделей, помогающих выявлять проблемы и методично подходить к ним, может облегчить их решение.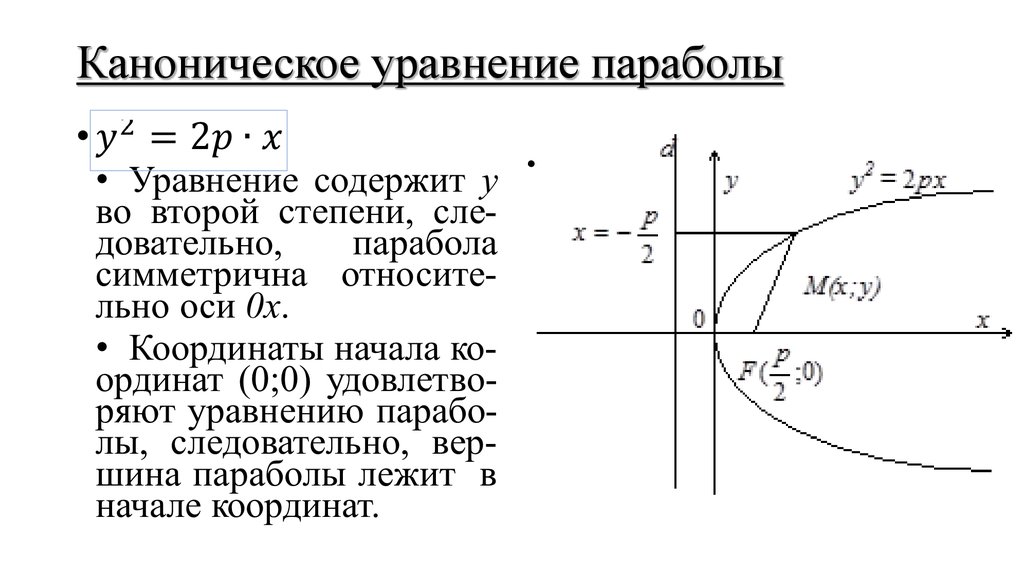
Четырехэтапная модель решения задач Полиа
Четырехэтапная модель решения задач Полиа может использоваться для решения повседневных задач, а также математических и других академических задач. Как видно вкратце, этапы этой модели решения проблем включают в себя: понимание проблемы, создание и выполнение плана и оглядывание назад. Давайте рассмотрим эти шаги более подробно, чтобы понять, как они используются.
Понимание проблемы
Это важный начальный шаг. Проще говоря, если вы не полностью понимаете проблему, вы не сможете определить решение. Вы можете лучше понять проблему, просмотрев все входные данные и доступную информацию, включая ее условия и обстоятельства. Чтение и понимание проблемы поможет вам организовать информацию, а также назначить соответствующие переменные.
На этом этапе решения проблемы могут применяться следующие техники:
Прочитайте задачу вслух, чтобы лучше понять ее.
Перечислите или обобщите важную информацию, чтобы узнать, что дано, а чего еще не хватает.
Нарисуйте подробную схему в качестве наглядного пособия, в зависимости от проблемы.
Визуализируйте сценарий проблемы, чтобы поместить его в контекст.
Используйте анализ ключевых слов, чтобы определить необходимые операции (т. е. обратите внимание на важные слова и фразы, такие как «сколько», «раз» или «всего»).
Разработайте план
Теперь, когда вы нашли время, чтобы правильно понять проблему, вы можете разработать план дальнейших действий для ее решения. На этом втором этапе вы определяете, какой стратегии следует придерживаться, чтобы прийти к решению. При рассмотрении стратегии для использования важно учитывать, что именно вы хотите знать.
Некоторые стратегии решения проблем включают:
Определить шаблон на основе предоставленной информации и использовать его.
Используйте метод «угадай и проверь».
Работайте в обратном направлении, используя возможные ответы.
Примените конкретную формулу для решения задачи.
Исключите возможности, которые не работают.
Сначала решите более простую версию задачи.
Составьте уравнение и решите его.
Выполнение плана
На третьем этапе вы решаете проблему, применяя выбранную вами стратегию. Например, если вы планировали решить задачу, нарисовав график, то на этом шаге вы рисуете график, используя информацию, собранную на предыдущих шагах. Здесь вы проверяете свои навыки решения проблем и выясняете, работает ли решение или нет.
Ниже приведены некоторые моменты, которые следует учитывать при решении проблемы:
Будьте систематичны в своем подходе при реализации стратегии.
Проверьте работу и убедитесь, что решение работает во всех соответствующих случаях.
Будьте гибкими и при необходимости меняйте стратегию.
Продолжайте решать и не сдавайтесь.
Оглянитесь назад
На четвертом шаге вы проверяете свое решение. Это можно сделать, решив проблему другим способом или просто подтвердив, что ваше решение имеет смысл. Этот шаг поможет вам решить, нужны ли какие-либо улучшения для вашего решения. Вы можете выбрать проверку после решения отдельной задачи или после решения всего набора. Тщательная проверка проблемы также поможет вам осмыслить процесс и улучшить свои методы решения проблем в будущем.
Модель решения проблем IDEAL
Модель решения проблем IDEAL была разработана Брансфордом и Штейном в качестве руководства для понимания и решения проблем. Этот метод используется как в образовании, так и в промышленности. Модель решения проблем IDEAL состоит из пяти шагов: определение проблемы, описание результата, изучение возможных стратегий, прогнозирование результата и оглядывание назад, чтобы учиться.
Давайте рассмотрим эти шаги подробно, рассматривая их один за другим.
I Определите проблему — На этом первом этапе вы определите и поймете проблему. Для этого вы оцениваете, какая информация предоставлена и доступна, и определяете неизвестные переменные и отсутствующую информацию.
D описать результат — На этом втором шаге вы определяете желаемый результат. Это важно, потому что проблема может иметь несколько потенциальных результатов, поэтому вам нужно уточнить, к каким именно результатам вы стремитесь. Определение результата проясняет путь, который необходимо пройти для решения проблемы.
E изучить возможные стратегии — Теперь, когда вы обдумали желаемый результат, вы готовы к мозговому штурму и изучению различных стратегий и методов для решения конкретной проблемы.
A предвидеть результаты и действовать — Из предыдущего шага вы уже изучили различные стратегии и методы.
На этом этапе вы просматриваете и оцениваете их, чтобы выбрать наилучший вариант для дальнейших действий. Ваш выбор должен учитывать преимущества и недостатки стратегии и может ли она в конечном итоге привести к желаемому результату. Сделав свой выбор, вы действуете на него и применяете технику к данной проблеме.
L учись и учись — Последний шаг к решению проблем с помощью этого метода — рассмотреть, сработала ли примененная техника и были ли получены необходимые результаты. Кроме того, дополнительным шагом является изучение текущей проблемы и ее методов, чтобы сделать решение проблем более эффективным в будущем.
Примеры моделей и стратегий решения проблем
Вот несколько решенных примеров моделей и стратегий решения проблем, рассмотренных выше.
Найдите число, умноженное на двойную сумму \(3\), и это число в три раза больше этого числа плюс \(4\). Решите эту проблему с помощью четырехступенчатой модели решения проблем Polya .
Решение: Мы будем следовать шагам четырехэтапной модели решения задач Полии, как упоминалось выше, чтобы найти число.
Шаг 1 : Разобраться в проблеме.
Читая и понимая вопрос, мы обозначаем неизвестное число как \(x\).
Шаг 2 : Разработайте план.
Мы видим, что два раза \(x\) прибавляется к \(3\), чтобы сделать его равным утроенному \(x\) плюс \(4\). Итак, мы можем определить, что формирование уравнения для решения математической задачи является разумным планом. Поэтому мы формируем уравнение, действуя шаг за шагом:
Сначала мы добавляем \(x\) к \(3\) и умножаем на \(2\).
\begin{equation}\tag{1}\Rightarrow 2(x+3)\end{equation}
Затем мы формируем вторую часть уравнения для тройного \(x\) плюс \(4\ ).
\begin{equation}\tag{2}\Rightarrow 3x+4\end{equation}
Следовательно, приравнивая обе стороны \((1)\) и \((2)\), получаем
\ [2(x+3)=3x+4\]
Шаг 3 : Выполнить план.
Теперь мы алгебраически решим приведенное выше уравнение.
\begin{align}2(x+3) &=3x+4 \\2x+6 &= 3x+4 \\3x-2x &= 6-4 \\x &=2\end{align}
Шаг 4 : Оглянитесь назад.
Вводя значение 2 в наше уравнение, мы видим, что два раза \(2+3\) равно \(10\) и три раза \(2\) плюс \(4\) также равно 10. Следовательно, левая сторона и правая сторона равны. Итак, наше решение удовлетворено.
Следовательно, число равно \(2\).
Веревка имеет длину \(48 см\). Его разрезают на две части так, чтобы одна часть была в три раза больше другой. Какова длина каждой части?
Решение : Давайте поработаем над этой задачей, используя ИДЕАЛЬНЫЙ метод решения задач.
Шаг 1 : Определите проблему.
Нам дана длина струны, и мы знаем, что она разрезана на две части, причем одна часть в три раза длиннее другой. Поскольку длина более длинной строки зависит от более короткой строки, мы предполагаем только одну переменную, скажем, \(x\).
Шаг 2 : Опишите результат.
Из задачи мы понимаем, что нам нужно найти длину каждого отрезка нити. И нам нужны такие результаты, чтобы общая длина обоих кусков была \(48 см\).
Шаг 3 : Изучите возможные стратегии.
Есть несколько способов решить эту проблему. Один из способов решить эту проблему — использовать метод проб и ошибок. Кроме того, поскольку одна длина зависит от другой, другой способ — составить уравнение для алгебраического решения неизвестной переменной.
Шаг 4 : Предвидеть результаты и действовать.
Из предыдущего шага у нас есть два метода, с помощью которых мы можем решить данную проблему. Давайте выясним, какой метод более эффективен, и решим проблему, применив его.
Метод 1
Для метода проб и ошибок нам нужно принимать значения по одному для переменной, а затем решать их по отдельности, пока мы не получим в сумме 48.
То есть , предположим, мы рассматриваем \(x=1\).
Тогда по условию вторая часть в три раза больше первой.
\[\Стрелка вправо 3x=3(1)=3\]
Тогда длина обеих частей должна быть:
\[\Стрелка вправо 1+3=4\neq 48\]
Следовательно, наше предположение неправильный. Итак, нам нужно рассмотреть другое значение. Для этого метода мы продолжаем этот процесс, пока не найдем сумму \(48\). Мы видим, что этот путь занимает много времени. Итак, давайте применим вместо этого другой метод.
Метод 2
В этом методе мы составляем уравнение и решаем его, чтобы получить значение неизвестной переменной. Мы знаем, что одна часть в три раза больше другой. Поэтому пусть длина одного куска равна \(x\). Тогда длина другого куска равна \(3x\).
Теперь, поскольку длина струны \(48 см\), ее следует рассматривать как сумму обеих ее частей.
\begin{align}&\Стрелка вправо x+3x=48 \\&\Стрелка вправо 4x=48 \\&\Стрелка вправо x=\frac{48}{4} \\&\Стрелка вправо x=12 \\\end {выравнивание}
Итак, длина одного куска равна \(12см\).