Лучший ответ по мнению автора | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||
Другие ответы
| ||||||||||||
09.15
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика
| Похожие вопросы |
Сестра нашла 27 грибов, а брат — .
Среди этих грибов было 3 несъедобных. Сколько всего съедобных грибов нашли дети? Заполни пропуск. Реши задачу разными способами.
Данный пример использовался на экзамене upsc в декабре 2013 и лишь один человек смог решить его … 1,3,5,7,9,11,13,15 нужно взять 3 числа и только сложением получить 30.
в зале на шести скамейках сидят 18 учеников . Сколько учеников на трех скамейках, если на каждой скамейке помещается одно и тоже число учеников
как решить задачу 1,3,5,7,9,11,13,15 используя 3 числа чтоб ответ получился 30 одно и тоже число можно использовать несколько раз несколько раз
Пользуйтесь нашим приложением
Презентация_по_алгебре_на_тему_Определение_квадратного_уравнения — презентация онлайн
ТЕМА
УРОКА:
Определение
квадратного уравнения.
Неполные квадратные
уравнения
2. Девиз урока: «Дорогу осилит идущий, а математику — мыслящий!»
Принцип урока:Я слышу, я вижу, я делаю.
3. Неполные квадратные уравнения
Цель урока:Научиться классифицировать
квадратные уравнения и решать неполные
квадратные уравнения различными способами.
Уравнение
Уравнением называется равенство,
содержащее переменную, значение которой
надо найти.
• Корень уравнения – значение переменной,
при котором получается верное равенство.
Решить уравнение — найти все его корни
(или убедиться, что их нет).
а) х — 5 = 0;
б) 2у- 4 = 0;
в) n(n + 5) = 0;
г) m² = 16;
д) c² – 9 = 0 ;
е) 5х = 0.
Определение квадратного
уравнения
Квадратным уравнением называется
уравнение вида ах²+вх+с=0, где х – переменная;
а, в, с – любые действительные числа,
причем а≠0.
Числа а, в, с – коэффициенты квадратного уравнения.
а – первый или старший коэффициент,
в – второй коэффициент или коэффициент при х,
с – свободный член.
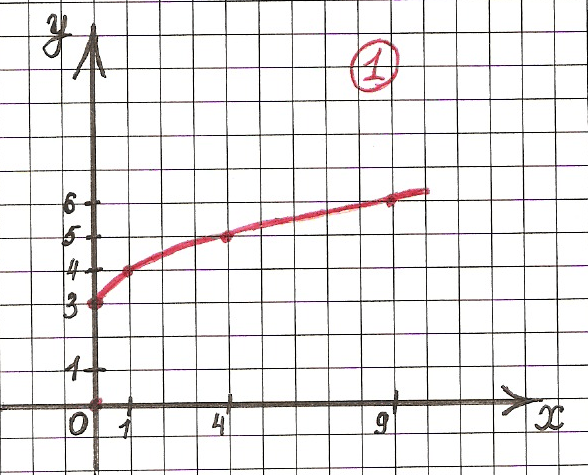
Является ли квадратным
уравнение?
• а) 2х² + 7х – 3 = 0;
д) х² – 6х + 1 = 0;
• б) 5х – 7 = 0;
е) 7х + 5х = 0;
• в) –х² – 5х – 1 = 0;
ж) 4х² + 1 = 0;
• г) 3х + 4 = 0;
з) х² – 36 = 0.
Приведите уравнение
к виду ах² + bх + с = 0
• а) –х + 2х² – 4 = 0;
г) 18 – 7х + х² = 0;
• б) 2х² – 3х = – 1;
д) 3 – х² + х = 0.
• в) х + 8 – 9х² = 0;
Определите коэффициенты
квадратного уравнения:
• 6х2 + 4х + 2 = 0
а=
b=
c=
• -2х2 + х — 1 = 0
а=
b=
c=
• 8х2 – 7х = 0
а=
b=
c=
• х2 – 0,7 = 0
а=
b=
c=
Приведённое и неприведённое
квадратное уравнение.
• Квадратное уравнение называют приведённым,
если его старший коэффициент =1.
х² – 6х + 1 = 0
• Квадратное уравнение называют неприведённым,
если старший коэффициент отличен от 1.
2х² + 10х – 6 = 0
• Чтобы квадратное уравнение стало приведённым
надо коэффициенты квадратного уравнения
разделить на старший коэффициент.
Преобразуйте квадратное
уравнение в приведённое:
• а) –х² + 2х – 5 = 0;
г) 3х² + 9х –21 = 0;
• б) х² + 3х – 1 = 0;
0;
д) 5х² + 10х + 20 =
• в) 2х² – 4х = 0;
е) 8х²+24 = 0.
Здоровьесберегающие технологии
Вперёд четыре шага,
Назад четыре шага.
Кружится, кружится
Наш хоровод.
Ручками похлопаем,
Ножками потопаем,
Плечиком подвигаем,
А потом попрыгаем.
Квадратное уравнение
Полное квадратное
уравнение — это
уравнение, в котором
присутствуют все три
слагаемых; иными словами, это
уравнение, у которого
коэффициенты в и с отличны от
нуля.
Неполное квадратное
уравнение — это
уравнение, в котором
присутствуют не все три
слагаемых; иными словами, это
уравнение, у которого хотя бы
один из коэффициентов в, с
равен нулю.
Виды неполных
квадратных уравнений
• Если b = 0, то уравнение имеет вид
ах2 + c=0
• Если с = 0, то уравнение имеет вид
ах2 + bx =0
• Если b = 0 и с = 0, то уравнение имеет
вид
ах2 =0
Способы решения
неполных квадратных
уравнений
Примеры неполных
квадратных уравнений
а) –х² +1,2=0
б) -3х² +7х=0
в) 5х² — 2=0
г) 7х² =0
д) х²+4х =0
,где а= , в= , с= ;
а= , в= , с= ;
а= , в= , с= ;
а= , в= , с= ;
а= , в= , с= .
Примеры решения неполных
квадратных уравнений
• ах2 + c=0
Пример №1
-3х2 +75=0
-3х2 = -75
х2 = -75:(-3)
х2 =25
х1 = 5 х2 = -5
Ответ: х1 = 5 х2 = 5
Пример №2
4х2 +8=0
4х2 = -8
х2 = -8:4
х2 = -2
Ответ: корней нет
• ах2 + bx =0
Пример №1
4х2 +12х=0
х(4х + 12) = 0
х = 0 или 4х + 12 = 0
х = -12:4
х = -3
Ответ: х1 = 0 х2 = -3
• ах2 =0
Пример №1
0,2х2 =0
х2 =0:0,2
х2 =0
х =0
Ответ: х = 0
Закрепление
• – Какое уравнение называется квадратным?
• – Может ли коэффициент а в квадратном уравнении
быть равным нулю?
• – Является ли уравнение 3х² – 7 = 0 квадратным? Назовите
коэффициенты этого уравнения.
• – Какое квадратное уравнение называется неполным?
• – Какое квадратное уравнение называется приведённым?
• – Как преобразовать неприведённое квадратное уравнение
в приведённое?
18. Какие из данных уравнений являются квадратными? а) 3х+х2=0; д) х2+8х+1=0; б) 2х-5=4; е) х2-9х=0; в) -3х2+2х-5=0; ж) 5х2=0; г)
Какие из данных уравнений являютсяквадратными?
а) 3х+х2=0;
б) 2х-5=4;
в) -3х2+2х-5=0;
г) 2х2-7=0;
д) х2+8х+1=0;
е) х2-9х=0;
ж) 5х2=0;
з) х+2=0;
Какие из этих уравнений являются неполными
квадратными?
Укажите коэффициенты уравнений в пунктах
а), в), д).
19. Исторические сведения.
А когда люди научились решать квадратные уравнения?Древние греки — Евклид и другие ученые – квадратные уравнения
решали геометрическим путем. Задачи, которые они решали, имели
практическую направленность. Например, найти сторону квадрата по его
площади, или радиус круга тоже по площади.
В Древнем Вавилоне образованные люди (жрецы и чиновники)
умели решать задачи на определение длины и ширины прямоугольника
по площади и периметру.
Багдад 9 век. Математик аль-Хорезми предлагает правило решения
квадратных уравнений в точности соответствующее действиям по
нашим формулам, но изложено риторически.
Выдающийся французский математик 16 века Франсуа Виет ввел для
коэффициентов буквы и получил равенство, связывающее корни
уравнения.
После трудов нидерландского математика Жирара, а также
Декарта и Ньютона способ решения квадратных уравнений
принял современный вид.
20. Домашнее задание: п.
28, № 638, 641, 64721. « Пусть каждый день и каждый час Вам новое добудет. Пусть добрым будет ум у вас, а сердце умным будет». С. Маршак
« Пусть каждый день и каждый часВам новое добудет.
Пусть добрым будет ум у вас,
а сердце умным будет».
С. Маршак
| 1 | Найти производную — d/dx | бревно натуральное х | |
| 2 | Оценить интеграл | интеграл натурального логарифма x относительно x | |
| 3 | Найти производную — d/dx | 92)||
| 21 | Оценить интеграл | интеграл от 0 до 1 кубического корня из 1+7x относительно x | |
| 22 | Найти производную — d/dx | грех(2x) | |
| 23 | Найти производную — d/dx | 9(3x) по отношению к x||
| 41 | Оценить интеграл | интеграл от cos(2x) относительно x | |
| 42 | Найти производную — d/dx | 1/(корень квадратный из х) | |
| 43 | Оценка интеграла 9бесконечность | ||
| 45 | Найти производную — d/dx | х/2 | |
| 46 | Найти производную — d/dx | -cos(x) | |
| 47 | Найти производную — d/dx | грех(3x) | 92+1|
| 68 | Оценить интеграл | интеграл от sin(x) по x | |
| 69 | Найти производную — d/dx | угловой синус(х) | |
| 70 | Оценить предел | ограничение, когда x приближается к 0 из (sin(x))/x 92 по отношению к х | |
| 85 | Найти производную — d/dx | лог х | |
| 86 | Найти производную — d/dx | арктан(х) | |
| 87 | Найти производную — d/dx | бревно натуральное 5х92 |
Уравнения окружности
В этом уроке мы поговорим о различных формах уравнений окружности на декартовой плоскости.
Давай начнем!
Уравнение окружности с центром (x
1 , y 1 ) и радиусом rЧтобы найти уравнение, мы выберем любую точку на окружности и установим некоторую связь между ее координатами, т.е. всегда истинный. Это соотношение и будет искомым уравнением.
Пусть C(x 1 , y 1 ) будет центром круга. Тогда для любой точки P(x, y) на окружности имеем:
CP = r
Почему? Потому что любая точка на окружности всегда находится на фиксированном расстоянии от центра окружности. И это фиксированное расстояние является радиусом.
Поскольку мы ищем связь между координатами, мы приведем некоторые формулы координатной геометрии. Используя формулу расстояния, мы можем переписать приведенное выше соотношение как: 92}=r\)
Наконец, чтобы это выглядело красивее, возведем в квадрат обе стороны, чтобы получить:
(x – x 1 ) 2 + (y – y 1 ) 2 = r 2
Поскольку приведенное выше соотношение верно для любых точек на окружности, оно является требуемым уравнением окружности.
Общее уравнение окружности
Теперь мы нашли стандартное уравнение, а также приведенное выше. Но какое уравнение вообще будет представлять круг?
Например, какое из следующих уравнений описывает окружность?
x 2 + y – 2x – 4 = 0
x + y 2 + 6x – 2y + 5 = 0
3x + 4y = 12
x 2 + y 2 – 2x + 4y + 1 = 0
Третье уравнение представляет собой линию, которую мы узнали на предыдущем уроке. А как насчет других?
So, let’s pick any circle, i.e. a circle with the center as (x 1 , y 1 ) and radius as r , where x 1 , y 1 и r (> 0) может иметь любое значение . Теперь мы найдем его уравнение и внимательно посмотрим на те термины, которые у нас получились.
Из предыдущего раздела уравнение этой окружности будет:
(x – x 1 ) 2 + (y – y 1 ) 2 = r 2
:
x 2 + y 2 – 2x 1 x – 2y 1 y + x 1 2 + y 1 2 – r 2 = 0
Уравнение содержит следующие типы членов.
Два семестра второй степени: x 2 and y 2
Two terms of first degree: –2x 1 x and –2y 1 y
One constant term: –r 2
Кроме того, члены второй степени имеют одинаковый коэффициент (в данном случае 1 ).
Теперь рассмотрим это уравнение:
x 2 + y 2 + 2gx + 2fy + c = 0
Это несколько похоже на предыдущее (т. е. в отношении количества и типов терминов).
Представляет ли это круг, потому что он выглядит как уравнение окружности?
Оказывается, да. Нам просто нужно сделать так, чтобы он выглядел точно так же, как в предыдущем разделе. Давайте сделаем это!
x 2 + Y 2 + 2GX + 2FY + C = 0
⇒ (x 2 + 2GX) + (Y 2 2 + 2GX) + (y 2 + 2 0 + 2 0 + 2. термины)
⇒ (x 2 + 2gx + g 2 ) + (y 2 + 2fy + F 2 ) + C = 0 + G 2 + F 2 (добавление G 2 и F 2 на SIPES) на обоих вехах) 99999999999. и F 2 на обоих вехах).