Планиметрия в тезисах и решениях. 9 класс
При решении задач на окружность и круг применяются следующие формулы:
если ? выражена в радианах. Sсегмента = Sсектора – Sтреугольника.
Вписанный в окружность угол равен половине центрального угла, опирающегося на ту же дугу.
Примеры решения задач
79. Даны две концентрические окружности. Длина одной из них равна 33?, другой 27?. Найдите ширину кольца (рис. 163). (1)
Рис. 163.
Решение. Очевидно, что ширина кольца hкольца = R – r (см. рис). Зная длины окружностей, найдём их радиусы.
Ответ: 3.
80. Найдите площадь сектора круга с радиусом R = 4 и центральным углом в 30°. (1)
Решение. Площадь сектора с углом в 30° в 36°/3° = 12 раз меньше площади всего круга. Значит, площадь сектора
Ответ: 4/3?.
81. Две окружности с радиусами R = 3 и r = 1 касаются внешним образом. Найдите расстояния от точки касания окружностей до их общих касательных (рис.
Рис. 164.
Решение. Из рисунка видно, что четырёхугольник АВ02О1 – трапеция. В самом деле, радиусы О1А и О2В перпендикулярны общей касательной АВ, а значит, параллельны друг другу. Проведём среднюю линию EF трапеции АВO2О1. По свойству средней линии трапеции находим
Легко видеть, что КМ – средняя линия трапеции EВО2F(см. рис. 164, б).
Ответ: 3/2.
82. В сектор с центральным углом в 60° вписан круг. При каком радиусе сектора площадь круга равна ? (рис. 165)? (2)
Рис. 165.
Решение. Пусть АО = ОВ = ОС = х (см. рис). D – центр вписанного в сектор круга. Тогда ОС – биссектриса ?АОВ и ?СОВ = 1/2 ?АОВ = 1/2 ? 60° = 30°. Из прямоугольного треугольника ODK:
Ответ: 3.
83. Диаметр окружности радиуса R является основанием правильного треугольника. Вычислите площадь той части треугольника, которая лежит вне данного круга (рис. 166). (2)
Рис. 166.
Решение. Как видно из рисунка, треугольники ADO и ОЕС – равносторонние (например, у ?ADO ?А = 60°; АО = OD, значит, ?ADO = 60°).
Как видно из рисунка, треугольники ADO и ОЕС – равносторонние (например, у ?ADO ?А = 60°; АО = OD, значит, ?ADO = 60°).
Искомая площадь:
Ответ:
84. На плоскости даны две окружности с радиусами 12 см и 7 см и центрами в точках О1 и О2 касающиеся некоторой прямой в точках М1 и М2 и лежащие по одну сторону от этой прямой. Отношение длины отрезка М1М2 к длине отрезка О1O2 равно
Вычислить длину отрезка М1М2 (рис. 167). (3)
Рис. 167.
Решение. Пусть S1 и S2 – две окружности, удовлетворяющие условию задачи. Поскольку точки М1 и М2 являются точками касания окружностей S1 и S2 с прямой М1М2, то О1М1 ? М1М2 и O2М2 ? М1М2. Соединим центры О1 и O2 этих окружностей и проведём через точку О1 прямую, параллельную прямой М1М2. Пусть точка К будет точкой пересечения прямых O2М2 и прямой, проведённой параллельно прямой М1М2 через точку О1. Получим прямоугольный треугольник O1O2K с гипотенузой O1O2. Применяя к прямоугольному треугольнику О1КO2 теорему Пифагора, имеем:
О1О22= O1K2+ KO22(1)
Поскольку
то
Поскольку КМ2 = О1М1 и КO2 = КМ2 – М2O2, то КO2 = 5 см. Наконец,
Наконец,
Теперь из равенства (1) с учётом (2) и (3), а также КO2 = 5 см, следует, что 5/4 М1М22= М1М22+ 25, откуда
Ответ: 10 см.
Задачи для самостоятельного решения
85. Дуги А1В1 и А2В2 равной длины 1 принадлежат разным окружностям с радиусами R1 и R2. Найдите отношение градусных мер центральных углов, соответствующих этим дугам. (1)
86. Точка лежит вне круга на расстоянии диаметра от центра круга. Найдите угол между касательными, проведенными из данной точки к данному кругу. (1)
87. В пересечение двух равных кругов вписан ромб с диагоналями 12 и 6 см. Найдите радиус окружностей. (2)
88. В равнобедренный треугольник, у которого боковая сторона равна 10 см, а основание 6 см, вписана окружность. Определите расстояние между точками касания, находящимися на боковых сторонах треугольника. (2)
89. Дано круговое кольцо, площадь которого Q. Определите длину хорды большего круга, касательной к меньшему. (2)
(2)
90. Круг радиуса
разделен на два сегмента хордой, равной стороне вписанного в этот круг правильного треугольника. Определите площадь меньшего из этих сегментов. (2)
91. Хорды АВ и АС имеют одинаковую длину. Величина образованного ими вписанного в окружность угла равна ?/6. Найти отношение площади той части круга, которая заключена в этом угле, к площади всего круга. (3)
§ Геометрические фигуры на плоскости. Прямоугольник, квадрат, треугольник, многоугольник, круг и окружность
Точка, прямая, луч, отрезок и ломаная Угол. Виды углов Фигуры и их свойства
Познакомимся с основными фигурами геометрии.
Прямоугольник
Запомните!
Прямоугольник — это фигура, которая имеет четыре стороны и четыре прямых угла.
У прямоугольника противоположные стороны равны.
В геометрии прямоугольник обозначают четырьмя заглавными латинскими буквами.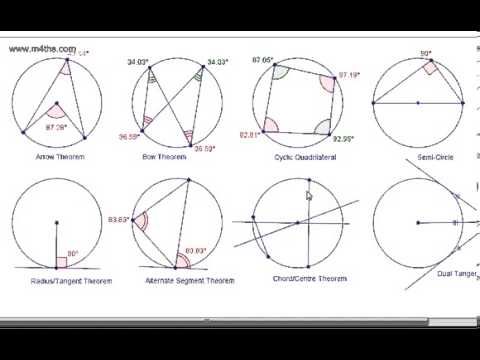
Противоположные стороны прямоугольника ABCD: AB = CD, BC = DA.
Углы:ABC = BCD = CDA = DAB = 90° — все углы прямые.
Квадрат
Запомните!
Квадрат — это прямоугольник, у которого все стороны равны.
В геометрии квадрат, также как и прямоугольник, обозначают четырьмя большими латинскими буквами.
Стороны квадрата KLFM: KL = LF = FM = MK.
Углы: KLF = LFM = FMK = MKL = 90° — все углы прямые.
На нашем сайте вы можете проверить свои вычисления, используя калькулятор расчёта периметра и площади квадрата онлайн.
Треугольник
Запомните!
Треугольник — это геометрическая фигура, которая имеет три стороны и три угла (вершины треугольника).
Треугольник обозначается тремя заглавными латинскими буквами, перед которыми ставится знак:
Треугольник EFG сокращенно обозначается как EFG.
Виды треугольников
| Вид треугольника | Пример |
|---|---|
| Прямоугольный (Один угол прямой, два других острых) | |
| Остроугольный (Все углы острые) | |
| Тупоугольный (Один угол тупой, два других — острые) |
Многоугольник
Многоугольники — это геометрические фигуры различной формы.
Вершины многоугольника — это точки, соединяющие отрезки, из которых состоит многоугольник.
Стороны многоугольника — это отрезки, из которых состоит многоугольник.
Многоугольник ELNFK.
- Вершины многоугольника — E, L, F, N, K.
- Стороны многоугольника — EL, LN, NF, FK, KE.
Окружность. Круг
Запомните!
Окружность — это геометрическая фигура, образованная замкнутой кривой линией, все точки которой находятся на одинаковом расстоянии от центра.
Круг — это геометрическая фигура, которая ограничена окружностью.
Окружность — это граница круга.
Радиус круга — это расстояние от центра окружности до любой её точки.
Диаметр круга — это отрезок, который соединяет две точки окружности и проходит через её центр.
Диаметр круга равен двум его радиусам.
- Точка O — центр круга.
- AB — диаметр круга (обозначается буквой «d»).

- OK — радиус круга (обозначается буквой «r»).
- АB = 2OK
Точка, прямая, луч, отрезок и ломаная Угол. Виды углов Фигуры и их свойства
Теоремы о восьми кругах страница
Вы здесь: Главная > Введение в математику > Теоремы круга первая страница > Восемь теорем
Теоремы
Загрузите их в виде файла .pdf, который обобщает теоремы — в основном печатная копия, 2 стороны A4, версия этой страницы.
Здесь я изложил восемь теорем, чтобы вы могли убедиться, что сделали правильные выводы на страницах динамической геометрии! Я включил диаграммы, которые представляют собой просто унылую статическую геометрию, отчасти в качестве резервной копии на случай, если динамические страницы не будут работать на вашем компьютере. Я также недавно добавил больше ссылок на страницы динамической геометрии: например, вы можете просто щелкнуть по диаграмме. Я заметил, что Google, похоже, выводит вас сюда, если вы искали «теоремы о кругах», так что вы, возможно, еще не видели всех динамических прелестей, скрывающихся всего за один клик !!!
Техническое примечание
Если повезет, следующий абзац должен быть неактуален — я обновил страницы динамической геометрии, чтобы использовать Geogebra 5 и Geogebra Tube.
Если вы получаете сообщение «Ошибка. Нажмите для подробностей» там, где должна быть динамическая геометрия, возможно, стоит перезагрузить страницу. Если это не сработает, это, вероятно, означает, что Geogebra изменила расположение важного файла, а я не обновил страницы!!
Если у вас проблемы со страницами, или вы хотите связаться, дайте мне знать.
Тим Деверо 02.02.15
- Теорема о первой окружности — углы в центре и на окружности.
- Теорема о второй окружности — угол в полуокружности.
- Третья теорема об окружности — углы в одном отрезке.
- Четвертая теорема об окружности — углы вписанного четырехугольника.
- Пятая теорема об окружности — длина касательных.
- Шестая теорема об окружности — угол между касательной к окружности и радиусом.
- Теорема седьмого круга — теорема об альтернативных сегментах.
- Восьмая теорема об окружности — перпендикуляр из центра делит хорду пополам
Круг Теорема 1
ссылка на динамическую страницу
Далее >
Угол в центре в два раза больше угла на окружности.

(Обратите внимание, что оба угла обращены к одной и той же части дуги, CB)
Теорема об окружности 2
ссылка на динамическую страницу
Далее >
Угол полукольца равен 90°.
(Это частный случай теоремы 1 с центральным углом 180°.)
Теорема о круге 3
ссылка на динамическую страницу
Далее >
Углы в одном отрезке равны.
(Оба угла находятся в большом сегменте; я выделил меньший сегмент серым цветом)
Теорема об окружности 4
ссылка на динамическую страницу
Далее >
Противолежащие углы вписанного четырехугольника в сумме составляют 180°.
Круг Теорема 5
ссылка на динамическую страницу
Далее >
Длины двух касательных из точки к окружности равны.
CD = CE
Круг Теорема 6
ссылка на динамическую страницу
Далее >
Угол между касательной и радиусом окружности равен 90°.
Круг Теорема 7
ссылка на динамическую страницу
Далее >
Теорема об альтернативном сегменте:
Угол (α) между касательной и хордой в точке контакта (D) равен углу (β) в альтернативном сегменте*.
*Спасибо, BBC Bitesize, за точную формулировку этой теоремы!
Вот ссылка на страницы с исправлениями их кругов.
Открытые учебники | Siyavula
Загрузите наши открытые учебники в различных форматах, чтобы использовать их так, как вам удобно. Нажмите на обложку каждой книги, чтобы увидеть доступные для загрузки файлы на английском и африкаанс. Лучше, чем просто бесплатные, эти книги также имеют открытую лицензию! См. различные открытые лицензии для каждой загрузки и пояснения к лицензиям в нижней части страницы.
Математика
- Читать онлайн
Учебники
Английский
- 7A PDF (CC-BY-ND)
- 7B PDF (CC-BY-ND)
Африкаанс
- 7A PDF (CC-BY-ND)
- 7B PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- 8A PDF (CC-BY-ND)
- 8B PDF (CC-BY-ND)
Африкаанс
- 8A PDF (CC-BY-ND)
- 8B PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- 9A PDF (CC-BY-ND)
- 9B PDF (CC-BY-ND)
Африкаанс
- 9A PDF (CC-BY-ND)
- 9B PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
Наука
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 7А
- PDF (CC-BY-ND)
Класс 7Б
- PDF (CC-BY-ND)
Африкаанс
Граад 7А
- PDF (CC-BY-ND)
Граад 7Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 8А
- PDF (CC-BY-ND)
Класс 8Б
- PDF (CC-BY-ND)
Африкаанс
Граад 8А
- PDF (CC-BY-ND)
Граад 8Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 9А
- PDF (CC-BY-ND)
Класс 9Б
- PDF (CC-BY-ND)
Африкаанс
Граад 9А
- PDF (CC-BY-ND)
Граад 9Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 4А
- PDF (CC-BY-ND)
Класс 4Б
- PDF (CC-BY-ND)
Африкаанс
Граад 4А
- PDF (CC-BY-ND)
Граад 4Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 5А
- PDF (CC-BY-ND)
Класс 5Б
- PDF (CC-BY-ND)
Африкаанс
Граад 5А
- PDF (CC-BY-ND)
Граад 5Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 6А
- PDF (CC-BY-ND)
Класс 6Б
- PDF (CC-BY-ND)
Африкаанс
Граад 6А
- PDF (CC-BY-ND)
Граад 6Б
- PDF (CC-BY-ND)
Лицензирование наших книг
Лучше, чем просто бесплатные, эти книги также имеют открытую лицензию! Один и тот же контент, но разные версии (фирменные или нет) имеют разные лицензии, как объяснено:
CC-BY-ND (фирменные версии)
Вам разрешается и поощряется свободное копирование этих версий.