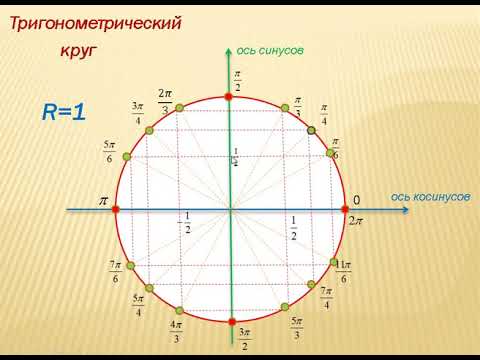
Тригонометрический круг синус и косинус
Тригонометрический круг представляет значения тригонометрических функций синус (sin) и косинус (cos) в виде координат точек единичной окружности при различных значениях угла альфа в градусах и радианах.
Поскольку я сам вечно путаюсь при переводе координат точек окружности в синусы и косинусы, для простоты все значения косинусов (cos) для углов от 0 до 360 градусов (от 0 пи до 2 пи) подчеркнуты зеленой черточкой. Даже при распечатке этого рисунка тригонометрического круга на черно-белом принтере все значения косинуса будут подчеркнуты, а значения синуса будут без подчеркивания. Если вам интересно, то можете посмотреть отдельные тригонометрические круги для синуса и косинуса.
Напротив указанных углов на окружности расположены точки, а в круглых скобках указаны координаты этих точек. Первой записана координата Х (косинус)
Давайте проведем обзорную экскурсию по этому уголку математического зоопарка.
В этой системе координат нарисована окружность радиусом, равным единице. Центр окружности находится в начале системы координат — там, где в центе рисунка пересекаются оси абсцисс (ось Х) и ординат (ось У)
.Из центра окружности проведены тоненькие черточки, которые показывают углы 30, 45, 60, 120, 135, 150, 210, 225, 240, 300, 315, 330 градусов.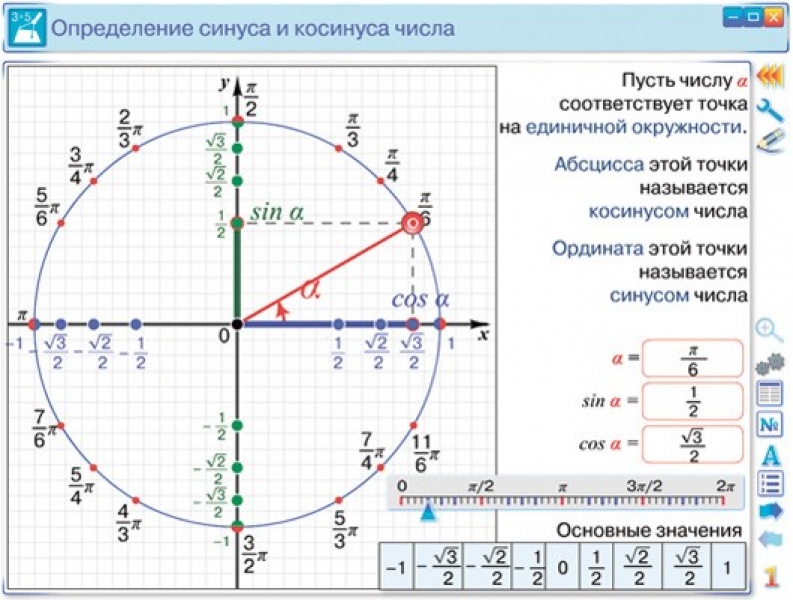
В радианной мере углов это пи деленное на 6, пи на 4, пи на 3, 2 пи на 3, 3 пи на 4, 5 пи на 6, 7 пи на 6, 5 пи на 4, 4 пи на 3, 3 пи на 2, 5 пи на 3, 7 пи на 4, 11 пи деленное на 6. С осями координат совпадают такие значения углов: 0, 90, 180, 270 градусов или 0 пи, пи деленное на 2, пи, 3 пи деленное на 2. Пользуясь картинкой, очень просто переводить углы из градусов в радианы и из радиан в градусы. Одинаковые значения в разных системах измерения углов написаны на одной линии, изображающей этот угол.
Линии углов заканчиваются точками на единичной окружности. Возле каждой точки, в круглых скобках, записаны координаты этой точки. Первой записана координата Х, которая соответствует косинусу угла, образовавшего эту точку. Второй записана координата
Главное, не перепутать синус с косинусом.Обращаю особое внимание на тот факт, что если вы по значению синуса или косинуса ищите угол, обязательно нужно дописывать период угла. Математики очень трепетно относятся к этому аппендициту тригонометрических функций и при его отсутствии могут влепить двойку за, казалось бы, правильный ответ. Что такое период при нахождении угла по значению тригонометрической функции? Это такая штучка, которая придумана математиками специально для того, чтобы запутываться самим и запутывать других. Особенно блондинок. Но об этом мы поговорим как-нибудь в другой раз.
Всё, что собрано в кучку на рисунке тригонометрического круга синуса и косинуса, можно внимательно рассмотреть на отдельных картинках с портретами синуса 0, 30, 45 градусов (ссылки на отдельные странички я буду добавлять по мере увеличения фотогалереи синусов и косинусов).
Найти решение:
Синусы и косинусы круг — здесь картинка во всей своей тригонометрической красе.
Угол 120 градусов в радианах — равен 2/3 пи или 2 пи деленное на 3, на картинке очень красиво нарисовано.
Значения синусов косинусов углов в радианах — на картинке есть такие, надеюсь, именно те углы, которые вы ищете.
Значение косинуса угла в 45 градусов — равно корню из двух деленному на два, можете проверить по рисунку.
Тригонометрическая окружность — я не совсем уверен, что представленная на картинке окружность является тригонометрической, но что-то от тригонометрии в этой окружности определенно есть, например, синусы и косинусы на окружности — вылитая тригонометрия.
Тригонометрический круг рисунок — есть здесь такой. Правда, не самый красивый рисунок, можно нарисовать гораздо красивее и понятнее. Мне минус в репутацию — почему я до сих пор не нарисовал его для блондинок? Представляете ситуацию в картинной галерее будущего: экскурсовод объясняет группе школьников «Перед вами всемирно известное полотно «Тригонометрическая мадонна с единичным отрезком на руках» — картина гениального художника эпохи Раннего Математического Возрождения .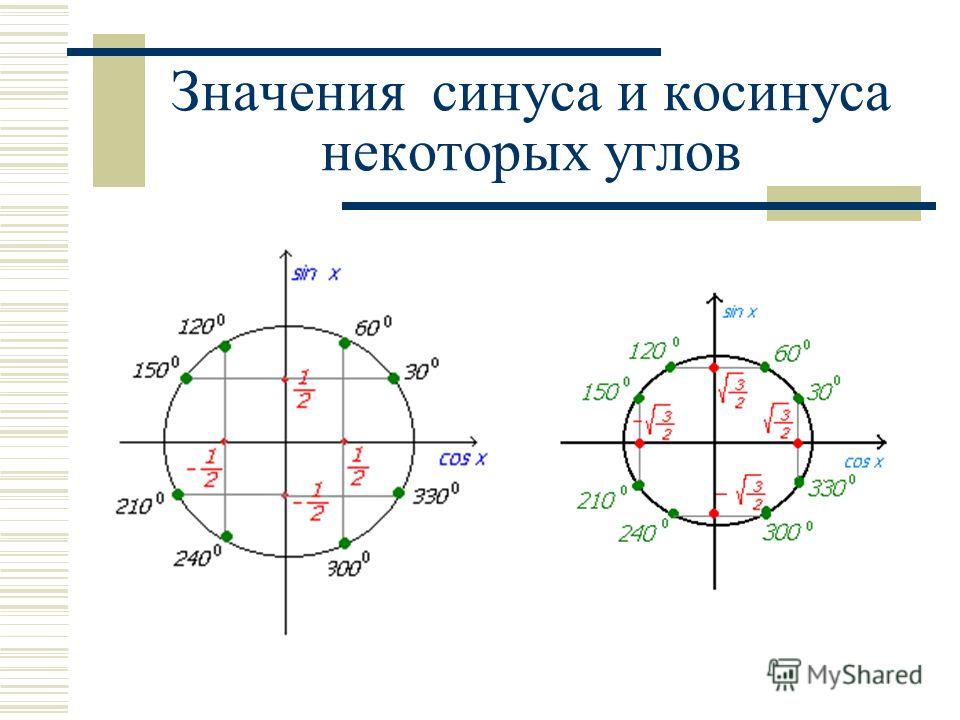
..» Дальше она называет имя этого самого художника (или художницы). Это имя может быть вашим!
Круг синусов и косинусов — именно такой круг совершенно случайно оказался здесь на картинке.
Угол 9 градусов сколько это в пи — в пи это 1/20 или пи/20.
Решение: для перевода градусов в пи радиан, нужно имеющиеся у нас градусы разделить на 180 градусов (это 1 пи радиан). У нас получается 9/180 = 1/20
Ответ: 9 градусов = 1/20 пи.
Синус это вверх или в сторону — синус — это вверх, в сторону — это косинус.
Комментарии к этой статье запрещены. Из-за огромного их количества мои ответы на ваши вопросы о тригонометрическом круге уже не публикуются. Вопросы можете задавать в комментариях к другим страницам. Постараюсь решить проблему за счет удаления части комментариев, тем самым освобожу место для новых.
Математика для блондинок: Тригонометрический круг
Более правильным названием этого произведения математического искусства является «единичная окружность», в простонародье больше прижилось название «тригонометрический круг».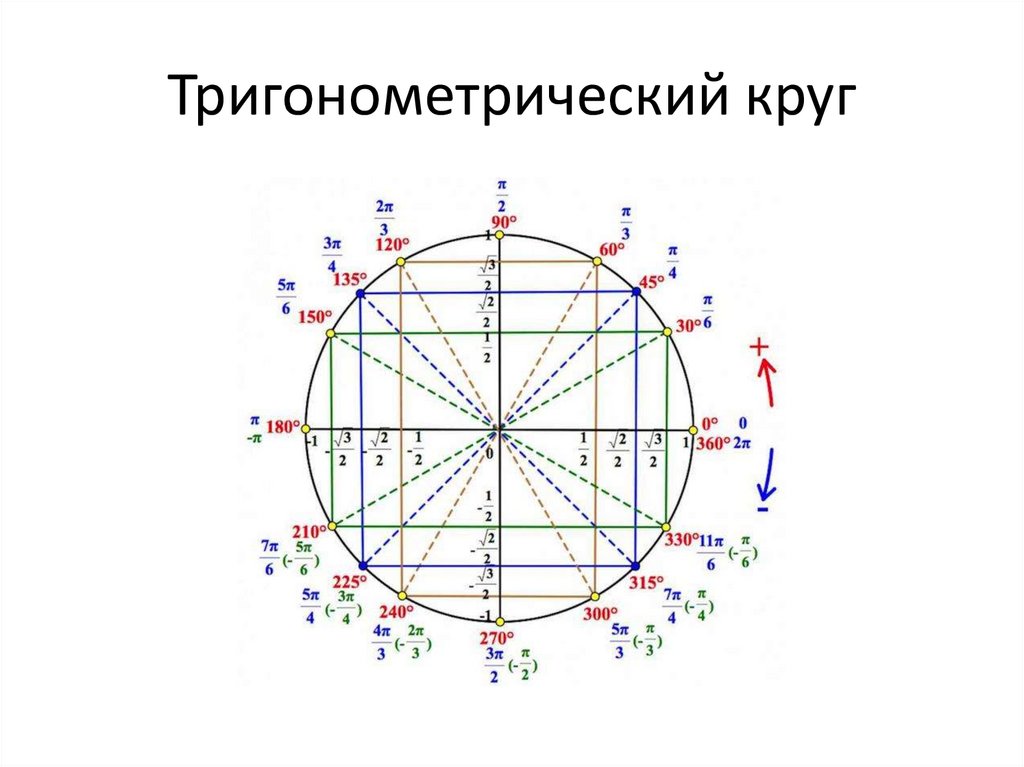
| Тригонометрический круг |
Если бы мне нужно было подобрать символ современного шаманства, то я бы выбрал тригонометрический круг. Почему именно тригонометрический круг? Своей формой он похож на шаманский бубен. Тригонометрический круг разрисован кабалистическими знаками, смысл которых нам могут поведать только шаманы. Свои танцы с бубном шаманы часто исполняют, двигаясь по кругу. По уровню интеллектуального наполнения тригонометрический круг находится где-то между полным идиотизмом и каменным веком. Шаманы с бубнами пляшут свои пляски, Великий Дух Единичной Окружности сообщает шаманам значения тригонометрических функций для определенных углов, шаманы пересказывают эти значения нам.
Если математики будут рассказывать вам, что тригонометрические функции — это координаты точек единичной окружности, не верьте им. Если взять конкретную точку на единичной окружности, то эта точка может принадлежать бесконечному множеству графиков совершенно других функций. Да, если значения тригонометрических функций брать в определенной последовательности и считать их координатами точек в декартовой системе координат, то можно получить окружность с радиусом, равным единице. Но не более того. С таким же успехом в декартовой системе координат можно набросать ваш портрет, но это не будет означать, что ваш портрет — это вы и есть.
Тригонометрический круг показывает значения синусов и косинусов при определенных углах. Для простоты давайте разделим этот круг на составляющие. Сперва уберем с картинки всё, что относится к синусам, и у нас получится тригонометрический круг косинусов.
| Тригонометрический круг косинус |
Теперь мы уберем с первоначальной картинки всё, что относится к косинусам и получим тригонометрический круг синусов.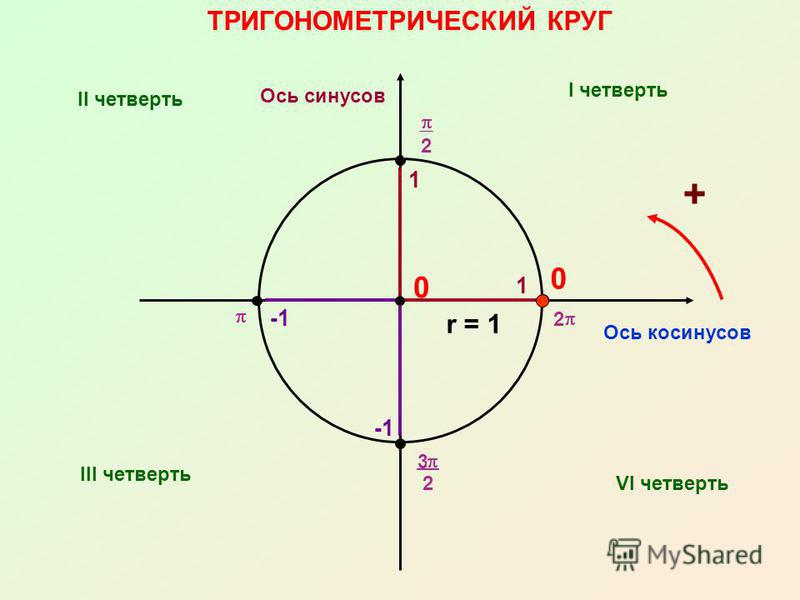
| Тригонометрический круг синус |
Но и это ещё не всё. Те картинки, которые вы здесь видите — это сериал под названием «Значения тригонометрических функций на окружности». Состоит этот сериал из отдельных кадров. Когда учитель математики просит вас показать значение определенной тригонометрической функции для определенного угла, он хочет, чтобы вы выбрали один кадр из всего сериала.
Когда-то, давным-давно, я нарисовал картинки для синусов, но так и не опубликовал их здесь. Наверное, на косинусы сил не хватило и это благородное дело не свершилось. Вот теперь настало время разобрать тригонометрический круг по косточкам на примере значений синуса.
Единица измерения окружности — понимание ее значения в математике
Если вы изучаете тригонометрию или готовитесь к ней, вам необходимо знать единицу измерения окружности. Этот круг служит важным инструментом, используемым для решения угловых синусов, косинусов и тангенсов, в конечном счете, длин треугольников.
Как они работают и какая информация требуется для их использования? В этой статье более подробно описывается единичный круг и его использование.
Единичная окружность обычно рисуется вокруг начала координат (0,0) осей X, Y с радиусом 1. Для прямой линии, проведенной от центральной точки окружности до точки вдоль края окружности, длина этой линии всегда равно 1. Это также означает, что диаметр круга равен 2, потому что диаметр равен удвоенной длине радиуса. Обычно центр единичной окружности — это точка пересечения осей x и y или координаты (0,0).
Это концепция триангуляции, которая позволяет математикам расширять синус, косинус и тангенс по частоте за пределами традиционного прямоугольного треугольника. Как вы помните, синус, косинус и тангенс — это отношение сторон треугольника к заданному углу, обычно называемому тета.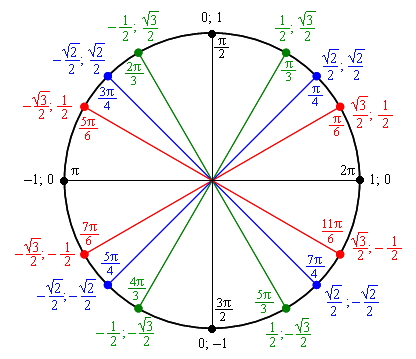
Используйте эти традиционные определения, чтобы ограничить описание углов в прямоугольном треугольнике от 0 до 90 градусов. В некоторых случаях вам нужно знать эти значения для углов больше 90, и единичный круг делает это возможным.
Они названы так потому, что имеют радиус в одну единицу. Его центр находится в начале координат, а все точки окружности удалены от центра на одну единицу. Если вы проведете линию от центра к точке на окружности, длина линии будет равна 1. Затем вы можете добавить линию, чтобы создать прямоугольный треугольник.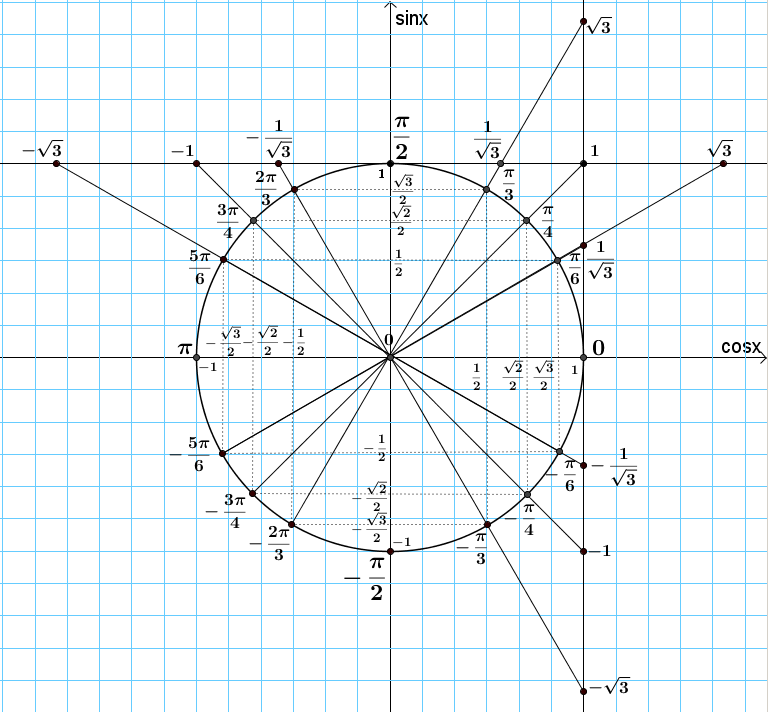
Этот треугольник будет иметь высоту, равную координате y, и длину, аналогичную координате x.
Как упоминалось выше, единичный круг позволяет быстро решить любой порядок радианного синуса, косинуса или тангенса. Знание графика круга особенно полезно, если вам нужно решить определенное значение триггера.
Ознакомьтесь с этими советами, чтобы сэкономить время на вводе чисел в калькулятор.Вот несколько советов, которые следует запомнить. Эти советы упрощают решение математических задач, требующих единичного круга.
Запомнить общие углы и координаты: Чтобы эффективно использовать единичный круг, вам необходимо запомнить наиболее распространенные углы (как в градусах, так и в радианах) и соответствующие им координаты x и y.
Узнайте, что такое негатив и позитив.
Чтобы найти правильное значение для задачи триггера, важно различать положительные и отрицательные координаты x и y.
Как решить тангенс
Наконец, важно знать, как использовать всю эту информацию о триангуляционных окружностях, синусе и косинусе для решения тангенса углов.
Прежде всего, просмотрите наши математические и другие ресурсы для получения дополнительной помощи по этому полезному тригонометрическому инструменту.
Об авторе
Сэм Кан
Сэм — создатель контента и специалист по SEO в Gooroo, репетиторском членстве и платформе онлайн-обучения, которая подбирает студентов к репетиторам, идеально подходящим для них, исходя из их уникальных потребностей в обучении. Gooroo предлагает репетиторство по математике, английскому языку, SAT, кодированию, испанскому языку и многому другому.
- Обучение
- математика
- тригонометрия
- единичный круг
ТРИГОНОМЕТРИЯ ДЛЯ СТАТИКИ. Часть 2
ТРИГОНОМЕТРИЯ ДЛЯ СТАТИКИ
ЧАСТЬ 2:
Единица Окружность и визуализация тригонометрических функций:
Фундаментальное соотношение предполагает, что синус и косинус могут быть
визуализируется с помощью круга единичного радиус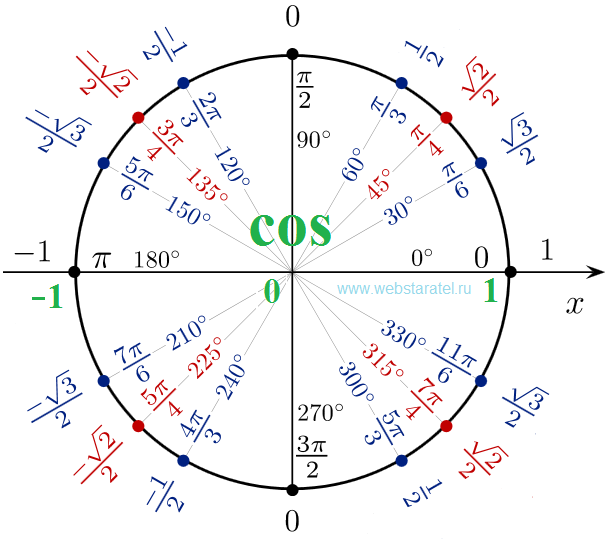а.
Для этого нарисуйте окружность единицы
радиус, как показано на рисунке. Затем нарисуйте радиальную линию от центра
круг к его дуге и образуя угол против часовой стрелки с горизонталью
оси, как показано на рисунке. Проекция этой линии на горизонталь
ось , проекция этой линии на вертикальную ось , и если
радиальная линия продлевается до пересечения с вертикальной линией AB можно получить, как показано на
фигура.
Из единичной окружности сразу видно, что синус и косинус функции могут принимать значения от -1 до 1, а тангенс может иметь любое значение форма для .
Единица обозначает квадранты единичного круга
как показано на рисунке. Видно, что синус имеет положительное значение.
первый и второй квадранты, и отрицательное значение в третьем и четвертом
квадранты. Косинус имеет положительное значение в первой и четвертой четверти и
отрицательное значение во втором и третьем квадрантах. Тангенс имеет положительный
значение в первом и третьем квадрантах и отрицательное значение во втором и
четвертые квадранты.
Единичный круг также может помочь запомнить значения тригонометрического функции. For example, at
At
At
At
Инверсия Тригонометрические функции:
Обратные тригонометрические функции: арксинус, арккосинус и арктангенс . Для конкретного значения z они записываются как: , , . За например, функция предоставляет углы, которые имеют . В подобном таким образом, и соответственно обеспечивают углы, для которых и .
Например, означает угол, для которого синус имеет значение 0,5. Таким образом,
одно решение есть. Аналогично, имеет решение.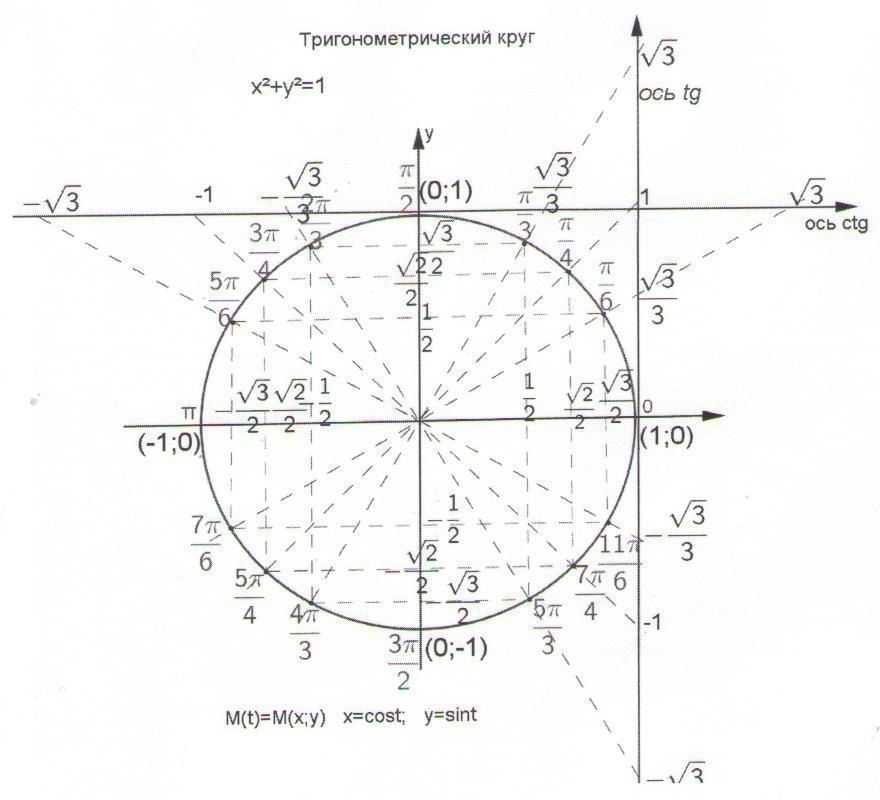
Обратные тригонометрические функции также записываются как sin -1 , cos -1 и тангенс -1 . Например, такое же, как . Это противоречит соглашение, установленное для положительных показателей. Следовательно, хотя
обратные тригонометрические функции кратны ценится. Например, все углы удовлетворяют соотношению и равны: поэтому решения для . Это хорошо видно на единичной окружности. так как проекция радиальных линий на 30 или и 150 или на вертикальная ось одинакова.
На единице.
новая радиальная линия, расположенная поверх исходной радиальной линии. Следовательно
значение любой тригонометрической функции под углом такое же, как и ее значение при . Это
также верно для сложения любого целого числа, кратного 360 или , чтобы
например, для любого целого числа n .