Какой формулой рассчитать мощность резисторов
Резисторы применяются практически во всех электросхемах. Это наиболее простой компонент, в основном, служащий для ограничения или регулирования тока, благодаря наличию сопротивления при его протекании.
Резисторы
Виды резисторов
Внутреннее устройство детали может быть различным, но преимущественно это изолятор цилиндрической формы, с нанесённым на его внешнюю поверхность слоем либо несколькими витками тонкой проволоки, проводящими ток и рассчитанными на заданное значение сопротивления, измеряемое в омах.
Существующие разновидности резисторов:
- Постоянные. Имеют неизменное сопротивление. Применяются, когда определенный участок электроцепи требует установки заданного уровня по току или напряжению. Такие компоненты необходимо рассчитывать и подбирать по параметрам;
- Переменные. Оснащены несколькими выводными контактами. Их сопротивление поддается регулировке, которая может быть плавной и ступенчатой. Пример использования – контроль громкости в аудиоаппаратуре;
- Подстроечные – представляют собой вариант переменных. Разница в том, что регулировка подстроечных резисторов производится очень редко;
- Есть еще резисторы с нелинейными характеристиками – варисторы, терморезисторы, фоторезисторы, сопротивление которых меняется под воздействием освещения, температурных колебаний, механического давления.
Важно! Материалом для изготовления практически всех нелинейных деталей, кроме угольных варисторов, применяемых в стабилизаторах напряжения, являются полупроводники.
Параметры резисторного элемента
- Для резисторов применяется понятие мощности. При прохождении через них электротока происходит выделение тепловой энергии, рассеиваемой в окружающее пространство. Мощность детали является параметром, который показывает, сколько энергии она может выделить в виде тепла, оставаясь работоспособной. Мощность зависит от габаритов детали, поэтому у маленьких зарубежных резисторов ее определяют на глаз, сравнивая с российскими, технические характеристики которых известны;
Важно! Импортные резисторные элементы идентичной мощности имеют несколько меньшие размеры, так как российские производятся с некоторым запасом по этому показателю.
На схеме мощность показана следующим образом.
Условное обозначение мощности
- Второй параметр – сопротивление элемента. На российских деталях типа МЛТ и крупных импортных образцах оба параметра указываются на корпусе (мощность – Вт, сопротивление – Ом, кОм, мОм). Для визуального определения сопротивления миниатюрных импортных элементов применяется система условных обозначений с помощью цветных полосок;
Цветовая маркировка резисторов
- Допуски. Невозможно изготовить деталь с номинальным сопротивлением, в точности соответствующим заявленному значению. Поэтому всегда указываются границы погрешности, называемые допуском. Его величина – 0,5-20%;
- ТКС – коэффициент температуры. Показывает, как варьируется сопротивление при изменении внешней температуры на 1°С. Желательно, но не обязательно подбирать элементы с близким или идентичным значением этого показателя для одной цепи.
Расчет резисторов
Для расчета сопротивления резистора формула применяемая в первую очередь – это закон Ома:
I = U/R.
Исходя из этой формулы, можно вывести выражение для сопротивления:
R = U/I,
где U – разность потенциалов на выводных контактах резистора.
Пример. Необходимо провести зарядку аккумулятора 2,4 В зарядным током 50 мА от автомобильной 12-вольтовой батареи. Прямое соединение сделать нельзя из-за слишком высоких показателей по току и напряжению. Но возможно поставить в схему сопротивление, которое обеспечит нужные параметры.
Предварительно нужно рассчитать резистор:
- Расчет начинается с определения падения напряжения, которое должен обеспечить резисторный элемент:
U = 12-2,4 = 9,6 B
- Протекающий по детали ток – 50 мА. Следовательно, R = 9,6/0,05 = 192 Ом
Теперь можно уже подобрать нужный резистор по одному показателю.
Если рассчитанной детали не нашлось, можно применить соединение из нескольких резисторных элементов, установив их последовательно или параллельно. Расчет сопротивлений при этом имеет свои особенности.
Последовательное соединение
Последовательно соединенные сопротивления складываются:
R = R1+ R2.
Если нужно получить общий результат 200 Ом, и имеется один резистор на 120 Ом, то расчет другого:
R2 = R-R1 = 200-120 = 80 Ом.
Последовательное соединение
Параллельное соединение
При параллельной схеме другая зависимость:
1/R = 1/R1 + 1/R2.
Или преобразованный вариант:
R = (R1 x R2)/ (R1 + R2).
Важно! Параллельное соединение можно использовать, когда в наличии детали с большим сопротивлением, чем требуется, последовательное наоборот.
Пример. Необходимо сопротивление 200 Ом. Имеется деталь R2 на 360 Ом. Какое сопротивление подобрать еще? R1 = R2/(R2/R-1) = 360/(360/200-1) = 450 Ом.
Параллельное соединение
Смешанное соединение
В смешанных схемах присутствуют последовательно-параллельные комбинации. Расчет таких схем сводится к их упрощению путем преобразований. На рисунке ниже представлено, как упростить схему, рассчитывая общий показатель для шести резисторов с учетом их соединения.
Расчет сопротивления в смешанной схеме
Мощность
Определив сопротивление, еще нельзя выбрать деталь. Чтобы обеспечить надежную работу схемы, необходимо найти и другой параметр – мощность. Для этого надо знать, как рассчитать мощность резисторного элемента.
Формулы, по которым можно рассчитать мощность резистора:
Пример. I = 50 мА; R = 200 Ом. Тогда P = I² x R = 0,05² x 200 = 0,5 Вт.
Если не учитывать значение тока, расчет мощности резистора ведется по другой формуле.
Пример. U = 9,6 В, R = 200 Ом. P = U²/R = 9,6²/200 = 0,46 Вт. Получился тот же результат.
Теперь, зная точные параметры рассчитываемого резисторного элемента, подберем радиодеталь.
Важно! При выборе деталей возможно их заменить на резисторы с мощностью, больше рассчитанной, но обратный вариант не подходит.
Это основные формулы для расчета резисторных деталей, на основании которых производится анализ узлов схемы, где главным является определение токов и напряжений, протекающих через конкретный элемент.
Видео
Оцените статью:elquanta.ru
параллельная, последовательная и комбинированная цепь
Решая задачи в области электроники и электрики, приходится сталкиваться с различными вычислениями. Чаще всего они связаны с упрощением электрических схем. Для этого используется метод эквивалента, когда часть цепи заменяется на один элемент с характеристиками, аналогичными ей. Но чтобы это сделать, необходимо знать, как посчитать сопротивление участка цепи и какие виды соединений бывают.
Определение величины
Ток — это упорядоченное движение носителей заряда под действием электрического поля. Способность вещества проводить ток называют электропроводимостью. Чем больше носителей частиц имеет материал, тем большей проводимостью он обладает
- Проводники. Характеризуются хорошей электропроводностью. К ним относят металлы и их сплавы, а также электролиты.
- Диэлектрики. Вещества, практически не проводящие электрический ток. В основном это газы, каучук, минеральные масла, пластмассы.
- Полупроводники. Материалы, обладающие двумя видами проводимости одновременно — дырочной и электронной. Это вещества, имеющие ковалентную связь: кремний, германий, селен.
Величина, обратная электропроводимости, называется электрическим сопротивлением. То есть это физическая величина, препятствующая прохождению тока. Кроме способности любого материала ограничивать количество проходящих через него зарядов, существует специальный радиоэлемент, ограничивающий силу тока — резистор
.Таким образом, существует два понятия сопротивления: радиоэлемент и физическая величина.
Сопротивление радиоэлемента
Термин «резистор» произошёл от латинского слова resisto — «сопротивляемость». Все резисторы делятся на постоянные и переменные. Последние позволяют изменять своё сопротивление. На схемах и в литературе такая радиодеталь подписывается латинской буквой R. Единицей измерения считается Ом. Графически резистор обозначается в виде прямоугольника с двумя выводами от середины краёв. Кроме номинального сопротивления, он характеризуется рассеиваемой мощностью и классом точности.
По своей сути это пассивный радиоэлемент, преобразующий часть электрической энергии в тепловую. Тем самым он ограничивает ток, линейно преобразовывая его силу в напряжение и наоборот. Главный параметр, описывающий сопротивление, находится согласно закону Ома для участка цепи по следующей формуле: R = U/I, где:
- R — электрическое сопротивление, Ом.
- U — разность потенциалов приложенная к элементу, В.
- I — сила тока, преходящая через резистор, А.
Но тут следует отметить, что этот закон справедлив только для резистивных цепей. То есть для тех, при расчёте которых ёмкостью и индуктивностью пренебрегают. Если же эту формулу применить к реактивным элементам, то для катушки индуктивности сопротивление будет равным нулю, а для конденсатора — бесконечным. Но это верно для постоянного тока и напряжения.
При переменных величинах напряжение на индуктивности не будет равно нулю, как и ток, проходящий через конденсатор. Такие случаи сопротивлением уже не описываются, поскольку оно предполагает постоянные значения тока и напряжения.
Удельный параметр вещества
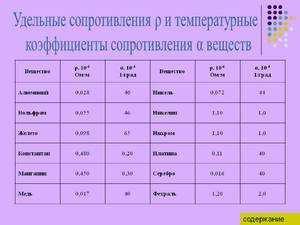Чтобы различать понятие и элемент, было введено название удельное электрическое сопротивление. Обозначается оно греческим символом ρ. В Международной системе единиц эта величина измеряется в Омах, умноженных на метр. Зависит она исключительно от свойства материала.
Для расчёта электрического сопротивления однородного вещества используется формула: R = ρ* l/S, где:
- l — длина проводника, м;
- S — площадь поперечного сечения, м2.
Поэтому в физическом смысле удельное сопротивление материала — это величина, обратная удельной проводимости, представляющая собой сопротивление однородного проводника единичной длины и площади поперечного сечения. А значит, она численно равна импедансу участка электрической цепи, выполненному из вещества длиною один метр и площадью поперечного сечения один метр квадратный.
Для каждого вещества удельное сопротивление известно и является справочной величиной. Например, для меди — 0,01724 Ом*мм2/м, алюминия — 0,0262 Ом*мм
Эквивалентная схема
При расчётах сопротивления электрических цепей широко используется понятие «эквивалентная схема замещения». Её назначение — упростить сложную схему до вида, состоящую из минимума элементов. Иными словами, каждый сложный радиоэлемент можно представить в виде соответствующих ему эквивалентных простых радиодеталей: резистор, ёмкость, индуктивность, источники тока и напряжения. Это позволяет не только математически описать любую схему, но и рассчитать её параметры.
При этом обычно радиоэлементы идеализируются, то есть их паразитные параметры не учитываются. Так и для подсчёта сопротивления цепи каждый компонент представляется как идеальный резистор. После чего схема перерисовывается, и в результате на ней остаются только подключённые разными способами друг к другу резисторы.
Существует два вида подключения:
- последовательное;
- параллельное.
Основными элементами электрической цепи являются узел, ветвь и контур. Узел — это место соединения двух и более ветвей. Ветвь — это последовательный участок цепи между двумя узлами, а контур — любая замкнутая цепь. Последовательное соединение состоит из элементов, при котором все компоненты цепи связаны так, что участок цепи, образованный из них, не имеет ни одного узла. А при параллельном соединении все компоненты электрической цепи контактируют между собой в двух узлах. При этом эти узлы напрямую не связаны.
Расчёт импеданса
Методы вычисления общего сопротивления зависят от способа соединения резисторов. При расчётах общего импеданса за основу берутся законы Кирхгофа.
Так, первый его закон гласит: сумма токов в узле равна нулю. Или, если его перефразировать, значение тока, втекающего в узел, равно сумме токов, вытекающих из этого узла. Второй закон связан с электродвижущей силой, и его формулировка звучит так: сумма разности потенциалов в контуре равна сумме падений разности потенциалов на каждом резисторе в цепи.
При последовательном соединении все элементы располагаются друг за другом без ответвлений. Так как согласно правилу Кирхгофа в любом месте ветви сила тока одинаковая I = I1 = In, то падение напряжения на первом элементе: U1 = I*R1, а на n: Un = I*Rn, где:
- In — сила тока, протекающая через резистор, А.
- Un — значение падения напряжения на резисторе, В.
- Rn — величина сопротивления элемента, Ом.
Общая разность потенциалов равна сумме всех напряжений, поэтому можно записать: U = U1+…+Un = I*(R1+…+Rn) = IRo.
В результате формула для расчёта сопротивления цепи в этом случае будет выглядеть следующим образом:
Ro = R1 +…+ Rn, где:
- Ro — общее сопротивление ветви.
- R1 — значение импеданса первого элемента.
- Rn — величина сопротивления n-го элемента.
Если цепь параллельная то это значит, что на этом участке несколько ветвей расходятся, а после опять соединяются. Получается, что сила тока в каждой ветви будет своя, а величина напряжения одинакова. Поэтому Uo = U1=…= Un, а Io = I1+…+In. Используя закон Ома, можно записать:
Uo/Ro = U1/R1+…+Un/Rn, или
1/Ro = 1/R1+…1/Rn.
В итоге эквивалентное сопротивление при параллельном соединении рассчитывается как произведение значений резисторов, делённое на сумму их произведений. Для двух резисторов формулу для нахождения общего сопротивления можно записать в виде: Ro = (R1*R2) / (R1+R2).
Браузерный онлайн-калькулятор
Если элементов в цепи немного, то, упрощая схему, довольно легко посчитать, используя формулы для параллельного и последовательного включения резисторов, общий импеданс цепи. Но если в схеме много элементов, да ещё она такая, что содержит и то, и другое соединение (комбинированная), проще воспользоваться браузерными онлайн-калькуляторами.
В их основе используются всё те же формулы для расчёта эквивалентного резистора, но все вычисления происходят автоматически. Существует огромное количество предложений таких калькуляторов. Но при этом все они работают одинаково. Онлайн-расчёт представляет собой программный код, в котором заложен алгоритм вычисления. Потребителю необходимо только в специальных ячейках указать, какой вид соединения используется, сколько элементов в контуре и сопротивления резисторов. Далее надо нажать кнопку «Рассчитать» и через считанные секунды получить ответ.
Необходимо отметить, что, если даже это в программе не указано, все значения вводятся только в Международной системе единиц, сила тока — ампер, напряжение — вольт, сопротивление — Ом. Тогда и ответ получится в Омах.
Бонусом является и то, что многие такие программы сразу рассчитывают и мощность элемента. Для этого используется формула: P = U2/Ro = I2*Ro, Вт.
Практическое применение
Чаще всего на практике расчёт общего сопротивления цепи выполняют для того, чтобы узнать потребляемую мощность той или иной схемы. При этом, зная общее сопротивление, можно найти и такие важные параметры цепи, как ток и напряжение. Поэтому и рисуют эквивалентную схему электрической цепи. Простые цепи состоят только из последовательных или параллельных участков, но чаще встречаются комбинированные соединения.
Перед тем как приступить к расчёту эквивалентного сопротивления, вся электрическая цепь разделяется на простые контуры. Как только импеданс каждого такого контура будет подсчитан, схема перерисовывается, но вместо контуров рисуется уже резистор. Затем всё повторяется, и это происходит до тех пор, пока не останется один элемент.
Простое соединение
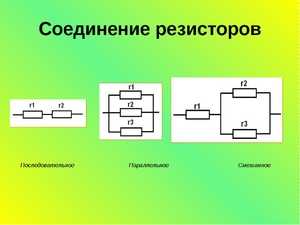Пусть будет дана схема, состоящая из трёх резисторов, включённых последовательно. При этом сопротивление R1и R2 одинаковое и равно 57 Ом, а сопротивление R3 составляет один килоОм. Для расчёта общего сопротивления цепи сначала понадобится привести значение R3 согласно Международной системе единиц.
R3 = 1 кОм = 1000 Ом.
Так как соединение последовательное, используется формула: Ro = R1+R2+R3. Подставив известные значения, рассчитывается эквивалентное значение: Ro = 57+57+1000 = 1114 Ом.
Если же те же самые резисторы будут расположены параллельно друг другу, то для расчёта общего сопротивления уже используется другое выражение:
1/Ro = 1/R1 + 1/R2 +1/R3.
Ro = R1*R2*R3 / (R1*R2+R2*R3+R1*R3).
Подставив исходные данные в эту формулу, получим:
Ro = 57*57*1000/ (57*57 +57*1000+ 57*1000) = 3249000/117249 = 27,7 Ом.
Комбинированный контур
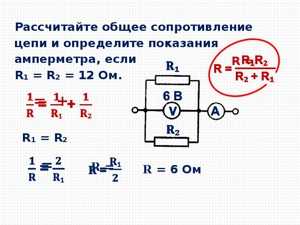Необходимо вычислить мощность и эквивалентное сопротивление смешанной цепи, состоящей из четырёх резисторов. Резистор R1 =R2 =5 Ом, R3= 10 Ом, R4 =3 Ом. На схему подаётся питание пять вольт.
Первоначально понадобится упростить схему. Сопротивления R3 и R4 включены относительно друг друга параллельно. Поэтому находится их объединённое сопротивление:
Rp = (R3*R4)/(R3+R4).
Rp = (10*3)/ (10+3) = 2,3 Ом.
Теперь схему можно перерисовать в виде трёх последовательно включённых резисторов и найти общее сопротивление путём сложения их величин:
Ro = R1+R2+Rp = 5+5+2,3 = 12,3 Ом.
Зная эквивалентное сопротивление, используя закон Ома, несложно вычислить силу тока в цепи и мощность эквивалентного резистора:
I = U/R = 5/2,3 = 2,2 A.
P = I*U = 2,2*5= 11 Вт.
Таким образом, путём постепенного упрощения схемы можно свести цепь из последовательно и параллельно соединённых резисторов к одному элементу. А затем рассчитать его сопротивление и требуемую мощность.
220v.guru
Полное сопротивление | Формулы и расчеты онлайн
В любой цепи переменного тока наряду с чисто реактивным сопротивлением присутствует омическое (активное) сопротивление, которое нужно учитывать при определении полного сопротивления.
Если
| Z | полное сопротивление, | Ом |
|---|---|---|
| R | омическое (активное) сопротивление, | Ом |
| X | реактивное сопротивление, | Ом |
| Y = 1/Z | полная проводимость, | сименс |
| G | активная проводимость, | сименс |
| B | реактивная проводимость, | сименс |
| U | полное напряжение (эффективное значение), | Вольт |
| I | полный ток (эффективное значение), | Ампер |
то имеем:
Полное сопротивление при последовательном соединении R и X
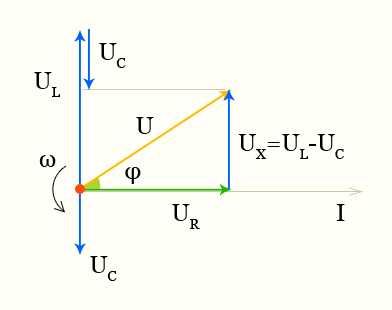
полное сопротивление векторная диаграмма тока и напряжений
При последовательном соединении активное и реактивное сопротивления складываются геометрически
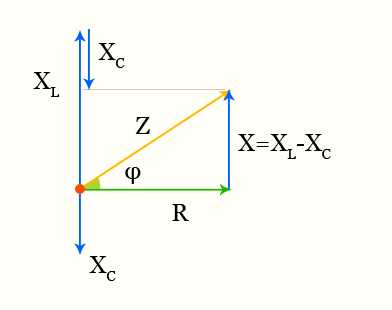
полное сопротивление векторная диаграмма
\[ Z = \sqrt{R^{2} + X^{2}} \]
и
\[ U = \sqrt{U^{2}_{R} + U^{2}_{X}} = IZ \]
Полное сопротивление при параллельном соединение R и X
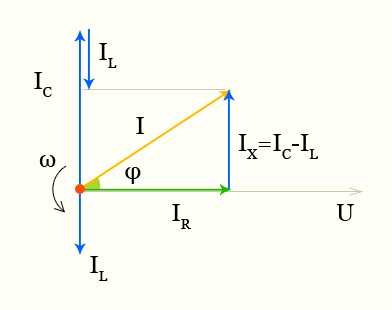
полное сопротивление векторная диаграмма тока и напряжений
При параллельном соединении активная и реактивная проводимости складываются геометрически
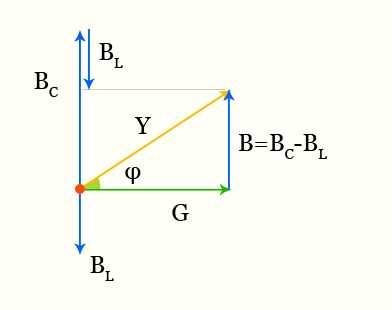
полное сопротивление векторная диаграмма
\[ Y = \sqrt{G^{2} + B^{2}} \]
и
\[ I = \sqrt{I^{2}_{R} + I^{2}_{X}} = UY \]
В помощь студенту
Полное сопротивление |
стр. 689 |
|---|
www.fxyz.ru
Емкостное сопротивление | Формулы и расчеты онлайн
Конденсатор емкостью C имеет в цепи постоянного тока бесконечно большое сопротивление. Если же приложить к конденсатору переменное напряжение, то он будет периодически перезаряжаться, и в цепи потечет ток. Напряжение на конденсаторе достигает максимального значения в те моменты, когда ток равен нулю.
Если R = 0, то напряжение на конденсаторе совпадает с приложенным напряжением и u = q/C. Мгновенное значение тока определяется выражением:
\[ i = \frac{dq}{dt} = C \frac{du}{dt} = C \frac{d}{dt}(U_{m} \sin(ωt)) \]
Отсюда следует
\[ i = ωCU_{m} \cos(ωt) = ωCU_{m} \sin(ωt + \frac{π}{2}) \]
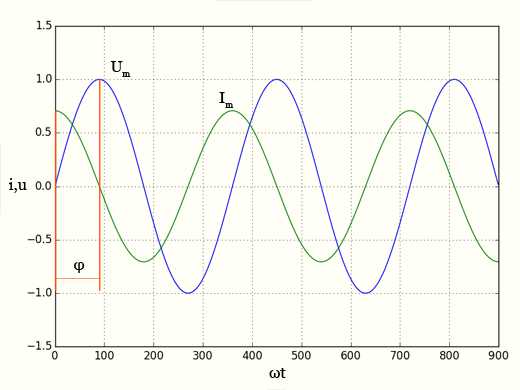
Емкостное сопротивление — график тока и напряжения
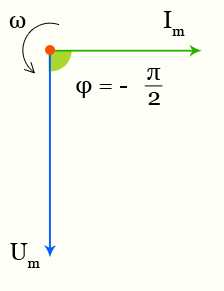
Между напряжением и током имеется разность фаз —π/2.
В чисто емкостной цепи переменного тока ток опережает напряжение на π/2 (или Т/4).
В соответствии с приведенным выше уравнением амплитуда тока Im = ωCUm. Сравнение с законом Ома U = RI показывает, что величина 1/ωС играет роль сопротивления.
Цепь переменного тока, содержащая емкость C, обладает сопротивлением переменному току; оно называется емкостным сопротивлением ХC.
Единица СИ емкостного сопротивления: [XC] = Ом.
Если
| ХC | емкостное сопротивление цепи переменного тока, | Ом |
|---|---|---|
| ω = 2πf | круговая частота переменного тока, | радиан/Секунда |
| C | емкость, | Фарад |
то
\[ X_{C} = \frac{1}{ωC} \]
$ $Ток в цепи, обладающей только емкостным сопротивлением, определяется выражением
\[ I = UωC \]
Вычислить, найти емкостное сопротивление
В помощь студенту
Емкостное сопротивление |
стр. 687 |
|---|
www.fxyz.ru
Как правильно расчитать сопротивление резистора ?
Расчет показан на примере светодиода и источника питания в 5 вольт. Такая связка часто встречается тем, кто занимается «украшательством» компьютеров. Наш светодиод «работает» при Напряжении 2,5 вольта и потребляет при этом 20mA (20 милиампер) . Нам известно, что напряжение на концах цепи равно сумме напряжений на всех её участках. Зная это мы можем узнать какое напряжение будет на нашем резисторе. Отнимаем от 5 вольт 2,5 которые идут на светодиод и получаем 2,5. Также нам известно, что сила тока на всех участках цепи одинаковая. Значит на нашем резисторе будет столькоже ампер, сколько и на светодиоде, а именно 20mA=0,02A/ Теперь нам известны 2 параметра резистора. Вычислить 3й нам поможет закон ома. P.S. И не забудь проголосовать за лучший ответ через три часа.. . Закон ома: I=U/R Отсюда следует, что R= U/I. По русски это звучит так: Сопротивление = Напряжение деленное на Силу тока. Подставим в формулу известные нам значения : R= 2,5В/0,02 = 125Ом. Если резистора с таким сопротивлением не существует, нужно взять резистор с сопротивлением немного больше (но не меньше) . Так будет выглядеть схема: <img src=»//otvet.imgsmail.ru/download/99b25fe0b6f2c319e810d42f4816dbc6_i-11.jpg» >
Откуда ты взял такую величину силы тока? Ведь ток надо брать для участка цепи. Надо 5в поделить на ток потребляемый светодиодом (это микроамперы). Только так всё получится.
Ну во-первых: ток в 10 А — очень большая величина для диода Во-вторых: ток для диода измеряеться не в микроамперах, а в миллиамперах. Попоробуй расчитать: I = 10 mА — 20 mA U = 1.35 — 5.5 V думаю получиться ))))
«Лишнее напряжение, вольт, делить на ток светодиода, миллиампер, получите сопротивление, килоом.
touch.otvet.mail.ru
Полное сопротивление цепи переменного тока
В предыдущих статьях мы узнали, что всякое сопротивление, поглощающее энергию, называется активным, а сопротивление, не поглощающее энергии, безваттным или реактивным. Кроме того, мы установили, что реактивные сопротивления делятся на два вида — индуктивные и емкостные.
Однако существуют цепи, где сопротивление не является чисто активным или чисто реактивным. То есть цепи, где вместе с активным сопротивлением включены в цепь, как емкости, так и индуктивности.
Введем понятие полного сопротивления цепи переменному току — Z, которое соответствует векторной сумме всех сопротивлений цепи (активных, емкостных и индуктивных). Понятие полного сопротивления цепи нам необходимо для более полного понимания закона Ома для переменного тока
На рисунке 1 представлены варианты электрических цепей и их классификация в зависимости от того какие элементы (активные или реактивные) включены в цепь.
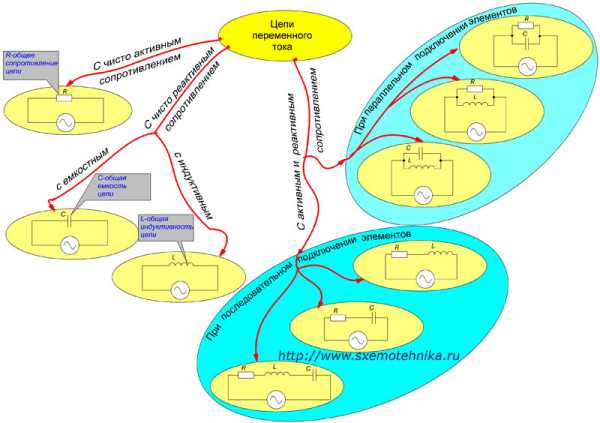
Рисунок 1. Классификация цепей переменного тока.
Полное сопротивление цепи с чисто активными элементами соответствует сумме активных сопротивлений цепи и рассматривалось нами ранее. О чисто емкостном и индуктивном сопротивлении цепи мы тоже с вами говорили, и оно зависит соответственно от общей емкости и индуктивности цепи.
Рассмотрим более сложные варианты цепи, где последовательно с активным сопротивлением в цепь включено индуктивное и реактивное сопротивление.
Полное сопротивление цепи при последовательном соединении активного и реактивного сопротивления.
В любом сечении цепи, изображенной на рисунке 2,а, мгновенные значения тока должны быть одинаковыми, так как в противном случае наблюдались бы скопления и разрежения электронов в каких-либо точках цепи. Иными словами, фазы тока по всей длине цепи должны быть одинаковыми. Кроме того, мы знаем, что фаза напряжения на индуктивном сопротивлении опережает фазу тока на 90°, а фаза напряжения на активном сопротивлении совпадает с фазой тока (рисунок 2,б). Отсюда следует, что радиус-вектор напряжения UL (напряжение на индуктивном сопротивлении) и напряжения UR (напряжение на активном сопротивлении) сдвинуты друг относительно друга на угол в 90°.
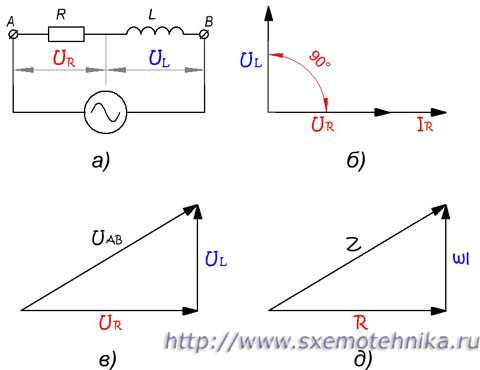
Рисунок 2. Полное сопротивление цепи с активным сопротивлением и индуктивностью. а) — схема цепи; б) — сдвиг фаз тока и напряжения; в) — треугольник напряжений; д) — треугольник сопротивлений.
Для получения радиуса-вектора результирующего напряжения на зажимах А и В (рис.2,а) мы произведем геометрическое сложение радиусов-векторов UL и UR. Такое сложение выполнено на рис. 2,в, из которого видно, что результирующий вектор UAB является гипотенузой прямоугольного треугольника.
Из геометрии известно, что квадрат гипотенузы равен сумме квадратов катетов.
По закону Ома напряжение должно равняться силе тока, умноженной на сопротивление.
Так как сила тока во всех точках цепи одинакова, то квадрат полного сопротивления цепи (Z2) будет также равен сумме квадратов активного и индуктивного сопротивлений, т. е.
(1)
Извлекая квадратный корень из обеих частей этого равенства, получим,
(2)
Таким образом, полное сопротивление цепи, изображенной на рис 2,а, равно корню квадратному из суммы квадратов активного и индуктивного сопротивлений
Полное сопротивление можно находить не только путем вычисления, но и путем построения треугольника сопротивлений, аналогичного треугольнику напряжений (рис 2,д), т. е. полное сопротивление цепи переменному току может быть получено путем измерения гипотенузы, прямоугольного треугольника, катетами которого являются активное и реактивное сопротивления. Разумеется, измерения катетов и гипотенузы должны производиться в одном и том же масштабе. Так, например, если мы условились, что 1 см длины катетов соответствует 1 ом, то число омов полного сопротивления будет равно числу сантиметров, укладывающихся на гипотенузе.
Полное сопротивление цепи, изображенной на рис.2,а, не является ни чисто активным, ни чисто реактивным; оно содержит в себе оба эти вида сопротивлений. Поэтому угол сдвига фаз тока и напряжения в этой цепи будет отличаться и от 0° и от 90°, то есть он будет больше 0°, но меньше 90°. К которому из этих двух значений он будет более близок, будет зависеть от того, какое из этих сопротивлений имеет преобладающее значение в цепи. Если индуктивное сопротивление будет больше активного, то угол сдвига фаз будет более близок к 90°, и наоборот, если преобладающим будет активное сопротивление, то угол сдвига фаз будет более близок к 0°.
В цепи, изображенной на рис 3,а, соединены последовательно активное и емкостное сопротивления. Полное сопротивление такой цепи можно определить при помощи треугольника сопротивлений так же, как мы определяли выше полное сопротивление активно-индуктивной цепи.
Рисунок 3. Полное сопротивление цепи с активным сопротивлением и емкостью. а) — схема цепи; б) — треугольник сопротивлений.
Разница между обоими случаями состоит лишь в том, что треугольник сопротивлений для активно-емкостной цепи будет повернут в другую сторону (рис 3,б) вследствие того, что ток в емкостной цепи не отстает от напряжения, а опережает его.
Для данного случая:
(3)
В общем случае, когда цепь содержит все три вида сопротивлений (рис. 4,а), сначала определяется реактивное сопротивление этой цепи, а затем уже полное сопротивление цепи.
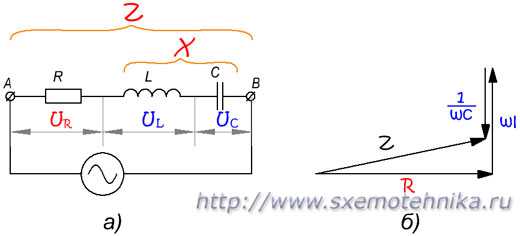
Рисунок 4. Полное сопротивление цепи содержащей R, L и C. а) — схема цепи; б) — треугольник сопротивлений.
Реактивное сопротивление этой цепи состоит из индуктивного и емкостного сопротивлений. Так как эти два вида реактивного сопротивления противоположны друг другу по своему характеру, то общее реактивное сопротивление цепи будет равно их разности, т. е.
(4)
Общее реактивное сопротивление цепи может иметь индуктивный или емкостный характер, в зависимости от того, какое из этих двух сопротивлений (XL или XC преобладает).
После того как мы по формуле (4) определили общее реактивное сопротивление цепи, определение полного сопротивления не представит затруднений. Полное сопротивление будет равно корню квадратному из суммы квадратов активного и реактивного сопротивлений, т. е.
(5)
Или
(6)
Способ построения треугольника сопротивлений для этого случая изображен на рис. 4 б.
Полное сопротивление цепи при параллельном соединении активного и реактивного сопротивления.
Полное сопротивление цепи при параллельном соединении активного и реактивного элемента.
Для того чтобы вычислить полное сопротивление цепи, составленной из активного и индуктивного сопротивлений, соединенных между собой параллельно(рис. 5,а), нужно сначала вычислить проводимость каждой из параллельных ветвей, потом определить полную проводимость всей цепи между точками А и В и затем вычислить полное сопротивление цепи между этими точками.
Рисунок 5. Полное сопротивление цепи при параллельном соединении активного и реактивных элементов. а) — параллельное соединение R и L; б) — параллельное соединение R и C.
Проводимость активной ветви, как известно, равна 1/R, аналогично проводимость индуктивной ветви равна 1/ωL , а полная проводимость равна 1/Z
Полная проводимость равна корню квадратному из суммы квадратов активной и реактивной проводимости, т. е.
(7)
Приводя к общему знаменателю подкоренное выражение, получим:
(8)
откуда:
(9)
Формула (9) служит для вычисления полного сопротивления цепи, изображенной на рис. 5а.
Нахождение полного сопротивления для этого случая может быть произведено и геометрическим путем. Для этого нужно построить в соответствующем масштабе треугольник сопротивлений, и затем произведение длин катетов разделить на длину гипотенузы. Полученный результат и будет соответствовать полному сопротивлению.
Аналогично случаю, рассмотренному выше, полное сопротивление при параллельном соединении R и С (рис 5б) будет равно:
(10)
Полное сопротивление может быть найдено также и в этом случае путем построения треугольника сопротивлений.
В радиотехнике наиболее часто встречается случай па¬раллельного соединения индуктивности и емкости, например колебательный контур для настройки приемников и передатчиков. Так как катушка индуктивности всегда обладает кроме индуктивного еще и активным сопротивлением, то эквивалентная (равноценная) схема колебательного контура будет содержать в индуктивной ветви активное сопротивление (рис 7).
Рисунок 6. Эквивалентная схема колебательного контура.
Формула полного сопротивления для этого случая будет:
(11)
Так как обычно активное сопротивление катушки (R) бывает очень мало по сравнению с ее индуктивным сопротивлением (ωL), то мы имеем право формулу (11) переписать в следующем виде:
(12)
В колебательном контуре обычно подбирают величины L и С таким образом, чтобы индуктивное сопротивление равнялось емкостному, т. е. чтобы соблюдалось условие
(13)
При соблюдении этого условия полное сопротивление колебательного контура будет равно:
(14)
где L—индуктивность катушки в Гн;
С—емкость конденсатора в Ф;
R—активное сопротивление катушки в Ом.
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Похожие материалы:
Добавить комментарий
www.sxemotehnika.ru
Расчёт сопротивления проводников и реостаты: формулы
Электрическое сопротивление проводника происходит из-за взаимодействия электрона с ионами кристаллической решетки.
Сопротивление проводника зависит от:
- — его длины,
- — площади поперечного сечения
- — от вещества из которого он изготовлен,
а также сопротивление прямо пропорционально длине проводника и обратно пропорционально площади его поперечного сечения и зависит от вещества проводника.
Чтобы посчитать зависимость сопротивления от вещества, из которого изготовляют проводник, надо вычислить его удельное сопротивление.
Удельное сопротивление — физическая величина которая определяет сопротивление проводника из данного вещества длиной 1м, и площадью поперечного сечения 1м^2.
- Удельное сопротивление обозначается буквой — p.
- Длина — l.
- Площадь поперечного сечения — S.
- Сопротивление проводника обозначим буквой R.
В итоге мы получим формулу:
R = p*l/S
Получим еще несколько разновидностей формул:
l = R*S/p ; S = p*l/R ; p = R*S/l
Единицей сопротивления является 1 Ом, следовательно единица удельного сопротивления будет:
1 Ом*1м^2/1м или 1 Ом*м, следуя из формулы p = R*S/l
Также площадь поперечного сечения можно выражать в квадратных миллиметрах, тогда мы получим такую формулу:
1 Ом*мм^2/м
Наименьшим удельным сопротивлением обладает серебро (0,016) и медь (0,017), следовательно они лучше проводят электричество.
Эбонит(10^20) и фарфор(10^19) имеют очень большое удельное сопротивление и почти не проводят электрический ток, их используют для изоляторов.
Реостаты
Реостат — прибор, который используется для регулирования силы тока в цепи.
Самый простой реостат — проволока с большим удельным сопротивлением , такая как никелиновая или нихромовая.
Виды реостатов:
Ползунковый реостат — еще один вид реостатов , в котором стальная проволока намотана на керамический цилиндр.Проволока покрыта тонким слоем окалины , которая не проводит электрический ток , поэтому ее витки изолированы друг от друга.Над обмоткой — металлический стержень по которому перемещается ползунок .
Он прижат к виткам обмотки.От трения ползунка о витки слой окалины стирается и электрический ток в цепи проходит от витков проволоки к ползунку, потом в стержень.Когда реостат подключили в цепь , можно передвигать ползунок , таким образом увеличивать или уменьшать сопротивление реостата.
Жидкостный реостат — представляет бак с электролитом, в который погружаются металлические пластины.
Проволочный реостат — cостоит из проволоки из материала в котором высокое удельное сопротивление, натянутый на раму.
Нельзя превышать силу тока реостата, потому что обмотка реостата может перегореть.
Реостат мы часто применяем в повседневной жизни, например, регулируя громкость телевизора и радио, увеличивая и уменьшая скорость езды на машине.
Нужна помощь в учебе?
Предыдущая тема: Закон Ома для участка цепи: формулировка и формула, применение
Следующая тема:   Последовательное и параллельное соединение проводников
Все неприличные комментарии будут удаляться.
www.nado5.ru