Определение синуса. Основные тригонометрические функции
Тригонометрия является важной частью математики, знания которой широко используются в астрономии и при ориентировании на местности. В данной статье рассматривается определение синуса, косинуса, тангенса и котангенса как основных тригонометрических функций.
Что такое тригонометрия?

Это наука, которая изучает количественные свойства треугольников, о чем говорит ее название. Процесс изучения этих простых плоских фигур осуществляется с использованием так называемых тригонометрических функций.
Еще в древнем Вавилоне и Египте люди сталкивались с задачами, требующими знания соотношения между сторонами и углами треугольника (например, при строительстве египетских пирамид). Однако до нашего времени не дошли точные свидетельства того, что вавилоняне и египтяне располагали необходимой математической теорией для решения задач подобного рода.

Развитие тригонометрия получила на заре нашей эры, благодаря достижениям древнегреческих ученых. Первые таблицы тригонометрических функций были составлены лишь во второй половине XV века.
Прямоугольный треугольник
Перед тем как давать определение синусу и другим тригонометрическим функциям, необходимо пояснить, что представляет собой прямоугольный треугольник. У него один из углов равен 90o.
Зная, что сумма углов в этой фигуре равна 180o, можно с уверенностью сказать, что два других угла в сумме составят 90o. При этом каждый из них будет меньше, чем прямой угол.
Стороны прямоугольного треугольника имеют названия. Отрезок, лежащий против прямого угла, называется гипотенузой. Две другие стороны — это катеты.
Введение тригонометрических функций
Теперь можно дать определение синусу и косинусу угла, а также тангенсу и котангенсу. Для этого построим окружность единичного радиуса. Ниже на рисунке представлен треугольник ABC, у которого отрезок AB = 1 — является гипотенузой (радиус окружности), AC и CB — катеты.
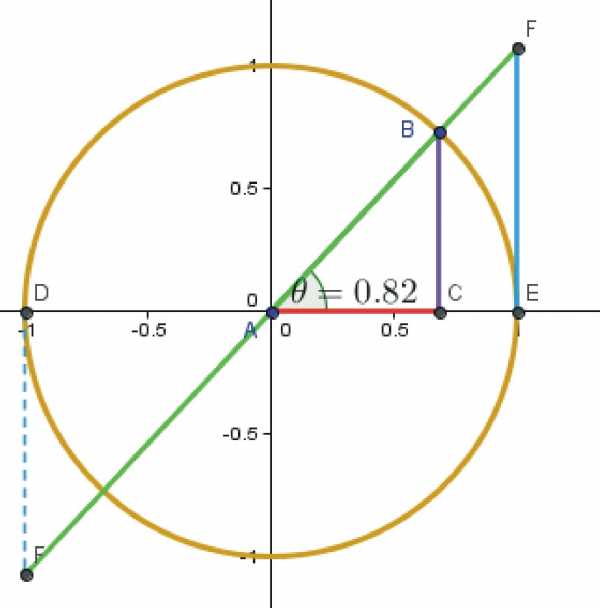
Давая определение синуса угла, следует сказать, что он равен отношению отрезка BC к отрезку AB. Записывается это следующим образом: sin(θ) = BC/AB. Поскольку AB = 1, то sin(θ) = BC. Иными словами, под синусом угла прямоугольного треугольника понимают отношение катета, лежащего напротив этого угла, к гипотенузе.
Теперь определение косинуса угла. Это отношение катета, прилежащего к рассматриваемому углу, к гипотенузе. Для рисунка выше имеем: cos(θ) = AC/AB = AC.
Тангенс угла — это тригонометрическая функция, которая определяется отношением катета, противолежащего к данному углу, к прилежащему катету. То есть tg(θ) = BC/AC.
Наконец, котангенс угла — это отношение прилежащего катета к противолежащему, то есть ctg(θ) = AC/BC.
Свойства синуса и других тригонометрических функций
Из введенных определений синуса, косинуса угла и других функций следуют несколько важных выводов об их свойствах:
- Во-первых, тригонометрические функции являются безразмерными величинами.
- Во-вторых, их значение не зависит от размеров треугольника. Последний факт легко доказать, если обратиться к тому же рисунку вверху и рассмотреть треугольники ABC и AFE. Эти треугольники являются подобными, так как имеют общий угол в вершине A, это означает, что выполняется следующее равенство: BC/AB = FE/AF = sin(θ). Аналогичные равенства можно привести для остальных тригонометрических функций.
- В-третьих, любая тригонометрическая функция может быть выражена с использованием максимум двух других. Это утверждение верно, поскольку все три стороны треугольника фигурируют в выражениях для двух тригонометрических функций. Например, tg(θ) = sin(θ)/cos(θ).
Периодичность функций
Это свойство специально было вынесено в отдельный пункт статьи, поскольку его рассмотрение заслуживает отдельного внимания.
Если вращать отрезок AB (см. рис. выше) против часовой стрелки, то точка B пробежит всю окружность единичного радиуса. Как при этом будут меняться тригонометрические функции?
Рассмотрим синус. Согласно определению синуса угла, когда θ = 0, то BC = 0, то есть sin(0o) = 0. По мере возрастания угла θ, увеличивается длина отрезка BC. При этом длина AB остается неизменной. Это означает, что sin(θ) постоянно увеличивается. Когда угол θ = 90o, то BC=AB и sin(90o) = 1.
Дальнейшее вращение AB против часовой стрелки приводит к уменьшению значения синуса до нуля при угле 180o (sin(180o)=0).
Для углов со значениями лежащими между 180o и 270o синус снова увеличивается по модулю, но уменьшается в абсолютных значениях, поскольку отрезок BC будет лежать в отрицательной области оси ординат. В итоге sin(270o) = -1.
Наконец, в 4-м квадранте окружности, когда угол меняется от 270o до 360o, абсолютное значение синуса увеличивается, но модуль его уменьшается до тех пор, пока при 360o он снова не станет равным нулю (sin(360o) = sin(0o) = 0).
Из проведенного анализа следует, что синус является периодической функцией, которая повторяет свои значения каждые 360o. В тригонометрии обычно пользуются не градусами, а радианами. Напомним, что 2*pi радиан равно 360o, где pi = 3,14 — число пи. График функции sin(x) приведен на главном фото статьи.
Если провести аналогичные рассуждения, то можно показать, что косинус — это периодическая функция с таким же периодом, как и для синуса, то есть T = 2pi. Тангенс и котангенс тоже являются периодическими, только для них T =pi.
Таблица значений тригонометрических функций
Эта таблица включает в себя данные о значениях синуса, косинуса, тангенса и котангенса для набора углов. Школьников заставляют учить эти значения наизусть.
В настоящее время, благодаря развитию информатики, все языки программирования и калькуляторы снабжены соответствующими библиотеками, которые позволяют быстро рассчитать значения любой тригонометрической функции за доли секунды.
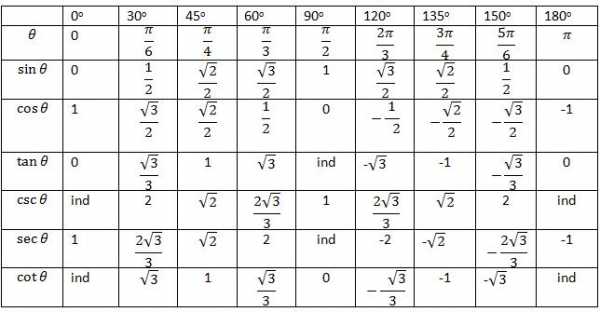
Ниже приводится таблица, в которой приведены значения для всех названных функций набора углов. Которые представлены, как в градусах, так и в радианах. Буквы «ind» означают, что функция для этого угла имеет неопределенное значение. Помимо основных четырех тригонометрических функций, в таблице также приводятся секанс (sec) и косеканс (csc), которые представляют собой обратные косинус и синус, соответственно.
Теорема Пифагора и связь синуса и косинуса
Поскольку определение синуса и косинуса угла основано на использовании прямоугольного треугольника, то эти функции можно связать, если воспользоваться теоремой Пифагора.
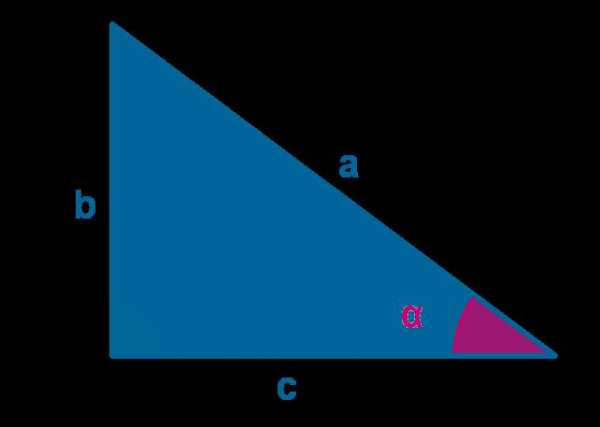
Для изображенного выше прямоугольного треугольника имеем: sin(α) = b/a и cos(α) = c/a. Теорема Пифагора записывается так: c2 + b2 = a2. Если левую и правую части этого выражения поделить на a2, а затем подставить формулы для синуса и косинуса, то получим: (sin(α))2 + (cos(α))2 = 1.
fb.ru
|
Деятельность учителя |
Деятельность учеников |
||||
1. |
Организационный этап Занятие сопровождается компьютерной Презентацией. Задачи: подготовка учащихся к работе на уроке, психологический настрой учащихся, организация внимания; — взаимное приветствие; |
Готовятся к уроку, приветствуют учителя. |
||||
2. |
Этап проверки домашнего задания Задача: проверить правильность, полноту и сознательность выполнения домашнего задания всем классом. |
Учащиеся сдают домашние задания, выполненные по карточкам. (Приложение 1) |
||||
3. |
Этап всесторонней проверки знаний Задача: проверить знания учащихся по теме «Угол поворота», «Измерение углов поворота в радианах»; закрепление, уточнение и систематизация знаний учащихся. |
Фронтальная устная работа по слайдам презентации. |
||||
Слайд 2: Выразить угол в радианах с помощью π. |
Выражают градусную меру углов в радианах с помощью π: 45°, 150°, 90°,360°, 30°, 270°,135°, 60°, 180°, -210°, -720° |
|||||
Слайд 3: Найти градусную меру угла по заданной радианной. |
Находят градусную меру угла по заданной радианной: ; ; 3π; ; . |
|||||
Слайд 4: Определить, какой координатной четверти принадлежит угол. |
Определяют, какой координатной четверти принадлежит угол: 45°; -80°; 150°; -120°; 250°; -200°; 400°; 820°; -460°; 450°. |
|||||
4. |
Этап усвоения новых знаний Задача: изучение понятий синуса, косинуса, тангенса и котангенса произвольного угла α; нахождение области определения и области значений выражений sin α, cos α, tg α, ctg α. |
|
||||
Слайд: Тема нового материала: «Определение косинуса, синуса, тангенса и котангенса». В курсе геометрии были определены косинус, синус и тангенс угла α при 0° ≤ α ≤ 180°. Распространим эти определения на случай произвольного угла α. Кроме того, введем понятие котангенса угла α. |
|
|||||
Слайд 6: Пусть при повороте около точки О на угол α начальный радиус ОА переходит в конечный радиус ОВ. Косинусом угла α называется отношение абсциссы точки В к длине радиуса. |
Записывают определение на лист с печатной основой. (Приложение 2) |
|||||
Слайд 7: Синусом угла α называется отношение ординаты точки В к длине радиуса. |
Записывают определение на лист с печатной основой. |
|||||
Слайд 8: Тангенсом угла α называется отношение ординаты точки В к ее абсциссе. |
Записывают определение на лист с печатной основой. |
|||||
Слайд 9: Котангенсом угла α называется отношение абсциссы точки В к ее ординате. |
Записывают определение на лист с печатной основой. |
|||||
Слайд 10: Докажем, что sin α, cos α, tg α, ctg α зависят только от угла α и не зависят от радиуса. Рассмотрим на примере sin α и cos α. Докажем, что для любого угла α отношение и не зависят от длины радиуса, а зависят только от угла α. |
Принимают участие в доказательстве (проводится в форме беседы). |
|||||
Слайд 11: 1. Возьмем два начальных радиуса ОА1 = R1, ОА2 = R2. 2. Повернем их около точки О на один и тот же угол α. 3. Получим радиусы ОВ1 и ОВ2, В1(х1; у1), В2 (х2; у2). 4. Построим прямоугольные треугольники ОВ1С1 и ОВ2С2 5. Треугольники ОВ1С1 и ОВ2С2 подобны по двум углам. |
1. Сколько окружностей надо построить? (Две.) 2. Что можно сказать о длине радиусов ОВ1 и ОВ2? (ОВ1= R1, ОВ2 = R2) 3. Найдите длины сторон В1С1 и В2С2, ОС1 и ОС2(х2 и х1; у2 и у1) 4. Что можно сказать о прямоугольных треугольниках ОВ1С1 и ОВ2С2? (Они подобны.) 5. По какому признаку? (По двум углам.) |
|||||
Слайд 12: 6. Из подобия треугольников (с учетом знака координат точек В1 и В2) следует, что и . Эти равенства верны и тогда, когда точки В1 и В2 попадают на какую-либо из осей. 7. Таким образом, для любого угла α отношение и не зависят от длины радиуса, а зависят только от угла α. |
6. Равенство каких отношений следует из подобия треугольников ОВ1С1 и ОВ2С2? ( и ) |
|||||
Слайд 13: Область определения выражений sin α, cos α, tg α, ctg α. 1. Выражения sin α и cos α определены при любом α, так как для любого угла поворота можно найти соответствующие значения дробей и . То есть областью определения этих выражений является промежуток (-∞; +∞). |
Отвечают на вопросы учителя, делают выводы, заполняют таблицу на листе с печатной основой. 1. Всегда ли определена дробь (Да, т.к. R≠0.) 3. Вывод? (Выражение cosα определено при любом α.) 4. Всегда ли определена дробь (Да, т.к. R≠0.) 5. Что можно сказать о выражении sin α? (Тоже всегда определено.) 6. Вывод? (Выражение sin α определено при любом α.) 7. То есть областью определения этих выражений является промежуток? (-∞; +∞) |
|||||
2. Выражение tg α имеет смысл при любом α , кроме углов поворота вида α = где n – целое число, т.к. для этих углов не имеет смысла дробь . |
1. Всегда ли определена дробь ? (Нет, не определена для углов поворота, у которых координата х равна 0.) 2. Какие это углы? (Углы вида α = где n – целое число.) 3. При каких значениях α имеет смысл выражение tg α ? (При любом α , кроме углов поворота вида α = n – целое.) |
|||||
3. Выражение сtg α имеет смысл при любом α , кроме углов поворота вида α = , где n – целое число, т.к. для этих углов не имеет смысла дробь . |
1. Всегда ли определена дробь ? (Нет, не определена для углов поворота, у которых координата у равна 0.) 2. Какие это углы? (Углы вида α = , где n – целое число.) 3. При каких значениях α имеет смысл выражение сtg α ? (При любом α , кроме углов поворота вида α = , где n – целое.) |
|||||
Область значений выражений 1. Областью значений синуса и косинуса является промежуток , т.к. при изменении угла поворота координаты х и у изменяются в пределах от –R до R, а значит, отношения и изменяются в пределах от -1 до 1. |
1. В каких пределах изменяются координаты х и у при изменении угла поворота? (Координаты х и у изменяются в пределах от –R до R.) 2. В каких пределах изменяются отношения и ? (От -1 до 1.) 3. Значит, областью значений выражений sin α и cos α является промежуток? () |
|||||
2. Областью значений тангенса и котангенса является промежуток (-∞; +∞) |
|
|||||
5. |
Этап закрепления новых знаний: Задача: закрепить в памяти учащихся знания и умения, необходимые им для самостоятельной работы по новому материалу; сформировать умения и навыки нахождения значений выражений, содержащих синусы, косинусы, тангенсы и котангенсы углов 0°, 30°, 45°, 60°, 90°, 180°, 270°, 360°. 1. Рассмотрим примеры вычисления значений выражений sin α, cos α, tg α, ctg α для некоторых углов поворота. — для углов 30°, 45°, 60° знакомы нам из курса геометрии. Слайд 14 — при повороте на угол α =180° точка В имеет координаты( -R; 0). Значит, 2. Заполнить таблицу на раздаточном листе. Проверка ответов по слайду презентации. Слайд 15 Резервные номера: № 1028 |
Отвечают на вопросы учителя, вместе разбирают пример при α = 180° , заполняют таблицу значений sin α, cos α, tg α, ctg α на листе с печатной основой. Проверяют ответы по слайду презентации. 1. Назовите координаты точки в при повороте на угол α = 180°? (Точка В имеет координаты(-R; 0).) Проверка правильности заполнения таблицы по слайду презентации. Для учеников, быстро справившихся с заданием: № 1028.
|
||||
Задание на листе с печатной основой. (Приложение 3) Проверка по слайду презентации. Слайд 16 |
Весь класс выполняет задание на листе с печатной основой. (Приложение 3) Проверка по слайду презентации. |
|||||
6. |
Этап подведения итогов урока, информации учащихся о домашнем задании, инструктаж по его выполнению Задачи: — подвести итоги урока; выставить оценки за работу на уроке; — сообщить учащимся о домашнем задании; разъяснить методику его выполнения; мотивировать необходимость его выполнения. Слайд 17 Подводим итог урока, предлагая учащимся вопросы: 1. Сформулировать определение синуса, косинуса, тангенса, котангенса. Задание на дом Пункт 45, № 1026, 1027. |
Ученики отвечают на вопросы учителя. Записывают домашнее задание в дневники: пункт 45, № 1026, 1027. |
urok.1sept.ru
math-public:opredelenie_sinusa [Президентский ФМЛ №239]
Общее определение синуса
Синус острого угла равен отношению перпендикуляра к наклонной.
Синус тупого угла равен синусу смежного острого угла.
Синус прямого угла равен единице.
Синус развернутого угла равен нулю.
Корректность определения синуса
Пусть из точки $B$, лежащей на стороне $p$ острого угла $A$, опущен перпендикуляр $BC$ на сторону $q$ этого угла. Тогда отношение перпендикуляра $BC$ к наклонной $BA$ не зависит от выбора точки $B$.
Доказательство
Первый способ (не использует подобия).
На стороне $q$ выберем любую точку $M$.
Выразим площадь $S$ треугольника $ABM$ двумя способами.
С одной стороны, $S=\dfrac{1}{2}ma$, где $a=BC, m=AM$.
C другой стороны, $S=\dfrac{1}{2}ch$, где $h=MD$ – высота треугольника $ABM$ и $c=BA$.
Поэтому $ma=ch$ или $\dfrac{a}{c}=\dfrac{h}{m}$.
Если на стороне $p$ взять другую точку $B_1$ и повторить проведенные рассуждения, то снова получим, что $\dfrac{a_1}{c_1}=\dfrac{h}{m}$, где $a_1=B_1C, c_1=AB_1$.
Поэтому $\dfrac{a_1}{c_1}=\dfrac{a}{c}$.
Отношение перпендикуляра к наклонной не зависит от того, на какую сторону угла опущен перпендикуляр.
Действительно, пусть, как и раньше, $M$ – точка на стороне $q$ угла $A$ и $MD\perp p$.
Вернемся к равенству $\dfrac{a}{c}=\dfrac{h}{m}$
В правой части этого равенства стоит отношение перпендикуляра к наклонной, которое с выбором точки $M$ не связано.
Значит правая часть этого равенства от выбора точки $M$ не зависит.
Второй способ (использует подобие).
Если на стороне $p$ взять точки $B$ и $B_1$ и опустить из них перпендикуляры $BC$ и $B_1C_1$ к стороне $q$ угла $A$, то треугольники $ABC$ и $AB_1C_1$ будут подобны по двум углам.
Следовательно, $\dfrac{BC}{AB}=\dfrac{B_1C_1}{AB_1}$.
Отношение перпендикуляра к наклонной не зависит от того, на какую сторону угла опущен перпендикуляр.
Действительно, пусть, как и раньше, $M$ – точка на стороне $q$ угла $A$ и $MD\perp p$.
Треугольники $ADM$ и $ABC$ подобны по двум углам ($\angle A$ – общий).
Следовательно, $\dfrac{MD}{AM}=\dfrac{BC}{AB}$, а отношение, стоящее в правой части этого равенства не зависит от выбора точки $M$.
Теорема
Синусы углов, имеющих равные величины, равны.
Доказательство
Возьмем два равных острых угла: $\angle A$ и $\angle M$.
Из некоторой точки $B$ на стороне угла $A$ опустим перпендикуляр $BC$ на другую сторону угла $A$.
Получим прямоугольный треугольник $ABC$.
Отложим на сторонах угла $M$ отрезки $MP=AB$ и $MQ=AC$.
Тогда $\triangle MPQ=\triangle ABC$ по первому признаку равенства.
Поэтому $\angle Q=\angle C=90^\circ$.
Итак $PQ$ – перпендикуляр, опущенный из точки $P$ одной стороны угла $M$ на другую его сторону.
Но тогда $\sin{\angle A}=\dfrac{BC}{AB}=\dfrac{PQ}{PM}=\sin{\angle M}$.
math-public/opredelenie_sinusa.txt · Последние изменения: 2016/04/07 22:56 — labreslav
wiki.sch239.net
что такое sin и cos и чему они равны??
Начерти прямоуголньный треугольник. sin угла равен отношению противолежащего катета к гипотенузе, cos — прилежащего к ней же
Встань и ляг.. вот и вся разница 90 градусов.
синус и косинус 90градусов
В общем то это синус и косинус. Их значения можно найти в учебнике по математике в школьной программе. Желаю успехов.
Тригонометрические функции — вид элементарных функций. Обычно к ним относят синус (sin x), косинус (cos x), тангенс (tg x), котангенс (ctg x), секанс (sec x) и косеканс (cosec x), последняя пара функций в настоящее время сравнительно малоупотребительна. Обычно тригонометрические функции определяются геометрически. Пусть дана декартова система координат на плоскости и построена окружность радиуса R с центром в начале координат O. <img src=»//content.foto.my.mail.ru/bk/rabids/_animated/i-16.gif» > Будем измерять углы как повороты от положительного направления оси абсцисс до луча OB. Направление против часовой стрелки считается положительным, по часовой стрелке отрицательным. Абсциссу точки В обозначим xB, ординату обозначим yB (см. рисунок) . Синусом называется отношение <img src=»//content.foto.my.mail.ru/bk/rabids/_answers/i-17.jpg» > Косинусом называется отношение <img src=»//content.foto.my.mail.ru/bk/rabids/_answers/i-18.jpg» >. Ясно, что значения тригонометрических функций не зависят от величины радиуса окружности R в силу свойств подобных фигур. Часто этот радиус принимают равным величине единичного отрезка, тогда синус равен просто ординате yB, а косинус — абсциссе xB. Если альфа — действительное число, то синусом альфа в математическом анализе называется синус угла, радианная мера которого равна альфа, аналогично для прочих тригонометрических функций. Во многих учебниках элементарной геометрии до настоящего времени тригонометрические функции острого угла определяются как отношения сторон прямоугольного треугольника. Пусть OAB — треугольник с углом альфа. <img src=»//content.foto.my.mail.ru/bk/rabids/_animated/i-19.gif» > Тогда: Синусом альфа называется отношение AB/OB (противолежащего катета к гипотенузе) . Косинусом альфа называется отношение ОА/OB (прилежащего катета к гипотенузе).
touch.otvet.mail.ru
это отношение чего к чему? Основы тригонометрии
Тригонометрия является одним из наиболее важных разделов алгебры и геометрии для изучения в средней школе. Эта наука берет свое начало еще со времен античной Греции. В средние века наиболее весомый вклад в изучение и применение на практике тригонометрии внесли страны Ближнего Востока, а также Индия.
Зачастую в процессе изучения нового материала учащиеся испытывают сложности в понимании новой терминологии, особенно если она никак не связана с уже полученными ранее знаниями. Однако важно осознавать важность усвоения базовых основ любой темы, ведь от этого, в первую очередь, зависит успешность дальнейшего обучения ребенка. В данной статье мы рассмотрим такой тригонометрический термин, как sin угла, с которого, можно сказать, и начинается вся тригонометрия.
Определение
Рассмотрим геометрический смысл данной функции.
Для определения синуса используется соотношение сторон прямоугольного треугольника. Рассмотрим подробнее. Sin — это отношение противолежащего катета к гипотенузе такого треугольника.
Для облегченного понимания объясним определение с использованием вспомогательного рисунка:
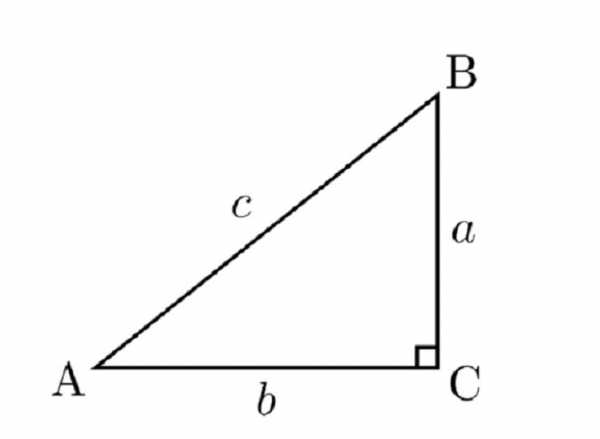
Применяя уже пройденные в геометрии термины, обозначим гипотенузу АВ маленькой латинской буквой с, а катеты прямоугольного треугольника АС и ВС примем за b и а соответственно. Таким образом, рассматривая угол А, его sin — это отношение a к с. Теперь рассмотрим другой, парный ему острый угол В. Его sin — это отношение b к с.
Теперь рассмотрим алгебраический смысл.
Если рассматривать термин «синус» с точки зрения этого раздела математики, то нам стоит обратиться к декартовой системе координат. Понадобится единичная окружность (радиус которой равен одной условной единице) с центром в начале координат.
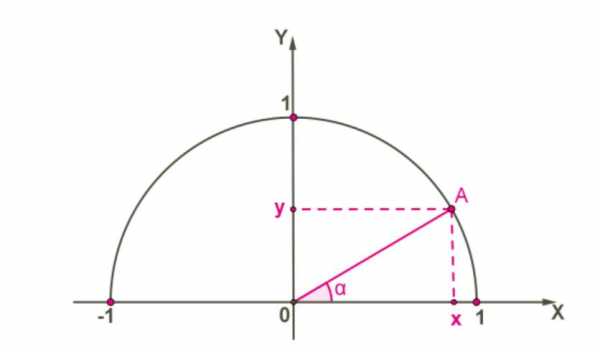
Отложим некий угол, равный альфа от оси абсцисс. Второй луч, образующий данный угол, пересекает единичную окружность в точке А. Она нам и потребуется, а именно ее вторая координата. Значение ее численно равно синусу отложенного угла.
Области определения и допустимых значений
Напоминаем общий случай. Область определения для функции принято обозначать как D(f), а находится она по оси абсцисс. В свою очередь область допустимых значений обозначается как E(f), а находить ее следует по оси ординат.
В нашем случае. Для синуса его область допустимых значений находится на отрезке от -1 до 1, а к области определения принадлежат все действительные числа. Также отметим, что функция синуса периодическая, а ее период равен пи.
Заключение
Теперь вы можете без толики сомнения ответить на все, связанные с определением sin угла вопросы, в том числе: sin — это отношение чего к чему, как он находится. Надеемся, что данная статья была полезной и понятной для вас.
fb.ru
